32
IV- Analyse de données et descriptive
Afin de mieux appréhender le sujet d'étude,
nous avons décidé d'effectuer une analyse de données du
modèle. Cette analyse sera confrontée à la
littérature dans le but de voir si les grandes périodes
définies par cette dernière se confirment dans nos
observations.
Dans un premier temps, on va présenter les
différentes variables dans un tableau. Il s'agit des variables qui sont
utilisées dans la partie économétrique.
Tableau 1 : Index de la base « Ide »
Nom de la variable
|
Description
|
Type de
variable
|
PIB_HAB
|
Produit intérieur brut par habitant
|
Quantitative
|
TX_CHA
|
Taux de change effectif réel basé sur le
coût
unitaire de fabrication pour la France
|
Quantitative
|
BENEF
|
Total des bénéfices tirés des ressources
naturelles
en pourcentage du PIB
|
Quantitative
|
TX_INT
|
Taux d'intérêt réel en France
|
Quantitative
|
IPC
|
Indice des prix à la consommation
|
Quantitative
|
BENEF_IMP
|
Bénéfices des entreprises après
impôt
|
Quantitative
|
EXP
|
Exportations : valeurs des biens pour la France
en
pourcentage du PIB
|
Quantitative
|
IMP
|
Importations : valeurs des biens pour la France
en
pourcentage du PIB
|
Quantitative
|
SAL_HOR
|
Salaire horaire
|
Quantitative
|
DEP_SCO
|
Dépenses de consommation des administrations
:
droits de scolarité et frais de formation
|
Quantitative
|
DUMMIES_EURO
|
=1 si le pays utilise l'euro comme monnaie durant
le
trimestre
|
Qualitative
|
DUMMIERS_CRISE
|
=1 si le pays est en période de crise durant le
trimestre
|
Qualitative
|
|
Dans le cadre de l'étude, la variable à
expliquer sera nommée « IDE ». Elle représente la
valeur de l'investissement direct étranger en France. Les histogrammes
de chaque variable se trouvent en annexe (annexe 1).
33
IV.1 Statistiques descriptives
Pour commencer, on va tout d'abord regarder un peu plus en
détail et essayer d'interpréter les statistiques liées aux
variables. Le logiciel R Studio donne le tableau des statistiques descriptives.
Afin de réaliser ces statistiques, on a utilisé la fonction
summary. Cette fonction permet d'obtenir les valeurs du minimum, le
premier quartile, la médiane, la moyenne, le troisième quartile
et le maximum. Elle permet également de connaître le nombre de
valeurs manquantes.
Tableau 2 : Statistiques descriptives du modèle :
Minimum, maximum, médiane, moyenne et
quartiles
Variables
|
Minimum
|
1er
quartile
|
Médiane
|
Moyenne
|
3ème
quartile
|
Maximum
|
IDE
|
-132,60
|
99,95
|
175,75
|
229,15
|
363,27
|
1 084,40
|
PIB_HAB
|
301,80
|
355,30
|
424,90
|
423,70
|
493,30
|
532,20
|
TX CHA
|
0,848
|
1,094
|
1,264
|
1,223
|
1,349
|
1,581
|
BENEF
|
122,80
|
127,70
|
138,90
|
144,40
|
160,40
|
175,70
|
TX INT
|
0,067
|
1,109
|
2,983
|
2,640
|
3,556
|
7,444
|
IPC
|
65,79
|
69,59
|
76,29
|
78,79
|
87,89
|
98,02
|
BENEF_IMP
|
467,60
|
533,40
|
947,90
|
1009,70
|
1406,60
|
1879,80
|
EXP
|
17,70
|
20,45
|
21,03
|
20,97
|
21,49
|
25,24
|
IMP
|
18,08
|
20,64
|
22,56
|
22,35
|
24,12
|
26,63
|
SAL HOR
|
58,41
|
65,82
|
78,12
|
78,00
|
89,47
|
97,72
|
DEP_SCO
|
30,53
|
41,40
|
56,59
|
55,55
|
69,04
|
79,89
|
|
|
0
|
1
|
DUMMIES_EURO
|
20
|
56
|
DUMMIES CRISE
|
64
|
12
|
|
A partir du tableau 2, on observe plusieurs points communs
entre les différentes variables. Plus de la moitié des variables
présentent un écart important entre leurs minimums et leurs
maximums. La série est composée de 76 observations (19
années de 4 trimestres).
On remarque que la répartition des importations et des
exportations sur la période d'étude semble assez proche. En
effet, les exportations moyennes sont de 20,97 tandis que les importations
moyennes sont de 22,35. L'investissement direct à l'étranger
moyen est de 175,75.
Le PIB par habitant moyen et médian est relativement
proche. A première vue, le PIB par habitant est représenté
de manière égalitaire entre les différentes années
d'études.
34
On observe que durant trois quarts des trimestres, l'IPC a une
valeur inférieure à 87 tandis qu'il a une valeur
inférieure à 69 durant un quart des trimestres.
Nous avons ensuite réalisé différents
tests sur les variables quantitatives afin de valider différentes
hypothèses du modèle.
Tableau 3 : Les différents tests du modèle
(valeurs statistiques ou p-value)
VARIABLES
|
SHAPIRO-WILK
|
KURTOSIS
|
SKEWNESS
|
KOLMOGOROV-SMIRNOV
|
IDE
|
W = 0,9305
p-value = 0,0004
|
5,8615
|
1,1731
|
D = 0,1121
p-value = 0,2952
|
PIB_HAB
|
W = 0,9224
p-value = 0,0002
|
1,6251
|
-0,1388
|
D = 0,1394
p-value = 0,0946
|
TX_CHA
|
W = 0,9189
p-value = 0,0001
|
2,5879
|
-0,7479
|
D = 0,1325
p-value = 0,1266
|
BENEF
|
W = 0,8967
p-value = 1,409E-05
|
1,8777
|
0,4649
|
D = 0,1487
p-value = 0,0694
|
TX_INT
|
W = 0,9439
p-value = 0,0022
|
3,1333
|
0,2833
|
D = 0,1018
p-value = 0,4097
|
IPC
|
W = 0,9030
p-value = 2,555E-05
|
1,7491
|
0,3998
|
D = 0,1269
p-value = 0,1729
|
BENEF_IMP
|
W = 0,8604
p-value = 6,308E-07
|
1,5614
|
0,3074
|
D = 0,2022
p-value = 0,0034
|
|
35
EXP
W = 0,9556
p-value = 0,0096
|
3,7600
|
0,2315
|
D = 0,1226
p-value = 0,1870
|
IMP
|
W = 0,9581
p-value = 0,0135
|
2,1601
|
-0,3418
|
D = 0,0906
p-value = 0,5301
|
SAL_HOR
|
W = 0,9347
p-value = 0,0007
|
1,6702
|
-0,0216
|
D = 0,0969
p-value = 0,4459
|
DEP_SCO
|
W = 0,9309
p-value = 0,0005
|
1,6346
|
-0,1185
|
D = 0,1135
p-value = 0,2611
|
|
Tout d'abord, le test de Shapiro-Wilk est
réalisé à l'aide de la matrice de variance-covariance afin
de pouvoir tester l'hypothèse H0 qui permet de savoir si la distribution
de la variable suit bien une loi normale. Pour l'ensemble du modèle, la
p-value est inférieur à 0,05. Par conséquent,
l'hypothèse H0 est rejetée au seuil de risque de 5% pour
l'ensemble des variables du modèle. Aucune variable ne suit donc la loi
normale. En revanche, le test de Kurtosis évalue la dispersion des
valeurs extrêmes en faisant référence à la loi
normale. Ce dernier sera nul pour une distribution normale. Dans le cas de ce
modèle, toutes les variables ont un coefficient de Kurtosis positif. On
peut donc en conclure que la distribution est plus aplatie que normale. Enfin,
nous allons analyser le test de Skewness. Pour les variables IDE, BENEF,
TX_INT, IPC, BENEF_IMP et EXP, le coefficient de ce test est positif. On peut
donc dire que sa distribution est étalée à droite. En
revanche, les variables PIB_HAB, TX_CHA, IMP, SAL_HOR et DEP_SCO ont un
coefficient négatif. La distribution de ces variables est donc
étalée à gauche. Cependant, le résultat de ces
tests ne permet pas de savoir si le modèle est normalement
distribué. On va donc réaliser un test non-paramétrique
dont l'objectif sera de tester le modèle avec plus de précision.
Ainsi, en réalisant le test de Kolmogorov-Smirnov sur notre
modèle ayant une loi normalement distribuée, la p-value est
supérieur à 0,05 pour toutes les variables sauf pour le
BENEF_IMP. On peut donc dire que l'hypothèse H0 est acceptée au
seuil de risque de 5% et la loi normale est bien suivie sauf
pour la variable BENEF_IMP.
36
Etant donné que la loi normale n'est pas suivie pour la
variable BENEF_IMP, une matrice de corrélation est
réalisée à partir de la méthode de Spearman afin de
détecter les éventuelles corrélations entre les
variables.
Graphique 12 : Matrice de corrélation de
Spearman
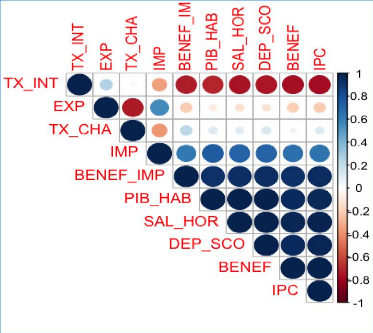
D'après la matrice de corrélation de Spearman
(graphique 12), les corrélations positives sont
représentées par des cercles bleus tandis que les
corrélations négatives sont visibles sur le graphique par des
cercles rouges. En effet, plus le cercle est foncé et donc plus la
corrélation est forte. Dans ce modèle, nous pouvons voir que le
TX_INT est corrélée négativement avec les variables
BENEF_IMP, PIB_HAB, SAL_HOR, DEP_SCO, BENEF et IPC. Cette corrélation
est très forte car le cercle de l'ensemble de ces variables est rouge
foncé. De plus, il y a des corrélations positives qui sont
très fortes. En effet, la variable BENEF_IMP est corrélée
positivement avec le PIB_HAB, SAL_HOR, DEP_SCO, BENEF et l'IPC. De plus, le
PIB_HAB est corrélée positivement avec le SAL_HOR, DEP_SCO, BENEF
et IPC. Il existe également une forte corrélation positive entre
le SAL_HOR et les DEP_SCO ainsi que le BENEF et l'IPC. Ensuite, le graphique
montre que la variable DEP_SCO est corrélée positivement avec le
BENEF et IPC. Enfin, la variable BENEF est
37
corrélée également positivement avec
l'IPC. Cette matrice montre également que la variable IMP est
corrélée positivement mais moins fortement avec les variables
BENEF_IMP, PIB_HAB, SAL_HOR, DEP_SCO, BENEF et l'IPC. Une autre version de
Spearman est disponible en fin de mémoire (annexe 3).
Par la suite, on a voulu déterminer la présence
ou non de valeurs atypiques dans le modèle. Cette partie est
détaillée en annexe (annexe 2) à la fin du
mémoire.
Graphique 13 : Boîte à moustache et valeurs
potentiellement atypiques du modèle
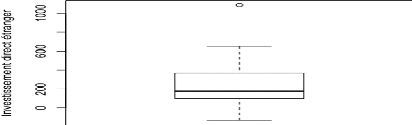
D'après le graphique 13, on observe que la variable
IDE a potentiellement une valeur atypique. Les autres boîtes à
moustache représentant les autres variables se trouve en annexe mais ne
présentent pas forcément de valeurs atypiques (annexe 2).
Si la variable n'avait qu'une valeur potentiellement
atypique, le test de Grubbs est réalisé. En revanche, si la
variable avait plusieurs valeurs potentiellement atypiques, le test de Rosner
est réalisé (annexe 2).
Après l'application du test de Rosner, les variables
TX_INT et EXP ont ressorties des valeurs qui n'étaient pas atypiques. En
revanche, la valeur de la variable IDE était atypique. Cette
dernière correspondait au quatrième trimestre 2007 (il s'agit de
la 52ième observations). Cependant, cette valeur atypique n'est pas
très surprenante est l'une des raisons pourrait être la crise
économique qui s'est déroulée au cours de cette
période. On ne va donc pas supprimer
38
cette valeur car le mémoire est basé sur des
séries temporelles mais il nous paraît tout de même
intéressant de comprendre les raisons de la présence de ces
valeurs.
|
|



