Déterminants des investissements directs étrangers en France.

1

MASTER 1 : ECONOMETRIE ET STATISTIQUE

PARCOURS : ECONOMETRIE APPLIQUEE

LES DETERMINANTS DES

INVESTISSEMENTS DIRECTS

ETRANGERS EN FRANCE

Présenté par : Sous la direction de :

FIGUREAU Bastien PHAM Thi-Hong-Hanh

Nantes, mai 2019

2

Remerciements

Dans cette première partie, je tiens à formuler tous mes remerciements à mon encadrante de mémoire Madame Thi-Hong-Hanh PHAM. Elle m'aura apportée tout son soutien au cours de la réalisation de ce mémoire.

Benoit SEVI et Olivier DARNE (responsables du Master Econométrie et Statistique) ont organisés durant l'année différentes réunions afin qu'on puisse réaliser un travail de qualité pour notre premier mémoire. Je leurs en suis très reconnaissant.

J'adresse également ma totale reconnaissance à tous les enseignants et personnels de l'IAE qui m'ont accordés leurs aides à travers des conseils dans le cadre de mes recherches. Par leurs disponibilités, j'ai pu créer un lien afin d'élaborer un travail de qualité.

J'apporte également des remerciements à mes parents, Bernadette et Thierry qui m'ont accordés de leurs temps durant la conception de ce dossier afin de mettre en place un travail de relecture permanent et efficace.

Enfin, je remercie mes amis et collègues de groupe pour leurs aides durant la réalisation de ce projet. Je les remercie pour la confiance qu'ils m'ont témoignée.

A l'ensemble de ces intervenants que j'ai eu l'occasion de nommer, je présente mes sincères remerciements, mon estime et ma gratitude.

3

Liste des abréviations

ACP : Analyse en Composante Principale

BLUE : Best Linear Unbiaised Estimator

FAC : Fonction d'AutoCorrélation

FACP : Fonction d'AutoCorrélation Partielle

IDE : Investissement Direct Etranger

IPC : Indice des Prix à la Consommation

MCO : Moindres Carrés Ordinaires

OLI : Ownership Localisation Internalisation advantages

PIB : Produit Intérieur Brut

RLM : Régression Linéaire Multiple

SMIC : Salaire Minimum Interprofessionnel de Croissance

TVA : Taxe sur la Valeur Ajoutée

VIF : Variance Inflation Factor

4

Sommaire

Résumé	5
Abstract	6
I- Introduction	.. 7		II- Revue de littérature
10	III- Modèle empirique et données
17	IV- Analyse de données et descriptive
32	V- Etude économétrique du sujet
43
Conclusion	..72
Bibliographie	73
Récapitulatif des graphiques et tableaux	. 77
Annexes du mémoire	79

5

Résumé

A travers ce mémoire, on cherche à analyser les déterminants macroéconomiques des entrées d'Investissements Directs Etrangers (IDE) en France. Notre projet est effectué sur la période allant du premier trimestre 1995 au quatrième trimestre 2013. Ce choix, nous permet d'avoir un maximum de données pour la conception de ce mémoire. L'IDE a un rôle dominant dans le cadre des stratégies de développement privilégiées à l'échelle nationale. Cependant, une variation de l'inflation aura probablement des conséquences négatives sur les IDE.

L'objectif de ce mémoire étant de s'appuyer sur la littérature économique afin de pouvoir caractériser les déterminants des IDE. Pour cela, nous allons regarder les différentes faiblesses empiriques qui portent sur ce thème. Ce mémoire ayant pour but de déterminer une nouvelle vision pour observer les actions des déterminants macroéconomiques sur l'entrée des IDE en France.

Au cours de l'ensemble de ce mémoire, on essayera de trouver des liens éventuels entre l'IDE et les variables qui semblent avoir un impact important sur ces derniers.

6

Abstract

This thesis seeks to analyze the macroeconomic determinants of Foreign Direct Investment (FDI) inflows in France. Our project is carried out over the period from the first quarter of 1995 to the fourth quarter of 2013. This choice allows us to have a maximum of data for the design of this memory. FDI has a dominant role in the development strategies favored at the national level. However, a change in inflation will likely have a negative impact on FDI.

The objective of this paper is to rely on the economic literature in order to characterize the determinants of FDI. For this, we will look at the different empirical weaknesses that bear on this theme. This thesis aims to determine a new vision to observe the actions of macroeconomic determinants on the entry of FDI in France.

Throughout this thesis, we will try to find possible links between IDE and variables that seem to have a significant impact on them.

7

I- Introduction

Au sein d'une économie globalisée, la question de la délocalisation occupe une place très importante au niveau de l'activité économique et social. On peut expliquer ce phénomène par la mondialisation qui représente la libre circulation des marchandises. En effet, depuis les années 90, les flux d'IDE ont beaucoup changé grâce à la mondialisation ¹ . Les Investissements Directs Etrangers (IDE) correspondent quant à eux aux investissements d'une entité résiduelle qui obtient un intérêt durable au sein d'une entité résidente d'une économie étrangère². L'analyse effectuée concerne en grande partie les IDE sortants qui sont réalisés par des groupes français mais n'écarte pas les IDE entrants qui sont exécutés par des groupes étrangers en France³. On peut donc dire que si une entreprise étrangère investit en France, c'est que cet investissement a une rentabilité élevée.

Les investissements directs étrangers peuvent également être vues comme les activités internationales de capitaux effectuées afin de concevoir et développer ou assurer de garder une filiale à l'étranger. Ils permettent aussi d'exercer l'inspection et d'avoir un effet significatif sur la gestion d'une firme. Au cours des décennies passées, il y a eu une hausse très importante des flux d'investissements directs étrangers au sein de l'économie internationale⁴. Ces derniers ont augmenté de plus de 12 millions d'euros en 2015 ⁵ . Aujourd'hui, les IDE sont très importants car ils participent à la croissance des pays du monde. Les deux principales motivations qui incitent les pays à investir sont la forte baisse des coûts de main-d'oeuvre moins chers ainsi qu'un rapprochement géographique vers les zones de ressources naturelles. Elles vont donc permettre aux pays de destination de réduire les prix de transport et ainsi faire de l'optimisation fiscale. Enfin, la conquête de nouveaux marchés difficiles à pénétrer par les exportations qui nécessitent automatiquement l'intervention des firmes locales afin de faire augmenter de manière spectaculaire la compétitivité. A travers les IDE, on peut également améliorer la macro-économie en utilisant le transfert de fonds financiers, le transfert de la technologie et du savoir-faire en gestion et capital humain ainsi que par la création d'emplois. En revanche, dans les entreprises

1 http://unpan1.un.org/intradoc/groups/public/documents/idep/unpan020634.pdf. Consulté le 16 décembre 2018.

2 https://www.insee.fr/fr/metadonnees/definition/c1263. Consulté le 16 décembre 2018.

3 FONTAGNE L. et TOUBAL F. 2010. « Investissement direct étranger et performances des entreprises ». La documentation française.

4 https://www.memoireonline.com/11/12/6447/m_Le-rle-des-IDE-Investissement-Direct-Etranger--dans-le-secteur-bancaire-algerien2.html. Consulté le 16 décembre 2018.

5 https://www.insee.fr/fr/statistiques/3303553?sommaire=3353488. Consulté le 16 décembre 2018.

8

étrangères, les revenus sont généralement plus élevés que dans les firmes locales (hausse d'environ 30%). On peut donc dire que l'IDE a un effet qui est très positif sur la croissance des pays d'accueil⁶.

Pour poursuivre, on peut dire que les flux d'investissements directs étrangers dépendent en grande partie de la stabilité des pays d'accueil, de leurs perspectives futures et enfin de leurs rentabilités. A ce jour, les mouvements d'investissements directs étrangers qui sont produits entres l'Union Européenne, le Japon et enfin les Etats-Unis sont les plus impressionnants au monde⁷. En 2015, les investissements entrants provenant de l'Union européenne sont d'environ 9,8 milliards d'euros tandis que ceux provenant des Etats-Unis et du Japon sont de 22,7 milliards d'euros ⁸. Au cours des dernières années, les flux ont globalement augmentés de manière significative dans les pays asiatiques et donc en particulier en Chine⁹. Cependant, depuis les années 1980, la France est devenu un des investisseurs les plus précieux au monde, avec des investissements sortants vers les pays développés, en particulier l'Union Européenne. En revanche, les activités d'investissements les plus solides se situent dans le secteur du commerce, de la manufacture et de plus en plus dans les services (marchands et non marchands). Les firmes françaises ayant une implantation à l'étranger sont en générale plus productives que les firmes locales pures. Les entreprises étrangères qui implantent des filiales en France sont très regroupées au nord du pays, à la frontière belge, en île de France et pour finir en Rhône-Alpes, en particulier dans le domaine industriel. En revanche, les firmes ayant leurs sièges sociaux en France (filiales française ou étrangère) sont bien plus productives, bien plus grandes et proposent donc des rémunérations à la hauteur des attentes de leurs salariés. Cependant, les investissements étrangers peuvent parfois occasionner des dégâts au niveau environnementaux¹⁰.

D'un point de vue théorique, des économistes ont essayés d'expliquer les facteurs qui pouvaient influencer les émissions d'investissements directs étrangers à partir de différentes théories. Ces dernières font références aux économistes DUNNING (1977), LEVIS (1979),

6 FONTAGNE L. et TOUBAL F. 2010. « Investissement direct étranger et performances des entreprises ». La documentation française.

7 https://news.un.org/fr/story/2008/01/123392-les-investissements-directs-etrangers-ont-battu-des-records-en-2007. Consulté le 16 décembre 2018.

8 https://www.insee.fr/fr/statistiques/2569430?sommaire=2587886. Consulté le 16 décembre 2018.

9 https://news.un.org/fr/story/2008/01/123392-les-investissements-directs-etrangers-ont-battu-des-records-en-2007. Consulté le 16 décembre 2018.

10 FONTAGNE L. et TOUBAL F. 2010. « Investissement direct étranger et performances des entreprises ». La documentation française.

9

FREY (1985), et MAYER (1999) par exemple¹¹. En effet, DUNNING a expliqué les flux d'IDE dans une économie pour la première fois. Concernant LEVIS, il a séparé les variables en deux groupes (celles politiques et celles économiques). A travers ce mémoire, on va présenter les facteurs économiques en faisant en sorte de ne pas tenir compte des facteurs politiques. On va s'appuyer sur certaines de ces théories afin d'élaborer notre modèle économique.

Dans ce mémoire, nous nous intéressons à l'importance d'étudier les déterminants de l'IDE. Nous allons comprendre le choix de la France comme pays d'étude dans ce mémoire. Ce choix est basé sur le fait que la France dispose d'un emplacement géographique stratégique.

Dans un premier temps, la littérature économique de ce mémoire avec des économistes ayant réalisés des travaux sur les déterminants des investissements directs étrangers sera présentée. Dans un second temps, le modèle empirique ainsi que les données seront exposées. La troisième partie sera réservée aux statistiques descriptives ainsi qu'aux tests économétriques. Enfin, la dernière partie aura pour mission de conclure l'ensemble du mémoire.

11 https://www.memoireonline.com/11/09/2898/m_Determinants-de-linvestissement-direct-a-letranger-dans-les-pays-en-voie-de-developpement-11.html. Consulté le 20 décembre 2018.

10

II- Revue de littérature

Tout d'abord, rappelons la définition des investissements directs étrangers. Les IDE¹² représentent les investissements qui permettent aux entités résidentes d'une économie d'obtenir un intérêt durable au sein d'une entité résidente d'une économie étrangère. Soulignons que l'investissement direct prend en compte l'ensemble des opérations, c'est-à-dire, l'opération initiale ainsi que les opérations financières.

Il y a trois grandes catégories d'IDE qui sont les investissements en capital social (prises en compte de la participation à hauteur de plus de 10% au sein des firmes), les bénéfices réinvestis qui correspondent à la partie qui n'est pas distribuée et enfin, les opérations diverses qui désignent les prêts entre les investisseurs directs et les firmes.

II.1 Travaux théoriques

Au préalable, soulignons que les IDE sont considérés comme important par certains pays comme la France. En effet, la république française pense que les IDE sont très utiles dans les pays en développement comme par exemple en Afrique. Dans cette partie, notre objectif est de monter une revue de littérature.

A travers plusieurs théories, les économistes ont évoqués les IDE sous différents aspects. Par exemple, DUNNING s'est intéressé aux flux d'IDE pour la première fois au début des années 1970. DUNNING a utilisé les travaux de HIRSCH en 1976. DUNNING va donc construire un modèle composé de deux entreprises en 1981¹³. DUNNING prouve que les décisions d'internationalisations sont justifiées par trois catégories d'avantages qui forment le modèle OLI¹⁴ :

Ø Ownership advantages (O) : Ils représentent le capital intellectuel, un avantage qui concerne la firme. Il s'agit d'un produit qui n'est pas possédé par les autres entreprises (brevet, licence,...).

12 https://www.tresor.economie.gouv.fr/Ressources/8235_les-investissements-directs-a-l-etranger-ide. Consulté le 05 février 2019.

13 https://www.memoireonline.com/04/12/5787/Les-investissements-directs-etrangers-dans-lespace-UEMOAdeterminants-et-analyse-dimpacts.html. Consulté le 20 décembre 2018.

14 https://www.glossaire-international.com/pages/tous-les-termes/modele-oli.html. Consulté le 05 février 2019.

Ø

11

Localisation advantages (L) : Il est préférable que le produit soit utilisé à l'étranger plutôt que dans le pays de provenance. L'objectif étant de limiter les coûts de production.

Ø Internalisation advantages (I) : Les avantages à sous-traiter sont moindres. Cependant, il y a des avantages en matières de transaction. C'est donc profitable à l'internalisation afin d'éviter la concurrence.

Les conditions évoquées ci-dessus ont un intérêt hiérarchisé car d'après DUNNING, les importances à l'internalisation sont concluantes.

Il est important de souligner que certains économistes émettent l'hypothèse que les IDE produisent de la croissance tandis que certains autres économistes pensent que les IDE apportent des retenues. Par exemple, SOLOW¹⁵ en 1956 a rédigé un article dans lequel il explique que les IDE connaissent une évolution. Cependant, il a souligné que les effets sont uniquement à court terme car l'économie a des rendements décroissants du capital qui entraine donc un taux de croissance de long terme plutôt stable.

Les IDE sont vues comme favorisant l'apparition de nouvelles variables économiques et technologiques indispensables aux pays développés aujourd'hui (LALL et NARULA, 2004)¹⁶. Les rendements de capitaux étant décroissants rendent les IDE et leurs apports technologiques sont importants.

Dans l'approche théorique, on peut identifier deux visions sur l'apport des IDE dans la croissance. Dans la première, on s'intéresse plus à l'apport de nouvelles technologies associées aux entreprises nationales grâce à leurs externalités (BLONIGEN et WANG, 2004)¹⁷ tandis que la seconde vision sera sur l'apparition de nouveaux biens de capitaux dus à l'action des IDE (BERTHELEMY et DEMURGER, 2000)¹⁸. Ces deux derniers auteurs ont développés un modèle basé sur le capital humain et les écarts technologiques dans le progrès technique à travers l'utilisation de biens intermédiaires. Ils se basent sur un marché composé de deux entreprises, une grande entreprise étrangère et high tech et une autre locale plus

15 https://www.memoireonline.com/01/14/8691/m_Investissements-directs-etrangers-et-developpement-durable-Cas-de-la-cte-d-Ivoire5.html. Consulté le 21 janvier 2019.

16 LALL S. et NARULA R. 2004. « FDI and its role in economic development: Do we need a new agenda? ». Research Memoranda 019. Maastricht : MERIT.

17 BLONIGEN B.A. et WANG M. 2004. « Inappropriate pooling of wealthy and poor countries in empirical FDI studies ». NBER Working Paper n° 10 378. Cambridge.

18 BERTHELEMY J.C et DEMURGER S. 2000. « Foreign Direct Investment and Economic Growth: Theory and Application to China ». Review of Development Economics. Wiley Blackwell, vol 4.

12

petite. Les deux vont sur ce marché pour produire mais aussi investir dans la recherche (R&D). La plus petite entreprise locale va pouvoir utiliser les connaissances supérieures de l'autre firme pour son R&D qui débouche sur un progrès technique de la firme locale. Leurs modèles sous entends que les Etats devraient favoriser les IDE afin d'augmenter le progrès technique de leurs entreprises locales.

KRUGMAN et OBSTFELD (2006)¹⁹ définissent les investissements directs étrangers comme les flux de capitaux avec pour objectif pour la firme d'ouvrir une filiale au sein d'un pays étranger. L'investissement direct étranger autorise la prise d'une possibilité de contrôle car les firmes ne disposent pas uniquement des obligations financières face au siège mais également se situe au sein de la même structure organisationnelle.

ANDREFF (2003)²⁰ définit les investissements directs étrangers comme : « un capital dans la propriété d'actifs réels pour implanter une filiale à l'étranger ou prendre le contrôle d'une firme étrangère existante. Il vise à établir des relations économiques durables d'une unité à l'étranger ».

LIPSEY (1999) ²¹ montre que la théorie économique qui utilise une analyse néoclassique de la modernisation recommande que les investissements directs étrangers encouragent la croissance économique à partir de l'accumulation du capital ainsi que le transfert technologique.

Dans leurs papiers, les économistes LOVE et LAGE HIDALGO (2000) ²² vont affirmer que les marchés, les stocks de capitaux ainsi que les facteurs macroéconomiques sont les déterminants les plus importants des IDE. Parmi cela, on retrouve les travaux de (TRUMAN et EMMERT, 1999)²³ qui vont dans ce même sens.

Pour conclure, la littérature économique caractérise plusieurs définitions sur les concepts des investissements directs étrangers présentés par des auteurs. Soulignons que ces définitions sont proposées par SOLOW (1956), DUNNING (1970), LIPSEY (1999), ANDREFF (2003) ainsi que KRUGMAN et OBSTFELD (2006).

19 KRUGMAN P. et OBSTFELD M. 2006. Economie internationale, 7^ème édition. Bruxelles 3. Nouveaux horizons.

20 ANDREFF W. 2003. « Les multinationales globales ». Paris, la Découverte, Repères.

21 LIPSEY R. 1999. « The location and characteristics of U.S affiliates in Asia. 6876 ». Cambridge. Mass.

22 LOVE et LAGE HIDALGO. 2000. « Analysing the determinants of US direct investment in Mexico ».

23 TRUMAN J. et EMMERT C. 1999. « Explaining Japanese Foreign Direct Investment in Latin America ». Social Science Quarterly 80. P. 539-541.

13

II.2 Travaux empiriques

Dans cette sous-partie, on va présenter les travaux empiriques portant sur les IDE réalisés par des économistes durant les dernières décennies.

Les études empiriques des IDE ont d'abord été menées dans les pays asiatiques à la fin des années 90, alors que ces pays étaient en pleine croissance. HUSSEIN et WANG en 1996 ont menés les travaux les plus significatifs pour montrer que les IDE ont un impact important dans le processus de développement des pays.

Cependant, l'analyse empirique des IDE à une limite méthodologique. En effet, les IDE sont variables et ne sont pas forcément constant. De plus, ils dépendent de très nombreuses variables et provoquent des difficultés d'estimations en plus du dynamisme des IDE. Comme cité, des variables explicatives telles que l'environnement (CHAKRABARTI, 2001)²⁴ sont difficiles à mesurer. Dans la littérature de la même période, des auteurs tel que (LEVASSEUR, 2002)²⁵ entre autres a réussi à trouver plusieurs facteurs des IDE tout aussi déterminant. On peut retrouver dans ses papiers les facteurs tels que le climat des affaires ou la conjoncture économique, la distance et le coût de transport, les différentes tailles de marchés domestiques, ainsi que le degré d'ouverture d'un pays, pour ne citer qu'eux, déterminent les IDE. On peut trouver des synthèses de l'analyse empirique des IDE qui ne gardent principalement qu'une vingtaine de déterminants triés de manière politique, institutionnel, économique et incitative.

Des études bien plus récentes, (BRUNO et MERVELEVEDE, 2011)²⁶ nous font remarquer que les externalités sont celles qui ont le plus d'impact. En effet, on peut voir que sur un ensemble d'études, seulement la moitié montre un effet positif des IDE sur la croissance et que même 39% n'ont aucun effet.

Cependant, une cassure est observée dans la littérature, caractérisée par les papiers de CARKOVIC et LEVINE (2005)²⁷. Ils vont prouver que les études précédentes utilisaient des

24 CHAKRABARTI A. 2001. « The Determinant of Foreign Direct Investment : Sensitivity Analyses of Cross-Country Regressions ». Kyklos, vol 54 Fasc. P. 114-189.

25 LEVASSEUR S. 2002. « Investissements directs à l'étranger et stratégies des firmes multinationales ». OFCE. Hors série.

26 MERVELEVEDE Y. et BRUNO J.F. 2011. « FDI Spillovers and the Time since Foreign Entry ». Working Papers of Faculty of Economics and Business Administration. Ghent University. Belgium.

27 CARKOVIC M. et LEVINE R. 2005. « Does foreign direct investment accelerate economic growth ? ». Institute for International Economics and Center for Global Development. Washington. DC. P.195-220.

14

techniques économétriques non adaptées. Pour cela, ils vont montrer les limites des études précédentes et utiliser une analyse empirique plus large et sur une plus longue période et réduire le plus possible la volatilité. Les conclusions de leurs études sont que certes les IDE ont un impact visible sur la croissance mais en revanche, cet impact n'est qu'éphémère et non durable à long terme.

Néanmoins, d'autres études tendent à prouver le contraire sur des périodes différentes et avec des techniques économétriques plus poussées (NEUHAUS, 2005). Les causes des différents résultats obtenus de chaque étude seront en partie expliquées par l'hétérogénéité de chaque pays (LIPSEY et SJÖHOLM, 2005)²⁸. Selon eux, deux niveaux interviennent pour considérer la capacité d'absorption des États. Le premier côté est le facteur de l'attrait des IDE et de l'autre côté, les facteurs qui régulent l'effet des IDE. Pour les facteurs de l'hétérogénéité, les auteurs évoquent le niveau de développement du pays, son capital humain, son ouverture économique et commercial, l'effort local d'innovation ainsi que son développement financier et matériel.

Le premier auteur qui a introduit les « effets externes » des IDE sur le bien être général se nomme MACDOUGALL en 1960. Un autre auteur du nom de CAVES en 1971 s'est intéressé aux différents effets des IDE sur le bien être social²⁹.

Un peu plus tôt, durant les années 1950, MUNDELL a mis en place un modèle ayant pour objectif de présenter les échanges commerciaux. Il utilise pour cela deux pays, deux facteurs de productions, deux produits ainsi qu'une fonction de production homogène pour chaque pays. En revanche, le modèle de MUNDELL n'est pas le meilleur afin d'expliquer les IDE³⁰.

De plus, KOIZUMI et KOPECKY ont mis en place en 1977 un modèle d'équilibre général. Ce dernier a pour mission de présenter les effets de diffusion des IDE sur la croissance. A travers ce modèle, on définit la technologie comme un « bien public »³¹.

28 LIPSEY R. et SJÖHOLM F. 2005. « The Impact of Inward FDI on Host Countries : Why Such Different Answers ? ». Chap 2 in Does Foreign Direct Investment Promote Development ? Editors Moran. P 23-43.

29 http://www.mafhoum.com/press4/135E18.pdf. Consulté le 20 décembre 2018.

30 https://tel.archives-ouvertes.fr/tel-01191817/document. Consulté le 20 décembre 2018.

31 https://www.memoireonline.com/02/11/4273/Les-effets-des-investissements-directs-etrangers-sur-la-croissance-des-pays-mediterraneens.html. Consulté le 21 décembre 2018.

15

BREWER a montré en 1991 qu'il y avait une corrélation négative entre la croissance économique et l'IDE³². On peut donc traduire cela par le fait que l'IDE peut avoir un effet totalement négatif sur la croissance économique.

A travers sa thèse de doctorat (soutenue en 1960 avant d'être diffusée en 1976)³³, HYMER essaye de faire la différence entre l'investissement étranger de portefeuille et l'IDE. Selon lui, la microéconomie financière donne des précisions uniquement sur les flux d'investissement de portefeuille. Dans son analyse, il commente que les différentes hypothèses de la microéconomie ne sont pas en accord avec l'attitude des entreprises multinationales.

Plus récemment, VAN HUFFEL ³⁴ en 2001 a trouvé deux stratégies permettant d'intégrer les IDE. Pour cela, il distingue l'intégration verticale (market-seeking) et horizontale (rent-seeking). L'objectif de l'intégration verticale est de créer des « filiales ateliers » par les firmes multinationales. En revanche, l'intégration horizontale est tout simplement un investissement dans le pays d'accueil afin d'éviter les contraintes lors des exportations.

Dans ce paragraphe, on va nommer quelques auteurs ayant réalisés des travaux sur une partie précise de la France³⁵. Par exemple, DUPUY et SAVARY en 1986 ainsi que KRIFA et HERAN en 1999 ont travaillés sur les régions de la France. KLEIN et ROSENGREN en 1994 ainsi que HINES en 1996 se sont intéressés aux métropoles. On peut dire que leurs travaux stipulent que les multinationales choisissent des investissements dans les régions où le nombre de concurrents est moindre.

On tient également à noter que de nombreuses études économiques prouvent que les entreprises ainsi que les secteurs les plus impliqués sur les IDE concernent ceux qui possèdent un leadership technologique. En revanche, les firmes les moins impliquées sur les IDE sont celles qui s'opposent aux firmes des pays ayant les salaires les plus faibles. En France,

32 https://www.memoireonline.com/02/11/4273/Les-effets-des-investissements-directs-etrangers-sur-la-croissance-des-pays-mediterraneens.html. Consulté le 21 décembre 2018.

33 HYMER S.H. 1976. « The International Operations of National Firms : A Study of Direct Foreign Investment 1976 ». Edition MIT Press. Cambridge (thèse de Doctorat. MIT. 1960).

34 https://www.memoireonline.com/01/14/8691/Investissements-directs-etrangers-et-developpement-durable-Cas-de-la-cte-d-Ivoire.html. Consulté le 21 janvier 2019.

35 El OUARDIGHI J., KAHN R. 07/2003. « Les investissements directs internationaux dans les régions Françaises ». Revue d'Economie Régionale et Urbaine. Page 10.

16

MESSERLIN en 1995 a prouvé que l'apparition de nouveaux emplois sur le sol national ont pour conséquence la sortie des flux d'IDE³⁶.

Pour conclure, il y a un grand nombre de littérature consacrée à ce thème. Cependant, il n'existe pas de cadre théorique précis afin d'analyser les déterminants des IDE. La littérature des IDE a connu une très forte augmentation depuis les années 2000³⁷.

36 AUSSILLOUX V., CHEVAL M-L. 2002. « Les investissements directs français à l'étranger et l'emploi en France ». Economie et prévision. Page 30.

37 http://dictionnaire.sensagent.leparisien.fr/Investissement%20direct%20à%20l%27étranger/fr-fr/. Consulté le 21 décembre 2018.

17

III- Modèle empirique et données

Cette section présente le modèle empirique et le choix des variables macroéconomiques. Pour atteindre l'objectif de recherche, les données exploitées sont en rapport avec le marché français et porte sur la période du premier trimestre 1995 au quatrième trimestre 2013. L'ensemble de la base de données a était réalisé à partir du site « fred.stlouisfed.org ».

Le modèle économétrique est défini comme suivant :

IDE_t = a + _{I31tPIB_HAB1t} + _{I32tTX_CHA2t} + _I33tBENEF3t + _{I34tTX_INT4t} + I3stIPCst

+ _I3_6tBENEF_IMP_6t + _I37tEXP7t + _I38tIMP8t + I39tSAL_HOR9t

+ _{I310tDEP_SCO10t} + _{I311tDUMMIES_EURO11t} + I312tDUMMIES_CRISE12t

+ £_t

Avec :

· IDE : Investissement direct étranger

· PIB_HAB : Produit intérieur brut par habitant

· TX_CHA : Taux de change en France

· BENEF : Total des bénéfices tirés des ressources naturelles en pourcentage du

PIB

· TX INT : Taux d'intérêt en France _

· IPC : Indice des prix à la consommation

· BENEF_IMP : Bénéfice des sociétés après impôt

· EXP : Exportations : valeurs des biens pour la France en pourcentage du PIB

· IMP : Importations : valeurs des biens pour la France en pourcentage du PIB

· SAL_HOR : Salaire horaire

· DEP_SCO : Dépenses de consommation des administrations : droits de scolarité et frais de formation

· DUMMIES_EURO : Utilisation de l'euro comme monnaie au cours du trimestre

· DUMMIES_CRISE : La crise est présente au sein du pays

18

III.1 L'investissement direct étranger en France (IDE)

Pour débuter, on va réaliser un graphique représentant l'investissement direct à l'étranger en France.

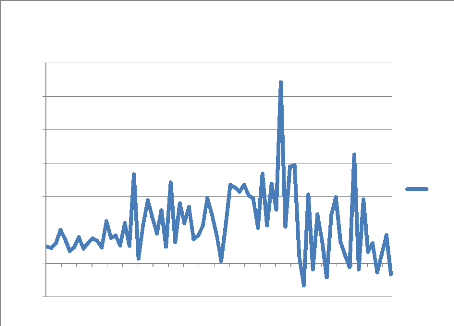
Graphique 1 : Investissement direct à l'étranger en France

1200.0

1000.0

-200.0

400.0

800.0

600.0

200.0

0.0

1995-01-01 1995-11-01 1996-09-01 1997-07-01 1998-05-01 1999-03-01 2000-01-01 2000-11-01 2001-09-01 2002-07-01 2003-05-01 2004-03-01 2005-01-01 2005-11-01 2006-09-01 2007-07-01 2008-05-01 2009-03-01 2010-01-01 2010-11-01 2011-09-01 2012-07-01 2013-05-01

Investissement direct à l'étranger en

France

IDE

Source : L'auteur, d'après les données de « fred.stlouisfed.org ».

A travers le graphique 1, on observe une forte augmentation de l'IDE au cours de l'année 1999. La volonté de l'État français à participer au développement de ces investissements pourrait être la raison de cette hausse des IDE. Il est probable que cette augmentation donne lieu à un investissement important de l'État dans les entreprises domestiques afin qu'elles s'internationalisent. Un autre objectif envisageable serait également d'augmenter la formation de la main d'oeuvre. Cependant, une forte dérèglementation et l'optimisation de la fiscalité pour les entreprises sont possibles³⁸. En effet, le secteur des services est le plus impliqué par ces investissements à cause de la tertiarisation des pays développés. A partir de 2006 et jusqu'à 2008, on remarque une très forte augmentation des

38 https://hal-sciencespo.archives-ouvertes.fr/hal-01017815/document. Consulté le 21 décembre 2018.

19

IDE en France. Le point le plus haut a probablement été atteint en 2007. Cette très forte hausse a pour conséquence la provocation de la crise économique qui s'est tenue jusqu'en 2008. Elle a eu des effets totalement négatifs sur la croissance. Depuis 2011, la tendance est à la croissance. Les IDE ont atteint voir dépassés les 600 (indice 1^er trimestre 1995 fixé à 100). En 2013, la France occupe une place très importante (5^ème rang) au niveau des stocks mondiaux d'investissements directs à l'étranger derrière les Etats-Unis, le Royaume-Uni, l'Allemagne et la Chine³⁹. Les principaux effets des IDE sur la croissance sont le transfert des connaissances, la productivité, la transformation de la spécialisation internationale pour le pays d'accueil ainsi que le renforcement du processus d'agglomération⁴⁰.

III.2 Le produit intérieur brut par habitant (PIB HAB)

On définit le PIB comme un indicateur ayant pour objectif de représenter le niveau de vie des habitants. On calcul cet indicateur à partir de la somme totale des valeurs ajoutées d'un pays à laquelle on ajoute les impôts et on soustrait les subventions sur les produits⁴¹.

Le PIB peut être un facteur totalement décisif dans un pays. On peut expliquer cela par le fait qu'un habitant qui a un revenu disponible plus élevé sera plus enclin à consommer, où bien investir dans une firme du territoire. A partir de son évolution, on peut avoir un aperçu de la croissance.

Cependant le PIB a deux gros problèmes. En effet, il ne prend en compte que les échanges marchands. L'autre problème avec cet indicateur est le fait qu'il ne donne pas assez d'importance à la destruction du stock des ressources naturelles⁴².

Cette variable est présente dans la base de données car les IDE contribuent à une relance de la croissance économique en stimulant les stocks de capitaux, ce qui est donc profitable pour le pays d'accueil.

39 https://www.tresor.economie.gouv.fr/Ressources/1837_les-investissements-francais-a-letranger. Consulté le 21 décembre 2018.

40 BOUOIYOUR J., HANCHANE H. et MOUHOUD E. 2009. « Investissements directs étrangers et productivité ». Revue Économique.

41 https://www.insee.fr/fr/statistiques/3315267?sommaire=3315331. Consulté le 21 décembre 2018.

42 https://www.les-crises.fr/historique-pib-france/. Consulté le 23 décembre 2018.

20

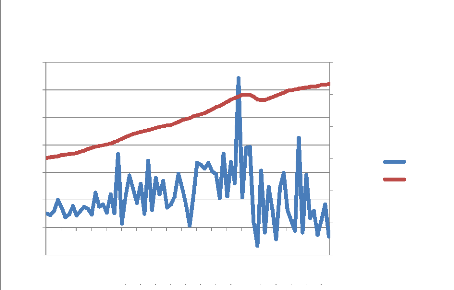
Graphique 2 : Relation entre l'IDE et le PIB par habitant

1200.0

1000.0

-200.0

400.0

800.0

600.0

200.0

0.0

1995-01-01 1996-01-01 1997-01-01 1998-01-01 1999-01-01 2000-01-01 2001-01-01 2002-01-01 2003-01-01 2004-01-01 2005-01-01 2006-01-01 2007-01-01 2008-01-01 2009-01-01 2010-01-01 2011-01-01 2012-01-01 2013-01-01

Relation entre l'IDE et le PIB par habitant en France

400.000

600.000

300.000

200.000

0.000

500.000

100.000

IDE

PIB_HAB

Source : L'auteur, d'après les données de « fred.stlouisfed.org ».

D'après le graphique 2, on aperçoit que le PIB a globalement crû de 1995 à 2013. Il a atteint environ 499 milliards d'euros en 2008 durant la crise économique.

Par conséquent, on ne sait pas quel lien on va obtenir entre le PIB par habitant et le volume des investissements directs étrangers.

III.3 Le taux de change en France (TXCHA)

Selon l'INSEE, le taux de change effectif correspond au taux de change d'une sphère monétaire. Ce dernier est calculé à partir d'une somme pondérée des taux de change pour les différents organismes commerciaux ainsi que pour les concurrents. En revanche, le taux de change effectif nominal est mesuré à partir des parités nominales. Pour cela, on ne prend pas en compte dans le calcul les différences possibles de pouvoir d'achat entre les deux devises et le taux de change effectif réel s'appui sur les indices de prix ainsi que leurs évolutions⁴³.

43 https://www.insee.fr/fr/metadonnees/definition/c1438. Consulté le 23 décembre 2018.

21

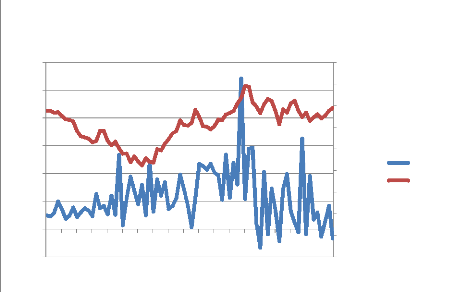
Graphique 3 : Relation entre l'IDE et le taux de change

1200.0

1000.0

-200.0

400.0

800.0

600.0

200.0

0.0

1995-01-01 1996-01-01 1997-01-01 1998-01-01 1999-01-01 2000-01-01 2001-01-01 2002-01-01 2003-01-01 2004-01-01 2005-01-01 2006-01-01 2007-01-01 2008-01-01 2009-01-01 2010-01-01 2011-01-01 2012-01-01 2013-01-01

Relation entre l'IDE et le taux de change en

France

0.80000

0.60000

0.40000

0.20000

0.00000

1.80000

1.60000

1.40000

1.20000

1.00000

IDE TX_CHA

Source : L'auteur, d'après les données de « fred.stlouisfed.org ».

D'après le graphique 3, on observe que le taux de change a beaucoup chuté jusqu'au début de l'année 2001. Ensuite, il a bien augmenté. Cette hausse s'est réalisée jusqu'à la période de crise (ce dernier était d'environ 1,58% en 2008). Après la crise, le taux de change est globalement en « dents de scie ».

Le taux de change est tout simplement un prix. Par exemple, le taux de change de l'euro en dollar correspond au nombre de dollar que l'on peut acheter avec un euro. Dans le cadre du taux de change, la cotation est réalisée soit à l'incertain, soit au certain. En Europe, on cote au certain.

Les principaux acteurs du taux de change sont principalement les institutions financières et les banques centrales. Ils permettent donc d'exécuter les ordres de leurs clients⁴⁴.

44 https://www.lafinancepourtous.com/decryptages/marches-financiers/fonctionnement-du-marche/taux-de-change/. Consulté le 23 décembre 2018.

22

III.4 Total des bénéfices tirés des ressources naturelles en

pourcentage du PIB (BENEF)

La France détient beaucoup de ressources naturelles qui constituent ainsi souvent un argument afin de pouvoir attirer un grand nombre d'IDE. La situation géographique de la France est un avantage car elle bénéficie de l'atlantique et de la Méditerranée. Enfin, elle dispose également d'un cadre physique favorable (forêt, sol, accessibilité naturelle et climat). Ces différents éléments vont permettent aux firmes de baisser de manière significative leurs coûts pour les matières premières et les énergies pour les productions. On peut donc dire qu'il y a un effet positif et significatif sur les IDE⁴⁵.

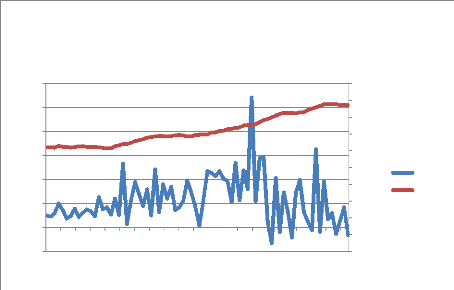
Graphique 4 : Relation entre l'IDE et le total des bénéfices tirés des ressources naturelles en

France

1200.0

1000.0

-200.0

400.0

800.0

600.0

200.0

0.0

1995-01-01 1995-12-01 1996-11-01 1997-10-01 1998-09-01 1999-08-01 2000-07-01 2001-06-01 2002-05-01 2003-04-01 2004-03-01 2005-02-01 2006-01-01 2006-12-01 2007-11-01 2008-10-01 2009-09-01 2010-08-01 2011-07-01 2012-06-01 2013-05-01

Relation entre l'IDE et le total des
bénéfices tirés des ressources naturelles
en france

40.0

200.0

80.0

60.0

20.0

0.0

180.0

160.0

140.0

120.0

100.0

IDE BENEF

Source : L'auteur, d'après les données de « fred.stlouisfed.org ».

D'après le graphique 4, on remarque que le total des bénéfices tirés des ressources naturelles est légèrement croissant. Cependant, on constate très clairement que cette hausse est progressive. En effet, ce dernier est d'environ 123 en 1995 pour atteindre environ 174 en 2013. Seulement une légère baisse a pu être constatée entre 2012 et 2013. Il est compliqué de

45 http://www.voyagesphotosmanu.com/ressources naturelles.html. Consulté le 23 décembre 2018.

23

savoir à quelle relation s'attendre entre les bénéfices tirés des ressources naturelles et le volume des IDE en France.

III.5 Le taux d'intérêt en France (TX INT)

Aujourd'hui, il y a deux types de taux d'intérêt. On distingue le taux d'intérêt de court terme qui s'oppose à celui de long terme⁴⁶. Le taux d'intérêt à court terme représente le taux d'emprunt. On les considère souvent comme des moyennes de taux journaliers. La valeur de ce taux est renseignée en pourcentage. En revanche, le taux d'intérêt de long terme représente les obligations d'États. Leurs échéances sont souvent de dix années. Ces derniers dépendent des prix facturés, du risque propre à l'emprunt et de la baisse nette de la valeur du capital. Ils interviennent donc sur des obligations. Le gouvernement se charge du remboursement du capital.

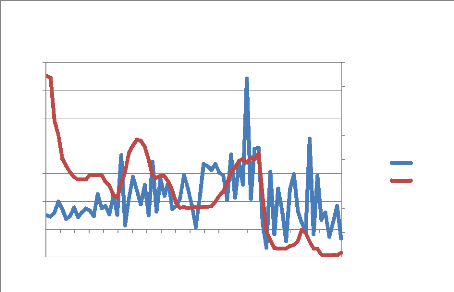
Graphique 5 : Relation entre l'IDE et le taux d'intérêt en France

1200.0

1000.0

-200.0

400.0

800.0

600.0

200.0

0.0

1995-01-01 1995-12-01 1996-11-01 1997-10-01 1998-09-01 1999-08-01 2000-07-01 2001-06-01 2002-05-01 2003-04-01 2004-03-01 2005-02-01 2006-01-01 2006-12-01 2007-11-01 2008-10-01 2009-09-01 2010-08-01 2011-07-01 2012-06-01 2013-05-01

Relation entre l'IDE et le taux d'intérêt en

France

4.0000

8.0000

7.0000

6.0000

3.0000

2.0000

0.0000

5.0000

1.0000

IDE TX_INT

Source : L'auteur, d'après les données de « fred.stlouisfed.org ».

D'après le graphique 5, on constate que le taux d'intérêt baisse beaucoup à partir de 2008. Cette baisse profite à l'économie car il favorise beaucoup l'accès aux crédits pour les entreprises. Depuis 2010, on constate que le taux d'intérêt est proche de zéro voir en dessous.

46 http://www.europarl.europa.eu/workingpapers/econ/pdf/116 fr.pdf. Consulté le 23 décembre 2018.

24

On peut donc dire que les ménages sont incités à baisser leurs épargnes et donc leurs consommations.

D'un point de vue théorique, les économistes ont des visions différentes sur les taux d'intérêt. Par exemple, on observe que pour les économistes classiques et les néoclassiques comme David HUME (1758) et Irving FISHER (1907), l'objectif du taux d'intérêt est de financer les épargnants en échange du fait qu'ils ne consomment plus. Ces économistes ont une attirance pour le présent et non pour le futur qui va s'expliquer en grande partie par un facteur d'ordre psychologique et également un facteur d'incertitude concernant la durée de la vie humaine⁴⁷.

En revanche, selon John Maynard KEYNES (1936), le taux d'intérêt n'est pas une récompense parfaite de la non-dépense immédiate car il admet qu'un individu qui accumule ses épargnes sous la forme d'argent liquide (monnaie fiduciaire) ne gagne absolument aucun intérêt. Il va donc montrer que les taux d'intérêt sont la pour convaincre les agent à diriger leurs épargnes vers des formes plus généreuses pour la société⁴⁸.

III.6 L'indice des prix à la consommation (IPC)

Selon l'INSEE, l'Indice des Prix à la Consommation (IPC) permet de déterminer l'inflation. Il va donc servir à estimer entre deux périodes, la variation moyenne des prix des biens qui vont être achetés par les ménages. Calculé à partir d'un panier fixe de produits, il s'appuie sur la masse du produit. Chaque mois, l'indice des prix à la consommation est publié au Journal Officiel. Apparu en 1914, la couverture de l'IPC s'est développée d'un point de vue géographique⁴⁹.

En revanche, afin que l'indice soit significatif, le panier est donc modifié chaque année au cours du mois de décembre afin de supprimer les biens et services anciens et insérer les nouveaux biens et services.

47 Alternatives économiques n°296, « Comment sauver la protection sociale », 11/2010, page 71. Consulté le 23 décembre 2018.

48 Alternatives économiques n°296, « Comment sauver la protection sociale », 11/2010, page 71. Consulté le 23 décembre 2018.

49 https://www.insee.fr/fr/metadonnees/source/indicateur/p1653/description. Consulté le 24 décembre 2018.

25

L'IPC a une utilité macroéconomique. Il est suivit par la banque centrale pour prendre en considération les prix à court terme et assurer le duel contre l'inflation. Cet indicateur est en relation avec le revenu des personnes et des firmes⁵⁰.

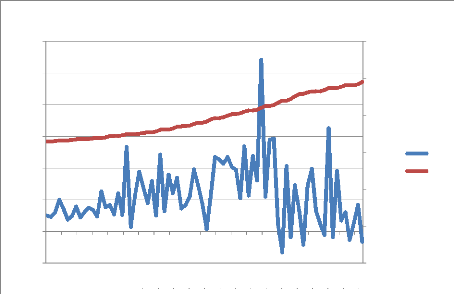
Graphique 6 : Relation entre l'IDE et l'IPC en France

1200.0

1000.0

-200.0

400.0

800.0

600.0

200.0

0.0

1995-01-01

1995-12-01

Relation entre l'IDE et l'IPC en France

1996-11-01

1997-10-01

1998-09-01

1999-08-01

2000-07-01

2001-06-01

2002-05-01

2003-04-01

2004-03-01

2005-02-01

2006-01-01

2006-12-01

2007-11-01

2008-10-01

2009-09-01

2010-08-01

2011-07-01

2012-06-01

2013-05-01

40.0

80.0

60.0

20.0

0.0

120.0

100.0

IDE IPC

Source : L'auteur, d'après les données de « fred.stlouisfed.org ».

D'après le graphique 6, on observe une augmentation légère de l'IPC entre 1995 et 2013. On remarque très clairement que la croissance de l'IPC n'est pas impactée par la crise financière de 2008. Un lien est possible entre l'IPC et l'IDE car si les prix baissent, les populations seront incitées à augmenter leurs investissements. On s'attend donc à une relation opposée entre l'IPC et l'IDE.

III.7 Le bénéfice des entreprises après impôt (BENEF IMP)

Dans notre société, la rivalité des fiscalités pour l'IDE est une réalité dans ce contexte de mondialisation. En effet, les investisseurs font des comparaisons au niveau des impôts qui représentent les différentes localisations et les impositions qui peuvent facilement jouer un rôle prépondérant dans le choix des investisseurs.

50 http://www.annales.org/gazette/memoire-51.pdf. Consulté le 24 décembre 2018.

26

En effet, une diminution de l'impôt sur les sociétés devrait probablement améliorer le niveau des salaires réels futurs. Cet impôt représente donc la part des profits qui est reversée à l'État⁵¹.

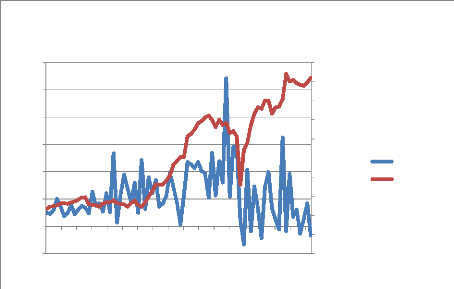
Graphique 7 : Relation entre l'IDE et le bénéfice des entreprises après impôt en France

1200.0

1000.0

-200.0

400.0

800.0

600.0

200.0

0.0

1995-01-01 1996-02-01 1997-03-01 1998-04-01 1999-05-01 2000-06-01 2001-07-01 2002-08-01 2003-09-01 2004-10-01 2005-11-01 2006-12-01 2008-01-01 2009-02-01 2010-03-01 2011-04-01 2012-05-01 2013-06-01

Relation entre l'IDE et le bénéfice des entreprises après impôt en France

400.000

2000.000

800.000

600.000

200.000

0.000

1800.000

1600.000

1400.000

1200.000

1000.000

IDE

BENEF_IMP

Source : L'auteur, d'après les données de « fred.stlouisfed.org ».

D'après le graphique 7, on constate que si le pays offre plus de faveurs fiscales aux investisseurs étrangers alors le pays va attirer davantage d'investisseurs. Il y a de forte chance qu'il existe une relation négative entre les impositions et l'IDE. Le bénéfice a tout d'abord connu une forte fluctuation jusqu'en 2006 avant de chuter jusqu'en 2008. Enfin, on constate qu'il a globalement augmenté jusqu'à la fin de notre période d'étude (2013).

En effet, les études récentes prouvent que l'IDE devient un élément de plus en plus sensible à la fiscalité. Ces dernières essayent de montrer qu'une augmentation du taux

51 STIMULA L. et TRANNOY A. 03/2009. « Incidence de l'impôt sur les sociétés ». Revue française d'économie. PP. 100-102.

27

d'impôt entrainera une baisse de l'IDE. L'ensemble de ces études est important sur le long terme afin de prédire l'impact de l'IDE sur la réforme de l'impôt sur les sociétés⁵².

III.8 Exportations : valeurs des biens pour la France (EXP)

Au sens de l'INSEE, les exportations représentent l'ensemble des biens et services qui sont livrés par des résidents à des populations non-résidentes⁵³.

Graphique 8 : Relation entre l'IDE et les exportations en France

1200.0

1000.0

-200.0

400.0

800.0

600.0

200.0

0.0

1995-01-01

Relation entre l'IDE et les exportations en

France

1995-12-01

1996-11-01

1997-10-01

1998-09-01 1999-08-01 2000-07-01 2001-06-01 2002-05-01 2003-04-01 2004-03-01 2005-02-01 2006-01-01

2006-12-01

2007-11-01

2008-10-01

2009-09-01 2010-08-01 2011-07-01 2012-06-01 2013-05-01

30.0

25.0

20.0

0.0

15.0

10.0

5.0

IDE EXP

Source : L'auteur, d'après les données de « fred.stlouisfed.org ».

D'après le graphique 8, on remarque une baisse des exportations après la crise jusqu'au premier trimestre 2009. Cette baisse provoque un déficit commercial de la France. On peut expliquer cette diminution des exportations par la hausse de l'euro. Ce dernier handicap les exportations. La compétitivité des entreprises s'est donc dégradée. Cependant, d'autres évènements peuvent expliquer la baisse des exportations comme la hausse du prix du pétrole et la présence de la concurrence entre les pays émergents⁵⁴.

52 https://www.oecd.org/fr/investissement/politiques-investissement/40251026.pdf. Consulté le 26 décembre 2018.

53 https://www.insee.fr/fr/metadonnees/definition/c1425. Consulté le 26 décembre 2018.

54 https://fr.slideshare.net/Nicolas Pomer/lvolution-des-exportations-en-France. Consulté le 26 décembre 2018.

28

En effet, cette baisse des exportations risque d'endommager le déficit de la balance des paiements. Le PIB risque également de baisser. Selon une analyse, vers 2050, la France devrait se situer au alentour de la sixième place mondiale au niveau des exportations. La reprise des exportations s'effectue depuis le début de l'année 2011⁵⁵. La crise économique de 2008 a eu des conséquences sur les exportations.

III.9 Importations : valeurs des biens pour la France (IMP)

Selon l'INSEE, on définit les importations comme l'ensemble des biens et services qui sont livrés par des non-résidents à des populations résidentes.

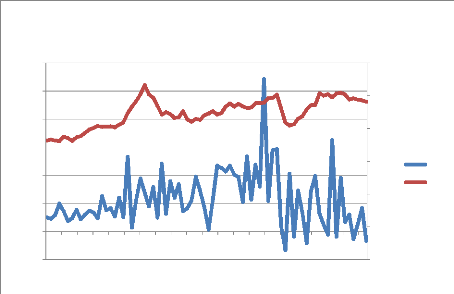
Graphique 9 : Relation entre l'IDE et les importations en France

1200.0

1000.0

-200.0

400.0

800.0

600.0

200.0

0.0

1995-01-01 1995-12-01 1996-11-01 1997-10-01 1998-09-01 1999-08-01 2000-07-01 2001-06-01 2002-05-01 2003-04-01 2004-03-01 2005-02-01 2006-01-01 2006-12-01 2007-11-01 2008-10-01 2009-09-01 2010-08-01 2011-07-01 2012-06-01 2013-05-01

Relation entre l'IDE et les importations en

France

30.0

25.0

20.0

0.0

15.0

10.0

5.0

IDE

IMP

Source : L'auteur, d'après les données de « fred.stlouisfed.org ».

D'après le graphique 9, pour l'année 2012, on observe une légère baisse des importations. L'une des causes de cette baisse pourrait être l'affaiblissement de la croissance dans la zone euro⁵⁶.

55 https://fr.slideshare.net/Nicolas Pomer/lvolution-des-exportations-en-France. Consulté le 26 décembre 2018.

56 https://www.insee.fr/fr/statistiques/1288375?sommaire=1288404. Consulté le 26 décembre 2018.

29

Afin de réaliser des importations en France, les résidents doivent payer une Taxe sur la Valeur Ajoutée (TVA). Cette taxe peut être accompagnée des droits de douane mais ces derniers ne sont pas systématiques. En effet, les droits de douane peuvent dans certains cas être relativement élevés comme par exemple pour le textile (12%) mais également pour les nouveaux produits comme les montres connectées et les drones (7%). En revanche, les droits de douane sont totalement différents pour l'insertion de billets de banque dans une enveloppe ainsi que les pièces de métaux précieux⁵⁷.

III.10 Salaire horaire (SALHOR)

On définit le salaire comme la rémunération du travail en commun accord entre un salarié et son employeur. Le salaire brut comptabilise l'ensemble des montants perçus avant la déduction des frais. En revanche, le salaire net est le salaire que va toucher le salarié⁵⁸.

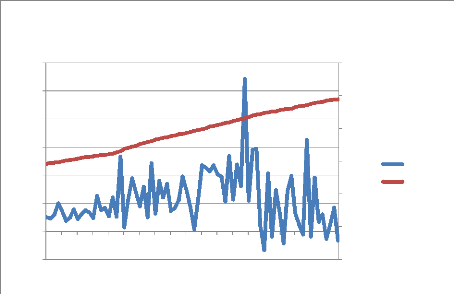
Graphique 10 : Relation entre l'IDE et le salaire horaire en France

1200.0

1000.0

-200.0

400.0

800.0

600.0

200.0

0.0

1995-01-01 1996-01-01 1997-01-01 1998-01-01 1999-01-01 2000-01-01 2001-01-01 2002-01-01 2003-01-01 2004-01-01 2005-01-01 2006-01-01 2007-01-01 2008-01-01 2009-01-01 2010-01-01 2011-01-01 2012-01-01 2013-01-01

Relation entre l'IDE et le salaire horaire en

France

40.0

80.0

60.0

20.0

0.0

120.0

100.0

IDE

SAL_HOR

Source : L'auteur, d'après les données de « fred.stlouisfed.org ».

57 http://blog.globeservices.fr/particuliers/hors-de-france/la-douane-francaise/importation-en-france/. Consulté le 26 décembre 2018.

58 https://www.insee.fr/fr/metadonnees/definition/c1211. Consulté le 27 décembre 2018.

30

D'après le graphique 10, on observe très clairement que le salaire horaire a tendance à augmenter. Certaines études récentes montrent que le salaire a un impact positif sur l'IDE. Enfin, d'autres études ont montrées que le salaire peut varié en fonction de la géolocalisation de la firme (locale ou étrangère)⁵⁹.

A ce jour, plus de 10,6% des salariés d'une entreprise du secteur privé sont rémunérés sur la base du Salaire Minimum Interprofessionnel de Croissance (SMIC). Cette augmentation du SMIC s'est réalisée sans l'aide du gouvernement afin de remplir les objectifs du Président MACRON⁶⁰.

III.11 Dépenses de consommation des administrations : droits de scolarité et frais de formation (DEPSCO)

On définit les droits de scolarité et les frais de formation comme l'ensemble des coûts afin d'assurer la scolarisation des enfants. Les frais de scolarité pour un élève de lycée professionnel est dotant plus important qu'un élève de lycée général⁶¹.

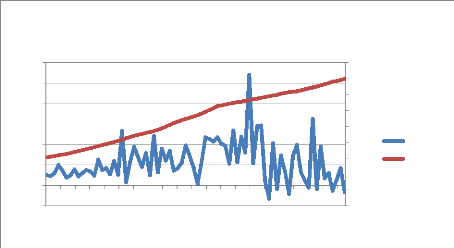
Graphique 11 : Relation entre l'IDE et les dépenses scolaires en France

1200.0

1000.0

-200.0

400.0

800.0

600.0

200.0

0.0

1995-01-01 1995-12-01 1996-11-01 1997-10-01 1998-09-01 1999-08-01 2000-07-01 2001-06-01 2002-05-01 2003-04-01 2004-03-01 2005-02-01 2006-01-01 2006-12-01 2007-11-01 2008-10-01 2009-09-01 2010-08-01 2011-07-01 2012-06-01 2013-05-01

Relation entre l'IDE et les dépenses scolaires en France

40.0

90.0

80.0

60.0

30.0

20.0

0.0

70.0

50.0

10.0

IDE

DEP_SCO

Source : L'auteur, d'après les données de « fred.stlouisfed.org ».

59 http://www.oecd.org/fr/daf/inv/mne/40889808.pdf. Consulté le 27 décembre 2018.

60 https://www.net-iris.fr/indices-taux/paye/1-salaire-minimum-smic-horaire-smic-mensuel. Consulté le 27 décembre 2018.

61 http://www.education.gouv.fr/cid92789/les-depenses-des-familles-pour-la-scolarisation-des-enfants.html. Consulté le 29 décembre 2018.

31

D'après le graphique 11, on observe que les dépenses de scolarité sont croissantes sur la période d'étude.

En effet, les frais de formation prennent en compte les frais d'inscription ainsi que les frais de scolarité. Une enquête concernant les frais de scolarité en 2013 montre que ces derniers sont plus importants que durant l'année 1995. Cette augmentation peut s'expliquer par l'amélioration du système d'éducation. On calcule la dépense moyenne d'éducation en faisant le rapport entre le total des dépenses et l'effectif total des élèves pour le niveau concerné⁶².

III.12 Utilisation de l'euro comme monnaie au cours du trimestre

(DUMMIESEURO)

Le choix de cette variable a été réalisé afin de déterminer si la présence de l'euro comme monnaie au sein du pays affecte les investissements directs étrangers. En effet, l'euro est devenu la monnaie officielle en France durant la période d'étude. Cette variable est qualitative qui sera codée 1, lorsque le pays utilise l'euro comme monnaie et 0 sinon.

L'utilisation de l'euro comme monnaie nationale a un impact positif sur les investissements directs étrangers. En effet, ces derniers étaient meilleurs à partir des années 2000 (utilisation de l'euro en monnaie). La forte baisse à partir de 2007 est causée par la crise économique.

III.13 La crise est présente au sein du pays (DUMMIESCRISE)

Cette variable qualitative est intégrée dans le modèle afin de voir si la crise au sein du pays a un impact sur les investissements directs étrangers. En effet, une crise économique a débutée en 2007. DUMMIES_CRISE est une variable qualitative codée 1, lorsque la France est en crise et 0 sinon.

La crise économique a un impact négatif sur les investissements directs étrangers. Les IDE ont beaucoup chutés durant la crise. Ces derniers étaient mêmes négatifs en 2009. Il y a donc une relation négative entre les IDE et l'existence de la crise économique en France.

62 http://www.education.gouv.fr/cid92789/les-depenses-des-familles-pour-la-scolarisation-des-enfants.html. Consulté le 29 décembre 2018.

32

IV- Analyse de données et descriptive

Afin de mieux appréhender le sujet d'étude, nous avons décidé d'effectuer une analyse de données du modèle. Cette analyse sera confrontée à la littérature dans le but de voir si les grandes périodes définies par cette dernière se confirment dans nos observations.

Dans un premier temps, on va présenter les différentes variables dans un tableau. Il s'agit des variables qui sont utilisées dans la partie économétrique.

Tableau 1 : Index de la base « Ide »

Nom de la variable	Description		Type de variable	PIB_HAB
Produit intérieur brut par habitant	Quantitative		TX_CHA
Taux de change effectif réel basé sur le coût unitaire de fabrication pour la France	Quantitative		BENEF
Total des bénéfices tirés des ressources naturelles en pourcentage du PIB	Quantitative		TX_INT
Taux d'intérêt réel en France	Quantitative		IPC
Indice des prix à la consommation	Quantitative		BENEF_IMP
Bénéfices des entreprises après impôt	Quantitative		EXP
Exportations : valeurs des biens pour la France en pourcentage du PIB	Quantitative		IMP
Importations : valeurs des biens pour la France en pourcentage du PIB	Quantitative		SAL_HOR
Salaire horaire	Quantitative		DEP_SCO
Dépenses de consommation des administrations : droits de scolarité et frais de formation	Quantitative		DUMMIES_EURO
=1 si le pays utilise l'euro comme monnaie durant le trimestre	Qualitative		DUMMIERS_CRISE
=1 si le pays est en période de crise durant le trimestre	Qualitative

Dans le cadre de l'étude, la variable à expliquer sera nommée « IDE ». Elle représente la valeur de l'investissement direct étranger en France. Les histogrammes de chaque variable se trouvent en annexe (annexe 1).

33

IV.1 Statistiques descriptives

Pour commencer, on va tout d'abord regarder un peu plus en détail et essayer d'interpréter les statistiques liées aux variables. Le logiciel R Studio donne le tableau des statistiques descriptives. Afin de réaliser ces statistiques, on a utilisé la fonction summary. Cette fonction permet d'obtenir les valeurs du minimum, le premier quartile, la médiane, la moyenne, le troisième quartile et le maximum. Elle permet également de connaître le nombre de valeurs manquantes.

Tableau 2 : Statistiques descriptives du modèle : Minimum, maximum, médiane, moyenne et

quartiles

Variables	Minimum	1er quartile	Médiane	Moyenne	3ème quartile		Maximum	IDE
-132,60	99,95	175,75	229,15	363,27	1 084,40		PIB_HAB
301,80	355,30	424,90	423,70	493,30	532,20		TX CHA
0,848	1,094	1,264	1,223	1,349	1,581		BENEF
122,80	127,70	138,90	144,40	160,40	175,70		TX INT
0,067	1,109	2,983	2,640	3,556	7,444		IPC
65,79	69,59	76,29	78,79	87,89	98,02		BENEF_IMP
467,60	533,40	947,90	1009,70	1406,60	1879,80		EXP
17,70	20,45	21,03	20,97	21,49	25,24		IMP
18,08	20,64	22,56	22,35	24,12	26,63		SAL HOR
58,41	65,82	78,12	78,00	89,47	97,72		DEP_SCO
30,53	41,40	56,59	55,55	69,04	79,89

	0		1	DUMMIES_EURO
20	56		DUMMIES CRISE
64	12

A partir du tableau 2, on observe plusieurs points communs entre les différentes variables. Plus de la moitié des variables présentent un écart important entre leurs minimums et leurs maximums. La série est composée de 76 observations (19 années de 4 trimestres).

On remarque que la répartition des importations et des exportations sur la période d'étude semble assez proche. En effet, les exportations moyennes sont de 20,97 tandis que les importations moyennes sont de 22,35. L'investissement direct à l'étranger moyen est de 175,75.

Le PIB par habitant moyen et médian est relativement proche. A première vue, le PIB par habitant est représenté de manière égalitaire entre les différentes années d'études.

34

On observe que durant trois quarts des trimestres, l'IPC a une valeur inférieure à 87 tandis qu'il a une valeur inférieure à 69 durant un quart des trimestres.

Nous avons ensuite réalisé différents tests sur les variables quantitatives afin de valider différentes hypothèses du modèle.

Tableau 3 : Les différents tests du modèle (valeurs statistiques ou p-value)

VARIABLES	SHAPIRO-WILK	KURTOSIS	SKEWNESS		KOLMOGOROV-SMIRNOV	IDE
W = 0,9305 p-value = 0,0004	5,8615	1,1731	D = 0,1121 p-value = 0,2952		PIB_HAB
W = 0,9224 p-value = 0,0002	1,6251	-0,1388	D = 0,1394 p-value = 0,0946		TX_CHA
W = 0,9189 p-value = 0,0001	2,5879	-0,7479	D = 0,1325 p-value = 0,1266		BENEF
W = 0,8967 p-value = 1,409E-05	1,8777	0,4649	D = 0,1487 p-value = 0,0694		TX_INT
W = 0,9439 p-value = 0,0022	3,1333	0,2833	D = 0,1018 p-value = 0,4097		IPC
W = 0,9030 p-value = 2,555E-05	1,7491	0,3998	D = 0,1269 p-value = 0,1729		BENEF_IMP
W = 0,8604 p-value = 6,308E-07	1,5614	0,3074	D = 0,2022 p-value = 0,0034

35

EXP

W = 0,9556 p-value = 0,0096	3,7600	0,2315	D = 0,1226 p-value = 0,1870	IMP
W = 0,9581 p-value = 0,0135	2,1601	-0,3418	D = 0,0906 p-value = 0,5301	SAL_HOR
W = 0,9347 p-value = 0,0007	1,6702	-0,0216	D = 0,0969 p-value = 0,4459	DEP_SCO
W = 0,9309 p-value = 0,0005	1,6346	-0,1185	D = 0,1135 p-value = 0,2611

Tout d'abord, le test de Shapiro-Wilk est réalisé à l'aide de la matrice de variance-covariance afin de pouvoir tester l'hypothèse H0 qui permet de savoir si la distribution de la variable suit bien une loi normale. Pour l'ensemble du modèle, la p-value est inférieur à 0,05. Par conséquent, l'hypothèse H0 est rejetée au seuil de risque de 5% pour l'ensemble des variables du modèle. Aucune variable ne suit donc la loi normale. En revanche, le test de Kurtosis évalue la dispersion des valeurs extrêmes en faisant référence à la loi normale. Ce dernier sera nul pour une distribution normale. Dans le cas de ce modèle, toutes les variables ont un coefficient de Kurtosis positif. On peut donc en conclure que la distribution est plus aplatie que normale. Enfin, nous allons analyser le test de Skewness. Pour les variables IDE, BENEF, TX_INT, IPC, BENEF_IMP et EXP, le coefficient de ce test est positif. On peut donc dire que sa distribution est étalée à droite. En revanche, les variables PIB_HAB, TX_CHA, IMP, SAL_HOR et DEP_SCO ont un coefficient négatif. La distribution de ces variables est donc étalée à gauche. Cependant, le résultat de ces tests ne permet pas de savoir si le modèle est normalement distribué. On va donc réaliser un test non-paramétrique dont l'objectif sera de tester le modèle avec plus de précision. Ainsi, en réalisant le test de Kolmogorov-Smirnov sur notre modèle ayant une loi normalement distribuée, la p-value est supérieur à 0,05 pour toutes les variables sauf pour le BENEF_IMP. On peut donc dire que l'hypothèse H0 est acceptée au seuil de risque de 5% et la loi normale est bien suivie sauf

pour la variable BENEF_IMP.

36

Etant donné que la loi normale n'est pas suivie pour la variable BENEF_IMP, une matrice de corrélation est réalisée à partir de la méthode de Spearman afin de détecter les éventuelles corrélations entre les variables.

Graphique 12 : Matrice de corrélation de Spearman

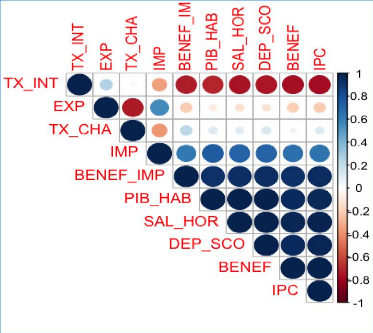
D'après la matrice de corrélation de Spearman (graphique 12), les corrélations positives sont représentées par des cercles bleus tandis que les corrélations négatives sont visibles sur le graphique par des cercles rouges. En effet, plus le cercle est foncé et donc plus la corrélation est forte. Dans ce modèle, nous pouvons voir que le TX_INT est corrélée négativement avec les variables BENEF_IMP, PIB_HAB, SAL_HOR, DEP_SCO, BENEF et IPC. Cette corrélation est très forte car le cercle de l'ensemble de ces variables est rouge foncé. De plus, il y a des corrélations positives qui sont très fortes. En effet, la variable BENEF_IMP est corrélée positivement avec le PIB_HAB, SAL_HOR, DEP_SCO, BENEF et l'IPC. De plus, le PIB_HAB est corrélée positivement avec le SAL_HOR, DEP_SCO, BENEF et IPC. Il existe également une forte corrélation positive entre le SAL_HOR et les DEP_SCO ainsi que le BENEF et l'IPC. Ensuite, le graphique montre que la variable DEP_SCO est corrélée positivement avec le BENEF et IPC. Enfin, la variable BENEF est

37

corrélée également positivement avec l'IPC. Cette matrice montre également que la variable IMP est corrélée positivement mais moins fortement avec les variables BENEF_IMP, PIB_HAB, SAL_HOR, DEP_SCO, BENEF et l'IPC. Une autre version de Spearman est disponible en fin de mémoire (annexe 3).

Par la suite, on a voulu déterminer la présence ou non de valeurs atypiques dans le modèle. Cette partie est détaillée en annexe (annexe 2) à la fin du mémoire.

Graphique 13 : Boîte à moustache et valeurs potentiellement atypiques du modèle

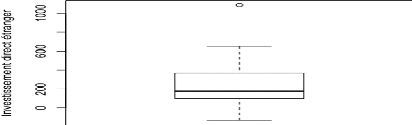
D'après le graphique 13, on observe que la variable IDE a potentiellement une valeur atypique. Les autres boîtes à moustache représentant les autres variables se trouve en annexe mais ne présentent pas forcément de valeurs atypiques (annexe 2).

Si la variable n'avait qu'une valeur potentiellement atypique, le test de Grubbs est réalisé. En revanche, si la variable avait plusieurs valeurs potentiellement atypiques, le test de Rosner est réalisé (annexe 2).

Après l'application du test de Rosner, les variables TX_INT et EXP ont ressorties des valeurs qui n'étaient pas atypiques. En revanche, la valeur de la variable IDE était atypique. Cette dernière correspondait au quatrième trimestre 2007 (il s'agit de la 52ième observations). Cependant, cette valeur atypique n'est pas très surprenante est l'une des raisons pourrait être la crise économique qui s'est déroulée au cours de cette période. On ne va donc pas supprimer

38

cette valeur car le mémoire est basé sur des séries temporelles mais il nous paraît tout de même intéressant de comprendre les raisons de la présence de ces valeurs.

IV.2 Analyse de données

Dans un premier temps, nous avons réalisé un graphique qui nous permet de ressortir la variance qui est expliquée par chaque dimension.

Graphique 14 : Variance expliquée par chaque dimension

Le graphique 14 montre que l'inertie ressort principalement des trois premières composantes. En effet, la première dimension est dominante car elle ressort 63% de l'inertie de l'analyse en composante principale tandis que la seconde dimension en ressort seulement 19,7%. Enfin, la troisième dimension ressort 10,7% de l'inertie de l'ACP. En observant le graphique, les autres dimensions ressortes très peu d'inertie voir pas du tout.

A présent, nous allons observer la qualité de la représentation de nos variables sur le graphique. Nous allons donc regarder les cosinus carrés associés à nos variables.

39

Graphique 15 : Cosinus des dimensions

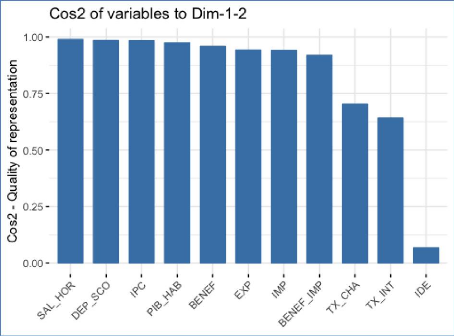
Tout d'abord, il est important de souligner que si la valeur du cosinus est élevée alors la variable aura une meilleure représentation sur les axes considérés. De plus, une variable dont le cosinus carré est élevé sera proche de l'origine du cercle de corrélation. D'après le graphique 15, les variables SAL_HOR, DEP_SCO, IPC et PIB_HAB sont très bien représentées. En effet, la valeur de leurs cosinus carrés est proche de un. Le TX_CHA présente un cosinus carré d'environ 0,70 tandis que celui du TX_INT est d'environ 0,65. En revanche, la variable à expliquer (IDE) ne semble pas bien représentée car la valeur de son cosinus est très faible (environ 0,10).

Dans l'étape suivante, nous allons procéder à la représentation de nos variables sur le cercle de corrélation. Pour cela, nous allons observer la contribution des variables dans la définition des composantes.

40

Graphique 16 : Contribution de chaque variable à la définition des composantes

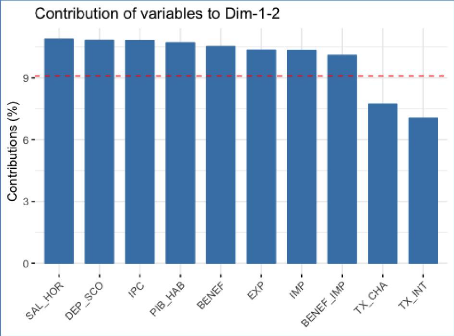
Le graphique 16 nous montre les contributions de chaque variable à la définition des composantes dans le cadre des deux premières dimensions. Les résultats obtenus à partir de ce graphique sont très similaires à ceux des corrélations variables composantes. En effet, les variables fortement corrélées avec la première dimension participent davantage à expliquer la variabilité de l'échantillon. De manière identique, les variables qui ne sont pas ou très peu corrélées avec une composante ne participent pas ou très peu à expliquer la variabilité de l'échantillon. Le trait en pointillé rouge représente la contribution moyenne. Les variables les mieux représentées dans le cadre des deux premières dimensions sont le SAL_HOR, DEP_SCO et l'IPC. Il est beaucoup plus simple d'observer ces indicateurs sur un graphique qui favorise l'interprétation des données.

41

Graphique 17 : Cercle de corrélation

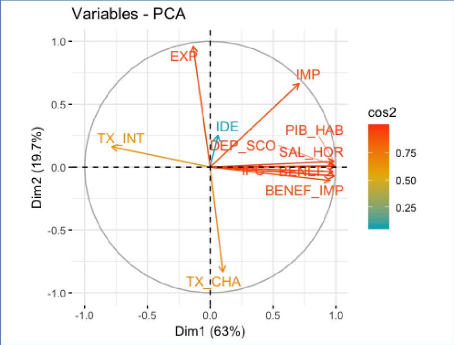
A partir du graphique 17 représentant le cercle de corrélation, les variables IDE, IMP, PIB_HAB, DEP_SCO, SAL_HOR, BENEF, BENEF_IMP, IPC et TX_CHA ont une corrélation positive avec la dimension 1. En revanche, les variables TX_INT et EXP sont corrélés négativement car elles se situent sur la partie gauche du cercle. Par exemple, les variables EXP, IMP et BENEF_IMP font parties des variables qui sont très bien représentées car leurs flèches sont très proches du cercle. Dans le cas de la seconde dimension, les variables IPC, BENEF, BENEF_IMP et TX_CHA sont corrélées négativement tandis que les variables SAL_HOR, DEP_SCO, PIB_HAB, IMP, IDE, EXP et TX_INT sont corrélés positivement. La somme des dimensions dépasse les 80%, ce qui permet d'affirmer que le modèle est bien représenté. Cependant, la variable à expliquer est très mal représentée car sa flèche est proche de l'origine du cercle. Pour conclure sur l'analyse en composante principale, il est possible de dire que le modèle semble plutôt satisfaisant et le choix des variables explicatives semble pertinent.

42

Graphique 18 : Représentation des observations

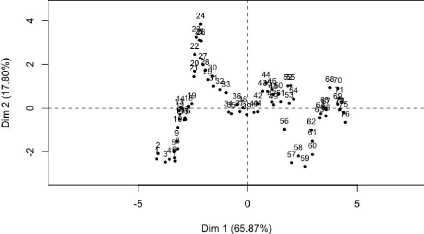
D'après le graphique 18, nous observons que les observations 75 et 76 contribuent très fortement à l'axe 1. En effet, ces deux observations correspondent au troisième et quatrième trimestre 2013. Par conséquent, on peut dire que les investissements directs étrangers ont été satisfaisants sur ces deux trimestres.

En revanche, pour l'axe 2, l'observation 24 semble la plus contributive. Elle représente le quatrième trimestre 2010. Ce point est le plus contributif car il s'agit du point le plus haut sur l'axe 2. Globalement, les observations les moins bien représentées sont celles qui correspondent à la période de crise économique.

43

V- Etude économétrique du sujet

Nous allons tout d'abord, présenter le modèle de régression multiple d'un point de vue théorique. Ensuite, nous réaliserons différents modèles dans le cadre de cette étude.

V.1 Modèle théorique RLM

V.1.1 Modèle de régression multiple

Le modèle de Régression Linéaire Multiple (RLM) se définit avec 12 variables explicatives :

???? = ?? + ? j =???? ?????????? + ???? pour i = 1,...,76

Avec :

· ???? : La variable à expliquer

· ??????, ... , ???????? : Les variables exogènes 1,...,12

· ?? : ????, ... , ?????? : Les paramètres du modèle

· ???? : L'erreur de spécification pour chaque année

· 76 : Le nombre de période de référence

On peut le réécrire sous forme matricielle :

??= ???? + ??

Avec :

Y1

1

X21

X31 ...

X121

á

E1

Y2

1

X22

X32 ...

X122

02

E2

Y =

Y3

; X =

1

X23

X33 ...

X123

; 0 _

03

;

E_

E3

...

...

...

... ...

...

...

...

Y76

1

X276

X376 ...

X12,76

B12

E76

44

V.1.2 Hypothèses du modèle

Il y a plusieurs hypothèses qui doivent être vérifiées dans le cadre d'un modèle de régression multiple. Les hypothèses à vérifier sont les suivantes :

· L'hypothèse fondamentale : E(ei) = 0 pour i = 1,..., co . L'espérance mathématique de l'erreur est nulle et les erreurs se compensent sur la totalité de l'échantillon.

· L'hypothèse d'homoscédasticité : Var(ei) = Qi ² pour i = 1,..., co. La variance de l'erreur est constante. On peut donc dire (du fait de la nullité de son espérance) que : E(ei²) = Qi².

· L'hypothèse de non-corrélation du terme d'erreur : E(eie1) = 0 pour i*j. Les erreurs sont indépendantes d'un élément à l'autre de l'échantillon.

· L'hypothèse de non-corrélation entre les variables exogènes et le terme d'erreur : les erreurs sont indépendantes des 12 variables explicatives.

· L'hypothèse de non-colinéarité des variables explicatives : si deux variables exogènes sont parfaitement colinéaires alors on dira que la matrice carrée X'X n'est plus inversible et donc la méthode des Moindres Carrés Ordinaires (MCO) n'est plus valide.

· L'hypothèse de normalité des erreurs : le terme d'erreur (e) suit une loi normale N(0, Q_i² )⁶³.

V.1.3 Estimation des paramètres du modèle

Il est important de rappeler que pour estimer le vecteur II par un vecteur b composé des estimateurs respectifs a, b1,.., b12 des paramètres a, II 1, ... , II12, la méthode des MCO sera appliquée. Pour cela, nous allons minimiser les carrés des erreurs par rapport à II. Nous allons donc résoudre le programme suivant :

76

Min Iei^2 i=1

= Min e^'e = Min (Y - XII)^'(Y - XII) = Min(Y^'Y - 2II^'X^'XII)

Ainsi, en différenciant cette quantité par rapport à la valeur de f.?, on obtient donc :

dII(e^'e) = -2X^'Y + 2X'XII

63 MIGNON V. « Econométrie : Théorie et application ». Chapitre 3. P 93-95. Consulté le 19 février 2019.

45

On suppose que les conditions de second ordre sont vérifiées. Pour cela, on admet que la matrice X'X est définie positive. La dérivée calculée ci-dessus s'annule bien en un point de minimum. Ce point est atteint pour -2X^'Y + 2X^'Xb = O, soit en b = (X^'X)^-1X'Y.

Soulignons, que ce minimum ne peut être atteint que dans l'hypothèse où la matrice X'X (matrice carrée d'ordre 12) est inversible. Pour que cette matrice soit inversible, deux variables explicatives ne doivent pas être parfaitement corrélées. En effet, X'X est la matrice des produits croisés des variables exogènes. De plus, s'il y a une colinéarité parfaite entre deux variables alors X'X ne sera plus invisible et par conséquent, la méthode MCO ne fonctionne plus.

Lorsque le vecteur b est obtenu, le modèle estimé s'écrit sous la forme :

12

+ ei

Yi= a+ LbjXji

j=1

Avec : ei résidu à la date i qui représente l'écart entre la valeur observée de la variable endogène et sa valeur estimée par le modèle.

V.1.4 Propriétés des estimateurs

On a démontré précédemment qu'on pouvait estimer les paramètres du modèle définie par : b = (X^'X)^-1X'Y.

Or, nous savons que le modèle théorique se présente sous la forme : Y = XII + E.

On obtient donc : b = (X^'X)^-1X^'(XII + E) = (X^'X)^-1X^'XII + (X^'X)^-1X^'E = II + (X^'X)^-1X'E.

L'espérance mathématique de b est donc la suivante : E(b) = E(II + (X^'X)^-1X^'e) = II + (X^'X)^-1X'E(e) par linéarité de l'espérance mathématique ⁶⁴ . Or, l'hypothèse fondamentale de la nullité de l'espérance de l'erreur est la suivante : E(e) = O. On peut donc

64 MIGNON V. « Econométrie : Théorie et application ». Chapitre 3. P 98-100. Consulté le 19 février 2019.

46

en déduire que : E(b) = j? et par conséquent, les estimateurs sont bien sans biais. On dira que l'estimateur est d'autant plus juste que le nombre d'observations est grand⁶⁵.

De plus, d'après le théorème de Gauss-Markov, l'estimateur des moindres carrés est un excellent estimateur linéaire sans biais. On dira même que cet estimateur est Best Linear Unbiaised Estimator (BLUE). Cela signifie qu'il fournit les variances les plus faibles parmi l'ensemble des estimateurs. On peut donc dire que cet estimateur est efficace et convergent⁶⁶.

V.2 Application économétrique du modèle

V.2.1 Premier modèle étudié

Tout d'abord, le premier modèle réalisé prendra en compte l'ensemble des variables étudiées dans ce dossier.

Tableau 4 : Régression linéaire 1 nommée « reg1 »

Variables	Estimate	Std.Error	T value	Pr (>|t|)	Significativité
CONSTANTE	4 375,503	1 545,775	2,831	0,006	**
PIB HAB	23,240	7,370	3,153	0,002	**
TX_CHA	-232,620	321,811	-0,723	0,472
BENEF	31,368	19,606	1,600	0,115
TX INT	-33,420	35,409	-0,944	0,349
IPC	-50,686	34,077	-1,487	0,142
BENEF IMP	0,168	0,201	0,838	0,405
EXP	-82,262	61,951	-1,328	0,189
IMP	26,216	48,838	0,537	0,593
SAL HOR	-192,080	88,030	-2,182	0,033	*
DEP_SCO	30,742	42,371	0,726	0,471
DUMMIES EURO	135,249	178,332	0,758	0,451
DUMMIES_CRISE	-63,550	104,478	-0,608	0,545
			Valeur
Multiple R-squared			0,427
Adjusted R-squared			0,318
F-statistic			3,919
P-value			0,000

D'après le tableau 4, nous remarquons que la qualité du modèle semble correcte mais pas suffisante. En effet, le coefficient de détermination (R²) est de 0,427. Cela signifie qu'environ 42,7% de la variance de l'IDE est expliquée par les variables explicatives choisies.

65 CREPON B. et JACQUEMET N. « Econométrie : méthode et applications ». Chapitre 2. Page 46. Consulté le 19 février 2019.

66 BOURBONNAIS R. « Econométrie ». Dunod. 9^ème édition. Consulté le 19 février 2019.

47

La constante est significative au seuil de risque de 1%. La variable PIB_HAB est également significative au seuil de risque de 1%. Lorsque le PIB_HAB augmente d'une unité, l'IDE augmente de 23,240 dollars. La croissance du PIB_HAB et les IDE sont fortement corrélés positivement. En effet, l'augmentation des IDE dans un pays est supérieure à sa croissance économique. L'augmentation des IDE d'une économie va permettre de manière générale de pouvoir produire plus, donc d'augmenter la productivité afin de créer de l'emploi, ce qui va améliorer le niveau de vie et donc le PIB par habitant. Concernant la variable SAL_HOR, cette dernière est significative au seuil de risque de 5%. On peut donc dire que lorsque le SAL_HOR augmente d'un point, l'IDE baisse de 192,080 dollars. L'un des objectifs principaux des IDE est de réduire ses coûts de production, et donc d'investir dans les pays ou les zones dans lesquels les coûts sont plus faibles que ceux où l'entreprise est implantée. Ainsi, les entreprises gagnant en productivité à moindre coût dans les pays moins strict en matière de fiscalité vont pouvoir répartir une partie de ses gains dans les salaires. On peut donc voir que les entreprises étrangères pratiquant des IDE dans un pays proposeront un salaire plus élevé à ses employés que les entreprises locales. Les IDE ont donc un impact positif sur les salaires qu'ils augmentent. Enfin, l'hypothèse H0 selon laquelle au moins une des variables explicatives à un impact significatif permet d'accepter le test de Fisher car la p-value est de 0,000 et elle est donc bien inférieure à 0,05.

Tableau 5 : Test des résidus du modèle « reg1 »

MODELE	SHAPIRO-WILK	BREUSCH-PAGAN	RAMSEY
Reg1	W = 0,963 p-value = 0,026	BP = 22,431 p-value = 0,033	RESET = 0,428 p-value = 0,654

D'après le test de Shapiro-Wilk dans le cadre du premier modèle de régression, l'hypothèse H0 de normalité des résidus est refusée car la p-value est inférieure à 0,05. On va donc modifier la forme fonctionnelle du modèle en passant par une estimation semi-logarithmique. Le test de Breusch-Pagan permet de vérifier l'hypothèse d'homoscédasticité des résidus. Dans ce modèle, on refuse l'hypothèse d'homoscédasticité des résidus au seuil de risque de 5% pour l'unique raison que la p-value est inférieure à 0,05. Nous allons essayer de résoudre cela par l'estimation d'un modèle semi-logarithmique. Enfin, le test de Ramsey permet de vérifier la linéarité du modèle. Ce test ne permet cependant pas d'en déduire s'il

48

s'agit du meilleur modèle à estimer. Dans notre cas, la forme fonctionnelle linéaire du modèle spécifié est acceptée au seuil de 5% car la p-value du test est de 0,654, ce qui est supérieure à 0,05. Par conséquent, on accepte l'hypothèse H0 au seuil de risque de 5%.

Tableau 6 : VIF du modèle « reg1 »

VARIABLE	VIF
PIB_HAB	824,854
TX_CHA	8,635
BENEF	322,454
TX_INT	9,487
IPC	340,665
BENEF_IMP	25,014
EXP	22,299
IMP	31,677
SAL_HOR	3274,557
DEP_SCO	1162,316
DUMMIES_EURO	17,036
DUMMIES_CRISE	4,010

La Variance Inflation Factor (VIF) permet de juger la colinéarité entre les variables explicatives du modèle. L'ensemble de nos variables sauf DUMMIES_CRISE, TX_CHA et TX_INT ont de la forte colinéarité car leurs valeurs dépassent 10.

Graphique 19 : Analyse de la normalité des résidus

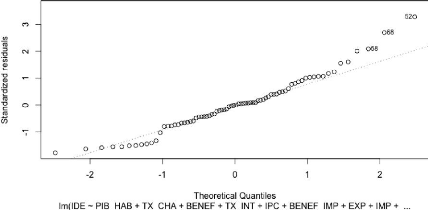
49

Ce modèle ne semble pas très satisfaisant. Les différents tests confirment ce que l'on peut supposer au vu du graphique 19. A priori la loi normale n'est pas suivie (il faut supprimer les observations 58, 68 et 52). Le modèle présente des problèmes au niveau de la normalité des résidus (test de Shapiro-Wilk). Le test de Breusch-Pagan a indiqué que le modèle refuse l'hypothèse d'homoscédasticité des résidus. La forme fonctionnelle du modèle va donc être modifiée en passant par un modèle semi-logarithmique. D'après le VIF, nous avons un souci de multicolinéarité. En revanche le modèle ne présente pas de problème de forme fonctionnelle (test de Ramsey). Les différents graphiques de ce modèle (reg1) ainsi que les distances de Cooks se trouvent en fin de dossier (annexe 4).

A présent, nous allons procéder à l'étude du modèle semi-logarithmique. Ce modèle sera réalisé avec les mêmes variables. Nous allons seulement tester le logarithme de ces variables.

Tableau 7 : Régression semi-logarithmique 1 nommée « reg1sl »

Variables	Estimate	Std.Error	T value	Pr (>|??|)	Significativité
CONSTANTE	7,695	30,838	0,250	0,804
Log(PIB HAB)	12,678	16,384	0,774	0,442
Log(TX CHA)	-2,090	1,693	-1,235	0,222
Log(BENEF)	26,373	12,051	2,188	0,033	*
Log(TX INT)	0,417	0,285	1,462	0,149
Log(IPC)	-3,991	13,951	-0,286	0,776
Log(BENEF IMP)	1,283	0,735	1,744	0,087	.
Log(EXP)	0,515	6,788	0,076	0,940
Log(IMP)	-3,701	5,273	-0,702	0,486
Log(SAL HOR)	-60,322	25,713	-2,346	0,022	*
Log(DEP_SCO)	17,810	9,283	1,919	0,060	.
DUMMIES EURO	0,126	0,742	0,169	0,866
DUMMIES_CRISE	0,160	0,506	0,316	0,753
			Valeur
Multiple R-squared			0,388
Adjusted R-squared			0,257
F-statistic			2,961
P-value			0,003

D'après le tableau 7, nous observons que la qualité explicative du modèle s'est légèrement dégradée. Le coefficient de détermination est de 0,388. Nous pouvons donc dire que 38,8% de la variance de l'IDE est expliquée par les variables explicatives choisies. En revanche, les variables BENEF et SAL_HOR ont un impact significatif au seuil de risque de 5% sur l'IDE. Par exemple, lorsque le BENEF augmente d'un point, l'IDE augmente de

50

log(26,373). Les IDE des entreprises, principalement celle étant dans des pays ou des zones à forte pression fiscale facilite l'investissement dans des pays où le contrôle fiscal est bien moins important et ainsi avoir une plus grande productivité pour des coûts réduits et de ce fait, faire des économies d'échelles. A travers les IDE, les entreprises essaient d'augmenter leurs bénéfices. Les variables BENEF_IMP et DEP_SCO ont un impact significatif au seuil de risque de 10% sur l'IDE. Par exemple, lorsque les DEP_SCO augmente d'une unité, l'IDE augmente de log(17,810). Soulignons que le fonctionnement de l'éducation national étant très liée à tout ce qui est de l'ordre des collectivités, leurs budgets provenant ainsi de l'Etat, des régions et des départements. Le niveau d'éducation favorisant à long terme la croissance, l'augmentation des IDE dans un pays et l'imposition auxquels ils sont soumis, permet à l'Etat et aux collectivités territoriales d'augmenter leur budget et ainsi d'avoir la possibilité de le réinvestir dans l'éducation. Les résultats de l'éducation étant eux aussi bénéfiques aux IDE à moyen et long terme. De plus, dans les pays à forte fiscalité, les IDE permettent d'échapper à l'impôt car étant tourné vers des pays où la fiscalité est moins contraignante. En effet, plus un pays recevra des IDE, moins il devra mettre en place une politique de fiscalité lourde pour éviter une baisse de ceux-ci. Ainsi, les IDE devrait avoir un impact positif sur les bénéfices après impôts avec des marges plus importantes pour les entreprises ayant investis dans un pays afin de moins payer d'impôts. On est donc en contradiction avec ce que l'on avait supposé dans la partie économique. Elle peut vendre au même prix avec les impôts en moins ce qui lui permet de faire plus de bénéfices. Enfin, le test de Fisher est accepté car la p-value est inférieure à 0,05. Soulignons que les résultats obtenus avec le premier modèle semi-logarithmique sont différents du modèle linéaire multiple. Le modèle logarithmique semble donc différent.

Tableau 8 : Test des résidus du modèle « reg1sl »

MODELE	SHAPIRO-WILK	BREUSCH-PAGAN	RAMSEY
Reg1sl	W = 0,936 p-value = 0,0012	BP = 10,962 p-value = 0,532	RESET = 3,694 p-value = 0,031

Dans ce modèle, nous constatons que l'hypothèse H0 de normalité des résidus est refusée (d'après le test de Shapiro-Wilk). De plus, la forme fonctionnelle linéaire du modèle spécifié est rejetée au seuil de 5% (d'après le test de Ramsey). En revanche, l'hypothèse

51

d'homoscédasticité des résidus est acceptée au seuil de risque de 5% (d'après le test de Breusch-Pagan). Les différents graphiques de ce modèle (reg1sl) se trouvent en fin de dossier (annexe 4).

Tableau 9 : VIF du modèle « reg1sl »

VARIABLE	VIF
PIB_HAB	1236,555
TX_CHA	9,730
BENEF	262,280
TX_INT	13,129
IPC	420,234
BENEF_IMP	18,021
EXP	30,771
IMP	41,682
SAL_HOR	2360,907
DEP_SCO	1056,814
DUMMIES_EURO	16,588
DUMMIES_CRISE	4,648

Dans ce modèle, l'ensemble des variables sauf TX_CHA et DUMMIES_CRISE ont de la forte colinéarité car leurs valeurs dépassent 10.

L'ensemble des graphiques de ce modèle se trouve en fin de dossier (annexe 4). Ce modèle semi-logarithmique est très similaire au modèle de régression 1 (reg1). Cependant, il semble moins bon à cause des différents tests effectués. Dans ce dernier, plus de variables sont ressorties significatives. Nous allons à présent étudier un nouveau modèle qui ne prendra pas en compte les variables corrélées fortement négativement à la variable TX_INT. Ce modèle ne prendra donc pas en compte les variables PIB_HAB, BENEF, IPC, BENEF_IMP, SAL_HOR et DEP_SCO.

V.2.2 Second modèle étudié

Le second modèle réalisé ne prend pas en compte les variables corrélées fortement négativement à la variable TX_INT. Les variables PIB_HAB, BENEF, IPC, BENEF_IMP, SAL_HOR et DEP_SCO ne figurent donc pas dans ce modèle. Nous avons réalisé ce choix afin de voir si notre modèle sans les variables corrélées négativement est meilleur que le modèle avec l'ensemble des variables.

52

Tableau 10 : Régression linéaire 2 nommée « reg2 »

Variables	Estimate	Std.Error	T value	Pr (>|??|)	Significativité
CONSTANTE	-1 090,780	803,118	-1,358	0,179
TX_CHA	251,758	276,115	0,912	0,365
TX INT	26,749	21,244	1,259	0,212
EXP	45,394	48,028	0,945	0,348
IMP	-3,887	29,615	-0,131	0,896
DUMMIES_EURO	83,380	86,270	0,966	0,337
DUMMIES CRISE	94,066	77,894	1,208	0,231
			Valeur
Multiple R-squared			0,19
Adjusted R-squared			0,12
F-statistic			2,71
P-value			0,02

D'après le tableau 10, ce modèle semble décevant. En effet, le coefficient de détermination (R²) est de 0,19. Cela signifie qu'environ 19% de la variance de l'IDE est expliquée par les variables explicatives choisies. De plus, aucune des variables ne sont significative. Ce modèle ne semble pas concluant. Enfin, l'hypothèse H0 selon laquelle au moins une des variables explicatives à un impact significatif permet d'accepter le test de Fisher car la p-value est de 0,02 et elle est donc bien inférieure à 0,05.

Tableau 11 : Test du modèle « reg2 »

MODELE	SHAPIRO-WILK	BREUSCH-PAGAN	RAMSEY
Reg2	W = 0,954 p-value = 0,008	BP = 11,841 p-value = 0,066	RESET = 0,039 p-value = 0,961

Dans ce modèle, l'hypothèse H0 du test de Shapiro-Wilk est refusée. La forme fonctionnelle du modèle va donc être modifiée en passant par une estimation semi-logarithmique. D'après le test de Breusch-Pagan, l'hypothèse d'homoscédasticité des résidus est acceptée au seuil de risque de 5% car la p-value est supérieure à 0,05. Enfin, d'après le test de Ramsey, nous observons que la forme fonctionnelle linéaire du modèle est acceptée au seuil de 5% car la p-value est supérieure à 0,05. Les différents graphiques de ce modèle (reg2) se trouvent en fin de dossier (annexe 4).

53

Tableau 12 : VIF du modèle « reg2 »

VARIABLE	VIF
TX_CHA	4,926
TX_INT	2,646
EXP	10,385
IMP	9,026
DUMMIES_EURO	3,089
DUMMIES_CRISE	1,727

Dans ce modèle, l'ensemble des variables sauf EXP n'a pas de la forte colinéarité car leurs valeurs sont en dessous de 10. L'ensemble des graphiques de ce modèle se trouve en fin de dossier (annexe 4).

Nous allons poursuivre avec l'étude du modèle semi-logarithmique. Il sera réalisé avec les mêmes variables que le modèle. Le logarithme de ces variables va être testé.

Tableau 13 : Régression semi-logarithmique 2 nommée « reg2sl »

Variables	Estimate	Std.Error	T value	Pr (>|??|)	Significativité
CONSTANTE	3,646	7,458	0,489	0,627
Log(TX_CHA)	-0,333	1,261	-0,264	0,793
Log(TX_INT)	0,246	0,148	1,663	0,101
Log(EXP)	-2,974	4,523	-0,657	0,513
Log(IMP)	3,357	3,152	1,065	0,291
DUMMIES EURO	0,214	0,373	0,573	0,569
DUMMIES_CRISE	0,195	0,370	0,527	0,600
			Valeur
Multiple R-squared			0,172
Adjusted R-squared			0,092
F-statistic			2,152
P-value			0,060

D'après le tableau 13, nous pouvons voir que la qualité explicative du modèle semble décevante. Le coefficient de détermination est de 0,172. Nous pouvons donc dire que 17,2% de la variance de l'IDE est expliquée par les variables explicatives choisies. Nous pouvons constater qu'aucune variable n'est significative comme dans le modèle de régression 2 (reg2). De plus, le test de Fisher est refusé car la p-value est supérieure à 0,05. Nous n'allons donc pas conserver ce modèle. Les différents graphiques de ce modèle (reg2sl) se trouvent en fin de dossier (annexe 4).

54

V.2.3 Troisième modèle étudié

Le troisième modèle réalisé ne prend pas en compte les variables corrélées fortement positivement à la variable IPC. Les variables PIB_HAB, BENEF, BENEF_IMP, SAL_HOR et DEP_SCO ne figurent donc pas dans ce modèle. Nous allons donc effectuer la nouvelle estimation afin d'observer si notre modèle est meilleur. En effet, ce choix est basé sur le fait que l'intégration des variables corrélées positivement peut entraîner une détérioration du modèle.

Tableau 14 : Régression 3 nommée « reg3 »

Variables	Estimate	Std.Error	T value	Pr (>|??|)	Significativité
CONSTANTE	79,586	1 104,672	0,072	0,943
TX_CHA	341,539	279,738	1,221	0,226
TX INT	-2,452	28,434	-0,086	0,932
IPC	-16,107	10,548	-1,527	0,131
EXP	-19,595	63,832	-0,307	0,760
IMP	59,810	50,997	1,173	0,245
DUMMIES EURO	92,999	85,681	1,085	0,282
DUMMIES_CRISE	82,229	77,542	1,060	0,293
			Valeur
Multiple R-squared			0,217
Adjusted R-squared			0,137
F-statistic			2,701
P-value			0,016

D'après le tableau 14, nous remarquons que la qualité du modèle semble décevante. En effet, le coefficient de détermination (R²) est de 0,217. Cela signifie qu'environ 21,7% de la variance de l'IDE est expliquée par les variables explicatives choisies. De plus, aucune variable n'est significative. Enfin, l'hypothèse H0 selon laquelle au moins une des variables explicatives à un impact significatif permet d'accepter le test de Fisher car la p-value est de 0,016 et elle est donc bien inférieure à 0,05. Ce modèle n'est donc pas conservé. Les différents graphiques de ce modèle (reg3) se trouvent en fin de dossier (annexe 4).

V.2.4 Quatrième modèle étudié

Le quatrième modèle réalisé prend en compte uniquement les variables qui étaient significatives dans le cadre du premier modèle. Nous avons donc refait un modèle avec uniquement les variables PIB_HAB et SAL_HOR. Le but d'enlever les variables non significatives de notre meilleur modèle (reg1) est d'observer une éventuelle amélioration du coefficient de détermination.

55

Tableau 15 : Régression 4 nommée « reg4 »

Variables	Estimate	Std.Error	T value	Pr (>|??|)	Significativité
CONSTANTE	79,586	1 104,672	0,072	0,943	***
PIB_HAB	341,539	279,738	1,221	0,226	***
SAL HOR	-2,452	28,434	-0,086	0,932	***
			Valeur
Multiple R-squared			0,337
Adjusted R-squared			0,319
F-statistic			18,57
P-value			3,022e-17

D'après le tableau 15, nous observons que l'ensemble des variables du modèle est significatif au seuil de risque de 1%. En revanche, le coefficient de détermination (R²) semble légèrement moins bon que celui du premier modèle. Nous n'allons donc pas conserver ce modèle car non seulement, le coefficient de détermination est moins bon mais de plus, étant donné que beaucoup de variables ont été supprimées, ce modèle ne semble donc pas représentatif. Les différents graphiques de ce modèle (reg4) se trouvent en fin de dossier (annexe 4).

V.2.5 Récapitulatif des modèles RLM

Le tableau ci-dessous résume les résultats que l'on a obtenus avec les différents modèles étudiés. Il va donc permettre de déterminer le meilleur modèle parmi l'ensemble des modèles que nous avons réalisé. Nous allons également observer les résultats du test de Shapiro des résidus, du test de Breush-Pagan et du test de Ramsey pour effectuer notre choix.

Tableau 16 : Récapitulatif des modèles

	Variables significatives	Coefficient de détermination (R^2)	Test de Shapiro des résidus (p-value)	Test de Breush-Pagan (p-value)	Test de Ramsey (p-value)
Reg1	CONSTANTE(**) PIB_HAB(**) SAL_HOR(*)	0,427	0,026	0,033	0,654
Reg1sl	BENEF(*) BENEF_IMP(.) SAL_HOR(*) DEP_SCO(.)	0,388	0,002	0,532	0,031

56

Reg2

		0,19	0,008	0,066	0,961
Reg2sl		0,172	2,201e-05	0,715	0,117
Reg3		0,217	0,009	0,157	0,361
	CONSTANTE(***)
Reg4	PIB_HAB(***)	0,337	0,232	0,000	0,976
	SAL_HOR(***)

D'après le tableau 16, nous ressortons que les modèles Reg1, Reg1sl et Reg4 sont les seuls modèles ayant des variables significatives. Le coefficient de détermination est également le plus élevé pour ces trois modèles. De plus, le test de Ramsey est accepté pour le modèle reg1. Nous allons donc retenir le premier modèle (reg1) comme notre modèle final et qui est le plus représentatif pour notre étude. Etant donné qu'il s'agit du modèle prenant en compte l'ensemble des variables, on peut donc dire que les variables ont correctement étaient choisies, ce qui confirme donc l'analyse de la partie économique.

V.3 Détermination du modèle ARIMA (p, d, q)(P, D, O)s pour l'IDE

Tout d'abord, soulignons que la série IDEt concerne l'investissement direct étranger en France du premier trimestre 1995 au quatrième trimestre 2013. Il s'agit donc d'une série temporelle car la série est exprimée en année. Nous allons commencer par déterminer le modèle ARIMA pour notre série IDEt.

57

Graphique 20 : Représentation de l'investissement direct étranger en France

Source : L'auteur sur Gretl, d'après les données de « fred.stlouisfed.org ».

D'après le graphique 20, nous observons que notre série sur l'investissement direct étranger semble stationnaire au niveau de la moyenne. Rappelons, que pour pouvoir construire les modèles ARIMA, la série doit être obligatoirement stationnaire au niveau de la variance et de la moyenne.

Graphique 21 : Corrélogramme pour l'investissement direct étranger

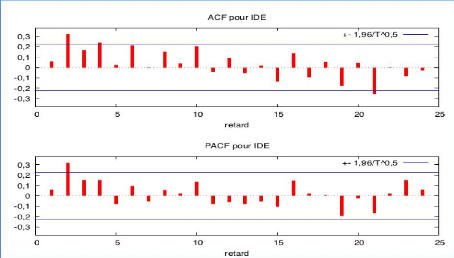
58

Nous observons très clairement que cette série est stationnaire. D'après le graphique 23, nous observons une décroissance rapide des corrélations

V.3.1 Estimation de notre modèle

Tout d'abord, représentons le tableau de la fonction d'autocorrélation (FAC) et d'autocorrélation partielle (FACP) pour notre série IDEt portant sur l'investissement direct étranger. Nous n'avons pas effectué de différenciation car notre série brute était stationnaire.

Tableau 17 : FAC et FACP

Fonction d'auto-corrélation pour IDE ***, **, * indicate significance at the 1%, 5%, 10% levels using standard error 1/T^0,5
RETARD	ACF	PACF	Q	P. Critique
1	0,057	0,057	0,254	0,615
2	0,319 ***	0,317 ***	8,408	0,015
3	0,165	0,151	10,627	0,014
4	0,237 **	0,149	15,261	0,004
5	0,025	-0,079	15,315	0,009
6	0,216 *	0,094	19,257	0,004
7	-0,003	-0,053	19,258	0,007
8	0,152	0,054	21,274	0,006
9	0,041	0,025	21,421	0,011
10	0,204 *	0,136	25,153	0,005
11	-0,045	-0,081	25,338	0,008
12	0,090	-0,058	26,095	0,010
13	-0,053	-0,081	26,363	0,015
14	0,016	-0,052	26,388	0,023
15	-0,139	-0,105	28,259	0,020
16	0,134	0,145	30,034	0,018
17	-0,097	0,021	30,972	0,020
18	0,052	0,007	31,252	0,027
19	-0,175	-0,192 *	34,444	0,016
20	0,043	-0,025	34,645	0,022
21	-0,255 **	-0,166	41,648	0,005
22	0,005	0,023	41,651	0,007
23	-0,084	0,151	42,442	0,008
24	-0,030	0,056	42,543	0,011

D'après le tableau 17, nous observons une corrélation significative et positive au seuil de risque de 1% concernant le second retard. Cette corrélation est visible aussi bien pour la FAC et la FACP. Nous observons également une corrélation au seuil de risque de 5% pour les retards quatre et vingt-un au niveau de la FAC. Notons que cette corrélation est négative pour le retard vingt-un. Enfin, nous observons pour les retards six et dix, une corrélation positive

59

au seuil de risque de 10% dans le cadre de la FAC uniquement ainsi qu'une corrélation négative au même seuil pour le retard dix-neuf dans le cadre de la FACP uniquement. Les autocorrélations significatives pour la FAC nous montre que le modèle peut être MA (2). Dans le cadre de la FACP, nous allons être amené à tester le modèle AR (2) grâce aux corrélations significatives. Il y a donc quatre modèles à tester, AR (2), MA (2), ARIMA (1, 0, 1) et enfin ARIMA (2, 0, 1).

V.3.1.1 Modélisation du premier modèle AR (2) Nous rappelons tout d'abord que l'équation du modèle AR (2) est :

ide_t = S + a_t + _{çp1idet_1} + çp2idet_2 où :
ide_t représente la série IDE_t
a_t représente le bruit blanc
S représente la tendance centrale de notre série

Nous allons à présent vérifier à partir du modèle obtenu sous le logiciel GRETL la significativité des paramètres.

Tableau 18 : Modélisation AR (2) avec la constante

Evaluations de la fonction : 20
Evaluations du gradient : 8
Modèle 1 : ARMA utilisant les observations 1995 : 1-2013 : 4 (T=76)
Paramètres	Coefficient		Erreur Std.		Z		P. critique		Significativité
CONSTANTE	224,728		33,698		6,669		2,58e-11		***
PHI_1	0,043		0,109		0,394		0,693
PHI 2	0,323		0,109		2,959		0,003		***
					Valeur
Moyenne variable dépendante					229,147
Ecart type variable dépendante					200,893
Moyenne des innovation					1,380
Ecart type des innovations					188,465
Log de vraisemblance					-506,109
Critère d'Akaike					1 020,217
Critère de Schwarz					1 029,540
Hannan-Quinn					1 023,943
Modèle		Réel		Imaginaire		Modulo		Fréquence
AR
RACINE 1		-1,828		0,000		1,828		0,500
RACINE 2		1,695		0,000		1,695		0,000

60

Dans un premier temps, nous avons modélisé le modèle AR (2). D'après le tableau 18, nous observons que la probabilité de la constante est inférieure à 0,05. Par conséquent, elle est significative donc nous la conservons dans le modèle. De plus, PHI_2 est significatif au seuil de risque de 1%. La valeur de PHI_2 est égale à 0,323. En revanche, PHI_1 n'est pas significatif donc nous allons observer notre second modèle. Les graphiques de ce modèle AR (2) se trouvent en fin de dossier (annexe 5).

V.3.1.2 Modélisation du second modèle MA (2) Pour commencer, rappelons que l'équation du modèle MA (2) est :

???????? = ?? + ???? - ??1????-1 - ??2????-2 où :

???????? représente la série ????????

???? Représente le bruit blanc

?? Représente la tendance centrale de notre série

Nous allons à présent contrôler à partir du modèle réalisé sous le logiciel GRETL la significativité des paramètres.

Tableau 19 : Modélisation MA (2) avec la constante

Evaluations de la fonction : 38
Evaluations du gradient : 13
Modèle 1 : ARMA utilisant les observations 1995 : 1											- 2013 : 4 (T=76)
Paramètres		Coefficient			Erreur Std.			Z			P. critique			Significativité
CONSTANTE		227,566			26,912			8,456			2,77e-17			***
THETA_1		-0,030			0,119			-0,254			0,800
THETA 2		0,263			0,104			2,524			0,012			**
											Valeur
Moyenne variable dépendante											229,147
Ecart type variable dépendante											200,893
Moyenne des innovation											0,730
Ecart type des innovations											191,279
Log de vraisemblance											-507,195
Critère d'Akaike											1 022,390
Critère de Schwarz											1 031,713
Hannan-Quinn											1 026,116
Modèle	Réel			Imaginaire			Modulo			Fréquence
MA
RACINE 1	0,058			-1,949			1,950			-0,245

61

RACINE 2

0,058

1,949

1,950

0,245

Ensuite, nous avons modélisé le modèle MA (2). D'après le tableau 19, nous observons que la probabilité de la constante est inférieure à 0,05. Par conséquent, elle est significative donc nous la conservons dans le modèle. De plus, THETA_2 est significatif au seuil de risque de 5%. La valeur de THETA_2 est égale à 0,263. En revanche, THETA_1 n'est pas significatif donc nous allons observer notre troisième modèle. Les graphiques de ce modèle MA (2) se trouvent en fin de dossier (annexe 5).

V.3.1.3 Modélisation du troisième modèle ARIMA (1, 0, 1) Nous rappelons tout d'abord que l'équation du modèle ARIMA (1, 0, 1) est :

ide_t = u + a_t - 81at_1 + (P1idet_1 où :
ide_t représente la série IDE_t
a_t représente le bruit blanc
u représente la tendance centrale de notre série

Nous allons à présent s'assurer à partir du modèle obtenu sous le logiciel GRETL que les conditions de stationnarités sont vérifiées ainsi que la significativité des paramètres. Nous essayerons également d'observer si nos résidus suivent bien un bruit blanc.

Tableau 20 : Modélisation ARIMA (1, 0, 1) avec la constante

Evaluations de la fonction : 59
Evaluations du gradient : 19
Modèle 1 : ARMA utilisant les observations 1995 : 1							- 2013 : 4 (T=76)
Paramètres	Coefficient		Erreur Std.		Z		P. critique		Significativité
CONSTANTE	207,645		56,736		3,660		0,000		***
PHI 1	0,920		0,076		12,100		1,12e-33		***
THETA 1	-0,786		0,104		-7,588		3,26e-14		***
							Valeur
Moyenne variable dépendante							229,147
Ecart type variable dépendante							200,893
Moyenne des innovation							4,385
Ecart type des innovations							190,174
Log de vraisemblance							-506,815
Critère d'Akaike							1 021,630
Critère de Schwarz							1 030,953
Hannan-Quinn							1 025,356

62

Modèle

	Réel	Imaginaire	Modulo	Fréquence
AR
RACINE 1	1,087	0,000	1,087	0,000
MA
RACINE 1	1,272	0,000	1,272	0,000

Dans ce modèle, nous envisageons des modèle mixtes : ARIMA (1, 0, 1), c'est une combinaison de AR (1) et MA (1). Cela veut dire que la performance présente est déterminée par la performance précédente et la valeur de référence évolue d'une mesure à l'autre. L'objectif essentiel de la modélisation est de déterminer combien de paramètre est nécessaires pour obtenir un modèle effectif. D'après le tableau 20, nous observons que la constante est significative. Par conséquent, elle est conservée dans ce modèle. De plus, PHI_1 et THETA_1 sont également significatifs au seuil de risque de 1%. La valeur de PHI_1 est égale à 0,920 et celle de THETA_1 est égale à -0,786. Comme on est dans un modèle mixte, il faut vérifier aussi les conditions de stationnarité et d'inversibilité avant l'estimation. Ici nous avons :

|ö₁| = |0,920| < 1,

|e₁| = |-0,786| < 1

Donc les conditions de stationnarité et d'inversibilité sont vérifiées.

Nous allons à présent vérifier les résidus de notre modèle à partir d'un corrélogramme. Nous ferons également une représentation de la FAC et de la FACP.

Graphique 22 : Corrélogramme pour les résidus

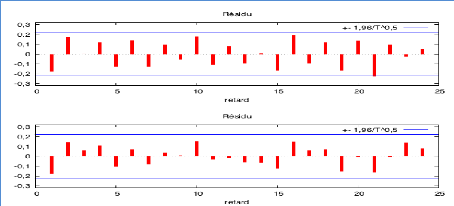
63

Dans cette étape de l'estimation, les vérifications essentielles à réaliser portent sur les résidus. Les valeurs de la fonction d'autocorrélation et d'autocorrélation partielle de la série des résidus doivent être toutes égales à zéro. Cela veut dire qu'ils ont une caractéristique qui correspond à celle d'un bruit blanc. Si les autocorrélations et les autocorrélations partielles ne sont pas nulles, on pourrait dire que le modèle ARIMA est probablement inapproprié. Ici on peut constater qu'aucun de nos résidus ne dépassent le seuil significatif, donc ils ont une caractéristique d'un bruit blanc.

Tableau 21 : FAC et FACP pour les résidus

Fonction d'auto-corrélation résiduelle ***, **, * indicate significance at the 1%, 5%, 10% levels using standard error 1/T^0,5
RETARD	ACF	PACF	Q	P. Critique
1	-0,180	-0,180
2	0,173	0,145
3	0,000	0,056	4,952	0,026
4	0,121	0,111	6,157	0,046
5	-0,127	-0,106	7,497	0,058
6	0,139	0,072	9,136	0,058
7	-0,129	-0,078	10,578	0,060
8	0,093	0,035	11,327	0,079
9	-0,052	0,006	11,568	0,116
10	0,181	0,152	14,521	0,069
11	-0,111	-0,033	15,648	0,075
12	0,082	-0,019	16,268	0,092
13	-0,092	-0,063	17,067	0,106
14	0,007	-0,066	17,072	0,147
15	-0,166	-0,123	19,745	0,102
16	0,194 *	0,148	23,461	0,053
17	-0,092	0,060	24,304	0,060
18	0,120	0,071	25,766	0,057
19	-0,166	-0,154	28,637	0,038
20	0,134	-0,005	30,552	0,032
21	-0,228 **	-0,164	36,148	0,010
22	0,093	-0,006	37,108	0,011
23	-0,030	0,138	37,206	0,016
24	0,048	0,079	37,468	0,021

Dans cette approche de Box et Jenkins, un autre test statistique souvent employé pour évaluer un bruit blanc est le test Q. Ce test dont le but est de vérifier si les résidus sont indépendants entre eux. Nous devons vérifier l'hypothèse H0 d'indépendance entre les résidus. Si la p-value est supérieure à 0,05, on accepte l'hypothèse H0 et on dira que les résidus sont indépendants. Dans le cas où la p-value est inférieure à 0,05, on refuse

64

l'hypothèse H0 et par conséquent, les résidus ne seront pas indépendants. D'après le tableau 21, on constate que la p-value est inférieure à 0,05. Les résidus ne sont donc pas indépendants entre eux.

Graphique 23 : Test de normalité des résidus

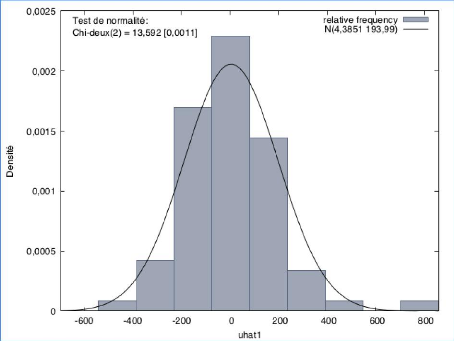
D'après le graphique 23, on peut voir si les résidus suivent une loi normale. On pose l'hypothèse H0 : les résidus suivent une loi normale. Il faut une p-value supérieure à 0,05 pour accepter H0, ici on a une p-value égale à 0,0011, ce qui est inférieure à 0,05, donc on rejette H0 et nos résidus ne suivent pas une loi normale.

65

Graphique 24 : Les valeurs observées et prédites

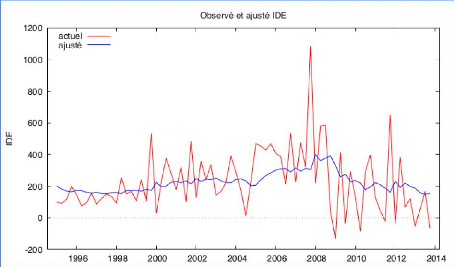
Tout d'abord, si le modèle est bien spécifié, l'ajustement réalisé selon ce modèle doit suivre les évolutions de la série empirique, donc on projette les valeurs observées et les valeurs prédites dans le même graphique. Selon le graphique 24, on constate visuellement que les deux lignes ont des tendances et des volatilités différentes. Nos qualités prédites ne sont pas satisfaisantes.

V.3.1.4 Modélisation du quatrième modèle ARIMA (2, 0, 1) Nous rappelons tout d'abord que l'équation du modèle ARIMA (2, 0, 1) est :

ide_t = u + a_t - 81at_1 + _{çP1idet_1} + çP2idet_2 où :

ide_t représente la série IDE_t

a_t représente le bruit blanc

u représente la tendance centrale de notre série

Nous allons à présent poursuivre avec la vérification des conditions de stationnarité et la significativité des paramètres. Nous essayerons également de vérifier si nos résidus suivent bien un bruit blanc.

66

Tableau 22 : Modélisation ARIMA (2, 0, 1) avec la constante

Evaluations de la fonction : 45
Evaluations du gradient : 16
Modèle 1 : ARMA utilisant les observations 1995 : 1							- 2013 : 4 (T=76)
Paramètres	Coefficient		Erreur Std.		Z		P. critique		Significativité
CONSTANTE	211,699		52,112		4,062		4,86e-05		***
PHI 1	0,534		0,219		2,442		0,015		**
PHI_2	0,294		0,124		2,368		0,018		**
THETA 1	-0,569		0,218		-2,616		0,009		***
							Valeur
Moyenne variable dépendante							229,147
Ecart type variable dépendante							200,893
Moyenne des innovation							3,66324
Ecart type des innovations							184,180
Log de vraisemblance							-504,450
Critère d'Akaike							1 018,901
Critère de Schwarz							1 030,554
Hannan-Quinn							1 023,558
Modèle		Réel		Imaginaire		Modulo		Fréquence
AR
RACINE 1		1,147		0,000		1,147		0,000
RACINE 2		-2,961		0,000		2,961		0,500
MA
RACINE 1		1,756		0,000		1,756		0,000

Dans ce modèle, nous envisageons également des modèle mixtes : ARIMA (2, 0, 1), c'est une combinaison de AR (2) et MA (1). D'après le tableau 22, nous observons que la constante est significative. Par conséquent, elle est conservée dans ce modèle. De plus, PHI_1, PHI_2 et THETA_1 sont également significatifs au seuil de risque de 5% pour PHI et de 1% pour THETA_1. La valeur de PHI_1 est égale à 0,534, PHI_2 est égale à 0,294 et celle de THETA_1 est égale à -0,569. Comme on est dans un modèle mixte, il faut vérifier aussi les conditions de stationnarité et d'inversibilité avant l'estimation. Ici nous avons :

|ö₂| = |0,294| < 1,

P₁ + P₂ = 0,534 + 0,294 = 0,828 < 1,

P₂ - P₁ = 0,294 - 0,534 = -0,240 < 1,

|e₁| = |-0,569| < 1

Donc les conditions de stationnarité et d'inversibilité sont vérifiées.

67

Nous allons à présent examiner les résidus de notre modèle à partir d'un corrélogramme. Nous réaliserons également une représentation de la FAC et de la FACP.

Graphique 25 : Corrélogramme des résidus

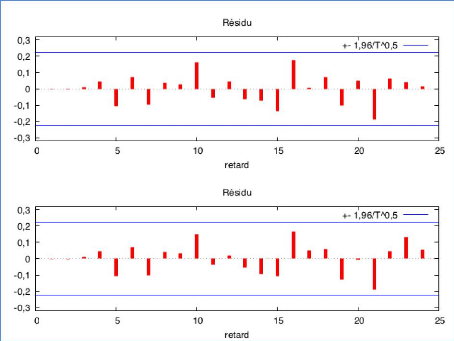
D'après le graphique 25, on peut constater qu'aucun de nos résidus ne dépassent le seuil significatif, donc ils ont une caractéristique d'un bruit blanc.

Tableau 23 : FAC et FACP pour les résidus

Fonction d'auto-corrélation résiduelle ***, **, * indicate significance at the 1%, 5%, 10% levels using standard error 1/T^0,5
RETARD	ACF	PACF	Q	P. Critique
1	-0,002	-0,002
2	-0,003	-0,003
3	0,009	0,009
4	0,045	0,045	0,178	0,673
5	-0,108	-0,108	1,149	0,563
6	0,071	0,072	1,571	0,666
7	-0,097	-0,101	2,379	0,666
8	0,036	0,041	2,495	0,777
9	0,026	0,032	2,555	0,862

68

10

	0,161	0,149	4,874	0,675
11	-0,055	-0,038	5,152	0,741
12	0,044	0,021	5,329	0,805
13	-0,063	-0,056	5,707	0,839
14	-0,072	-0,093	6,202	0,860
15	-0,136	-0,105	7,987	0,786
16	0,177	0,165	11,091	0,603
17	0,007	0,052	11,096	0,678
18	0,069	0,060	11,588	0,710
19	-0,104	-0,128	12,706	0,694
20	0,051	-0,007	12,977	0,738
21	-0,190 *	-0,188	16,851	0,533
22	0,061	0,046	17,264	0,572
23	0,039	0,130	17,437	0,624
24	0,015	0,054	17,464	0,683

D'après le tableau 23, on constate que la p-value est égale à 0,683 ce qui est supérieure à 0,05. Les résidus sont donc indépendants entre eux. La p-value étant relativement élevée, on peut donc dire que le modèle est bon.

Graphique 26 : Test de normalité des résidus

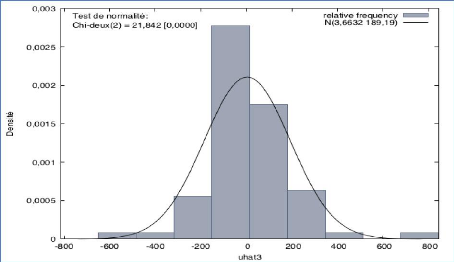
D'après le graphique 26, on a une p-value égale à 0,0000, ce qui est inférieure à 0,05, donc on rejette H0 et nos résidus ne suivent pas une loi normale.

69

Graphique 27 : Les valeurs observées et prédites

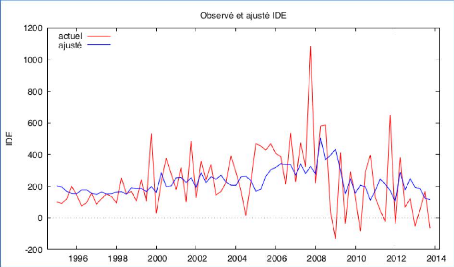
D'après le graphique 27, on observe visuellement que les deux lignes ont des tendances et des volatilités différentes. Nos qualités prédites semblent décevantes.

V.3.2 Récapitulatif des modèles ARIMA

Le tableau ci-dessous résume les résultats que l'on a obtenus avec les différents modèles étudiés.

Tableau 24 : Comparaison des quatre modèles

MODELE	Q TEST	LA FORME	NORMALITE DES RESIDUS
AR (2)	0,706	idet = at + 0,043idet-1 + 0,323ide??-2	NON
MA(2)	0,417	idet = at + 0,030a??-1 - 0,263a??-2	NON
ARIMA (1, 0, 1)	0,021	idet = at + 0,786a??-1 + 0,920ide??-1	NON
ARIMA (2, 0, 1)	0,683	idet = at + 0,569a??-1 + 0,534ide??-1 + 0,294ide??-2	NON

Le tableau 24, va nous permettre de déterminer le modèle le plus adapté pour notre série. Dans ces quatre modèles, on constate que la méthode d'estimation postule que les résidus ne sont pas auto-corrélés, et possède que du bruit. En revanche, la distribution ne suit pas la loi normale. Un bon modèle consiste à construire les résidus et à les analyser pour voir s'il existe des directions systématiques, et a une valeur de Q test la plus élevée possible. Dans ce cas-là, on trouve que notre premier modèle AR (2) paraît le plus pertinent pour notre série.

70

Cependant, nous ne pouvons pas conserver ce modèle car le coefficient PHI_1 n'est pas significatif. La situation est similaire pour le modèle MA (2) avec un coefficient THETA_1 qui n'est pas significatif. En revanche, la valeur du Q Test est relativement faible pour le modèle ARIMA (1, 0, 1), ce qui signifie que les résidus ne sont pas indépendants entre eux. Nous allons donc sélectionner le modèle ARIMA (2, 0, 1) comme notre meilleur modèle.

A partir du logiciel R, nous avons pu déterminer si le modèle retenu était le meilleur. Pour cela, nous avons utilisé la fonction auto.arima proposée par le logiciel R. Le résultat est que le modèle que nous avons sélectionné est le plus pertinent selon ce logiciel.

Nous allons à présent procéder à la prévision pour la série sur l'IDE. Cette prévision va être réalisée pour le modèle retenu : ARIMA (2, 0, 1). Rappelons que la série n'a pas été différenciée car la série brute était déjà stationnaire.

Comme nous n'avons pas différenciée notre série, nous écrivons :

??_t = IDE_t

Notons également que :

??_t = ô + a_t - ??1at_1 + P1??????t_1 + P2??????t_2

On a donc :

IDE t = ô - ??1at_1 + P1??????t_1 + P2??????t_2

P₁ = 0,534

P₂ = 0,294

ô = 211,699

??????t_1 = -65,6

??????t_2 = 168,2

??₁ = -0,569
at_1 = -26,608

71

On obtient donc comme résultat : 211,699 + 0,569*(-26,608) + 0,534*(-65,6) + 0,294*168,2 = 210,979

A présent, nous pouvons calculer le pourcentage d'erreur par la formule suivante :

Valeur observée-valeur théorique	210,979+65,6 * 100 = -4,216% -65,6
|valeur théorique |

Pour notre meilleur modèle, nous pouvons observer qu'à court terme, les prévisions sont satisfaisantes. En effet, les prévisions du modèle ne se trompent que de -4,216%, ce qui est relativement faible. Le modèle ARIMA (2, 0, 1) est donc validé. La série IDE peut donc être estimée par le modèle ARIMA (2, 0, 1).

Nous avons étudié le modèle ARIMA dans le cadre de la série IDE afin de mettre en avant la méthode de Box et Jenkins. Contrairement à la régression linéaire multiple qui est basée sur la partie économique (construction du modèle), la modélisation ARIMA nous permet de faire la prévision en se basant sur un modèle totalement statistique. C'est la raison pour laquelle, nous avons réalisé la modélisation ARIMA.

72

Conclusion

Tout d'abord, rappelons que l'objectif de notre modèle était de présenter les déterminants du niveau d'investissement direct étranger en France. Nous avons réalisé une régression linéaire multiple qui se base sur la partie économique ainsi qu'une modélisation ARIMA qui se base sur un modèle totalement statistique. On a pu remarquer que la qualité de nos modèles est assez moyenne au niveau de la régression linéaire multiple. Dans le cas de notre meilleur modèle de régression prenant en compte l'ensemble des variables, les hypothèses de normalité des résidus et d'homoscédasticité sont rejetées. En revanche, l'erreur de prévision de la série IDE est de -4,216% d'après la modélisation ARIMA, ce qui est assez faible. L'analyse en composante principale a confirmée que le choix des variables est pertinent. En effet, la somme des dimension de l'analyse en composante principal est d'environ 80%, ce qui montre que notre modèle est bien représenté.

Etant donné que notre modèle comporte un problème d'homoscédasticité, il est donc possible que notre modèle se base sur des observations représentatives de moyenne et dont la variance de l'erreur serait liée aux valeurs des variables explicatives.

Pour pouvoir améliorer notre modèle, nous pourrions déjà corriger le problème d'homoscédasticité. Une autre façon d'améliorer notre modèle serait d'ajouter ou supprimer des variables explicatives. En effet, l'IDE est une composante de l'économie qui repose sur un certains nombre de facteurs, il est donc très difficile de l'expliquer à partir d'un nombre relativement faible de variables. Le coefficient de détermination (R²) pourrait également augmenter.

73

Bibliographie

Ouvrages et articles :

Ø Alternatives économiques n°296, « Comment sauver la protection sociale », 11/2010, page 71.

Ø ANDREFF W. 2003. « Les multinationales globales ». Paris, la Découverte, Repères.

Ø AUSSILLOUX V., CHEVAL M-L. 2002. « Les investissements directs français à l'étranger et l'emploi en France ». Economie et prévision. Page 30.

Ø BERTHELEMY J.C et DEMURGER S. 2000. « Foreign Direct Investment and Economic Growth: Theory and Application to China ». Review of Development Economics. Wiley Blackwell, vol 4.

Ø BLONIGEN B.A. et WANG M. 2004. « Inappropriate pooling of wealthy and poor countries in empirical FDI studies ». NBER Working Paper n° 10 378. Cambridge.

Ø BOUOIYOUR J., HANCHANE H. et MOUHOUD E. 2009. « Investissements directs étrangers et productivité ». Revue Économique.

Ø BOURBONNAIS R. « Econométrie ». Dunod. 9^ème édition.

Ø CARKOVIC M. et LEVINE R. 2005. « Does foreign direct investment accelerate economic growth ? ». Institute for International Economics and Center for Global Development. Washington. DC. P.195-220.

Ø CHAKRABARTI A. 2001. « The Determinant of Foreign Direct Investment : Sensitivity Analyses of Cross-Country Regressions ». Kyklos, vol 54 Fasc. P. 114-189.

Ø CREPON B. et JACQUEMET N. « Econométrie : méthode et applications ». Chapitre 2. Page 46.

Ø El OUARDIGHI J., KAHN R. 07/2003. « Les investissements directs internationaux dans les régions Françaises ». Revue d'Economie Régionale et Urbaine. Page 10.

Ø FONTAGNE L. et TOUBAL F. 2010. « Investissement direct étranger et performances des entreprises ». La documentation française.

Ø HYMER S.H. 1976. « The International Operations of National Firms : A Study of Direct Foreign Investment 1976 ». Edition MIT Press. Cambridge (thèse de Doctorat. MIT. 1960).

Ø KRUGMAN P. et OBSTFELD M. 2006. Economie internationale, 7^ème édition. Bruxelles 3. Nouveaux horizons.

Ø

74

LALL S. et NARULA R. 2004. « FDI and its role in economic development: Do we need a new agenda? ». Research Memoranda 019. Maastricht : MERIT.

Ø LEVASSEUR S. 2002. « Investissements directs à l'étranger et stratégies des firmes multinationales ». OFCE. Hors série.

Ø LIPSEY R. 1999. « The location and characteristics of U.S affiliates in Asia. 6876 ». Cambridge. Mass.

Ø LIPSEY R. et SJÖHOLM F. 2005. « The Impact of Inward FDI on Host Countries : Why Such Different Answers ? ». Chap 2 in Does Foreign Direct Investment Promote Development ? Editors Moran. P 23-43.

Ø LOVE et LAGE HIDALGO. 2000. « Analysing the determinants of US direct investment in Mexico ».

Ø MERVELEVEDE Y. et BRUNO J.F. 2011. « FDI Spillovers and the Time since Foreign Entry ». Working Papers of Faculty of Economics and Business Administration. Ghent University. Belgium.

Ø MIGNON V. « Econométrie : Théorie et application ». Chapitre 3. P 93-95.

Ø MIGNON V. « Econométrie : Théorie et application ». Chapitre 3. P 98-100.

Ø STIMULA L. et TRANNOY A. 03/2009. « Incidence de l'impôt sur les sociétés ». Revue française d'économie. PP. 100-102.

Ø TRUMAN J. et EMMERT C. 1999. « Explaining Japanese Foreign Direct Investment in Latin America ». Social Science Quarterly 80. P. 539-541.

Sites consultés :

Ø BOUABDI O. « Libéralisation financière et investissement direct à l'étranger : un mode de financement qui s'impose pour le développement des PED : cas du Maroc ». 07/11/2014. Archives-ouvertes.

Ø CANINGAN L.K. 2012. « Investissements directs étrangers et développement durable. Cas de la côte d'Ivoire ». Mémoire Online.

Ø Carnet Photographique. « Les ressources naturelles de la France ». 30/12/2017.

Ø Globe services. « Douane et importation en France ».

Ø Glossaire international. « Modèle OLI ». Le dico du commerce international.

Ø HANANE M. 2009. « Le rôle des IDE (Investissement Direct Etranger) dans le secteur bancaire algérien ». Mémoire Online.

Ø

75

INSEE, Comptes nationaux trimestriels au 4^e trimestre 2017. « Produit Intérieur Brut (PIB) et ses composantes ». 26/03/2018.

Ø INSEE, Exportations de biens et de services : définition. 13/10/2016.

Ø INSEE, Indice des prix à la consommation : définition. 06/05/2019.

Ø INSEE, Investissements directs étrangers : définition. 13/10/2016.

Ø INSEE, Salaire : définition. 13/10/2016.

Ø INSEE, Tableaux de l'économie française. « Importations-Exportations ». 19/02/2014.

Ø INSEE, Tableaux de l'économie française. « Investissements internationaux ». 27/02/2018.

Ø INSEE, Tableaux de l'économie française. « Investissements internationaux ». 02/03/2017.

Ø INSEE, « Taux de change effectif nominal et réel ». 13/10/2016.

Ø La finance pour tous. « Taux de change ». 06/02/2018.

Ø Les Crises. « Historique du PIB de la France ». 21/01/2013.

Ø LEVASSEUR S. 2002. « Investissements directs à l'étranger et stratégies des entreprises multinationales ». Archives-ouvertes.

Ø MIKIMER L. 2009. « Les effets des investissements directs étrangers sur la croissance des pays méditerranéens ». Mémoire Online.

Ø Ministère de l'économie et des finances. « Les investissements directs à l'étranger (IDE) ». 27/04/2014. Trésor.

Ø Ministère de l'économie et des finances. « Les investissements français à l'étranger ». 27/04/2014. Trésor.

Ø Ministère de l'éducation nationale et de la jeunesse. « Les dépenses des familles pour la scolarisation des enfants ». 09/2015. Education.gouv.

Ø MUHINDO NGELEZA A.M. 2009. « Déterminants de l'investissement direct étranger dans les pays en voie de développement : application faite a la RDC ». Mémoire Online.

Ø Net-iris. « SMIC 2019 : salaire minimum horaire et mensuel ». Révisé le 11/01/2019.

Ø OCDE. « Incidence de l'impôt sur l'investissement direct étranger ». 03/2008.

Ø OECD. « L'impact de l'investissement direct étranger sur les salaires et les conditions de travail ». 23/06/2008.

Ø ONU Info. « Les investissements directs étrangers ont battu des records en 2007 ». 08/01/2008.

Ø

76

PATTERSON B. et LYGNERUD K. 1999. « Détermination des taux d'intérêt ». Europarl.europa.

Ø PILLOT T., RIGAIL A.C. et VIRLET H. 2008. « Mais où est donc passé notre pouvoir d'achat ? ». Annales.org.

Ø POMER N. « L'évolution des exportations en France ». 27/05/2009. SlideShare.

Ø T. KOUKPO M. Unpan1.un.org. 2005. « Analyse des déterminants des investissements directs étrangers dans les pays de l'UEMOA ».

Ø TOUFIK S. 09/2002. « Interaction entre investissements directs étrangers, productivité et capital humain : cas des industries manufacturières marocaines ». Mafhoum.com.

Ø ZALLE O. 2011. « Les investissements directs étrangers dans l'espace UEMOA : déterminants et analyse d'impacts ». Mémoire online.

77

Récapitulatif des graphiques et tableaux

GRAPHIQUES

Graphique 1 : Investissement direct à l'étranger en France 18

Graphique 2 : Relation entre l'IDE et le PIB par habitant .. 20

Graphique 3 : Relation entre l'IDE et le taux de change 21

Graphique 4 : Relation entre l'IDE et le total des bénéfices tirés des ressources naturelles en

France .. 22

Graphique 5 : Relation entre l'IDE et le taux d'intérêt en France .. 23

Graphique 6 : Relation entre l'IDE et l'IPC en France 25

Graphique 7 : Relation entre l'IDE et le bénéfice des entreprises après impôt en France 26

Graphique 8 : Relation entre l'IDE et les exportations en France ... 27

Graphique 9 : Relation entre l'IDE et les importations en France .. 28

Graphique 10 : Relation entre l'IDE et le salaire horaire en France 29

Graphique 11 : Relation entre l'IDE et les dépenses scolaires en France 30

Graphique 12 : Matrice de corrélation de Spearman 36

Graphique 13 : Boîte à moustache et valeurs potentiellement atypiques du modèle .. 37

Graphique 14 : Variance expliquée par chaque dimension . 38

Graphique 15 : Cosinus des dimensions .. 39

Graphique 16 : Contribution de chaque variable à la définition des composantes . 40

Graphique 17 : Cercle de corrélation .. 41

Graphique 18 : Représentation des observations 42

Graphique 19 : Analyse de la normalité des résidus 48

Graphique 20 : Représentation de l'investissement direct étranger en France 57

Graphique 21 : Corrélogramme pour l'investissement direct étranger 57

Graphique 22 : Corrélogramme pour les résidus . 62

Graphique 23 : Test de normalité des résidus 64

Graphique 24 : Les valeurs observées et prédites 65

Graphique 25 : Corrélogramme des résidus 67

Graphique 26 : Test de normalité des résidus 68

Graphique 27 : Les valeurs observées et prédites 69

TABLEAUX

Tableau 1 : Index de la base « Ide » 32

Tableau 2 : Statistiques descriptives du modèle : Minimum, maximum, médiane, moyenne et

quartiles 33

Tableau 3 : Les différents tests du modèle (valeurs statistiques ou p-value) .. 34

Tableau 4 : Régression linéaire 1 nommée « reg1 » 46

Tableau 5 : Test des résidus du modèle « reg1 » . 47

Tableau 6 : VIF du modèle « reg1 » 48

Tableau 7 : Régression semi-logarithmique 1 nommée « reg1sl » . 49

Tableau 8 : Test des résidus du modèle « reg1sl » .. 50

Tableau 9 : VIF du modèle « reg1sl » . 51

Tableau 10 : Régression linéaire 2 nommée « reg2 » . 52

Tableau 11 : Test du modèle « reg2 » . 52

Tableau 12 : VIF du modèle « reg2 » .. 53

Tableau 13 : Régression semi-logarithmique 2 nommée « reg2sl » 53

78

Tableau 14 : Régression 3 nommée « reg3 » .. 54

Tableau 15 : Régression 4 nommée « reg4 » .. 55

Tableau 16 : Récapitulatif des modèles .. 55

Tableau 17 : FAC et FACP . 58

Tableau 18 : Modélisation AR (2) avec la constante .. 59

Tableau 19 : Modélisation MA (2) avec la constante . 60

Tableau 20 : Modélisation ARIMA (1, 0, 1) avec la constante .. 61

Tableau 21 : FAC et FACP pour les résidus ... 63

Tableau 22 : Modélisation ARIMA (2, 0, 1) avec la constante .. 66

Tableau 23 : FAC et FACP pour les résidus 67

Tableau 24 : Comparaison des quatre modèles 69

79

Annexes du mémoire

Annexe 1 : Présentation des variables pour la base « Ide »

Nature des variables du modèle

Variables	Type de variable	1ère valeur	2ème valeur	3ème valeur	4ème valeur	5ème valeur
IDE	Numérique	100	91,1	118,6	199,3	144,3
PIB_HAB	Numérique	302	304	306	307	311
TX CHA	Numérique	1,35	1,35	1,33	1,34	1,3
BENEF	Numérique	124	124	124	126	125
TX INT	Numérique	7,44	7,37	5,62	5,01	4,04
IPC	Numérique	65,8	65,8	66	66,3	66,4
BENEF_IMP	Numérique	468	491	499	506	525
EXP	Numérique	18,9	19,4	18,7	18,9	19,4
IMP	Numérique	18,1	18,3	18,2	18,1	18,7
SAL HOR	Numérique	58,4	58,9	59,1	59,3	59,8
DEP_SCO	Numérique	30,5	30,9	31,3	31,8	32,2
DUMMIES_EURO	Numérique	0	0	0	0	0
DUMMIES CRISE	Numérique	0	0	0	0	0

Le tableau ci-dessus permet de connaître la nature des variables du modèle. Nous voyons très clairement que l'ensemble des variables sont quantitatives sauf les variables DUMMIES_EURO et DUMMIES_CRISE. Par conséquent, il a fallu les recoder car ces deux variables étaient qualitatives et non des variables numériques. Enfin, ce tableau a été obtenu à l'aide de la fonction str sur le logiciel R Studio.

Histogrammes de fréquences de chaque variable quantitative

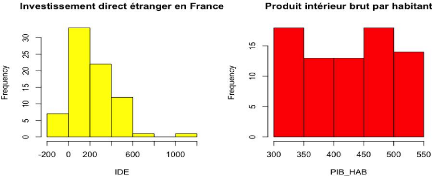
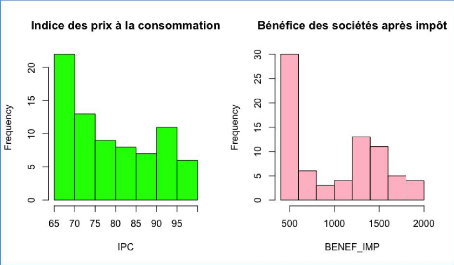
80

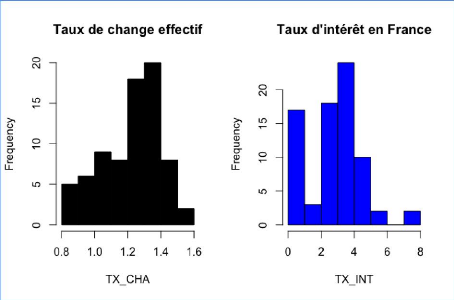
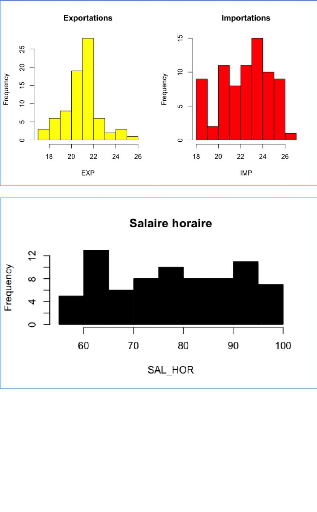
81

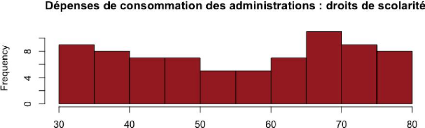
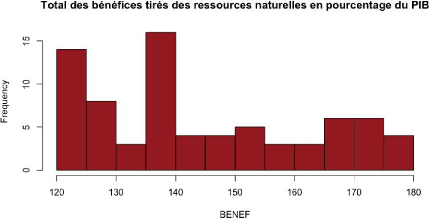
82

Les histogrammes ci-dessus représentent chaque variable quantitative. Par exemple, dans le cas de l'IDE, la fréquence la plus élevée (environ 35) est obtenue pour une valeur de l'IDE comprise entre 0 et 200.

Dans le cas des variables DUMMIES_EURO et DUMMIES_CRISE qui sont des variables qualitatives (binaire), nous avons réalisé des diagrammes en barre afin de les représenter.

83

Diagramme en barre de chaque variable qualitative

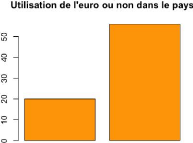
Annexe 2 : Valeurs atypiques du modèle

Cette deuxième annexe a pour but de déterminer les éventuelles valeurs atypiques pour chaque variable du modèle. Deux tests sont effectués en fonction du nombre de valeurs atypiques : test de Grubbs dans le cas où une seule observation est potentiellement atypique et le test de Rosner dans le cas où au moins deux observations sont potentiellement atypiques.

Boxplot de chaque variable quantitative

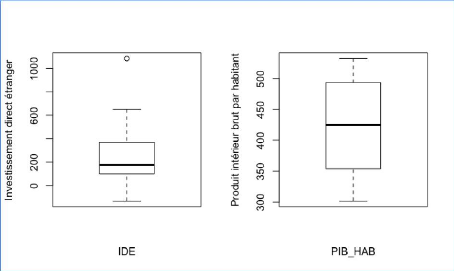
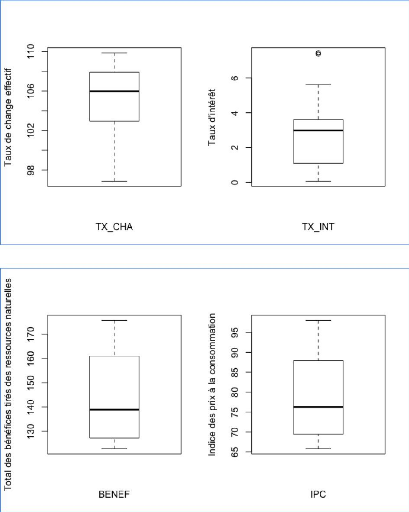
84

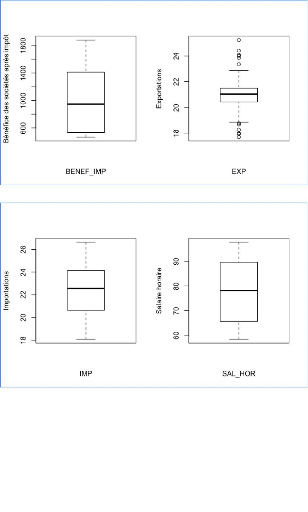
85

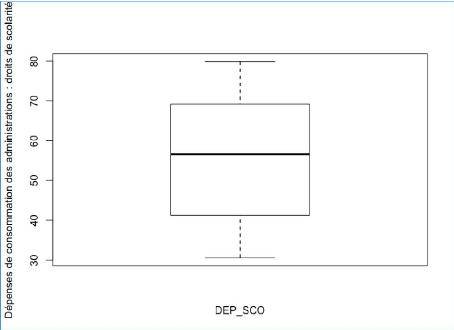
Test de Grubbs pour la variable IDE

GRUBBS TEST FOR ONE OUTLIER

Data : Ide$IDE

G = 4,2573

U = 0,7551

P-Value = 0,0004

86

Pour la variable IDE, la p-value du test de Grubbs est inférieure à 0,05 et donc par conséquent, l'hypothèse H0 est refusée au seuil de risque de 5%. La variable IDE a donc une valeur atypique.

Suppression de l'observation atypique

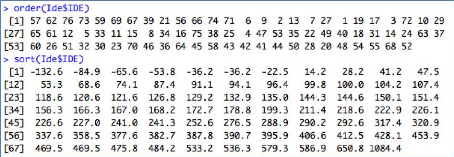
87

D'après le tableau ci-dessus, on observe que la valeur atypique correspond donc à la cinquante-deuxième observation. Il s'agit du quatrième trimestre 2007.

Test de Rosner pour la variable TX INT

NUMERO	OUTLIERS	TEST STATISTIQUE	CRITICAL VALEUR
1	1	2,883	3,288
2	2	3,034	3,283
3	3	2,089	3,278
4	1	1,749	3,273
5	2	1,674	3,268
6	3	1,688	3,263
7	1	1,652	3,257
8	2	1,694	3,252
9	3	1,738	3,247
10	1	1,788	3,241
11	2	1,837	3,236
12	3	1,848	3,230

Dans le test de Rosner, si le test statistique est supérieur à la critical valeur alors l'observation sera considérée comme atypique. Dans le cas ou ce test est inférieur, l'observation ne sera pas atypique. Pour la variable TX_INT, il n'y a pas de valeurs potentiellement atypiques.

Test de Rosner pour la variable EXP

NUMERO	OUTLIERS	TEST STATISTIQUE	CRITICAL VALEUR
1	1	2,922	3,288
2	2	2,532	3,283
3	3	2,425	3,278
4	1	2,482	3,273
5	2	2,498	3,268
6	3	2,548	3,263
7	1	2,506	3,257
8	2	2,586	3,252
9	3	2,484	3,247
10	1	2,442	3,241
11	2	2,280	3,236
12	3	2,296	3,230

Pour la variable EXP, il n'y a pas de valeurs potentiellement atypiques car le test statistique est inférieur à la critical valeur pour l'ensemble des observations.

88

Annexe 3 : Corrélations des variables

Corrélation de Spearman (autre version)

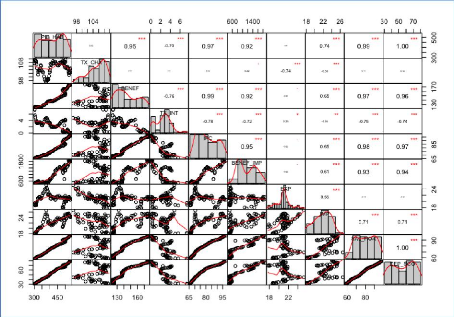
Tests de Spearman pour les variables corrélées

					SPEARMAN'S RANK CORRELATION RHO
					Data : PIB HAB and DEP SCO
S =		420			P-Value < 2,2e-16
					Alternative hypothesis : true rho is not equal to 0
					Rho = 0,994
				SPEARMAN'S RANK CORRELATION RHO
				Data : SAL_HOR and DEP_SCO
S =			0	P-Value < 2,2e-16
				Alternative hypothesis : true rho is not equal to 0
				Rho = 1
					SPEARMAN'S RANK CORRELATION RHO
					Data : PIB HAB and SAL HOR
S =		420			P-Value < 2,2e-16
					Alternative hypothesis : true rho is not equal to 0
					Rho = 0,994

89

									SPEARMAN'S RANK CORRELATION RHO
									Data : PIB_HAB and IPC
S =	437,01								P-Value < 2,2e-16
									Alternative hypothesis : true rho is not equal to 0
									Rho = 0,994
										SPEARMAN'S RANK CORRELATION RHO
										Data : BENEF and IPC
S = 1		439,1								P-Value < 2,2e-16
										Alternative hypothesis : true rho is not equal to 0
										Rho = 0,980
							SPEARMAN'S RANK CORRELATION RHO
							Data : IPC and SAL_HOR
S =					13		P-Value < 2,2e-16
							Alternative hypothesis : true rho is not equal to 0
							Rho = 1
											SPEARMAN'S RANK CORRELATION RHO
											Data : BENEF and SAL HOR
S = 1		402,6									P-Value < 2,2e-16
											Alternative hypothesis : true rho is not equal to 0
											Rho = 0,981
							SPEARMAN'S RANK CORRELATION RHO
							Data : IPC and DEP_SCO
S =					13		P-Value < 2,2e-16
							Alternative hypothesis : true rho is not equal to 0
							Rho = 1
										SPEARMAN'S RANK CORRELATION RHO
										Data : IPC and BENEF_IMP
S = 5				717,1						P-Value < 2,2e-16
										Alternative hypothesis : true rho is not equal to 0
										Rho = 0,922
											SPEARMAN'S RANK CORRELATION RHO
											Data : PIB HAB and BENEF
S = 1			864,6								P-Value < 2,2e-16
											Alternative hypothesis : true rho is not equal to 0
											Rho = 0,974
											SPEARMAN'S RANK CORRELATION RHO
											Data : BENEF and DEP_SCO
S = 1		402,6									P-Value < 2,2e-16
											Alternative hypothesis : true rho is not equal to 0
											Rho = 0,981

90

		SPEARMAN'S RANK CORRELATION RHO
		Data : BENEF_IMP and DEP_SCO
S = 5	690	P-Value < 2,2e-16
		Alternative hypothesis : true rho is not equal to 0
		Rho = 0,922

J'ai réalisé le test de Spearman pour l'ensemble des variables dont la corrélation était supérieure ou égale à 0,95. Comme dans l'ensemble des cas, la p-value est inférieure à 0,05, les variables sont donc corrélées positivement et significativement au seuil de risque de 1%.

Annexe 4 : Régressions linéaires multiples du modèle

Dans cette première partie de l'annexe, nous avons réalisé les graphiques de la première régression (« reg1 »).

Analyse de l'homoscédasticité des résidus du modèle reg1

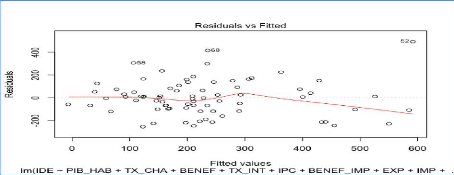
Analyse de la forme fonctionnelle du modèle reg1

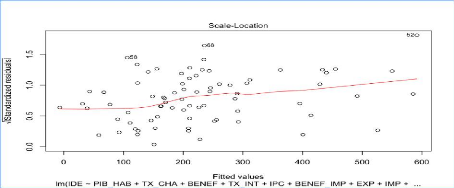
91

Analyse des informations qui influencent l'information du modèle reg1

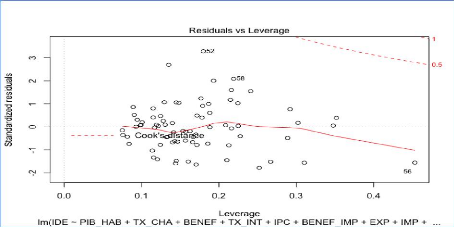
Distance de Cooks du modèle reg1

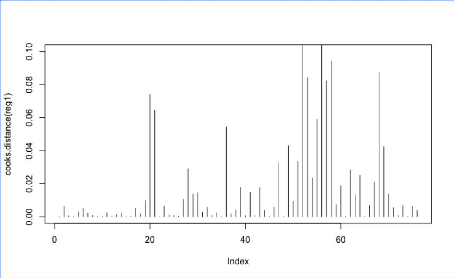
92

Nous allons poursuivre avec les graphiques du modèle de régression linéaire 1 semi logarithmique (« reg1sl »).

Analyse de l'homoscédasticité des résidus du modèle reg1sl

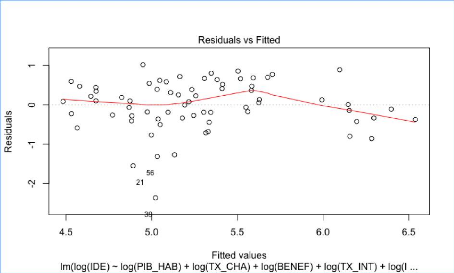
Analyse de la forme fonctionnelle du modèle reg1sl

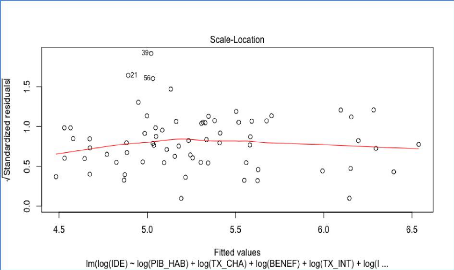
93

Analyse des informations qui influencent l'information du modèle reg1sl

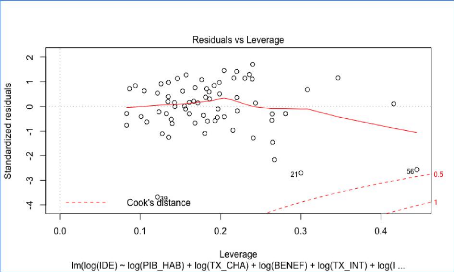
Analyse de la normalité des résidus du modèle reg1sl

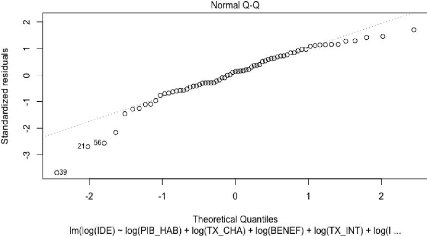
94

Nous allons poursuivre avec les graphiques du modèle de régression linéaire 2 (« reg2 »).

Analyse de l'homoscédasticité des résidus du modèle reg2

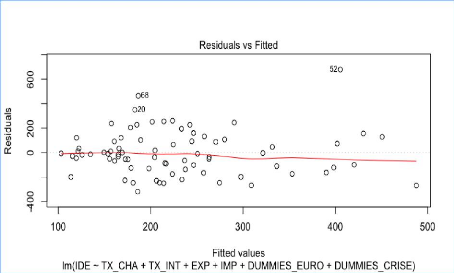
Analyse de la forme fonctionnelle du modèle reg2

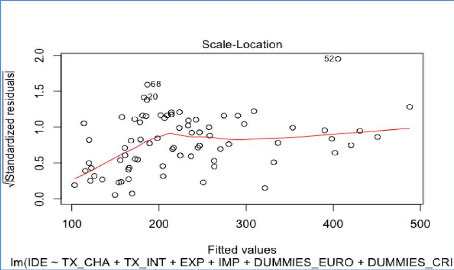
Analyse des informations qui influencent l'information du modèle reg2

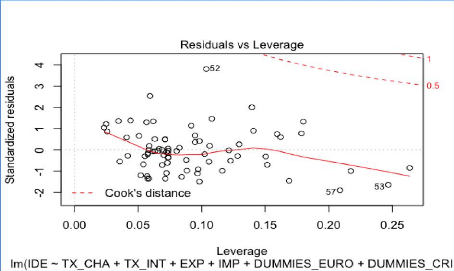
95

Analyse de la normalité des résidus du modèle reg2

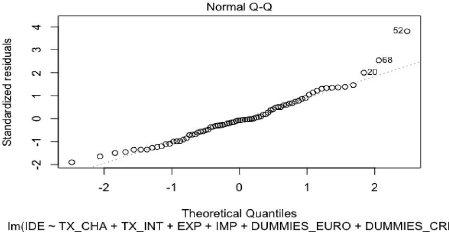
96

Les graphiques suivants sont ceux du modèle de régression linéaire 2 semi logarithmique (« reg2sl »).

Analyse de l'homoscédasticité des résidus du modèle reg2sl

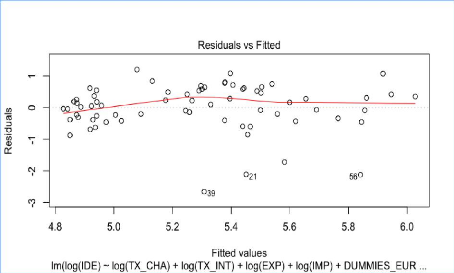
Analyse de la forme fonctionnelle du modèle reg2sl

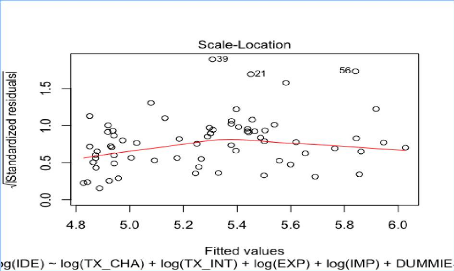
Analyse des informations qui influencent l'information du modèle reg2sl

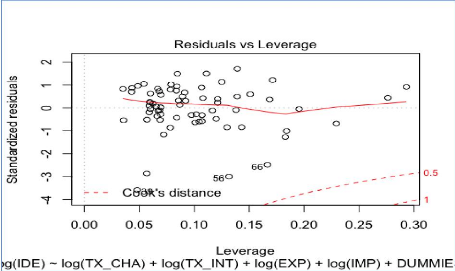
97

Analyse de la normalité des résidus du modèle reg2sl

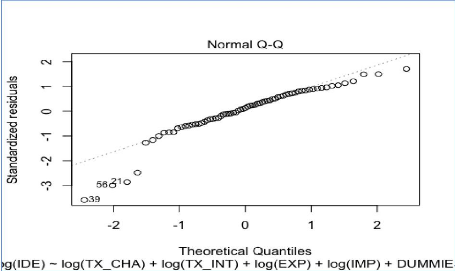
98

Nous allons poursuivre avec les graphiques du modèle de régression linéaire 3 (« reg3 »).

Analyse de l'homoscédasticité des résidus du modèle reg3

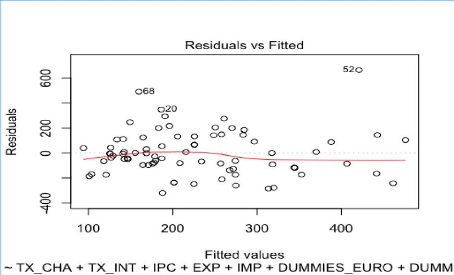
Analyse de la forme fonctionnelle du modèle reg3

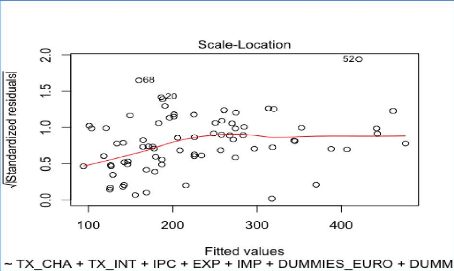
Analyse des informations qui influencent l'information du modèle reg3

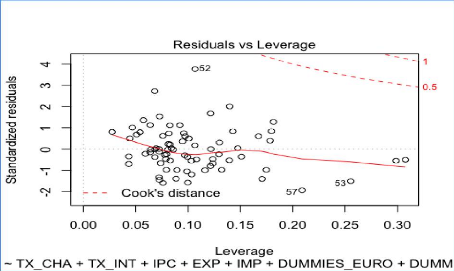
99

Analyse de la normalité des résidus du modèle reg3

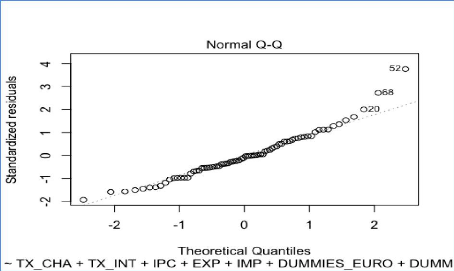
100

Enfin, nous allons terminer avec les graphiques du modèle de régression linéaire 4 (« reg4 »).

Analyse de l'homoscédasticité des résidus du modèle reg4

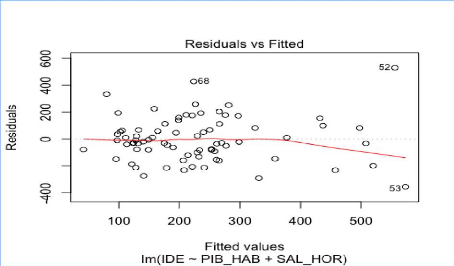
Analyse de la forme fonctionnelle du modèle reg4

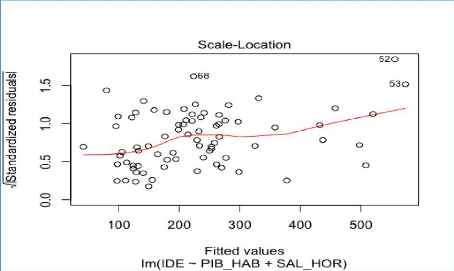
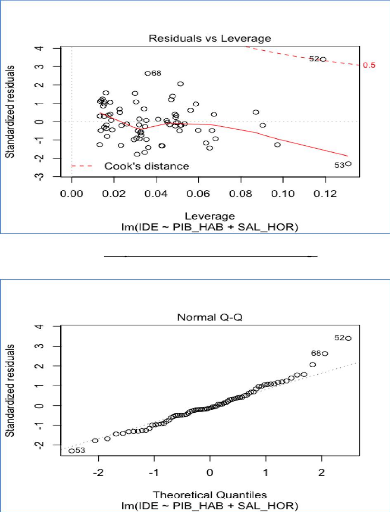
Analyse de la normalité des résidus du modèle reg4

101

Analyse des informations qui influencent l'information du modèle reg4

102

Annexe 5 : Modélisation ARIMA pour l'IDE

Dans cette première partie de l'annexe, nous avons réalisé les graphiques du modèle AR (2).

Corrélogramme des résidus de AR (2)

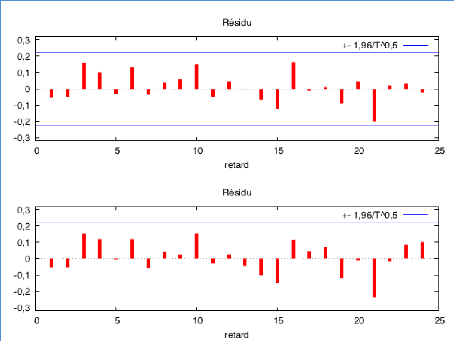
FAC et FACP des résidus de AR (2)

Fonction d'auto-corrélation résiduelle ***, **, * indicate significance at the 1%, 5%, 10% levels using standard error 1/T^0,5
RETARD	ACF		PACF		Q		P. Critique
1	-0,0524		-0,0524
2	-0,0513		-0,0542
3	0,1576		0,1528		2,4440		0,118
4	0,1014		0,1179		3,2914		0,193
5	-0,0327		-0,0057		3,3809		0,337
6	0,1325		0,1203		4,8679		0,301
7	-0,0367		-0,0604		4,9839		0,418
8	0,0371		0,0390		5,1041		0,531
9	0,0577		0,0249		5,3989		0,611

103

10

	0,1508	0,1545	7,4409	0,490
11	-0,0504	-0,0276	7,6730	0,567
12	0,0463	0,0227	7,8714	0,641
13	-0,0010	-0,0469	7,8714	0,725
14	-0,0652	-0,1038	8,2776	0,763
15	-0,1221	-0,1497	9,7253	0,716
16	0,1618	0,1165	12,3122	0,581
17	-0,0112	0,0470	12,3248	0,654
18	0,0128	0,0718	12,3417	0,720
19	-0,0896	-0,1180	13,1759	0,724
20	0,0439	-0,0116	13,3796	0,769
21	-0,2017 *	-0,2364 **	17,7631	0,538
22	0,0215	-0,0160	17,8137	0,600
23	0,0332	0,0857	17,9369	0,653
24	-0,0241	0,1028	18,0033	0,706

Test de normalité des résidus de AR (2)

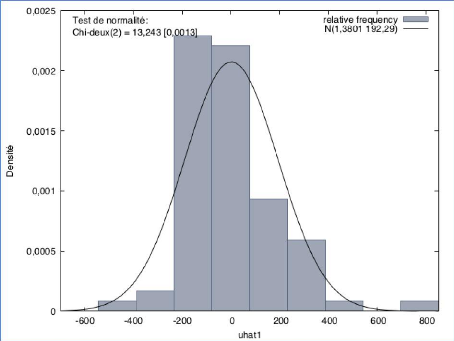
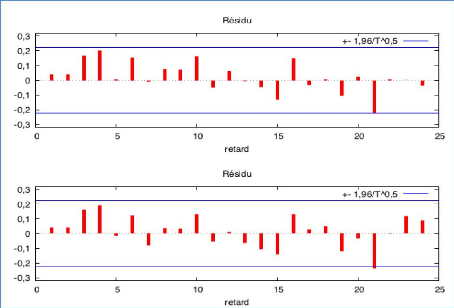
104

Valeurs observées et prédites de AR (2)

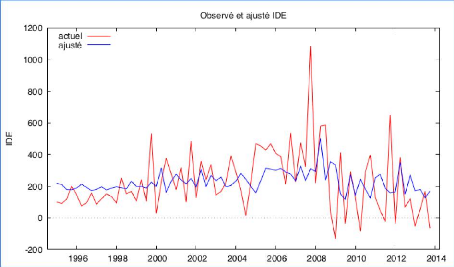
Dans cette seconde partie de l'annexe, nous avons réalisé les graphiques du modèle MA (2).

Corrélogramme des résidus de MA (2)

105

FAC et FACP des résidus de MA (2)

Fonction d'auto-corrélation résiduelle ***, **, * indicate significance at the 1%, 5%, 10% levels using standard error 1/T^0,5
RETARD	ACF	PACF	Q	P. Critique
1	0,0424	0,0424
2	0,0430	0,0412
3	0,1661	0,1632	2,5299	0,112
4	0,2024 *	0,1942 *	5,9029	0,052
5	0,0060	-0,0150	5,9059	0,116
6	0,1533	0,1215	7,8968	0,095
7	-0,0097	-0,0814	7,9048	0,162
8	0,0749	0,0364	8,3940	0,211
9	0,0716	0,0343	8,8480	0,264
10	0,1639	0,1328	11,2610	0,187
11	-0,0483	-0,0558	11,4735	0,245
12	0,0648	0,0113	11,8621	0,294
13	-0,0064	-0,0642	11,8660	0,374
14	-0,0438	-0,1059	12,0496	0,442
15	-0,1298	-0,1386	13,6879	0,396
16	0,1474	0,1330	15,8348	0,324
17	-0,0317	0,0277	15,9355	0,386
18	0,0047	0,0497	15,9378	0,457
19	-0,1070	-0,1205	17,1292	0,446
20	0,0250	-0,0324	17,1956	0,510
21	-0,2237 *	-0,2376 **	22,5901	0,256
22	0,0061	0,0022	22,5941	0,309
23	0,0020	0,1184	22,5946	0,366
24	-0,0355	0,0891	22,7381	0,417

Test de normalité des résidus de MA (2)

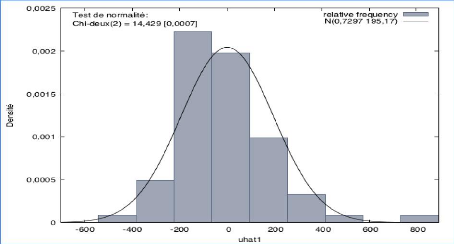
106

Valeurs observées et prédites de MA (2)

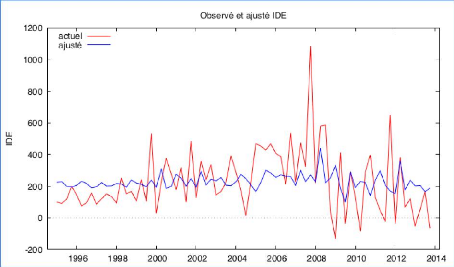
107

Table des matières

Remerciements 2

Liste des abréviations . 3

Sommaire . 4

Résumé 5

Abstract 6

I- Introduction .. 7

II- Revue de littérature 10

II.1 Travaux théoriques 10

II.2 Travaux empiriques .. 13

III- Modèle empirique et données 17

III.1 L'investissement direct étranger en France (IDE) 18

III.2 Le produit intérieur brut par habitant (PIB_HAB) 19

III.3 Le taux de change en France (TX_CHA) 20

III.4 Total des bénéfices tirés des ressources naturelles en pourcentage du PIB

(BENEF) . 22

III.5 Le taux d'intérêt en France (TX_INT) 23

III.6 L'indice des prix à la consommation (IPC) 24

III.7 Le bénéfice des entreprises après impôt (BENEF_IMP) 25

III.8 Exportations : valeurs des biens pour la France (EXP) .. 27

III.9 Importations : valeurs des biens pour la France (IMP) .. 28

III.10 Salaire horaire (SAL_HOR) .. 29

III.11 Dépenses de consommation des administrations : droits de scolarité et frais de

formation (DEP_SCO) 30

III.12 Utilisation de l'euro comme monnaie au cours du trimestre

(DUMMIES_EURO) .. 31

108

III.13 La crise est présente au sein du pays (DUMMIES_CRISE) IV- Analyse de données et descriptive IV.1 Statistiques descriptives IV.2 Analyse de données		. 31 32 33 38
V- Etude économétrique du sujet		43
V.1 Modèle théorique RLM		43
V.1.1 Modèle de régression multiple		43
V.1.2 Hypothèses du modèle		44
V.1.3 Estimation des paramètres du modèle		44
V.1.4 Propriétés des estimateurs		.. 45
V.2 Application économétrique du modèle		. 46
V.2.1 Premier modèle étudié		46
V.2.2 Seconde modèle étudié		51
V.2.3 Troisième modèle étudié		54
V.2.4 Quatrième modèle étudié		54
V.2.5 Récapitulatif des modèles RLM		55
V.3 Détermination du modèle ARIMA (p, d, q)(P, D, Q)s pour l'IDE		56
V.3.1 Estimation de notre modèle		58
V.3.1.1 Modélisation du premier modèle AR (2)		. 59
V.3.1.2 Modélisation du second modèle MA (2)		..60
V.3.1.3 Modélisation du troisième modèle ARIMA (1, 0,	1)	61
V.3.1.4 Modélisation du quatrième modèle ARIMA (2, 0,	1)	65
V.3.2 Récapitulatif des modèles ARIMA		69
Conclusion		72
Bibliographie		73

109

Récapitulatif des graphiques et tableaux . 77

Annexes du mémoire 79

Annexe 1 : Présentation des variables pour la base « IDE » 79

Annexe 2 : Valeurs atypiques du modèle 83

Annexe 3 : Corrélation des variables 88

Annexe 4 : Régressions linéaires multiples du modèle 90

Annexe 5 : Modélisation ARIMA pour l'IDE 102