3. La matrice de transition
Comme décrit ci-haut, les matrices de transitions ont
été appliquées afin de quantifier les différentes
transitions observées au courant des années en étude.
4. Analyse de la structure spatiale du paysage
Dans la structure spatiale du paysage, l'étude se
concentre à deux niveaux : le niveau global du paysage et le niveau
spécifique. Au niveau global, les analyses portent sur le nombre de
taches par type (classe). Au niveau spécifique (tache par tache) les
analyses portent sur :
? L'aire de tâche :
l'aire totale ; l'aire moyenne et l'aire maximale ;
? Le périmètre de tâche :
le périmètre total, le périmètre moyen et le
périmètre maximal) ;
? La dominance Dj (a) : indique la proportion
d'aire occupée par la tache dominante dans la classe j.

Il s'agit de la part occupée dans l'aire totale par la
plus grande tache de la classe j notée amax .J. Plus la valeur
de la dominance est grande, moins la classe est fragmentée. (McGarigal
& Marks, 1995) :

? La forme des tâches : Celle-ci est
calculée par l'indice de la forme de tâche.
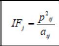
La forme est un élément difficile à
quantifier et qui peut donner libre cours à différentes
interprétations (Krummel et al., 1987). Plus les taches ont des
formes allongées ou irrégulières, plus la valeur de
l'IFj sera élevée et cette valeur décroîtra
à mesure que les formes deviennent circulaires (Bogaert et al.,
2000).
Afin d'évaluer la dispersion des superficies et des
périmètres autour de leurs moyennes, nous avions calculé
la variance, l'écart-type et le coefficient de variation.
? La variance ó2 j(a) :
représente la moyenne des carrés des écarts
à la moyenne. Elle permet de caractériser la dispersion des
valeurs par rapport à la moyenne.
|
ó2 ??(??) = 1 ? (??????
????
??=1 - ???? )2
????
|
? Le Coefficient de variation (CVj) : il est un
indicateur de dispersion. Il est égal au rapport de la racine
carrée de la variance par la moyenne de la classe j
CVj (a) = v???? ??(??)
??
????
5. Identification des processus de transformation
spatiale
Pour identifier les transformations spatiales, la typologie
proposée par Bogaert et al. (2004) a été
appliquée.

? Dynamique prospective du paysage
Pour cette étude, le Land Change Modeler (LCM) a
été utilisé comme outil de Modélisation. Les
étapes de la modélisation prédictive de l'occupation des
sols à l'aide du module LCM sont donc structurées selon le
cheminement présenté dans la figure 13.

Fig.13. Prédiction du changement de l'occupation du
sol à l'aide LCM En effet, les changements historiques sont d'abord
déterminés à partir d'une série multi-temporelle de
cartes de l'occupation des sols. Puis, les facteurs les plus significatifs
(variables explicatives) dans ces changements sont déterminés.
Le nombre de variables explicatives à intégrer
aux modèles de simulation des changements des modes d'occupation et
d'usage du sol est contraint par leur disponibilité ainsi que leur
spatialisation. Le tableau 6 présente les variables explicatives
retenues pour cette étude.

Tableau 6 : Facteurs explicatifs des
changements
|
|
Variables explicatives
|
Description
|
|
0.
|
Le réseau routier
|
Facilite l'accès aux ressources et leur
évacuation
|
1.
|
Le réseau hydrographique
|
Influe sur la répartition des types d'occupation du
sol
|
2.
|
Les pentes
|
Influe sur l'accessibilité à certaines
ressources
|
3.
|
L'agriculture
|
Important facteur de déforestation
|
4.
|
Les agglomérations humaines
|
Accélèrent la déforestation
|
5.
|
|
L'aspect
|
Influe sur l'accessibilité et l'utilisation certaines
ressources
|
|
a. Modélisation du potentiel pour le
changement
? Création du sous-modèle de
transition
Après avoir étudié les changements
historiques, la première étape est ici consacrée à
la construction du sous-modèle. Ceci permet ainsi l'introduction des
variables sur lesquelles se produisent des transitions potentielles. Dans cette
étude, nous avons déterminé 20 transitions possibles entre
l'occupation des sols de 1995 et 2009.
Afin d'éviter les transitions impossibles dans le
modèle, seules 6 transitions potentielles ont été retenues
(tableau 7). Deux options pour la modélisation des transitions
potentielles sont proposées : le Perceptron Multi-Couche (PMC) ou la
Régression logistique (Reloger). Dans cette étude, le Perceptron
Multi-couche a été appliqué.
? Evaluation de la qualité des variables
explicatives
La deuxième étape permet d'explorer la puissance
potentielle des variables explicatives qui sont considérées comme
importantes dans le processus de prédiction. Elle permet
également de calculer l'indice de Cramer's V et la probabilité
associée. La puissance potentielle des variables explicatives est
évaluée à l'aide des outils de transformation variable.
Ces outils lient les changements de l'occupation des sols observés aux
variables explicatives. Celles-ci ont été
sélectionnées en fonction de leur potentiel explicatif, et
évaluées grâce au coefficient de Cramer's V, utilisé
dans ce cas comme une valeur de probabilité associée à la
variable explicative. Une valeur élevée de ce coefficient marque
l'importance de cette variable explicative. Ainsi, une valeur supérieure
ou égale à 0.15 est considérée comme acceptable.
Au-delà de 0.4, les variables explicatives sont
considérées comme très satisfaisantes.

Six variables explicatives ont été
évaluées : la distance autour du réseau routier, la
distance autour du réseau hydrographique, la distance autour des
agglomérations, l'aspect du terrain, la pente ainsi que la distance aux
champs. La figure 1 (aux annexes) présente les rendus visuels des
variables explicatives retenues. La relation entre les variables explicatives
et les principales transitions sont décrites dans le tableau 7
ci-dessous.
Tableau 7 : Coefficient de Cramer's V des variables
explicatives
Légende : D.A.H : distances aux
agglomérations humaines ; D.C : Distances aux champs ;
P : la pente ; AT : Aspect du terrain ;
RT : réseau routier ; RH :
réseau hydrographique.
|
Variables
|
FP-TBN
|
FS-TBN
|
CL.A-TBN
|
FP-CL.A
|
FS-CL.A
|
FS-FP
|
|
D.A.H
|
0.25
|
0.25
|
0.24
|
0.25
|
0.25
|
0.26
|
|
D.C
|
0.25
|
0.25
|
0.25
|
0.25
|
0.24
|
0.25
|
|
P
|
0.23
|
0.23
|
0.24
|
0.26
|
0.23
|
0.24
|
|
AT
|
0.23
|
0.26
|
0.26
|
0.32
|
0.32
|
0.19
|
|
RT
|
0.18
|
0.18
|
0.18
|
0.18
|
0.18
|
0.18
|
|
RH
|
0.12
|
0.12
|
0.12
|
0.12
|
0.12
|
0.12
|
Le tableau 30 montre que les distances au réseau
hydrographique constituent la variable explicative la moins importante pour les
principales transitions retenues. Ses coefficients globaux de Cramer's V
étant inférieurs à 0.15.
Dans l'ensemble, les distances aux agglomérations
humaines, les distances aux champs, la pente et l'aspect du terrain,
constituent des variables explicatives ayant de plus, influencé les
transitions observées entre 1995 et 2009.
Les plus fortes corrélations avec les changements
observés entre 1995 et 2009 se sont observées entre l'aspect du
terrain et les transitions forêts primaires-classe agricole, forêts
secondaires-classe agricole. L'aspect du terrain a en effet, enregistrés
des coefficients globaux de Cramer's V les plus élevés (0.32).
Ceci indique la forte contribution de l'aspect du terrain dans la
répartition des champs dans la région de Yangambi.
Les évaluations vues dans le tableau 21 montrent que
les variables explicatives étudiées et l'occupation du sol de la
région de Yangambi, à l'exception du réseau
hydrographique, sont relativement assez bien corrélées. Par
conséquent, toutes ces variables, excepté le réseau
hydrographique, ont utilisées dans le sous-modèle pour la
modélisation prédictive de l'occupation du sol.

Afin de se passer de la subjectivité et du manque de
précision d'une approche comparative purement visuelle entre une carte
de référence (2018) et la simulation (2018), R. G. Pontius et al.
(2004) montrent l'intérêt d'une comparaison statistique entre les
cartes.
Les auteurs distinguent quatre catégories de pixels
avec (i) les pixels corrects en raison d'une constance observée et
prédite (null successes [N]), (ii) les erreurs en raison d'une constance
observée mais prédite comme changée (false alarms [F]),
(iii) les pixels corrects dus à un changement observé et
prédit (hits [II]) et (iv) les erreurs dues à un changement
observé mais prédit comme constant (misses [M]). Pour juger la
précision de la prédiction globale des changements à
travers l'ensemble du paysage, ils avancent une méthode permettant de
mesurer les erreurs (en % du paysage) en raison de la quantité et de
l'allocation en se basant sur les résultats de la budgétisation
susmentionnée. Le tableau 8 ci-dessous montre les mesures des erreurs et
des exactitudes.
Tableau 8 : Mesure des erreurs et des
exactitudes
OC : changement observé en pourcentage
du paysage
PC : changement prédit
Q : erreur en raison de la quantité des
changements prédits
Q = |pc - oc| = |(f+h) - (m+h)| = |f-m|
A : erreur en raison de l'allocation des
changements prédits
A = (f+m) - q
T : erreur totale
T = f+m = q + a
L'erreur due à la quantité de changement
prédite mesure le pourcentage d'imperfection de la correspondance entre
la quantité de changement observée et prédite. L'erreur
due à l'allocation mesure le degré d'approximation de la
correspondance dans l'allocation spatiale des changements, compte tenu de la
spécification de la quantité des changements dans les cartes de
changements observés et prédits.
c. Traitement et analyse des données
climatiques
Les données climatiques (les données de
température et celles des précipitations)
prétraitées et organisées sous Excel, sont
importées sous le logiciel Statistica dans le but de calculer les
statistiques descriptives d'une part, et d'autres parts déterminer si la
relation entre les variables dépendantes (température et
précipitation) et indépendante (superficie forestière) est
au moins approximativement linéaire afin de définir les
équations de la prédiction climatique.

? Courbes de fluctuation climatique et les
statistiques descriptives
Pour chaque variable climatique, les courbes de fluctuation
spatio-temporelle sont produites. Elles retracent les variations annuelles des
précipitations et de la température. Les statistiques
descriptives (la moyenne ; le maximum ; le minimum) et les statistiques de
dispersion (la variance ; l'écart-type ; le coefficient de variation)
viennent à l'appui des courbes d'évolution et décrivent la
variabilité et les écarts autour des valeurs moyennes au courant
de trois décennies en étude.
? Prédiction des variables climatiques à
court, moyen et long terme
La prédiction climatique pour le court, le moyen et le
long terme dans le cadre de ce travail s'est reposée sur la
méthode de régression simple. En effet, trois modèles sont
testés et comparés. Il s'agit du modèle linéaire,
du modèle logarithmique et du modèle exponentiel.
De ce fait, les moyennes décennales des superficies
forestières sont considérées dans le cadre de cette
étude comme les seules variables indépendantes, desquelles
dépendent la fluctuation de la température et les
précipitations au.
? Evaluations des modèles
Pour chaque modèle un diagramme de dispersion est
produit. Ce diagramme permet de mesurer la corrélation « r »
entre les variables et la dépendance (R2) de
la variable Y à la variable X. Ces coefficients sont utiles dans la
régression car ils permettent d'évaluer les modèles
à travers leurs valeurs. Ils mesurent ainsi la force de la relation
(association) entre les variables et la qualité du modèle.
d. Traitement et analyse des données des
moteurs de déforestation
L'impact de chaque facteur de déforestation est
analysé sur une échelle annuelle. Ce qui a permis en
définitive, de déduire le principal moteur de
déforestation dans la zone d'étude. Chaque moteur de
déforestation est pondéré au nombre
d'enquêtés afin déduire l'activité autour de
laquelle, la majorité de la population s'adhère.
Le recours aux statistiques descriptives a permis de
décrire chaque moteur de déforestation. Pour cela, la moyenne, le
maximal, le minimal et les paramètres de dispersion ont
été appliqués.

| 


