GUESMI Thouraya
Chapitre 2 : Les techniques de filtrages

Figure 2.1. La Transformée de
Fourier
Cette méthode est un moyen qui assure le passage du
domaine temporel vers le domaine fréquentiel selon la formule:
?? (??) = ?~??(??).
??-2???????????? (2.1)
Néanmoins, la transformée de Fourier n'est pas
capable de déterminer les phases du signal reconstruit à
l'inverse malgré qu'elle peut extraire les informations sur le temps par
la transformée de Fourier inverse :
??(??) = ? ??(??).
??2????????????
8 (2.2)
-8
La transformée de Fourier est appliquée pour
retirer les informations fréquentielles d'un signal, mais le grand
inconvénient de cette transformation est son absence de
résolution temporelle. Cela désigne la capacité du TR de
révéler les fréquences dans le signal par contre elle est
inapte d'identifier à quel instant elles se produisent dans le
signal.
Il existe une transformée de Fourier plus «
locale » donnant des informations mieux localisées, il s'agit de la
transformée de Fourier Fenêtrée [29]
La transformée de Fourier Fenêtrée (STFT)
est introduite afin de corriger les limites de la TF. Elle emploi une «
Fenêtre glissante ».
Le principe général de la technique de la STFT
pour l'analyse d'un signal est le suivant : il s'agit d'utiliser un masque sous
forme d'une fenêtre glissante où le signal est stationnaire au
niveau local puis il se décale le long du signal.
GUESMI Thouraya
Chapitre 2 : Les techniques de filtrages
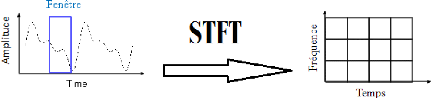
Figure 2.2. La Transformée de
Fourier par fenêtre glissante.
La figure 2.2 indique que les sinus de la transformée
de Fourier (TF) sont remplacés par des sinus multipliés dans une
fenêtre temporellement glissante.
La STFT est définie par:
????????(??,??) = ?[x(t).??*(t -
s)].??-??2????????t (2.3)
Avec :
· x (t) : signal d'origine.
· ??* : le conjugué de la fonction
fenêtrée (t) .
· ?? : la fréquence.
· s : l'échelle temporelle.
Comme l'équation suggère, cette méthode
est la multiplication de la TF avec une fonction fenêtrée. Cette
technique garantit une résolution invariable pendant toute la
durée du signal aussi la fenêtre g est invariante qui ne
dépend pas de l'échelle s c'est-à-dire
l'enveloppe de la fenêtre glissante est stable.
En outre, la taille de l'enveloppe définit la
précision d'interprétation du signal avec la STFT :
· En cas de petite fenêtre : les harmoniques basses
fréquences n'y seront pas contenues.
· En cas de grande fenêtre : les renseignements
sur les harmoniques à haute fréquence sont inclus dans les
informations sur la période complète de la fenêtre.
Alors le majeur désavantage de cette méthode
est l'invariance de la taille de la fenêtre, ce qui entraine la
nécessité d'une méthode où la fenêtre
s'adapte avec le changement de fréquence dans le signal à
analyser, cette technique est appelée analyse en ondelette.
| 


