IV- Statistiques descriptives et analyse des
données
Les données recueillies dans le cadre de ce travail
sont des données de très hautes fréquences
collectées pratiquement à la seconde. Une journée
d'activité de trading commence de 9:30 am et se termine a 16 :00 PM du
lundi au vendredi pour les jours non fériés de l'année en
question19. Nous avons donc dans un premier temps regroupé
les données en fréquences de 5 minutes ce qui nous donne 78
observations de prix pour chaque journée. Dans un second temps on a
calculé la fréquence optimale à partir de la formule de
Bandi et Russel M* (h?/(?(?)2)2)1/3 où
`h' est l'unité de période en secondes (dans notre cas `h'
correspond a une journée d'activité de trading soit 23,400
secondes),`Q20' est appelé `integreted quarticity' et est
généralement remplacé par
|
son estimateur Q?
|
??? ? ?r
? 4 21 et `?' est la microstructure noise. Pour arriver à
la fréquence
??? j
|
optimale, on a choisit dans un premier temps, pour le calcul
de r?4 et de ?Q, une fréquence relativement basse
de 15 minutes qui permette de rendre négligeable l'effet de la «
microstructure noise du marché » sur leur calcul. Ensuite, on
calcul un Mj22 pour chacun des 252 jours d'activités de
l'année 2010 et on détermine sa valeur moyenne de sorte qu'on ait
une valeur unique M*. Dans le cadre de ce travail on a trouvé une valeur
M* avoisinant les 9 minutes et de ce fait, pour la simplicité des
calculs on a considéré M*=9 minutes.
Le modèle HAR(3)-RV consiste à faire la
régression ??????
(?) = c+ â(d) ???(?)+ â(w)
???(?)+
â(m) ???(?)+ùt+1d.. Dans ce
modèle, ??????
(?) est la volatilité réalisée
journalière au temps t+1, ???(?) est la volatilité
réalisée journalière au temps t, ???(?) est la
volatilité réalisée hebdomadaire obtenue en faisant la
moyenne arithmétique simple de la volatilité
réalisée pour 5 jours ouvrables consécutifs et
???(?)est la volatilité réalisée
mensuelle obtenue en faisant la moyenne arithmétique simple de 20 jours
ouvrables consécutifs. De ce fait, on a pu déterminer les
volatilités réalisées ???(?) en prenant la racine
carrée de la somme des carrés du logarithme
? )1/2.
des pris par intervalles de 5 minutes et de 9 minutes ???(?)= (?
r
???
??? ???.?'
19 Cete consideration d'un journee d'activité est selon le
New York Stock Exchange (NYSE).
20 `Q' est considéré comme la variance du signal
21 Pour le calcul le calcul de Q? on a pris M=15 minutes afin
d'éviter la microstructure noise contamination.
22 Mj est une valeur journalière
10
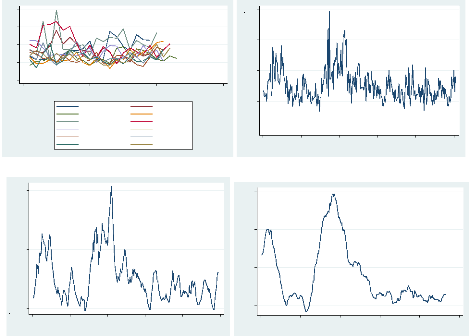
Volatilité Réalisée du CHK stock:
Données regroupées par fréquences de 5 minutes
Les graphiques présentés dans cette partie du
travail font ressortir les tendances des volatilités
réalisées regroupées par fréquences de 5 minutes.
La comparaison de ces dernières, mois par mois (de janvier 2010 à
décembre 2010), laisse ressortir une certaine consistance dans les
données sauf pour les mois de Février, Mai et Juin où il y
a certaine hausse à leur début. Cette variation peut
également être observée quand un graphique chronologique
annuelle est réalisé et également en observant les
volatilités hebdomadaires et mensuelles.
.01 .02
0
0 10 20 30
days 2
Jan freq 5 Fev freq 5
Mars freq 5 AVRIl freq 5
MAY
freq 5 JUIN freq 5
JUILLET freq 5 AOUT freq 5
SEPT freq 5 OCT freq 5
NOV
freq 5 DEC freq 5
.02
.015
.01
.005
0
0 50 100 150 200 250
days
.015
.01
.005
0 50 100 150 200 250
Weeks
.012
.01
.006 .008
0 50 100 150 200 250
Months
Figure 1 : Volatilités réalisées des
données regroupées en fréquence de 5 minutes
11
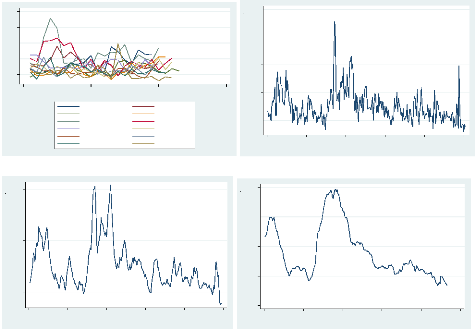
Volatilité Réalisée du CHK stock:
Données regroupées par fréquences optimale de 9
minutes
A peu près les mêmes tendances sont observées
quand les volatilités réalisées sont regroupées par
fréquences de 9 minutes que quand elles le sont par fréquences de
5 minutes. Les graphiques suivant en attestent cette similitude.
Figure 2 : Volatilités réalisées des
données regroupées en fréquence de 9 minutes
.01 .02
0 10 20 30
days 2
Jan freq 9 Fev freq 9
Mars freq 9 AVRIl freq 9
MAY
freq 9 JUIN freq 9
JUILLET freq 9 AOUT freq 9
SEPT freq 9 OCT freq 9
NOV
freq 9 DEC freq 9
.025
.02
.015
.01
.005
0 50 100 150 200 250
days
.015
.01
.005
0 50 100 150 200 250
Weeks
.012
.01
.004 .006 .008
0 50 100 150 200 250
Months
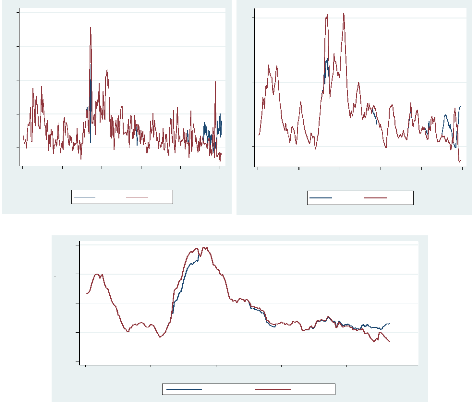
Volatilité Réalisée,
fréquences de 5 minutes et de 9 minutes : Comparaison
En dehors des similitudes observées au niveau de leur
tendance, on a jugé bon de mettre sur un même repère les
volatilités réalisées de même type. Ce faisant, on
peut remarquer que les graphes sont presque toujours confondus dans le cas des
volatilités journalières et hebdomadaires, sauf à quelques
rares endroits. En ce qui concerne leurs volatilités
réalisées
12
considérées mensuellement, les données
regroupées en fréquence de 9 minutes attestent de
volatilités généralement plus élevées que
ceux regroupées en fréquence optimale de 5 minutes.
Figure 3 : Volatilités réalisées :
graphiques comparés des données de 5 minutes et de 9 minutes
.01
. 0 1 . 0 2
.0 1
0 50 100 150 200 250
days
0 50 100 150 200 250
Weeks
RV(d)5 RV(d)9
RV(w)5 RV(w)9
0 50 100 150 200 250
Months
RV(m)5 RV(m)9
Une analyse descriptive des donnés journalières
permet de tirer les même conclusions que précédemment.
13
Tableau 1 : Statistiques descriptives
. tabstat rvd5 rvd9 rvw5 rvw9 rvm5 rvm9, statistics( mean
sd skewness kurtosis ) columns(variables)
|
stats
|
rvd5
|
rvd9
|
rvw5
|
rvw9
|
rvm5
|
rvm9
|
|
mean
|
.0075705
|
.0075156
|
.0075754
|
.0075559
|
.0079124
|
.0076104
|
|
sd
|
.0025741
|
.0028641
|
.0019837
|
.00223
|
.0018749
|
.0017779
|
|
skewness
|
1.404292
|
1.650738
|
1.191229
|
1.299055
|
1.317743
|
.9857251
|
|
kurtosis
|
5.802221
|
7.374368
|
4.238651
|
4.662374
|
3.685027
|
2.791721
|
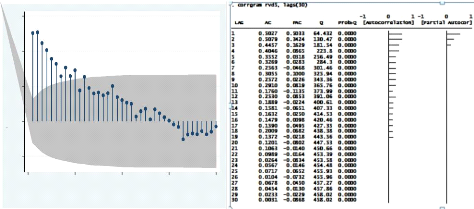
Auto-Corrélation des Volatilités
réalisées pour les séries journalières
L'analyse des graphiques et tableaux
d'auto-corrélations pour les séries de volatilités
réalisées attestent d'une éventuelle stationnarité
(sous l'hypothèse que la variable en question est homoskedastique) pour
les deux séries (Volatilités réalisées
journalières regroupées en fréquences de 5 minutes et en
fréquences de 9 minutes) quand on fait le calcul avec 30 retards pour
les deux séries. En effet, l'auto-corrélation des erreurs tend
vers 0 à partir de 19ème retard pour la série
RV(d)5 et à partir du 22ème retard pour la
série RV(d)9.
14
Figure 4 : Auto-corrélation des volatilités
réalisées journalières : fréquence de 5 minutes
0.00 0 . 2 0 0 . 4 0 0 . 6 0
-0.20
0 10 20 30 40
Lag
Bartlett's formula for MA(q) 95% confidence bands

0 . 0 0 0 . 2 0 0 . 4 0 0 . 6 0
- 0 . 2 0
0 10 20 30 40
Lag
Bartlett's formula for MA(q) 95% confidence bands
Figure 5 : Auto-corrélation des volatilités
réalisées journalières : fréquence de 9 minutes
15
V- Estimation et prévision
Les variables en questions sont toutes les volatilités
calculées à partir du logarithme du prix du stock CHK,
considérées de manière journalières, hebdomadaires
ou mensuelles pour des données regroupés en fréquences de
5 et de 9 minutes. Dans le cadre de l'estimation et pour la prévision,
les variables dépendantes sont notées RV(d)5 et RV(d)9 et se
réfèrent respectivement aux volatilités
réalisées journalières pour la période « t+1
» des séries regroupées en fréquences de 5 et 9
minutes. Les variables explicatives RV(d)5t, RV(w)5t, RV(m)5t, RV(d)9t,
RV(w)9t, RV(m)9t sont respectivement les volatilités
réalisées journalières, hebdomadaires et mensuelles pour
la période « t » respectivement pour les séries
regroupés en fréquences de 5 et 9 minutes. Le modèle HAR
utilisé régresse la volatilité journalière sur la
volatilité journalière retardée ainsi que sur les
volatilités hebdomadaire et mensuelle, également
retardées, c'est-à-dire de la période « t ».
Cette partie du travail présente dans un premier temps les testes de
stationnarité puis les estimations ensuite les prévisions pours
les deux séries sous études.
Test de Stationnarité et relation de long
terme
Avant de procéder à l'estimation des
paramètres du modèle, nous allons utiliser les tests
Dickey-Fuller Augmenté (ADF) et Phillips-Perron (PP) pour
déterminer si les séries de volatilités
réalisés journalières, hebdomadaires et mensuelles sont
stationnaires à travers le temps. L'hypothèse nulle de ces tests
stipule que la variable contient une racine unitaire, tandis que
l'hypothèse alternative indique que la série est
générée par un processus stationnaire. Pour choisir le
nombre optimal de retards à inclure dans la régression, nous
avons utilisé le critère d'information AIC23 (Akaike
Information Criteria).
23 Voir tableau # 9 à tableau #14 en annexe.
16
Tableau# 2 Test de stationnarité ADF et PP
|
Augmented Dickey-Fuller
|
Test Stat
|
5% critical Value
|
RV(d)5t -4.284 -2.881
RV(w)5t -2.182 -2.882
RV(m)5t -2.349 -2.881
RV(d)9t -3.912 -2.881
RV(w)9t -2.084 -2.882
RV(m)9t -2.306 -2.882
|
Phillips-Perron Test
|
Test Stat
|
5% critical Value
|
RV(d)5t -9.017 -2.881
RV(w)5t -3.006 -2.881
RV(m)5t -1.313 -2.881
RV(d)9t
RV(w)9t
RV(m)9t
|
-6.849
|
-2.881
|
|
-3.004
|
-2.881
|
|
-1.024
|
-2.881
|
Source : Calculs effectués à partir de
Stata
Le tableau ci-haut présente les résultats des
deux tests (ADf et PP) pour les différentes séries
utilisées dans l'estimation des volatilités
réalisées journalières regroupées en
fréquences de 5 et de 9 minutes. Selon le test ADF seulement les
séries de volatilités réalisées journalières
(fréquences de 5 et 9 minutes) sont stationnaires tandis que le test PP
dénote la stationnarité des séries de volatilités
hebdomadaires également en plus. Ceci est assez juste car le test PP est
habituellement plus puissant que celui d'ADF. Michael et al (1997), soutiennent
que ces problèmes peuvent être dus soit à des erreurs de
mesure dans les données soit à cause de la faible puissance des
tests, ou tout simplement à cause de l'absence de
linéarité dans les séries. Toutefois on suppose que toutes
les variables sont stationnaires pour pouvoir poursuivre notre étude.
17
Estimation
L'estimation des paramètres du modèle HAR(3)-RV
est faite par la méthode des moindres carrés ordinaires
(MCO)24. On considère toutes les variables de
l'équation ??????
(?) = c+ â(d) ??? (?)+ â(w) ??? (?)+
â(m) ??? (?)+ùt+1d comme étant observées
et on estime les paramètres. Cependant, dans le but de palier
d'éventuels problèmes d'auto-corrélation des erreurs dans
les données, on a appliqué la méthode de correction de
covariance pour les séries corrélées de Newey-West. Le
tableau suivant présente les résultats obtenus de
l'estimation.
Tableau# 3 HAR(3)-RV estimation

Source : Calculs effectués à partir de
Stata
Le seuil critique pour un niveau d'erreur de 5% est de
1,81225 et en comparant les « t » statistiques (les
valeurs entre parenthèses) à ce seuil on remarque que pour le
modèle avec fréquences de 5 minutes, seulement le coefficient de
la volatilité réalisée hebdomadaire est significativement
différent de 0 tandis que pour le modèle avec fréquences
de 9 minutes seulement le coefficient de la volatilité
réalisée journalière l'est. Cette non
significativité de la plus part des paramètres peut être du
au fait que certaines séries ne sont pas stationnaires ou bien à
cause d'une présence importante de « microstructure noise»
dans les séries. Comme expliqué par Corsi 2009, la non
significativité des paramètres en question peut être due au
fait
24 Le principe des MCO est d'estimer les coefficients de
façon à minimiser l'erreur d'estimation.
25 Valeur tirée de Hamilton, page 755.
18
de l'estimation de séries fortement affectées
par la microstructure noise. En effet c'est possiblement le cas des
séries RV(d)5t; RV(w)5t; RV(d)9t et RV(w)9t qui sont toutes
stationnaires selon les résultats du test PP a 5%.
Une analyse d'un modèle AR(5)26 sur les
volatilités journalières regroupées suivant les deux
fréquences utilisées, nous permet de soutenir l'hypothèse
d'un possible problème de microstructure noise au niveau des
données. En effet l'estimation des modèles AR(5), avec la
correction de Newey West, nous montre que seulement les coefficients des
volatilités réalisées avec un seul retard sont
significativement différents de « 0 ».
Afin de pouvoir continuer avec notre travail et
réaliser les prévisions, on va supposer que toutes les
séries sont stationnaires et que les résultats d'estimations sont
concluants.
Prévisions hors échantillons
Dans cette partie du travail on va procéder des
exercices de prévisions hors échantillon afin de
déterminer lequel des séries du CHK stock, regroupées soit
en fréquences de 5 minutes soit en fréquences optimales de 9
minutes de Bandi et Russell (2007), est plus performant en utilisant le model
HAR(3)-RV de Corsi (2009). En effet, l'une des utilités principales de
l'estimation de volatilités est la réalisation de
prévisions pouvant servir à la prise de décision.
Pour évaluer et comparer les prévisions du
modèle HAR(3)-RV appliqué aux séries de CHK stock
regroupées en fréquences de 5 minutes et en fréquences
optimale de 9 minutes, on priorise dans le cadre de ce travail la
méthode de fenêtre récursive. On a choisit de faire la
prévision sur deux mois soit 40 jours ouvrables, selon notre
définition d'un mois, dans le cadre de notre travail. Soit R le nombre
d'observations pour l'estimation et P celui pour la prévision, on a donc
a R=192 et P=40 pour les deux variables sous études (séries de
volatilités réalisées journalières
regroupées en fréquences de 5 minutes et de 9 minutes). Le
principe de la fenêtre récursive est la suivante: On estime le
modèle sur les observations de 1 à R et on fait une
prévision pour R + h27. On ajoute alors une nouvelle
observation à l'échantillon et on ré-estime le
modèle pour les
26 Voir tableau # 23 et 24 en annexe
27 ` h' varie de 1 à P
19
observations 1 à R+1et on fait une prévision
pour R+1+h. L'échantillon avec lequel nous faisons l'estimation augmente
à chaque fois.
Le processus de prévision hors échantillon se
fera donc comme suit:
Premièrement on estime le modèle ??????
(?) = c+ â(d) ???
(?)+ â(w) ??? (?)+
â(m) ???
(?)+ùt+1d en utilisant les
données pour les jours de 1 à 192 et on détermine
â? (d)(192), â? (w)( 192), â? (m)( 192),
??28(192). Ensuite on produit la prévision de RV(d, 193) et
on la note ??? (d, 193). Ensuite on estime à nouveau le même
modèle mais en considérant maintenant les données se 1
à 193 pour déterminer â? (d)(193), â? (w)(
193), â? (m)( 193), ??(193) puis produire la prévision
de RV(d, 194)
|
qu'on note ???
|
(d, 194). On continue ainsi jusqu'à la prévision
de RV(d, 232) qu'on note
|
?
?? (d, 232).
L'objectif de ce travail étant de comparer
l'efficacité d'un regroupement des volatilités
réalisées , journalières, hebdomadaires et mensuelles ,en
fréquence de 5 minutes et en fréquence optimale ( qui est de 9
minutes dans notre cas), on va calculer le « Heteroskedasticity adjusted
root meam square error (HRMSE) » tel que proposé par Corsi, Pirino
et Renò (2010) pour chacune des deux projections et ensuite les
comparer. Le modèle qui produira le HRMSE le plus faible sera
considéré comme étant le meilleur dans le cadre bien
précis du CHK stock. L'expression du
?
HRMSE est ?? ? ? ? ????????? ??? ? .
???
Les projections et calculs des HRMSE se trouvent dans les deux
tableaux suivants.
28 C? eslt la valeur estimée de la constante C du
modèle.
20
Tableau # 4 Prévisions des volatilités
réalisées journalières regroupées en
fréquences de 5 minutes

Jour
Volatilites Observees
Constante et Coefficients estimes du modele
Valeures projetees et Calcul du HRMSE
RV(d)5tf RV(w)5tf RV(m)5tf c" b1" b2" b3" Y" Y Y-Y"
(Y-Y")/Y ((Y-Y")/Y)"2 (1/40)* ((Y-Y")/Y)"2
|
0.0018459
|
0.1563002
|
0.6018683
|
0.0076421
|
|
0.0017772
|
0.1645432
|
0.5858661
|
0.0220828
|
|
0.0017479
|
0.1651393
|
0.5815531
|
0.0286278
|
|
0.0017428
|
0.1636357
|
0.5827547
|
0.0293956
|
|
0.0018368
|
0.1725239
|
0.5702962
|
0.0236012
|
|
0.0018747
|
0.1720189
|
0.5685132
|
0.0220048
|
|
0.0018578
|
0.1713607
|
0.5704522
|
0.0224127
|
|
0.0018637
|
0.1709753
|
0.5706345
|
0.0220171
|
|
0.001829
|
0.1722678
|
0.5700312
|
0.0248247
|
|
0.0018153
|
0.172427
|
0.5704733
|
0.0256084
|
|
0.0018023
|
0.172894
|
0.5701506
|
0.0268075
|
|
0.0017804
|
0.170913
|
0.5728039
|
0.0283278
|
|
0.0018097
|
0.1709216
|
0.5725243
|
0.0255466
|
|
0.0018138
|
0.1705714
|
0.5728131
|
0.0251709
|
|
0.00177
|
0.1675821
|
0.5783849
|
0.0270914
|
|
0.0017913
|
0.1670175
|
0.5782288
|
0.0255592
|
|
0.0017537
|
0.1658684
|
0.5773317
|
0.0315081
|
|
0.001782
|
0.1648022
|
0.5784558
|
0.0284316
|
|
0.0017729
|
0.1662356
|
0.5770919
|
0.0293317
|
|
0.0016938
|
0.1664063
|
0.5707775
|
0.0434201
|
|
0.0016851
|
0.1641059
|
0.5723782
|
0.0449302
|
|
0.0017792
|
0.1501784
|
0.5898017
|
0.0314926
|
|
0.0017234
|
0.1566712
|
0.5798423
|
0.0407615
|
|
0.0016855
|
0.1530694
|
0.5807374
|
0.0471365
|
|
0.0017167
|
0.1557225
|
0.577874
|
0.0442253
|
|
0.0017442
|
0.158738
|
0.5723437
|
0.0439705
|
|
0.0017771
|
0.1592116
|
0.568745
|
0.0436602
|
|
0.001772
|
0.1588429
|
0.5698252
|
0.0434721
|
|
0.0017849
|
0.1586889
|
0.5685018
|
0.0435955
|
|
0.0017709
|
0.1595789
|
0.5691348
|
0.0435511
|
|
0.0017296
|
0.1586224
|
0.5742235
|
0.0437012
|
|
0.0017297
|
0.1586182
|
0.5742241
|
0.0436986
|
|
0.0016885
|
0.1566861
|
0.5787317
|
0.045387
|
|
0.0016946
|
0.1562236
|
0.5792334
|
0.044698
|
|
0.0016601
|
0.159206
|
0.5747735
|
0.049852
|
|
0.0016252
|
0.1613872
|
0.5690936
|
0.0569481
|
|
0.0016141
|
0.1629218
|
0.5662217
|
0.0594351
|
|
0.0015826
|
0.1594892
|
0.5661395
|
0.0659914
|
|
0.0016092
|
0.1587013
|
0.5688399
|
0.061456
|
|
0.0016032
|
0.1579979
|
0.5692925
|
0.0622881
|
|
0.005868819
|
|
|
|
|
|
0.007035562
|
0.004248532
|
-0.00278703
|
-0.655998308
|
0.43033378
|
0.010758345
|
|
0.007520017
|
0.00634207
|
-0.001177947
|
-0.185735409
|
0.034497642
|
0.000862441
|
|
0.007776141
|
0.007737261
|
-3.88804E-05
|
-0.005025087
|
2.52515E-05
|
6.31287E-07
|
|
0.008009672
|
0.010947599
|
0.002937927
|
0.268362687
|
0.072018532
|
0.001800463
|
|
0.006985544
|
0.007909681
|
0.000924137
|
0.116836185
|
0.013650694
|
0.000341267
|
|
0.006452743
|
0.005889717
|
-0.000563026
|
-0.09559475
|
0.009138356
|
0.000228459
|
|
0.006601513
|
0.006711692
|
0.000110179
|
0.016415996
|
0.000269485
|
6.73712E-06
|
|
0.006485142
|
0.005281377
|
-0.001203766
|
-0.227926485
|
0.051950483
|
0.001298762
|
|
0.006743892
|
0.006047966
|
-0.000695926
|
-0.115067763
|
0.01324059
|
0.000331015
|
|
0.006618745
|
0.006172305
|
-0.000446441
|
-0.072329678
|
0.005231582
|
0.00013079
|
|
0.006692729
|
0.005999666
|
-0.000693063
|
-0.115516972
|
0.013344171
|
0.000333604
|
|
0.006958394
|
0.007826758
|
0.000868364
|
0.110948083
|
0.012309477
|
0.000307737
|
|
0.006712663
|
0.006497243
|
-0.00021542
|
-0.033155529
|
0.001099289
|
2.74822E-05
|
|
0.00634954
|
0.004813758
|
-0.001535782
|
-0.319040104
|
0.101786588
|
0.002544665
|
|
0.006578762
|
0.007142242
|
0.00056348
|
0.078893986
|
0.006224261
|
0.000155607
|
|
0.006362125
|
0.005652878
|
-0.000709247
|
-0.125466593
|
0.015741866
|
0.000393547
|
|
0.007227727
|
0.007616882
|
0.000389155
|
0.051091075
|
0.002610298
|
6.52574E-05
|
|
0.006574
|
0.005820431
|
-0.000753568
|
-0.129469527
|
0.016762358
|
0.000419059
|
|
0.006147081
|
0.003517128
|
-0.002629953
|
-0.747755821
|
0.559138768
|
0.013978469
|
|
0.007344819
|
0.00738077
|
3.59509E-05
|
0.004870885
|
2.37255E-05
|
5.93138E-07
|
|
0.007900158
|
0.010424015
|
0.002523858
|
0.242119517
|
0.05862186
|
0.001465547
|
|
0.006648317
|
0.004473709
|
-0.002174608
|
-0.486086137
|
0.236279733
|
0.005906993
|
|
0.006931213
|
0.005434635
|
-0.001496579
|
-0.275377982
|
0.075833033
|
0.001895826
|
|
0.007524139
|
0.008566717
|
0.001042578
|
0.121700962
|
0.014811124
|
0.000370278
|
|
0.007040897
|
0.007886634
|
0.000845737
|
0.107236784
|
0.011499728
|
0.000287493
|
|
0.006588018
|
0.007531939
|
0.000943922
|
0.125322541
|
0.015705739
|
0.000392643
|
|
0.006161541
|
0.005886214
|
-0.000275327
|
-0.046774834
|
0.002187885
|
5.46971E-05
|
|
0.006103207
|
0.006475832
|
0.000372625
|
0.057540904
|
0.003310956
|
8.27739E-05
|
|
0.005936236
|
0.005228465
|
-0.000707771
|
-0.135368821
|
0.018324718
|
0.000458118
|
|
0.005791484
|
0.004346462
|
-0.001445021
|
-0.332459157
|
0.110529091
|
0.002763227
|
|
0.00617182
|
0.006004133
|
-0.000167686
|
-0.027928441
|
0.000779998
|
1.94999E-05
|
|
0.006012499
|
0.004565474
|
-0.001447025
|
-0.316949503
|
0.100456987
|
0.002511425
|
|
0.006472666
|
0.006708174
|
0.000235507
|
0.035107493
|
0.001232536
|
3.08134E-05
|
|
0.006480789
|
0.005215601
|
-0.001265188
|
-0.242577562
|
0.058843874
|
0.001471097
|
|
0.006717458
|
0.005446289
|
-0.001271169
|
-0.233400871
|
0.054475967
|
0.001361899
|
|
0.007243671
|
0.006585228
|
-0.000658443
|
-0.099987956
|
0.009997591
|
0.00024994
|
|
0.007190466
|
0.005662202
|
-0.001528263
|
-0.269906167
|
0.072849339
|
0.001821233
|
|
0.007718061
|
0.008778895
|
0.001060834
|
0.120839166
|
0.014602104
|
0.000365053
|
|
0.007274014
|
0.006955459
|
-0.000318555
|
-0.045799325
|
0.002097578
|
5.24395E-05
|
|
0.007452727
|
0.008403169
|
0.000950442
|
0.113105178
|
0.012792781
|
0.00031982
|
|
0.004248532
|
0.007437029
|
0.006477798
|
|
0.00634207
|
0.007765266
|
0.006786572
|
|
0.007737261
|
0.00783919
|
0.006693154
|
|
0.010947599
|
0.007348013
|
0.006578023
|
|
0.007909681
|
0.006368086
|
0.006458978
|
|
0.005889717
|
0.006020611
|
0.006457826
|
|
0.006711692
|
0.006042601
|
0.006539937
|
|
0.005281377
|
0.006265614
|
0.006498663
|
|
0.006047966
|
0.006508787
|
0.006558386
|
|
0.006172305
|
0.006261946
|
0.006517411
|
|
0.005999666
|
0.006455934
|
0.006426119
|
|
0.007826758
|
0.006386576
|
0.006426342
|
|
0.006497243
|
0.006344601
|
0.006263278
|
|
0.004813758
|
0.006209238
|
0.006273825
|
|
0.007142242
|
0.005949912
|
0.006293917
|
|
0.005652878
|
0.005997618
|
0.006209119
|
|
0.007616882
|
0.006951845
|
0.006255737
|
|
0.005820431
|
0.006323211
|
0.006158003
|
|
0.003517128
|
0.006246051
|
0.006305926
|
|
0.00738077
|
0.007255969
|
0.006477842
|
|
0.010424015
|
0.007357142
|
0.006528962
|
|
0.004473709
|
0.006778727
|
0.00632396
|
|
0.005434635
|
0.007061228
|
0.006426751
|
|
0.008566717
|
0.007269467
|
0.006485111
|
|
0.007886634
|
0.006601817
|
0.006355011
|
|
0.007531939
|
0.005893783
|
0.006252902
|
|
0.005886214
|
0.005588221
|
0.006161543
|
|
0.006475832
|
0.005324073
|
0.006182722
|
|
0.005228465
|
0.005370542
|
0.006158296
|
|
0.004346462
|
0.005367969
|
0.006242826
|
|
0.006004133
|
0.005587934
|
0.006432462
|
|
0.004565474
|
0.005704153
|
0.006480055
|
|
0.006708174
|
0.005923499
|
0.006719377
|
|
0.005215601
|
0.006337643
|
0.006720978
|
|
0.005446289
|
0.006685615
|
0.006971874
|
|
0.006585228
|
0.007276991
|
0.007276991
|
|
0.005662202
|
0.007437161
|
0.007449931
|
|
0.008778895
|
0.007426378
|
0.008045841
|
|
0.006955459
|
0.007188374
|
0.007679314
|
|
0.008403169
|
0.007023501
|
0.008403169
|
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
Ó 0.055865745
HRMSE 0.027932873
Tableau réalisé à partir de
donnés tirées de Stata
21
Tableau # 5 Prévisions des volatilités
réalisées journalières regroupées en
fréquences optimales de 9 minutes

Jour
Volatilites Observees
Constante et Coefficients estimes du modele
Valeures projetees et Calcul du HRMSE
RV(d)9tf RV(w)9tf RV(m)9tf c" b1" b2" b3" Y" Y Y-Y"
(Y-Y")/Y ((Y-Y")/Y)"2 (1/40)* ((Y-Y")/Y)"2
|
0.004248532
|
0.007437029
|
0.006379598
|
|
0.00634207
|
0.007765266
|
0.006688372
|
|
0.007737261
|
0.00783919
|
0.006594954
|
|
0.010947599
|
0.007348013
|
0.006479822
|
|
0.007909681
|
0.006368086
|
0.006360778
|
|
0.005889717
|
0.006020611
|
0.006359626
|
|
0.006711692
|
0.006042601
|
0.006441737
|
|
0.005281377
|
0.006265614
|
0.006400463
|
|
0.006047966
|
0.006508787
|
0.006460186
|
|
0.006172305
|
0.006261946
|
0.006419211
|
|
0.005999666
|
0.006455934
|
0.006327919
|
|
0.007826758
|
0.006386576
|
0.006328142
|
|
0.006497243
|
0.0059518
|
0.006165078
|
|
0.004813758
|
0.005816437
|
0.006175624
|
|
0.007142242
|
0.005557111
|
0.006195717
|
|
0.005652878
|
0.005604817
|
0.006110919
|
|
0.005652878
|
0.006559044
|
0.006157536
|
|
0.005820431
|
0.006323211
|
0.006158003
|
|
0.003517128
|
0.006246051
|
0.006150091
|
|
0.00738077
|
0.007255969
|
0.006249331
|
|
0.010424015
|
0.007357142
|
0.006165095
|
|
0.004473709
|
0.006778727
|
0.005901533
|
|
0.005434635
|
0.007061228
|
0.005921585
|
|
0.008566717
|
0.007269467
|
0.00596387
|
|
0.007886634
|
0.006601817
|
0.005856193
|
|
0.007531939
|
0.005893783
|
0.005650987
|
|
0.005886214
|
0.005588221
|
0.005539465
|
|
0.006475832
|
0.005324073
|
0.00544073
|
|
0.005228465
|
0.005370542
|
0.00532952
|
|
0.004346462
|
0.005367969
|
0.005465916
|
|
0.006004133
|
0.005587934
|
0.005594856
|
|
0.004565474
|
0.005704153
|
0.005472397
|
|
0.006708174
|
0.005923499
|
0.005982961
|
|
0.005215601
|
0.005714305
|
0.005984453
|
|
0.005446289
|
0.00577157
|
0.005911916
|
|
0.006585228
|
0.005821523
|
0.00582443
|
|
0.005662202
|
0.005535032
|
0.005701916
|
|
0.005662202
|
0.00537754
|
0.005634773
|
|
0.00550193
|
0.005501166
|
0.005500463
|
|
0.005696053
|
0.005683414
|
0.005436699
|
|
0.005152772
|
0.005300706
|
0.005347576
|
|
0.0016343
|
0.4988372
|
0.2190531
|
0.0789913
|
|
0.0015735
|
0.5045644
|
0.2082028
|
0.0900205
|
|
0.0015446
|
0.5049687
|
0.2049135
|
0.0957035
|
|
0.0015167
|
0.4983139
|
0.2097454
|
0.1001111
|
|
0.001601
|
0.5046873
|
0.2017939
|
0.0933165
|
|
0.0016411
|
0.5041005
|
0.2007061
|
0.0909254
|
|
0.0016186
|
0.5034672
|
0.2024683
|
0.0920309
|
|
0.0016335
|
0.5026033
|
0.2029615
|
0.0908822
|
|
0.0016023
|
0.5036406
|
0.2022821
|
0.0936587
|
|
0.0015894
|
0.5038038
|
0.2024889
|
0.0945826
|
|
0.0015807
|
0.5040811
|
0.2022566
|
0.0954257
|
|
0.0015481
|
0.5016975
|
0.2050819
|
0.0982425
|
|
0.0015793
|
0.5022696
|
0.2034937
|
0.0960373
|
|
0.0015993
|
0.5011631
|
0.2038083
|
0.0947347
|
|
0.001548
|
0.4973144
|
0.2111833
|
0.0964418
|
|
0.0015752
|
0.4971371
|
0.2099546
|
0.0950001
|
|
0.0015571
|
0.4981234
|
0.2086602
|
0.0971989
|
|
0.0015386
|
0.4987583
|
0.2080517
|
0.0991009
|
|
0.0015557
|
0.4964643
|
0.210267
|
0.097359
|
|
0.0014701
|
0.4965922
|
0.2038865
|
0.1123259
|
|
0.0014411
|
0.4912439
|
0.2064881
|
0.1179327
|
|
0.0015748
|
0.4764531
|
0.2275757
|
0.0971853
|
|
0.0015246
|
0.4806918
|
0.2199227
|
0.1059929
|
|
0.001468
|
0.4772629
|
0.2182951
|
0.1169314
|
|
0.0014982
|
0.4789231
|
0.2177648
|
0.1126093
|
|
0.0015219
|
0.4804558
|
0.2161432
|
0.1101519
|
|
0.001563
|
0.4805763
|
0.2153835
|
0.1062996
|
|
0.0015474
|
0.4799933
|
0.2163888
|
0.1075804
|
|
0.0015695
|
0.479653
|
0.216393
|
0.1054701
|
|
0.0015643
|
0.479908
|
0.2162551
|
0.1059211
|
|
0.0015111
|
0.479429
|
0.2177645
|
0.1106778
|
|
0.0015249
|
0.4786584
|
0.2185117
|
0.1091777
|
|
0.0014766
|
0.4770252
|
0.2213892
|
0.1129838
|
|
0.0014959
|
0.4763711
|
0.2212694
|
0.1117119
|
|
0.0014761
|
0.4768629
|
0.2213596
|
0.1132328
|
|
0.0014494
|
0.4760472
|
0.2227128
|
0.1155342
|
|
0.0014636
|
0.4760072
|
0.2223139
|
0.1144428
|
|
0.0014548
|
0.4759681
|
0.2226839
|
0.1150718
|
|
0.0014474
|
0.4760374
|
0.2227438
|
0.1157511
|
|
0.0014323
|
0.4761774
|
0.2226057
|
0.117418
|
|
0.005868819
|
|
|
|
|
|
0.005886663
|
0.004248532
|
-0.001638131
|
-0.385575644
|
0.148668577
|
0.003716714
|
|
0.006992323
|
0.00634207
|
-0.000650253
|
-0.102530152
|
0.010512432
|
0.000262811
|
|
0.007689191
|
0.007737261
|
4.80704E-05
|
0.006212839
|
3.85994E-05
|
9.64984E-07
|
|
0.009161955
|
0.010947599
|
0.001785644
|
0.163108302
|
0.026604318
|
0.000665108
|
|
0.007471522
|
0.007909681
|
0.000438159
|
0.055395276
|
0.003068637
|
7.67159E-05
|
|
0.006396734
|
0.005889717
|
-0.000507017
|
-0.086085187
|
0.007410659
|
0.000185266
|
|
0.006813991
|
0.006711692
|
-0.000102299
|
-0.015241876
|
0.000232315
|
5.80787E-06
|
|
0.006141304
|
0.005281377
|
-0.000859927
|
-0.162822564
|
0.026511187
|
0.00066278
|
|
0.006569965
|
0.006047966
|
-0.000521999
|
-0.086309872
|
0.007449394
|
0.000186235
|
|
0.006574151
|
0.006172305
|
-0.000401846
|
-0.065104711
|
0.004238623
|
0.000105966
|
|
0.006514619
|
0.005999666
|
-0.000514954
|
-0.085830403
|
0.007366858
|
0.000184171
|
|
0.007406229
|
0.007826758
|
0.00042053
|
0.053729729
|
0.002886884
|
7.21721E-05
|
|
0.006645899
|
0.006497243
|
-0.000148656
|
-0.022879823
|
0.000523486
|
1.30872E-05
|
|
0.005782262
|
0.004813758
|
-0.000968504
|
-0.201194949
|
0.040479407
|
0.001011985
|
|
0.006871035
|
0.007142242
|
0.000271207
|
0.037972274
|
0.001441894
|
3.60473E-05
|
|
0.00614275
|
0.005652878
|
-0.000489873
|
-0.086658975
|
0.007509778
|
0.000187744
|
|
0.006340048
|
0.005652878
|
-0.00068717
|
-0.12156115
|
0.014777113
|
0.000369428
|
|
0.006367407
|
0.005820431
|
-0.000546976
|
-0.093975088
|
0.008831317
|
0.000220783
|
|
0.005213934
|
0.003517128
|
-0.001696806
|
-0.482440679
|
0.232749009
|
0.005818725
|
|
0.007316689
|
0.00738077
|
6.40813E-05
|
0.008682194
|
7.53805E-05
|
1.88451E-06
|
|
0.008808063
|
0.010424015
|
0.001615953
|
0.155022097
|
0.024031851
|
0.000600796
|
|
0.005822528
|
0.004473709
|
-0.001348819
|
-0.301499105
|
0.090901711
|
0.002272543
|
|
0.006317555
|
0.005434635
|
-0.00088292
|
-0.162461691
|
0.026393801
|
0.000659845
|
|
0.007840829
|
0.008566717
|
0.000725888
|
0.084733511
|
0.007179768
|
0.000179494
|
|
0.007372396
|
0.007886634
|
0.000514238
|
0.065203718
|
0.004251525
|
0.000106288
|
|
0.007037032
|
0.007531939
|
0.000494907
|
0.06570784
|
0.00431752
|
0.000107938
|
|
0.006184229
|
0.005886214
|
-0.000298014
|
-0.050629231
|
0.002563319
|
6.4083E-05
|
|
0.006393142
|
0.006475832
|
8.26904E-05
|
0.012769079
|
0.000163049
|
4.07623E-06
|
|
0.005801601
|
0.005228465
|
-0.000573137
|
-0.109618529
|
0.012016222
|
0.000300406
|
|
0.005390009
|
0.004346462
|
-0.001043546
|
-0.240090933
|
0.057643656
|
0.001441091
|
|
0.006225736
|
0.006004133
|
-0.000221602
|
-0.036908287
|
0.001362222
|
3.40555E-05
|
|
0.00555409
|
0.004565474
|
-0.000988616
|
-0.21654188
|
0.046890386
|
0.00117226
|
|
0.006663944
|
0.006708174
|
4.42294E-05
|
0.006593367
|
4.34725E-05
|
1.08681E-06
|
|
0.005913397
|
0.005215601
|
-0.000697796
|
-0.133790128
|
0.017899798
|
0.000447495
|
|
0.006020249
|
0.005446289
|
-0.000573959
|
-0.105385377
|
0.011106078
|
0.000277652
|
|
0.006553728
|
0.006585228
|
3.14999E-05
|
0.004783421
|
2.28811E-05
|
5.72028E-07
|
|
0.006041907
|
0.005662202
|
-0.000379704
|
-0.067059493
|
0.004496976
|
0.000112424
|
|
0.005995723
|
0.005662202
|
-0.00033352
|
-0.058902939
|
0.003469556
|
8.67389E-05
|
|
0.00592856
|
0.00550193
|
-0.00042663
|
-0.077541879
|
0.006012743
|
0.000150319
|
|
0.006048158
|
1.00550193
|
0.999453771
|
0.993984936
|
0.988006053
|
0.024700151
|
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
Ó 0.046503711
HRMSE 0.023251856
Tableau réalisé à partir de
donnés tirées de Stata
22
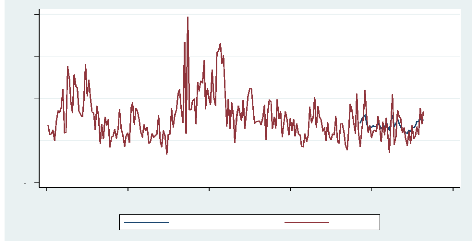
Figure 6 : Prévision à partir du
193ème jour de RV(d)5
.01 .02
0
0 50 100 150 200 250
date
Prevision RV(d)5 RV(d)5
.01 .02
0 50 100 150 200 250
date
Prevision RV(d)9 RV(d)9
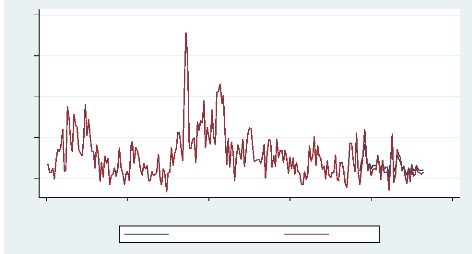
Figure 7 : Prévision à partir du
193ème jour de RV(d)9
'
23
La réalisation d'une prévision hors
échantillon suivant le principe de la fenêtre récursive
nous a permis de calculer le HRMSE pour les deux modèles. Dans les
tableaux précédents `??
représente la projection de la volatilité
réalisée journalière pour les 2 modèles et `Y' est
la volatilité réalisée observée. Les
dernières colonnes des mêmes tableaux ont servi au calcul du HRMSE
au fin de comparaison de la performance des deux modèles. En terme de
HRMSE on peut remarquer que le modèle HAR(3)-RV regroupée suivant
la fréquence optimum de 9 minutes et appliqué à la
série CHK Stock du 4 janvier 2010 au 31 décembre 2010 donne une
meilleure performance que si la série est regroupée en
fréquence de 5 minutes. Le HRMSE de ce dernier qui est 0,027932873 est
en effet supérieur à celui du précédent qui est de
0,023251856 pour une des prévisions hors échantillons sur 40
jours suivant le principe de la fenêtre récursive.
24
| 

