A. QED
Proof of Proposition 1: By Lemma 1, a strategy profile forms a
subgame perfect equilibrium if and only if there is no profitable one shot
deviation from that strategy at any stage in the game.
Our candidate equilibrium, me-M, is that, for any CUT , miners
chain their block to the most recent block in the original chain.
To prove that this is a Markov perfect equilibrium we now show
that, in any state wt, any miner prefers to follow the equilibrium, and chain
his block to the most recent one in the original chain, rather than engaging in
a one shot deviation, chaining his block to another block, B, at time T, and
then reverting to the equilibrium strategy.
To do so, consider three cases, whose probabilities are
independent of the miners' actions (since they reflect the distributions of
independent Poisson processes whose intensities are exogenous)
27
Proof of Proposition 2: Denote by n(T) the index of the last
block solved by time T, by Bn(T) the corresponding block and by I f
the first time at which the sunspot variable is above 1 -- E and f <
n(T).
Our candidate equilibrium strategy profile, a* , specifies the
following:
a) Before the fork: If T < T f , miners chain
their block to the most recent block in the original chain.
b) At the fork inception: If T Tf , or T > T
f and cut does not include an edge (Bn(Tf) f, Bk+l), with k >
n(T), miners chain their block to
c) After the fork: If T > T f and WT includes
an edge Bk+l), with k > n(T f ), miners chain
their block to
the most recently solved block in the chain including (Bn(Tf) f, Bk*+l), (with
k* = min{k n(T f )
s.t. there exists an edge (Bn(Tf) f, Bk+l)}), whose index is the
index of its parent plus one or, if such a block does not exist, to B/c* +1.
Note that if all miners follow a* , their behaviour on the
equilibrium path is as described in Proposition 2. To prove that this is a
Markov perfect equilibrium, we need to prove that a miner does not have a
profitable one shot deviation from o*. We hereafter consider the three cases
a), b) and c) in turn.
a) Before the fork: Bearing in mind that miner's actions
don't affect the occurrence of the sunspot, at all times before T/ the proof of
a) operates along the same line as the proof of Proposition 1.
b) At the fork inception: Compare m's expected gain if he
follows the equilibrium strategy (chaining his block to Bn(Tf) f) to his
expected gain from deviating once by chaining his block to # and then reverting
to the equilibrium strategy. As earlier, the only relevant case is when the
next event is that m solves If he had chained to B, then he expects that at
later stages no miner (including himself) will chain any block to since he
anticipates the equilibrium strategy to be followed. Consequently, his reward
for mining attached to B is 0 (and therefore less than his gain if he had
followed the equilibrium). Moreover, as before, his expected payoff from
previously solved blocks as well as from future blocks, is unaffected by which
block he has just mined.
58
29
c)
59
After the fork: If T > Tf , Condition 2 holds
and the new chain exists, then miners m < K chain their block to the last
block on the new chain, while miners m > K chain their block to the last
block on the original chain.
d) After the fork off-path: Suppose there are two consecutive
times T and T' such that Condition 2 holds at T but not at T'. Note that this
can only happen after a deviation from the strategy prescribed in b) and c)
where BH is either chained to the last block on the new chain (or Bn(Tf) f) by
a miner m > K or chained to the last block on the original chain by a miner
m < K. The equilibrium strategy then prescribes that miners exclude BT'.
More precisely, suppose BT/ was chained to the original chain by m < K. Then
at and after H, miners m < K chain their block to the last block on the new
chain. At T/ miners m > K chain their block to the last block solved by time
T on the original chain, B} and do so until a new block BnewO is
solved and chained to B O After Bneu,O is solved, miners
m > K chain their block to the last block on the chain that contains (Bn(T)
O BnewO ) that preexists all chains that contain (B n(T)
O BnewO ). This chain then replaces the original chain in
Condition 2. Symmetrically, if Bf/ was chained to the new chain by m > K,
then at and after T', miners m > K chain their block to the last block on
the original chain, while miners m < K exclude BT/ by mining from the last
block solved by time T on the new chain, and then mining from the chain that
originates from that fork. This chain then replaces the new chain in Condition
2.
As will become explicit below, the specification of the
equilibrium strategy in states described in d) is useful to rule out certain
types of deviations. Note that if the state is as described in d) and all
miners play the equilibrium strategy, then the expected payoff of a miner, say
m < K, at T1 is
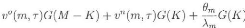
which is exactly his expected payoff at T under the equilibrium
strategy described in b) and c). This also holds for miners m > K.
We need to prove that a miner does not have a profitable one
shot deviation from a*. We hereafter consider each of the cases above in
turn.
31
Hence, one can set E so that, Pr(T f < z Iw z and
correspondingly the gain from reducing the likelihood of a fork via a
deviation, is arbitrarily close to 0.
Next consider the second effect. If miner m solves but this block
is not on the original chain, no further block will be chained to it, since all
miners henceforth will follow a*. Hence the expected payoff for this block is
0. If instead m was following the equilibrium strategy when he solved
the expected payoff from this block is strictly positive.
Overall, the first effect, which reflects the maximum gain from a
one shot deviation can be set arbitrarily close to 0, while the second effect,
which reflects the cost of a one shot deviation, is bounded away from 0. Hence,
there is no profitable one shot deviation.
b) c) At or after the fork:
1) Consider first a deviation by a miner m > K.
Any deviation other than chaining to the last block on the new
chain is ruled out by similar arguments as in Proposition 1. Hence we just have
to check that rn, prefers to chain his block to the last block on the original
chain, rather than to the last block on the new chain. As in the previous
60
proofs, this one shot deviation affects rn's payoff only if the
next stopping time T/ corresponding to two possible events: either m solves his
block, or zrn occurs.
(i) Suppose miner m solves a block at T', i.e., IVm(T/) --
Nm(T) = 1. If Condition 2 is still true at T', since every miner, including m,
reverts to the equilibrium strategy from T' on, the only impact of the
deviation is that m earns G(K) for block Bn(T/) instead of G(M -- K) under the
equilibrium strategy. If Condition 2 is not true at T', the only impact of the
deviation is that m earns 0 for block Bn(T') instead of G(M -- K) under the
equilibrium strategy. Indeed both under the equilibrium strategy and the
deviation, his expected payoff at T' is his expected payoff at T plus the
reward he receives for block Bn(T'), which is 0 under the deviation when
Condition 2 does not, hold since from d) no miner will ever chain a block to
Bn(T/) .
(ii) Suppose miner 'm, is hit, by a liquidity shock at, T',
i.e., zm, = T'. Then his payoff under the deviation is
33
Last, see that inequality (1) in Condition 1 guarantees that
(2) and (3) cannot be satisfied jointly for the same miner m.
d) After the fork off-path
Suppose is as described in d) and consider a deviation by miner m
before block is solved. If m chains his block to Bn(TI) and the next event is
not that m solves his block, then his deviation is irrelevant. If the next
event is that he solves his block, then the only impact of the deviation is
that m earns 0 for this block, since all miners play the equilibrium strategy
going forward so that no
miner will ever chain his block to
Suppose that miner m deviates and chains his block to a block
that was solved before Bn(+). Then, as above, the only relevant deviations are
for a miner m K to mine a block chained to the last block on the original chain
solved by time T or for m > K to mine a block chained to the last block on
the new chain solved by time T. By construction, the payoffs from these
deviations and from adhering to the equilibrium strategy are identical to the
payoffs derived in b) and c). Furthermore, given that no miner chains his block
to Bn(T') which therefore yields 0 to the miner who solved it, a deviation is
not profitable if Condition 2 holds when block Bn(T') is substracted from
miners' vested interests vo (m, H) and on (m, H), that is, if v
o (m, T) and on (m, T) are such that Condition 2 holds,
which is true.
Finally, consider a deviation by miner m after block Bn(T0+1 is
solved, then the state is such that Condition 2 holds, hence, from b) and c),
there is no profitable one shot deviation. QED
| 


