CHAPITRE III. ANALYSE ET
INTERPRETATION DES RESULTATS
Cette partie va essayer de faire une présentation des
variables démographiques de l'échantillon, quelques statiques
avec le test de chi-deux, elle présentera aussi les résultats des
analyses économétriques mais aussi la discussion des
résultats.
III.1. Variables
démographiques de l'échantillon
Tableau n°4 : Répartition de
l'échantillon selon le statut de l'institution
|
Statut de l'institution
|
|
Effectifs
|
Pourcentage
|
Pourcentage valide
|
Pourcentage cumulé
|
|
Valide
|
Société de microfinance
|
4
|
16,0
|
16,0
|
16,0
|
|
Coopérative
|
21
|
84,0
|
84,0
|
100,0
|
|
Total
|
25
|
100,0
|
100,0
|
|
Source : Elaboré par nous sur base de notre
enquête
Ce tableau nous montre que 4 institutions
enquêtées sur les déterminants de la diversification des
produits dans la ville de Goma soit 16% ont comme statut
« Société de microfinance » et 21
institutions soit 84.0% ont comme statut
« coopérative ».
Tableau n°5 : Répartition de
l'échantillon selon les postes occupés par les
enquêtés.
|
Poste occupé
|
|
Effectifs
|
Pourcentage
|
Pourcentage valide
|
Pourcentage cumulé
|
|
Valide
|
Agent de crédit
|
1
|
4,0
|
4,0
|
4,0
|
|
Chargé de clientèle
|
2
|
8,0
|
8,0
|
12,0
|
|
Autre
|
4
|
16,0
|
16,0
|
28,0
|
|
Chargé de développement et gestion de nouveaux
produits
|
8
|
32,0
|
32,0
|
60,0
|
|
Gérant
|
10
|
40,0
|
40,0
|
100,0
|
|
Total
|
25
|
100,0
|
100,0
|
|
Source : Nos calculs sur base de notre enquête.
Il ressort de ce tableau que sur 25 personnes
enquêtés dans les IMF, 1 personne soit 4.0% est un agent de
crédit, 2 personnes soit 8% sont des chargé de la
clientèle, 4 personnes soit 16% sont des chargés de
développement et gestion de nouveaux produits et 10 personnes soit 40%
sont des gérants.
III.2. Quelques
statistiques avec le test de Chi-deux
Tableau n°6 : Diversification et capacité de
l'instituions ?
|
Tableau croisé
|
|
Capacité
Diversification
|
Capacité de l'institution
|
Total
|
|
Nous avons fait recours aux spécialistes externes
|
Par nos agents eux-mêmes sur base de leur
capacité
|
|
Diversification
|
non
|
Effectif
|
3
|
1
|
4
|
|
% compris dans Diversification
|
75,0%
|
25,0%
|
100,0%
|
|
oui
|
Effectif
|
4
|
17
|
21
|
|
% compris dans Diversification
|
19,0%
|
81,0%
|
100,0%
|
|
Total
|
Effectif
|
7
|
18
|
25
|
|
% compris dans Diversification
|
28,0%
|
72,0%
|
100,0%
|
Source : Nos calculs sur base de notre enquête
Il ressort de ce tableau que sur 4 institutions n'ayant pas
diversifié leurs produits, 3 d'entre elles soit 75.0% ont fait recours
aux spécialistes externes pour les produits qu'ils ont, 1 institution
soit 25.0% a développé le produit qu'elle a sur base de la
capacité de ses agents. Pour les 21 IMF ayant diversifié leurs
produits, 4 d'entre elles soit 19.0% affirment avoir fait recours aux
spécialistes externes pendant que 17 IMF soit 81.0% affirment avoir
développés leurs produits eux-mêmes sur base de la
capacité de leurs agents.
Sur base de ces calculs, nous avons calculé les ratios
de vraisemblance de la manière suivante :
· La probabilité pour qu'une IMF diversifie ses
produits par ses agents sur base de leur capacité est de
p1=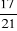 =0,81 =0,81
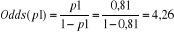
On comprend par ici que les IMF ont 4,26 fois la chance de
diversifier leurs produits sur base de la capacité de leurs de leurs
agents eux-mêmes que de faire recours aux spécialistes
externes.
· La probabilité pour qu'une IMF diversifie ses
produits en faisant recours aux spécialistes externes est de p0= =0,19 =0,19

Le rapport de chance (rapport de cote) est de 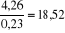
Comme le Odds-ratio est supérieur à 1, nous
pouvons alors dire que les IMF qui diversifient leurs produits par leurs agents
sur base de leur capacité ont plus de chances de diversifier leurs
produits que celles qui le font en faisant recours aux spécialistes
externes.
Tableau n°7 : Test de Chi-deux sur la
diversification des produits et la capacité de l'institution.
|
Valeur
|
ddl
|
Signification asymptotique (bilatérale)
|
|
Khi-deux de Pearson
|
5,218a
|
1
|
,022
|
|
Rapport de vraisemblance
|
4,699
|
1
|
,030
|
|
Association linéaire par linéaire
|
5,009
|
1
|
,025
|
Ce tableau issu du croisement des variables
« capacité de l'institution » et « ont
diversifié leurs produits ou non » nous montre que la valeur
de la signification du Khi-deux est de 0,022 à 1ddl, laquelle est
inférieure à 0,05 notre seuil de signification. Ceci nous permet
de rejeter l'hypothèse d'indépendance des
sous-échantillons et par là, nous pouvons affirmer qu'il y a
un lien d'association entre ces deux variables croisées au tableau
précédent. La capacité de l'institution peut donc influer
sur la décision de diversifier les produits.
Tableau n° 8 : Diversification et besoins des
clients
|
Tableau croisé
|
|
Besoins des clients
Diversification
|
Besoins des exclus
|
Total
|
|
Besoins en services non financiers
|
Les besoins de développer les AGR et de consommation
|
Autres besoins
|
|
Diversification
|
non
|
Effectif
|
1
|
3
|
0
|
4
|
|
% compris dans Diversification
|
25,0%
|
75,0%
|
0,0%
|
100,0%
|
|
oui
|
Effectif
|
0
|
15
|
6
|
21
|
|
% compris dans Diversification
|
0,0%
|
71,4%
|
28,6%
|
100,0%
|
|
Total
|
Effectif
|
1
|
18
|
6
|
25
|
|
% compris dans Diversification
|
4,0%
|
72,0%
|
24,0%
|
100,0%
|
Source : nos calculs sur base de notre enquête
Il ressort de ce tableau que sur 4 institutions n'ayant pas
diversifié leurs produits, 1 d'entre elles analyse les besoins en
services non financiers et 3 ont analysé les besoins de
développer les AGR et de consommation. Pour les 21 institutions ayant
diversifié leurs produits, aucune d'entre elles n'a analysé les
besoins des clients en services non financiers, 15 d'entre elles soit 71,4% ont
analysé les besoins de développer les AGR et de consommation
alors que 6 d'entre elles soit 28,6% ont analysé les autres besoins.
De ces calculs :
· La probabilité pour qu'une IMF ayant
analysé les besoins de développer les AGR et de consommation
diversifient ses produit est de : de p1=

· La probabilité pour qu'une institution ayant
analysé les autres besoins des clients diversifie ses produits est de
p2=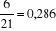

· Le rapport de chance entre les groupes d'IMF est
donné par : 
L'Odds ratio étant supérieur à 1, ce ceci
nous permet de dire que les institutions qui analysent les besoins de
développer les AGR et de consommation ont plus de chance de diversifier
leurs produits que celles qui analysent les autres besoins. Ceci s'explique par
le fait même que la microfinance permet aux pauvres de développer
leurs activités génératrices des revenus. Les clients de
la microfinance comprennent de petits agriculteurs du monde rural, des taximen,
des coiffeurs, des artisans et dont le revenu, bien que faible est relativement
stable. Comme le dit LEDGERWOOD(1999) cité par BUGANDWA (2014), ces
clients certes pauvres, ne sont pas « les plus pauvres des
pauvres ».
Tableau n°9 : Test de chi-deux sur la
diversification et les besoins des clients
|
Tests du Khi-deux
|
|
Valeur
|
ddl
|
Signification asymptotique (bilatérale)
|
|
Khi-deux de Pearson
|
6,399a
|
2
|
,041
|
|
Rapport de vraisemblance
|
5,763
|
2
|
,056
|
|
Association linéaire par linéaire
|
3,857
|
1
|
,050
|
Il ressort de ce tableau issu du croisement des variables
« besoins des clients » et « ont
diversifié leurs produits ou non » que la valeur de la
signification du Khi-deux est de 0,041 à 2ddl, laquelle est
inférieure à 0,05 notre seuil de signification. Ceci nous pousse
à rejeter l'hypothèse d'indépendance des
sous-échantillons et par là, nous pouvons affirmer qu'il y a
un lien d'association entre ces deux variables croisées.
Tableau n°10 : Diversification et concurrence
|
Tableau croisé
|
|
Concurrence
Diversification
|
Concurrence
|
Total
|
|
Non
|
Oui
|
|
Diversification
|
non
|
Effectif
|
4
|
0
|
4
|
|
% compris dans Diversification
|
100,0%
|
0,0%
|
100,0%
|
|
oui
|
Effectif
|
6
|
15
|
21
|
|
% compris dans Diversification
|
28,6%
|
71,4%
|
100,0%
|
|
Total
|
Effectif
|
10
|
15
|
25
|
|
% compris dans Diversification
|
40,0%
|
60,0%
|
100,0%
|
Source : Nos calculs sur base de notre enquête
Ce tableau nous permet de constater que pour les 4
institutions n'ayant pas diversifié leurs produits, les toutes n'ont pas
tenues compte de leurs concurrents. Pour les 21 institutions ayant
diversifié leurs produits, 15 d'entre elles soit 71,4% ont tenu compte d
la connaissance des produits de leurs concurrents alors que 6 d'entre elles
soit 28,6% n'ont pas tenue compte de la connaissance des produits de leurs
concurrents.
De ces calculs :
· La probabilité pour qu'une IMF ayant
analysé fait connaissance des produits de ses concurrent diversifie ses
produits est de : p1=
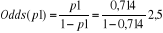
· La probabilité pour qu'une institution n'ayant
pas fait connaissance des produits de ses concurrents diversifie ses produits
est de : p0=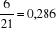

· Le rapport de chance entre les deux groupes d'IMF est
donné par : 
L'Odds ratio étant supérieur à 1, nous
pouvons par là dire que les IMF qui font connaissance des produits de
leurs concurrents ont beaucoup plus de chance de diversifier leurs produits que
celles qui n'ont pas fait connaissance des produits de leurs concurrents. Ceci
peut s'expliquer par l'idée de Nhu-An Tran (2000)
issue de la revue empirique qui stipule que, la concurrence qui se
développe entre les prestataires de services, et les IMF doivent avant
tout améliorer leur réactivité aux besoins des clients et
la diversification de leurs produits.
Tableau n°11 : Test de chi-deux sur la
diversification et la concurrence
|
Valeur
|
Ddl
|
Signification asymptotique (bilatérale)
|
|
Khi-deux de Pearson
|
7,143a
|
1
|
,008
|
|
Rapport de vraisemblance
|
8,523
|
1
|
,004
|
|
Association linéaire par linéaire
|
6,857
|
1
|
,009
|
Il ressort de ce tableau issu du croisement des variables
« concurrence » et « ont diversifié leurs
produits ou non » que la valeur de la signification du Khi-deux est
de 0,008 à 1ddl, laquelle est inférieure à 0,05 notre
seuil de signification. Ceci nous pousse à rejeter l'hypothèse
d'indépendance des sous-échantillons et par là, nous
pouvons affirmer qu'il y a un lien d'association entre ces deux variables
croisées.
Tableau n°12 : Diversification & risques des
clients et des IMF
|
Tableau croisé
|
|
Risques des clients et des
IMF
Diversification
|
Risques des clients et des IMF
|
Total
|
|
Non
|
Oui
|
|
Diversification
|
non
|
Effectif
|
4
|
0
|
4
|
|
% compris dans Diversification
|
100,0%
|
0,0%
|
100,0%
|
|
oui
|
Effectif
|
11
|
10
|
21
|
|
% compris dans Diversification
|
52,4%
|
47,6%
|
100,0%
|
|
Total
|
Effectif
|
15
|
10
|
25
|
|
% compris dans Diversification
|
60,0%
|
40,0%
|
100,0%
|
Source : Nos calculs sur base de notre enquête
Il ressort de ce tableau que les 4 IMF n'ayant pas
diversifié leurs produits n'ont pas tenu compte de leurs risques et des
risques de leurs membres, par contre, sur les 21 IMF ayant diversifié
leurs produits, 11 d'entre elles soit 52,4% n'ont tenu compte des risques
auxquelles elles font face et leurs clients, alors que 10 d'entre elles soit
47,6% affirment avoir tenu compte des risques auxquelles elles font face et
leurs clients. A notre avis, ceci est possible du fait que les IMF qui sont
tombées sont accusées parfois de n'avoir pas bien pesé les
risques auxquelles elles faisaient face et leurs clients, elles ont
développé des produits qui n'ont pas réussi.
Tableau n°13 : Test de chi-deux sur la
diversification et les risques des clients et des IMF
|
Valeur
|
ddl
|
Signification asymptotique (bilatérale)
|
|
Khi-deux de Pearson
|
3,175a
|
1
|
,075
|
|
Rapport de vraisemblance
|
4,586
|
1
|
,032
|
|
Test exact de Fisher
|
|
|
|
|
Association linéaire par linéaire
|
3,048
|
1
|
,081
|
Il ressort de ce tableau issu du croisement des variables
« risques des clients et des IMF» et « ont
diversifié leurs produits ou non » que la valeur de la
signification du Khi-deux est de 0,075 à 2ddl, laquelle est
supérieure à 0,05 notre seuil de signification. Ceci nous permet
de ne pas rejeter l'hypothèse d'indépendance des
sous-échantillons. Cela étant, nous rejetons notre
hypothèse nulle qui préconisait que les risques des clients et
des IMF pouvaient influer la diversification des produits dans les IMF de la
ville de Goma.
Tableau n°14 : Diversification et
Fidélisation et Attrait de nouveaux clients
|
Tableau croisé
|
|
Fidélisation et attrait de
nouveaux clients
Diversification
|
Fidélisation et Attrait de nouveaux clients
|
Total
|
|
La fidélisation
|
L'attrait de nouveaux clients
|
les autres raisons
|
|
Diversification
|
non
|
Effectif
|
1
|
2
|
1
|
4
|
|
% compris dans Diversification
|
25,0%
|
50,0%
|
25,0%
|
100,0%
|
|
oui
|
Effectif
|
6
|
7
|
8
|
21
|
|
% compris dans Diversification
|
28,6%
|
33,3%
|
38,1%
|
100,0%
|
|
Total
|
Effectif
|
7
|
9
|
9
|
25
|
|
% compris dans Diversification
|
28,0%
|
36,0%
|
36,0%
|
100,0%
|
Source : élaboré par nous sur base de notre
enquête
Ce tableau nous fait voire que sur les 4 IMF n'ayant pas
diversifié leurs produits, 1 recherche la fidélisation de ses
client, 2 cherchent à attirer de nouveaux clients et 1 avance les autres
raisons. Pour les 21 IMF ayant diversifié leurs produits, 6 d'entre
elles soit 28,6%% cherchent à fidéliser leurs clients, 7 soit
33,3% l'ont fait à cause de l'attrait de nouveaux clients alors que 8
d'entre elles soit 38,1% évoquent les autres raisons.
Tableau n°15 : Test de chi-deux sur la
diversification & la fidélisation et attrait de nouveaux
clients
|
Tests du Khi-deux
|
|
Valeur
|
ddl
|
Signification asymptotique (bilatérale)
|
|
Khi-deux de Pearson
|
,435a
|
2
|
,805
|
|
Rapport de vraisemblance
|
,428
|
2
|
,807
|
|
Association linéaire par linéaire
|
,046
|
1
|
,830
|
Il ressort de ce tableau issu du croisement des variables
« fidélisation et attrait de nouveaux clients» et
« ont diversifié les produits ou non » que la valeur
de la signification du Khi-deux est de 0,805 à 2ddl, laquelle est
supérieure à 0,05 notre seuil de signification. Ceci nous permet
de ne pas rejeter l'hypothèse d'indépendance des
sous-échantillons. Cela étant, nous rejetons notre
hypothèse nulle qui préconisait que la fidélisation des
clients et l'attrait de nouveaux clients pouvaient influer la diversification
des produits dans les IMF de la ville de Goma.
Tableau n° 16 : diversification et segmentation des
marchés?
|
Tableau croisé
|
|
Segmentation des
marchés
Diversification
|
Segmentation des marchés
|
Total
|
|
Age
|
Niveau d'étude
|
Type d'activités
|
|
Diversification
|
non
|
Effectif
|
1
|
0
|
3
|
4
|
|
% compris dans Diversification
|
25,0%
|
0,0%
|
75,0%
|
100,0%
|
|
oui
|
Effectif
|
5
|
1
|
15
|
21
|
|
% compris dans Diversification
|
23,8%
|
4,8%
|
71,4%
|
100,0%
|
|
Total
|
Effectif
|
6
|
1
|
18
|
25
|
|
% compris dans Diversification
|
24,0%
|
4,0%
|
72,0%
|
100,0%
|
De ce tableau, nous constatons que pour les 4 IMF n'ayant
pas diversifié leurs produits, 1 d'entre elles a segmenté ses
marché sur base de l'âge alors que 3 ont segmenté leurs
marchés sur base du type d'activités. De 21 IMF qui ont
diversifié leurs produits, 5 d'entre elles soit 23,8% ont
segmenté leurs produits par le critère d'âge, 1 soit 4,8% a
segmenté ses marché par le critère du niveau
d'études et 15 soit 71,4% ont segmenté leurs marchés par
le critère type d'activités. A notre avis, ce résultat est
cohérent car les IMF ciblent les pauvres économiquement actifs,
c'est-à-dire ceux qui ont des activités
génératrices des revenus.
Tableau n°17 : Test du chi-deux sur la
diversification et segmentation des marchés.
|
Tests du Khi-deux
|
|
Valeur
|
ddl
|
Signification asymptotique (bilatérale)
|
|
Khi-deux de Pearson
|
,198a
|
2
|
,906
|
|
Rapport de vraisemblance
|
,357
|
2
|
,837
|
|
Association linéaire par linéaire
|
,000
|
1
|
,987
|
Il ressort de ce tableau issu du croisement des variables
« segmentations des marchés» et « ont
diversifié les produits ou non » que la valeur de la
signification du Khi-deux est de 0,906 à 2ddl, laquelle est
supérieure à 0,05 notre seuil de signification. Ceci nous permet
de ne pas rejeter l'hypothèse d'indépendance des
sous-échantillons. Cela étant, nous rejetons notre
hypothèse nulle qui préconisait que la segmentation des
marchés pouvait influer la diversification des produits dans les IMF de
la ville de Goma.
Tableau n°18 : diversification des produits et
statut de l'institution
|
Tableau croisé Diversification * Statut de
l'institution
|
|
Statut de l'institution
|
Total
|
|
Société de microfinance
|
Coopérative
|
|
Diversification
|
non
|
Effectif
|
0
|
4
|
4
|
|
% compris dans Diversification
|
0,0%
|
100,0%
|
100,0%
|
|
oui
|
Effectif
|
4
|
17
|
21
|
|
% compris dans Diversification
|
19,0%
|
81,0%
|
100,0%
|
|
Total
|
Effectif
|
4
|
21
|
25
|
|
% compris dans Diversification
|
16,0%
|
84,0%
|
100,0%
|
Source : Nos calculs sur base de notre enquête
Nous comprenons par ce tableau que les 4 IMF qui n'ont pas
diversifié leurs produits ont comme statut
« coopérative ». Sur les 21 IMF ayant
diversifié leurs produits, 4 soit 19,0% ont comme statut
« société de microfinance » et 17 d'entre
elles soit 81,0% ont comme statut « coopérative ».
Tableau n°19 : Test de chi-deux sur la
diversification et le statut de l'institution.
|
Valeur
|
ddl
|
Signification asymptotique (bilatérale)
|
|
Khi-deux de Pearson
|
,649a
|
1
|
,420
|
|
Rapport de vraisemblance
|
1,121
|
1
|
,290
|
|
Association linéaire par linéaire
|
,623
|
1
|
,430
|
Il ressort de ce tableau issu du croisement des variables
« statut de l'institution» et « ont diversifié
les produits ou non » que la valeur de la signification du Khi-deux
est de 0,420 à 1ddl, laquelle est supérieure à 0,05 notre
seuil de signification. Ceci nous permet de ne pas rejeter l'hypothèse
d'indépendance des sous-échantillons. Cela étant, nous
rejetons notre hypothèse nulle qui préconisait que le statut de
l'institution pouvait influer la diversification des produits dans les IMF de
la ville de Goma.
Tableau n°20 : Diversification et diversifier
les sources des revenus
|
Tableau croisé
|
|
Diversifier les sources des
revenus
Diversification
|
Diversifier les sources des revenus
|
Total
|
|
Non
|
Oui
|
|
Diversification
|
non
|
Effectif
|
2
|
2
|
4
|
|
% compris dans Diversification
|
50,0%
|
50,0%
|
100,0%
|
|
oui
|
Effectif
|
2
|
19
|
21
|
|
% compris dans Diversification
|
9,5%
|
90,5%
|
100,0%
|
|
Total
|
Effectif
|
4
|
21
|
25
|
|
% compris dans Diversification
|
16,0%
|
84,0%
|
100,0%
|
Source : Nos calculs sur base de notre enquête
Ce tableau nous montre que sur les 4 IMF n'ayant pas
diversifié leurs produits, 2 d'entre elles ne cherchent pas à
diversifier leurs sources des revenus et deux cherchent à diversifier
leurs sources des revenus. Pour les 21 ayant diversifié leurs produits,
2 d'entre elles soit 9,5% ne cherchent pas à diversifier leurs sources
des revenus et 19 soit 90,5% cherchent à diversifier leurs sources des
revenus. A notre avis, ceci est cohérent par le fait que les IMF
poursuivent la rentabilité en vue d'atteindre la
pérennité.
Tableau n°21 : Test de chi-deux sur
diversification et diversifier les sources des revenus.
|
Valeur
|
ddl
|
Signification asymptotique (bilatérale)
|
|
Khi-deux de Pearson
|
4,096a
|
1
|
,043
|
|
Rapport de vraisemblance
|
3,230
|
1
|
,072
|
|
Association linéaire par linéaire
|
3,932
|
1
|
,047
|
Il ressort de ce tableau issu du croisement des variables
« diversifier les sources des revenu » et « ont
diversifié les produits ou non » que la valeur de la
signification du Khi-deux est de 0,043 à 1ddl, laquelle est
inférieure à 0,05 notre seuil de signification. Ceci nous permet
rejeter l'hypothèse d'indépendance des sous-échantillons.
Cela étant, nous pouvons dire qu'il y a un lien d'association entre les
variables croisées au tableau précédent.
Tableau n°22 : Diversification des produits et
le nombre d'années
|
Tableau croisé
|
|
Nombre d'années
Diversification
|
Nombre d'années
|
Total
|
|
3 à 6 ans
|
Plus de 6 ans
|
|
Diversification
|
non
|
Effectif
|
4
|
0
|
4
|
|
% compris dans Diversification
|
100,0%
|
0,0%
|
100,0%
|
|
oui
|
Effectif
|
4
|
17
|
21
|
|
% compris dans Diversification
|
19,0%
|
81,0%
|
100,0%
|
|
Total
|
Effectif
|
8
|
17
|
25
|
|
% compris dans Diversification
|
32,0%
|
68,0%
|
100,0%
|
Source : Nos calculs sur base de notre enquête
Ce tableau nous permet d'affirmer que pour les 4 IMF n'ayant pas
diversifié leurs produits existent il y a 3 à 6 ans. Pour les IMF
ayant diversifié leurs produits, 4 d'entre elles soit 19,0% existent il
y a 3 à 6 ans alors que 17 d'entre elles soit 81,0% existent il y a plus
de 6 ans.
Sur base de ces calculs, nous avons calculé les ratios
de vraisemblance de la manière suivante :
· La probabilité pour qu'une IMF ayant 3 à
6 ans diversifie ses produits est : p1=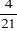 =0,19 =0,19

· La probabilité pour qu'une IMF ayant plus de 6
ans diversifie ses produits p2=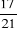 =0,81 =0,81

Le rapport de chance est de 
Comme le Odds ratio est inférieur à 1, nous
pouvons dire alors que les IMF ayant plus de 6 ans ont beaucoup plus de chance
des diversifier leurs produits que celles ayant 3 à 6 ans. A notre avis,
ce résultat est cohérent par le fait qu'une IMF qui se lance au
sitôt sur le marché ne peut pas se lancer dans le processus de
diversification des produits comme celle qui a déjà
maitrisé le marché.
Tableau n°23 : Test de chi-deux sur diversification
et nombre d'années.
|
Valeur
|
Ddl
|
Signification asymptotique (bilatérale)
|
|
Khi-deux de Pearson
|
10,119a
|
1
|
,001
|
|
Rapport de vraisemblance
|
10,893
|
1
|
,001
|
|
Association linéaire par linéaire
|
9,714
|
1
|
,002
|
Il ressort de ce tableau issu du croisement des variables
« nombre d'années » et
« diversification » que la valeur de la signification du
Khi-deux est de 0,008 à 1ddl, laquelle est inférieure à
0,05 notre seuil de signification. Ceci nous pousse à rejeter
l'hypothèse d'indépendance des sous-échantillons et par
là, nous pouvons affirmer qu'il y a un lien d'association entre ces
deux variables croisées au tableau ci-haut.
Le test de chi-deux sur base de croisement entre les
différentes variables indépendantes et la variable
dépendante nous montre que les variables dont : les risques des
clients et des IMF, fidélisation et l'attrait de nouveaux clients et la
segmentation des marchés n'ont pas de lien avec la variable
dépendante du fait que leurs significations sont supérieures
à 0,05 notre seuil de signification.
Il importe aussi que le modèle mis à
l'épreuve soit correctement spécifié, c'est à dire
que les variables vraiment importantes pour prédire une variable
dépendante doivent être présentes dans l'équation,
alors que les variables non pertinentes ne doivent pas en faire partie
(ww.ctqn.ca). Ceci nous pousse donc à ne pas introduire ces
variables dans notre modèle de régression.
L'équation fonctionelle de notre modèle de
regression s'ecrira alors :
 Avec Y la variable dépendante ; Avec Y la variable dépendante ;
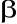 un vecteur des éléments explicatifs associés au
vecteur x ; un vecteur des éléments explicatifs associés au
vecteur x ;
Cap, Besoin, Concur, DivSouR, NbrAn un vecteur des variables
explicatives ;
Ui bruits ou perturbations.
Comme Y ne peut prendre que deux valeurs (0 et 1), il en est
de même de la perturbation ui .
ui prendra la valeur 1-xi.b(si yi=1) ou la valeur
-xi.b (si yi=0).
On ne peut donc pas faire l'ypothèse d'une loi continue
sur les résidus, à fortiori celle d'une loi normale. Si E(ui)=0,
le parametre b doit vérifier les contraintes 0=xi.b=1 pour tout i=1
....n (Alain JACQUOT, 2000).
|
|



