Conception et dimensionnement d'un pont en ba.

Page 1 sur 115

Epigraphe

« Le passage du quartier Abattoir vers le quartier NDANU ne peut
être rendu possible que par un pont jeter sur la rivière Njili. Nous
voici réfléchir sur comment jeter le pont nonobstant ce qui est
déjà fait ne dit-on pas que l'abondance n'a jamais été nuisible ! »

MERVEIL ASALAKOW

Page 2 sur 115

Dédicace

Nous dédions ce travail à nos chers parents : JEAN ASALAKOW et FLORENCE KAYOKO, pour leur dévouement.

MERVEIL ASALAKO MBANGU

Page 3 sur 115

Avant-propos

Au terme du premier cycle en Bâtiment et Travaux Publics, qui sanctionne notre formation à l'I.N.B.T.P, n'est pas le fruit de nos seules capacités. Il est le couronnement des efforts de plusieurs personnes auxquelles nous voulons ici réitérer l'expression de notre gratitude.

De prime à bord, nous rendons un vibrant hommage au Dieu tout puissant, source de toute inspiration, pour le souffle de vie et la protection dont nous étions bénéficiaire tout au long de ces 4 années d'études.

Nous remercions plus particulièrement le Chef des travaux DEDE BIVULU, qui malgré ses multiples occupations, a accepté de diriger et de mener à bout ce travail.

Notre gratitude va en outre à l'endroit de tout le corps académique, scientifique et professoral de l'Institut National du Bâtiment et des Travaux Publics en sigle (I.N.B.T.P.), qui s'est donné corps et âme pour notre formation.

Nous pensons également à nos soeurs GRACIEL ASALAKOW, BENEDICTE KAYOKO, MERRY TABUKU, PLAMEDIE ASALAKOW, LUMIERE MONI, CLARISSE ASAKAKOW, LAURETTE ASALAKOW, JAEL MONI et CHRISTELLE KAYOKO, à nos frères REAGAN ASALAKOW, TCHAN MONI, HYGO MONI ARISTOTE MAZELE, SOU MONI, WANG MONI et ENOCK GAGA, ainsi qu'à mes nièces et neveux KERTICHE KIBUNGI, MIKE ASALAKOW, ESDY ASALAKOW et KATHIE ASALAKOW.

Nous ne pouvons pas oublier les combattants et camarades de lutte, avec qui nous avons enduré et parcouru le cycle à savoir GLOIRE BONKINGA, JOHN ILUNGA, GEDEON MUNGEDI, GEULORD KAZEMBE, JEAN BLESE MUKOKO, ELIE KABONGO.

Sans oublier nos camarades de chambre PATRICK LOKATIKALA, EMMANUEL LUMENE, KEVINE ITOLE, THE GAME KUYANA, DON BENIE, LADY ASANZI, TELICA MADECO et LOVE MANDWENI.

Enfin à toute la famille de l'Institut National du Bâtiment et des Travaux Publics et à ceux qui, de loin ou de près, ont apporté leur pierre à la mise au point de ce travail et dont les noms ne figurent pas ici, qu'ils se sentent concernés par ces remerciements.

Page 4 sur 115

SYMBOLES, SIGLE ET ABREVIATIONS

: Section d'armature be : base de l'entretoise ;

b : Base de la poutre ;

c : Enrobage

d : Hauteur utile

e : Excentricité

Fv : somme force verticale

Fh : somme des forces horizontales

H : Hauteur de la poutre ;

h₀ : épaisseur de la dalle ;

H : Effort du freinage

H : Poussée due à la surcharge du remblai

H3 : poussée du remblai (terre)

He = hauteur de l'entretoise ;

Hr : hauteur (épaisseur) de revêtement

: Kilo newton

: Portée du pont ;

: Largeur du pont ;

lC : largeur de la chaussée ;

Lxe : écartement entre nus de l'entretoise ;

l1x : distance entre axe des poutres ;

lx : écartement des poutres ;

Lx : petite portée de la dalle ;

Ly : grande portée de la dalle ;

M : Méga newton

Page 5 sur 115

M : moment fléchissant ;

M₀ : moment fléchissant à l'axe 0 du pont ;

M+ : moment positif ;

M- : moment négatif ;

Mtt : moment en travée ;

MtA : moment sur l'appui ;

Mser : moment de service ;

MR : moment reversant ;

Ms : moment stabilisant

Ne : nombre d'entretoise ;

n : nombre de voies de circulation ;

N1e : nombre d'entretoise ;

Np : nombre de poutre ;

P( KN) : Charge unitaire

P : charge permanente

Q1 : surcharge sur le remblai

Q2 : réaction des charges

Q3 : poids de la culée

Q4 : poids propre de la superstructure

Q5 : poids du remblai q- : charge négative _q+ : charge positive

: Résultant des forces

S+ : surface positive

S- : surface négative

t : trottoir ;

T : effort tranchant ;

Page 6 sur 115

Tmax : effort tranchant max ;

U et V : côtés de rectangle d'impact ;

x : bras de levier ;

: Contrainte ;

: Contrainte maximale ;

: Contrainte minimale ;

: Contrainte admissible d'acier ;

: Contrainte maximale du béton ;

: Contrainte admissible du béton ;

: Coefficient d'impact dynamique ;

: Diamètre de barres en acier (haute adhérence) ;

: Tension tangentielle ;

: Rapport entre lx et ly ;

: Angle de frottement naturel.

Page 7 sur 115

CHAPITRE 0 INTRODUCTION

1. Problématique

Afin de contribuer à la modernité de notre pays, nous avons bien jugé de concevoir un ouvrage d'art de franchissement. Les quartiers NDANU et ABATTOIR présentent des divers problèmes d'enclavement et de sérieux problèmes pour pouvoir même traverser l'obstacle naturel (rivière NDJILI) sans problème pour bien se communiquer.

S'agissant de la conception et dimensionnement d'un nouvel ouvrage sur le site, cette étude menée dans la perspective de construire un pont en béton armé de 18m de portée à deux voies s'est révélée urgente.

2. Hypothèses

Notre souci sur ce sujet n'est rien d'autre que de répondre aux questions essentielles ci-après :

Comment faut - il concevoir un pont adapté aux réalités du milieu ?

Quels sont des méthodes et normes des calculs qu'il faut utiliser et les matériaux qui peuvent nous servir pour arriver à réaliser l'ouvrage ?

3. Objectif et intérêt

Le but poursuivi dans cette étude est la conception et dimensionnement d'un ouvrage à un prix moindre pouvant tenir face aux sollicitations telles que :

> Les inondations ;

> Le poids propre de l'ouvrage ;

> Le convoi ; > La foule...

4. Canevas du travail

Ce présent travail est divisé en 7 chapitres à savoir :

> Généralités sur le pont

> Description de l'ouvrage

> pré dimensionnement du pont

> Calcul de la poutre et l'entretoise

> Calcul du trottoir et la dalle

> Calcul de l'infrastructure

> Evaluation du projet

Page 8 sur 115

Chapitre I. Généralités sur les ponts

I.1. Définitions

Le pont est une construction, qui permet de franchir une dépression ou un obstacle (cours d'eau, voie de communication, vallée, etc.) en passant par-dessus cette séparation. Le franchissement supporte le passage d'hommes et de véhicules dans le cas d'un pont routier ou d'eau dans le cas d'un aqueduc¹.

Il fait partie de la famille des ouvrages d'art et leur construction relève du domaine du génie civil.

Toutefois, ce sont généralement des ouvrages de portée supérieure à 8m, qui reposent sur des culées et peuvent comporter plus d'une travée. Ce qui nécessite alors la construction d'une ou de plusieurs piles.²

Ponceau ou dalot : c'est un pont de longueur inférieur à 8m.

Une buse : c'est un ouvrage permettant de faire passer l'eau de pluie ou un ruisseau sous la route. Cette dernière n'est jamais appelée Pont même si elle remplit la définition du pont.

I.2. Types de ponts3

Ces derniers sont distingués d'après

? Le matériau constitutif ;

? L'utilisation future ;

? Le mode de conception suivant les règles de la Résistance des matériaux ;

? La forme des poutres ;

? La forme en plan et la durée du service envisagée.

Certes, l'existence de plusieurs possibilités de différencier les ponts entre eux ne permet pas d'en établir une classification unique et indiscutable.

I.2.1. selon les matériaux constitutifs

Ponts en bois : sa durée de vie est limitée, il est employé pour les ponts provisoires. Les formes les plus usitées sont les poutres à treillis et les arcs.

Ponts en pierre : étant donné que la construction en maçonnerie résiste très bien aux efforts de compression, et très mal à la traction, la réalisation des voûtes en pierre pour lesquelles chaque section reste constamment comprimée est employée. Par contre, celui-ci est en nette régression parce que les conditions actuelles, principalement de main-d'oeuvre et de temps, ne permettent plus la taille de la pierre.

¹ Wikipédia, encyclopédie, dictionnaire libre.

2 Guide : aménagement des ponts et des ponceaux dans le milieu forestière

3 REUNION D'INGENIEURS ; Cours de ponts

Page 9 sur 115

Ponts en béton : le béton non armé a été utilisé comme la pierre de taille pour la réalisation de voûtes, car il n'est pas susceptible de s'opposer aux grands efforts de traction.

Ponts en béton armé : le mode de mise en oeuvre du béton armé permet d'envisager la réalisation de toutes les formes d'ouvrages que l'on peut imaginer. Cependant, dans un but d'économie, le projeteur recherche les formes simples qui permettent de réduire au minimum le prix des coffrages.

Ponts en béton précontraint : il permet en particulier de réaliser de travées indépendantes par poutres préfabriquées de plus grande portée et à un prix moindre lorsqu' il y a un grand nombre de poutres identiques. Grâce à celui-ci, des méthodes nouvelles de construction sont apparues, telle la construction par encorbellement, qui permet de supprimer les cintres et les échafaudages.

Ponts en métal

? Ponts en fonte et en fer : pour la réalisation des ponts, ces matériaux sont maintenant abandonnés par ce que :

( La fonte est trop fragile, résiste mal à l'application de surcharges dynamiques et se fissure ;

( Le fer est plus cher et moindre résistant que l'acier.

? Ponts en acier : diverses nuances d'acier, de qualités différentes, permettent la réalisation de ponts métallique modernes. Les pièces métalliques élémentaires (fers plats, cornière...) sont assemblées soit par rivetage, soit par soudure, soit par boulonnage. Un ouvrage métallique réclame une surveillance et un entretient permanents, après son achèvement.

? Ponts mixtes : ce sont des ouvrages métalliques pour lesquels la dalle de couverture en Béton Armé intervient dans la résistance générale de l'ensemble à la flexion longitudinale.

? Ponts en alliages légers.

Il existe quelques cas particuliers des grains de poids assez importants.

I.2.2. selon la conception mécanique. On distingue deux catégories :

Les ouvrages isostatiques :

> Arcs à trois articulations ;

> Pont à travées indépendantes ;

> Ponts cantilever ou ponts GERBER ; > Les consoles.

Les ouvrages hyperstatiques : > Les ponts cadres ;

Page 10 sur 115

> Ponts à travées continues ; > Les ponts à béquilles.

Le calcul des premiers est généralement plus simple et plus rapide.

Ponts à travées indépendantes : ce sont des ouvrages isostatiques : Poutres sur appuis simple. On réalise ainsi des ouvrages ayant jusque 30m en béton armé, 50m en béton précontraint et jusque 80m en métal.

C'est la solution quasi idéale que l'on rencontre par exemple dans les viaducs d'accès aux grands ouvrages ou dans les ponts particulièrement longs.

Fig. I.1 pont à travée indépendante

Ponts en poutres continues : ce sont des ouvrages hyperstatiques, qui répondent bien au franchissement de larges brèches avec implantation d'appuis intermédiaires.

La continuité permet de réduire les moments en travée et fait apparaître des moments négatifs sur appuis. Ceci permet une variation de la hauteur des poutres, donc de respecter, dans certains cas, les gabarits imposés par la voie franchie.

Fig. I.2 pont à poutre continue

Ponts cantilevers : ce sont des ouvrages isostatiques que les projeteurs n'envisagent plus guère actuellement à cause des problèmes qui se posent au droit de l'articulation pour le joint de chaussée et qui n'ont pas trouvé de solution jugée acceptable.

Fig. I.3 pont cantilever

Ponts Voûtes et arcs : ces sont des ouvrages hyperstatiques, qui engendrent des poussées horizontales sur le sol de fondation, d'où la nécessité pour celui-ci d'être particulièrement résistant.

Ponts en portiques : ils engendrent des poussées horizontales à leur base comme les arcs. L'évolution de la précontrainte permet la réalisation de formes nouvelles

Fig. I.4 pont arc

dans les portiques.

Fig.I.5 Portique

I.2.3. Selon l'utilisation

> Ponts rail : est destiné à supporter une ou plusieurs voies ferrées.

> Ponts routes : supporte des voies de circulation routière.

> Passerelles : c'est un ponceau réservé aux piétons. Il est de faible largeur, avec des rampes ou des escaliers d'accès.

> Ponts canaux : le problème de l'étanchéité y est particulièrement important.

> Aqueducs et bâches : c'est un petit ouvrage généralement voûte et inférieur à 2m utilisé pour le transport de l'eau potable.

On appelle bâche, un petit aqueduc.

> Ponts Oléoduc : c'est un pont, qui livre passage à une canalisation conçue pour le transport des huiles.

> Poutres en caissons : elles sont constituées par deux âmes ou plus reliées entre elles par des membrures supérieure et inférieure. Ces membrures s'appellent également hourdis dans les ouvrages en béton précontraint.

Page 11 sur 115

En métal (a) Fig.I.7 En béton précontraint(b)

> Poutres à âme pleine : c'est le cas des ponts à poutres latérales de hauteur relativement faible ou des poutres multiples sous chaussée.

> Poutres à treillis : lorsque la hauteur des poutres devient trop importante (cas des ouvrages à poutres latérales de grande portée), et afin de réduire le poids du matériau utilisé, on réalise des poutres treillis. Ceci est une forme des poutres très répandue dans les ouvrages métalliques.

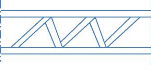
Fig.I.8 poutre en treillis

Page 12 sur 115

Poutres de hauteur constante ou variable : la hauteur, plus grande sur appui qu'à la clé, peut varier suivant une loi parabolique sur toute la longueur de la travée.

Mais, la hauteur peut également varier paraboliquement ou linéairement sur une partie de la portée : Ce sont les poutres à goussets.

Ponts dalles : il n'y a plus de poutre, la dalle est à la fois élément de couverture et élément porteur. Ils sont souvent réalisés pour les ouvrages de faible portée et pour lesquels le gabarit de la voie franchie et le profil en long de la voie portée ne permettent qu'une faible hauteur du tablier.

I.2.4. Selon la forme en plan. ? Ponts droits.

Ce sont ceux pour lesquels l'axe de la voie portée est perpendiculaire à l'axe de la voie franchie (ou à la direction principale du courant de la rivière).

	Fig.I.9
? Ponts biais.

Dont l'angle des deux axes c'est -à-dire l'axe de la voie de circulation et celle de la rivière sont différent de 9Ø°.

? Ponts courbes.

Est un pont dont l'axe de circulation décrit une courbe.

Fig.I.10 Pont Courbe

Page 13 sur 115

I.2.5. Selon la durée du service envisagé > Ponts provisoires.

Ils doivent être construits rapidement et pour une durée relativement brève permettant la construction d'un ouvrage définitif.

Ils sont en bois ou métal (poutres de récupération). On utilise également les ponts militaires Bellay.

> Ponts définitifs.

Ils sont théoriquement pour une durée de l'ordre d'un siècle et sont évidemment beaucoup plus soignés que les ponts provisoires.

> Pont semi définitif.

Est un pont intermédiaire entre le pont provisoire et le pont définitif.

I.2.6. utres types d'ouvrages selon leur transmission des charges. > Ponts à Haubans.

Cette forme d'ouvrage peut être intéressante pour franchir des portées supérieures à 100 mètres. Les haubans (câbles obliques) introduisent dans le tablier une composante horizontale de compression, ce qui permet d'économiser une grande partie des câbles intérieur.

Le tablier peut être constitué par des poutres sous chaussée ou par des caissons. C'est sont des ponts à efforts normaux de type spéciale.

> De Pont Bow - String.

Un pont bow-string est une catégorie de pont munie d'un tablier faisant aussi fonction de tirant et de poutres latérales (en arc au-dessus du tablier) qui sont encastrés l'un dans l'autre aux extrémités. En travée, le tablier est tenu par des suspentes souvent à la verticale.

> Ponts Vierendeel.

Pont de type treillis dont les diagonales sont enlevées et les membrures sont encastrées.

> Ponts suspendus.

Ponts de portée supérieur supérieure à 300m constitués par des câbles porteurs ou suspends, pylônes, poutre maîtresse et les massifs d'encrages.

> Ponts hybrides.

C'est la combinaison des ponts suspendus et les ponts Haubans.

Page 14 sur 115

? Ponts Radier.

C'est un dalot avec chaussée submersible.

I.3. Historiques4.

L'historique peut se résumer en différentes périodes ci-

dessous :

Avant 1500 (après J.C.).

C'est la période empirique, la conception des ponts sans les calculer. Il s'agit de construction de ponts voûte en maçonnerie par des romains avant 1500.

Période de 1500 à 1700-1800.

C'est la période de grands savants (Newton, Hooke, Galilée) ; c'est le climat des études théoriques des ponts, naissance de l'acier.

Période de 1800-1900.

Naissance de l'industrialisation, d'où début de chemins de fer et construction des 1er Ponts métalliques pour des chemins de fer.

A la fin de cette période, il y a apparition du Béton Armé (B.A).

Période de 1900-1950.

pparition des voitures, d'où des ouvrages d'arts routiers (ponts,...) ;

Apparition du béton précontraint.

Période de 1950-1975

Développement de l'autoroute, à partir de 975, à cause de la crise pétrolière qui a entraîné la crise tout court et de l'apparition des écologistes, fin de la construction des routes.

Ecologistes : les gens destinés à conserver la nature c.-à-d. qui est contre ceux qui détruisent la nature.

Les grandes lignes de l'évolution de la construction des ponts ces dernières années sont les suivantes :

Evolution du trafic en flèche : le trafic a évolué quantitativement et qualitativement et le confort aussi.

4 MUTONDO, « Cours de ponts », BTP3/INBTP 2014-2015.

Evolution des techniques des constructions : les techniques à mettre à la disposition des ingénieurs, des moyens de plus en plus sûrs du point de vue matériaux, calculs et exécutions.

I.4. Éléments constitutifs des ponts5.

Le pont est constitué de deux grandes parties qui sont : la superstructure et l'infrastructure.

I.4.1. La superstructure

La superstructure est constituée de : I.4.1.1. Le tablier

C'est la partie de l'ouvrage supportant la chaussée (ou la voie ferrée) au-dessus de la brèche à franchir. Dans les ponts à poutres, on distingue les ponts à poutres latérales et les ponts à poutres sous chaussée. Que ce soit dans l'un ou dans l'autre cas, une dalle, des entretoises et parfois des longerons, sont associés aux poutres pour former le tablier.

I.4.1.1.1. Dalle

La dalle ou hourdis sert d'élément de couverture ; c'est elle qui reçoit la couche de roulement de la chaussée et les surcharges des véhicules.

Outre celui de couverture, le rôle de la dalle est de reporter les charges permanentes et les surcharges sur les poutres, les longerons et les entretoises.

I.4.1.1.2. Entretoises

Les entretoises intermédiaires ont pour but de solidariser les poutres entre-elles ; elles reportent l'effet des charges sur les différentes poutres. Elles doivent être rigides et avoir une hauteur sensiblement identique à celle des poutres (rigidité). Elles sont à âme pleine mais le plus souvent elles sont triangulées car les efforts qui les sollicitent sont faibles et la couverture repose sur les poutres à faible écartement. Entre les entretoises d'appuis et du milieu on place les autres uniformément à une distance de 7 à 10m. Les entreprises d'appuis répartissent les réactions d'appui entre les différentes poutres et transmettent aux appareils d'appuis les efforts dus au vent.

I.4.1.1.3. Longerons

Les longerons, essentiellement utilisés dans les ponts métalliques, sont disposés parallèlement à l'axe longitudinal de l'ouvrage et relient entre elles les différentes entretoises.

Page 15 sur 115

5 REUNION D'INGENIEURS ; Op. cit

Page 16 sur 115

I.4.1.1.4. Les poutres principales

Il s'agit de l'organe essentiel porteur de l'ouvrage. Les poutres transmettent aux appuis les efforts des charges permanentes et des surcharges. Elles sont parallèles à l'axe longitudinal du pont.

I.4.1.1.4. Poutres latérales

Elles sont également appelées poutres de rive, poutres maitresses ou, encore, poutres principales.

Dans ce type d'ouvrage, les charges sont supportées par deux poutres parallèles à l'axe longitudinal de la chaussée et situées aux bords extrêmes du tablier.

I.4.1.1.5. Poutres sous chaussée

Pour des raisons d'esthétique, dans les agglomérations, pour dégager la visibilité ou pour réserver un gabarit au-dessus de la brèche, la hauteur de la poutre se trouve être imposée. On a alors recours aux ponts à poutres sous chaussée. Un tel type d'ouvrage comporte un certain nombre de poutres sensiblement identiques, réparties de façon uniforme sous le tablier.

I.4.1.1.6. Contreventement

Le contreventement est constitué par une poutraison croisée horizontale entre poutres latérales destiné à assurer la stabilité du tablier sous les efforts du vent.

I.4.1.1.7. La chaussée

Elle reçoit les surcharges et peut être en béton ou en d'autres matériaux. Le drainage des eaux de pluie est assuré par deux pentes opposées dirigées vers les trottoirs et par les canalisations d'évacuation des eaux à travers les trottoirs.

I.4.1.1.7.1. Profil en travers

Pour les ponts droits, ce profil normal est celui qui comprend deux pentes de sens contraire de 2 à 3 % raccordées par un arc parabolique sur une largeur de 0,5 à ,5 m de part et d'autre de l'axe. Pour les ponts courbes, il faut prévoir un devers de 2%.

I.4.1.1.7.2. Profil à long

Sa pente ne dépassera pas 4% et ne sera pas inférieure à 1% afin de permettre un écoulement normal des eaux.

Page 17 sur 115

I.4.1.1.7.3. Le revêtement

Le revêtement comprend essentiellement une couche d'étanchéité et une couche de roulement.

Couche d'étanchéité en béton

Le béton étant un matériau poreux, même bien comprimé, il n'est jamais parfaitement étanche.

Pour protéger les armatures il est nécessaire de disposer d'une chape d'étanchéité sur toute la couverture en béton. L'étanchéité peut être :

? base d'asphalte coulée naturel ou synthétique utilisant des résines

synthétique ;

? Par feuilles préfabriquées revêtues d'asphalte ; ? Par moyens à haute cadence (MHC)

Couche de roulement

La couche de roulement doit, sur un ouvrage d'art comme en section courante, présenter un bon Uni (confort) et offrir des bonnes caractéristiques antidérapantes. Les couches de roulement classiques ne sont pas étanches, il faut alors étudier les dispositions constructives pour éviter la stagnation de l'eau entre la couche de roulement et l'étanchéité proprement dite (drains, pentes, ...).

I.4.1.1.8. Les trottoirs⁶

C'est l'espace latéral du profil en travers dûment identifié par une surélévation par rapport au niveau des voies de circulation des véhicules et dont la fonction principale est de supporter une piste piétonne.

Il est limité, côté circulation par une marche ou par un dispositif de retenue et, côté vide, par un grand corps (ou une barrière de sécurité qui assurera aussi la fonction de sécurité des piétons).

Cette position en surélévation est usuellement utilisée pour faire transiter sur l'ouvrage des canalisations de services publics ou de concessionnaires.

Le trottoir peut être utilisé moyennant certaines adaptations pour permettre une cohabitation comme support d'une piste cyclable.

6 Service d'études techniques des routes et autoroutes : « SETRA » ; Guide technique ; Août 2005 ; France Page 5

Page 18 sur 115

I.4.1.1.8.1. Le revêtement

Il dépend de l'utilisation et du type de l'ouvrage. Dans le cas où le trottoir ne comporte pas d'alvéoles, on peut le consulter par le béton maigre recouverte d'asphalte (en ville) ou non revêtu (en rase campagne) ou simplement comblé du sable.

Pour les trottoirs à dalot (dallette) préfabriqué, il n'y a pas de revêtements. I.4.1.1.8.2. Les bordures des trottoirs⁷

Les bordures de trottoir sont généralement en béton (en site urbain, on emploie parfois des bordures en granit, plus robustes) et leurs dimensions sont normalisées. Leur hauteur varie de 20 à 30 Cm, leur poids de 0,56 à 1,65 KN/m et son parement est incliné de 1/20. La bordure est en saillie de 16 à 20m.

I.4.1.1.8.3. Les canalisations

Les compagnies de gaz, de l'eau, de l'électricité peuvent solliciter de faire franchir leur conduite et leur câble par le pont. On ménage ainsi des galeries visitables sous les trottoirs pour les recevoir. Il faut alors prévoir d'alvéoles en créant des compartiments sous la dallette car certaines canalisations ne peuvent pas être mises côte à côte telles que les conduites des gaz et les câbles électriques.

I.4.1.1.8.4. Les garde-corps

Ils ont essentiellement pour objet la protection des piétons. Ils doivent être constitués des matériaux non fragiles ; on utilise souvent l'acier doux ou les alliages légers. La hauteur minimale est égale à :

hmin = Min (1,20m ; 0,95m + 0,005H #177; 0,05m).

Avec H = la hauteur en mètre du trottoir au-dessus du sol ou de l'eau.

Jusqu'à une hauteur de 0,60m au-dessus du trottoir, les vides doivent être suffisamment réduits pour qu'on ne puisse pas y faire pénétrer un cylindre de plus de 5cm de diamètre afin d'assurer la sécurité des jeunes enfants.

Les différentes parties d'un garde-corps sont :

? La main courante ou lisse (elle est dépourvue de souillée) ;

? Une ou plusieurs sous lisses (facultatives suivant le type de garde-corps) ; ? Les montants principaux scellés dans le tablier ;

? Les barreaux ou montants secondaires (facultatifs).

7 J. Armand CALGARO: `` Projet et construction des ponts ; Presses de l'école nationale des ponts et chaussées. Paris 1999.page 220-221''.

Page 19 sur 115

I.4.1.1.8.5. Canalisation d'eau

Les eaux de pluie sont évacuées hors du pont par des drains (ouvertures, orifice, tuyaux, conduite...) à travers les trottoirs (conduites à plastique, en métal, en amiante ciment).

I.4.1.1.8.6. Les corniches

La corniche a essentiellement un rôle esthétique. En plus de ce rôle elle doit également servir de lamier afin d'éviter le ruissellement de l'eau de pluie sur le parement. La corniche en béton peut être coulée en place ou préfabriquée.

I.4.2. L'infrastructure

L'infrastructure est constituée de :

I.4.2.1. Les piles et les culées

Les piles et les culées dépendent des deux éléments qu'elles unissent :

? Le sol

? le tablier

Elles sont donc conçues au mieux, en tenant compte de ces facteurs, ce qui se traduit par la résistance mécanique, la stabilité et l'aspect.

En plus de leur rôle de support des extrémités des ouvrages d'art, les culées doivent souvent soutenir les terres des ouvrages d'accès et sont étudiées en conséquence.

I.4.2.2. Les appareils d'appui

Sous l'effet des différences de température, ou sous l'application des surcharges, les tabliers se déplacent par rapport aux piles et aux culées. Il est donc nécessaire d'interposer entre eux des dispositifs permettant ces mouvements : ce sont les appareils d'appui.

Ces appareils d'appui peuvent être fixes ou mobiles ; ils sont différents selon que l'ouvrage est en béton armé ou précontraint, à poutres préfabriquées (appuis en Néoprène, par exemple) ou coulé en place (noyau Freyssinet) ou métallique (balanciers ou rotules...).

I.4.2.3. Le sommier

Il s'agit de la maçonnerie au-dessus des appuis sur laquelle repose une voûte ou des poutres et servant à transmettre et à répartir les charges des tabliers sur les piles et culées. Il joue le rôle d'une poutre ceinture ou chaînage dans la construction des ponts.

Page 20 sur 115

I.4.2.4. La dalle de transition

Il s'agit d'une dalle en béton armé placée sous la chaussée à l'entrée du pont, elle est appuyé sur l'arrière de la culée et sur le remblai. Elle a pour rôle d'éviter la dénivellation qui risque de se produire entre la chaussée courante et le pont en cas de tassement du remblai. Si ce tassement se produit elle remplace une différence brutale de niveau par une légère augmentation de la pente.

Page 21 sur 115

Chapitre II. Description de l'ouvrage II.1. Description de site

Le présent pont sera érigé dans la ville province de Kinshasa, entre le quartier NDANU dans la commune de LIMETE et le quartier ABATTOIR dans la commune de MASINA.

II.1.1. Données hydrographiques

Le quartier NDANU et ABATTOIR sont séparés par une grande rivière dénommée « rivière N'DJILI »

II.1.2. Données naturelle

Les données naturelles étant l'ensemble des éléments techniques de l'environnement qui influence directement la structure. Cela nous permettrait d'avoir :

a) Données géologiques

Le site de Kinshasa a deux zones géomorphologiques :

? La plaine du pool bordant le fleuve Congo au nord constituée par deux terrasses emboîtées dont l'altitude varie de 275 à 340m

? La zone des collines dont le sommet culmine à 550m d'altitude présentant dans l'ensemble des pentes de l'ordre de 2 à30% pour des altitudes de 345 à 550m. elle est située au sud-est et sud-ouest de la ville.

b) Données hydrologiques

Lorsqu'un ouvrage d'art franchit un cours d'eau ou un canal, un certain nombre des renseignements sont nécessaire. En dehors du relevé précis de la topographie de lit, il convient de connaitre les niveaux des eaux qui influencent sur la conception de l'ouvrage et son implantation dans l'espace et permet d'apprécier l'opportunité de certaines méthodes d'exécution.

Débit d'étiage : 0,140m³/s

Vitesse d'écoulement : 0,7m/s avec une profondeur de 0,65m

Précipitation annuelle : 1500mm

Débit de crue : 14,7 m³/s

PHE : 2,5m

PBE : 0,5m

Profondeur de la nappe phréatique : pas présence de la nappe phréatique.

c) Les données géotechniques

Les données géotechniques sont évidemment fondamentales dans l'étude d'un ouvrage. Non seulement elles déterminent les types de fondations des appuis, mais elles constituent l'une des éléments de choix de la solution pour le franchissement.

Page 22 sur 115

Elles sont obtenues à partir de la reconnaissance du sol. Les essais in situ mettent en évidence les sols ci-après.

Nature du sol	Contrainte admissible Kg/cm^2
Sable fin moyennement compact	2 à 3
Sable fin assez compact	3 à 6
Sable fin très compact	6 à 12

Comme nous sommes face à un sable fin assez compact, les résultats proposent un mode de fondation directe et travaillant avec une contrainte admissible de 3,5 kg/cm² (0,35 MPa).

? Capacité portante : 0,35 MPa ? Profondeur du sol : 2,5m

II.2. Description de l'ouvrage

II.2.1. Présentation de l'ouvrage

Notre ouvrage est un pont-route de 18m de portée avec une travée isostatique, qui contient deux bandes de 3,5m, deux trottoirs de 1,5m, deux caniveaux de 0,35m et deux bordures de 0,15m.

II.2.2. Les données fonctionnelles

Elles rassemblent l'ensemble des caractéristiques permettant au point d'assurer la fonction de l'ouvrage de franchissement.

II.2.2.1. Données relatives à la voie portée

Le dimensionnement à adopter pour les différentes caractéristiques de la route répond à une nécessité de permettre l'écoulement du trafic dans les conditions de fluidité et de confort lié à l'importance de l'itinéraire. Ces données concernent :

a) Le tracé en plan

C'est la ligne définissant la géométrie de l'axe de la voie portée. Il définit aussi les ouvrages droits, biais et courbes. Il convient d'éviter les deux cas derniers pour des raisons qu'ils sont difficiles à calculer et à exécuter.

b) Le profil en long

C'est la ligne située sur l'estrade de l'ouvrage définit en élévation le tracé en plan. Il doit être défini en tenant compte des nombreux paramètres liés aux contraintes fonctionnelles de l'obstacle franchi.

Page 23 sur 115

c) Le profil en travers

Il définit la géométrie et les équipements de la voie dans le sens transversal. Les pentes transversales de la chassée ont une valeur variante entre 0 et 2%.

II.2.2.2. Données relatives à l'obstacle franchi

Lorsqu'un ouvrage projeté franchit une voie de communication (route, voie ferrée ou voie navigable), il convient naturellement de respecter les caractéristiques relatives à cette voie. Il s'agit de respecter les ouvertures.

Les gabarits définissent la hauteur libre minimale à dégager au-dessus de la voie franchie les ouvertures de la largeur minimale à dégager parfois appelée « gabarit horizontale ».

> Dans notre cas l'ouvrage franchi une voie non navigable, mais il est important de définir les gabarits à respecter. Car au cas contraire l'ouvrage sera englouti par des eaux de la rivière. Nous devrons donc définir la période des plus hautes eaux (PHE) et celle des plus basses eaux (PBE).

> Le gabarit maximal du véhicule est fixé à 4m.

II.3. Les données architecturales

Ces données rassemblent les éléments qui vont guider la conception esthétique de la structure.

II.4. Conception de l'ouvrage

II.4.1. Choix du type de l'ouvrage

Ce choix est une démarche qui nous aide bien de trouver la variante qui s'inscrit le mieux dans le contexte naturel du franchissement de l'obstacle.

II.4.2. Critère de choix du type d'ouvrage Il nous est de tenir compte de :

> L'obstacle à franchir : la rivière

> Voie portée : un pont-route

> Matériaux : un pont en béton armé

> Fonctionnement mécanique : un pont fixe

> Durée de vie de l'ouvrage : un pont définitif

Suivant les critères nous sommes face à un pont en béton arme de 18 m de portée à une travée isostatique, deux culées gauche et droite.

Page 24 sur 115

II.5. Base de calcul

Les charges et règlement de calcul adoptés pour le présent travail sont relatifs aux normes belges en particulier NBN B03-101 qui fixe les actions à considérer pour le calcul des ponts routes. La méthode de calcul est celle des états limites.

Page 25 sur 115

Chapitre III Pré dimensionnement

III.1. Définition

Le pré dimensionnement d'une structure consiste à fixer les dimensions de différents éléments de la structure ou de l'ouvrage en respectant certain règles et principes pratique de la construction.

Etant donné que la superstructure est composée des éléments en béton armé et autre, le pré dimensionnement de la structures se portera sur : la poutre (nervure longitudinale), la dalle et l'entretoise nervure transversale).

Partant sur le renseignement reçu de l'office de route, relative à l'ouverture de deux bouts de la rivière sur laquelle nous voulons placer le pont et suivant l'utilité du projet, nous recueillons les données ci-dessous :

élément	Nombre	longueur (m)	longueur total
Bande	2	3,50 m	7 m
Caniveaux	2	0,35 m	0,70 m
Bordure	2	0,15 m	0,30 m
Trottoir	2	1,50m	3 m
Largueur de la chaussée 11 m

III.2. La poutre

a) Hauteur de la poutre Hp

Pour déterminer la hauteur de la poutre, il est mieux de respecter la condition avec L : la portée du pont

8

0

85 H

,2 H ,8

D'où nous adoptons Hp= ,2m

b) Epaisseur de la poutre (bo)

La condition pour déterminer l'épaisseur de la poutre est donnée par :

0,30	Hp	bo	0,40Hp
0,30	,2	bo	0,40	,2
0,36	bo	0,48

Nous adoptons bo=0,40m

c) Nombre des poutres (Np)

Le nombre des poutres est fonction de la longueur totale du pont. Le cours de pont « Réunion des ingénieurs⁸ » recommandé dans la page 305, l'utilisation de l'abaque ci-après pour déterminer le nombre des poutres.

Largueur	à 6m	6 à 9m	9 à 11m		11 à 14 m	Np
2	3	4	5

Etant donné que la largeur totale du pont est de 11 m et pour mieux repartir les

charges sur toutes les poutres nous prendrons = 4 .

d) Distance entraxe des poutres L1x

La distance entraxe L x est déterminée par l'expression =
Avec l : la largeur du pont

=

4 = 2,8 m

e) Ecartement des poutres

b0

= 2 2

= b0 = 2,75 0,40 = 2,4m

f) Porte à faux

Les portes à faux sont aux extrémités de la largeur du pont suivant le profil en

travers p = ,

= = ,4 m

g) Les goussets

Les dimensions des goussets sont tirées de l'expérience pratique soit une largeur de 030 m et 010 m de hauteur.

h) Encorbellement 2

Alors ,

d où 0,60 m

Nous adoptons alors 0,55m qui équivaut à 55cm

⁸ Réunion des ingénieurs, op.cit.

Page 26 sur 115

Page 27 sur 115

III.3. La dalle

L'épaisseur de la dalle est toujours 6m

pour 16m, nous avons une distance entraxe de 2m pour 18m, nous avons une distance entraxe de 3m pour 20m, on nous avons distance entraxe de 4m

D'où pour notre cas, maintenons la valeur de 18m vu que L1x est égale à 2,75m.

III.4. L'entretoise

Les entretoises sont des éléments en béton armé considérées comme poutres disposée perpendiculairement aux poutres principales reliant celle-ci, alors qu'elles sont placées transversalement par rapport à la portée du pont.

a) Hauteur de l'entretoise (He)

En travée He = Hp ed = ,20 0, 8 = ,02m

Aux appuis He = 2 = 2 ,

= 0,68m

b) Epaisseur de l'entretoise

L'épaisseur de l'entretoise est à celle des poutres longitudinales.

= 5 :

Cette expression est destinée dans l'ouvrage « calcul et vérification des ouvrages en béton armé de Pierre Chavron » 9

Alors be = 40 5 = 35cm

c) Distance entraxe d'entretoise

Elle varie entre 5m 8m
nous adoptons 6m

d) Ecartement des entretoises Cet écartement est donné par la relation

be

= 2 2

si nous simplifions, l expressiondevient = be = 6 0,35 = 5,65m

e) Nombre d'entretoise Ne

⁹ Pierre Chavron, calcul et vérification des ouvrages en béton armé

Partant de la théorie du cours de pont, il exige qu'on place une entretoise au droit de la section médiane et deux autres aux extrémités et de placer encore une si possible dans les deux parties récentes. Mais nous les

déterminons par la relation Ne =

Ne =	8 0,35	= 2,94 = 3,94m 4 entretoises
	6

Page 28 sur 115

III.5. Trottoir

Le trottoir est constitué de :

Sable de 0cm d'épaisseur Mortier de 1cm d'épaisseur Dallette de 3cm d'épaisseur Chape de protection

Pierre de taille

Représentation transversale de la superstructure

Page 29 sur 115

Représentation longitudinale du la superstructure

Page 30 sur 115

CHAP IV. CALCUL DE LA POUTRE ET L'ENTRETOISE

IV.1. La poutre

IV.1.1. Répartition des charges transversales10

En considérant l'hypothèse où = pour le calcul des lignes

d'influence, le croquis ci-dessous représente la coupe transversale du pont.

Partant de la ligne d'influence de la poutre une, nous la définissons comme étant la déformation de l'entretoise sous l'effet d'une charge unitaire située au droit de cette poutre, ce raisonnement est valable pour les poutres 2, 3,4, et 6.

Comme l'entretoise , les lignes d'influences sont des droites, il suffit de connaitre deux points pour le tracer.

Plaçons en premier une charge unitaire en 0 c.-à-d. dans l'axe du point. Le coefficient de répartition des charges est de 1/4 car chaque poutre est estimée charger de la même manière, alors que le point 0 est commun à toutes les

poutres. Ces qui vient à dire qu'à ce point on a = 0,25t.

Plaçons une charge unitaire de 1t sur la poutre une, à ce point nous aurons une flexion composée car l'effort normal de t et un moment réduit au centre de la section M = P d apparaissent et on obtient R = R2 = R3 pour la commodité de calcul, nous replaçons I par le moment d'inertie de la section fictive S tel que :S = S2 = S3 = S4 = . d où St = ? Si

= 4 dans cette condition I=Sd² par

symétrie I= (S1d²+S2d2²) 2

Avec une charge unitaire de 1t, sur la première poutre on a une rotation de la section de 0, l'axe de la coupe transversale. On a Q1, Q2, Q3, Q4, Q5 et Q6

Avec

Q1= d où P =Q1S1

¹⁰ Mutondo, op.cit.

Page 31 sur 115

Q2= d où P =Q2S2 Q3=

doù P =Q3S3

Q4= doù P =Q4S4

Nous savons que ? P =

= 4,2 ; = ,4

= (4,2) ( ,4) 2

= 9,33 et_, = 28

= ( 7,64 ,96)

= 39,2 Pd1=( 4,2) = 4,2

On aura alors = ,

Donc Q1= , =0,70 d oùP = 0,70 = 0,70t

,

Q2= , = 0,40 doù P2 = 0,40 = 0,40t

Q3= ,

= 0, 0 doù P2 = 0, 0 = 0, 0t

^,Q4= = 0,20 d oùP2 = 0,20 = 0,20t

,

Vérification de ?Pi = t alors prenons: (0,7 0,4 0, 0,2) = t cqfd

Page 32 sur 115

IV.1.1.1. Traçage des lignes d'influences

IV.1.1.2. Evaluation des surfaces des diagrammes obtenus

Ligne d'influence	Surfaces positives		Surfaces négatives					Surfaces totales
1 et 4	0,7 8,6	3,0	0,2		2,4	=	0,24	2,77
	2 =			2
2 et 3	(0,09 0,4)		0					2,70
	2
	= 2,70

IV.1.1.3. Utilisation des lignes d'influences

Pour le poids propre de l'ouvrage, il n'y a pas des répartitions transversales, chaque poutre repend de même charge.

Pour le surcharge fixe, il est de même que le poids propre. La foule à son tour on considère le coefficient d'impact dynamique de ,2 avec la charge ed4KN. Faisons

alors 0,4 ,2 = 0,48tm.

Cette charge est la seule qui se répartie sur toute la surface du tablier du pont ; d'où nous allons la multiplier par les surfaces des lignes d'influences transversales.

Page 33 sur 115

Lignes d'influences

	Surfaces positives				Surfaces négatives
1 et 4	0,48	3,0	=	,44	0,48	0,24	= 0,	5
2 et 3	0,48	2,7	=	,30		0

Pour le convoi nous supposons que chaque véhicule ne peut se mouvoir que dans la bande de circulation. D'où la recherche de la répartition maximale par usage des lignes d'influences avec l'utilisation de deux véhicules à la fois.

	R	R	R	R	Total
P1	0,46	0,31	0,2	0,04	1,01
P2	0,32	0,27	0,13	0,18	1
P3	0,18	0,23	0,27	0,32	1
P4	0,04	0,19	0,3	0,46	0,99
Total	1	1	1	1	4

IV.1.1.4. Calcul des coefficients d'impact dynamique

,

III.1.1.4.1. Coefficient d'impact dynamique pour la dalle

Elle est donnée par la relation = , ,

? Charges permanentes Pour la dalle : =

Alors P = 0, 8 25 8 7 = 567KN
Pour la chaussée

- Couche de forme en béton

P = (0,04	23	8	7)	= 5,92KN
- Couche d'isolation P = (0,02	23	8	7)	= 57,96KN

Page 34 sur 115

- Couche de revêtement

P = (0,03 23 8 7) = 86,94KN

Le poids propre de la chaussée = 5,92 57,96 86,94 = 260,82
Tablette

P = 0,30 25 8 0, 5 = 20,25KN

Le poids total Pt=poids de la dalle + poids de la chaussée + poids de la tablette

P = 567 260,82 20,25 = 848,07KN

? Charge d'exploitation

Nous n'avons que deux bandes de 3,5m, donc nous considérons deux camions de 32t roulant à coté ; la position la plus défavorable. D'où Q=32t 2=64t=640KN

,

,

Alors = ,

( , )

= , 8 ,2

IV.1.1.4.2. Coefficient d'impact dynamique pour la poutre

? Charges permanentes

Pour la chaussée

- Couche de forme en béton armé

P = (0,04 23 8 7) = 5,92KN
- Couche d'isolation

P = (0,02 23 8 7) = 57,96KN
- Couche de revêtement

P = (0,003 23 8 7) = 86,94KN

D'où le poids pour la chaussée =

Alors on a : = 5,92 57,96 86,94) = 260,82

Pour l'entretoise - En travée :

3 = ,02 0,35 3 2,8 2 25 = 49,94

- Aux appuis : on applique la même formule est on a

0,68 0,35 3 2,8 2 25 = 99,96KN

D'où le poids de l'entretoise = 49,94 99,94 = 249,9

Pour la poutre

= = ,20 0,40 8 25 4 = 864

Trottoir

= 0,05 ,5 8 25 = 33,75
Garde-corps : 1KN 8 = 8KN

Pour la tablette la valeur déjà calculée dans la partie haute = 20,25

' ù = = (33,75 20,25 8) = 72

Cette valeur on le multiplie par deux parce que qu'on a deux trottoirs, qui donnent 144KN

=

= (260,82 249,9 864 44 567) = 2085,72KN

Charge d'exploitation

= 32 2 = 64 = 640

,

,

( , )

Alors =

, = , 3

Page 35 sur 115

IV.1.1.5. Choix de la poutre la plus chargée

La valeur de la poutre la plus chargée est de 1,01(de la poutre une), cette poutre tiendra compte du coefficient d'impact dynamique de

1, 3, alors l'effet maximum réduit pour KN par essieu k =

Avec n : nombre des bandes, c : la valeur de la poutre la plus chargée

k = 2

= 0,57

,0 , 3

IV.1.2. Détermination de la poutre longitudinale la plus chargée

Etablissons les lignes d'influences des moments (M) et l'effort tranchant (T) en 10 points de notre poutre et déterminons la courbe enveloppe de ces deux derniers dans ce dix ponts.

IV.1.2.1. Le moment fléchissant à chaque section a) Calcul du moment fléchissant

Mmax =

L ; x = L x _;P = t

Pxx

alors Mmax =	Px(L x)
	L
pour x = 0; M =			0( 8 0) 8		= 0tm

pour x = .8_; M = pour x = 3.6_; M = pour x = 5.4; M = pour x = 7.2; M =

.8( 8 .8)

8

3.6( 8 3.6)

8

5.4( 8 5.4)

8

7.2( 8 7.2)

8

= .62tm

= 2.88tm

= 3.78tm

= 4.32tm

pour x = 9; M =		9( 8 9) 8	= 4.5tm

pour x = 0.8_; M = pour x = 2.6_; M = pour x = 4.4; M = pour x = 6.2; M =

0.8( 8 0.8)

8

2.6( 8 2.6)

8

4.4( 8 4.4)

8

6.2( 8 6.2)

8

= 4.32tm

= 3.78tm

= 2.88tm

= .62tm

Page 36 sur 115

pour x = 8; M =	8( 8 8)	= 0tm
	8

b) Evaluation des surfaces des lignes d'influence du moment fléchissant

Les surfaces du diagramme des moments fléchissant à chaque section de la poutre sont des triangles dont la base est la portée du pont et la hauteur est la valeur du moment fléchissant en ce point de la poutre.

Comme nous venons de remarquer ci-haut que :

S = S ; S = S ; S = S ; S = S ; etS = S

Alors on fait :

0 8

S= S =		= 0m
	2

.62 8

S= S =		= 4.58m
	2

2.88 8

S= S =		= 25.92m
	2

3.78 8

S= S =		= 34.02m
	2

4.32 8

S= S =				= 38.88m
		2
S=	4.5 8		= 40.5m
	2

IV.1.2.2. Effort tranchant à chaque section

( )

= =

a) Effort tranchant positif

( 8 0)

T 0 = 8

= t

T = 8

= 0.9t

( 8 .8)

T 2 = 8

( 8 3.6)

T 3 = 8

( 8 5.4)

T 5 = 8

= 0.5t

( 8 9)

T 6 = 8

= 0.4t

( 8 0.8)

Page 37 sur 115

T 4 = ( 8 7.2)

8

= 0.8t

= 0.7t

= 0.6t

T 7 = 8

( 8 2.6)

= 0.3t

T 8 = 8

= 0.2t

( 8 4.4)

T 9 = 8

= 0. t

( 8 6.2)

T 0 = 8

( 8 8)

Page 38 sur 115

= Ot

b) Effort tranchant négatif T i = P T i

T 0 = = 0t

T = 0.9 = 0. t

T 2 = 0.8 = 0.2t

T 3 = 0.7 = 0.3t

T 4 = 0.6 = 0.4t

T 5 = 0.5 = 0.5t

T 6 = 0.4 = 0.6t

T 7 = 0.3 = 0.7t

T 8 = 0.2 = 0.8t

T 9 = 0. = 0.9t

T 0 = 0 = t

c) Evaluation des surfaces des lignes d'influences de l'effort tranchant

Les surfaces des lignes d'influences sont des triangles

dont la base est la portée du pont en ce point et la hauteur est la valeur de l'effort tranchant en ce point.

T X

S=
	2

v Effort tranchant positif

S 0 =			8 = 9m

0.9 6.2

S= S 2 = S 3 = S 4 =			= 7.29m = 5.76m = 4.4 m = 3.24m

S 5 =	0.5 9		= 2.25m

S 6 =

S 7 =

S 8 =

S 9 =

0.4 7.2

2

0.3 5.4

2

0.2 3.6

2

0. .8

2

= .44m

= 0.8 m

= 0.36m

= 0.09m

S 0 =	0 0		= 0m

v Effort tranchant négatif

0 0

S 0 =		= 0m
	2

0. .8

S=		= 0.09m
	2

0.2 3.6

S 2 =		= 0.36m
	2

0.3 5.4

Page 39 sur 115

S 3 =

S 4 =

2

0.4 7.2

2

= 0.8 m

= .44m

Page 40 sur 115

0.5 9

S 5 =		= 2.25m
	2

0.6 0.8

S 6 =		= 3.24m
	2

0.7 2.6

S 7 =				= 4.4 m
	2
S 8 = S 9 =	0.8 4.4			= 5.76m = 7.29m
	2 0.9 6.2
	2
S 0 =			8= 9m
		2

? Surface totale

La surface totale est la différence entre la surface positive et la surface négative.

St = Si Si

On a :

St = 9 0 = 9m

St = 7.29 0.09 = 7.2m

St = 5.76 0.36 = 5.4m

St = 4.4 0.8 = 3.6m

St = 3.24 .44 = .8m
St = 2.25 2; 25 = 0m

St = .44 3.24 = .8m

St = 0.8 4.4 = 3.6m
St = 0.36 5.76 = 5.4m St = 0.09 7.29 = 7.2m St = 0 9 = 9m

Page 41 sur 115

IV.1.2.3. Diagrammes des lignes d'influences IV.1.2.3.1. Lignes d'influence des moments

IV.1.2.3.2. Lignes d'influences des efforts tranchants

IV.1.3. Application

Déterminons d'abord la largeur de la table de compression :

Page 42 sur 115

b

		b0	= Min = Min = .4 = 2(	L Lx [ ] .11
b	2	b0		0' 2 [ 8 2.81
b	2	b0		.4)	0' 2 J
b	2	b0

b = 2.8 0.4 b = 3.20m

IV.1.3.1. Poids propre

a) Poutre

> Dalle (table de compression)

S = 0. 8 3.20 = 0.578m > Nervure

S2 = 0.40 .02 = 0.408m
> Les deux goussets

0. 0.3

S4 = S3 = 2		= 0.03m
	2

St = S S2 (S3 4) = 0.576 0.408 0.03 = .0 4m

D où Pp = St b = .0 4 25 = 25.35 KN m

¹¹ Pratique du BAEL 91, cours et exercices corrigés

Page 43 sur 115

b) Entretoise

Les effets des entretoises extrêmes sont directement reprisent par les appuis, les autres entretoises (intermédiaires) peuvent être considérées comme ponctuelles ou uniformément réparties ; nous considérons ce dernier cas :

Pentr =	Nentr be(he e de la dalle)(b b0) b
	L
Pentr =	2 0.35( .02 0. 8)(3.20 0.40)25	= 2.28KN
	2

Alors :

P = Pp Pentr

P = 2.28 25.35 = 27.6KN = 2.76t m IV.1.3.2. Surcharge fixe sur la moitié du pont > Garde-corps : 0,05t/m > Chape de protection : 0,15t/m
>	Revêtement asphalté :	7 0.03 2.3 = 0.483 t/m
>	Mortier de port : 0.0	.5	2.2 = 0.033 t/m
>	Sable (trottoir) : 0.	.5	.8 = 0.27t/m
>	Couche d'isolation : 7	0.02	2.3 = 0.322 t/m
>	Couche de forme : 7	0.04	2.3 = 0.6 4 t/m
>	Pierre de taille : 0. 5	0. 5	2.3 = 0.052 t/m
>	Dallette : 0.03 .5	2.2 =	0. 08 t/m

? = .79 ^t /_m

Etant donné que la moitié du pont comporte deux poutres, on aura comme solution :

.72 P = 2

= 0.895t/m

D'où Pt = P P = 2.76 0.895 = 3.66 t/_m en ELS Et Pt = 4.94 ^t /_m en ELU

IV.1.3.3. Foule

Charge positive : en ELS .44 t/_m et en ELU 2. 6 t/_m

Charge négative : en ELS 0. 5 t/_m et en ELU 0. 7 t/_m

IV.1.3.3. Convois

Le convoi de 32t mis dans la position la plus défavorable. La position longitudinale de convois produit un moment maximum.

La norme NBN considère la charge suivant pour le pont route par rapport à la bande de circulation, un convoi routier de 32t (12t, 6t, 6t, 4t, 4t) ? Les essieux étant permutable et écartés de 4m

IV.1.3.3.1. Valeurs des moments dus au convoi

On calcul ces valeurs suivant la règle de triangle semblable en tenant compte du déplacement du convoi au long du pont.

Cas 1 où le convoi est fixe sur le pont Au point 1

/ .l v .	. = alors Y =			= 0.9 (4t)

/ .	/	. = alors Y2 =			= .3 (6t)

/ .	/	. = alors Y3 =			= 0.9 ( 2t)

/ .	/	. = alors Y4 =			= 0.5 (6t)

/ .	/	. = alors Y5 =			= 0. (4t)

s . .		. = alors Y =				= 0.8 (4t)
	. = alors Y2 =			= 2.6 (6t)

Page 44 sur 115

Au point 2

s .		. = alors Y2 =			= .8 ( 2t)

s .		. = alors Y4 =			= (6t)

s .		. = alors Y5 =			0.2 (4t)

Au point 3

s .		=
.		s .
=
.		s .
=
.		s .
=
.		s .
=

.

.

.

.

.

.

Au point 4

.

alors Y =

.

alors Y2 =

.

alors Y3 =

.

alors Y4 =

.

alors Y5 =

= 0.7 (4t)

= 3.5 (6t)

= 2.7 ( 2t)

= .5 (6t)

= 0.3 (4t)

.

/ .:

V .

= 0.6 (4t)

.

= alors Y =

.

/ .: V .

= 3 (6t)

.

= alors Y2 =

/ .	/	. = alors Y3 =			= 3.6 ( 2t)

/ .	/	. = alors Y4 =			= 2 (6t)

/ .	/	. = alors Y5 =		= 0.4 (4t)
	.		.

Page 45 sur 115

Page 46 sur 115

Au pont 5

? . alors Y = .

= = 2.5 = Y4 (6t)

? . alors Y2 = .

= = 0.5 = Y5 (4t)

? Y3 = 4.5 ( 2t)

IV.1.3.4.1.1. Tableau récapitulatif du moment

Section	4t			6t			12t		somm e	0.57M
	Y1	Y2	(Y1+Y2)4 t	Y1	Y2	(Y1+Y2)6 t	Y	12Y
	0.	0.
1	9	1	4	1.3	0.5	10.8	0.9	10.8	25.6	14.60
	0.	0.
2	8	2	4	2.6	1	21.6	1.8	21.6	47.2	26.9
	0.	0.
3	7	3	4	3.5	1.5	30	2.7	32.4	66.4	37.85
	0.	0.
4	6	4	4	3	2	30	3.6	43.2	77.2	44
	0.	0.
5	5	5	4	2.5	2.5	30	4.5	54	88	50.16
Somm										173.5
e			20			122.4		162	304.4	1

Cas 2 où le convoi se déplace sur le pont Au point 1

ü Y = .62 (4t)

ü . =

. .

alors Y2 = . . . = .22 (6t)

ü .

.

=

.

alors Y3 = . .

= 0.82 ( 2t)

ü .

.

=

.

alors Y4 = . .

= 0.42 (6t)

ü .

.

=

.

alors Y5 = . .

= 0.02 (4t)

Au point 2

ü Y = 2.88 (4t)

ü . = . .

alors Y2 = . .

. = 2.08 (6t)

ü . = . .

. . = .28 ( 2t)

alors Y3 =

ü .

.

=

.

alors Y4 = . .

= 0.48 (6t)

ü .

.

=

.

alors Y2 = . .

= 2.58 (6t)

ü .

.

=

.

alors Y3 =

. . = .38 ( 2t)

ü .

.

=

.

alors Y4 = . .

= 0. 8 (6t)

Page 47 sur 115

Au point 3

ü Y = 3.78 (4t)

Au point 4

ü Y = 4.32 (4t)

ü .

.

=

.

alors Y2 = . .

= 2.72 (6t)

ü .

.

=

.

alors Y3 =

. . = . 2 ( 2t)

Au point 5

ü Y ü .	= = =	4.5 (4t) . Y2 alors =	=		2.5 (6t) 0.5 ( 2t)	ü .
ü		=

Pour les points :

P = P9; P2 = P8; P3 = P7; P4 = P6, vus que le diagramme est symétrique IV.1.3.4.1.2. Tableau récapitulatif

section	4t			6t			12t		somme	0.57M
	Y1	Y2	(Y1+Y2)4t	Y1	Y2	(Y1+Y2)6t	Y	12Y
1	1,62	0,02	6,56	1,22	0,42	9,84	0,82	9,84	26,24	14,96
2	2,88	0	11,52	2,08	0,48	15,35	1,28	15,36	42,24	24,08
3	3,78	0	15,12	2,58	0,18	16,56	1,38	16,56	48,24	27,50
4	4,32	0	17,28	2,72	0	16,32	1,12	13,44	47,04	26,81
5	4,5	0	18	2,5	0	15	0,5	6	39	22,23

Page 48 sur 115

somme

202,76

115,57

73,07

68,48

61,2

IV.1.3.4.1.3. Tableau synthèse des deux cas

Section	CAS 1		CAS 2		Mcrt	A RETENIR
	M	M*Mcrt	M	M*Mcrt
1	25,6	14,59	26,24	14,96	0,57	14,96
2	47,2	26,90	42,24	24,08	0,57	26,9
3	66,4	37,85	48,24	27,50	0,57	37,85
4	77,2	44,00	47,04	26,81	0,57	44
5	88	50,16	39	22,23	0,57	50,16
Somme		173,51		115,57		173,87

Comme nous venons de trouver les moments de fléchissant dus aux trains des charges de convoi, alors trouvons les moments dus à la foule et au poids propre de la poutre en fin de faire la sommation de tous les trois moments.

IV.1.3.4.1.4. Tableau des moments dus à la foule

Section	S+	q+ EN ELS	q+ EN ELU	q+S+ ELS	q+S+ ELU
1	14,58	1,44	2,16	21,00	31,49
2	25,92	1,44	2,16	37,32	55,99
3	34,02	1,44	2,16	48,99	73,48
4	38,88	1,44	2,16	55,99	83,98
5	40,05	1,44	2,16	57,67	86,51

Page 49 sur 115

Page 50 sur 115

IV.1.3.4.1.5. Tableau des moments dus au poids propre

Section	S+	Pt	Pt'	S+Pt	S+Pt'
1	14,58	3,66	4,94	53,36	72,03
2	25,92	3,66	4,94	94,87	128,04
3	34,02	3,66	4,94	124,51	168,06
4	38,88	3,66	4,94	142,30	192,07
5	40,05	3,66	4,94	146,58	197,85

IV.1.3.4.2. Valeurs des efforts tranchants dus aux convois

L'effort tranchant est maximal aux appuis et on peut le calculer toujours suivant la règle de triangle semblable en tenant compte du déplacement du convoi tout au long du pont.

Cas 1 où le convoi est fixe sur le pont Au point 0

? olrs Y0 =

= = 0.94 (4t)

? lors Y =

= = 0.72 (6t)

? alors Y2 =

= = 0.5 ( 2t)

? alors Y3 =

= = 0.27 (6t)

? alors Y3 =

= = 0.05 (4t)

Page 51 sur 115

Au point 1

Nous appliquons la même procédure, et on a des valeurs :

1' Y0 =		0 (4t)
1' Y	=	0.72 (6t)
1' Y2	=	0.5 ( 2t)
1' Y3	=	0.27 (6t)
1' Y4	=	0.05 (4t)

Au point 2

1'	Y0=0 (4t)
1'	Y1=0.72 (6t)
1'	Y2=0.5 (12t)
1'	Y3=0.27 (6t)
1'	Y4=0.05 (4t)

Au pont 3

1'	Y0=0 (4t)
1'	Y1=0 (6t)
1'	Y2=0.5 (12t)
1'	Y3=0.27 (6t)
1'	Y4=0.05 (4t)

Page 52 sur 115

Au point 4

1'	0	=	0 (4	)
1'		=	0 (6	)
1'	2	=	0.5 (	2 )
1'	3	=	0.27	(6 )
1'	4	=	0.05	(4 )

Au point 5

1'	0	=	0 (4	)
1'		=	0 (6	)
1'	2	=	0.5 (	2 )
1'	3	=	0.27	(6 )
1'	4	=	0.05	(4 )

Au point 6

1'	0	=	0 (4 )
1'		=	0(6 )
1'	2	=	0( 2 )
1'	3	=	0.27 (6 )
1'	4	=	0.05 (4 )

Page 53 sur 115

Au point 7

1'	0	=	0 (4 )
1'		=	0 (6 )
1'	2	=	0 ( 2 )
1'	3	=	0.27 (6 )
1'	4	=	0.05 (4 )

Au point 8

1'	0	=	0 (4 )
1'		=	0 (6 )
1'	2	=	0 ( 2 )
1'	3	=	0 (6 )
1'	4	=	0.05 (4 )

Au point 9

1'	0	=	0 (4 )
1'		=	0 (6 )
1'	2	=	0 ( 2 )
1'	3	=	0 (6 )
1'	4	=	0.05 (4 )

Au point 10

1'	0	=	0	(4 )
1'		=	0	(6 )
1'	2	=	0	( 2 )
1'	3	=	0	(6 )
1'	4	=	0	(4 )

IV.1.3.4.2.1. Tableau récapitulatif des efforts tranchant

section	4t			6t			12t		somme	0.57M
	Y1	Y2	(Y1+Y2)4t	Y1	Y2	(Y1+Y2)6t	Y	12Y
0	0.94	0,05	3,96	0,72	0,27	5,94	0,5	6	15,9	9,063
1	0	0,05	0,2	0,72	0,27	5,94	0,5	6	12,14	12,14
2	0	0,05	0,2	0,72	0,27	5,94	0,5	6	12,14	12,14
3	0	0,05	0,2	0	0,27	1,62	0,5	6	7,82	7,82
4	0	0,05	0,2	0	0,27	1,62	0,5	6	7,82	7,82
5	0	0,05	0,2	0	0,27	1,62	0,5	6	7,82	7,82
6	0	0,05	0,2	0	0,27	1,62	0	0	1,82	1,82
7	0	0,05	0,2	0	0,27	1,62	0	0	1,82	1,82
8	0	0,05	0,2	0	0	0	0	0	0,2	0,2
9	0	0,05	0,2	0	0	0	0	0	0,2	0,2
10	0	0,05	0	0	0	0	0	0	0	0
somme			5,76			25,92		36	67,68	38,58

Page 54 sur 115

Page 55 sur 115

Cas 2 où le convoi se déplace sur le pont Au point 0

	0	=	(4	)
		=	0.77	(6	)
	2	=	0.55	(	2 )
	3	=	0.33	(6	)
	4	=	0.	(4	)

Au point 1

	0	= =	0.9 (4 ) 0.67 (6 )
	2	=	0.45	( 2 )
	3	=	0.23	(6 )
	4	=	0.0	(4 )

Au point 2

	0		=		0.8 (4 )
			=		0.57 (6 )
	2		=		0.35 ( 2 )

Page 56 sur 115

1'

	3	=	0.35	(6 )
1'	4	=	0. 3	(6 )

Au point 3

1'	0	=	0.7 (4 )
1'		=	0.47 (6 )
1'	2	=	0.25 ( 2 )
1'	3	=	0.033 (6 )
1'	4	=	0 (4 )

Au point 4

1' 1'	0	= =	0.6 (4 0.37 (6		) )
1'	2	=	0. 5	(	2 )
1'	3	=	0 (6	)
1'	4	=	0 (4	)

Au point 5

1'		0		=		0.5 (4 )
1'				=		0.27 (6 )
1'		2		=		0.05 ( 2 )

Page 57 sur 115

	3	=	0	(6 )
	4	=	0	(4 )

Au point 6

	0	=	0.4 (4 )
		=	0. 7 (6 )
	2	=	0 ( 2 )
	3	=	0 (6 )
	4	=	0 (4 )

Au point 7

	0	= =	0.3 (4 ) 0.07 (6 )
	2	=	0 ( 2 )
	3	=	0 (6 )
	4	=	0 (4 )

Au point 8

	Y0=0.2 (4t)
	Y1=0 (6t)
	Y2=0 (12t)
	Y3=0 (6t)
	Y4=0 (4t)

Page 58 sur 115

Au point 9

1' Y0=0.1 (4t) 1' Y1=0 (6t)

1' Y2=Y3=Y4=0

Au point 10

Nous avons pour valeur zéro dans tous les tronçons. IV.1.3.4.2.2.Tableau récapitulatif de l'effort tranchant

section	4t			6t			12t		somme	0.57M
	Y	Y	(Y +Y )4t	Y	Y	(Y +Y )6t	Y	12Y
0	1,00	0,11	4,44	0,77	0,33	6,60	0,55	6,60	17,64	10,05
1	0,90	0,01	3,65	0,67	0,23	5,40	0,45	5,40	14,45	8,24
2	0,80	0,00	3,20	0,57	0,13	4,20	0,35	4,20	11,60	6,61
3	0,70	0,00	2,80	0,47	0,03	3,02	0,25	3,00	8,82	5,03
4	0,60	0,00	2,40	0,37	0,00	1,48	0,15	1,80	5,68	3,24
5	0,50	0,00	2,00	0,27	0,00	1,08	0,05	0,60	3,68	2,10
6	0,40	0,00	1,60	0,17	0,00	0,68	0,00	0,00	2,28	1,30
7	0,30	0,00	1,20	0,07	0,00	0,28	0,00	0,00	1,48	0,84
8	0,20	0,00	0,80	0,00	0,00	0,00	0,00	0,00	0,80	0,46
9	0,10	0,00	0,40	0,00	0,00	0,00	0,00	0,00	0,40	0,23
10	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00

somme

22,74

38,09

21,60

22,49

66,83

Page 59 sur 115

IV.1.3.4.2.3. Tableau synthèse de trois cas

Section	CAS 1		CAS 2		A RETENIR
	T	T*crt	T	T*crt
0,00	15,90	9,06	17,64	10,05	10,05
1,00	12,14	6,92	14,44	8,23	8,23
2,00	12,14	6,92	11,60	6,61	6,92
3,00	7,82	4,46	8,82	5,03	5,03
4,00	7,82	4,46	5,68	3,24	4,46
5,00	7,82	4,46	3,68	2,10	4,46
6,00	1,82	1,04	2,28	1,30	1,30
7,00	1,82	1,04	1,48	0,84	1,04
8,00	0,20	0,11	0,80	0,46	0,46
9,00	0,20	0,11	0,40	0,23	0,23
10,00	0,00	0,00	0,00	0,00	0,00
SOMME		38,58		38,09	42,18

IV.1.3.4.2.4. Tableau des efforts tranchant dus au poids propre

Section	St		Pt ELS		Pt ELU		St*Pt ELS		St*Pt ELU
0	9		3,66		4,94		32,94		44,46
1	7,2		3,66		4,94		26,352		35,568
2	5,4		3,66		4,94		19,764		26,676
3	3,6		3,66		4,94		13,176		17,784
4	1,8		3,66		4,94		6,588		8,892
5	0		3,66		4,94		0		0

Page 60 sur 115

6

	-1,8	3,66	4,94	-6,588	-8,892
7	-3,6	3,66	4,94	-13,176	-17,784
8	-5,4	3,66	4,94	-19,764	-26,676
9	-7,2	3,66	4,94	-26,352	-35,568
10	-9	3,66	4,94	-32,94	-44,46

IV.1.3.4.2.5. Tableau des efforts tranchant dus à la foule

S-q-

ELU 0,00 0,02 0,06 0,14 0,24 0,38 0,55 0,75 0,98 1,24 1,53

section	S POS	S NEG	q POS ELS	q POS ELU	q NEG ELS	q NEG ELU	S+q+ ELS	S+q+ ELU	S-q-ELS
0	9	0	1,44	2,16	0,115	0,17	12,96	19,44	0,00
1	7,29	0,09	1,44	2,16	0,115	0,17	10,50	15,75	0,01
2	5,76	0,36	1,44	2,16	0,115	0,17	8,29	12,44	0,04
3	4,41	0,81	1,44	2,16	0,115	0,17	6,35	9,53	0,09
4	3,24	1,44	1,44	2,16	0,115	0,17	4,67	7,00	0,17
5	2,25	2,25	1,44	2,16	0,115	0,17	3,24	4,86	0,26
6	1,44	3,24	1,44	2,16	0,115	0,17	2,07	3,11	0,37
7	0,81	4,41	1,44	2,16	0,115	0,17	1,17	1,75	0,51
8	0,36	5,76	1,44	2,16	0,115	0,17	0,52	0,78	0,66
9	0,09	7,29	1,44	2,16	0,115	0,17	0,13	0,19	0,84
10	0	9	1,44	2,16	0,115	0,17	0,00	0,00	1,04

IV.1.3.4.3. Courbe enveloppe

Après avoir trouvé les moments fléchissant et les efforts tranchant dus au poids propre et aux surcharges fixes à la foule et au convoi, nous pouvons bien faire la sommation pour tracer la courbe enveloppe.

IV.1.3.4.3.1. valeurs des moments fléchissant

Section	POIDS PROPRE (1)		FOULE (2)		CONVOIS (3)		MOMENT (1)+(2)+(3)
	ELS	ELU	ELS	ELU	ELS	ELU	ELS	ELU
1,00	53,36	72,03	21,00	31,49	14,96	22,44	89,32	125,96
2,00	94,87	128,04	37,32	55,99	26,90	40,35	159,09	224,38
3,00	124,51	168,06	48,99	73,48	37,85	56,78	211,35	298,32
4,00	142,30	192,07	55,99	83,98	44,00	66,00	242,29	342,05
5,00	146,58	197,85	57,67	86,51	50,16	75,24	254,42	359,60

IV.1.3.4.3.1.1. Graphique de la courbe enveloppe du moment

IV.1.3.4.3.2. Valeurs des efforts tranchant

section	CONVOIS (1)		FOULE (2)				poids propre (3)		(1)+(2)+(3)
	ELS	ELU	T+ ELS	T- ELS	T+ ELU	T-ELU	ELS	ELU	ELS	ELU
0	10,05	15,08	12,96	0,00	19,44	0,00	32,94	44,46	55,95	78,98
1	8,23	12,35	10,50	0,01	15,75	0,02	26,35	35,57	45,09	63,67
2	6,92	10,38	8,29	0,04	12,44	0,06	19,76	26,68	35,02	49,56

Page 61 sur 115

3	5,03	7,55	6,35	0,09	9,53	0,14	13,18	17,78	24,65	34,99
4	4,46	6,69	4,67	0,17	7,00	0,24	6,59	8,89	15,88	22,83
5	4,46	6,69	3,24	0,26	4,86	0,38	0,00	0,00	7,96	11,93
6	1,30	1,95	2,07	0,37	3,11	0,55	-6,59	-8,89	-2,84	-3,28
7	1,04	1,56	1,17	0,51	1,75	0,75	-13,18	-17,78	- 10,46	- 13,72
8	0,46	0,69	0,52	0,66	0,78	0,98	-19,76	-26,68	- 18,12	- 24,23
9	0,23	0,35	0,13	0,84	0,19	1,24	-26,35	-35,57	- 25,15	- 33,79
10	0,00	0,00	0,00	1,04	0,00	1,53	-32,94	-44,46	- 31,91	- 42,93

IV.1.3.4.3.2.1. Graphique de la courbe enveloppe de l'effort tranchant

Page 62 sur 115

Page 63 sur 115

IV.1.4. Calcul des armatures de la poutre

M = 359,60tm = 3,5960MNm M = 254,44tm = 2,5442MNm T = 78,98t = 0,7898MN

T = 55,95t = 0,55MN

f = 30MP f = 400MP

Contrainte de calcul du béton

f=	0,85 f

avec = ; = ,5

alors f =	0,85 30	= 7MPa
	,5

f = 0,6 0,06fc28 = 2.4MPa

Contrainte de calcul de l'acier

f st =		avec s = , 5
st =	400		= 348MPa
	, 5

Calcul du moment de table de compression Mt

M = f h b (d h 2 )

M = 7 3,2 0, 8 ( , 5 0, 8 2 )

Page 64 sur 115

M = 0,38MNm Mu = 3,5960MNm

Dans ce cas l'axe neutre est dans la table de compression. La poutre sera calculée comme une poutre rectangulaire b h.

Calcul du moment réduit

Mu 3,5960

= bd fbu =
	3,2( , 5) 7

,

= ,

= 0,05 0, 89, , Donc, la poutre n'a

pas besoin des armatures comprimées.

=	,25(
		v	2	)
=	,25(	v	2		0,05)
=	0,064

Y = d = 0,064 , 5

Y = 0,073m

H = 0,20Y 0,8Yu = 0,059

dans ce cas une partie de la dalle est comprimée Bras de levier

z = d( 0,4 )

z = , 5( 0,4 0,064) = , 2m
Section d'armatures tendues s

3,5960

M

=

=

, 2 348

z

= 0,009226 52m qui equivaut à 92,26cm

On utilise des barres à haute adhérence HA comprise entre HA 20 à HA 32 voire

, ( , )

même HA 40 ; prenons HA 32 avec une section de S = = 8,04cm

Soit 12HA32 avec une section réelle d'armatures de 98,51cm2.12 Calcul et vérification des contraintes à l'état limite de service¹³ Axe neutre

¹² J. Pierre Mougin, Pratique du BAEL 91, page 117

¹³ Pascal Legrand, cours de béton armé suivant les règles de BAEL 91 et modifications 99, page 84

by

n (y C ) n (d Y ) (b b0) (y h0

2 ) = 0

Avec A=Asu ; '=0 On a :

b y 2(b b )h 30 s y (b b )h 30 d = 0

40y 2(320 40) 8 30 98,5 y (320 40)( 8) 30 98,5 5

= 0

y 325,88y 622,48 = b 4ac

= (325,88) 4 ( 6228,48)
= 395

Après calcul nous avons trouvé y =34,56cm et y =-360,44 qui est la valeur à ne pas utiliser.

Le moment d'inertie par rapport à l'axe neutre Y

bY

I =

n s(d y )

3

40 (34,56)

I =

Page 65 sur 115

5 98,5 ( 5 34,56)

3

= , = ,

Contrainte maximale dans le béton comprimé

= =	2,5442 0,3456	= 8,7MPa bc adm = 8MPa
	0, 0

La contrainte de traction des aciers

st =

= 5 0, 0

( , 5 0,3456)

n(d y )

I

= 303,94MPa st adm = 348MPa (la fissuration préjudiciable)

Contrainte de cisaillement

= bd min [0, 5fc28

V ; 4MPa] , é

= 0,4 , 5 min [0, 5 30

0,7898 ,5 ; 4MPa]

Page 66 sur 115

= ,72MPa 3MPa

Détermination des armatures transversales des poutres et leur espace

V =	=	0,7898	=	,72MPa
bd		0,40 , 5

Dimensionnement des armatures transversales

Les armatures transversales sont estimées à partir de la relation : 35 ; 32; 400

t min [h 0 ]

t min 34,28; 32; 40 prenons 32mm

Pour la petite section = = 0,7mm, d oùnous optons our t = 2mm Disposition des étriers

Selon le cours de pont, il nous est recommandé de diviser le mi porté de la poutre en trois zones, puis effectué les espacements comme suit :

Zone 1 : de l'appui à 3m 5cm d espacement

Zone 2 : de 3m à 6m 20cm d espacement

Zone 3 : de 6m au mi porté 25cm

Il est souhaitable d'utiliser les armatures inclinées de 45° dans la première zone afin d'éviter de manière efficace le phénomène de rupture du à la traction du béton. Cependant dans les deux dernières zones, les armatures resteront verticales d'autant plus que dans ces derniers les efforts de cisaillement deviennent de plus en plus faibles.

Page 67 sur 115

Plan d'armature

Page 68 sur 115

IV.2. Calcul de l'entretoise

IV.2.1. Définition

Dans le pont, nous désignons par entretoise une sorte de poutre secondaire disposée perpendiculairement aux poutres principales qu'elle relie pour la plupart des cas. (Sauf dans des ponts biais, où celle-ci est parallèle aux appareils d'appui).

La présence des entretoises dans le pont se justifie du fait qu'elles assurent non seulement la solidarité effective des poutres mais aussi pour leur rôle du contreventement transversal de ce dernier.

En plaçant une charge au point 0, chacune des quatre poutres reçoit une portion de 1/4 en se référant de ligne d'influences transversales.

M = 4 (d d ) = 4 ( ,4 4,2) = ,3tm

En plaçant une charge unitaire sur la poutre principale n°1 on obtient :

M = (0,7 4,2) 0,4( ,4) (4,2)

M = 0,7tm

En plaçant une charge sur la poutre n°2

P = 0,4		=	0,4t
P =	0,3	=	0,3t
P =	0,2	=	0,2t
On a : ,4 = 0,25 9,3				= 0,4t

= 0,25 28

= 0,3t

,4

= 0,25 28

= 0,2t

,4

Page 69 sur 115

P d = ,4 = ,4tm

P = S P = S P = S P = S	Pd2
	I d2 Pd
	I d Pd
	I d Pd
	I

alors P = S

alors P = S

alors P = S

alors P = S

P

=

S 4

d

0,25t

=
m

I = (P d P d ) 2

I = (4,2) ( ,4) 2 alors I = 39,2m

I 39,2		= 9,33m
d 4,2
I = d	39,2		= 28m
	,4

= 0,25 9,3

= 0, 0t P = 0, 0 = 0, 0t

,4

M = (0,4 4,2) (0,3 ,4) ( ,4) = 0,7tm

Surface du diagramme

Surface positive S+	Surface négative S-
= , , ,	, , =	= ,

IV.2 2. Application

Nous avons 4 entretoises distantes de 5,88 m sur 4 poutres distantes de 2,8 m. IV.2 2.1. Poids propre et surcharges fixes

Ces éléments ne causent pas de flexion de l'entretoise. Tout est repris par les poutres principales. Tout le pont fléchit et les entretoisent parallèles à elles-mêmes.

IV.2 2.2. La foule

Il faut chercher la ligne d'influence de la réaction de la dalle sur l'entretoise considérée liée iso statiquement à celle-ci.

Surface d'influence

S = 2	bh	= 2	5,88	= 5,88m
	2		2

Page 70 sur 115

La charge de la foule

q=	0,48t		5,88 =	2,82t
	m			m

IV.2 2.2.1. Valeurs des moments fléchissant dû à la foule Moment positif : M+=2,82 3,5 = 9,89tm

Moment négatif : M = 2,82 ,05 = 2,96tm

Page 71 sur 115

IV.2.3. Convoi

On a pris un convoi de 32t disposé de 5 essieux de 4t, 6t, 12t, 6t et 4t.

Et on a des valeurs comme suite : y= y = 0,

y = y = 0,55

y=

IV.2.3.1. Valeur de la réaction

Q = 2( ) 2(6 0,55) (4 2 0, ) = 9,48t

Etant donné que nous avons deux fils de roues, nous aurons comme valeur de ,

Q = = 9,74t

IV.2.3.2. Les lignes d'influences des moments

1er cas : deux véhicules roulent dans leur bande habituelle

Par la règle de triangles semblables, nous auront : y = ,0 et y = 0,096

Alors ?y = 2 (0,096 ,0 ) = 2,2 4

2eme cas : un véhicule avec un fil de roue sur l'axe

Page 72 sur 115

y = ,0 ; y = 0,096_; y = ,3 et y = 0,385

?y = ,0 0,096 ,3 0,385 = 2,792
?y = 0

Nous retenons ? = ,

IV.2.3.3. Valeur de moment dû au convoi

M = Q ?y = 9,74 2,792 ,2 = 32,63tm

IV.2.3.4. Tableau synthèse des moments

Type des charges	M tm
Foule (q)	9,89
Convoi (Q)	32,63
Mser=Q+q	42,52
Mu=1,5(Q+q)	63,78

IV.2.4. Calcul d'armatures

Comme pour la poutre et la dalle, nous calculons les armatures à l'ELU_; puis si possible, nous vérifierons à l'ELS.

= 0,35

= 0, 8

= ,02

= 0,9 = 0,9 8

= 2 = 2 0, 8 0,35 = 2,5

Calcul du moment dans la table de compression

Mt = bf h0 (d h 2 ) fbu

Mt = 2,5 0, 8 (0,9 8

0, 8 2 ) 7

' ù = 6,35 = 0,6378 ; Ainsi l'entretoise sera armée comme

une poutre rectangulaire de section = .

		,		=	0,0 7
uu=	=	, (	, )
= ,25	(	v	2(0,0	7))=	0,02143
= .	=	0,02	43	0,9 8	= 0,0 96
0,8 =	0,0	5	=	0, 8

D'où, l'axe neutre passe dans la table de compression ; Cela étant, nous aurons :

= ( 0,4 ) = 0,9 8( 0,4 0,02 43) = 0,9

As=	, =		= 0,0020 4 = 20, 4

Page 73 sur 115

,

7H 20, pour une bonne disposition on prend

é,

Armatures de répartition :

,

Ar= = = 6,2825 5HA14 (7,70 cm²)

Armatures transversales (étriers) : le diamètre des armatures transversales est de :

øt= = 6,66

Nous adoptons øt=10 mm

Espacement de armatures transversales : e= 25 cm

Plan d'armature de l'entretoise

Page 74 sur 115

Page 75 sur 115

Chap. V. Calcul du trottoir et la dalle

V.1. Calcul du trottoir

Le calcul du trottoir se fait comme une poutre encastrée et libre de l'autre côté et dans une tranche d'un mètre.

Schéma statique de cet élément en porte-à-faux est :

V.1.1. Evaluation des charges sur le trottoir Surcharge fixe

a) Charges permanentes

,

Pierre de taille : ,5 2,3 =

Chape de protection : ,

,

: 0,03 ,5 2,2 =

,

Mortier : 0,0 ,5 2,2 =

,

Poids propre : ,5 0, 8 2,5 =

,

Bordure : 2,5 0, 5 0,04 =

,

Corniche : 2,5 0,20 ,5 =
D'où ? = ,

b) Charges concentrées

La force horizontale : ,

Garde-corps : ,

D'où ? = ,

Page 76 sur 115

La foule

La norme belge prévoit une charge de 0,4t/m² avec un coefficient dynamique

0,72

= ,2

= 0,4 ,5 ,2 =

La combinaison en ELU nous donne :

= ,35 ,5 = ( ,35 3,727) ( ,5 0,72)

6,

=

= , 7 ,35 = 0,23

V.1.2. Sollicitation

=		6, =		= 3,055
	2		2

= = 0,23 = 0, 7

= = 3,055 0,23 = 3,285

V.1.3. Calcul des armatures Nous avons :

= ,5 ; = 0, 8 ; = 0, 8 0,02 = 0, 9

= 3,225 = 0,03825

= =	0,03825	= 0,035 0,39
	,5 0, 9 7

= ,25( V 2 )

= ,25( V 2 0,035) = 0,0875

= = 0,0875 0, 9 = 0,0 66

0 0,8 0, 8 0,0 3

e é .

= ( 0,4 ) = 0, 9 ( 0,4 0,0875) = 0, 8
lors la section d'armatures s sera :

= =	0,03825	= 6, 0
	0, 8 348

Page 77 sur 115

8HA10 par mètre avec une section réelle de 6,28cm² Espacement

St (2 0 ; 25 ), é
M (36 ; 25 )

25 , ù 20 .

Plan d'armature

Page 78 sur 115

V.2. Calcul de la dalle

V.2.1. Introduction

La dalle est avant tout une plaque, c.à.d. un élément horizontal de la structure dont l'une des dimensions est plus petite que les deux autres.

La dalle que nous aurons à calculer est en béton armé, c.à.d. constituée de béton et des aciers armatures) dont nous déterminerions la section.

Pour ce faire, nous utiliserons les règles de béton armé aux états limites (BAEL). Mais en cela, nous signalons que pour la détermination des moments fléchissant dus aux charges roulantes, nous nous servirons des Abaques de PIGE UD qui s'avèrent les plus pratiques et les plus utilisés dans le calcul des charges mobiles.

V.2.2. Calcul proprement dit

Considérons un panneau de dalle

Élancement

= = , = 0,424 ,

étant supérieur à 0,4 ; ce qui revient à dire que la dalle porte dans les deux sen. C.à.d. suivant la petite portée (lx) et suivant la grande portée (ly).

Configuration de la dalle

Page 79 sur 115

V.2.2.1. Les charges en présences ? Charges permanentes

Comme charges permanentes, nous considérerons le poids propre de la dalle et celle de la chaussée.

Nous aurons :

Dalle : =0,18×25KN/m³ = 4,50 KN/m²

Chaussée : = 2,07 KN/m²

? = = ,

? La foule

La norme Belge 003-01 nous recommande de prendre pour foule :

= 4KN/m²×1,2= 4,80 KN/m²

? Le convoi

A ce stade, nous prendrons en compte les effets de la roue la plus chargée sur le panneau considéré.

D'après la norme, l'essieu le plus chargé est de celui de 2t. insi, la roue la plus chargée sera celle de 6t d'autant plus que la charge d'un essieu se reparti équitablement sur deux roues.

Les roues sont en contact avec la chaussée sur un rectangle de dimensions a1 et a2, définies par la norme.

Ainsi, la norme nous prescrit les dimensions ci-après :

U0= a2= 0,30m V0= a1= 0,10m

Page 80 sur 115

La charge de la roue sur la chaussée fait fléchir une bande de longueur et de largeur respectivement V et U.

V= V0+1,5hr+2hd+ Avec hr : épaisseur du revêtement

U= U0+1,5hr+2hd hd : épaisseur de la dalle

L1 : entre-axes des poutres

Cela étant, nous aurons :

V= 0,15+1,5(0,09) +2(0,18) + ,

= 1,57 m

U= 0,20+1,5(0,09) +2(0,18)

= 0,725 m

Surface d'impact

S= U×V= 0,725m×1,57m

= 1,138 m²

Densité de la charge (roue)

Pr = 6t= 60 KN (poids de la roue)

La densité de la roue sera déterminée par la formule ci-après :

d= Avec Pr : poids de la roue

: coefficient d'impact applicable à la dalle S : surface d'impact

Nous aurons :

d=		,2 = 53,2

,

Page 81 sur 115

V.2.2.2. Calcul des moments (par rapport à la plaque considérée) Soit un panneau:

Le rapport = = 0,49 0,4 ; donc la dalle est sollicitée dans les deux sens.

Dans ce cas, l'étude de cet élément consiste à travailler sur une bande d'un mètre dans le sens perpendiculaire à celui de la portée considérée.

Abaques de Pigeaud

PIGEAUD a publiée dans les annales des ponts et chaussées (janvier-février 1921), des abaques permettent de déterminer les moments maximaux suivant la petite et la grande portée pour les plaques rectangulaires simplement appuyées sur leur pourtour et pour les cas de charges suivants :

Charge uniformément repartie sur toute la surface de la plaque

Charge uniformément repartie sur un rectangle concentrique à la plaque

Les moments au centre de la plaque ont les valeurs suivantes :

Sens de Lx ? ??x = (M1+??M2) P

Sens de Ly? ??y = (??M1+M2) P

Avec :

1' M1 : obtenue par l'abaque en fonction de 1 = Lx/Ly= 0,49;

1' M2 : obtenue par l'abaque en fonction de 2 = Ly/Lx= 2,01 ;

1' ?? : Coefficient de poisson, on prend ??= 0,15 pour le béton armé ;

P= charge totale agissant sur la plaque (P= Pi x Lx x Ly). Dans le cas de notre projet, nous avons :

1 = 0,49? M1 = 0,048

2 = 2,01? M2 = 0,009.

Moment du aux charges permanentes

= 6,57 Or la section du panneau est S= Lx x Ly= 13,56m²

= = 6,57 3,56 = 89,08

= (0,049+0,15 x 0,009) x 89,08 = 4 ,48517 KNm/m

= (0,15 x 0,049+0,009) x 89,08 = 1,45645 KNm/m

Moment dû à la foule

P= ×lx×ly= 4,80KN/m²×2,4m×5,65m

= 65,088 KN

La charge repartie sur une bande d'un mètre est: = 65,088

= (0,049+0,15 x 0,009) x 65,088 = 3,27718 KNm/m

= (0,15 x 0,049+0,009) x 65,088 =1,06418 KNm/m

Moment du aux charges roulantes (trains de charge)

,

,

= =

= 0,33

,

= =

= 0,27

Page 82 sur 115

,

Elancement 0,795 = = ,53

= 0,52

Après dans les Abaques, nous avons trouvé les valeurs suivantes : m1= 0,16 m2= 0,068 Calcul des moments

= (m1+nm2) P Pour ce type de charge, n= 0,15

= (nm1+m2) P

La charge P à considérer suivant le sens de la circulation est : =

= 53,2				,53 =	96,69
= (0,	6	0,	5	0,068)	96,69	=	6,456
= (0,	6	0,	5	0,068)	96,69	=	8,895

V.2.2.3. Combinaison des charges à ELU

= ,35 ,5( )

= ,35 4 ,485 7 ,35 (3,277 8 6,456 )

= 32,694

= ,35 ,5( ) = ,35 ,45645 ,5( ,064 8 8,895 )

= 6,9

Moment aux appuis

= 0,5 = 6,347 (Suivant la petite portée)

= 0,5 = 8,45 (Suivant la grande portée)
Moment en travée

= 0,75 = 24,52 (Suivant la petite portée)

= 0,75 = 2,675 (Suivant la grande portée)
V.2.2.4. Calcul des armatures

Comme toujours, la dalle sera calculée comme étant une poutre rectangulaire de

largeur b= 1m et de hauteur = 0, 8 . D'où la distance utile d= 0,9hd= 0,162m ? Armatures en travée

Suivant la petite portée : = 24,52 = 0,02452

u= avec b=1m

Nous aurons :

u=	,	= 0,055 0,186 Pivot A
	( , )
u=	,		= 0,028< 0,186 pivot A
	( , )

Page 83 sur 115

= ,25( -J 2 ) = 1,25(1-J 2(0,055))

= 0,07

= ( 0,4 ) = 0, 62( 0,4 0,07) = 0, 57

La section d'armatures est :

= , As= ,		= 4,48cm^2

4HA12 pm avec une section réelle de 4,52cm²

Suivant la grande portée: avec Mu= 2,675 =0,0126752 MNm

= ,25( J 2(0,028)) = 0,035

= ( 0,4 ) = 0, 62( 0,4 0,035) = 0, 59

La section d'armatures est:

As= , = 2,29cm²

4HA10 pm avec une section réelle de 3,14cm² ? Armatures aux appuis

Suivant la petite portée : avec Mu= 6,34 = 0,01634MNm

u= avec b=1m

Nous aurons :

u=	,	= 0,036 0,186 Pivot A
	( , )

= ,25( -J 2 ) = 1,25(1-J 2(0,036))

= 0,045

= ( 0,4 ) = 0, 62( 0,4 0,045) = 0, 59
La section d'armatures est :

= , As= ,		= 2,95cm^2

Soit, 4HA10 pm avec une section réelle de 3,14cm²

Suivant la grande portée: avec Mu= 8,45 =0,00845MNm

u=	,	= 0,018< 0,186 pivot A
	( , )

Page 84 sur 115

= ,25( J 2(0,0 8)) = 0,023

= ( 0,4 ) = 0, 62( 0,4 0,023) = 0, 6

La section d'armatures est:

As= , = 1,51cm²

,

4HA8 avec une section réelle de 2,01cm²

Plan armature de la dalle

Page 85 sur 115

Page 86 sur 115

CHAPITRE VI CALCUL DE L'INFRASTRUCTURE

VI.1. Données naturelles

VI.1.1. Données géotechniques

Sable :

Contrainte admissible : 0,35MPa L'angle de frottement : 30°

VI.1.2. Données hydrologiques

Niveau des bases eaux (NBE) : c'est le niveau d'une cour d'eau en temps normal, pour notre projet NBE est 0,50m.

Niveau des hautes eaux (NHE) : c'est le niveau d'une cour d'eau en temps de crue, pour notre projet NHE est 2,50m.

VI.2. Pré dimensionnement de la culée

Page 87 sur 115

VI.2.1. Charges en présence

Avec :

- : û

- : é û à

- H : é ( )

- :

- : é

- : é

- :

- :

VI.3. Evaluation des charges horizontales sur la culée

VI.3.1. Effort dû au freinage

,93

= = 0,333 232 =

L'excentricité est = 7, 25

Avec :

: Convoi de 32t N : nombre de voie

: :

= ( _{4 2}) = 0,333

Page 88 sur 115

VI.3.2. Poussée due à la surcharge de remblai

= = 7,75 0,333 = 2,58

é é = 2 = 3,875

8

Avec =

VI.3.3. Poussée dû au remblai (terre)

=

2 = 2 ,8 7,75 0,333 =

é é = 3 = 2,58

Tableau récapitulatif des forces horizontales

	( )		é	)
	1,93	1,93	7,125	13,75
	2,55	2,55	3,875	9,88
	18	18	2,58	56,44
?	22,48	22,48		70,07

D'où le moment de renversement dû aux charges horizontales est :

= 70,07

= ,

= 70,07 = 22,48

= 3,

VI.4. Evaluation des charges verticales

La culée et la dalle se calcule sur une bande de un mètre

VI.4.1. Surcharge de remblai

,4

2 7,75

= =

é 0 = 4

VI.4.2. Réaction des charges

9,35

= ( ) = 55,95 36,6 =

Comme il y a 4 appuis sur la culée, on fait

9,35 4 = =	7,036

é = 2,4

33, 5

=

,89

= 2,788

= é ? =	2,5	,89 =	29,725

Page 89 sur 115

VI.4.3. Poids de la superstructure

,58

=

= 208,572

=

=

8

5,79

=

2

é = 2,4

VI.4.4. Poids de remblai

27,9		= ( , =		,25 0,2 = 0,25 , ) , 0, 4 =		; ; = 3,67 4 ,33	= 3	= 3,	2,9
2 7,75 = ,8 = é 4 VI.4.5. Poids de la culée · . Surface 1 (rectangle) : · . Surface 2 (trapèze) : · . Surface 3 (rectangle) : · . Surface 4 (triangle) : · . Surface 5 (rectangle) : · . Surface 6 (rectangle) : · . Surface 7 (triangle) :
		= =		6,5 = 6,5 ; , 0,5 = ; =
		= = =		2 = 2 ; = 2 = 2 ; = , 0,5 = ; =
N°	S (m^2)		e (m)
1	0,25		2,9		0,725
2	0,14		3,1		0,434
3	6,5		3		19,5
4	0,5		3,67		1,835
5	2		1		2
6	2		4		8
7	0,5		1,33		0,665
?	11,89				33,159

Le moment stabilisant = = 33, 5

Tableau récapitulatif des forces verticales

N°		Q (t/m)	e (m)	Moment (tm)
1		1,41	4	5,64
2		7,036	2,4	16,87
3		5,79	2,4	13,896
4		27,9	4	111,6
5		29,159	2,788	81,29
?		71,295		229,296
= 229,296 = 7 ,295	= 3,2

VI.5. Vérification de la stabilité

La présente vérification consiste à vérifier l'aptitude du mur à pouvoir résister aux forces qui sollicitent l'ouvrage et si cette vérification donne un coefficient de sécurité insuffisante, il faut modifier les dimensions du mur de la culée.

a) Stabilité au renversement

2

Condition de vérification : ? ?

229,296

68,037 ,5 3,37 ,5 ù .

b) Stabilité des contraintes sur le sol Condition de vérification :

Calcul de l'excentricité =

? ?

= ?

2

3 3

229,296 68,037

= 2,26

=

7 ,295

,66 3,33

Page 90 sur 115

Dans le cours de résistance de matériaux, une pièce soumise à la flexion composée développe les contraintes telles que :

=

= ; = ? ; = ? ; = =

2 2

Page 91 sur 115

?

= a			?

2

=

2 = 2,5 2,26 = 0,24

( 6

) = 7 ,295 5 ( 6 0,24

5 )

8,36 0,0 836 = =				= 0,0 836
0, 4 0,0 0 4 = =				= 0,0 0 4

ù = 0,0 836 = 0,35

c) Stabilité au glissement sur la base

Condition de vérification : 0,788 ? ,5

?

7 ,295

0,788 _22,48 ,5

2,47 ,5

d) Stabilité à la fissuration

Pour que la stabilité à la fissuration soit vérifiée, il faut que la résultante des forces verticales R tombe à l'intérieur du tiers central ; 0

: 0 0,24 0,83 ù é .

e) Diagramme de compression

Page 92 sur 115

VI.6. Calcul de la culée

Le calcul de la culée se fait dans les sections dangereuses. Il est simplifié, car nous ne considérons que la flexion simple, alors qu'il s'agit d'une flexion composée. Nous allons utiliser que les efforts horizontaux.

Les sections 4-4 et 5-5 seront déterminées dans le calcul de la semelle.

VI.6.1. Calcul des efforts

1) effort de freinage

2,895

= ,93 = ,5 ,93 = { . .

2) poussée de remblai

=

2

Section 1-1

,288

= 2,083 = 2 (2,083) 0,33 ,8 =

Section 2-2

5, 39

= 4, 6 = 2 (4, 6) 0,33 ,8 =

Section 3-3

Page 93 sur 115

,6

= 6,25 = 2 (6,25) 0,33 ,8 =

Toutes ces différentes valeurs à l'E.L.U deviennent :

Section 1-1 : = ,35 ,288 = ,7388

Section 2-2 : = ,35 5, 39 = 6,937

Section 3-3 : = ,35 ,6 = ,

La poussée due à la surcharge = Avec k : hauteur de la section

0,33

=

l'E.L.U : = 0,33 ,5 = ,

VI.6.2. Calcul des moments et efforts tranchants Section 1-1

2,895 =	; = 2 =	2,083	= ,04 5
		2

,7388

=

; = 3 = 0,694

0,495

5,66

= 2 = 2,083

2,083 = ,03 ; =

= = ,04 5 0,694 ,03 =

= ( ) ( ) ( )

= (2,895 ,04 5) ( ,7388 0,694) ( ,03 ,04 5) = 5

Section 2-2

2,895 =

; =2 = 3, 24

,7388

=

; = 3 = ,388

0,495

= 2 = 2,083

4, 66 = 2,062 ; =

= = 2,895 6,937 2,062 = ,894

= ( ) ( ) ( )

22,96

= (2,895 3, 24) (6,937 ,388) (2,062 2,083) =

Section 3-3

2,895

=

; = 2 =5,2

m

,7388

=

; =₃ = 2, 6

0,495

= 2 = 3,25

6,5 = 2,062 ; =

2 ,77

= = 2,895 5,66 3,2 75 =

= ( ) ( ) ( )

59,3

= (2,895 5,2) ( 5,66 2, 6) (3,2 75 3,25) =

Tableau récapitulatif des moments dans le mur

Section	Moment (t/m)	Effort tranchant (t)
1-1	5	5,66
2-2	22,96	11,894
2-3	59,31	21,77

VI.6.3. Calcul des armatures

v Géométrie de la section

= ; = 0,05 = 0,95 ; = 0,05

Nous prenons la valeur max pour dimensionner la culée pour des raisons sécuritaires, d'où on a :

59,3

=

2 ,77

= 0,593

=

0,2 77

=

v

Page 94 sur 115

Moment réduit

=

Page 95 sur 115

=

	0,593	= 0,038
	0,95 7

0, 89, , é .

= ,25 ( v 2 )

= ,25 ( v 2 0,038) = 0,048

? Bras de levier

= ( 0,4 ) = ( 0,4 0,048) = 0,98
? Section d'acier

0,593 7,39

= =		=

0,98 348

Soit é 24, 3

? Espacement

00

=		= 25
	4

? Armatures de répartition

=	6,032 =

4

Soit

?

00

	= 25
4

VI.7. Calcul de la semelle

Page 96 sur 115

VI.7.1. Calcul des surfaces

= = 2 0,9 = ,8

= =

2

2 0,5 = 2

= 0,5

= ,4 = ,4

= 6

VI.7.2. Poids propre

= = 6 2,5 = 5

La contrainte

=

5 5 = 3

Réaction de sol

= 8,36

= 0, 4

VI.7.3. Charges supportées par la semelle

> Mur de front : 5 2,5 = 2,5

> Mur de garde-grève : ,25 0,2 2,5 = 0,625

? = 2,5 0,625 = 3, 25

> Poussée des terres : 6,25 2 ,8 = 22,5

,

> Effort normal dû au tablier : R = = = 2,43

:

· :

· :

· = é

> Surcharge du remblai : 2 =2

= 3, 25 22,5 2,43 2 = 50,055

Contrainte : , = 6,685

? Diagramme des contraintes sur la semelle

VI.7.4. Calcul des contraintes ? Au point A

= = 8,36 3 = 5,36

? Au point B

( 8,36 0, 4)	=		= 3,288
5		2

Page 97 sur 115

= = 5,072

= = 6,685 3 5,072 = 4,6 3

= = 5,072 3 = 2,072
? Au point C

= = 6,685 3 0, 4 = 9,545

Chaque partie de la semelle a pour valeur une résultante. Tronçon AB

( 5,36 2,072) = 2

2 = 27,432

, ,

Point d'application = =

= ,039

, ,

Tronçon BC

(9,545 4,6 3)

= 3 = 2 ,237
2

Point d'application = = , , ,	,	= ,67

Page 98 sur 115

VI.7.5. Les moments pour les sections d'encastrement

v Semelle avant : = = 27,432 ,039 = 28,50

v Semelle arrière : = ( ) = 2 ,237 ( ,67 ) = 4,22

: .

Combinaison à l'E.L.U

a) Semelle avant (section 5-5)

= ,35 = ,35 28,50 = 38,475 = 0,38475

b) Semelle arrière (section 4-4)

= ,35 = ,35 4,22 = 9, 97 = 0, 9 97

Pour des raisons sécuritaires, utilisons le moment le plus grand dans toutes les sections de la semelle.

VI.7.6. Calcul des armatures

On a = ; = ,4 ; = ,4 0,05 = ,35

Page 99 sur 115

? Moment réduit

=

=	0,38475	= 0,0 2
	,35 7

0, 89, , é .

= ,25 ( v 2 )

= ,25 ( v 2 0,0 2) = 0,0 5

? Bras de levier

= ( 0,4 ) = ( 0,4 0,0 5) = ,34
? Section d'acier

0,38475 8,25

= =		=

,34 348

Soit é 9,42

? Armatures de répartition

=	2,355 =

4

Soit

?

00

	= 25
4

Page 100 sur 115

Plan d'armatures de l'infrastructure

Page 101 sur 115

VI.8. Dalle de transition (flottante) VI.8.1. Définition

Une dalle de transition est une dalle en béton armé reposant sur le remblai dans la partie arrière de la culée recouverte par la chaussée et assurant la transition entre le tablier et le remblai d'accès.

Nous adoptons une épaisseur de 30cm de la dalle de transition, = 6 sur le

sens de circulation et = suivant la largeur du pont.

6

= = = 0,54 0,4, é ,

= =

6 = ,83,

= 0,0475 = 0,0 2 VI.8.2. Evaluation des charges ? Poids propre de la dalle : = 49,5			é	é = 2,5	= 0,3 6 =
			,2	= 79,2
? Surcharge la dalle 6 sur : =
VI.8.3. Calcul des moments
? Charge permanente
? Dans le sens de la petite portée
= ( ) = (0,0475	0,	5	0,0	2) 49,5	=	2,44035
? Dans le sens de la petite portée = ( ) = (0,0475	0,	5	0,0	2) 49,2	=	0,940456

· . Surcharge sur la dalle

2)	79,2	=		3,9045	2)
49,2	=	,5 47

> Dans le sens de la petite portée

= ( ) = (0,0475 0, 5 0,0
> Dans le sens de la grande portée

= ( ) = (0, 5 0,0475 0,0

VI.8.4. Combinaison à l'E.L.U

> Dans le sens de la petite portée

= ,35 ,5 = ,35 2,44035 ,5 3,00456
= 9, 5 3 3

> dans le sens de la grande portée

= ,35 ,5 = ,35 0,940456 ,5 ,5 47

= 7,5432

VI.8.5. Calcul des armatures

La géométrie de l'élément est : = ; = 0,30 ; = 0,30 0,05 = 0,25

a) dans le sens de la petite portée

= 9, 5 3 3 = 0, 5 3 3

· . Moment réduit

=	0, 5 3 3		= 0,086 0, 86

Page 102 sur 115

= ,25( J 2(0,086)) = 0,112

· . Bras de levier

= ( 0,4 ) = 0,25( 0,4 0, 2) = 0,23

· . La section d'armatures est:

As= , = 11,43cm²

,

6HA16 pm avec une section réelle de 12,06cm² b) Dans le sens de la grande portée

= 7,5432 = 0,075432

· . Moment réduit

,

u= ( , )

= 0,07< 0,186 pivot A

= ,25( J 2(0,07)) = 0,09

? Bras de levier

= ( 0,4 ) = 0,25( 0,4 0,09) = 0,24
? La section d'armatures est:

As= , = 8,99cm²

,

7HA14 pm avec une section réelle de 10,78cm²

Plan armature de la dale de transition

VI.9. Dimensionnement des appareils d'appuis

Rappelons que l'appareil d'appui est conçus pour transmettre des

efforts essentiellement verticaux, ou, à la fois des efforts verticaux et des efforts horizontaux. Il permet le mouvement de rotation dû aux charges d'exploitations ou aux déformations imposées.

On distingue deux sortes d'appareils d'appuis :

? les appareils d'appui fixes ;

? Les appareils d'appui mobiles qui permettent à la poutre une libre dilatation.

Page 103 sur 115

Nous optons pour choix, un appareil d'appui à néoprène. Il est formé de plusieurs plaques constituées, chacune par une feuille de caoutchouc colée à une plaque de tôle d'acier dont le rôle est de fretter le néoprène.

VI.9.1. Caractéristiques de l'élastomère frette

L'épaisseur des frettes est comprise entre et 3mm et l'épaisseur des feuilles d'élastomère est, en général, de 8, 10,12 et 16mm. Leurs dimensions en plan sont 100x100mm².

Des tels appareils d'appui sont vérifiés à la compression et à la distorsion.

VI.9.2. Calcul de la surface de plaque

La surface de la plaque doit satisfaire à la condition suivante :

S>

avec = = 559,5 KN et = 100Kg/cm² = 1KN/cm²

S> , = 559,5cm²

La longueur du néoprène étant de 30 cm, sa largeur sera :

l= = ,

= 18,65 cm.

Donc la surface S = L x l = 30cm x 18,65cm = 559,5cm² 560cm²

VI.9.3. Vérification des contraintes

Pour les contraintes de compression on a :

= 0,95 KN cm cas de l'ouvrage non chargé ;

= ,35 KN cm pour l'ouvrage chargé

Avec P1= poids propre de la poutre et P2 = Poids max de l'effort tranchant Rappelons que P1 = 25KN/m³ x 0.40m x ,20m x 8m = 2 6 KN est le poids d'une poutre et P2 = 559,5KN.

= = 0,385 0,95

=	559,5		= 0,999 ,35

Page 104 sur 115

Pour la distorsion on a :

= 0,5 e avec e = l'épaisseur de la plaque = 2cm.

.

=

.

Page 105 sur 115

vec F = l'effort de freinage= ; Q = 60 KN (convoi pour une roue),

Np (nombre des poutres) = 4 et = nombre d'appui par poutre = 2.

F = 7,5 KN.

G (le module d'élasticité transversal du néoprène) qui est généralement pris égal à 0,1019 KN/cm²

La distorsion totale d=d1+d2 0,7.e.

= ,

D'où d = 0,5 2 = et d = ,

,

Donc d = 1cm + 0,26cm = 1,26cm < 0,7.e = 1,4 cm.

Toutes les conditions étant vérifiées, ceci revient à dire que les dimensions choisies conviennent et notre néoprène transmettra aussi bien les poids du tablier aux appuis.

Page 106 sur 115

Chapitre VII : EVALUATION QUANTITATIVE DES MATERIAU ET DEVIS ESTIMATIF

Sur cette évaluation, nous tenons compte qu'aux matériaux utilisés (le béton armé).

Nous n'allons pas tenir compte aussi des travaux préparatifs.

VII.1. Evaluation quantitative des matériaux

a) Qualification des éléments de l'infrastructure > béton de propreté : L=11m, l=5m, H=0,10

V= 2 x L x l x H

= 2 5 0, 0 =

> béton semelle : L=11m, l=5m, H=1,40m

V= 2 x L x l x H

= 2 5 ,40 = 54

> culée :

-mur de front : V= 5 x 11 x 1 x 2

V=110m

-mur garde grève : V= 1,25 x 11 x 0,2 x 2

V= 5,5m

> dalle de transition : V=0,3 x 11 x 6 x 2

V= 39,6m

b) quantification de la superstructure

> dalle : = 0, 8 8 = 35,64

> trottoir : = 8 ,5 0,30 2 = 6,2

> poutre : = 0,40 ,02 0,30 4 = 29,376

> entretoise : = 0,35 2 (0,84 0,50) 7,2 = 6,7536

VII.2. Devis quantitatif et estimatif des matériaux de constructions du pont

N°	désignation	unité	quantité	P.U USD	P.T USD
I	travaux préliminaires
I.1	installation chantier 2,5%	%	-	-	-
sous total 0
II	terrassement
II.1.	démolition d'ouvrage existant		-	-	-		II.2.
aménagement voie d'accès (passerelle)	Ff	-	-	-	II.3.
fouille		-	25	-

Page 107 sur 115

II.4. déviation de la rivière - - -

sous total 1 -
III.	infrastructure							III.1.
semelle	m^3		154	800	123.200	III.2.
culé	m^3		115,5	800	92.400	III.3.
dalle de transition	m^3		39,6	800	31.680	Sous total 2
247.280						IV.
Superstructure
IV.1	dalle dosé à 450kg/m		m^3	35,64	750	26.730
IV.2	poutres dosé à 450kg/m		m^3	29,38	750	22.035
IV.3	entretoises dosé à 450kg/m		m^3	6,76	750	5.070
IV.4.	trottoir		m^3	16,2	750	12.150			IV.5.
appareils d'appuis	Ff		8	100	800
sous total 3						66.785
total travaux						314.065

Page 108 sur 115

Conclusion

Le présent travail a pour intérêt de concevoir et dimensionner un pont en béton armé de 18m de portée sur la rivière NJILI entre le quartier ABATTOIR et le quartier NDANU, pouvant résister face aux diverses sollicitations ci-dessus énumérées.

L'objectif atteint, il nous a amené finalement de déterminer un coût des travaux d'exécution du projet de 314.065 USD.

Il nous a permis d'avoir une idée clef sur le fonctionnement du pont en tant que étudiants finalistes du premier cycle ou Ingénieur technicien en devenir dans le domaine du bâtiment et travaux publics, BTP en sigle.

Page 109 sur 115

BILIOGRAPHIE

I. Ouvrages

> Réunion d'ingénieurs, cours de pont ;

> Guide d'aménagement des ponts et des ponceaux dans le milieu

forestière ;

> Wikipédia, encyclopédie, dictionnaire libre ;

> Service d'étude technique des routes et autoroutes « SETRA » ;

> Projet et construction des ponts ;

> Calcul et vérification des ouvrages en béton armé ;

> Pratique du BAEL 91 ;

> Béton armé BAEL 91 modifié 99.

II. Notes de cours

5. Prof. RUFIN MUTONDO, cours de pont, 3ièmeBTP/INBTP, Kinshasa

6. Prof. MBUYAMBA, cours de résistance des matériaux, 2ièmeBTP/INBTP, Kinshasa

7. Prof. MUZYUMBA, cours de mécanique de sol, 2ièmeBTP/INBTP, Kinshasa

8. Prof. MUKENDI, cours d'initiation à la recherche scientifique, 2ièmeBTP, Kinshasa

9. CT. KUK , cours de l'analyse des travaux, 3ièmeBTP/INBTP, Kinshasa

10. CT MANGINZI, cours de calcul des structures, 3ièmeBTP/INBTP, Kinshasa

11. Ass. NZENZA, cours de béton armé, 2ièméBTP/INBTP, Kinshasa

12. ss. K PEBW , cours de l'Expression Orale et Ecrite, 1ièmeBTP, Kinshasa

Page 110 sur 115

Table des matières

Epigraphe 1

Dédicace 2

Avant-propos 3

SYMBOLES, SIGLE ET ABREVIATIONS 4

CHAPITRE 0 INTRODUCTION 7

1. Problématique 7

2. Hypothèses 7

3. Objectif et intérêt 7

4. Canevas du travail 7

? Généralités sur le pont 7

? Description de l'ouvrage 7

? pré dimensionnement du pont 7

Chapitre I. Généralités sur les ponts 8

I.1. Définitions 8

I.2. Types de ponts 8

I.2.1. selon les matériaux constitutifs 8

I.2.2. selon la conception mécanique. 9

I.2.3. Selon l'utilisation 11

I.2.4. Selon la forme en plan. 12

I.2.5. Selon la durée du service envisagé 13

I.2.6. utres types d'ouvrages selon leur transmission des charges. 13

I.3. Historiques. 14

I.4. Éléments constitutifs des ponts. 15

I.4.1. La superstructure 15

Chapitre II. Description de l'ouvrage 21

II.1. Description de site 21

II.1.1. Données hydrographiques 21

II.1.2. Données naturelle 21

II.2. Description de l'ouvrage 22

II.2.1. Présentation de l'ouvrage 22

II.2.2. Les données fonctionnelles 22

II.2.2.1. Données relatives à la voie portée 22

II.2.2.2. Données relatives à l'obstacle franchi 23

II.3.

Page 111 sur 115

Les données architecturales 23

II.4. Conception de l'ouvrage 23

II.4.1. Choix du type de l'ouvrage 23

II.4.2. Critère de choix du type d'ouvrage 23

II.5. Base de calcul 24

Chapitre III Pré dimensionnement 25

III.1. Définition 25

III.2. La poutre 25

III.3. La dalle 27

III.4. L'entretoise 27

III.5. Trottoir 28

CH P IV. C LCUL DE L POUTRE ET L'ENTRETOISE 30

IV.1. La poutre 30

IV.1.1. Répartition des charges transversales 30

IV. . . . Traçage des lignes d'influences 32

IV.1.1.2. Evaluation des surfaces des diagrammes obtenus 32

IV. . .3. Utilisation des lignes d'influences 32

IV. . .4. Calcul des coefficients d'impact dynamique 33

III. . .4. . Coefficient d'impact dynamique pour la dalle 33

IV. . .4.2. Coefficient d'impact dynamique pour la poutre 34

IV.1.1.5. Choix de la poutre la plus chargée 35

IV.1.2. Détermination de la poutre longitudinale la plus chargée 35

IV.1.2.1. Le moment fléchissant à chaque section 36

IV.1.2.2. Effort tranchant à chaque section 37

IV.1.2.3. Diagrammes des lignes d'influences 41

IV. .2.3. . Lignes d'influence des moments 41

IV. .2.3.2. Lignes d'influences des efforts tranchants 41

IV.1.3. Application 41

IV.1.3.1. Poids propre 42

IV.1.3.2. Surcharge fixe sur la moitié du pont 43

IV.1.3.3. Foule 43

IV.1.3.3. Convois 44

IV.1.3.3.1. Valeurs des moments dus au convoi 44

IV.1.3.4.2. Valeurs des efforts tranchants dus aux convois 50

Page 112 sur 115

IV.1.3.4.3. Courbe enveloppe 60

IV.1.4. Calcul des armatures de la poutre 63

IV.2. Calcul de l'entretoise 68

IV.2.1. Définition 68

IV.2 2. Application 70

IV.2 2.1. Poids propre et surcharges fixes 70

IV.2 2.2. La foule 70

IV.2 2.2.1. Valeurs des moments fléchissant dû à la foule 70

IV.2.3. Convoi 71

IV.2.3.1. Valeur de la réaction 71

IV.2.3.2. Les lignes d'influences des moments 71

IV.2.3.3. Valeur de moment dû au convoi 72

IV.2.3.4. Tableau synthèse des moments 72

IV.2.4. Calcul d'armatures 72

Chap. V. Calcul du trottoir et la dalle 75

V.1. Calcul du trottoir 75

V.1.1. Evaluation des charges sur le trottoir 75

V.1.2. Sollicitation 76

V.1.3. Calcul des armatures 76

V.2. Calcul de la dalle 78

V.2.1. Introduction 78

V.2.2. Calcul proprement dit 78

V.2.2.1. Les charges en présences 79

V.2.2.2. Calcul des moments (par rapport à la plaque considérée) 81

V.2.2.3. Combinaison des charges à ELU 82

V.2.2.4. Calcul des armatures 83

CHAPITRE VI CALCUL DE L'INFRASTRUCTURE 86

VI.1. Données naturelles 86

VI.1.1. Données géotechniques 86

VI.1.2. Données hydrologiques 86

VI.2. Pré dimensionnement de la culée 86

VI.2.1. Charges en présence 87

VI.3. Evaluation des charges horizontales sur la culée 87

VI.3.1. Effort dû au freinage 87

Page 113 sur 115

VI.3.2. Poussée due à la surcharge de remblai 88

VI.3.3. Poussée dû au remblai (terre) 88

VI.4. Evaluation des charges verticales 88

VI.4.1. Surcharge de remblai 88

VI.4.2. Réaction des charges 88

VI.4.3. Poids de la superstructure 89

VI.4.4. Poids de remblai 89

VI.4.5. Poids de la culée 89

VI.5. Vérification de la stabilité 90

VI.6. Calcul de la culée 92

VI.6.1. Calcul des efforts 92

VI.6.2. Calcul des moments et efforts tranchants 93

VI.6.3. Calcul des armatures 94

VI.7. Calcul de la semelle 95

VI.7.1. Calcul des surfaces 96

VI.7.2. Poids propre 96

VI.7.3. Charges supportées par la semelle 96

VI.7.4. Calcul des contraintes 97

VI.7.5. Les moments pour les sections d'encastrement 98

VI.7.6. Calcul des armatures 98

VI.8. Dalle de transition (flottante) 101

VI.8.1. Définition 101

VI.8.2. Evaluation des charges 101

VI.8.3. Calcul des moments 101

VI.8.4. Combinaison à l'E.L.U 102

VI.8.5. Calcul des armatures 102

VI.9. Dimensionnement des appareils d'appuis 103

VI.9. . Caractéristiques de l'élastomère frette 104

VI.9.2. Calcul de la surface de plaque 104

VI.9.3. Vérification des contraintes 104

Chapitre VII : EVALUATION QUANTITATIVE DES MATERIAU ET DEVIS ESTIMATIF 106

Sur cette évaluation, nous tenons compte qu'aux matériaux utilisés (le béton armé). 106

Nous n'allons pas tenir compte aussi des travaux préparatifs. 106

VII.1. Evaluation quantitative des matériaux 106

Page 114 sur 115

VII.2. Devis quantitatif et estimatif des matériaux de constructions du pont 106

Conclusion 108

BILIOGRAPHIE 109

Table des matières 110

Page 115 sur 115

ANNEXES