E-(;) = E(2,-;) serait une fenêtre de la forme E#172;
b(;) = v-0
~ ~;~ -- v-(;), b ç 0 où
v est définie par le produit de deux fenêtres
passe-bas mono-dimensionnelles.
CHAPITRE IV : DECOMPOSITION D'UN SIGNAL EN CURVELETS :
APPLICATION A LA
COMPRESSION D'IMAGES FIXES
Ceci nous permet de séparer les échelles dans le
domaine Cartésien ; il nous reste alors à étudier le cas
de la séparation angulaire. En supposant que la fenêtre V
respecte la condition d'admissibilité de l'Erreur : source de la
référence non trouvée, on peut poser :
£
Y-(;) = Y(2
:8:) La fenêtre Cartésienne recherchée sera
alors :
8ê
Rapport Rédigé et présenté par SIMO
TEGUEU et EMBOLO AURELIEN Page 35
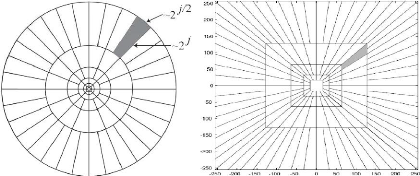
(a) Pavage du plan fréquentiel (b) Pavage du plan
fréquentiel
dans le domaine continu dans le domaine discret
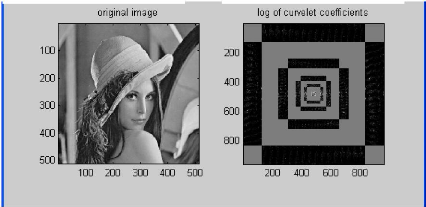
Figure 10 Pavage du plan fréquentiel de l'image de
Lenna sous MATLAB dans le
domaine discret
Rapport Rédigé et présenté par SIMO
TEGUEU et EMBOLO AURELIEN Page 36
CHAPITRE IV : DECOMPOSITION D'UN SIGNAL EN CURVELETS :
APPLICATION A LA
COMPRESSION D'IMAGES FIXES
I.2 COMPRESSION D'UNE IMAGE SOUS MATLAB SELON L'ALGORITHME
FCDT
L'idée est de déterminer les coefficients de
décomposition de l'image en curvelets en utilisant le script
FCDT_usfft_matlab de la boîte à outils Curvelab
développée récemment par l'université Stanford,
leur appliquer un seuillage dont le coefficient dépend du taux de
compression espéré. Nous avons à cet effet
développé une interface ergonomie d'appréciation des
résultats.
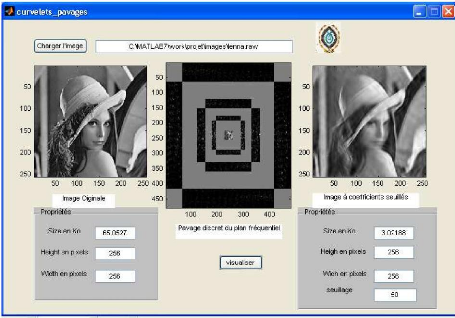
Figure 11 Décomposition et approximation d'une image
par pavage du plan fréquentiel
dans le domaine discret sous MATLAB
| 


