Chapitre 3
Programmation sur Matlab
Matlab est un langage de programmation adapté aux
divers domaines scientifique, il permet de résoudre différents
problèmes de calcul numérique. On l'utilise dans ce chapitre pour
mettre en oeuvre les méthodes numériques (Euler et Runge-Kutta
d'ordre 2) étudiées dans le chapitre 2.
3.1 La méthode d'Euler
Cette section est consacré à l'écriture
du programme matlab qui nous permet de résoudre le problème de
Cauchy (2.1.1) par la méthode numérique d'Euler.
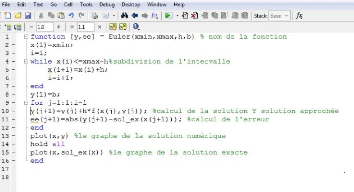
Euler
3.2 La méthode de Runge-Kutta 18
3.2 La méthode de Runge-Kutta
Cette section est consacré à l'écriture du
programme matlab qui nous permet de résoudre le problème de
Cauchy (2.1.1) par la méthode numérique de Runge-Kutta 2.
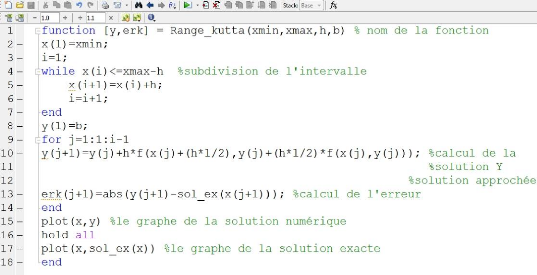
RK2
3.3 L'application 19
3.3 L'application
Les résultats numériques de la résolution
du problème de Cauchy (2.1.1) par les deux méthodes
numériques (Euler et Runge-Kutta 2) obtenus en utilisant le programme de
Matlab.
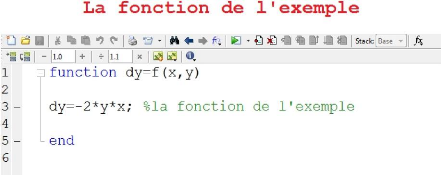
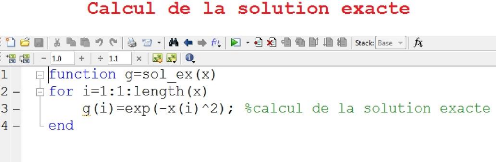
3.3 L'application 20
Les résultats numériques de la solution
approchée et les erreurs comises sont comme suit
>> xmin=0
xmin =
0
>> xmax=0.5
xmax =
0.5000
>> h=0.05
h=
0.0500
>> b=1
b=
1
>> [y,ee] = Euler(xmin,xmax,h,b)
y=
1.0000 1.0000 0.9950 0.9850 0.9703 0.9509 0.9271 0.8993 0.8678
0.8331 0.7956 ee =
0 0.0025 0.0050 0.0073 0.0095 0.0115 0.0132 0.0146 0.0157 0.0164
0.0168 >> [y,erk] = Range_kutta(xmin,xmax,h,b)
y=
|
1.0000 0.9975 0.9900
|
0.9777
|
0.9607
|
0.9393
|
0.9138
|
0.8846
|
0.8520
|
0.8165
|
0.7786
|
|
erk =
|
|
|
|
|
|
|
|
|
|
1.0e-03 *
|
|
|
|
|
|
|
|
|
|
0 0.0031 0.0124
|
0.0274
|
0.0474
|
0.0716
|
0.0987
|
0.1275
|
0.1565
|
0.1845
|
0.2100
|
| 


