Résolution numérique des équations différentielles ordinaires linéaires

UNIVERSITÉ ABDELHAMID IBN BADIS-MOSTAGANEM
FACULTÉ DES SCIENCES EXACTES ET SCIENCES DE LA NATURE ET
DE LAVIE
DÉPARTEMENT DE MATHÉMATIQUES



Mémoire de licence

Spécialité Contrôle et Analyse de Système

Thème

Résolution Numérique Des Equations Différentielles

Ordinaires Linéaires

Présenté par

BAALI Fakhreddine

RAiIS Omar

Soutenu le 11 /06/2013
Devant le jury

Mr BAHRI Sidi Mohamed Examinateur U. MOSTAGANEM.

Mme BENSIKADDOUR Dj Encadreur U. MOSTAGANEM.

Table des matières

1	Introduction Rappels et notations		1 2
	1.1	Généralités	2
	1.2	Équations différentielles du premier ordre	2
		1.2.1 Classification des équations différentielles du premier ordre	2
		1.2.2 Les équations différentielles linéaires du premier ordre	3
	1.3	Équations différentielles linéaires d'ordre n	6
		1.3.1 Cas d'une équation non homogène	6
		1.3.2 Cas d'une équation homogène	7
	1.4	Problème avec conditions initiales	8
2	La solution numérique des équations différentielles		10
	2.1	Méthode d'Euler	10
	2.2	Méthode Runge-Kutta	12
		2.2.1 Méthode Runge-Kutta d'ordre 1 (RK1)	12
		2.2.2 Méthode Runge-Kutta d'ordre 2 (RK2)	13
		2.2.3 Méthode Runge-Kutta d'ordre 4 (RK4)	13
	2.3	La convergence des méthodes numériques	14
		2.3.1 L'erreur locale et l'erreur globale	14
		2.3.2 Définition de la convergence	15

TABLE DES MATIÈRES 3

3 Programmation sur Matlab 17

3.1 La méthode d'Euler 17

3.2 La méthode de Runge-Kutta 18

3.3 L'application 19

Conclusion 21

Bibliographie 22

INTRODUCTION

Les équations différentielles constituent l'un des domaines les plus importants de l'analyse grâce à leurs nombreuses applications. Elles permettent de modéliser mathématiquement plusieurs phénomènes physiques et biologiques et d'étudier des problèmes de population, de métrologie...

Dans ce mémoire on présente un rapide survol de quelques méthodes de résolution des équations différentielles ordinaires linéaires en illustrant quelques exemples. Il n'est pas toujours possible de résoudre les équations différentielles et trouver leurs solutions analytiques, pour tels problèmes on applique des méthodes numériques pour déterminer des solutions approchées aux équations différentielles du type problème de Cauchy qui ce formule de la manière suivante :

~

y'(t) = f(t, y(t)), Vt E [t0, t0 + T ] (0.0.1)
y(t0) = y0 où f(t, y(t)) est une fonction de Rⁿ⁺⁴ dans Rⁿ et y0 E Rⁿ est une condition intiale. La

résolution du problème de cauchy consiste à trouver une fonction unique y(t) qui soit une solution de (0.0.1) dérivable sur un intervalle fini [t0, t0 + T] c R.

On a divisé le mémoire en trois chapitres :

1. Dans le premier on rappelle les définitions, les différents types et des méthodes de base de résolution d'équations différentielles ordinaires.

2. Le second chapitre est consacré à la présentation des méthodes d'approximation pour la résolution numérique d'équations différentielles linéaires.

3. Le troisième chapitre consiste à illustrer ces méthodes par des exemples à l'aide de logiciel de calcul numérique Matlab.

Chapitre 1

Rappels et notations

1.1 Généralités

Une équation différentielle est une relation entre la variable x, une fonction inconnue y = y(x) et ses dérivées y',y'', ..., y(n)

y(n) = f (x, y^', y^'', ..., y(fl_1)) : (1.1.1)

L'entier n s'appelle ordre de l'équation différentielle (1.1.1).

Intégrer l'équation différentielle (1.1.1), c'est trouver toutes les fonctions y qui vérifie la relation (1.1.1), le graphe de la fonction y est appelé courbe intégrale de l'équation différentielle (1.1.1). Intégrer l'équation (1.1.1) revient à trouver toutes les courbes intégrales.

1.2 Équations différentielles du premier ordre

1.2.1 Classification des équations différentielles du premier ordre

Définition 1.2.1 Une équation différentielle du premier ordre est de la forme :

y' = f(x,y) (1.2.1)

On distingue trois classes principales d'équations différentielles du premier ordre :

1. Équations dont on peut séparer les variables.

2. Équations homogènes (où y' ne dépend que du rapport y/x).

3. Équations linéaires.

1.2 Équations différentielles du premier ordre 3

Ces dernières peuvent être à coéfficients constants ou non, sans second membre (équations homogènes) ou avec second membre. Ce sont les équations différentielles les plus utilisées dans toutes les branches de la physique (mécanique, électricité,...).

1.2.2 Les équations différentielles linéaires du premier ordre

Définition 1.2.2 Une équation différentielle linéaire du premier ordre est une équation de la forme

y' (x) + a(x)y (x) = b(x), (1.2.2)

où a et b sont deux fonctions de la variable réelle x continues sur le même intervalle I C II1. On appelle solution de (1.2.2) toute fonction y dérivable sur I qui vérifie (1.2.2).

Lorsque le second membre b (x) est nul, on dit que l'équation différentielle (1.2.2) est sans second membre.

Résolution d'une équation différentielle linéaires sans second membre

Proposition 1.2.1 Soit a(x) est une fonction continue sur un intervalle ouvert I de II1_; la solution générale de l'équation différentielle sans second membre

y' + a(x)y = 0 (1.2.3)

est

y = k exp(--A(x))

où A(x) est une primitive de a(x) et k est une constante réelle. Preuve Si y ne s'annule pas sur I on peut séparer les variables

_y'

y

= --a(x). (1.2.4)

_Z

ln(jyj) =

I

--a(x)dx

En intégrant les deux membres de (1.2.4), on obtient

1.2 Équations différentielles du premier ordre 4

fOn déduit que si A = I

a(x)dx est une primitive de a(x) sur I alors

ln(jyj) = --A(x) + c, (c 2 II1).

D'où

jyj = e(A(x)+c) = y = e^ce^~A(x).

En posant k = #177;e^c, la solution de l'équation différentielle ( 1.2.3) devient

y = ke~A(x) = ke

Z~ I

a(x)dx , (k 2 II1). (1.2.5)

y = k(x)e_A(x),

Exemple 1.2.1 Soit l'équation différentielle du premier ordre sans second membre suivante:

y' + y sinx = 0.

La solution générale de cette équation est :

y = k _ecos x, (k 2 II1).

Résolution d'une équation différentielle non homogène avec second membre Théorème 1.2.1 La solution générale de l'équation avec second membre (1.2.2) est

fy = eA(x) I

b(x)e^A(x)dx

où A(x) est une primitive de a(x).

Preuve Pour résoudre l'équation différentielle (1.2.2) , on procède de la manière suivante : Etape 1 Résolution de l'équation homogène (1.2.3) (sans second membre).

Etape 2 On applique la méthode de variation de la constante

En posant k k(x), la solution (1.2.5) de l'équation différentielle (1.2.3) devient

1.2 Équations différentielles du premier ordre 5

k

y = k exp(-- ln(x)) =

x

, (xE1I8*).

et on a

y' = k^'(x)e^-A(x) -- A^'(x)k(x)e^-A(x) = k^'(x)e^-A(x) -- a(x)k(x)e^-A(x)

En remplaçant y et yi dans l'equation (1.2.2), on obtient :

k^'(x)e^-A(x) -- a(x)k(x)e^-A(x) + a(x)k(x)e^-A(x) = b(x)

D'où

k^'(x)e^-A(x) = b(x) =) k^'(x) = b(x)e^A(x) (1.2.6)

En intégrant les deux membres de l'équation (1.2.6), on trouve

Zk(x) = I

b(x)e^A(x)dx.

Donc la solutions générale de l'équation (1.2.2) est

Zy = e-A(x) I

b(x)e^A(x)dx

Exemple 1.2.2 On considère l'équation différentielle suivante

1 y' + x

y = 3x, (x E 1[8^*) . (1.2.7)

Etape 1 : On commence par la résolution de l'équation homogène

1

y = 0, (x E 1[8^*) . (1.2.8)

y' +

x

On écrit l'équation différentielle (1.2.8) sous la forme

dy y

dx

= --. (1.2.9)
x

En intégrant les deux membres de (1.2.9), on obtient

1.3 Équations différentielles linéaires d'ordre n 6

Etape 2 : La méthode de variation de la constante. On pose k - k(x), comme

, (xEIIB^*)

k(x)

y(x) = x

est une solution de l'équation différentielle (1.2.7), alors

x k^'(x) - k(x) + x2

1 k (x) x x

= 3x

ce qui implique

k^'(x) = 3x².

on intègre cette dernière équation, on trouve

k(x) = x³ + c, (c E I[8)

Donc la solution générale de l'équation (1.2.7) est

x3 + c

y=

, où c est une constante réelle et (x E II8^*) .

x

1.3 Équations différentielles linéaires d'ordre n

1.3.1 Cas d'une équation non homogène

Une équation différentielle linéaire d'ordre n, (n E N) à coéfficients fonctions continues à valeurs réelles est de la forme suivante

y(n) + _an-1 (x)y^(n-1) + ... + ai (x)y⁽ⁱ⁾ + ... + a1 (x)y⁽¹⁾ + a0 (x)y = r (x) (1.3.1)

où y⁽ⁱ⁾, 1 < i < n sont les dérivées d'ordre i de la fonction y par rapport à x, et ai , 1 < i < n sont des fonctions continues à valeurs réelles.

Une solution de cette équation est une fonction y (x) , n fois dérivable sur un intervalle ouvert I de IL

Cependant pour trouver cette solution, on commence tout d'abord par la résolution de l'équation homogène associée pour trouver la solution dite homogène ou complémentaire puis on utilise une méthode analogue à la méthode de variation de la constante définie précédement (1.2.1).

1.3 Équations différentielles linéaires d'ordre n 7

1.3.2 Cas d'une équation homogène

L'équation homogène associée à l'équation différentielle (1.3.1) est

y(n) + _an-1 (x) ^y(n-1) + ... + ai (x) y⁽ⁱ⁾ + ... + a1 (x) y⁽¹⁾ + a0 (x) y = 0 (1.3.2)

Proposition 1.3.1 Toute combinaison linéaire de fonctions solutions de l'équation différentielle homogène (1.3.2) est aussi une solution de cette équation.

Preuve Si les fonctions y1, y2, ...y_n sont toutes solutions de (1.3.2) linéairement indépendantes, alors

8 <>>>>>>> >>>>>>>:

(n) y1 + an-1 (x) y(n-1) 1 + ... + ai (x) y^(i)1 + ... + a1 (x) y(1) 1 + a0 (x) y1 = 0 y2 + an-1 (x) y(n-1) (n) 2 + ... + ai (x) y^(i)2 + ... + a1 (x) y(1) 2 + a0 (x) y2 = 0 : : : yn + an-1 (x) y(n-1) (n) n+ ... + ai (x) y^(i)n + ... + a1 (x) y(1) n + a0 (x) yn = 0

(1.3.3)

_Xn i=1

(n)

(n-1)

(i)

En multipliant chaque ligne i du système (1.3.3) par une constante Ci,1 < i < n , on obtient

i=1 i=1

n

n

!Ciyi + _an-1 (x) XCiy_i! + ... + ai (x) XCiyi +

!Ciyi + a0 (x) XCiy_i! = 0

(1)

+ a1 (x)

i=1

n

i=1

Donc

Xn i=1

Ciyi est solution de (1.3.2).

Définition 1.3.1 La solution générale de l'équation homogène est une combinaison linéaire des n formes solutions y₁, ... , y_n toutes linéairement indépendantes

yh = c1y1 + ... + cny_n

Lorsque les fonctions y1, ... , y_n sont toutes linéairement indépendantes, on dit que l'ensemble {y1, ... , y_n} forme une base de solutions de l'équation (1.3.2).

1.4 Problème avec conditions initiales 8

Remarque 1.3.1 Si les fonctions ai ; 1 < i < n sont toutes constantes sur 1[8, l'équation (1.3.1) est dite équation différentielle d'ordre n à coéfficients constants avec second membres.

y(n) + a_n-1y^(n-1) + ::: + aiy⁽ⁱ⁾ + ::: + a1y⁽¹⁾ + a0y = r (x) (1.3.4)

Définition 1.3.2 On définit le polynôme caractéristique de l'équation (1.3.4) par

P(À) = Aⁿ + an-1À^n-1 + ::: + a1io + a0 (1.3.5)

Théorème 1.3.1 ([2]) Lorsque le polynôme caractéristique p(À) a des racines A1_; :::; Àk d'ordre de multiplicité respectif r1_; :::; rk l'ensemble des solutions de l'équation différetielle (1.3.2) est le (C-espace vectoriel de dimension m ayant pour base les fonctions

yj_;q (x) = tqeA3x ; 1 < j < k ; 0 < q < rj - 1.

1.4 Problème avec conditions initiales

En général, les problèmes physiques font intervenir des conditions initiales sur la fonction y et ses dérivées y^'_; y^''_; :::; y⁽ⁿ⁾ afin d'obtenir un certain comportement de la solution y de l'équation différentielle (1.3.1). Dans cette section on s'intéresse à la résolution des équations différentielles (homogènes ou non-homogènes) d'ordre n et de n conditions initiales de type

{

y(n) + _an-1 (x) ^y(n-1) + ::: + ai (x) y⁽ⁱ⁾ + ::: + a1 (x) y⁽¹⁾ + a0 (x) y = r (x)

y (0) = k0

y' (0) = k1

.

.

.

y(n-1) = kn-1

(1.4.1)

Théorème 1.4.1 ([2], [1])"Existence et unicité de la solution" Si les fonctions an-1; :::; a1_; a0 sont toutes continues sur un intervalle ouvert I C 1[8, alors le problème (1.4.1) a une solution unique.

1.4 Problème avec conditions initiales 9

Exemple 1.4.1 On résout le problème:

y'' - 4y 8 y(0) < : y^'(0)

= = =

0 1 2

(a) (b) (c)

(1.4.2)

où (a) est une équation différentielle linéaire d'ordre deux à coefficients constants sans second membre, (b) et (c) sont deux conditions initiales.

L'équation caractéristique associée à (a) est

r2 - 4 = 0 (1.4.3)

elle admet deux racines r1 = 2 et r2 = -2. L'ensemble des solutions de l'équation (a) est l'ensemble des fonctions y définies sur par:

y(x) = c1e^2x + c2e_^2x, c1, c2 E .

Comme y vérifie les conditions initiales (b) et (c) , alors :

J

c1 + c2 = 1
c1 - c2 = 1

d'où

J c1 = 1 c2 = 0 :

Donc l'ensemble des solutions du système (1.4.2) est la fonction y définie sur par y(x) = e2x.

T

h = N

Chapitre 2

La solution numérique des équations

différentielles

L'objet de ce travail se porte sur la rèsolution numérique des équations différentielles linéaires. En effet pour résoudre ce problème plusieurs méthodes numériques sont possibles parmis les quelles on présente la méthode d'Euler et celle de Runge-Kutta.

2.1 Méthode d'Euler

En mathématiques, la méthode d'Euler, du mathématicien Leonhard Euler, est une procédure numérique pour résoudre par approximation des équations différentielles du premier ordre avec une condition initiale. C'est la plus ancienne et la plus simple des méthodes de résolution numérique des équations différentielles.

Définition 2.1.1 La méthode d'Euler est une méthode numérique élémentaire de résolution d'équations différentielles du premier ordre avec condition initiale (problème de Cauchy)

~

y'(x) = f(x, y(x)), Vx E I (2.1.1)
y(x0) = a où I est un intervalle de de longueur T et y une fonction réelle définie sur I, a E est

une constante donnée (condition initiale).

On subdivise l'intervalle I en N intervalles [x_n, xn+1], avec n = 0, 1, ..., N - 1 et on définit le pas h par

2.1 Méthode d'Euler 11

La méthode d'Euler pour la résolution des problèmes de Cauchy (2.1.1) consiste à calculer les quantités y_m E II1 qui représentent des approximations de y(x_n), définies ci-dessous. La méthode explicite Pour 0 Ç n Ç N - 1, on pose

y(xm+1) = y (x_n) + hf(x_n, y (x_n)). (2.1.2)

La formule (2.1.2) est appelée schéma d'Euler. Exemple 2.1.1 Soit le problème de Cauchy

~y (x) = -2xy, Vx E I = [0, 0.5] y0 = 1

.

(2.1.3)

La solution analytique du système (2.1.3) est y = e_^x2, x E II1.

On subdivise l'intervalle I en 10 intervalles, donc le pas h = 0, 05. Comme xn+1 = x + h, alors en appliquant la formule (2.1.2) on obtient le tableau suivant :

x	0	0.05	0.10	0.15	0.20	0.25	0.30	0.35	0.40	0.45	0.50
y	1.0000	1.0000	0.9950	0.9850	0.9703	0.9509	0.9271	0.8993	0.8678	0.8331	0.7956
y	1.0000	0.9975	0.9900	0.9778	0.9608	0.9394	0.9139	0.8847	0.8521	0.8867	0.7788

avec y est la solution approchée, et y _n est la solution exacte du problème de Cauchy (2.1.3).

Remarque 2.1.1 On remaque que les solutions obtenues s'écartent au für et à mesure de la solution exacte, voir figure 1.



2.2 Méthode Runge-Kutta 12

Cette méthode est équivalente à la méthode d'Euler, on l'applique généralement pour résoudre les équations différentielles du 1^er ordre.

Figure 1

2.2 Méthode Runge-Kutta

Les méthodes de Runge-Kutta (RK) d'ordre 1,2 ou 4 sont des méthodes d'approximation de solutions des équations différentielles, elles ont été nommées en l'hommeur des mathématiciens Carl Range et Martin Wilhelm Kutta (1901).

C'est méthode reposent sur le principe de l'intération, c'est à dire qu'une première estimation de la solution est utilisée pour calculer une seconde estimation, plus précise, et ainsi de suite, ce sont des méthodes à pas unique, directement dérivées de la méthode d'Euler.

2.2.1 Méthode Runge-Kutta d'ordre 1 (RK1)

2.2 Méthode Runge-Kutta 13

On considére le problème de Cauchy suivant :

J y/ = f(t_; y) (2.2.1)

l y(t0) = y0

La méthode RK1 utilise la formule (2.1.2) pour résoudre le système (2.2.1).

2.2.2 Méthode Runge-Kutta d'ordre 2 (RK2)

La méthode RK du deuxième ordre produit deux coéfficients K1_; K2 qui permettent d'écrire

	=
{K1 K2	=
Yn+ 1	=

_h

h:f (x_n; yn) l
h:f (x_n + _2;yn + 21 I

+ xl+K2 /

Yn 2

:

2.2.3 Méthode Runge-Kutta d'ordre 4 (RK4)

On applique la méthode de Runge-Kutta d'ordre plus élevé (RK4) pour obtenir plus de précision ; mais en doublant le temps de calcul puisqu'on procède de 4 évaluations de f.

{

K1 = h:f (xn; yn) h K1 K2 = h:f(~ xn+2;yn+ 2 h K2 K3 = h:f(xn+2;yn+ 2 K4 = h:f (xn + h;yn + K3)

:

K4

K2

6

3 +

K1 + 6

K3 + 3

yn+1 = y_n +

Exemple 2.2.1 On considère l'exemple (2.1.1) et on applique la méthode de Runge-Kutta d'ordre 2 (RK2).

On a :

h h

yn+1 = y_n + hf(x_n + _2;yn + ₂f(x_n;y_n))

Alors, pour n = 0 :

h h

y1 = y0 + hf(x0 + 2 ; y0 + ₂ f(x0_; y0))

0:05 0:05

= 1 + 0:05f(0 + 2 ; 1 + ₂ f(0;1))

= 1 + 0:05f(0:025_; 1) = 0:9975

2.3 La convergence des méthodes numériques 14

e, = jy (x_n) - ynj

En suivant les mêmes étapes de calcul, on obtient le tableau suivant :

x,

0

0:05

0:10

0:15

0:20

0:25

0:30

0:35

0:40

0:45

0:50

y,

1:0000

0:9975

0:9900

0:9777

0:9607

0:9393

0:9138

0:8846

0:8520

0:8165

0:7786

y0 ,

1:0000

0:9975

0:9900

0:9778

0:9608

0:9394

0:9139

0:8847

0:8521

0:8167

0:7788

avec y, est la solution approchée, et y0 , est la solution exacte du problème de Cauchy (2.1.3).

Remarque 2.2.1 On remaque que les solutions obtenues sont très proches de la solution exacte, voir figure 2.



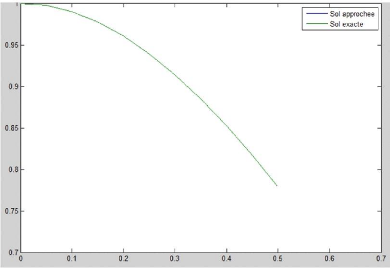
Figure 2

2.3 La convergence des méthodes numériques

2.3.1 L'erreur locale et l'erreur globale

Définition 2.3.1 "L'erreur locale" Soit y (x_n) la solution exacte de l'équation différentielle et y, sa solution approchée. On appelle l'erreur locale d'étape n la quantité

2.3 La convergence des méthodes numériques 15

Erreur globale l'erreur globale est définit par la formule suivante :

e = max jy_n - y (x_n)j 0~n~N

2.3.2 Définition de la convergence

La méthode numérique est dite convergente si

lim h--!0

e = lim h--!0

max jenj = 0 0<n<N

Exemple 2.3.1 Om calcule l'erreur comise dans le calcul de la solution approchée du problème de Cauchy (2.1.1)

1. Par la méthode d'Euler

Pour n = 0, on a

e1 = jy(x1) - y1j ~

e(_(0;05)2 - 1

~~~~

=

= j0_;9975 - 1j

= 0_;0025

pour les autres ordres, on a

n	0	1	2	3	4	5	6	7	8	9		10	en
0	0:0025	0:0050	0:0073	0:0095	0:0115	0:0132	0:0146	0:0157	0:0164	0:0168

2. Par la méthode de Runge-kutta : les erreurs calculées sont présentées dans le tableau ci-dessous

n	0	1	2	3	4	5	6	7	8	9	10
en	0	0:0000	0:0000	0:0001	0:0001	0:0001	0:0001	0:0001	0:0001	0:0002	0:0002



2.3 La convergence des méthodes numériques 16

Figure 3

Remarque 2.3.1 A la lumière de tout ce qu'on vient d'énumerer dans ce chapitre on peut conclure que la méthode de Range-Kutta nous permet d'avoir une meilleure approximation pour la résolution d'une équation différentielle linéaire ordinaire que la méthode d'Euler.

Chapitre 3

Programmation sur Matlab

Matlab est un langage de programmation adapté aux divers domaines scientifique, il permet de résoudre différents problèmes de calcul numérique. On l'utilise dans ce chapitre pour mettre en oeuvre les méthodes numériques (Euler et Runge-Kutta d'ordre 2) étudiées dans le chapitre 2.

3.1 La méthode d'Euler

Cette section est consacré à l'écriture du programme matlab qui nous permet de résoudre le problème de Cauchy (2.1.1) par la méthode numérique d'Euler.



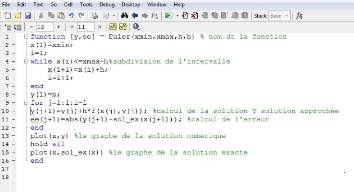
Euler

3.2 La méthode de Runge-Kutta 18

3.2 La méthode de Runge-Kutta

Cette section est consacré à l'écriture du programme matlab qui nous permet de résoudre le problème de Cauchy (2.1.1) par la méthode numérique de Runge-Kutta 2.



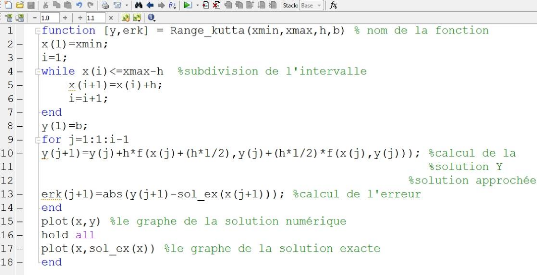
RK2

3.3 L'application 19

3.3 L'application

Les résultats numériques de la résolution du problème de Cauchy (2.1.1) par les deux méthodes numériques (Euler et Runge-Kutta 2) obtenus en utilisant le programme de Matlab.





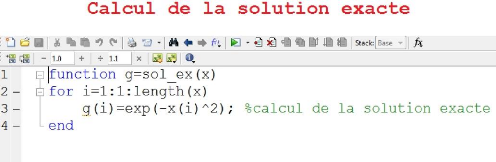
3.3 L'application 20

Les résultats numériques de la solution approchée et les erreurs comises sont comme suit

>> xmin=0

xmin =

0

>> xmax=0.5

xmax =

0.5000

>> h=0.05

h=

0.0500

>> b=1

b=

1

>> [y,ee] = Euler(xmin,xmax,h,b)

y=

1.0000 1.0000 0.9950 0.9850 0.9703 0.9509 0.9271 0.8993 0.8678 0.8331 0.7956 ee =

0 0.0025 0.0050 0.0073 0.0095 0.0115 0.0132 0.0146 0.0157 0.0164 0.0168 >> [y,erk] = Range_kutta(xmin,xmax,h,b)

y=

1.0000 0.9975 0.9900	0.9777	0.9607	0.9393	0.9138	0.8846	0.8520	0.8165	0.7786
erk =
1.0e-03 *
0 0.0031 0.0124	0.0274	0.0474	0.0716	0.0987	0.1275	0.1565	0.1845	0.2100

CONCLUSION

Les méthodes numériques de résolution des équations différentielles sont nombreuses, dans ce mémoire on a présenté la méthode d'Euler et les méthodes de Runge-kutta, cettes dernières sont les préférées mais elles ne sont pas toujours les meilleures, pour chaque problème, on peut toujours trouver une méthode optimal de résolution.

Bibliographie

[1] S,Benzoni-Gavage,. : Calcul Différentiel et Équations Différentielles. Dunod, Paris, (2010).

[2] S,Guerre-Delabrière,. M,Postel,. : Méthodes d'Approximation, Équations Différentielles, Applications Scilab. Ellipses Edition Marketing S.A, (2004).

[3] J-M, Ledermann,. : Équations Différentielles. Cours, Paris, (2012).

[4] J,Quinet,. : Cours Élémentaire de Mathématiques Supèrieures, 4 Équations Différentielles. BORDAS, Paris, Dunod, (1977).

[5] B,Stout,. : Méthodes Numériques de Résolution d'Équations Différentielles. Université de Provence, France, (2007).