C. Axes factoriels :
Les coordonnées des n points-individus sur l'axe factoriel
normé ( vecteur propre de
la matrice C associé à la valeur
propre) sont les n composantes du vecteur :
Le vecteur est une combinaison linéaire des variables
initiales.
p r ?
?a =
U X = U
i a j ij a
jS
j = 1 j
r j
Puisque le nuage des individus est centré sur le centre de
gravité (les masses affectées aux
individus étant égales à ), la moyenne du
facteur est nulle :
Et sa variance vaut :
La coordonnée du point-individu sur cet axe s'écrit
explicitement :
j
p
1
n
III. Analyse du nuage des variables : ? distance entre
points-variables :
La distance entre variables découle de l'analyse dans .
Calculant la distance euclidienne usuelle entre deux variables et
:
Soit :
2 ( ) ? ? ?
d j j x ij
, 2
n
2
? = + x 2
? - x x
ij ij ij ?
n n
i=1 i=1
Remplaçant par sa valeur tirée
précédemment et tenant compte du fait que
On obtient : et également :
D'où la relation liant la distance dans entre deux
points-variables et et le coefficient de
corrélation entre ces variables :
Dans l'espace de, le cosinus de l'angle de deux
vecteurs-variables est le coefficient de
corrélation entre ces deux variables .
-Deux variables centrées réduites fortement
corrélées sont très proches l'une de l'autre
ou au contraire les plus éloignées possible .
-Deux variables orthogonales sont linéairement
indépendantes.
v ? Xu
IV. Axes factoriels ou composantes principales
:
Une fois connus les vecteurs propres et les valeurs propresde la
matrice C=X'X d'ordre
(p, p), il est inutile de procéder à la
diagonalisation de la matrice XX' d'ordre (n, n).
a ? a
|
1
a
Le vecteur
|
est en effet un vecteur propre unitaire de XX', relativement
à la
? ? X? V ? 1
X? XU ? U ?
|
même valeur propre . Le facteur dans s'écrit :
? ? ? ? ?
? ?
Comme , on a :
Alors les coordonnées factorielles des points-variables
sur l'axe sont les composantes de
soit encore de :
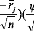
Et l'on a :
(Références bibliographiques: Ouvrages, [1])

Tableau croisant genre véhicule avec tranche d'âge
correspondant à l'année 2009
|
M5
|
5à9
|
10à14
|
15à19
|
P20
|
|
VT
|
2883367
|
1630851
|
2046311
|
3053306
|
10681365
|
|
CT
|
527242
|
174860
|
292236
|
684852
|
2684467
|
|
C
|
399067
|
384648
|
494212
|
1265222
|
3164961
|
|
TA
|
115410
|
73902
|
41861
|
104741
|
357897
|
|
R
|
58238
|
31723
|
58057
|
160361
|
353925
|
|
TR
|
65307
|
86147
|
140993
|
231340
|
554507
|
|
AA
|
44313
|
32581
|
33801
|
11637
|
74907
|
|
M
|
43945
|
78848
|
137105
|
174711
|
329378
|
|
VS
|
3006
|
2367
|
4510
|
18896
|
49781
|
Tableau croisant genre véhicule avec tranche de puissance
correspondant à l'année 2009
|
VT
|
CM
|
CMT
|
AA
|
TR
|
TA
|
VS
|
M
|
|
1 à 2
|
196881
|
0
|
0
|
0
|
0
|
0
|
0
|
22946
|
|
3 à 5
|
3387463
|
0
|
478774
|
0
|
0
|
0
|
319
|
23025
|
|
6 à 7
|
5672018
|
21562
|
933678
|
1644
|
1294
|
6972
|
602
|
13476
|
|
8 à 10
|
3939884
|
214963
|
3043181
|
102946
|
1222
|
32990
|
717
|
9978
|
|
11 à
16
|
754700
|
1464512
|
266907
|
132363
|
7500
|
721736
|
7107
|
257
|
|
17 à
20
|
102806
|
50570
|
30260
|
18201
|
1885
|
54901
|
1630
|
200
|
|
21 à
25
|
325428
|
130560
|
94194
|
21335
|
5007
|
15389
|
2395
|
16
|
|
PLUS 25
|
785878
|
530109
|
293820
|
127853
|
382633
|
106562
|
10577
|
4155
|

|
les tableaux bruts (genre/wilaya) :
|
les taux des tableaux bruts :
|
|
p0=read.table("nom du tableau 1.txt")
|
t00=round(t(t(p0)/apply(t(p0),1,sum)),3)*100
|
|
p1=read.table("nom du tableau 2.txt")
|
t01=round(t(t(p1)/apply(t(p1),1,sum)),3)*100
|
|
p2=read.table("nom du tableau 3.txt")
|
t02=round(t(t(p2)/apply(t(p2),1,sum)),3)*100
|
|
p3=read.table("nom du tableau 4.txt")
|
t03=round(t(t(p3)/apply(t(p3),1,sum)),3)*100
|
|
p4=read.table("nom du tableau 5.txt")
|
t04=round(t(t(p4)/apply(t(p4),1,sum)),3)*100
|
|
p5=read.table("nom du tableau 6.txt")
|
t05=round(t(t(p5)/apply(t(p5),1,sum)),3)*100
|
|
p6=read.table("nom du tableau 7.txt")
|
t06=round(t(t(p6)/apply(t(p6),1,sum)),3)*100
|
|
p7=read.table("nom du tableau 8.txt")
|
t07=round(t(t(p7)/apply(t(p7),1,sum)),3)*100
|
|
p8=read.table("nom du tableau 9.txt")
|
t08=round(t(t(p8)/apply(t(p8),1,sum)),3)*100
|
|
p9=read.table("nom du tableau 10.txt")
|
t09=round(t(t(p9)/apply(t(p9),1,sum)),3)*100
|
|
Les centres de gravités :
|
Centrage des tableaux de taux :
|
|
CG0=colMeans(t00)
|
tc0=scale(t00,center=T,scal=F)
|
|
CG1=colMeans(t01)
|
tc1=scale(t01,center=T,scal=F)
|
|
CG2=colMeans(t02)
|
tc2=scale(t02,center=T,scal=F)
|
|
CG3<-colMeans(t03)
|
tc3=scale(t03,center=T,scal=F)
|
|
CG4<-colMeans(t04)
|
tc4=scale(t04,center=T,scal=F)
|
|
CG5<-colMeans(t05)
|
tc5=scale(t05,center=T,scal=F)
|
|
CG6<-colMeans(t06)
|
tc6=scale(t06,center=T,scal=F)
|
|
CG7<-colMeans(t07)
|
tc7=scale(t07,center=T,scal=F)
|
|
CG8<-colMeans(t08)
|
tc8=scale(t08,center=T,scal=F)
|
|
CG9<-colMeans(t09)
|
tc9=scale(t09,center=T,scal=F)
|
Le tableau des centres de gravité :
g<-matrix(c(CG0,CG1,CG2,CG3,CG4,CG5,CG6,CG7,CG8,CG9),nrow=10,
ncol=6, byrow=T)
|
Transformations les tableaux centrés en matrices :
|
Les matrices variance-covariance :
|
|
tc0=as.matrix(tc0)
|
v0<- (1/48)*(t(tc0)%*%tc0)
|
|
tc01<-as.matrix(tc1)
|
v1<- (1/48)*(t(tc01)%*%tc01)
|
|
tc02<-as.matrix(tc2)
|
v2<- (1/48)*(t(tc02)%*%tc02)
|
|
tc03<-as.matrix(tc3)
|
v3<- (1/48)*(t(tc03)%*%tc03)
|
|
tc04<-as.matrix(tc4)
|
v4<- (1/48)*(t(tc04)%*%tc04)
|
|
tc05<-as.matrix(tc5)
|
v5<- (1/48)*(t(tc05)%*%tc05)
|
|
tc06<-as.matrix(tc6)
|
v6<- (1/48)*(t(tc06)%*%tc06)
|
|
tc07<-as.matrix(tc7)
|
v7<- (1/48)*(t(tc07)%*%tc07)
|
|
tc08<-as.matrix(tc8)
|
v8<-(1/48)*(t(tc08)%*%tc08)
|
|
tc09<-as.matrix(tc9)
|
v9<- (1/48)*(t(tc09)%*%tc09)
|
La matrice du compromis
v=v0+v1+v2+v3+4+v5+v6+v7+v8+v9
Programmation du premier critère
Les vecteurs propres
uij tel que i=2000,..., 2009 et j=1,2
u01=c(-0.513,-0.397,-0.531,-0.44,-0.29,-0.137)
u02=c(-0.248,0.165,-0.252,-0.171,0.622,0.657)
u11=c(0.479,0.352,0.36,0.521,0.495,0.022)
u12=c(-0.176,-0.118,-0.371,0.007,0.548,-0.719)
u21=c(-0.186,-0.261,-0.186,-0.569,-0.551,-0.484)
u22=c(0.811,0.181,0.441,-0.174,-0.084,-0.279)
u31=c(-0.488,-0.35,-0.358,-0.524,-0.485,-0.023)
u32=c(-0.143,-0.122,-0.362,0.013,0.521,-0.749)
u41=c(-0.493,-0.346,-0.353,-0.532,-0.478,-0.022)
u42=c(0.115,0.134,0.35,-0.072,-0.431,0.809)
u51=c(-0.5,-0.344,-0.354,-0.533,-0.47,-0.022)
u52=c(-0.082,-0.136,-0.335,0.089,0.377,-0.844)
u61=c(-0.509,-0.341,-0.358,-0.529,-0.465,-0.022)
u62=c(0.049,0.15,0.311,-0.111,-0.319,0.874)
u71=c(-0.505,-0.341,-0.405,-0.438,-0.461,-0.246)
u72=c(0.456,-0.102,0.135,0.308,-0.483,-0.66)
u81=c(-0.474,-0.394,-0.375,-0.456,-0.451,-0.261)
u82=c(-0.416,0.219,-0.033,-0.339,0.152,0.8)
u91=c(-0.531,-0.345,-0.365,-0.499,-0.465,-0.026)
u92=c(-0.021,0.155,0.237,-0.109,-0.213,0.929)
U1 <-
matrix(c(u01,u11,u21,u31,u41,u51,u61,u71,u81,u91),6)
U2 <-
matrix(c(u02,u12,u22,u32,u42,u52,u62,u72,u82,u92),6)
Les valeurs propres
lambda1 <-
c(24.525,55.029,43.607,56.313,58.14,59.328,60.408,20.795,20.801,58.401)
lambda2 <-
c(2.242,2.128,6.451,2.083,2.031,1.974,1.918,3.118,2.743,1.756)
k <- 1 ## pour 2000
Q0 <- vector()
for (j in 1:10){
Q0[j] = round(((lambda1[k]+lambda2[k] - (t(U1[,j]) %*% v0
%*% U1[,j]) -
(t(U2[,j]) %*% v0 %*% U2[,j]) )) *
(lambda1[k]+lambda2[k])^(-1),2)
I
k <- 2 ## pour 2001
Q1 <- vector()
for (j in 1:10){
Q1[j] = round(((lambda1[k]+lambda2[k] - (t(U1[,j]) %*% v1
%*% U1[,j]) -
(t(U2[,j]) %*% v1 %*% U2[,j]) )) *
(lambda1[k]+lambda2[k])^(-1),2)
I
|
k <- 3 ## pour 2002
Q2 <- vector()
for (j in 1:10){
Q2[j] = round(((lambda1[k]+lambda2[k] - (t(U1[,j]) %*% v2
%*% U1[,j]) - (t(U2[,j]) %*% v2 %*% U2[,j]) )) *
(lambda1[k]+lambda2[k])^(-1),2) I
k <- 4 ## pour 2003
Q3 <- vector()
for (j in 1:10){
Q3[j] = round(((lambda1[k]+lambda2[k] - (t(U1[,j]) %*% v3
%*% U1[,j]) -
(t(U2[,j]) %*% v3 %*% U2[,j]) )) *
(lambda1[k]+lambda2[k])^(-1),2)
I
k <- 5 ## pour 2004
Q4 <- vector()
for (j in 1:10){
Q4[j] = round(((lambda1[k]+lambda2[k] - (t(U1[,j]) %*% v4
%*% U1[,j]) - (t(U2[,j]) %*% v4 %*% U2[,j]) )) *
(lambda1[k]+lambda2[k])^(-1),2) I
k <- 6 ## pour 2005
Q5 <- vector()
for (j in 1:10){
Q5[j] = round(((lambda1[k]+lambda2[k] - (t(U1[,j]) %*% v5
%*% U1[,j]) - (t(U2[,j]) %*% v5 %*% U2[,j]) )) *
(lambda1[k]+lambda2[k])^(-1),2) I
k <- 7 ## pour 2006
Q6 <- vector()
for (j in 1:10){
Q6[j] = round(((lambda1[k]+lambda2[k] - (t(U1[,j]) %*% v6
%*% U1[,j]) - (t(U2[,j]) %*% v6 %*% U2[,j]) )) *
(lambda1[k]+lambda2[k])^(-1),2) I
k <- 8 ## pour 2007
Q7 <- vector()
for (j in 1:10){
Q7[j] = round(((lambda1[k]+lambda2[k] - (t(U1[,j]) %*% v7
%*% U1[,j]) - (t(U2[,j]) %*% v7 %*% U2[,j]) )) *
(lambda1[k]+lambda2[k])^(-1),2) I
k <- 9 ## pour 2008
Q8 <- vector()
for (j in 1:10){
Q8[j] = round(((lambda1[k]+lambda2[k] - (t(U1[,j]) %*% v8
%*% U1[,j]) - (t(U2[,j]) %*% v8 %*% U2[,j]) )) *
(lambda1[k]+lambda2[k])^(-1),2) I
k <- 10 ## pour 2009
Q9 <- vector()
for (j in 1:10){
Q9[j] = round(((lambda1[k]+lambda2[k] - (t(U1[,j]) %*% v9
%*% U1[,j]) - (t(U2[,j]) %*% v9 %*% U2[,j]) )) *
(lambda1[k]+lambda2[k])^(-1),2) I
|
MQ0 <- mean(Q0)
MQ1 <- mean(Q1)
MQ2 <- mean(Q2)
MQ3 <- mean(Q3)
MQ4 <- mean(Q4)
MQ5 <- mean(Q5)
MQ6 <- mean(Q6)
MQ7 <- mean(Q7)
MQ8 <- mean(Q8)
MQ9 <- mean(Q9)
minimum<-min(MQ0,MQ1,MQ2,MQ3,MQ4,MQ5,MQ6,MQ7,MQ8,MQ9)
Résultats :
|
Ö(00,00)= 0
|
Ö(01,00)=0.09
|
Ö(02,00)=0.17
|
Ö(03,00)=0.09
|
Ö(04,00)=0.09
|
|
Ö(00,01)=0.05
|
Ö(01,01)= 0
|
Ö(02,01)=0.32
|
Ö(03, 01)=0.00
|
Ö(04,01)=0.00
|
|
Ö(00,02)=0.08
|
Ö(01,02)= 0.11
|
Ö(02,02)= 0
|
Ö(03, 02)=0.11
|
Ö(04,02)=0.11
|
|
Ö(00,03)=0.06
|
Ö(01,03)=0
|
Ö(02, 03)=0.32
|
Ö(03, 03)= 0
|
Ö(04, 03)=0
|
|
Ö(00,04)=0.06
|
Ö(01,04)=0
|
Ö(02,04)= 0.31
|
Ö(03, 04)=0
|
Ö(04, 04)= 0
|
|
Ö(00,05)=0.06
|
Ö(01,05)=0
|
Ö(02, 05)=0.30
|
Ö(03, 05)=0
|
Ö(04, 05)=0
|
|
Ö(00,06)=0.06
|
Ö(01,06)=0
|
Ö(02, 06)=0.29
|
Ö(03, 06)=0
|
Ö(04, 06)=0
|
|
Ö(00,07)=0.03
|
Ö(01,07)=0.05
|
Ö(02, 07)=0.15
|
Ö(03,07)=0.05
|
Ö(04,07)=0.04
|
|
Ö(00,08)=0.06
|
Ö(01,08)= 0.03
|
Ö(02, 08)=0.18
|
Ö(03, 08)=0.02
|
Ö(04,08)=0.02
|
|
Ö(00,09)=0.06
|
Ö(01,09)= 0.01
|
Ö(02, 09)=0.27
|
Ö(03, 09)=0.00
|
Ö(04,09)=0.00
|
|
D(., 00)=0.052
|
D(.,01)=0.029
|
D(., 02)= 0.231
|
D(., 03)=0.027
|
D(.,04)= 0.026
|
|
Ö(05,00)=0.09
|
Ö(06,00)=0.09
|
Ö(07,00)=0.02
|
Ö(08,00)=0.03
|
Ö(09,00)=0.08
|
|
Ö(05,01)=0.00
|
Ö(06,01)=0.00
|
Ö(07, 01)=0.10
|
Ö(08,01=0.06
|
Ö(09,01)=0.01
|
|
Ö(05,02)=0.11
|
Ö(06,02)=0.10
|
Ö(07,02)=0.06
|
Ö(08,02)=0.07
|
Ö(09,02)=0.09
|
|
Ö(05,03)=0
|
Ö(06,03)=0.00
|
Ö(07,03)=0.10
|
Ö(08,03)=0.06
|
Ö(09,03)=0.01
|
|
Ö(05,04)=0
|
Ö(06,04)=0.00
|
Ö(07,04)=0.09
|
Ö(08,04)=0.05
|
Ö(09,04)=0.00
|
|
Ö(05,05)= 0
|
Ö(06,05)=0.00
|
Ö(07,05)=0.08
|
Ö(08,05)=0.04
|
Ö(09,05)=0.00
|
|
Ö(05,06)=0
|
Ö(06,06)= 0
|
Ö(07,06)=0.08
|
Ö(08,06)=0.04
|
Ö(09,06)=0.00
|
|
Ö(05,07)=0.04
|
Ö(06,07)=0.04
|
Ö(07,07)= 0
|
Ö(08,07)=0.01
|
Ö(09,07)=0.03
|
|
Ö(05,08)=0.02
|
Ö(06,08)=0.01
|
Ö(07,08)=0.02
|
Ö(08,08)= 0
|
Ö(09,08)=0.01
|
|
Ö(05,09)=0.00
|
Ö(06,09)=0.00
|
Ö(07,09)=0.06
|
Ö(08,09)=0.02
|
Ö(09,09)= 0
|
|
D(.,05)=0.026
|
D(.,06)=0.024
|
D(., 07)=0.061
|
D(., 08)=0.038
|
D(.,09)=0.023
|
les trajectoires : (Alger, Adrar, Chlef)
chlef=read.table("nom du tableau des
coordonnées chlef.txt")
attach(chlef)
ard=read.table("nom du tableau des coordonnées
de Adrar.txt")
attach(ard)
alger=read.table("nom du tableau des
coordonnées de Alger.txt")
attach(alger)
plot(axe1,axe2,type="p",pch=3,xlim=c(-10,20),ylim=c(-2.5,5),col="red")
lines(axe1,axe2,lty=3,col="red")
abline(v=0,h=0,panel.first=grid(col="gray"))
text(chlef,labels
=c("00","01","02","03","04","05","06","07","08","09"),cex =1, col =
"red")
points(ax1,ax2,pch=4,col="blue")
lines(ax1,ax2,lty=3,col="blue")
text(adrar,labels
=c("00","01","02","03","04","05","06","07","08","09"),cex =1, col
= "blue")
points(a1,a2,pch=4,col="blue")
lines(a1,a2,lty=3,col="blue")
text(alger,labels
=c("00","01","02","03","04","05","06","07","08","09"),cex =1, col
= "blue")
text(15,-1,"Alger")
text(1,1,"adrar")
text(-1,-1,"chlef")

|
Références bibliographiques
|
:
|
? Ouvrages :
[1] Ludovic Lebart Marie Piron Alain Morineau :
« Statistique exploratoire multidimensionnelle » Dunod
3e (18 août 2000)
[2] Gilbert Saporta :
« L'Analyse des données évolutives:
Méthodes et applications » Technip (3 mai 2000)
? Mémoires :
[1] Zitouni Kamel - Imoudache Farouk
« Analyse et prévision du budget en matières
d'explorations bancaires » Mémoire d'ingéniorat. Promotion
2010-2011. USTHB.
[2] Haddadou Fouad - Maloum Aghiles
« Modélisation et prévision de la part de
marché d'Air Algérie sur les différentes réseaux
internationaux affectés par la concurrence »
Mémoire d'ingéniorat. Promotion 2008-2009.
USTHB.
[3] Merieme Bensalloua - Nora cherfi
« Modélisation et prévision des
paramètres du marché pétrolier algérien »
Mémoire d'ingéniorat. Promotion 2004-2005. USTHB.
|
|



