Le point de départ de cette méthode
réside dans l'existence d'une relation théorique que les
paramètres considérés doivent satisfaire. L'idée de
base est qu'il faut choisir les estimateurs des paramètres de telle
sorte qu'ils soient le plus proches de la relation théorique. Ces
estimateurs sont choisis pour minimiser la distance pondérée
entre les valeurs théoriques et les valeurs observées.
Autrement, on introduit un ensemble de
paramètres auxiliaires, facilement estimables, et l'on estime les
paramètres du modèle à partir de ces estimatuers
auxiliaires.
Toutefois, s'il on retient un nombre important des
paramètres auxiliaires que des paramètres
d'intérêts, cela devrait améliorer la précision des
estimateurs des moments.
Notons que l'estimateur GMM (Generalized method of moments)
est robuste au sens où il ne nécessite pas des informations
particulières sur la vraie distribution des erreurs.
L'estimateur GMM consiste en une restriction sur les moments,
appelée conditions d'orthogonalité :
E (W', X,) = 0 (1)
Où W' est un vecteur des paramètres auxiliaires,
X, un vecteur des paramètres d'intérêts et un vecteur des
paramètres inconnus.
En notant G (X, W, ) la contrepartie empirique de (1), il
vient :
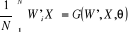
(2)
L'estimateur GMM de est tel que la moyenne empirique G (X,
W', ) soit aussi proche de zéro. Cet estimateur est alors la valeur de
qui minimise la fonction critère suivante :
G' (X, W',) A G ( X, W',) (3)
Où A est une matrice de pondération, de poids ou
de distance.
Si le système est juste identifié, le nombre des
paramètres d'intérêts égale celui des
paramètres auxiliaires, la fonction critère (3) est
minimisée pour la valeur de vérifiant : G (X, W', ) = 0
Signalons que de très nombreuses méthodes
d'estimation sont des cas particuliers de la méthode des moments
généralisés. Ainsi, l'estimateur des moindres
carrés ordinaires est un cas particulier de l'estimateur GMM en posant
que les variables endogènes et exogènes ne sont pas
corrélées avec le terme résiduel.
2. Outputs des estimations
Tableau 6: estimation de within avec
dette/pib
|
Dependent Variable: TXCROIS
|
|
Method: Least Squares
|
|
Date: 01/14/06 Time: 13:17
|
|
Sample(adjusted): 2 200
|
|
Included observations: 196
|
|
Excluded observations: 3 after adjusting endpoints
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
C
|
18.85207
|
7.695677
|
2.449696
|
0.0153
|
|
LPNBHAB(-1)
|
-2.762817
|
0.901151
|
-3.065877
|
0.0025
|
|
TEXCH
|
0.041704
|
0.030377
|
1.372874
|
0.1715
|
|
APD
|
0.000917
|
0.003519
|
0.260655
|
0.7947
|
|
LTXPOP
|
2.375701
|
1.907803
|
1.245255
|
0.2147
|
|
SERVEXP
|
0.005483
|
0.043105
|
0.127198
|
0.8989
|
|
TXINV
|
0.470486
|
0.104114
|
4.518945
|
0.0000
|
|
DEFICIT
|
0.434792
|
0.136100
|
3.194656
|
0.0017
|
|
OPEN
|
-0.064350
|
0.049735
|
-1.293850
|
0.1974
|
|
LDEPIB
|
-0.577571
|
2.351299
|
-0.245639
|
0.8062
|
|
LDEPIB2
|
-0.933932
|
1.139759
|
-0.819412
|
0.4137
|
|
D1
|
3.555428
|
3.423063
|
1.038669
|
0.3004
|
|
D2
|
-0.451753
|
3.037599
|
-0.148720
|
0.8819
|
|
D3
|
-1.935853
|
2.539689
|
-0.762240
|
0.4469
|
|
D4
|
0.666388
|
2.934215
|
0.227109
|
0.8206
|
|
D5
|
0.172904
|
2.941162
|
0.058788
|
0.9532
|
|
D6
|
-1.176215
|
2.935830
|
-0.400641
|
0.6892
|
|
D7
|
2.794441
|
3.400393
|
0.821800
|
0.4123
|
|
D8
|
-4.933572
|
3.635712
|
-1.356975
|
0.1765
|
|
D9
|
-0.513478
|
2.986656
|
-0.171924
|
0.8637
|
|
R-squared
|
0.275222
|
Mean dependent var
|
1.842857
|
|
Adjusted R-squared
|
0.196979
|
S.D. dependent var
|
7.585411
|
|
S.E. of regression
|
6.797395
|
Akaike info criterion
|
6.767407
|
|
Sum squared resid
|
8132.006
|
Schwarz criterion
|
7.101908
|
|
Log likelihood
|
-643.2059
|
F-statistic
|
3.517530
|
|
Durbin-Watson stat
|
2.006632
|
Prob(F-statistic)
|
0.000005
|
Tableau 7: estimation de within avec
dette/exportation
|
Dependent Variable: TXCROIS
|
|
Method: Least Squares
|
|
Date: 01/14/06 Time: 13:18
|
|
Sample(adjusted): 2 200
|
|
Included observations: 196
|
|
Excluded observations: 3 after adjusting endpoints
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
C
|
21.04443
|
14.65775
|
1.435721
|
0.1529
|
|
LPNBHAB(-1)
|
-2.735285
|
0.904724
|
-3.023338
|
0.0029
|
|
TEXCH
|
0.041395
|
0.030352
|
1.363813
|
0.1744
|
|
APD
|
0.000945
|
0.003519
|
0.268665
|
0.7885
|
|
LTXPOP
|
2.379889
|
1.907609
|
1.247577
|
0.2138
|
|
SERVEXP
|
0.005458
|
0.043098
|
0.126648
|
0.8994
|
|
TXINV
|
0.467935
|
0.104138
|
4.493412
|
0.0000
|
|
DEFICIT
|
0.434998
|
0.136058
|
3.197142
|
0.0016
|
|
OPEN
|
-0.061663
|
0.049817
|
-1.237803
|
0.2174
|
|
LDEXP
|
-1.733347
|
2.285464
|
-0.758422
|
0.4492
|
|
LDEXP2
|
-0.368872
|
1.178106
|
-0.313106
|
0.7546
|
|
D1
|
3.637165
|
3.420753
|
1.063264
|
0.2891
|
|
D2
|
-0.390532
|
3.036333
|
-0.128620
|
0.8978
|
|
D3
|
-1.895929
|
2.539590
|
-0.746549
|
0.4563
|
|
D4
|
0.743085
|
2.935547
|
0.253134
|
0.8005
|
|
D5
|
0.212515
|
2.938622
|
0.072318
|
0.9424
|
|
D6
|
-1.096113
|
2.935062
|
-0.373455
|
0.7093
|
|
D7
|
2.904663
|
3.396796
|
0.855119
|
0.3936
|
|
D8
|
-4.856862
|
3.629710
|
-1.338086
|
0.1826
|
|
D9
|
-0.486829
|
2.983761
|
-0.163160
|
0.8706
|
|
R-squared
|
0.275430
|
Mean dependent var
|
1.842857
|
|
Adjusted R-squared
|
0.197209
|
S.D. dependent var
|
7.585411
|
|
S.E. of regression
|
6.796422
|
Akaike info criterion
|
6.767120
|
|
Sum squared resid
|
8129.677
|
Schwarz criterion
|
7.101622
|
|
Log likelihood
|
-643.1778
|
F-statistic
|
3.521192
|
|
Durbin-Watson stat
|
2.007274
|
Prob(F-statistic)
|
0.000005
|
Tableau 8:Estimation GMM avec dette/pib
|
Dependent Variable: TXCROIS
|
|
Method: Generalized Method of Moments
|
|
Date: 01/18/06 Time: 09:31
|
|
Sample(adjusted): 3 181
|
|
Included observations: 179 after adjusting endpoints
|
|
No prewhitening
|
|
Bandwidth: Fixed (4)
|
|
Kernel: Bartlett
|
|
Convergence achieved after: 10 weight matricies, 11 total coef
|
|
iterations
|
|
Instrument list: D(TXCROIS) D(LPNBHAB(-1)) D(TEXCH) D(LTXPOP)
|
|
D(APD) D(SERVEXP) D(DEFICIT) D(TXINV) D(OPEN)
D(LDEPIB)
|
|
D(LDEPIB2)
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
C
|
29.44941
|
16.89479
|
1.743106
|
0.0831
|
|
LPNBHAB(-1)
|
-4.336943
|
1.938552
|
-2.237207
|
0.0266
|
|
TEXCH
|
0.006446
|
0.041848
|
0.154026
|
0.8778
|
|
LTXPOP
|
2.064860
|
2.613222
|
0.790159
|
0.4305
|
|
APD
|
0.005453
|
0.002065
|
2.641009
|
0.0090
|
|
SERVEXP
|
-0.151259
|
0.101448
|
-1.491007
|
0.1378
|
|
DEFICIT
|
0.228554
|
0.181099
|
1.262038
|
0.2087
|
|
TXINV
|
0.571036
|
0.160461
|
3.558730
|
0.0005
|
|
OPEN
|
-0.035450
|
0.064594
|
-0.548820
|
0.5839
|
|
LDEPIB
|
-1.408378
|
5.037171
|
-0.279597
|
0.7801
|
|
LDEPIB2
|
-0.565325
|
2.258483
|
-0.250312
|
0.8027
|
|
R-squared
|
0.119854
|
Mean dependent var
|
1.770391
|
|
Adjusted R-squared
|
0.067464
|
S.D. dependent var
|
6.070426
|
|
S.E. of regression
|
5.862083
|
Sum squared resid
|
5773.154
|
|
Durbin-Watson stat
|
1.710482
|
J-statistic
|
0.045428
|
Tableau 9: Estimation GMM avec dette/export
|
Dependent Variable: TXCROIS
|
|
Method: Generalized Method of Moments
|
|
Date: 01/18/06 Time: 09:32
|
|
Sample(adjusted): 3 181
|
|
Included observations: 179 after adjusting endpoints
|
|
No prewhitening
|
|
Bandwidth: Fixed (4)
|
|
Kernel: Bartlett
|
|
Convergence achieved after: 12 weight matricies, 13 total coef
|
|
iterations
|
|
Instrument list: D(TXCROIS) D(LPNBHAB(-1)) D(TEXCH) D(LTXPOP)
|
|
D(APD) D(SERVEXP) D(DEFICIT) D(TXINV) D(OPEN) D(LDEXP)
|
|
D(LDEXP2)
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
C
|
33.81051
|
24.60346
|
1.374218
|
0.1712
|
|
LPNBHAB(-1)
|
-4.470962
|
1.959561
|
-2.281613
|
0.0238
|
|
TEXCH
|
0.008734
|
0.041198
|
0.211999
|
0.8324
|
|
LTXPOP
|
2.133572
|
2.581795
|
0.826391
|
0.4098
|
|
APD
|
0.005301
|
0.002003
|
2.647066
|
0.0089
|
|
SERVEXP
|
-0.147657
|
0.102043
|
-1.447013
|
0.1498
|
|
DEFICIT
|
0.213474
|
0.180485
|
1.182783
|
0.2386
|
|
TXINV
|
0.582907
|
0.161716
|
3.604503
|
0.0004
|
|
OPEN
|
-0.054244
|
0.066484
|
-0.815901
|
0.4157
|
|
LDEXP
|
-2.176813
|
4.542123
|
-0.479250
|
0.6324
|
|
LDEXP2
|
-0.132237
|
2.568427
|
-0.051486
|
0.9590
|
|
R-squared
|
0.124803
|
Mean dependent var
|
1.770391
|
|
Adjusted R-squared
|
0.072708
|
S.D. dependent var
|
6.070426
|
|
S.E. of regression
|
5.845578
|
Sum squared resid
|
5740.692
|
|
Durbin-Watson stat
|
1.719906
|
J-statistic
|
0.045930
|
|
Dependent Variable: TXINV
|
|
Method: Least Squares
|
|
Date: 01/20/06 Time: 22:10
|
|
Sample: 1 200
|
|
Included observations: 200
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
C
|
-13.06925
|
5.126555
|
-2.549325
|
0.0116
|
|
AIDE
|
0.001213
|
0.002471
|
-2.490712
|
0.0342
|
|
LPNBHAB
|
4.761445
|
0.590170
|
8.067921
|
0.0000
|
|
SERVEXP
|
-0.011298
|
0.030338
|
2.372409
|
0.0370
|
|
OPEN
|
0.172154
|
0.031111
|
5.533475
|
0.0000
|
|
LDEPIB
|
-7.155756
|
1.523858
|
-4.695816
|
0.0000
|
|
LDEPIB2
|
2.611271
|
0.747353
|
3.494028
|
0.0006
|
|
D1
|
4.959196
|
2.115953
|
2.343717
|
0.0202
|
|
D2
|
0.206611
|
2.012250
|
0.102677
|
0.9183
|
|
D3
|
4.753549
|
1.666340
|
2.852688
|
0.0048
|
|
D4
|
3.683322
|
1.939713
|
1.898900
|
0.0591
|
|
D5
|
0.501738
|
1.993377
|
0.251703
|
0.8016
|
|
D6
|
4.029906
|
1.909829
|
2.110088
|
0.0362
|
|
D7
|
11.26193
|
2.094612
|
5.376617
|
0.0000
|
|
D8
|
11.48801
|
2.344449
|
4.900088
|
0.0000
|
|
D9
|
2.385389
|
1.992298
|
1.197305
|
0.2327
|
|
R-squared
|
0.735212
|
Mean dependent var
|
17.32150
|
|
Adjusted R-squared
|
0.713626
|
S.D. dependent var
|
9.222285
|
|
S.E. of regression
|
4.935210
|
Akaike info criterion
|
6.107286
|
|
Sum squared resid
|
4481.558
|
Schwarz criterion
|
6.371151
|
|
Log likelihood
|
-594.7286
|
F-statistic
|
34.05964
|
|
Durbin-Watson stat
|
2.206456
|
Prob(F-statistic)
|
0.000000
|
|
Dependent Variable: TXINV
|
|
Method: Least Squares
|
|
Date: 01/20/06 Time: 22:11
|
|
Sample: 1 200
|
|
Included observations: 200
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
C
|
-41.28530
|
9.746545
|
-4.235891
|
0.0000
|
|
AIDE
|
0.001228
|
0.002474
|
-2.496247
|
0.0320
|
|
LPNBHAB
|
4.758744
|
0.591126
|
8.050309
|
0.0000
|
|
SERVEXP
|
-0.011315
|
0.030377
|
2.372493
|
0.0370
|
|
OPEN
|
0.171222
|
0.031179
|
5.491518
|
0.0000
|
|
LDEXP
|
5.166659
|
1.497983
|
3.449076
|
0.0007
|
|
LDEXP2
|
-3.539599
|
0.762927
|
-4.639501
|
0.0000
|
|
D1
|
4.903493
|
2.117539
|
2.315656
|
0.0217
|
|
D2
|
0.150129
|
2.013271
|
0.074570
|
0.9406
|
|
D3
|
4.730356
|
1.668171
|
2.835655
|
0.0051
|
|
D4
|
3.658096
|
1.943219
|
1.882492
|
0.0613
|
|
D5
|
0.441447
|
1.993969
|
0.221391
|
0.8250
|
|
D6
|
3.980266
|
1.911292
|
2.082500
|
0.0387
|
|
D7
|
11.19431
|
2.095342
|
5.342473
|
0.0000
|
|
D8
|
11.42606
|
2.345772
|
4.870918
|
0.0000
|
|
D9
|
2.340733
|
1.993862
|
1.173969
|
0.2419
|
|
R-squared
|
0.734529
|
Mean dependent var
|
17.32150
|
|
Adjusted R-squared
|
0.712887
|
S.D. dependent var
|
9.222285
|
|
S.E. of regression
|
4.941571
|
Akaike info criterion
|
6.109862
|
|
Sum squared resid
|
4493.118
|
Schwarz criterion
|
6.373727
|
|
Log likelihood
|
-594.9862
|
F-statistic
|
33.94045
|
|
Durbin-Watson stat
|
2.210681
|
Prob(F-statistic)
|
0.000000
|
LES STATISTIQUES DESCRIPTIVES
|
APD
|
DEFICIT
|
DEPIB
|
DEPIB2
|
DEXP
|
DEXP2
|
OPEN
|
PNBHAB
|
SERVEXP
|
TEXCH
|
TXCROIS
|
TXINV
|
TXPOP
|
|
Mean
|
227.7450
|
-5.155500
|
86.48500
|
2445.040
|
394.1650
|
109.4400
|
57.10000
|
752.1500
|
18.16400
|
89.58835
|
1.786000
|
17.32150
|
2.705000
|
|
Median
|
183.5000
|
-4.250000
|
68.00000
|
1035.500
|
321.5000
|
46.50000
|
50.00000
|
297.5000
|
14.00000
|
89.50000
|
2.100000
|
14.90000
|
3.000000
|
|
Maximum
|
2034.000
|
6.100000
|
243.0000
|
46099.00
|
2147.000
|
589.0000
|
160.0000
|
5100.000
|
112.0000
|
180.3000
|
34.40000
|
59.70000
|
15.00000
|
|
Minimum
|
35.00000
|
-26.90000
|
16.00000
|
45.00000
|
67.00000
|
2.000000
|
5.000000
|
80.00000
|
0.100000
|
7.900000
|
-50.20000
|
1.800000
|
-21.00000
|
|
Std. Dev.
|
200.0568
|
4.874729
|
59.02593
|
4626.440
|
299.3147
|
144.2802
|
25.43017
|
1094.666
|
15.37000
|
20.02649
|
7.551785
|
9.222285
|
2.024467
|
|
Skewness
|
4.699553
|
-1.058228
|
1.085566
|
5.640847
|
2.076604
|
1.811527
|
1.409821
|
2.488725
|
2.378966
|
0.485244
|
-0.758504
|
1.613233
|
-6.960521
|
|
Kurtosis
|
36.94112
|
4.883159
|
3.228515
|
45.93284
|
9.861182
|
5.247823
|
5.538105
|
8.092166
|
12.30248
|
6.260334
|
16.08036
|
6.363473
|
101.8979
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jarque-Bera
|
10336.19
|
66.88059
|
39.71695
|
16420.88
|
536.0412
|
151.4936
|
119.9364
|
422.5430
|
909.7834
|
96.43019
|
1444.977
|
181.0253
|
83121.61
|
|
Probability
|
0.000000
|
0.000000
|
0.000000
|
0.000000
|
0.000000
|
0.000000
|
0.000000
|
0.000000
|
0.000000
|
0.000000
|
0.000000
|
0.000000
|
0.000000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Observations
|
200
|
200
|
200
|
200
|
200
|
200
|
200
|
200
|
200
|
200
|
200
|
200
|
200
|
LA MATRICE DES CORRELATIONS
|
APD
|
DEFICIT
|
DEPIB
|
DEPIB2
|
DEXP
|
DEXP2
|
OPEN
|
PNBHAB
|
SERVEXP
|
TEXCH
|
TXCROIS
|
TXINV
|
TXPOP
|
|
APD
|
1.000000
|
-0.196527
|
0.434168
|
0.144966
|
0.305313
|
0.421004
|
-0.103610
|
-0.288980
|
0.081268
|
-0.218194
|
-0.041200
|
-0.242136
|
-0.010125
|
|
DEFICIT
|
-0.196527
|
1.000000
|
-0.424584
|
-0.103089
|
-0.245565
|
-0.387639
|
-0.021618
|
0.166950
|
-0.132152
|
0.347015
|
0.240261
|
-0.091087
|
-0.019489
|
|
DEPIB
|
0.434168
|
-0.424584
|
1.000000
|
0.199662
|
0.410691
|
0.969053
|
0.407233
|
-0.045708
|
0.077639
|
-0.155415
|
-0.222427
|
0.096683
|
0.048765
|
|
DEPIB2
|
0.144966
|
-0.103089
|
0.199662
|
1.000000
|
0.911166
|
0.160424
|
-0.300189
|
-0.206215
|
0.493774
|
0.028556
|
-0.165918
|
-0.238545
|
0.060278
|
|
DEXP
|
0.305313
|
-0.245565
|
0.410691
|
0.911166
|
1.000000
|
0.343043
|
-0.359317
|
-0.325363
|
0.500594
|
-0.032320
|
-0.192474
|
-0.311957
|
0.029297
|
|
DEXP2
|
0.421004
|
-0.387639
|
0.969053
|
0.160424
|
0.343043
|
1.000000
|
0.399498
|
-0.100248
|
0.013353
|
-0.110122
|
-0.193507
|
0.067504
|
0.043147
|
|
OPEN
|
-0.103610
|
-0.021618
|
0.407233
|
-0.300189
|
-0.359317
|
0.399498
|
1.000000
|
0.491426
|
-0.291591
|
0.088122
|
-0.018215
|
0.622178
|
0.074856
|
|
PNBHAB
|
-0.288980
|
0.166950
|
-0.045708
|
-0.206215
|
-0.325363
|
-0.100248
|
0.491426
|
1.000000
|
-0.140557
|
0.054086
|
-0.001504
|
0.608742
|
0.082350
|
|
SERVEXP
|
0.081268
|
-0.132152
|
0.077639
|
0.493774
|
0.500594
|
0.013353
|
-0.291591
|
-0.140557
|
1.000000
|
-0.184582
|
-0.038739
|
-0.104001
|
0.007328
|
|
TEXCH
|
-0.218194
|
0.347015
|
-0.155415
|
0.028556
|
-0.032320
|
-0.110122
|
0.088122
|
0.054086
|
-0.184582
|
1.000000
|
0.139766
|
-0.078412
|
0.164242
|
|
TXCROIS
|
-0.041200
|
0.240261
|
-0.222427
|
-0.165918
|
-0.192474
|
-0.193507
|
-0.018215
|
-0.001504
|
-0.038739
|
0.139766
|
1.000000
|
0.181904
|
0.157631
|
|
TXINV
|
-0.242136
|
-0.091087
|
0.096683
|
-0.238545
|
-0.311957
|
0.067504
|
0.622178
|
0.608742
|
-0.104001
|
-0.078412
|
0.181904
|
1.000000
|
0.106495
|
|
TXPOP
|
-0.010125
|
-0.019489
|
0.048765
|
0.060278
|
0.029297
|
0.043147
|
0.074856
|
0.082350
|
0.007328
|
0.164242
|
0.157631
|
0.106495
|
1.000000
|
| 


