II.- REVUE DE LITTÉRATURE
2.1. Prévision pour les changements climatiques
sur le plan mondial
Au début du XXIe siècle, on prévoit de
nombreux impacts sur les systèmes naturels. On s'attend, par exemple,
à ce que des changements dans les précipitations ainsi que dans
la fonte des glaces et des neiges augmentent les risques d'inondation dans
certaines régions et provoquent des sécheresses dans d'autres. En
cas de réchauffement important, la capacité des
écosystèmes à s'adapter sera dépassée, ce
qui entraînera des effets néfastes, comme l'accroissement du
risque d'extinction d'espèces. Les populations les plus pauvres sont
généralement les plus vulnérables, parce que leur
capacité d'adaptation est moindre et que leurs moyens d'existence
dépendent souvent de ressources qui sont liées au climat
(GIEC, 2007).
Vers le milieu du XXIe siècle, le débit moyen
annuel des cours d'eau et la disponibilité en eau devraient augmenter en
raison du changement climatique aux latitudes élevées et dans
certaines zones tropicales humides, et diminuer dans des régions
sèches aux latitudes moyennes et dans les régions tropicales
sèches, d'où la variation des caractéristiques
hydrologiques. L'augmentation de l'intensité des pluies et de la
variabilité des précipitations devrait augmenter les risques de
crues et de sécheresses dans plusieurs régions. La
fréquence des épisodes de fortes précipitations (ou la
partie des précipitations totales imputables à de fortes pluies)
augmentera de manière très probable dans la plupart des
régions au cours du XXIe siècle, ce qui augmentera le risque de
crues d'origine pluviale. (GIEC, 2008).
2.2. Bassin versant
2.2.1. Concepts et définition
Un bassin versant est un espace géographique dont les
apports hydriques sont alimentés exclusivement par les
précipitations et dont les excès en eau sont drainés vers
un point unique appelé exutoire.
6
analytique à considérer pour toute prise de
décision en matière d'aménagement. C'est pourquoi les
gestionnaires et les décideurs réclament des outils
opérationnels adaptés à cette échelle. Mais le
bassin versant est une unité complexe : l'ensemble des composantes du
cycle hydrologique y est représenté et des facteurs anthropiques
perturbateurs s'y ajoutent souvent.
2.2.2. Fonctions d'un bassin versant
Un bassin versant peut être normalement
multifonctionnel dans son ensemble, les plus évidentes de ses fonctions
peuvent être écologiques, hydrologiques et
socio-économiques.
2.2.2.1. Fonction écologique
Écologiquement, un bassin versant représente :
Ø Un réservoir de biodiversité animale et
végétale;
Ø Un site d'échange pour les réactions
nécessaires aux organismes vivant (GANGBAZO, 2004 cité par
DURANDISSE, 2010).
2.2.2.2. Fonctions hydrologiques
Hydrologiquement, un bassin versant remplit les fonctions
suivantes :
Ø Recueillir les eaux des précipitations ;
Ø Restituer l'eau de pluie sous forme d'émergences
(GANGBAZO, 1995 cité par NELSON, 2008).
2.2.2.3. Fonctions
socio-économiques
Chaque individu vit au dépend des ressources du bassin
versant dans lequel il évolue. En ce sens, les bassins versants doivent
être protégés pour assurer leur fonction économique.
Chacun vit dans un bassin versant et chaque action a un impact sur la situation
du BV ainsi que celle de ses ressources (GANGBAZO, 2004).
2.2.3. Caractéristiques physiographiques d'un
bassin versant
Selon GIL (1986), un bassin versant possède quatre (4)
parties fondamentales de terrain qui sont : Les sommets, les flancs, les
ravines et les zones de déposition.
7
2.2.3.1. Les sommets
Ce sont en général, les parties aériennes
du BV, ils consistent le plus souvent en des surfaces planes et
légèrement convexes, le plus souvent allongées, parfois
étroites situées de part et d'autres de la ligne de crête.
Ils sont dans la plus part des cas de faible pente, ce qui leur rend peu sujets
à l'érosion.
2.2.3.2. Les flancs
Ce sont les portions du BV qui sont parfois concaves, parfois
convexes et généralement pentues. Leurs pentes entrainent des
ruissellements pouvant provoquer de l'érosion du sol en cas de mauvais
aménagements des versants. Ce sont les parties du BV où de
solides structures de conservation s'avèrent nécessaires
(DESORMES, 1998).
2.2.3.3. Les ravines
Ce sont des cours d'eau permanents ou temporaires qui
participent au drainage du bassin versant. Leur profondeur varie de quelques
décimètres à quelques mètres. Dessinant les creux
topographiques, elles forment le réseau de drainage naturel du BV,
c'est-à-dire les canaux d'écoulement des eaux pluviales en
montagnes (DEVIENNE, 1997 cité par PIERRE, 2002). Selon DESORMES (1998),
leur géométrie affecte valablement la vitesse de
l'écoulement durant l'averse. Généralement, elles sont le
résultat d'un affouillement graduel et continu des versants sous
l'influence de plusieurs facteurs comme la pente locale, la nature du sol et
celle de la roche mère, le couvert végétal et le
régime des pluies. Donc, leur développement est favorisé
par l'érosion qu'elles matérialisent elles même.
2.2.3.4. Les zones de
déposition
Ces sont les parties du terrain qui reçoivent les
matériaux entrainés par les écoulements depuis les sommets
et les flancs du BV (DESORMES, 1998). Autrement dit, ce sont des portions du
terrain à pentes faibles au niveau desquelles les eaux perdent leur
vitesse et du même coup, une partie de leur charriage (PIERRE, 2002). Ces
zones comprennent les piedmonts, les plaines et les vallées:
2.2.3.4.1. Les piedmonts
Ce sont les zones de dépositions rencontrées au
contact des flancs et des plaines.
8
2.2.3.4.2. Les plaines
Celles-ci représentent les lieux d'accumulation des
matériaux plus ou moins grossiers et/ou fins qui ont traversé les
zones de piedmonts. Elles sont généralement de pentes assez
faibles (DURANDISSE, 2010).
2.2.3.4.3. Les vallées
Ce sont les lieux d'accumulation d'alluvions et de colluvions.
Elles sont caractérisées par leur profondeur plus ou moins
importante et leur richesse en limon et en matière organique (PIERRE,
2002).
2.2.4. Délimitation d'un bassin
versant
La délimitation du bassin versant se fait au moyen des
lignes de plus grande pente et de la ligne de crête qui correspond
souvent à la ligne de partage des eaux. Le bassin versant est
entièrement caractérisé par son exutoire, à partir
duquel on peut tracer les points de départ et d'arrivée de la
ligne de partage des eaux qui le délimite. Elle passe par le sommet des
courbes convexes tandis que l'axe principal du cours d'eau passe par le sommet
des courbes concaves. C'est en suivant cette logique qu'on délimite un
bassin versant.
2.2.5. Comportement hydrologique d'un bassin
versant
L'analyse du comportement hydrologique d'un bassin versant en
tant que système hydrologique s'effectue le plus souvent par le biais de
l'étude de sa réaction hydrologique face à une
sollicitation (la précipitation). Cette réaction est
mesurée par l'observation de la quantité d'eau qui
s'écoule à son exutoire en fonction du temps dont la
représentation graphique constitue donc un hydrogramme de crue. La
réaction du bassin versant peut également être
représentée par un limnigramme qui n'est autre que la
représentation de la hauteur d'eau mesurée en fonction du
temps.
2.2.6. Caractérisation de la réaction
hydrologique d'un bassin versant
La réaction hydrologique d'un bassin versant à
une sollicitation (précipitation) particulière est
caractérisée par sa vitesse (temps de montée
tm, défini comme le temps qui s'écoule
entre l'arrivée de la crue et le maximum de l'hydrogramme) et son
intensité
9
(débit de pointe Qmax, volume
maximum Vmax, etc.). Ces deux caractéristiques
sont fonction du type et de l'intensité de la précipitation qui
le sollicite mais aussi du temps de concentration des eaux sur le BV qui est
une variable caractérisant l'état de ce dernier.
2.2.7. Le régime hydrologique du cours principal
d'un bassin versant
Le régime hydrologique d'un cours d'eau résume
l'ensemble de ses caractéristiques hydrologiques et de son mode de
variation. Il se définit par les variations moyennes de son débit
en fonction du temps. Les débits moyens des cours d'eau, aussi
appelés modules, sont très dépendants de la
pluviométrie. (P. BREIL et A. MALAFOSSE, 1994).
2.2.8. Variabilité de la pluie au niveau du
bassin versant
La pluviométrie d'une zone représente un facteur
écologique déterminant de la caractéristique d'un BV car
elle permet de différencier les climats de cette zone. Le
développement des formations végétales dépend non
seulement de la hauteur de precipitation, mais aussi de sa répartition
temporelle. Cette quantité de pluie observée à une
période donnée n'est pas constante pour quel que soit la
période considérée, d'où la fluctuation effective
des régimes pluviométriques. (M. B. SALEY et al,
2006).
2.2.9. Le temps de concentration d'un bassin
versant
Le temps de concentration est le temps écoulé
entre le début de la pluie et le temps où le ruissellement
effectif arrive à l'exutoire. Il se définit comme le maximum de
durée nécessaire à une goutte d'eau pour parcourir le
chemin hydrologique entre un point du bassin et l'exutoire de ce dernier
(GONOMY, 2011). Il est estimé à partir de plusieurs
formules empiriques dont, celle qui suit, formule de Ventura, en est une :
|
Tc = 76,3*(A/P) 0.5 avec :
|
· S : superficie du Bassin versant en
km2 ;
· I : pente en % ;
· Tc : Temps de concentration en mn.
|
2.3. Caractéristiques physiques des BV et leurs
influences sur l'écoulement Les caractéristiques
physiographiques d'un bassin versant influencent fortement sa réponse
hydrologique, et notamment le régime des écoulements en
période de crue ou d'étiage. Le temps de concentration
tc qui, caractérise en partie la
vitesse et l'intensité de la réaction du bassin versant à
une sollicitation, est influencé par diverses
10
caractéristiques morphologiques : en premier lieu, la
taille du bassin, sa forme et sa pente. A ces facteurs s'ajoutent le type de
sol, le couvert végétal et les caractéristiques du
réseau hydrographique. Ces facteurs, d'ordre purement
géométrique ou physique, se sont estimés aisément
à partir de cartes adéquates ou en recourant à des
techniques digitales et à des modèles numériques (Musy,
2005).
2.3.1. Les caractéristiques
géométriques
2.3.1.1. La forme
La forme d'un bassin versant influence l'allure de
l'hydrogramme à son exutoire. Par exemple, un BV de forme
allongée favorise, pour une même pluie, les faibles débits
de pointe de crue, ceci en raison des temps d'acheminement de l'eau à
l'exutoire plus importants. Ce phénomène est lié à
la notion de temps de concentration. En revanche, les bassins en forme
d'éventail, présentant un temps de concentration plus court,
donnent lieu à de forts débits de pointe (Musy, 2005). Il existe
différents indices morphologiques permettant de caractériser le
milieu, mais aussi de comparer les bassins versants entre eux. À titre
d'exemple, on a l'indice de compacité de Gravélius
(1914) KG, défini comme étant le rapport du
périmètre du bassin au périmètre du cercle ayant la
même surface.
2.3.1.2. L'aire
Le bassin versant étant l'aire de réception des
précipitations et d'alimentation des cours d'eau, les débits vont
être en partie reliés à sa surface.
2.3.1.3. Le relief
L'influence du relief sur l'écoulement se
conçoit aisément, car de nombreux paramètres
hydrométéorologiques (précipitations, températures,
etc.) varient avec l'altitude et la morphologie du bassin. En outre, la pente
influe sur la vitesse d'écoulement. Le relief se détermine lui
aussi au moyen d'indices ou de caractéristiques suivants.
2.3.1.3.1. La courbe hypsométrique
Elle fournit une vue synthétique de la pente du bassin,
donc du relief. Elle exprime le pourcentage de superficie, au-delà d'une
certaine altitude. Elle demeure un outil pratique pour comparer plusieurs
bassins entre eux ou les diverses sections d'un seul bassin.
11
2.3.1.3.2. Les altitudes caractéristiques
Ø Les altitudes maximales et
minimales
Obtenue directement à partir de cartes topographiques,
l'altitude maximale représente le point le plus élevé du
bassin tandis que l'altitude minimale est considérée comme le
point le plus bas, généralement à l'exutoire. Elles
déterminent l'amplitude altimétrique du bassin versant et
interviennent également dans le calcul de la pente.
Ø L'altitude moyenne
Déduite directement de la courbe hypsométrique
ou de la lecture d'une carte topographique, elle est peu représentative
de la réalité. Toutefois, elle est parfois utilisée dans
l'évaluation de certains paramètres
hydrométéorologiques ou dans la mise en oeuvre de modèles
hydrologiques.
Ø Les altitudes
médianes
L'altitude médiane correspond à l'altitude lue
au point d'abscisse 50% de la surface totale du bassin, sur la courbe
hypsométrique. Cette grandeur se rapproche de l'altitude moyenne dans le
cas où la courbe hypsométrique du bassin concerné
présente une pente régulière.
2.3.1.3.3. La pente moyenne du bassin versant
La pente moyenne (im) est une
caractéristique importante qui renseigne sur la topographie du bassin.
Elle est considérée comme une variable indépendante. Elle
donne une bonne indication sur le temps de parcours du ruissellement direct et
influence directement le débit de pointe lors d'une averse.
2.3.2. Le réseau hydrographique
2.3.2.1. La différenciation du réseau
hydrographique
Étant l'ensemble des cours d'eau naturels ou
artificiels, permanents ou temporaires, qui participent à
l'écoulement dans un BV, le réseau hydrographique est sans doute
l'un des éléments les plus importants d'un bassin versant. Il est
sujet à une multitude de formes et, sa différenciation est due
à quatre facteurs principaux.
12
Ø La géologie
Par sa plus ou moins grande sensibilité à
l'érosion, la nature du substratum influence la forme du réseau
hydrographique. Le réseau de drainage n'est habituellement pas le
même dans une région où prédominent les roches
sédimentaires, par comparaison à des roches ignées
(proviennent du refroidissement du magma). La structure de la roche, sa forme,
les failles, les plissements, forcent le courant à changer de
direction.
Ø Le climat
Le réseau hydrographique est dense dans les
régions montagneuses très humides et tend à
disparaître dans les régions désertiques.
Ø La pente du terrain
La pente du terrain détermine si les cours d'eau sont
en phase érosive ou sédimentaire. Dans les zones plus
élevées, les cours d'eau participent souvent à
l'érosion de la roche sur laquelle ils s'écoulent, ce qui donne
lieu à des réseaux jeunes. Au contraire, en plaine, les cours
d'eau s'écoulent sur un lit où la sédimentation
prédomine, donc des réseaux plus anciens.
2.3.2.2. La topologie (Structure et Ordre du
cours d'eau)
La topologie est définie comme étant
l'étude des propriétés géométriques se
conservant après déformations continues. Appliquée
à l'hydrologie, elle s'avère utile dans la description du
réseau hydrographique notamment en proposant une classification de
ceux-ci. À titre d'exemple, on trouve les types dendritiques, en
treillis, en parallèle, rectangulaire, à méandre,
anastomosé, centripète, etc.
Cette classification est facilitée par un
système de numérotation des branches des cours d'eau
(rivière principale et affluents), elle reflète donc la
ramification du cours d'eau. Il existe plusieurs types de classifications des
tronçons des cours d'eau, dont celle de Strahler (1957) est la plus
utilisée. Un bassin versant détient l'ordre de son cours d'eau
principal à l'exutoire. Il existe d'autres classifications de ce type
comme celle de Horton (1945) qui est parfois utilisée dans le même
but (Musy, 2005).
13
2.3.2.3. Les longueurs et les pentes
caractéristiques du réseau
2.2.2.3.1. Les longueurs caractéristiques
Le bassin versant se caractérise principalement par les
deux longueurs suivantes :
Ø Longueur du bassin versant
C'est la distance curviligne mesurée le long du cours
d'eau principal depuis l'exutoire jusqu'à un point représentant
la projection du centre de gravité du bassin sur un plan (Snyder,
1938).
Ø Longueur du cours d'eau principal
C'est la distance curviligne depuis l'exutoire jusqu'à
la ligne de partage des eaux, en suivant toujours le segment d'ordre le plus
élevé (Snyder, 1938).
2.3.2.3.2. Le profil en long du cours d»eau
C'est une représentation graphique de la variation
altimétrique du fond du cours d'eau en fonction de la distance à
l'émissaire. Le profil en long d'un cours d'eau permet de définir
sa pente moyenne.
2.3.2.3.3. La pente moyenne du cours d'eau principal
La pente moyenne du cours d'eau détermine la vitesse
avec laquelle l'eau se rend à l'exutoire du bassin, donc le temps de
concentration. Une pente abrupte favorise et accélère
l'écoulement superficiel, tandis qu'une pente douce ou nulle donne
à l'eau le temps de s'infiltrer, entièrement ou en partie, dans
le sol.
Les pentes moyennes des cours d'eau se calculent à
partir du profil longitudinal du cours d'eau principal. La méthode la
plus fréquemment utilisée consiste à diviser la
différence d'altitude entre les points extrêmes du profil par la
longueur totale du cours d'eau. On peut aussi l'assimiler à la pente de
la droite tracée entre les points situés à 15% et 90% de
distance à partir de l'exutoire, suivant le cours d'eau principal
(Benson, 1959).
14
2.3.2.4. Le degré de développement du
réseau
2.3.2.4.1. La densité de drainage
La densité de drainage, introduite par Horton, est la
longueur totale du réseau hydrographique par unité de surface du
bassin versant. Elle dépend de la géologie, des
caractéristiques topographiques du bassin versant et, dans une certaine
mesure, des conditions climatologiques et anthropiques. En pratique, les
valeurs de densité de drainage varient de 3 à 4 pour des
régions où l'écoulement n'atteint qu'un
développement très limité et se trouve centralisé.
Elles dépassent 1000 pour certaines zones où l'écoulement
est très ramifié avec peu d'infiltration.
Selon Schumm, la valeur inverse de la densité de
drainage, appelé « constante de stabilité du cours d'eau
», elle représente la surface du bassin nécessaire pour
maintenir des conditions hydrologiques stables dans un vecteur hydrographique
unitaire.
Les bassins ayant une densité de drainage
élevée réagissent rapidement aux sollicitations (Campeau,
2005 cité par Vallière, 2010). Tel qu'énoncé
précédemment, l'effet principal d'une densité de drainage
élevée, autant pour des cours d'eau naturels qu'artificiels, est
l'augmentation des vitesses d'écoulement (Cosandey et al, 2003
cité par Vallière, 2010).
2.3.2.4.2. La densité hydrographique
La densité hydrographique représente le nombre
de canaux d'écoulement par unité de surface.
2.3.2.4.3. Le rapport de confluence (bifurcation
ratio)
Le rapport de confluence est un nombre sans dimension
exprimant le développement du réseau de drainage. Il varie
suivant l'ordre considéré. C'est un élément
important à considérer pour établir des
corrélations d'une région à une autre. Selon Strahler
(1964), il varie de 3 à 5 pour une région où la
géologie n'a aucune influence. La réponse hydrologique d'un
bassin est fortement liée à son rapport de confluence.
15
2.3.3. Les caractéristiques
agro-pédo-géologiques 2.3.3.1. La couverture du
sol
2.3.3.1.1. La couverture végétale
L'activité végétative et le type de sol
sont intimement liés et leurs actions combinées influencent
beaucoup l'écoulement en surface. La forêt, par exemple, exerce
une action limitatrice importante sur le ruissellement superficiel. Elle
régularise le débit des cours d'eau et amortit les crues de
faibles et moyennes amplitudes. À l'inverse, le sol nu, de faible
capacité de rétention favorise un ruissellement très
rapide.
Suivant l'importance de la couverture en question, sa
présence se traduit par un indice (K) qui n'est que le rapport de la
surface occupée sur la surface totale du bassin.
Ce type d'indice se calcule aussi avec d'autres couvertures
végétales telles que les cultures vivrières, le
vétiver, le pâturage etc.
2.3.3.1.2. Le coefficient de ruissellement
Pour caractériser la capacité d'un bassin
versant à ruisseler un indice est très souvent utilisé en
hydrologie de surface : le coefficient de ruissellement
(Cr). Son calcul et son emploi sont simples, mais
notons qu'il peut conduire à commettre de grossières erreurs. Ce
coefficient est défini comme étant le rapport de la hauteur de la
lame ruisselée sur la hauteur d'eau précipitée (Cr =
R/P). Il est aussi estimé dans des abaques suivant les
caractéristiques de l'impluvium.
2.3.3.2. La géologie du
substratum
L'étude géologique d'un bassin versant dans le
cadre d'un projet hydrologique a surtout pour objet de déterminer la
perméabilité du substratum. Celle-ci intervient sur la vitesse de
montée des crues, sur leur volume et sur le soutien apporté aux
débits d'étiage par les nappes souterraines. Soumis à une
même averse, un bassin à substratum imperméable
présente une crue plus rapide et plus violente qu'un bassin à
substratum perméable.
16
2.3.3.3. La nature du sol
La nature du sol intervient sur la rapidité de
montée des crues et sur leur volume. En effet, le taux d'infiltration,
le taux d'humidité, la capacité de rétention, les pertes
initiales et le coefficient de ruissellement (Cr) sont fonction du type de sol
et de son épaisseur1.
2.4. Traitement statistique des données
hydrologiques
L'ensemble des données d'une station de mesures
pluviométriques constitue une information considérable qu'il est
souhaitable de condenser à l'aide de caractéristiques bien
choisies. On applique ainsi des lois et d'autres techniques de la statistique
aux relevés pluviométriques pour en tirer des informations utiles
aux études et travaux envisagés. On détermine de la sorte
:
· Valeurs de tendances centrales ou dominantes (moyenne,
médiane,...) ;
· Dispersion ou fluctuation des observations autour de
la valeur centrale (écart-type, quantiles,..) ;
· Lois de distribution statistiques (loi normale,
log-normale, Pearson...).
L'ensemble de ces valeurs ponctuelles, condensées sous
forme statistique, est utilisé pour déterminer la
fréquence et les caractéristiques d'un événement
pluvieux isolé.
Que ce soit pour anticiper les apports qui viendront remplir
un réservoir, ou pour décider de ce que peut être une
sècheresse sévère et s'en prémunir, les
démarches employées s'appuieront toujours sur les données
observées dans le passé.., et en tireront des conclusions pour le
futur. Normalement, ces données du passé peuvent être
décrites par une ou plusieurs lois de probabilité courantes (dans
une certaine gamme de probabilité). Il est alors intéressant de
chercher à ajuster sur ces données une, ou des lois pour
faciliter l'utilisation numérique et parfois, sous certaines
réserves, pour en tirer des informations de type probabiliste (GONOMY,
2012).
1 SRC: Le bassin versant et son
complexe
17
2.4.1. Choix d'une loi
Le choix d'une loi est une opération assez
méthodologique en ce sens qu'il faut tester quelle loi interprète
ou non bien, la tendance de l'échantillon. Il s'agit d'un test de
validité. Chaque famille de lois fait appel à un ensemble de
méthodes de détermination des paramètres de
définition de l'échantillon. La méthode qu'on utilise dans
ce document est la méthode graphique. Cette méthode consiste
à trouver un diagramme fonctionnel tel que : si l'échantillon
suit raisonnablement la loi pour laquelle ce diagramme a été
conçu, alors cela se traduira par un alignement, selon une droite,
facile à apprécier à l'oeil (GONOMY, 2012).
2.4.2. Quelques familles de lois en hydrologie
statistiques 2.4.2.1. Famille des lois normales
Cette famille de lois contient la loi de GAUSS (dite Loi
Normale), la loi de Galton (dite loi LogNormale) et leur
dérivées. Pour cette famille de loi, on ne tiendra pour ce
travail que la loi de Gauss. On sait aussi que ces lois suivent assez bien la
tendance des données moyennes (Obled et al, 2007).
Ø Loi de Gauss
C'est une loi à 2 paramètres ; la moyenne f3 et
l'écart-type á. La densité de probabilité
s'écrit :
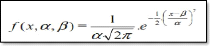
sa fonction de répartition notée N(f3, á)
s'écrit :
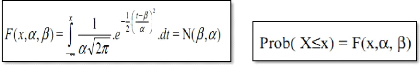
Selon cette loi, si on effectue sur x
la transformation linéaire : x ? u = (x - f3)/á, il
est démontrable que la nouvelle variable u suit encore une loi de Gauss.
(Obled et al., 2007).
18
2.4.2.2. Familles des lois exponentielles et des
valeurs extrêmes
Cette famille de lois contient les Lois exponentielles, la Loi
de Gumbel et d'autres lois de valeurs extrêmes (Weibull et GEV). Dans le
cadre de ce travail, on ne se statue que sur celle de Gumbel.
Ø La loi de Gumbel
C'est une loi très importante, qui sert dans l'analyse
fréquentielle des valeurs extrêmes, et sera notamment
l'ingrédient essentiel, en hydrologie opérationnelle, de la
méthode du Gradex pour le calcul des crues de projet (Obled et al.,
2007).
C'est une loi à 2 paramètres á et f3,
fonctions respectivement de l'écarts-type et la moyenne de
l'échantillon, donc de même dimension que x. Elle est
définie pour toute valeur de x par sa fonction de répartition
F(x, á , f3) et sa densité sont respectivement :
On désigne en général par "averse" un
ensemble de pluies associé à une perturbation
météorologique bien définie. Sa durée peut donc
varier de quelques minutes à une
Avec :
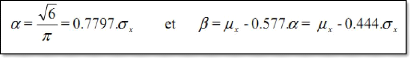
Où o?? et ????
sont respectivement l'écart-type et la moyenne de
l'échantillon, d'où :
XF = â + á.UF
|
UF = -Ln [-Ln(F)]
|
F = 1 - 1
T
|
T : temps de retour
|
|
2.5. Notion d'averse et d'intensités
2.5.1. Concepts et définition
C'est la représentation graphique de
l'intensité d'une averse en fonction de sa durée et de sa
récurrence.
19
centaine d'heures et intéresser une superficie allant
de quelques kilomètres carrés (km2) (orages) à
quelques milliers de km2 (pluies cycloniques). On définit
finalement une averse comme un épisode pluvieux continu, pouvant avoir
plusieurs pointes d'intensité. La notion d'averse est très
importante au niveau des petits bassins versants car elle s'avère
déterminante pour l'estimation des débits de crue (GEORGES,
2008).
Deux types de courbes déduites des enregistrements
d'un pluviographe (pluviogramme) permettent d'analyser les averses d'une
station :
Ø La courbe des hauteurs de pluie cumulée ;
Ø Le hyétogramme.
2.5.1.1. La courbe des hauteurs de pluie
cumulées
Représente en ordonnée, pour chaque instant
t, l'intégrale de la hauteur de pluie tombée depuis le
début de l'averse.
2.5.1.2. Le hyétogramme
Le hyétogramme est la représentation, sous la
forme d'un histogramme, de l'intensité de la pluie en fonction du temps.
Les éléments importants d'un hyétogramme sont le pas de
temps ?t et sa forme. Sa forme est en général
caractéristique du type de l'averse et varie donc d'un
événement à un autre.
2.5.2. Intensité d'une averse
L'intensité moyenne d'une averse désigne et
s'exprime par le rapport entre la hauteur de pluie observée et la
durée t de l'averse :
2.5.3. Courbe
Intensité-Durée-Fréquence (IDF) et
construction
Courbe donnant la probabilité de diverses
intensités de pluie pour diverses durées en un lieu donné.
Il s'agit souvent d'une famille de courbes, dont chacune représente une
certaine fréquence d'occurrence ou une certaine période de retour
exprimée en années.
20
2.5.3.1. Lois de la pluviosité
définissant les IDF
L'analyse des pluies a permis de définir deux lois
générales de pluviosité qui peuvent s'exprimer de la
manière suivante :
· Pour une même fréquence d'apparition
(même temps de retour) l'intensité d'une pluie est d'autant plus
forte que sa durée est courte.
· Ou encore, en corollaire, à durée de pluie
égale, une précipitation sera d'autant plus intense que sa
fréquence d'apparition sera petite (donc que son temps de retour sera
grand).
Les courbes (IDF) sont en générales
définies par ces deux lois précédentes.
2.5.3.2. Utilisation des courbes
IDF
Les courbes IDF ne sont pas une fin en soi, mais sont
construites dans un but bien précis. Elles permettent d'une part de
synthétiser l'information pluviométrique au droit d'une station
donnée et, d'autre part de calculer succinctement des débits de
projet et d'estimer des débits de crue ainsi que la détermination
des pluies de projet.
2.5.3.3. Construction des courbes
IDF
Les courbes IDF sont établies sur la base de l'analyse
d'averses enregistrées à une station au cours d'une longue
période. Les courbes obtenues peuvent donc être construites de
manière analytique ou statistique.
2.5.3.3.1. Représentation analytique
Différentes formules sont proposées pour
représenter l'intensité d'une pluie en fonction de sa
durée.
La forme la plus générale (avec T variable) est la
suivante
· Formule de Montana : i =
t?a ?
· Formule de Talbot : i =
a
(b+t)
Où a et b sont des paramètres d'ajustement en
fonction de la région.
L'intensité de la pluie peut être traduite par une
formule dérivée de celle de TALBOT:
21
2.5.3.3.2. Représentation statistique de la courbe
IDF
Les courbes IDF sont établies sur la base de l'analyse
d'averses journalières enregistrées à une station au cours
d'une longue période. L'analyse fréquentielle peut s'appliquer si
on ne présuppose pas une loi connue (de type Montana, etc.) et si on
s'intéresse à des événements rares, donc
extrêmes. Les données recueillies sont alors ajustées,
à un pas de temps choisi, à une loi statistique qui doit
décrire relativement bien la répartition des extrêmes. La
loi de Gumbel est la plus utilisée. Si l'opération est
répétée sur plusieurs pas de temps, on obtient la
variation de l'intensité avec la durée de la pluie pour
différents temps de retour, c'est à dire des courbes IDF de la
station considérée sur la période analysée. Au
niveau de ce document, on ne retient que celle-là.
2.5.4. Temps de retour d'un événement
pluvieux
Les projets d'aménagements hydrauliques ou
hydrologiques sont souvent définis par rapport à une averse type
associée aux fréquences probables d'apparition. En fait,
l'étude des grandeurs comme les précipitations, sert en
règle générale, à déterminer par exemple la
probabilité qu'une hauteur de pluie h ne soit pas atteinte ou
dépassée dans le temps. Cette probabilité est
donnée, si h est une variable aléatoire, par F(xi) =
P(h~ xi). On nomme cette probabilité
fréquence de non-dépassement ou probabilité de
non-dépassement. Son complément à l'unité
[1- F(xi)] est appelé probabilité de
dépassement, fréquence de dépassement ou encore
fréquence d'apparition. On définit alors le temps de retour T
d'un événement comme étant l'inverse de la
fréquence d'apparition de
l'événement. Soit : T = 1
P(x) ou T =
1
1-F(x)
Ainsi, l'intensité d'une pluie de temps de retour T
est l'intensité qui sera dépassée en moyenne toutes
les T années (GONOMY, 2012).
22
| 


