Comment le cadre théorique de la problématisation dans le paradigme de l'enseignement par compétences peut éclairer sur le processus engagé par un élève de lycée professionnel dans sa résolution d'un problème mathématiques

Master MEEF : Métiers de l'Enseignement, de l'Éducation et de la Formation

Option : Pratiques et Ingénierie de la Formation

Parcours: Expertise de l'Enseignement et des Apprentissages

COMMENT LE CADRE THEORIQUE DE LA PROBLEMATISATION
DANS LE PARADIGME DE L'ENSEIGNEMENT PAR COMPETENCES
PEUT ECLAIRER SUR LE PROCESSUS ENGAGE
PAR UN ELEVE DE LYCEE PROFESSIONNEL
DANS SA RESOLUTION D'UN PROBLEME MATHEMATIQUE

Mémoire présenté en vue de l'obtention du grade de master

Soutenu par

Christelle BREMAUD Le 8 juillet 2019

En présence de la commission de soutenance composée de : Magali HERSANT, directrice de mémoire

Bruno LEBOUVIER, membre de la commission

Christelle Brémaud_E179552Q

Christelle Brémaud_E179552Q

REMERCIEMENTS

A Philippe Briaud qui m'a mise sur la voie de ce master de recherche,

A Magali Hersant et Bruno Lebouvier, responsables de ce parcours EEA, qui nous ont ouverts à la richesse de la didactique, et nous ont sensibilisés aux éléments théoriques nécessaires à ce travail de recherche,

Et tout particulièrement à Magali, ma directrice de mémoire, qui m'a permis d'avancer sur ma réflexion avec son regard de didacticienne experte,

A Pierre-Charles Gauthier, alors enseignant stagiaire, qui a gentiment et efficacement accepté de prendre en charge la mise en oeuvre de certaines activités en classe avec mes élèves, pour me permettre de constituer le corpus nécessaire à cette étude,

Et plus largement, aux stagiaires de l'ESPE de ces deux dernières années, qui sans le savoir, ont nourri ma réflexion lors des activités engagées en formation le jeudi après-midi autour de la construction des compétences professionnelles,

Aux élèves de la promotion 2019 du bac Technicien en Etude du Bâtiment du lycée des métiers de Michelet, qui ont accepté d'être filmés ou enregistrés, qui m'ont fait confiance en m'autorisant à diffuser leurs productions écrites pour pouvoir mener l'analyse didactique que demandait ce travail de recherche,

A mes collègues de Michelet qui, parfois sans le savoir, ont fait avancer ma réflexion sur mon objet d'étude,

A mes amis, qui de près ou de loin ont suivi ce travail de recherche, et qui occasionnellement ou régulièrement, m'ont permis de « souffler » dans le cadre de ce travail de longue haleine, avec qui j'ai partagé des moments toujours chaleureux, qui m'ont permis de me ressourcer,

A ma famille, et tout particulièrement

à mes enfants, Arthur et Chloé, à qui je promets de me remettre à cuisiner leurs petits plats favoris, trop souvent bâclés par manque de temps ces derniers mois,

et à ma soeur, Laetitia, qui a toujours été présente dans tous les moments de ma vie où j'ai eu besoin de soutien et d'encouragements,

Merci à tous.

Christelle Brémaud_E179552Q

SOMMAIRE

INTRODUCTION : LE PROJET ET SON CONTEXTE 1. LE PARADIGME DES COMPETENCES		5 7
1.1. Quelques questions que pose cette notion de compétence	7
i. Légitimité des compétences dans l'enseignement	7
ii. Compétences : première réflexion	8
iii. Les situations	9
iv. L'évaluation	9
1.2. Où en est-on aujourd'hui dans les espaces d'enseignement ?	10
i. Un éclairage sur l'approche par compétences	11
ii. Quelques définitions : les programmes, les référentiels, le curriculum	11				iii. Les compétences dans les documents officiels
12
iv. Evaluation des compétences ou évaluation par compétences	14
v. Tension entre le prescrit et la réalité	15
vi. Pour conclure sur le sujet des compétences dans les classes	16
2. OBJET D'ETUDE ET QUESTION DE RECHERCHE		17
2.1. Eclairage sur certains termes	17
i. Les compétences dans le cadre de ce travail de recherche	17					ii. Un détour par quelques définitions pour mieux éclairer l'objet d'étude
18
iii. La problématisation dans le paradigme des compétences	19
2.2. Question de recherche	20
3. CADRES THEORIQUES POUR PENSER LES COMPETENCES		22
3.1. La dévolution pour positionner l'élève comme acteur de ses apprentissages	22

3.2. La problématisation pour mieux comprendre les processus de résolution d'une situation-

problème	23
3.3. Outil d'analyse : le losange de la problématisation	25
3.4. La problématisation dans une activité de recherche en mathématiques	26
i. L'activité de recherche dans une situation ordinaire de classe	26
ii. La situation-problème proposée aux élèves	27
iii. Contexte de mise en oeuvre	27
iv. Potentiel de problématisation de la situation et analyse a priori	28
4. METHODE DE RECHERCHE ET RECUEIL DE DONNEES		32
4.1. Les intentions	32
4.2. Conditions de mise en oeuvre de cette situation	32
4.3. Constitution du corpus	33
4.4. Méthode d'analyse du corpus	34

Christelle Brémaud_E179552Q

5. ANALYSE DU CORPUS 38

5.1. Première analyse (phase 1) des recherches individuelles 38

i. Premier relevé d'indices parmi les traces écrites (documents 1) 39

ii. Deuxième relevé d'indices parmi les traces écrites (documents 1) 41

iii. Troisième relevé d'indices parmi les traces écrites (documents 1) 46
5.2. Complément de la première analyse (phase 2) : ce que révèle l'enregistrement audio de la

phase de synthèse collective des recherches préliminaires à la résolution 49

i. Formalisation de certaines contraintes paralysantes comme sous problèmes à résoudre

(voire à évacuer) pour s'engager dans une résolution mathématique : 50

ii. Abandon de certaines contraintes non mathématiques faisant obstacles à la

construction du problème 52

iii. Recherche de données non explicites : « on n'a pas assez d'informations » 55 5.3. Deuxième analyse (phase 3) : ce que révèlent les traces écrites des recherches de protocole de

résolution lors du travail de groupe (documents 2) 57

5.4. Complément de la deuxième analyse (phase 3) : ce que révèlent les enregistrements lors du

travail de groupe pour la recherche d'un protocole de résolution 61

i. Séquences 1 et 2 : construction du problème 1 et calculs envisagés par les élèves au

regard du savoir à construire 62

ii. Séquence 3 : Construction du problème 2 68
5.5. Troisième analyse (phase 4) : comment les élèves doivent revenir sur des problèmes soulevés

précédemment mais non résolus pour répondre à la situation-problème i. Analyse des traces écrites (documents 3) ii. Analyse non formalisée de la transcription	69 69 75
6. DISCUSSION, LIMITES DE LA RECHERCHE ET PERSPECTIVES		76
6.1. Discussion	76
6.2. Limites de cette recherche :	81
6.3. Perspectives :	83
CONCLUSION		85
BIBLIOGRAPHIE		87
REFERENCES ELECTRONIQUES		88
ANNEXES		89

Christelle Brémaud_E179552Q

[5]

INTRODUCTION : LE PROJET ET SON CONTEXTE

Depuis la rénovation de la voie professionnelle en 2009, les enseignants de mathématiques et sciences physiques et chimiques des lycées professionnels ont en charge la gestion des épreuves certificatives pour les diplômes de niveau V (Certificat d'Aptitude Professionnelle (CAP) et le Brevet d'Etudes Professionnelles (BEP)) ainsi que pour celui de niveau IV (Baccalauréat Professionnel (BCP)).

Dans ce cadre, ils ont été mis face à la notion de compétences par lesquelles il s'agit d'évaluer dans des épreuves de contrôles en cours de formation¹ (CCF).

Par voie de fait, la nécessaire pédagogie appelée approche par compétences (APC) devait alors être mise en oeuvre sans que le temps et les conditions de réflexion sur sa mise en place ne permettent toujours aux acteurs de réellement s'en saisir, de voir quels en sont les modalités et tous les enjeux pour pouvoir définir clairement un cadre pédagogique et didactique pertinent.

Les cinq compétences à développer dans ces disciplines (s'approprier, analyser - raisonner, réaliser, valider, communiquer) ne présentent pas, semble-t-il de prime abord, de difficultés particulières dans leur signification première et ne font pas l'objet d'une réelle polémique à ce niveau.

La réforme est engagée depuis presque dix ans et pourtant, force est de constater que, beaucoup d'enseignants semblent encore mal à l'aise avec cette notion de compétences, tant elle est polysémique, avec un contour « flou », sans outil métrique donné pour pouvoir objectivement répondre aux exigences de l'évaluation demandée par l'Institution.

L'APC nécessite de repenser en partie les méthodes d'enseignement et donc les pratiques existantes encore parfois et depuis si longtemps sur des schémas transmissifs. D'autres focales sont alors mobilisées pour regarder l'apprenant, l'observer, l'écouter pour l'évaluer différemment, en le considérant comme acteur conscient de son apprentissage. Même si ces pratiques s'inscrivent en partie dans l'éducation dite nouvelle avec le courant constructiviste pensé par Piaget² et socioconstructiviste par Vygotski³, elles soulèvent encore bon nombre de questionnements quant à leur pertinence, leur efficacité pour répondre aux injonctions de l'Institution au sujet de leur évaluation.

Les textes officiels font apparaitre bon nombre de prescriptions et recommandations autour des compétences sans pour autant vraiment éclairer cette notion, laissant les enseignants dans un certain flou. Le travail que ces derniers engagent alors, dans ce cadre, relève plus souvent d'une tentative de mesure

¹ Annexe 1 : la grille nationale d'évaluation en mathématiques et en sciences physiques et chimiques initialement différentes pour les CAP, BEP (en certification intermédiaire dans le cursus de formation BCP) et les BCP est dorénavant unique pour les deux diplômes depuis la rentrée 2013.

² Pédagogue psychologue (1896-1980)

³ Pédagogue psychologue (1896-1934)

Christelle Brémaud_E179552Q

[6]

(comment évaluer ?) que d'une réflexion pour comprendre les enjeux didactiques et les possibilités que l'APC peut offrir en termes de choix pédagogiques pour proposer des activités qui mettent les compétences au travail. Et le sujet de l'évaluation reste encore polémique tant il soulève une certaine forme d'incompréhension, de doutes et de questions. L'approche par compétences est même encore parfois contestée en faisant valoir entre autre son « incompatibilité » avec les savoirs.

Au-delà de vouloir éclaircir ce dernier point dans cette étude, nous tenterons dans ce travail de recherche, de préciser quelques conditions pour que les compétences soient mises au travail chez les élèves dans le cadre d'activités mathématiques et comment certains cadres théoriques de la didactique

pourraient aider peut-être à mieux les éclairer, en comprendre les mécanismes voire les enjeux. Nous ciblerons notre travail sur deux des cinq compétences citées précédemment : s'approprier et analyser-raisonner. Nous considérerons en effet que ces compétences sont les premières à se mettre au travail chez l'élève dans une activité de recherche en mathématiques avant d'envisager une quelconque résolution (réaliser), une critique éventuelle des résultats (valider) et un compte rendu (communiquer), ce dernier faisant souvent obstacle à la visibilité de certaines compétences mises en jeu dans les processus de résolution de problèmes.

En préambule de ce travail heuristique, nous chercherons, au travers d'une revue de littérature sur le sujet, à définir en partie ce qu'est une compétence dans le cadre réduit de l'enseignement des mathématiques. Après une définition rapide et non exhaustive de l'approche par compétences, et d'autres termes connexes, nous pourrons alors préciser notre objet d'étude et la problématique à laquelle nous voulons répondre.

Nous ancrerons notre travail dans un cadre théorique de la didactique qui nous parait le plus adapté pour envisager un scénario a priori d'une activité à proposer à des élèves qui mobilisent les compétences qui nous intéresseront ici. Ce cadre nous permettra de préciser plus finement notre travail de recherche que nous focaliserons sur l'analyse d'une situation-problème que des élèves en classe de première bac pro ont à résoudre en mathématiques.

Nous espérons que l'analyse de notre corpus nous permettra de voir, au-delà de mettre les élèves en activité, les faire raisonner, se poser des questions, si la situation proposée a permis aux élèves de problématiser et de développer les compétences visées. Nous tenterons, le cas échéant, d'en préciser certains mécanismes dans la construction du savoir en jeu qui nous semble indissociable des compétences à développer dans le cadre de l'enseignement des mathématiques. Nous pourrons par la suite discuter de ce que les résultats de cette étude permettent d'éclairer quant aux injonctions ministérielles concernant l'évaluation en maths dans le cadre de la rénovation de la voie professionnelle de 2009.

Christelle Brémaud_E179552Q

[7]

1. LE PARADIGME DES COMPETENCES

L'émergence de la notion de compétences dans les années 1980 dans le monde de l'entreprise, semble correspondre à une volonté des directions des ressources humaines de penser et surtout d'évaluer le travail différemment. Au-delà des résultats, il s'agit d'observer également les moyens d'y arriver pour mesurer entre autre la performance des processus mis en jeu et éventuellement les optimiser. Nous ne nous intéresserons pas ici, faute de temps, aux résultats des recherches issues de la didactique professionnelle sur le sujet des compétences dans le secteur du travail, même si cela pourrait nous éclairer sur la définition de ce terme de compétence (VERGNAUD, 2004).

Après quelques prémices dans les années 1990⁴, la notion, voire le paradigme, de compétences, apparaît clairement dans le système éducatif français en 2005 via la loi d'orientation et de programme pour l'avenir de l'Ecole⁵, et plus particulièrement dans le secondaire avec la mise en place devenue incontournable du socle commun⁶ faisant partie de cette loi. Il officialise l'entrée des compétences à l'Ecole avec la volonté affichée d'un enseignement curriculaire.

Le débat s'ouvre alors sur cette nouvelle dimension à intégrer dans les pratiques pédagogiques.

1.1. Quelques questions que pose cette notion de compétence

i. Légitimité des compétences dans l'enseignement

Certains s'interrogent sur la finalité même de ce nouveau paradigme.

Bernard REY pose la question embarrassante « et si l'on avait affaire à un produit idéologique ne correspondant à rien de réel et répondant aux seuls besoins sociaux du moment ? » (REY, 1996). Loin de se restreindre à cette question, il contribuera largement à avancer sur le sujet des compétences, de leur définition et du cadre d'exercice qu'elles nécessitent.

D'autres alertent sur un certain danger que présente l'approche par compétences. Les situations d'apprentissage (enseignement par compétences) et les situations d'enseignement (enseignement par objectifs axés sur les savoirs à enseigner) « ne doivent être considérées comme antinomiques » car le « risque est grand de croire qu'apprendre de façon structurée est ennuyeux ! » écrit Gérard BOUTIN qui parle d' « amalgame paradigmatique » quand il s'agit de l'APC en éducation (BOUTIN, 2004).

⁴ Texte officiel « les cycles à l'Ecole » (1991) intégrant les instructions officielles de 1985 ( http://www.formapex.com/telechargementpublic/textesofficiels/1991_1.pdf)

⁵ Loi n° 2005-380 du 23 avril 2005 d'orientation et de programme pour l'avenir de l'école

⁶ Le socle commun de connaissances, de compétences et de culture présente ce que tout élève doit savoir et maîtriser à la fin de la scolarité obligatoire. Il rassemble l'ensemble des connaissances, compétences, valeurs et attitudes nécessaires pour réussir sa scolarité, sa vie d'individu et de futur citoyen. ( http://www.education.gouv.fr/cid2770/le-socle-commun-de-connaissances-et-de-competences.html)

Christelle Brémaud_E179552Q

[8]

Au-delà des questions polémiques sur la légitimité des compétences dans l'enseignement, sur laquelle nous ne nous attarderons pas, fleurit nombre de publications sur le sujet tentant d'éclaircir cette notion sans pour autant arriver à un réel consensus.

La lecture d'une partie de la littérature relativement récente sur ce thème, nous permettra de nous éclairer sur le terme de compétences à l'Ecole. Il ne s'agit pas d'en faire une description épistémologique, notre recherche ne portant pas sur ce sujet en lui-même. Mais il nous parait incontournable de tenter d'en éclaircir la signification, d'avoir une idée précise de ce qui nous parait faire obstacle dans ce qu'est l'approche par compétences (APC) dans le système éducatif, et d'essayer de voir en quoi elle met parfois en contradiction savoirs et compétences.

Revenir à la genèse des compétences dans l'enseignement, nous permettra peut-être de désarticuler certaines des tensions autour de cette notion afin de comprendre ce qui peut se jouer dans l'APC. Nous pourrons alors en raison, mobiliser des cadres théoriques de la didactique pour proposer une situation permettant de mieux éclairer l'APC et les compétences visées dans la mise en activités des élèves en mathématiques.

ii. Compétences : première réflexion

A la fin des années 1990, en sciences de l'éducation, PERRENOUD réinterroge la transposition didactique interne qui s'opère entre le curriculum réel (contenus de l'enseignement) et les apprentissages des élèves et préfère parler de transposition pragmatique (PERRENOUD, 1998) mettant en avant la nécessaire mise en action de l'apprenant pour l'appropriation des savoirs ou tout au moins la construction des connaissances.

Sans définir le « concept » de compétence, il l'évoque lorsqu'il explique qu'une action (réussie ou pas) nécessite des ressources cognitives mobilisées d'une part et des schèmes opératoires pour une mobilisation efficace des ressources. Il précise qu'il est impossible d'enseigner des compétences, et qu'il s'agit plutôt de « créer les conditions de leur développement, au gré de dispositifs d'entraînement ».

Il va même jusqu'à prédire l'approche par compétences dans les systèmes éducatifs (PERRENOUD, 1997). Il soulignera la pertinence du terme savoir-agir dans les nouveaux programmes québécois de 2000⁷, terme qui pour lui, permet de mieux distinguer la compétence du savoir-faire.

Par la suite, ROEGIERS proposera de lever le « malentendu » sur le terme de compétence en le distinguant de celui de capacité. Si les deux nécessitent de mobiliser un ensemble de ressources, la compétence doit avoir un « caractère finalisé » (donner lieu à une production, un résultat), en lien avec une famille de situations dans un contexte disciplinaire (ROEGIERS, 1999).

⁷ Ces nouveaux programmes préconisent l'APC à tous les niveaux d'enseignement et dans toutes les formations.

Christelle Brémaud_E179552Q

[9]

Il distingue l'approche par capacités (acquisition de connaissances et de savoir-faire généraux) de l'approche par compétences (enseignement plus spécifique, plus opérationnel) qui pour lui sont complémentaires dans la construction des savoirs à la base des connaissances des élèves. Il précise que « la recherche d'un équilibre entre ces deux approches constitue un enjeu majeur de nos systèmes éducatifs de demain » (ROEGIERS, 1999) pour ne pas opposer le développement des connaissances à celui des savoir-faire transversaux.

iii. Les situations

Parmi les prescripteurs pédagogiques, certains préconisent d'autres situations que la situation d'apprentissage (correspondant à des situations de recherche préconisée dans l'enseignement par compétences). Certains préférant l'expression « approche centrée sur le développement des compétences » (TARDIFF J., 2013) plutôt que APC, posent le problème du transfert de compétences mettant en avant la nécessité de remettre à l'épreuve les compétences travaillées dans d'autres contextes nouveaux. Ils parlent de décontextualisation et de situations de recontextualisation.

On voit alors apparaitre l'importance des situations, ou plutôt des familles de situations dans l'approche par compétences que JONNAERT d'ailleurs appelle approche située ou approche par situations car pour lui les compétences sont indissociables des situations dans lesquelles elles sont mises en jeu (JONNAERT, 2010). Même si par ailleurs CRAHAYE alerte encore sur la question des familles de situations, qui pour lui est problématique « car ni opérationnalisée, ni conceptualisée » (CRAHAYE, 2006).

Pour JONNAERT « l'apport essentiel de cette notion (de compétence), est le retour des situations, et par là celui du sens des apprentissages » (JONNAERT, 2011). Et REY explique qu' « une compétence comporte non seulement une démarche, mais aussi intrinsèquement la détermination des situations dans lesquelles on va pouvoir la mettre en oeuvre » (REY, 2014).

iv. L'évaluation

L'évaluation de compétences peut se faire par le prisme d'une appréciation très personnelle, avec un manque d'objectivité, ce qui nécessite de nouveaux critères d'observation, d'autant que « le jugement de compétences se nourrit de bien d'autres éléments que de la performance » (VERGNAUD, 2001).

D'ailleurs de son côté, CRAHAYE mettra en garde sur le côté élitiste de l'APC et surtout sur le danger d'évaluer les compétences. L'APC pour lui ne répond pas à la difficulté de certains élèves à mobiliser les ressources (connaissances) pour le transfert qu'exigent les résolutions de « tâches complexes et inédites » (CRAHAYE, 2006) dans les activités proposées pour le développement des compétences. Peut-on déclarer incompétent un élève qui a du mal à mobiliser les ressources pour les transferts nécessaires à une résolution de tâche ?

Christelle Brémaud_E179552Q

[10]

Pour DE KETELE, évaluer est « une démarche qui consiste à confronter un ensemble d'informations à un ensemble de critères en vue de prendre une décision ». Il rappellera dans une conférence en 2016 sur l'évaluation des compétences, qu'évaluer c'est :

- recueillir un ensemble d'informations suffisamment pertinentes, valides et fiables

- et examiner le degré d'adéquation entre cet ensemble d'informations et un ensemble de critères

adéquats aux objectifs fixés au départ ou ajustés en cours de route,

- en vue de prendre une décision.

Cette définition nous semble prendre tout son sens dans le paradigme des compétences alors qu'aujourd'hui aucun concept n'est réellement défini et qu'il n'existe pas encore de modèle de validation de mesure des compétences (DE KETELE et GERARD, 2005). KETELE précise que l'observation, « processus au service de l'évaluation » est une des stratégies possibles du recueil d'informations d'où l'importance des critères d'observations pour l'enseignant.

Pour ROEGIERS, si les capacités ne sont pas évaluables, les compétences le sont puisqu'elles peuvent se mesurer « à la qualité de l'exécution de la tâche, et à la qualité du résultat » (ROEGIERS, 1999). Encore faut-il savoir ce que l'on entend par « qualité de l'exécution de la tâche » ce qui remet en perspective l'importance de bien définir ce que l'on met à l'observation pour recueillir suffisamment de données pertinentes, viables et fiables pour pouvoir faire cette appréciation que demande l'évaluation. Nous notons au passage qu'il distingue la situation d'exploration de la situation d'intégration (dite également situation d'apprentissage de l'intégration), cette dernière permettant à l'élève de remobiliser la compétence visée et il précise que si l'on doit évaluer par compétences, la situation doit être de ce

type.

Bernard REY affirme de son côté que « l'approche par compétences ne facilite pas l'évaluation... qu'elle en subvertit les instruments traditionnels et en retour l'exigence d'évaluation vient interroger la notion de compétences » (REY, 2014, p.88). Car pour lui « La tâche proposée doit être inédite et complexe... et sa réalisation requiert donc un temps important » (ibid., p.89)... remettant en cause l'assurance de la justesse d'une évaluation de compétence.

Nous ne faisons ici qu'évoquer cet aspect de l'évaluation dans le cadre de l'APC pour peut-être mieux répondre par la suite à certaines questions que cette approche pose dans notre objet d'étude. Mais nous ne nous intéresserons ici, dans le cadre réduit de cette recherche, qu'aux démarches et processus engagés par un élève pour résoudre un problème, ce qui nous semble être une « condition indispensable pour pouvoir, dans l'enseignement... aider le sujet à construire ses compétences » (REY, 2014).

1.2. Où en est-on aujourd'hui dans les espaces d'enseignement ?

Force est de constater que malgré une littérature conséquente sur la notion de compétence, il n'existe actuellement aucun modèle théorique permettant de définir unanimement cette notion. Et les

Christelle Brémaud_E179552Q

[11]

nombreux écrits sur le sujet ne contribuent pas toujours à sa clarification d'autant que les qualificatifs sont nombreux : « compétences de base », « clé », « transversales, « spécifiques ».

i.

Un éclairage sur l'approche par compétences

On rappelle ici quelques définitions (issues des corps d'inspection⁸) pour mieux éclairer les termes utilisés dans la définition de l'approche par compétences faite par la suite. Nous précisons que dans le cadre de ce travail de recherche, « connaître » n'est pas « savoir », et le terme connaissance sera dans la recherche menée ici, utilisé comme ce qu'il reste chez l'élève du savoir enseigné (MARGOLINAS, 2014).

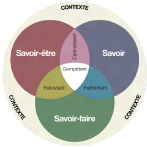
L'approche par compétences peut alors se définir en partie comme une pratique pédagogique visant à construire l'enseignement sur la base d'une conjugaison entre savoirs, savoir-faire et savoir-être, évalués lors de réalisation de tâches complexes utilisant les compétences à travailler comme point d'entrée dans la conception de l'activité.

Le travail de l'enseignant s'est structurellement

transformé sans que les conditions pour exercer son activité ne l'aient été. Les élèves sont les mêmes, les programmes de mathématiques n'ont pas été modifiés en profondeur (au regard de l'APC alors même

que l'on parle plus de curriculum que de référentiel et de programme) et ils laissent encore cette liberté pédagogique souvent bien embarrassante quand il s'agit de penser et agir différemment dans ce paradigme des compétences.

ii. Quelques définitions : les programmes, les référentiels, le curriculum

L'article 5 de la loi d'orientation du 10 juillet 1989 précise que « les programmes définissent les savoirs essentiels (en parlant toujours de connaissances plutôt que de savoirs) qui doivent être acquis ainsi que les méthodes qui doivent être assimilées. Ils constituent le cadre national au sein duquel les enseignants organisent leurs enseignements en prenant en compte les rythmes d'apprentissage de chaque élève. »

La charte des programmes élaborée par le Conseil Supérieur des Programmes en 2014, reprécise le caractère officiel des programmes : « Les programmes d'enseignement s'inscrivent dans le cadre de

⁸ Marie-Blanche MAUHOURAT et Frédéric THOLLON Inspecteurs Généraux de l'Education Nationale

Christelle Brémaud_E179552Q

[12]

la loi, non seulement en ce qu'elle définit leur mode d'élaboration, mais aussi en ce qu'elle fixe un certain nombre de principes ou de prescriptions qui s'imposent à eux ».

Le terme de référentiel apparait dans les années 1980 dans le monde professionnel mais plus tardivement dans le monde éducatif avec le socle commun de connaissances et de compétences⁹. Publiés sous forme de Bulletins Officiels, les référentiels (intégrant référentiel de formation et référentiel de certification) sont élaborés à partir des programmes sous forme d'un ensemble articulé de capacités, de connaissances dans une discipline, explicitant les attendus et la progression éventuelle des apprentissages. Il est la partie technique intégrante d'un curriculum prescrit par la loi de refondation de l'école de la République du 08 juillet 2013 avec les quatre parcours éducatifs¹⁰ visant à favoriser la continuité des apprentissages et à créer les conditions de réussite tout au long de la scolarité.

Si le programme est un produit fini, le curriculum est un processus. Les premiers sont clairs et précis pour les enseignants qui avec un peu d'expérience savent à quel niveau de complexité situer leurs interventions. Mais une lecture linéaire des programmes n'est plus en adéquation avec l'approche par compétences prescrite implicitement par les textes officiels. Une progression dite spiralée¹¹ des programmes doit alors être envisagée au travers de différentes situations pour permettre aux élèves de développer les compétences citées dans les textes officiels (sans pour autant être définies et sans que les modalités d'un enseignement adapté ne soit précisées).

Les termes de référentiel disciplinaire et curriculum de formation remplacent alors peu à peu ceux de programmes et des documents dits d'accompagnement, voire vade-mecum, sont publiés sur les sites officiels pour éclairer certains points des référentiels voire faire des propositions de mise en oeuvre.

iii. Les compétences dans les documents officiels

Dans les référentiels de formation post rénovation de la voie professionnelle (2009), les compétences visées ne sont pas toujours clairement définies. Christian ORANGE précise même que leur définition dans les disciplines scientifiques, « va rarement au-delà de la tautologie ou des évidences » et parle « d'intentions banales et bien générales » (ORANGE, 2012).

Dans les référentiels de l'enseignement professionnel¹², les compétences à développer sont déclinées en capacités pour lesquelles les tâches préconisées sont précisées ainsi que les conditions de réalisation, les connaissances et attitudes associées et enfin les critères d'évaluation.

⁹ Loi n° 2013-595 du 8 juillet 2013 d'orientation et de programmation pour la refondation de l'école de la République

¹⁰ Parcours citoyen, parcours d'éducation artistique et culturelle, parcours avenir, parcours santé

¹¹ Une progression "en spirale" permet à l'élève de revenir plusieurs fois sur la même notion au cours de la formation, lui laissant ainsi le temps de la maturation, de l'assimilation et de l'appropriation. (Extrait du Bulletin officiel spécial n° 2 du 19 février 2009)

¹² Annexe 2 : extrait d'un référentiel d'enseignement professionnel

Christelle Brémaud_E179552Q

[13]

En enseignement général, dans le programme de mathématiques et sciences physiques et chimiques de lycée professionnel, on relève souvent dans son préambule, le terme de compétence avec des qualificatifs qui lui sont associés sans plus de description et/ou explicitation:

- compétences du programme, compétences exigibles,

- les compétences scientifiques doivent être construites, ... pour développer des compétences en mathématiques..., compétences expérimentales de base,

- réinvestir ces compétences comme outils de résolution,

- compétences en calcul mental, compétences pour étudier et exploiter de nouvelles fonctions, compétence de géométrie,

- compétence en prise d'informations.

Le mot compétence revient de façon récurrente sans plus d'informations sur le contexte dans lequel ces compétences doivent être développées, ni de réel éclairage sur les conditions de réalisation voire de critères d'évaluation.

Les cinq compétences à développer et à évaluer sont mentionnées une seule fois dans ce référentiel et ne sont détaillées que dans la grille nationale d'évaluation¹³ (seul document considéré comme référentiel des compétences en maths sciences en lycée professionnel), à partir de laquelle doivent se réaliser les épreuves certificatives laissant les acteurs de leur mise en oeuvre dans une nébuleuse tant sur la définition de ces compétences que dans le choix pédagogique pour leur mise au travail. Même si comme nous l'avons vu, une compétence ne se réduit pas à une capacité, paradoxalement les seules indications que donne actuellement cette grille (dans le référentiel de certification) déclinent les compétences en capacités :

Compétences :	Capacités à :
S'approprier	Rechercher, extraire et organiser l'information.
Analyser Raisonner	Émettre une conjecture, une hypothèse. Proposer une méthode de résolution, un protocole expérimental.
Réaliser	Choisir une méthode de résolution, un protocole expérimental. Exécuter une méthode de résolution, expérimenter, simuler.
Valider	Contrôler la vraisemblance d'une conjecture, d'une hypothèse. Critiquer un résultat, argumenter.
Communiquer	Rendre compte d'une démarche, d'un résultat, à l'oral ou à l'écrit.

Le reste du programme liste les objectifs d'enseignement relatifs aux savoirs à enseigner, en décrivant distinctement d'une part les capacités à développer et d'autre part les connaissances à acquérir pour les différents domaines du programme. Certains documents d'accompagnement de cette grille¹⁴

¹³ Annexe 1

¹⁴ Annexe 1 bis : DOCUMENT D'ACCOMPAGNEMENT de la grille nationale d'évaluation en mathématiques et en sciences physiques et chimiques

Christelle Brémaud_E179552Q

[14]

proposés par les corps d'inspection, en donnent une explicitation dans laquelle on retrouve cette tendance à réduire les compétences aux seules capacités détaillées.

Malgré les documents d'accompagnement pour expliciter les compétences, les référentiels dans leur forme actuelle, tiennent du paradigme de l'enseignement tel que décrit par TARDIF (TARDIF, 2013) alors que le modèle d'enseignement prescrit par l'Institution se veut curriculaire et donc dans le paradigme des compétences d'où une certaine incohérence peut-être aussi en partie à l'origine du malaise des acteurs dans la mise en oeuvre de l'APC.

iv. Evaluation des compétences ou évaluation par compétences

Le sujet de l'évaluation des compétences est encore un vaste sujet en réflexion laissant les enseignants oeuvrer de façon souvent expérimentale sans avoir le temps nécessaire et la démarche de s'emparer des travaux issus de la recherche pouvant éclairer.

Il nous semble important à ce stade de notre réflexion, de distinguer l'évaluation DES compétences de l'évaluation PAR compétences. Les documents institutionnels sont souvent ambigus au sujet de ce qui pourrait apparaitre comme une nuance entre l'évaluation DES compétences et l'évaluation PAR compétences

En effet, nous pouvons relever, par exemple, 325 fois le mot « compétence(s) », 31 fois le mot « évaluer » et 97 le mot « évaluation » dans les 51 pages du document d'accompagnement donnant des « repères pour la mise en place du livret personnel de compétences au collège »¹⁵ avec, pour illustrer l'ambiguïté évoquée ici :

- « évaluer positivement l'acquisition de compétences » (p. 32),

- « évaluer une compétence » (p. 13),

- « s'assurer que l'évaluation porte bien sur des compétences » (p. 10),

- « évaluer les compétences » (p. 2), « évaluer positivement des connaissances et des capacités »

(p. 14), ...

Autant d'extraits pour faire apparaitre qu'il est question explicitement d'évaluer LES compétences dans ce document alors même que dans le document d'accompagnement : « Former et évaluer PAR compétences dans le cadre des activités expérimentales »¹⁶, il est question d'évaluer PAR compétences. Pour information et pour faire un parallèle avec ce qui précède, nous relevons dans ce document 24 fois le mot « compétence(s) », 5 fois le mot « évaluer » et 8 fois le mot « évaluation » dans les 11 pages du document. Ces mots clés interviennent, dans une proportion moindre certes dans ce document mais de façon significative, en précisant (pour illustration) :

¹⁵ https://media.eduscol.education.fr/file/socle_commun/97/5/ReperesLivretcompetences_145975.pdf

¹⁶ https://media.eduscol.education.fr/file/PC/66/5/Ressources PC former evaluer competences exp grilles 144665.pdf

Christelle Brémaud_E179552Q

[15]

- « évaluer PAR compétences » (p.2) mais aussi « l'acquisition des compétences ne peut se faire

sans une évaluation de leur maîtrise » (p.2) distinguant plus subtilement l'acquisition de compétences de leur évaluation (sans plus de précision pour lever l'ambigüité pointée ici),

- « évaluer les acquis » et non évaluer les compétences (p.2).

Se poser la question de la nuance entre ces deux appellations nous permet de pointer l'importance des critères d'observations et aussi de nous poser la question de la corrélation entre la lisibilité de ces critères (et par conséquence des objectifs réels de l'enseignant) et de l'évaluation des compétences et/ou de l'évaluation des savoirs sous prétexte de compétences (évaluation par compétences). Ce manque de clarté dans cette corrélation nous semble être une des raisons de tension lorsqu'il s'agit de l'APC.

En effet, actuellement les grilles d'évaluation, pensées et construites activité par activité par les enseignants auteurs des sujets proposés en CCF à leurs élèves et également évaluateurs de ces épreuves certificatives, portent le plus souvent sur des critères de résultats à obtenir¹⁷ au regard des savoirs visés mais non explicitement sur la façon d'y parvenir. Les grilles d'observation (et/ou d'évaluation) pourraient révéler une certaine forme d'évaluation des compétences (plus qu'une évaluation par compétences) si les critères de réussite ne portaient pas exclusivement sur des résultats à obtenir mais bien sur des preuves que la compétence a été mise au travail¹⁸ mais force est de constater qu'il n'en est pas toujours ainsi. Nous pouvons nous interroger sur ce point et réfléchir sur les causes de ce que nous pourrions ici caractériser de « nébuleuse » tant ce qui nous parait évaluable n'est pas en adéquation avec une évaluations des compétences. Nous pourrons y revenir en fin d'étude pour voir comment ce travail de recherche pourrait apporter certaines réponses à ce sujet que l'on qualifie très souvent d' « usine à gaz » tant il parait peu clair et donne lieu à bon nombre d'expérimentations diverses et variées lorsqu'il s'agit d'évaluer dans le cadre des CCF (entre autre).

v. Tension entre le prescrit et la réalité

Au-delà d'une définition consensuelle à trouver sur la notion de compétences, il serait déjà nécessaire que l'intention institutionnelle en plus d'être explicite, soit lisible par l'ensemble des acteurs. « Le Curriculum d'un système éducatif doit être unifié et cohérent » (JONNAERT, 2009).

Michèle DELL'ANGELO s'intéresse en 2011 dans son article « les tâches complexes et l'évaluation de compétences dans l'investigation » à différents documents d'accompagnement sur le sujet des programmes récents (relatifs aux maths, physiques et chimie, SVT et technologie), et à différents outils mis à disposition des enseignants pour évaluer les compétences. Après une analyse de 69 tâches (situations) complexes répertoriées sur différents sites institutionnels, elle pointe le « flou qui entoure la vocation de ses activités » et conclut que peu de ces situations permettent à l'élève de se poser

¹⁷ Annexes 14 bis et 14 ter

¹⁸ Annexe 14

Christelle Brémaud_E179552Q

[16]

lui-même des questions, énoncer des hypothèses et que rares sont celles qui intègrent les attitudes en supposant que ces dernières « entrent dans les rubriques de façon explicite (et que) les enseignants s'interrogent sur les moyens de les construire ». « En fait, tout reste à améliorer ...C'est toute la construction des programmes qui est peut-être à repenser » (DELL'ANGELO, 2011).

Maggy SCHNEIDER et Alain MERCIER (SCHNEIDER M, et MERCIER A., 2014) vont même jusqu'à mettre en garde en soulignant que « le travail pédagogique d'un curriculum didactiquement cohérent et socialement acceptable est un chantier politique et technique qui devrait être ouvert, faute de quoi, les réformes des systèmes d'enseignement sont et demeureront pour les professeurs la source d'injonctions paradoxales et paralysantes ». Et JONNAERT précise également, qu'« avant d'entrer dans un processus de réécriture de programmes de formation, un certain nombre d'activités, de débats et de réflexions doit avoir eu lieu. Une réforme curriculaire ne se réduit pas à une simple écriture de programmes de formation. Les programmes ne sont que des moyens au service de finalités présentées dans différents documents curriculaires, leur analyse est préalable à l'élaboration de programmes de formation » (JONNAERT, 2010).

vi. Pour conclure sur le sujet des compétences dans les classes

Autour des compétences, Xavier ROEGIERS (2010) considère qu'aujourd'hui il y a consensus sur le fait que les contenus d'enseignement vont au-delà des savoirs (assimilés aux connaissances dans les textes officiels institutionnels) et savoir-faire (assimilés aux capacités), que l'élève est acteur des apprentissages et que le savoir-agir en situation est valorisé. Il précise que l'Ecole ne peut plus se passer de mettre les situations complexes au centre des apprentissages.

Bernard REY (2014, pp. 92-94) propose, lorsque les conditions sont suffisantes pour pouvoir observer des compétences en action, d'observer si l'élève

- Cherche à interpréter la situation qu'il a à traiter,

- Fait appel pour cela à un système de références extérieur à la situation et/ou aux savoirs scolaires,

- Maitrise les procédures nécessaires à l'accomplissement des actions nécessaires,

- Possède les savoirs informatifs nécessaires à l'accomplissement des actions.

Ceci « pour faire la différence entre une manière compétente d'aborder une situation et une manière non compétente » (REY, 2014, p. 93).

La question épineuse pour l'enseignant, reste toutefois comment faire cette différence ? Pour cela souvent ils créent des outils d'observation¹⁹ qui renseignent plus précisément les élèves sur les attendus en termes de compétences lorsqu'ils sont mis en situation de résolution de problème.

¹⁹ Extrait de l'Annexe 3 : Grille détaillée des compétences conçue par l'auteure de cette recherche et distribuée aux

élèves en début de formation (avec préambule sur les attitudes, savoir-être, requises) inspirée du manuel scolaire Mathématiques CAP groupement A et Editions Foucher, 2016, pp.5 et 6.

Christelle Brémaud_E179552Q

[17]

2. OBJET D'ETUDE ET QUESTION DE RECHERCHE

2.1. Eclairage sur certains termes

i. Les compétences dans le cadre de ce travail de recherche

Nous allons tenter de dépasser les doxas sur les compétences, voire les polémiques que soulève cette notion dans le cadre scolaire (DEL REY A., 2009), pour mener un travail heuristique sur le(s) processus mis en jeu lors d'une activité construite dans le cadre de l'approche par compétences.

On convient ici, que la compétence est la « capacité d'agir efficacement dans un type défini de situations, capacité qui s'appuie sur des connaissances, mais ne s'y réduit pas » (PERRENOUD, 1998). Elle nécessite la mobilisation d'un ensemble de ressources (savoirs, savoir-faire, savoir être) en vue de résoudre une situation complexe appartenant à une famille de situations problèmes (ROEGIERS, 2010).

Il y a consensus sur le fait que la construction d'une compétence est avant tout un processus d'adaptation à des situations (JONNAERT, 2011) et que cela se réalise dans l'action. Nous ne nous interrogerons pas ici sur la pertinence de ces situations, ni sur la fiabilité des résultats observés au travers des performances de l'élève, ni sur la validité de leur évaluation que DE KETELE et GERARD définissent comme étant « l'adéquation entre ce que l'outil mesure et ce qu'il prétend mesurer » (DE KETELE et GERARD, 2005).

Si sur le sujet des familles de situations, beaucoup de questions restent en suspens, Bernard REY montre qu'il n'y a pas incompatibilité entre savoirs et compétences. Et il va plus loin en affirmant que ces dernières se construisent par le savoir « textualisé » (REY, 2014, p.64). Il met ainsi en évidence la pertinence des situations-problèmes qui par le biais de la problématisation permettent d'observer le processus de construction de la compétence pour mieux l'évaluer.

Maggy SCHNEIDER considère le savoir comme une « compétence technique forte » (SCHNEIDER M, et MERCIER A., 2014) et Christian ORANGE et Michel FABRE, les savoirs scientifiques comme « des compétences pour maitriser des problèmes » (FABRE M., ORANGE C., 1997).

Le champ d'investigation semble alors très large lorsque l'on parle d'approche (voire d'apprentissage) par compétences. Nous ne pourrons examiner dans le cadre réduit de ce travail de recherche, en quoi l'APC peut modifier la posture de l'élève quant à son engagement dans les apprentissages. Mais nous postulons qu'il n'y a pas d'apprentissage par compétences s'il n'y a pas certaines attitudes de l'ordre du « vouloir comprendre » (REY, 2014, p.77). Nous nous limiterons alors à étudier quand et comment une compétence se met au travail dans le cadre de l'apprentissage par situations-problèmes que nous définirons dans le paragraphe suivant.

Christelle Brémaud_E179552Q

[18]

Nous proposerons donc une situation de recherche dite situation-problème, permettant aux élèves de construire un raisonnement en vue de sa résolution. Plutôt que de ne nous attacher qu'aux résultats de la résolution, nous observerons la façon dont les élèves se sont appropriés ce problème, comment ils réfléchissent à sa résolution, c'est-à-dire comment ils l'analysent et raisonnent pour envisager d'y répondre. Cela nous permettra également de discuter des conditions pour que s'engagent les processus en jeu. Même si notre recherche s'envisage dans le paradigme des compétences, ne pouvant prétendre apporter de réponses à ce que soulève la notion de compétences de façon générale, nous élargirons notre enquête sur les enjeux didactiques que peut offrir une activité pensée dans le cadre d'un travail par compétences.

ii. Un détour par quelques définitions pour mieux éclairer l'objet d'étude

En mathématiques, une situation complexe n'est pas nécessairement compliquée et doit permettre à l'élève d'entrevoir des possibilités de résolution. Ce critère d'accessibilité apparente est une condition pour que l'élève s'engage dans l'activité proposée. Traiter une situation complexe fait appel à l'analyse de l'élève pour envisager des étapes dans son processus de résolution pour répondre à la situation donnée. Il s'agit alors pour l'élève de mobiliser à bon escient divers savoirs (non nécessairement scolaires), savoir-faire et savoir-être (attitudes) et la mise en situation de résolution d'une situation complexe conduit souvent l'élève à choisir et utiliser différentes ressources.

Un problème en mathématiques sera envisagé dans ce travail de recherche, comme une question à laquelle la réponse ne va pas de soi pour l'élève. Il nécessite un traitement des données, des allers retours entre certitudes et doutes, entre tentatives, erreurs et réussites, chaque étape mobilisant différentes procédures ou savoirs qui peuvent être élémentaires.

Nous parlerons de situation-problème quand il s'agit de traiter une situation d'apprentissage organisée autour d'un savoir à construire selon la définition qu'en donne Christian ORANGE. « Une situation-problème est une situation où l'élève est confronté à un problème dans lequel il peut s'engager... mais qu'il ne peut résoudre car ses connaissances font obstacle au savoir nécessaire à cette résolution ; la situation doit de plus permettre aux élèves de décider par eux-mêmes de la réussite ou de l'échec de leur tentative pour résoudre le problème et les conduire à dépasser l'obstacle pour accéder aux savoirs visés » (ORANGE C., 2012, p.33).

Cette situation présente alors un défi à la portée de l'élève dans la mesure où la résolution du problème à traiter (une fois identifié) peut se faire avec des connaissances et savoir-faire antérieurs. L'objectif d'une telle activité étant alors de faire apparaître le savoir en jeu comme l'outil mathématique le plus performant pour cette résolution. Pour l'enseignant, l'important n'est alors pas que l'élève produise LA bonne réponse en évitant des erreurs, mais de lui permettre, une fois qu'il a accepté la non évidence immédiate de la solution, d'engager différentes tentatives pour élaborer un raisonnement vers

Christelle Brémaud_E179552Q

[19]

la réponse. Nous supposons alors qu'un élève qui s'est engagé positivement dans cette situation de recherche, a mobilisé les compétences d'appropriation, d'analyse, de raisonnement visées dans le référentiel de mathématiques actuellement en lycée professionnel dans la mesure où ces compétences paraissent être celles en jeu dans toute résolution d'un problème en mathématiques. Il nous paraît alors important que l'enseignant traduise clairement ses intentions sous-jacentes en objectifs à évaluer pour que l'observation de ce travail par compétences se fasse de façon le moins aléatoire possible²⁰.

Une fois le concept de problème clarifié, comment comprendre alors ce qu'est « une problématique », terme qui revient de façon récurrente lorsque l'on parle de problème à résoudre en mathématiques ? La définition qu'en donne le Larousse « Ensemble des questions, des problèmes concernant un domaine de connaissances ou qui sont posés par une situation » mérite d'être explicitée dans un cadre disciplinaire. Nous considérons que la (ou les) problématique(s) d'un problème de mathématiques peut/peuvent être révélée(s) par la construction de sa résolution. En cela la définition proposée par le Petit Robert nous parait plus explicite dans notre étude : « La problématique est l'art, la science de poser les problèmes. C'est un questionnement aboutissant à un ensemble de problèmes dont les éléments sont liés ». Nous distinguerons l'exposé de ce questionnement (la problématique) du questionnement en lui-même pour lequel nous parlerons de problématisation. La problématique expose la manière dont le problème central se décompose en sous problèmes unis par des liens à définir (NONNON, 2002).

Nous donnons ici comme première définition de la problématisation²¹, « action volontaire, de définir un problème dans le but de l'analyser et à terme de le résoudre en expliquant son raisonnement. Ce qui revient à envisager la problématisation comme étant un processus permettant de passer d'une question de départ à des hypothèses de travail précises procédant par étapes successives d'exploration des possibles et de choix d'options qui délimitent pas à pas le travail entrepris. La problématisation est un cadre théorique de la didactique que nous développerons plus précisément dans le chapitre suivant.

iii. La problématisation dans le paradigme des compétences

Si la problématique n'est pas encore vraiment un terme clé dans les Instructions Officielles pour le lycée professionnel, la notion de problème est largement évoquée pour mettre l'élève en situation de « raisonner ». Nous notons dans les nouveaux documents d'accompagnement de la transformation de la voie professionnelle pour la rentrée 2019²², l'apparition de termes plus explicites sur ce sujet, comme « situations professionnelles problématisées ».

²⁰ http://www.pratiquemath.org/spip/spip.php?article283

²¹ https://www.linternaute.fr/dictionnaire/fr/definition/problematisation/

²² Vade-mecum : La mise en oeuvre de la co-intervention (maths/sciences et enseignement professionnel) préconise

« l'analyse de situations problématisées, déterminées conjointement par les deux professeurs à partir du référentiel d'activités professionnelles »

Christelle Brémaud_E179552Q

[20]

Mais nous touchons ici un point critique de l'enseignement car bien souvent la problématisation est implicitement envisagée (à défaut d'être nommée) comme moyen de mobiliser des connaissances et des capacités personnelles à l'élève plutôt que comme démarche à enseigner.

« Les notions de problème et de problématisation fonctionnent ainsi comme norme, au sens d'un principe régulateur qui oriente le travail des enseignants et les objectifs qu'ils se donnent... Mais cet objectif reste en fait peu opérationnalisable, il donne souvent lieu à des recommandations ou une imprégnation, un esprit plus qu'à une prise en charge explicite,... on n'enseigne pas bien à problématiser » (NONNON E., 2002).

Nous nous interrogerons dans cette étude, sur ce que les traces écrites des élèves renseignent quant à la problématisation dans le cas d'une pratique ordinaire de mise en activité de recherche.

Nous pourrons nous poser également la question du manque de cohérence lorsqu'il s'agit d'évaluer et qu'un élève ayant produit un résultat considéré comme pertinent, n'a renseigné en rien dans sa trace écrite sur ses procédures de résolution. Doit-on alors tacitement déclarer que l'élève a su « s'approprier » la situation à traiter, a su « analyser » le problème, à la seule constatation qu'il a réussi à « réaliser » pour parvenir à une solution ? Enseigner et évaluer par compétences ne peut se satisfaire de ce raccourci.

2.2. Question de recherche

Les enseignants constatent que les élèves de lycée professionnel ont souvent (pour ne pas dire toujours) des difficultés à formaliser par écrit un raisonnement en mathématiques pour rendre compte de la démarche de résolution d'un problème donné alors qu'ils se sont mis au travail, se sont posés des questions et parfois parviennent même à un résultat correct.

Comment peut s'apprécier alors leur analyse et la façon dont ils se sont appropriés la situation ?

Enseigner par compétences, permet de les mettre régulièrement en activité pour travailler entre autre le « communiquer » mais là n'est pas le coeur de notre sujet d'étude. Nous n'en parlons que pour mettre en perspective notre postulat qu'un élève raisonne, se questionne pour s'emparer des problèmes qui se posent à lui, et les résoudre, malgré les difficultés récurrentes à rendre compte de ce raisonnement.

Nous pourrons dans la discussion à laquelle donnera lieu l'analyse du corpus sur l'activité de l'élève, revenir plus précisément sur cette difficulté à « communiquer » qui peut être un réel obstacle dans l'évaluation que demande l'Institution dans le cadre des contrôles en cours de formation (CCF) que représentent les épreuves certificatives. Cela nous permettra également de mettre en perspective les conditions pour qu'une épreuve dite d'évaluation par compétences prenne tout son sens.

Pour nous recentrer sur notre objet d'étude, l'expérience montre qu'à partir du moment où l'élève accepte de s'engager dans un travail de résolution d'une situation-problème, on note un certain nombre de questionnements dans la construction de son raisonnement quel que soit le problème dévolu. Nous

[21]

Christelle Brémaud_E179552Q

chercherons ici à observer ce questionnement car observer s'il y a compétence c'est regarder la performance au travers du résultat auquel parvient l'élève mais aussi la façon dont il y arrive. D'où notre question de recherche :

COMMENT LE CADRE THEORIQUE DE LA PROBLEMATISATION
DANS LE PARADIGME DE L'ENSEIGNEMENT PAR COMPETENCES
PEUT ECLAIRER SUR LE PROCESSUS ENGAGE
PAR UN ELEVE DE LYCEE PROFESSIONNEL
DANS SA RESOLUTION D'UN PROBLEME MATHEMATIQUE

Christelle Brémaud_E179552Q

[22]

3. CADRES THEORIQUES POUR PENSER LES COMPETENCES

L'élaboration et la mise en oeuvre des activités s'envisagent dans ce travail de recherche, dans le cadre de la théorie des situations didactiques. En effet, nous considèrerons dans cette étude, que les compétences en question ici pour résoudre un problème en mathématiques, ne se mettent au travail que s'il y a adaptation au milieu, dans le cadre d'un contrat didactique implicitement établi pour que l'élève s'engage dans l'activité. Nous ne développerons ce cadre théorique que sommairement dans la mesure où nous choisirons celui de la problématisation pour analyser notre corpus.

3.1. La dévolution pour positionner l'élève comme acteur de ses apprentissages

Guy BROUSSEAU dans la théorie des situations didactiques, définit la dévolution comme étant un acte par lequel l'enseignant fait accepter à l'élève la responsabilité d'une situation d'apprentissage (adidactique). Il définit également la situation adidactique comme étant une situation didactique (construite avec des contenus et objectifs d'enseignement clairs et précis relatifs à un savoir visé) qui ne fait pas apparaitre directement à l'élève l'intention d'enseignement. Elle peut alors paraitre non didactique à l'élève qui doit alors faire des choix, prendre des décisions, engager des stratégies et évaluer leur efficacité pour parvenir à un résultat.

La dévolution correspond alors à une démarche pédagogique (mais aussi à un choix de gestion de classe) favorisant les initiatives des élèves qui en s'emparant d'un problème vont entreprendre de nouveaux apprentissages (consciemment ou pas). Elle doit être anticipée, contrôlée et lisible pour les élèves. L'enseignant reste le concepteur des apprentissages visés et détermine ce que tous doivent apprendre.

Dans ce travail de recherche, l'activité dévolue aux élèves leur est implicitement présentée comme un objet d'apprentissage dans le cadre d'un contrat didactique déjà éprouvé entre l'enseignant et les élèves en relation avec le savoir. Nous envisageons ici le contrat didactique comme défini par BROUSSEAU, étant ce qu'attendent les élèves de l'enseignant et inversement relativement à un contenu d'enseignement : « un contrat qui détermine (explicitement pour une petite part, mais surtout implicitement) ce que chaque partenaire, l'enseignant et l'enseigné, a la responsabilité de gérer et dont il sera d'une manière ou d'une autre responsable devant l'autre. Ce qui nous intéresse ici est le contrat didactique, c'est-à-dire la part du contrat qui est spécifique du "contenu" : la connaissance mathématique » (BROUSSEAU, 1983).

Dans cette étude, les élèves ont régulièrement en charge de résoudre des situations-problèmes proposées par l'enseignante (auteure de ce mémoire) et toujours basées sur des contenus d'enseignement.

Christelle Brémaud_E179552Q

[23]

Nous soulignons de façon non exhaustive que l'acte de dévolution

- impose à l'enseignant de se surveiller pour ne pas donner la solution en même temps, tout en
veillant à ne pas laisser l'élève chercher seul sans aide (ce qui peut parfois créer des paradoxes dans le contrat didactique établi),

- nécessite de reconsidérer le statut de l'erreur dans les apprentissages. Il faut accepter que les
élèves ne répondent pas exactement comme envisagé a priori, et les solutions construites par les élèves doivent souvent être interprétées et traitées pour être raccrochées aux objectifs d'apprentissage. En effet si l'enseignant dévolue, il a préalablement défini ce qu'il voulait que les élèves apprennent. La dévolution ne s'improvise pas et la définition des contenus d'enseignement reste un préalable incontournable.

La situation-problème semble répondre aux conditions nécessaires pour une dévolution

permettant entre autre (dans le cadre de cette recherche) à l'élève d'exercer ces compétences. Nous considérerons ici qu'observer les compétences s'approprier et analyser-raisonner quand un élève aborde et traite une situation-problème, doit se faire en cherchant à comprendre les processus en jeu. Il nous parait alors pertinent de mobiliser le cadre théorique de la problématisation tel que défini par Christian ORANGE et Michel FABRE.

3.2. La problématisation pour mieux comprendre les processus de résolution d'une situation-problème

Si la résolution d'un problème nécessite la construction de problématiques alors problématiser relève d'une procédure, un (des) choix à faire, une stratégie. Nous entendons problématique ici dans le sens où « construire une problématique consiste à élaborer un énoncé de problème » (FABRE, 2017). Nous avons présenté précédemment la problématisation comme étant le processus mené dans le cadre d'un travail heuristique pour résoudre un problème donné. Mais il ne suffit pas de se poser des questions pour résoudre un problème.

Nous précisons ici les éléments de ce processus qui se définit comme le cheminement fait lors du questionnement qui s'impose dans la résolution du problème, entre les faits (ou données) et les nécessités (ou conditions) qui en découlent en raison d'explications.

Les faits et les nécessités ne vont pas toujours de soi (données et conditions parfois non explicitées par l'énoncé du problème) et dans ce cas, ils peuvent faire suite à une construction de l'élève dans une critique raisonnée de ces questions.

ORANGE distinguent trois registres pour catégoriser ces éléments constituant l'enquête menée :

Christelle Brémaud_E179552Q

[24]

- Le registre explicatif (ou paradigme): dans lequel s'organisent les explications, les solutions du

problème travaillé.

- Le registre empirique : où sont notés les faits repérés comme pertinents pour le

problème,

- Le registre des modèles : dans lequel se développent les nécessités mais où ne sont
notées que celles construites.

Les nécessités apparaissent alors comme étant les conditions de possibilités des explications ou solutions du problème. Elles apparaissent en raison d'un cadre explicatif mobilisé (consciemment ou non) qui est didactiquement important car structurant les explications des élèves et donc leur façon de travailler les problèmes (ORANGE, 2012).

Les nécessités construites dans le registre des modèles ne viennent pas uniquement des faits. Elles apparaissent comme répondant à des raisons dans le registre explicatif convoqué dans le problème travaillé. La construction du problème se fait alors par des interactions entre les éléments du registre empirique et ceux du registre des modèles.

Et ORANGE précise que « le développement des nécessités se fait toujours, même si ce n'est pas explicite dans les argumentations, par la combinaison de plusieurs références et jamais à partir d'éléments empirique seuls. Ce travail qui consiste, par l'examen critique des solutions, à explorer et à délimiter les possibles en identifiant des nécessités, constitue ce que nous appelons le travail du problème ou sa construction ou encore la problématisation » (ORANGE, 2012, p.42). Et il propose le schéma suivant de l'activité scientifique prenant en compte les trois registres :

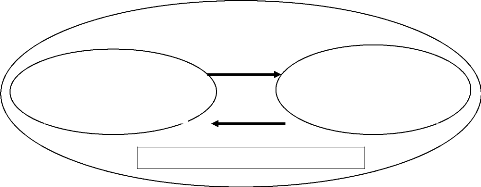
REGISTRE DES
MODELES :
Monde des idées
explicatives imaginées

REGISTRE EXPLICATIF ou paradigme

Communauté scientifique critique

REGISTRE
EMPIRIQUE :
Monde des faits
observés

ORANGE souligne l'importance des échanges argumentatifs qui trouvent tout leur sens ici pour explorer et délimiter de champ des possibles pour repérer les conditions de possibilité des solutions, les nécessités. Et même si « on peut problématiser seul, au moins en partie... les échanges dans la classe peuvent être une aide à la problématisation des élèves, de par la confrontation d'idées différentes, et un moment où ce travail de construction de problème est bien visible » (ORANGE, 2012, p.43).

[25]

3.3. Outil d'analyse : le losange de la problématisation

Les trois dimensions (position du problème, construction et résolution) dans le processus de traitement d'un problème sont à considérer « comme des orientations cognitives qui interfèrent dans le processus de recherche » et non comme des étapes qui se suivent (FABRE, 2017). Et ORANGE propose, pour illustrer la « délinéarisation de la démarche » le schéma suivant (ORANGE, 2012, p.127) :

Situation de
départ

Savoirs =

Possibles identifiés
+ nécessités

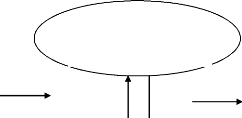
Construction de
modèles explicatifs

Exploration des possibles et recherche des nécessités

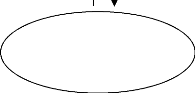
Investigations empiriques

Christelle Brémaud_E179552Q

FABRE précise que l'interaction entre le sujet et la tâche décrite définissant le problème compose la situation (FABRE, 2016, p.9), la tâche est constituée de buts, de données et de conditions. Les données pouvant être explicitement renseignées par l'énoncé du problème ou construites par le sujet : « les données sont ce qu'elles sont mais elles pourraient être autrement » (FABRE, 2016, p.31). Ce sont les hypothèses d'explications qui construisent les données « comme autant d'indices venant les conforter ou les invalider » (FABRE, 2016, p.35). FABRE précise qu'il n'y a pas de données, de conditions ou de solutions en soi, « tout dépend du contexte problématique dans lequel tel ou tel élément est inséré » (FABRE, 2016, p.40) en parlant de mobilité fonctionnelle de ces trois éléments. « L'articulation entre données et conditions s'opère dialectiquement » (FABRE, 2016, p.33), les conditions précisant le but, organisant le choix des données et leur contrôle.

La position du problème et sa solution représente la dimension horizontale de la résolution.

Sur cet axe apparaissent à gauche une des questions posées par l'énoncé et/ou que se pose l'élève dans sa construction du problème et à droite la réponse à laquelle il parvient pour avancer vers la solution de la situation. Il y aura autant de losanges de problématisation à construire dans cette analyse de corpus que de problèmes rencontrés par les élèves dans leur recherche de résolution.

Si le but est de trouver une solution, la construction du problème pour y parvenir en constitue sa substance. Cette construction est visible dans les traces que laisse apparaitre le cheminement entre les données et les conditions du problème. Ces deux éléments fonctionnels (données et conditions) dans le losange de la problématisation que propose FABRE représentent la dimension verticale de la

Christelle Brémaud_E179552Q

[26]

construction du problème. Sans cette dimension il n'y aurait pas de processus de construction de solution, FABRE parle de « pensée plate » dans le cas où la solution ne nécessite aucun questionnement, aucune construction de données qui appellent des conditions et réciproquement (FABRE, 2017, p.52).

On retient alors que la problématisation se caractérise par l'examen d'une question qui se fait par une pensée articulant données et conditions du problème dans un cadre déterminé, cette pensée se surveillant elle-même par des allers retour entre doutes et certitudes, tout ceci dans une perspective heuristique (une enquête est menée).

La position du problème définit le cadre de la résolution qui est l' « instance normative qui définit ce à quoi il convient de donner le statut de donnée, de condition ou de solution » (FABRE, 2016, p.23). Les données représentent la dimension empirique du problème et les conditions (relevant d'un jugement de nécessités) la dimension apodictique du problème (ce qui est comme ça et ne peut être autrement). FABRE parle alors de « dialectique de l'apodictique et l'assertorique » (FABRE, 2016, p.45) dans les allers retours entre les doutes et les certitudes de l'enquête.

La position de ces quatre éléments (problème, données, conditions, solution) peut être schématisée par le losange de la problématisation suivant que propose FABRE (FABRE, 2016, p.21) :

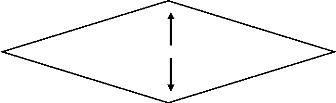
Position du problème Conditions

Construction résolution

Données

Cadre

Nous reprécisons que ce qui est pris en compte à gauche sur la dimension horizontale du losange, ne se limite pas nécessairement aux informations de l'énoncé du problème, mais peut être un des problèmes soulevés par l'élève au cours de sa résolution.

3.4. La problématisation dans une activité de recherche en mathématiques

i. L'activité de recherche dans une situation ordinaire de classe

Différentes situations de recherche sont régulièrement proposées aux élèves dans le cadre d'un enseignement par compétences, où l'enseignante (auteure de cette étude) cherche à proposer des situations conjuguant savoirs, savoir-faire et savoir-être des élèves pour pouvoir développer entre autre les compétences d'appropriation et d'analyse décrites précédemment. Nous en préciserons les modalités de mise en oeuvre dans la partie méthode de recherche.

Christelle Brémaud_E179552Q

[27]

Nous tenterons d'analyser a priori ici la situation proposée aux élèves dans le cadre de ce travail de recherche pour voir en quoi elle semble pertinente en termes de problématisation ou plus exactement de potentiel de problématisation. Seule l'analyse du corpus nous permettra d'en relever d'éventuelles traces dans l'activité de l'élève comme autant de preuves qu'il y a eu problématisation.

Nous pouvons espérer alors que l'analyse que nous ferons du processus de problématisation engagé par l'élève dans la construction de la résolution du problème à traiter, nous permettra de voir quand et comment les compétences nécessaires à la résolution d'un problème en mathématiques sont mises au travail pour mieux évaluer le processus permettant à l'élève d'arriver à un résultat.

ii. La situation-problème proposée aux élèves

La légende raconte que l'inventeur du jeu d'échecs demanda à son souverain comme récompense de lui donner 1 grain de riz pour la première case de l'échiquier, 2 pour la deuxième et ainsi de suite, le nombre de grains étant doublé d'une case à l'autre. La requête est-elle réalisable ?

iii. Contexte de mise en oeuvre

Pour mieux comprendre en quoi cette situation-problème offre suffisamment de résistance aux élèves, pour envisager qu'ils se posent un certain nombre de questions en vue de trouver des solutions au terme d'enquêtes, nous pensons qu'il nous faut expliciter certains points en amont.

L'activité est proposée à des élèves de première baccalauréat professionnel spécialité technicien en étude du bâtiment, qui à ce stade de leur cursus de formation n'ont pas encore travaillé sur les suites numériques (outils de résolution le plus performant pour cette situation-problème).

Ces élèves, depuis la classe de seconde, sont régulièrement mis en travail de recherche (démarche d'investigation, situations-problèmes) et s'y engagent de bon gré sans attacher plus d'importance aux compétences à développer et/ou à acquérir ni même vraiment à la rigueur des raisonnements permettant d'arriver aux résultats attendus.

A ce stade de leur formation, les habitudes prises en classe de mathématiques de travailler sur des activités de recherche avec des phases de recherche individuelle et des phases de travail en groupes, leur ont permis de comprendre l'importance de la trace écrite et surtout l'intérêt des brouillons. Le statut d'erreur n'est plus envisagé comme celui de fautes mais comme celui de tentatives, ce qui permet des allers retours dans leur raisonnement et surtout de pouvoir laisser des traces de leur cheminement vers des solutions potentielles.

Christelle Brémaud_E179552Q

[28]

Le niveau de ces élèves est très hétérogène et les savoirs de base fragiles. Ils connaissent l'ensemble du programme de mathématiques abordé au collège sans toutefois suffisamment le maitriser pour pouvoir toujours s'y référer et le (re)mobiliser à bon escient lorsque cela est nécessaire.

Pour préciser le savoir à construire en jeu dans la situation-problème donnée, nous précisons deux extraits du programme de maths :

- pour la classe de première :

- pour la classe de terminale :

Dialectiquement au travail engagé autour des compétences, l'objectif didactique pour l'enseignante est ici de faire générer expérimentalement une suite numérique à l'aide d'un tableur, de mettre en évidence l'intérêt des notations indicielles et l'importance de certains termes.

iv. Potentiel de problématisation de la situation et analyse a priori

Pour envisager une analyse a priori des problèmes que va soulever cette situation et que les élèves auront à résoudre, nous nous référerons aux documents de préparation de l'enseignant²³.

Nous schématiserons dans un premier temps cette analyse a priori de la situation sous la forme d'un losange de problématisation, pour mettre en évidence le potentiel de problématisation de la situation. Elle nous renseignera par la suite sur les démarches, raisonnements, procédures et solutions que l'élève peut mettre en oeuvre compte tenu de ses connaissances supposées en plus de recenser les difficultés qu'il peut rencontrer. Elle indiquera aussi la chronologie a priori de cette résolution.

²³ Annexe 4 : Documents de préparation de l'enseignant pour la mise en oeuvre de l'activité « grains de riz »

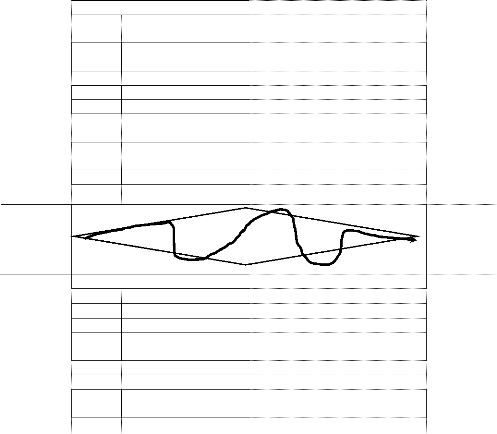
[29]

Conditions :

C1 : 63 calculs doivent être envisagés pour connaître le nombre de
grains de riz de chaque case ;

: Le nombre de grains de riz est doublé d'une case à l'autre, La
multiplication par 2 est le calcul récurrent ;

C3 : Les calculs doivent être organisés les uns après les autres...

C4 : ... à partir du nombre 1 ;

C5 : La somme des 64 résultats doit être envisagée (résultat 1);

C6 : Comparer le résultat 1 à une donnée (résultat 2) qui a du sens

pour pouvoir conclure ;

C7 : Le résultat 1 doit être dans la même unité de mesure que la
donnée (résultat2) à laquelle le comparer ;

C8 : Résultat1/ résultat2 = résultat3

C9 : La requête est réalisable si résultat3 est très inférieur à 1.

Problème :
La requête
est-elle
réalisable ?

Solution :

Non la

requête n'est pas réalisable

Données :

D1 : L'échiquier a 64 cases ;

D2 : 1 seul grain de riz dans la première case ;

D3 : 2 dans la deuxième case et ainsi de suite

D4 : La totalité des grains de riz sur l'échiquier (= résultat1) sera

la récompense ;

D5 : Le résultat 1 est un très grand nombre

D6 : Résultat 2 = production mondiale de riz en 2018 ;

D7 : Le quotient de deux grandeurs positives permet leur

comparaison ;

D8 : Grandeur1/grandeur2 <1 signifie que grandeur1<grandeur2.

Christelle Brémaud_E179552Q

Le losange précédent ne permet pas d'analyse a priori des sous-problèmes que posent la situation. En effet, l'élève ne pourra pas répondre directement à la question posée s'il ne repère pas et ne traite pas les problématiques soulevées par le problème posé.

En regardant plus finement cette première analyse a priori du potentiel de problématisation de la situation, il apparait que la problématique de la situation est double ici. Le problème 1 est défini comme étant celui à résoudre pour obtenir le nombre total de grains de riz et déterminer les calculs à effectuer pour obtenir le résultat en suivant l'algorithme défini par la situation. Deux cas de figures s'envisagent alors, selon si on se place :

- dans le registre de la multiplication dans lequel la suite des 64 termes correspondant au nombre de
grains par case est obtenue par multiplications successives par 2 avec un+1 = u_n×2 (pour n entier compris entre 1 et 63, avec u1=1) ce que fait apparaitre le losange précédent.

- dans le registre des exposants, où les 64 termes sont calculés indépendamment les uns des autres
avec pour expression un = u1×2^n-1 (pour n entier compris entre 1 et 64, avec u1=1),

[30]

Le problème 2 est défini comme étant celui qui révélera les contraintes permettant de conclure sur la faisabilité de la requête. Il pourra alors être considéré comme une critique du résultat du problème 1, pour pouvoir répondre à la question posée.

Ces problèmes ne sont pas explicites dans l'énoncé. Ils sont à construire pour pouvoir répondre au problème ouvert proposé.

Pour le problème 1 dans le registre de la multiplication, nous pouvons alors plus précisément envisager le losange de problématisation suivant :

Conditions :

C1 : 63 calculs doivent être envisagés pour connaître le nombre de grains de riz de chaque case ;

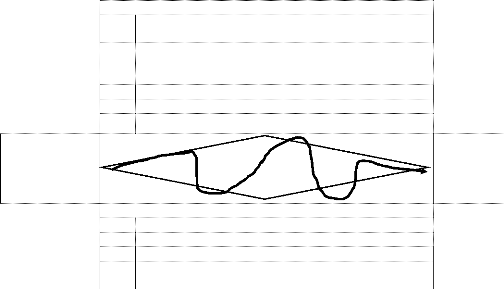
Christelle Brémaud_E179552Q

La multiplication par 2 est le calcul récurrent pour obtenir le

: nombre de grains de riz par case avec pour la case n+1, le nombre un+1 = u_n×2 (pour n entier entre 0 et 63 et u0=1);

C3 : Les calculs doivent être organisés les uns après les autres...

C4 : ... à partir du nombre 1 ;

C5 : La somme des 64 résultats doit être envisagée (résultat 1);

Solution 1 : Le résultat 1

Problème 1 :

Comment obtenir le nombre de grains de riz

total ?

Données :

D1 : L'échiquier a 64 cases ;

D2 : 1 seul grain de riz dans la première case ;

D3 : 2 dans la deuxième, ainsi de suite...

D4 : La totalité des grains de riz sur l'échiquier (=résultat1) sera

la récompense ;

Si le problème 1 est traité dans le registre des exposants, il sera renommé alors problème 1 bis.

Problème 1 bis :
Comment obtenir le
nombre de grains de
riz total ?

Données :

D1 : L'échiquier a 64 cases ;

D2 : 1 seul grain de riz dans la première case ;

D3 : 2 dans la deuxième, ainsi de suite...

D4 : La totalité des grains de riz sur l'échiquier (=résultat1) sera la récompense ;

Conditions :

C1 : 63 calculs doivent être envisagés pour connaître le nombre de grains de riz de chaque case ;

La multiplication par 2 est le calcul récurrent pour obtenir le

: nombre de grains de riz par case avec pour la case n, le nombre u_n = u1×2^n-1 (pour n entier entre 1 et 64 et u1=1) ;

C5 : La somme des 64 résultats doit être envisagée (résultat 1);

Solution 1 bis:

Le résultat 1

Nous pouvons alors plus précisément envisager le losange de problématisation suivant :

Christelle Brémaud_E179552Q

[31]

Nous faisons remarquer ici dans le problème 1 bis la réduction des conditions à 3, au lieu de 5 dans le problème 1. La condition permettant d'établir le calcul des grains par case est modifiée et les conditions C3 et C4 n'ont plus lieu d'être dans la mesure où les termes calculés en fonction de n (numéro de la case correspondant) peuvent se calculer les uns indépendamment des autres.

Mais il ne suffit pas d'obtenir un résultat chiffré pour répondre à la situation-problème donnée à résoudre. Encore faudra-t-il interpréter, critiquer ce résultat pour pouvoir conclure sur la faisabilité de la requête. Ce n'est en effet pas avec ce résultat brut que l'on peut conclure sur la faisabilité de la requête. On doit le confronter à une donnée qui a du sens, ce qui soulèvera une autre question quant au choix de cette nouvelle donnée. Nous pouvons proposer un troisième losange a priori dans lequel n'est pas discuté le choix de cette donnée mais qui permet de critiquer le nombre de grains de riz trouvé pour pouvoir conclure :

Problème 2 :
La requête
est-elle
réalisable ?

Données :

D5 : Le résultat 1 est un très grand nombre

D6 : Résultat 2 = production mondiale de riz en 2018 ;

D7 : Le quotient de deux grandeurs positives permet leur

comparaison ;

D8 : Grandeur1/grandeur2 <1 signifie que grandeur1<grandeur2.

Conditions :

C6 : Comparer le résultat 1 à une donnée (résultat 2) qui a du sens
pour pouvoir conclure ;

C7 : Le résultat 1 doit être dans la même unité de mesure que la
donnée (résultat2) à laquelle le comparer ;

C8 : Résultat1/ résultat2 = résultat3

C9 : La requête est réalisable si résultat3 est très inférieur à 1.

Solution 2: Non la requête n'est pas réalisable

Un certain nombre de problèmes connexes, apparaissent clairement dans cette analyse a priori, et sont à envisager comment autant d'obstacles à surmonter par les élèves. Cela ne présage pas que ce soient les seuls problèmes rencontrés par les élèves et nous pouvons envisager que d'autres problèmes se posent. Certains problèmes liés à une maitrise fragile des savoirs fondamentaux mathématiques peuvent aussi donner lieu à d'autres problématisations dans le cadre de difficultés que l'on qualifiera de techniques à surmonter. Mais nous n'en tiendrons ici pas compte dans cette analyse didactique et épistémologique a priori dans laquelle nous recherchons principalement à mettre en évidence le rapport entre problématisation et construction des savoirs en jeu.

Christelle Brémaud_E179552Q

[32]

4. METHODE DE RECHERCHE ET RECUEIL DE DONNEES

4.1. Les intentions

Nous avons précédemment mis à l'épreuve de la problématisation la situation-problème que nous soumettrons aux élèves dans le cadre de ce travail de recherche. Cela nous a permis de construire une analyse a priori du problème à résoudre pour mettre en évidence le potentiel de problématisation et identifier certains des obstacles à surmonter pour réussir cet exercice.

Le traitement du problème que l'élève aura à prendre en charge devra permettre de voir en quoi ce dernier est compétent. La question n'est pas simplement de savoir s'il a réussi (le cas échéant) mais comment il a réussi. Pour cela nous devons garantir dans un premier temps, qu'il soit seul et autonome dans ce travail d'appropriation et d'analyse de la situation et que la solution qu'il propose ainsi que sa démarche pour y parvenir soit bien de lui.

Comme évoqué dans le chapitre précédent, on peut problématiser seul, jusqu'à un certain point parfois, mais les interactions entre pairs aident à la problématisation et l'observation des interactions langagières à la visibilité de celle-ci.

Nous devons donc aussi envisager que le travail de groupe puisse être un des éléments ressources dont l'élève peut disposer pour avancer dans la résolution du problème. Il s'agira de permettre à l'élève de s'emparer des ressources extérieures qu'il aura définies (explicitement ou non et/ou consciemment ou non) au préalable.

4.2. Conditions de mise en oeuvre de cette situation

L'activité construite par l'enseignante chercheuse a été mise en oeuvre par un enseignant stagiaire en stage d'observation depuis plusieurs semaines dans cette classe de Première bac pro. Les modalités de mise en oeuvre ont été convenues en amont entre l'enseignante chercheuse et l'enseignant stagiaire qui anime cette séquence relativement ordinaire. Ce dernier ne doit intervenir, le cas échéant, que par des feedbacks pour faire reformuler les questions des élèves et/ou leur faire préciser leurs doutes et/ou certitudes. L'enseignante chercheuse est présente pour enregistrer mais étant l'enseignante responsable de la classe elle se donne également la possibilité d'intervenir dans la mise en oeuvre pour repréciser éventuellement les consignes de mise au travail et guider les élèves comme défini avec l'enseignant stagiaire.

Christelle Brémaud_E179552Q

[33]

4.3. Constitution du corpus

Quatre phases de travail seront envisagées sur deux séances de cours. La question de recherche nécessite que les éléments du corpus constitué mettent en perspective des traces de problématisation que nous repérerons au travers de différents épisodes. Pour cela, trois documents supports permettront de relever les traces écrites des élèves engagés dans ce travail de recherche et des enregistrements audio et vidéo permettront des transcriptions.

Pour information, sur 18 élèves de la classe, 17 étaient présents à la première séance et seulement 13 parmi ces 17 élèves, à la deuxième séance. Chaque élève devait renseigner chacun des trois documents à rendre (y compris lorsqu'il devait rendre compte d'un travail de groupe).

Etapes dans la résolution de la situation-problème		Eléments constituant le corpus
Phase 1 (10 minutes) :	Recherche individuelle pour l'appropriation de la situation-problème donnée à résoudre	Document 1		17 recherches individuelles (appropriation de la situation)
Phase 2 (10 minutes) :	Synthèse collective faite par la classe	Enregistrements vidéo et/ou audio	Photos de la trace écrite au tableau et 1 enregistrement vidéo (transcrit) de la synthèse collective sur l'appropriation de la situation
Phase 3 (30 minutes) :	Travail de groupe (en trinômes) pour l'élaboration d'un protocole de résolution		Document 2	14 comptes rendus de l'analyse de la situation (proposition de protocole de résolution), 1 vidéo (avec transcription) et 2 enregistrements audio (dont 1 transcrit)
Phase 4 (50 minutes) :	Travail de groupe (mêmes groupes constitués que pour la phase 3) pour la résolution et le compte rendu de l'activité de recherche		Document 3	12 comptes rendus de la résolution du problème et 2 enregistrements audio (dont 1 transcrit)

Pour des raisons de lisibilité du corpus nous indiquons la constitution des groupes de

travail constitués par affinités :

Groupe 1 : David, Erwan (absent à la séance 2), Inès

Groupe 2 : Dorian, Elsa, Maxime

Groupe 3 : Evan, Gabin, Romain

Groupe 4 : Coralie (absente à la séance 2), Jordan, Léa

Groupe 5 : Hugo, Marie, Rozenn

Groupe 6 : Axel, Théo (absents à la séance 2).

Le corpus sera donc constitué de documents écrits et d'enregistrements audio et vidéo comme

détaillés ci-après :

Christelle Brémaud_E179552Q

[34]

- 17 productions écrites d'élèves « document 1 »²⁴. Ces documents 1 renseignent sur la

compréhension individuelle de chaque élève du problème à traiter.

- 14 productions écrites d'élèves « document 2 »²⁵ sur les 17 attendues* (pouvant se résumer à 6
groupes de travail). Ces documents 2 rendent compte des protocoles de résolution envisagés par chacun des groupes de travail.

*On note que 3 élèves n'ont pas rendu leur production écrite (Erwan, Axel et Théo)

- 12 productions écrites d'élèves « document 3 »²⁶ sur 13 attendues** (pouvant se résumer à 5
groupes de travail car les élèves du groupe 6 étaient absents à cette séance). Ces documents 3 répondent à la question initiale posée dans la situation-problème.

**On note qu'un élève (David) n'a pas rendu son écrit considérant qu'il avait écrit la même chose que son binôme (Inès).

Les enregistrements audio et vidéo viennent étoffer le corpus avec des transcriptions²⁷ :

- La transcription de l'enregistrement audio de la phase 2²⁸, avec 117 tours de parole,

- La transcription de l'enregistrement audio du groupe 1 lors de la phase 3²⁹, avec 157 tours de

parole,

- 2 enregistrements audio (non transcrits) du groupe 2 lors des phases 3 et 4,

- La transcription des échanges filmés entre élèves du groupe 3 lors de la phase 3³⁰, avec 140

tours de parole,

- La transcription des échanges enregistrés du groupe 3 lors de la phase 4³¹, avec 226 tours de
parole.

On codera dans les transcriptions par Ens les prises de parole de l'enseignante chercheuse et par ES celles de l'enseignant stagiaire.

4.4. Méthode d'analyse du corpus

Afin de repérer des traces de problématisation, une lecture globale des productions écrites se fera document par document pour chacune des trois phases 1, 3 et 4, pour :

- relever les éléments de réponses des élèves dans la globalité des productions écrites qui
renseignent sur les problèmes que les élèves se sont posés et qu'ils devront résoudre,

24 ANNEXE 5 : Relevés des traces écrites_RECHERCHE INDIVIDUELLE_ phase 1

25 ANNEXE 7 : Relevés de traces écrites_Proposition de protocole de résolution_ phase 3

26 ANNEXE 10 : Relevés de traces écrites_résolution_ phase 4

27 Les prises de parole de l'enseignante chercheuse sont codées par Ens et celles de l'enseignant stagiaire sont codées par ES.

28 ANNEXE 6 : TRANSCRIPTION synthèse de classe_ phase 2 APPROPRIATION DE LA SITUATION PROBLEME

29 ANNEXE 8 : TRANSCRIPTION travail de groupe_ Proposition de protocole de résolution_ phase 3 Transcription investigation 1 TEB_ phase 3 Groupe 1 : David Erwan Inès

30 ANNEXE 9 : TRANSCRIPTION travail de groupe_ Proposition de protocole de résolution_ phase 3 Transcription investigation 1 TEB_ phase 3 Groupe 3 : Gabin Evan Romain

31 ANNEXE 11 : TRANSCRIPTION travail de groupe_ RESOLUTION DE LA SITUATION PROBLEME grains de riz Transcription investigation 1 TEB_ phase 4 groupe 3 : Gabin Evan Romain

Christelle Brémaud_E179552Q

[35]

- et observer les éventuelles procédures mises en oeuvre permettant de résoudre ces problèmes

après avoir délimiter les cadres explicatifs dans lesquels les élèves émettent leurs hypothèses et/ou les résultats auxquels ils parviennent.

Nous noterons Pb les problèmes que les élèves font apparaitre pour les distinguer des problèmes envisagés dans l'analyse a priori.

Les transcriptions des enregistrements nous permettront d'éclairer certains éléments relevés dans les traces écrites pour affiner cette observation par une analyse complémentaire (toujours phase par phase).

Nous nommons « éléments », des extraits des traces écrites dans les copies d'élèves. Ces éléments renseignent directement mais nous aurons parfois à les interpréter pour comprendre le problème que les élèves se posent. Nous nommerons donc par la suite, informations ces éléments extraits des traces écrites ou leur interprétation.

Nous coderons par ^n°phaseIn°d'ordre les informations relevées nous semblant importantes (issues des traces écrites et/ou des transcriptions) et à éventuellement catégoriser en données et en conditions par la suite.

Le numéro de phase (n° phase) sera 1, 2, 3 ou 4 relativement à chacune des quatre phases explicitées précédemment. Le numéro de l'ordre (n° ordre) correspondra à l'ordre dans lequel seront relevées ces informations pour chacune des quatre phases de travail comme autant de renseignements pouvant éclairer sur les problèmes construits par les élèves dans leur résolution. Il sera automatiquement réinitialisé à 1 à chaque nouvelle phase.

De façon exceptionnelle, pour les analyses des traces écrites, si certaines informations relevées n'apparaissent que de façon singulière dans une seule copie (ou en très petit nombre), nous préciserons l'auteur avec en complément son prénom dans l'indice porté en bas à droite avant le numéro d'ordre. On aura par exemple ¹IEvan_5 pour la cinquième information relevée dans la phase 1, cette information n'ayant été relevée que dans le document 1d'Evan.

Nous préciserons systématiquement dans la phase 2, le prénom de l'élève à l'origine de l'information relevée dans la transcription des échanges faits collectivement dans la classe. On codera alors par ²Iprénom_N°d'ordre et le numéro de l'ordre sera fonction de la chronologie des relevés et non de l'auteur de la donnée construite. On aura par exemple ²IElsa_1, ²IMaxime_2 et ²IDavid_3 pour chacune des trois premières informations relevées.

Nous précisons pour les phases 3 et 4, que le codage des informations suite aux lectures des productions écrites (documents 2 et 3) se fera comme pour la phase 1 mais en précisant systématiquement le groupe pour lequel l'information a été relevée avant le numéro d'ordre hiérarchisant l'information. Nous aurons par exemple ³Igroupe2_1, ³Igroupe2__2 et ³Igroupe2_3 pour chacune des trois premières informations

Christelle Brémaud_E179552Q

[36]

relevées dans les documents 2 du groupe 2, lors de la phase 3. Nous notons que de façon exceptionnelle si une information n'a été relevée que dans un seul des documents du groupe nous spécifierons le nom de l'élève auteur de cette information.

Pour le codage des informations relevées lors des analyses des transcriptions des phases 3 et 4, se fera comme pour la phase 2. Nous aurons par exemple ³IGabin_1, ³IRomain_2 et ³IGabin_3 pour chacune des trois premières informations relevées dans un extrait de la transcription de la phase 3 (ces informations étant relatives à des élèves d`un même groupe).

Nous relèverons le maximum d'informations et nous mettrons en caractères gras celles qui nous semblent indispensables à la construction du problème. Nous précisons ici que les informations non directement issues des traces écrites mais qu'il nous semble nécessaire de formaliser pour mieux en éclairer d'autres, ne seront pas mises en caractères gras.

Si une information est relevée plusieurs fois à différents moments de l'analyse selon le problème qui se construit alors nous la relèverons comme expliqué précédemment avec un numéro d'ordre correspondant à la chronologie du relevé mais ce codage sera entre parenthèse et on préfèrera rappeler le codage précédent. Par exemple, si la première information relevée dans le groupe 2 lors de la phase 3, ³I2_1 est identique à la neuvième relevée en phase 2, ²Iélève_9, alors nous préciserons (³I2_1=) ²Iélève_9, et ne mentionnerons que ²Iélève_9 pour la suite.

Les problèmes construits par les élèves seront notés comme précisé plus haut par Pb avec comme pour les informations relevées des indications sur le numéro de la phase à laquelle ils ont été repérés et en indice (si plusieurs problèmes se présentent dans une même phase) le numéro d'ordre d'apparition dans la phase. Nous aurons par exemple, ⁴Pb2 pour le deuxième problème construit par les élèves en phase 4. Nous nous réservons la possibilité d'y ajouter, pour plus de clarté, le groupe en indice car nous envisageons que la résolution d'un problème puisse se faire sur plusieurs phases et par morceaux de façon non linéaire.

Après avoir repéré ce qui semble être un des problèmes qui se posent, nous chercherons à catégoriser les informations ^n°phaseIn°d'ordre recueillies, en données D, conditions C et solution S (ou résultat) pour voir comment les élèves cheminent dans leur analyse et leur raisonnement pour élaborer une stratégie de résolution. Nous précisons que les numéros d'ordre pour les données (et conditions) pourront être différents de ceux des informations qui seront peut-être mobilisées dans un ordre différent de celui de leur recensement. Pour les données (et les conditions) le numéro d'ordre respectera l'ordre dans lequel elles seront construites dans chaque phase.

Le I de ^n°phaseIn°d'ordreI deviendra alors D dans la données ^n°phaseDn°d'ordreD, C dans la condition ^n°phaseCn°d'ordreC et S dans la solution ^n°phaseSn°d'ordreS. Les informations catégorisées comme données devront permettre de construire des conditions, qui comme nous le verrons au cours de l'analyse,

Christelle Brémaud_E179552Q

[37]

deviendront peut-être pour certaines à leur tour des données pour un autre problème posé dans la résolution du problème initial.

Ce codage nous permettra de voir au fur et à mesure des deux séances quelle chronologie suit la construction du problème. Nous nous attendons à ce que certaines informations tirées de phases ultérieures puissent venir compléter celles d'une phase précédente.

Au fur et à mesure de l'analyse, nous répertorierons les informations relevées ainsi que le statut qui leur est attribué dans un tableau dont nous rendrons compte en fin d'analyse sous la forme suivante :

Analyse a priori

phase 1

Analyse a priori

Récapitulatifs des informations recueillies et des données et conditions

construites :

D1

¹I4 ¹C1

¹I3 ¹C2

¹I4

Phase 1 Analyse 1

¹C1

Phase 1
Analyse 1 bis

Phase 2 Analyse 2

Phase 3 Analyse 3

Phase 4 Analyse 4

Nous indiquerons en rouge les informations qui auront été relevées à plusieurs stades de l'analyse en les faisant correspondre à celles qui les précèdent (déjà relevées et mentionnées dans le tableau).

Si par exemple, la quatrième information relevée dans l'analyse de la phase 1 (¹I4 considérée comme première condition apparaissant dans le problème à résoudre dans cette phase ¹C1) correspond à la donnée D1 de l'analyse faite a priori, elle sera notée comme indiqué dans l'extrait de tableau ci-dessus

- en noir sur la ligne correspondant au relevé de l'information puis surlignée en jaune

- et en rouge sur la ligne correspondant à D1

Ce tableau³² pourra par la suite nous renseigner plus globalement sur la construction que font les élèves du problème à résoudre. Les cases coloriées en bleu correspondront à des informations qui auront permis de construire un losange de problématisation suite aux analyses des productions et/ou enregistrements des élèves.

Les copies d'élèves pourront être mises de côté au fur et à mesure de l'avancée dans la recherche d'indices relevés parmi les informations écrites car elles ne révèleront plus rien au stade où en sera la recherche. Nous préciserons par document N^°prénom les copies d'élèves mises de côtés et ne faisant plus partie du corpus en cours d'analyse avec 1, 2 ou 3 pour n°, selon le document correspondant à la phase 1, 3 ou 4 (on rappelle qu'aucun document n'est relevé pour la phase 2 de débat).

³² Annexe 13 : RECAPITULATIF de l'ANALYSE DU CORPUS

Christelle Brémaud_E179552Q

[38]

5. ANALYSE DU CORPUS

5.1. Première analyse (phase 1) : ce que révèlent les traces écrites des recherches individuelles des élèves³³

A la première lecture des productions écrites individuelles des élèves, aucune trace d'un quelconque questionnement n'apparait de façon flagrante malgré des éléments de réussite certaine dans la construction du problème et parfois même d'une réponse (sans fondement puisque sans preuve) à la question posée dans cette situation-problème. Nous ne relevons directement aucune question, aucune trace de cheminement faisant apparaître de problématique ce à quoi nous pouvions nous attendre dans la mesure où une éventuelle problématisation se fera de façon inconsciente car la procédure qu'elle impose est inconnue des élèves. Nous devons alors mener l'enquête permettant de la mettre à jour.

Un décodage, une relecture plus minutieuse est nécessaire pour relever les informations qui peuvent se révéler être d'éventuelles données et conditions et surtout mettre à jour des relations entre certaines de ces données et certaines de ces nécessités pour recenser les problèmes posés que nous devons identifier (car pas explicités en général) et auxquels les élèves cherchent à répondre.

Nous rappelons qu'il ne s'agissait pas, lors de cette phase de recherche individuelle, de résoudre le problème donné mais bien de déterminer les problématiques qu'il soulève, et envisager les conditions qui permettent d'y répondre. Nous voyons alors apparaitre suite à la lecture de l'énoncé, une appropriation des élèves qui nécessite

- pour certains de réécrire et/ou modéliser certaines données de l'énoncé,

- pour d'autres (voir les mêmes) de les interpréter,

- pour d'autres (voire les mêmes) d'en construire de nouvelles et/ou d'en expliciter, afin de proposer

des hypothèses voire des solutions (que l'on peut voir également comme des résultats intermédiaires) pour répondre à la question (voire y répondre directement sans que la résolution ne fasse apparaître de résultats chiffrés preuve d'une démarche et d'une construction aboutie). Les 17 documents 1 sont lus globalement et permettent rapidement de faire un tri selon des lectures

organisées en plusieurs étapes autour des critères d'appropriation précisés précédemment :

- recherche d'éléments dans les traces écrites directement liées à l'énoncé du problème posé,

- recherche d'éléments correspondant à une tentative de modélisation (par un schéma et/ou un

calcul) de la situation,

- recherche d'autres éléments extérieurs pour envisager de répondre au problème posé,

³³ Annexe 5

Christelle Brémaud_E179552Q

[39]

Ceci en tenant compte d'une réduction du corpus au fur et à mesure de l'avancée de l'analyse comme expliqué dans le chapitre précédent lors de l'exposé de la méthodologie. Le document 1Inès indiquant uniquement « je ne comprends pas » sera exclu de cette première analyse même si nous tenterons ultérieurement des explications sur les raisons de cette incompréhension. De plus, bien que la consigne soit de formaliser ce que l'élève comprenait ou pas de la situation posée, sans nécessité de résoudre et donc sans chercher d'emblée à répondre à la question posée, 8 documents 1 font apparaitre une réponse à la question « la requête est-elle réalisable ? ». Le document 1Erwan indiquant uniquement « la requête est réalisable » sans plus d'information écrite sera également retiré du corpus. Le corpus sera donc réduit à 15 documents pour cette première analyse.

i. Premier relevé d'indices parmi les traces écrites (documents 1)

L'énoncé de ce problème ouvert révèle peu de données explicites. On en relève 3 :

- le plateau de l'échiquier (et les conditions qu'il peut imposer dans une éventuelle modélisation
et/ou formalisation d'un calcul),

- la première case contient 1 grain de riz, la deuxième 2,

- le nombre de grains de riz est doublé d'une case à l'autre de l'échiquier.

Nous répertorions dans les 15 copies, la façon dont est traité l'énoncé afin de repérer les problèmes que se posent les élèves :

Recherche d'éléments directement liées à l'énoncé du problème posé		copies
Le plateau de l'échiquier est représenté		9/15
- intégralement faisant apparaitre les cases 8×8	^1I1	7/9
o sans distinction de couleur	^1I2	6/9		o avec l'alternance de cases blanches et noires (document 1_Léa)
^1ILéa_3	1/9	- sa représentation n'est qu'évoquée (comme une nécessité « il faut représenter le plateau » document 1_Elsa)
	1/9	Le nombre de 64 apparait
	13/15	- de façon explicite comme étant le nombre de cases
	12/13	o par un calcul
	3/12
^1I4		o par une légende sur le schéma du plateau (document 1_Léa)
	1/12	o sans plus d'information sur ce résultat
	8/12	- de façon implicite dans un calcul proposé
	1/13	les cases sont ordonnées de la première à la dernière
	6/15	- de façon explicite sur un schéma avec cases numérotées
	1/6
^1I5		- de façon explicite sur un schéma
	3/6	- de façon implicite dans une suite de résultats chiffrés (grains par case ?)
	2/6	1 grain de riz sur la première case, 2 sur la deuxième
	6/15	- de façon explicite
	5/6	o par une réécriture littérale de l'information (document 1_Gabin)
^1I6	1/5	o par un marquage sur le schéma du plateau
	4/5	- de façon implicite dans un calcul
	1/6

Christelle Brémaud_E179552Q

[40]

Le nombre de grains est doublé d'une case à l'autre			6/15	- information réécrite littéralement
1I7	2/6		- information révélée par un marquage dans chaque case ou par une succession de nombres
	4/6		Les cases contiennent toutes des grains de riz
	6/15		- de façon explicite sur un schéma avec grains de riz sur chacune des premières cases
^1I8	4/6		- de façon implicite dans une suite de résultats chiffrés (grains par case ?)
	2/6

Nous faisons remarquer que les informations ¹I4 (le nombre 64 apparait), ¹I5 (les cases sont ordonnées de la première à la dernière) et ¹I8 (les cases contiennent toutes des grains de riz) ne sont pas des données explicites dans l'énoncé. Elles permettent déjà d'entrevoir la modélisation que les élèves vont faire pour résoudre le problème 1 pour obtenir le nombre de grains de riz total. On peut prévoir de les retrouver dans la deuxième analyse qui suivra à ce sujet.

Certains élèves cherchent ici à matérialiser (décrire physiquement) les conditions de la situation (pour mieux la comprendre semble-t-il) par les contraintes imposées par le plateau du jeu.

Nous voyons apparaitre ici une difficulté d'interprétation de l'énoncé pour certains élèves qui ne parviennent pas à aller au-delà de ce qu'il décrit. Des parties de l'énoncé sont directement reprises dans certaines copies de façon très explicite (¹ILéa_3) alors que dans d'autres copies, elles sont prises en compte de façon implicite comme si ce problème d'interprétation était déjà traité (comme dans l'analyse didactique a priori faite dans le chapitre 3 où nous n'avions pas évoqué le problème que semble vouloir ici résoudre certains élèves). Nous le nommerons ¹Pb1 et nous posons la question de savoir s'il doit présager d'une difficulté d'appropriation de la situation empêchant certains élèves d'aller au-delà dans la construction du problème (document 1_Léa, document 1_Jordan, document 1_Hugo).

Quel statut donner alors aux informations relevées pour mieux comprendre la construction de ce problème ? Nous considérons ici que le problème ¹Pb1 est de trouver les contraintes qu'impose le plateau de l'échiquier pour mieux comprendre ce qui est demandé et qui sera à traiter par la suite.

Pour savoir quel statut donner aux informations, nous devons discuter de ces informations en nous posant la question ici « ce qui est comme ça et ne peut être autrement » afin de répertorier les conditions qui permettront la modélisation d'un calcul répondant au problème que se posent déjà certains élèves dans cette phase 1.

Le plateau est constitué de 8 cases sur 8 cases (¹I1 donnée par l'illustration rappelant le design du plateau de l'échiquier) : nous considèrons que c'est une donnée qui imposera de travailler avec 64 cases ¹I4 que l'élève prend en compte comme contrainte et qui conditionnera le calcul par la suite. ¹I4 prend alors le statut de condition.

Le design du plateau impose la donnée de l'alternance de couleurs ¹ILéa_3 (mais pourrait en imposer une autre) dont il ne faut nécessairement pas tenir compte mais qui permet de construire la condition ¹I5 car seul l'ordre des cases, les unes par rapport aux autres ¹I6 (pour donner du sens à « 1 grain sur la première, 2 sur la suivante »), semble une condition à prendre en compte pour la suite.

Christelle Brémaud_E179552Q

[41]

La dernière donnée de l'énoncé ¹I7 « le nombre de grains est doublé d'une case à l'autre » présage que toutes les cases seront remplies (¹I8) et qu'il n'en sera pas autrement. La solution du problème ¹Pb1 posé est alors qu'il y a 64 cases à remplir de grains sans autre distinction que leur place sur le plateau les unes par rapport aux autres (¹S1).

Nous pouvons envisager le losange de problématisation suivant qui permet de conclure que l'échiquier impose qu'il y a 64 cases à remplir :

Problème ¹Pb1 :
Quelles
contraintes
impose le
plateau de jeu ?

Données :

¹I1 Plateau de jeu 8 cases X 8 cases ¹D1

¹ILéa_3 Alternance de cases blanches et noires ¹D2

¹I6 1 grain dans la case 1, 2 sur la deuxième ¹D3

Conditions :

¹I4 Plateau de jeu de 64 cases ¹C1

¹I2 Aucune distinction de couleur à faire d'une case

à l'autre pour les 64 cases

¹I5 Les cases sont implicitement numérotées de 1 à

64

¹I8 Les cases contiennent toutes des grains de riz ¹C4

¹I7 Le nombre de grains est doublé d'une case à

l'autre

¹C2

¹C3

¹D4

Solution ¹S1:

64 cases à remplir les unes après les

autres

Nous n'avions pas envisagé dans l'analyse a priori, la résolution de ce problème dont la solution pourrait paraitre tacite (comme c'est le cas pour certains élèves), mais il nous parait important de ne pas le passer sous silence car il peut expliquer certaines difficultés que semblent avoir eu plus de la moitié des élèves (9/17) pour envisager d'avancer plus loin dans la construction du problème posé initialement par l'énoncé et principalement pour le problème 1 du calcul à engager. Nous remarquons d'ailleurs que moins de la moitié des élèves (seuls 6 élèves sur 17) ont réussi à formaliser les informations ¹I5 et ¹I8 que l'on a précisées plus haut comme étant des éléments non explicites de l'énoncé.

ii. Deuxième relevé d'indices parmi les traces écrites (documents 1)

Nous relevons également dans ces documents 1, des éléments permettant d'envisager la résolution du problème 1 posé dans l'analyse a priori.

Nous apercevons dans ces copies, les prémices de cette résolution aux travers des informations relevées ci-après :

Recherche d'éléments correspondant à une tentative de modélisation			Copies	Le nombre de 64 apparait
(^1I9 =) ^1I4		13/15	les cases sont ordonnées de la première à la dernière
(^1I10 =) ^1I5		6/15

Christelle Brémaud_E179552Q

[42]

Un grain de riz sur la première case		6/15			- de façon explicite
	5/6			o par une réécriture littérale de l'information (document 1_Gabin)
		1/5
(^1I11 =) ^1I6				o par un marquage sur le schéma du plateau
		4/5		- de façon implicite dans un calcul
	1/6			Le nombre de grains est doublé d'une case à l'autre
	6/15			- information réécrite littéralement
	2/6			- information révélée par un marquage dans chaque case du plateau ou par une succession de nombres
(^1I12 =) 1I7	4/6			Les cases contiennent toutes des grains de riz
(^1I13 =) ^1I8	6/15			Un calcul récurrent apparait
^1I14	6/15			- à partir du nombre 1
^1I15				- multiplication par 2 pour obtenir le nombre de grains d'une case à l'autre
	4/6
^1I16				- n° de la case au carré pour obtenir le nombre de grains d'une case
	2/6			Interpréter des données non explicites* :
	9/15			- 63 Calculs doivent être envisagés avec de quantifier la récompense
				o Explicitement exprimé de façon littérale
^1I17	4/9			o Succession de premiers calculs laissant supposer une suite
	6/9			- La récompense est la totalité des grains sur le plateau
^1I18				- Il faut additionner tous les grains obtenus sur chacune (des 64) cases
	4/15			o Exprimé de façon littérale
^1I19		2/4		o Exprimé par un calcul
		2/4

Le problème que nous noterons ici ¹Pb2, ici fait suite à la résolution du problème ¹Pb1 précédent. La solution ¹S1 formulée précédemment sera donc en partie reprise dans la construction de ce nouveau problème ¹Pb2 avec des données et des nécessités (pour arriver à ¹S2) reprises pour certaines (¹I4, ¹I5, ¹I6, ¹I7, ¹I8) ici mais pouvant éventuellement changer de statut.

Pour comprendre ce que l'on appelle des « données non explicites* », et mieux voir quels sont les enjeux et obstacles que présente ce problème ouvert, nous devons éclaircir certains points. Ceci nous permettra de discuter par la suite le statut attribué à ces nouvelles informations pour proposer le losange de problématisation ci-après.

L'énoncé ne dit pas, par exemple, que chaque case contient des grains (¹I8), ni que la totalité des grains du plateau compose la récompense (¹I18). Nous parlerons de « supposés » que les élèves verront (ou pas). Ce que nous cherchons dans leurs copies, peut se résumer ici à : quels sont les éléments dans les traces écrites qui nous renseignent sur la compréhension des supposés de l'énoncé ?

Lorsqu'il s'agit d'interpréter des éléments de l'énoncé et/ou d'en créer de nouveaux avec les supposés de l'énoncé selon s'ils sont (les éléments créés) implicitement exprimées par un calcul ou explicitement (par une phrase), l'information que nous relevons, peut ne pas avoir le même statut.

Par exemple, pour exprimer l'implicite que chaque case doit être remplie (¹I8 qui avait le statut de condition ¹C4 dans le problème ¹Pb1 à résoudre précédemment), l'élève peut :

Christelle Brémaud_E179552Q

[43]

- soit le formuler littéralement (document 1_Dorian : « il faudra calculé le nombre de grain de riz par

case ») ce qui nous donne une information ¹I8 qui aura alors le statut de donnée (¹D6) comme précédemment dans le problème ¹Pb1,

- soit l'interpréter et faire apparaitre l'information au travers d'un calcul ce qui nous donne alors une

autre information ¹I17 qui elle aura le statut de condition (¹C5). Nous imaginons la discussion critique (consciente ou pas) qu'un élève peut avoir avec lui-même lorsqu'il dépose cela à l'écrit : « si nous avons bien compris l'implicite de l'énoncé alors nous pouvons dire qu'il y a nécessité de faire ces calculs ».

Nous remarquons également comme pour ¹I8, que ¹I4 ici n'a plus le statut de condition mais de

donnée ¹D5 (dans le losange de problématisation proposé ci-après) puisqu'ici la compréhension des contraintes qu'impose le plateau de l'échiquier n'est plus à discuter. De même avec ¹I8 qui perd son précédent statut de condition (¹D5) car le problème ¹Pb1 est résolu, l'élève se place dans le cadre explicatif des données qu'impose le plateau et la règle imposée par le souverain « les 64 cases sont remplies de grains ». Ce qui fait apparaitre la nécessité des 64 résultats intermédiaires et donc des 63 calculs donnant à l'information ¹I17 le statut de condition (¹C5). Nous remarquons ici qu'il faut les deux données ¹D5 et ¹D6 pour construire la nouvelle condition ¹C5.

Mais il peut en être un peu différemment pour certains éléments non explicites de l'énoncé. Par exemple, pour exprimer l'implicite que la totalité des grains du plateau compose la récompense (¹I18), les élèves n'évoquent pas la somme en tant que récompense mais l'addition nécessaire pour y parvenir (¹I19). Que ce soit de façon littérale (document 1_Elsa : « puis il faut additionner toutes les cases » et document 1_Dorian : « ...et ensuite tout additionné ») ou au travers d'un calcul (document 1_Evan et document 1_Rozenn), on voit apparaitre le caractère de nécessité de convoquer l'addition pour obtenir cette somme donnant à ¹I18 le statut de donnée (¹D9) et à ¹I19 celui de condition (¹C10). ¹I18 n'est alors ici pas issue directement des traces écrites mais a été envisagée par l'auteur pour permettre d'éclairer ¹I19. Elle ne sera donc pas mise en caractères gras dans le losange de problématisation suivant (et par voie de fait ¹D9 non plus).

Les informations relevées lors de l'analyse précédente ¹I7 (le nombre de grains est doublé d'une case à l'autre) et ¹I6 (un grain dans la première case) sont des données explicites de l'énoncé. Elles ne font donc pas référence à des éléments non supposés de l'énoncé comme celles évoquées précédemment mais elles donnent lieu à une interprétation. Ce qui explique que nous leur conférons le statut de données (respectivement ¹D7 et ¹D8) comme dans l'analyse précédente pour la construction du problème ¹Pb1.

En effet, « un grain de riz sur la première case » qui n'est pas un supposé de l'énoncé puisqu'exprimé littéralement en toutes lettres (¹I6), va générer implicitement l'information ¹I15 qui allant au-delà de la réécriture de l'énoncé (¹I6 aura alors de statut de données ¹D8) implique une nécessité dans le calcul que l'élève tente. L'information ¹I15 aura alors ici le statut de condition (¹C9).

[44]

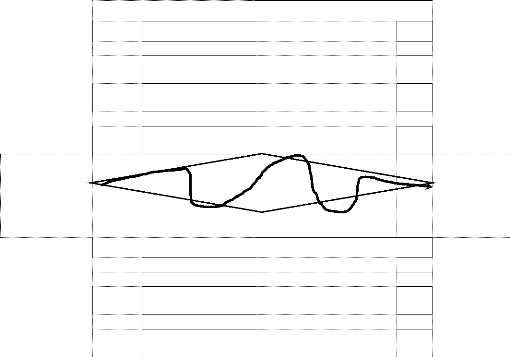
Pour ¹I7, il y a 2 informations que nous aurions pu distinguer : « le nombre de grains est doublé » et l'information complémentaire « d'une case à l'autre » donnant lieu à deux autres informations ¹I16 et ¹I5. ¹I7 donne lieu à ces deux conditions comme faisant suite à une interprétation. « Le nombre de grains est doublé » donne lieu d'emblée à la nécessité de convoquer la multiplication par 2 (bien qu'après plus de réflexion et pour des raisons d'évidence certains élèves utiliseront les puissances de 2) d'où la condition ¹C7. Et « d'une case à l'autre » déjà évoquée précédemment impose un ordre dans les calculs successifs à envisager ce qui fait référence à l'information relevée précédemment ¹I5 avec toujours un statut de condition. Nous remarquons qu'ici pour le problème ¹Pb2 en cours de construction, ¹C8 « les calculs doivent être organisés les uns après les autres » est différente de la condition découlant de la même information lors de la construction du problème ¹Pb1 précédent, ¹C3 « les cases sont ordonnées ». L'information n'est pas traitée de la même façon dans la mesure où elle ne construit pas le même problème.

Nous pouvons alors envisager le losange de problématisation suivant qui permet de schématiser la construction du problème 1 envisagé dans l'analyse a priori.

Conditions :

1I17 64 résultats intermédiaires 1C5

¹I14 Récurrence d'un calcul ¹C6

¹I16 La multiplication par 2 est envisagée comme calcul

récurrent (ou 2n°case-1)

¹C7

¹I5 Les calculs doivent être organisés les uns après les

autres...

¹C8

¹I15 ... à partir du nombre 1 ; ¹C9

¹I19 La somme des 64 résultats doit être

envisagée (résultat 1);

¹C10

Problème ¹Pb2 :
Comment
obtenir le
nombre de
grains de riz
total ?

Solution ¹S2: Résultat 1

Données :

¹I4 L'échiquier a 64 cases ; ¹D5

¹I8 Chaque case contient des grains de riz ¹D6

¹I7 Le nombre de grains de riz est doublé

d'une case à l'autre ;

¹D7

¹I6 1 seul grain de riz dans la première case ; ¹D8

¹I18 La totalité des grains de riz sur l'échiquier

(=résultat1) sera la récompense ;

¹D9

Christelle Brémaud_E179552Q

Les élèves ne se posent pas ici le problème de faire aboutir le calcul de la somme des 64 termes pour obtenir concrètement le résultat 1 final. Cela s'engagera peut-être en phase 2 de débat ou phase 3 lors de la recherche de protocole de résolution.

Christelle Brémaud_E179552Q

[45]

Nous remarquons que même si structurellement, ce problème est quasiment identique à celui de l'analyse a priori, deux informations supplémentaires apparaissent :

- une donnée (« chaque case contient des grains » considérée comme implicite dans l'analyse a
priori)

- et une condition supplémentaire faisant suite au dédoublement d'une condition (C2) pour mieux
mettre en perspective les deux informations qu'elle comportait : nécessité d'un calcul récurrent (¹C6) et nécessité de convoquer la multiplication par 2 ou les puissances de 2 (¹C7).

Pour illustrer les informations recueillies dans les traces écrites des documents 1 lors de ces deux premiers relevés, nous proposons ci-dessous des extraits du corpus :

^1ILéa_3		Figure 1 : Léa « Il y a 64 cases en tout, à chaque lignes il y a 4 noires et 4 blanches, il y a exactement le même nombre de cases noir et de cases blanches (32) »				^1I1 ^1ILéa_3 ^1I4
Figure 4: Elsa		^1I4 ^1I5 ^1I8 1I11 ^1I13 ^1I14
Figure 5: Rozenn Nous ne retenons ici que la nécessité d'additionner à ce qui est attendu (ici les numéros de cases au			ne correspondent pas
Figure 7 : David Figure 8 : Rozenn

Christelle Brémaud_E179552Q

[46]

^1I1
			^1I6
			^1I7
			^1I8
			^1I9
			^1I10
Figure 9 : Romain Figure 10 : Maxime	^1I13
	^1I7
Figure 11: Jordan « on dit dans l'énoncer que le nombre de grains était doublé d'une case à l'autre »	^1I4
	^1I8
	1I9
Figure 12: Gabin « un échiquier est composé est composé de 64 cases. On nous dit que le souverain doit
donner grain de riz lorsque celui-ci est sur la première case, et ainsi de suite. »

iii. Troisième relevé d'indices parmi les traces écrites (documents 1)

Nous reprenons le point évoqué en préambule de ce paragraphe 5.1 pour mieux éclairer la lecture suivante des copies et ce troisième relevés d'informations. Bien que la consigne soit de formaliser ce que l'élève comprenait ou pas de la situation posée, sans nécessité de résoudre et donc sans chercher d'emblée à répondre à la question posée, 9 documents 1 font apparaitre une réponse à la question « la requête est-elle réalisable ? » et 4 interrogent (ou semblent interroger) les conditions de faisabilité ce que nous décidons d'observer ici.

Nous retirons des copies (en plus de celles d'Inès et d'Erwan déjà retirées) celles d'Evan, d'Hugo et de Marie qui ne nous renseigneront plus sur ce que nous voulons lire. Le corpus se réduisant à 12 copies.

Nous précisons qu'une copie (document 1Rozenn) se décompose en deux parties présentant deux points de vue différents, nous la comptabiliserons comme 2 copies.

Donc 13 documents 1 retiennent notre attention ici dont 9 statuent sur la faisabilité ou non de la requête :

- 5 concluent sur la faisabilité de la requête :

o 1 élève (partie 1 de document 1 Rozenn) obtient un résultat faux (somme des 64 premiers entiers
= 2080) mais peut conclure sur la faisabilité de cette requête, ce qui sous-entend que si le

Christelle Brémaud_E179552Q

[47]

calcul est possible en parvenant à un résultat correspond à une quantité raisonnable, la requête est réalisable,

o 2 autres pointent des contraintes (pressentant une quantité « illimitée » et donc ce qui semble être un problème de stockage (document 1 Coralie) qui ne leur semble pas insurmontable pour que la requête soit réalisable ;

o 2 élèves posent que la requête est réalisable sans amener de preuve ni étayer leur réponse posée comme une vérité (document 1Gabin et document 1Léa) ;

- 4 concluent clairement sur la non faisabilité de la requête laissant apparaitre une quantité totale de
grains pressentie comme trop importante (mais non calculée) ;

- 1 élève ne se prononce pas mais précise que « cela dépend » en exprimant des conditions de façon
littéraire (document 1Dorian) ;

- 3 élèves (document 1 Théo, document 1 Axel et document 1 David). Le document 1 Axel est une copie
conforme de document 1 Théo par recopiage d'Axel sur Théo semble-t-il. Elles ne précisent rien au sujet de la faisabilité cependant elles mettent des contraintes en perspective. Pour information, Théo (élève de seconde générale réorienté en première bac professionnel) a peut-être déjà traité cette situation. Mais même si tel est le cas, comment peut-il se rappeler de cette ressource extérieure « production de grains de riz par : 429 200 000 000 kilo/an » ? Le corpus ne permet pas de répondre à cette question. Se pose alors la question du respect des règles qui étaient ici que la recherche se faisait individuellement et sans aucun accès à internet ou autre source d'informations que celles de l'énoncé.

La réponse à la question posée étant binaire « oui la requête est réalisable » ou « non elle ne l'est pas », nous n'accorderons aucune crédibilité aux réponses amenées à ce stade sans raisonnement construit et abouti en amont. Mais nous retenons ici l'émergence de contraintes qui semblent poser problème aux trois élèves (évoqués dans le dernier point) sans qu'ils formulent pour autant de conclusion hâtive.

Recherche des contraintes pour envisager de répondre au problème posé			Copies	Contraintes à prendre en compte pour conclure sur la faisabilité de la requête
		10/13	- Evocation de l'importante quantité que représentera le résultat
^1I20		8/10	- Evocation et/ou recherche de contraintes de faisabilité
		5/10	o « la richesse du roi » ? (pour comparaison au nombre de grains à disposition)
^1IDorian_21		1/5	o l'espace de stockage ? o cette dernière étant rejetée
1IDavid_22 ^1ICoralie_23		2/5	o Mobilisation de données extérieures au problème (pour comparaison ?)
^1IThéo_24		2/5

A ce stade là de raisonnement, il est difficile de donner un statut aux cinq nouvelles informations recueillies qui présage d'un problème qui se pose pour conclure sur la faisabilité de la requête et qui met en évidence l'obstacle pour les élèves de mobiliser des ressources extérieures au problème posé (mais

Christelle Brémaud_E179552Q

[48]

qui doivent avoir du sens) pour ce problème mathématique à résoudre pendant cette séquence. Nous y reviendrons en phase 2 où certaines de ces informations seront remobilisées et éclairées.

Pour illustrer les informations recueillies dans les traces écrites des documents 1 lors de ce troisième relevé, nous proposons ci-dessous des extraits du corpus :

^1IDorian_21		Figure 13: Dorian "Cela dépend de la taille de l'échiquier, du nombre de grains de riz que possède le souverain, de la richesse du roi. Il faudra calculer le nombre de grain de riz par case et ensuite tout additionné"	^1IDavid_22
F igure 14 : David. L'élève épaissit le plateau (pour que chaque case puisse contenir plus ?)		^1ICoralie_23
Figure 15 : Coralie « Cette enquête est réalisable car on ne dit pas qu'il faut mettre le riz sur la case, donc le souverain peut donner à l'inventeur un nombre illimité de grains de riz. S'il faut poser les grains de riz sur les cases c'est possible car selon la taille du plateau ça passe sur les cases »		^1IThéo_24
Figure 16: Théo

Nous précisons que certains élèves ont rendu leur feuille pensant, semble-t-il, qu'ils avaient répondu à la situation-problème posée (alors même qu'ils n'avaient pas le nombre total de grains de riz), d'où un certain malentendu qui a eu, à notre sens, comme conséquence que certains groupes n'ont pas

[49]

réinterroger et critiquer en phase 3, le travail fait en phase 1 et ne l'ont fait qu'en ultime phase 4 alors qu'ils devaient formaliser leur raisonnement pour parvenir à un résultat.

Nous réinterrogerons alors le fait que certains éléments pouvant aider à problématiser et ayant été relevés par certains élèves n'ont pas été discutés lors du débat en phase 2 comme nous allons le voir.

5.2. Complément de la première analyse (phase 2) : ce que révèle l'enregistrement audio³⁴ de la phase de synthèse collective des recherches préliminaires à la résolution

Le tout début de la transcription de la phase 2 (alors que les élèves rendaient leur document 1) fait apparaitre des échanges entre élèves permettant de remettre à jour les informations ²IMaxime_1, ¹I18, ¹I19 relevées lors de la résolution du problème ¹Pb1 :

- L'information ²IMaxime_1 prise alors comme condition ¹C1 (aucune distinction de couleur à faire
d'une case à l'autre pour les 64 cases) dans la construction du raisonnement.

9

Maxime

Bah c'est un damier blanc

Christelle Brémaud_E179552Q

- L'information ¹I18 était la donnée ¹D9 (la récompense est la totalité des grains sur le plateau) qui a

donné à l'information ¹I19 le statut de condition ¹C10 (il faut additionner tous les grains obtenus sur chacune (des 64) cases) :

10	Elsa	Bah non après faut additionner toutes les cases		^1I19	11
Evan	Bah non, faut pas additionner toutes les cases			12
Elsa	Bah si parce qu'il faut savoir combien de grains de riz... après faut savoir...	^1I18

Nous précisons cela pour illustrer le fait que certaines informations sont discutées à différents moments de la séquence pour plusieurs raisons nous semble-t-il :

- Les interactions entre élèves peuvent permettre à certains qui n'auraient pas relevé, ou compris, ou
utilisé certaines informations, de s'en saisir suite aux moments d'échanges,

- Une information relevée à un moment du raisonnement pour une raison particulière peut être
convoquée à un autre moment pour d'autres raisons (comme nous l'avons vu dans le paragraphe précédent pour ¹I4, ¹I5, ¹I6, ¹I7, ¹I8).

Nous pouvons alors envisager que l'échange lors de la phase 2, permette de mettre à jour les données et conditions suffisantes pour avancer dans la construction du problème amorcé précédemment.

A ce stade de leur réflexion, un certain nombre d'élèves semblent avoir admis qu'un calcul était envisageable pour trouver le nombre total de grains de riz à donner en récompense même si la procédure de calcul n'est pas encore aboutie, comme nous le verrons plus loin. Mais un manque certain d'informations semble apparait alors :

³⁴ Annexe 6

Christelle Brémaud_E179552Q

[50]

- certains élèves en font abstraction et parviennent à envisager un début de modélisation pour

engager un calcul

- et d'autres ne semblent pas parvenir à dépasser certaines contraintes que fait apparaitre la situation.
Cette phase de discussion collective pourrait permettre de régler cette difficulté pour que les élèves puissent s'engager dans une résolution mathématique.

i. Formalisation de certaines contraintes paralysantes comme sous problèmes à résoudre (voire à évacuer) pour s'engager dans une résolution mathématique :

La photo du tableau en fin de synthèse collective sur l'appropriation de la situation-problème fait apparaître des nécessités qui ne sont pas directement d'ordre mathématique et qui laissent à croire que les élèves se trouvent confrontés à un problème de la vie quotidienne et non à un problème mathématique qui leur est donné à résoudre.

Nous pouvions pressentir cet échange au travers des recherches individuelles de certains élèves qui

- sans pouvoir le formuler, ne parvenaient peut-être pas à dépasser certaines contraintes logistiques
sous-jacentes à l'énoncé pour engager un raisonnement (on ne peut ici que le supposer dans la mesure où l'élève ne laisse aucune réelle explication):

Figure 18 : seule information écrite sur document 1 (Inès)

Figure 17: Seule information écrite sur document1 (Hugo)

- explicitaient clairement ces contraintes : Figure 19: Dorian « Cela dépend de la taille de l'échiquier, du

nombre de grains de riz que possède le souverain, de la richesse du roi. Il faudra calculer le nombre de grains de riz par case et ensuite tout additionner. »

Le tableau suivant permet de mettre en parallèle certaines des informations relevées lors de la phase 1 et ces nouvelles informations relevées en phase 2.

Traces écrites au tableau				« Il n'y aura pas assez de grains de riz »
^2I1		^1I16	« Il n'y a pas assez de place sur l'échiquier (dépend de l'échiquier) »
^2I2		^1IDavid_22	« On ne demande jamais de poser les grains de riz sur l'échiquier »
^2I3		^1ICoralie_23	« Ça met du temps mais c'est possible »
^2I4			« au pire, on le fait à la calculatrice, au tableur... »
^2I5			« il n'y a pas assez d'informations : on ne connaît pas la quantité de riz dont dispose le2
		^1IDorian_21	souverain »
I6		1IThéo_24

Beaucoup d'élèves ayant engagé une procédure de calcul lors de leur recherche individuelle, nous aurions pu imaginer que lors de cette synthèse collective sur l'appropriation de la situation, certains

Christelle Brémaud_E179552Q

[51]

éléments de la discussion auraient porté sur l'aspect calculatoire et les problèmes éventuels qu'il pouvait faire apparaitre.

Mais nous voyons clairement ici que le calcul pour obtenir une réponse chiffrée ne semble pas le problème principal qui fait obstacle pour comprendre « le réalisable » de la situation.

Apparaissent des contraintes qui font obstacles :

o Nécessité d'une importante capacité de stockage ²I2 ;

o Nécessité d'un temps important pour comptabiliser le nombre de grains de riz à livrer au créateur du jeu d'échecs ²I4 ;

o Nécessité de trouver plus d'informations ²I6.

Nous voulons chercher à voir ici comment et quand les élèves parviennent à abandonner ce qi nous semble de prime abord comme de fausses contraintes, et que nous nommerons « conditions paralysantes » qui sont de l'ordre de la vie quotidienne, liées à des questions logistiques. L'information ²I3 (« On ne demande jamais de poser les grains de riz sur l'échiquier ») peut laisser percevoir un début de réponse sans pour autant présager que la nécessité ²I6 (« il n'y a pas assez d'informations : on ne connaît pas la quantité de riz dont dispose le souverain ») permette d'aboutir à un résultat (nécessité d'une ressource extérieure à l'énoncé).

L'échange laisse apparaitre que des élèves créent des nécessités qui ferment le problème et qui font obstacles à la création de données pour avancer dans la résolution (comme évoqué avec ²I6). Le problème ne se pose alors pas à ce stade de réflexion dans un cadre mathématique pour eux et ils ne peuvent alors pas entrer dans une démarche mathématique pour engager la suite d'un raisonnement.

Il faut lire la transcription de l'enregistrement audio des échanges lors de cette phase 2³⁵ pour mieux comprendre les obstacles qui se posent aux élèves et comment ces derniers parviennent à en abandonner certains qui soulèvent de « faux » problèmes dans le cadre d'une résolution mathématique de la situation à traiter.

Le questionnement ici met en évidence que le nouveau problème qui se pose, apparait comme les prémisses du problème 2 envisagé dans l'analyse a priori. Nous avions alors envisagé de mobiliser une ressource extérieure (la production mondiale de riz en 2018) comme une donnée (D6) pour pouvoir construire le problème 2. Les élèves ici s'interrogent pour déterminer cet élément qui apparait alors comme une nécessité pour pouvoir envisager de résoudre le problème 2. Comment vont-ils alors résoudre ce nouveau problème qui se pose à eux et que nous coderons ²Pb1?

³⁵ Annexe 6

Christelle Brémaud_E179552Q

[52]

ii. Abandon de certaines contraintes non mathématiques faisant obstacles à la construction du problème

Dans la suite de cette analyse, nous surlignons en jaune les extraits des échanges qui nous permettent de relever les informations consignées dans la colonne de droite.

Les élèves lors de cet échange ont supposé préalablement la nécessité d'un calcul (vu dans l'analyse précédente) même si ce dernier n'a pas été construit pour parvenir au nombre total de grains de riz.

L'extrait suivant le prouve (²IMaxime_1) et nous renseigne également sur le nombre très important pressenti par les élèves (²IMaxime_3) en plus de laisser entrevoir un autre problème qui est que certaines incertitudes se présentent (²IMaxime_2) certainement dues à un manque d'informations révélées par l'énoncé :

		Bah on peut trouver le nombre de grains de riz qu'il faut	^2I7	^2IMaxime_1
69	Maxime	mais on ne peut pas savoir si...	^2I8	^2IMaxime_2
		il est assez énorme	^2I9	^2IMaxime_3

Nous avions précédemment relevé ¹IDavid_22 (figure 13 : l'élève épaissit le plateau (pour que chaque case puisse contenir plus ?)) après avoir interprété le dessin que l'élève avait fait d'une partie de l'échiquier épaissit en 3D et qui nous semblait prouver qu'il s'interrogeait sur la possibilité de stocker tous les grains de riz sur chacune des casses. Nous avions également relevé ¹ICoralie_23 (« on ne dit pas qu'il faut mettre le riz sur la case ») qui telle que décrite très clairement de façon littérale par l'élève, paraissait avoir alors le statut de condition pour le problème soulevé alors du stockage d'une quantité pressentie comme très importante. Ces deux informations sont reprises ici et donnent lieu à un échange pour résoudre le « problème de stockage » :

Contrainte de la nécessité d'une importante capacité de stockage :
32	Evan	Il n'y a pas assez de place	^2I10	^2IEvan_4
33	Maxime	... même pour euh
34	PS (note)	Il n'y a pas assez de place
35	Elsa	Bah ça dépend de l'échiquier ! Tout dépend de l'échiquier...	2I11	(^2IElsa_5=) 1IDavid_22
36	Maxime	La taille de l'échiquier... l'échelle de l'échiquier. Donc il ne va pas s'amuser à compter un million de grains de riz non plus quoi !	^2I12	^2IMaxime_6
45	Coralie	On n'a jamais dit qu'il fallait les poser sur le cadre	^2I13	(^2ICoralie_7=) ^1ICoralie_23 2IDavid_S
48	Erwan	C'est pas marqué !	2I14
49	David	Voilà... en gros c'est obligé !	^2I15	^2IDavid_9
69	Maxime	Bah on peut trouver le nombre de grains de riz qu'il faut mais on ne peut pas savoir si... il est assez énorme !	^2I7 ^2I8 ^2I9	^2IMaxime_1 ^2IMaxime_2 ^2IMaxime_3
77	Elsa	La taille de l'échiquier
84	David	Est-ce que, non... est-ce que les grains de riz doivent rester absolument sur les cases ou euh
85		Non !
86	PS	On a déjà posé la question... on ne demande jamais de poser les grains de riz sur l'échiquier...
89	Ens.	Est-ce que c'est écrit ? Quelqu'un a dit tout à l'heure « ce n'est pas écrit »
90	David	Bah oui
91	Romain	Ce qui n'est pas écrit n'est pas écrit	^2I16	^2IRomain_10

Christelle Brémaud_E179552Q

[53]

Les élèves discutent ici de la nécessité ou pas, de prendre en compte un problème logistique de stockage. Nous le réduisons à un extrait de 14 tours de paroles mais nous attirons l'attention sur le fait qu'il mobilisera les élèves pendant tout l'échange nous permettant de penser qu'ils ont du mal à abandonner cette contrainte et nous interrogeant sur le fait qu'ils y parviendraient plus facilement s'ils pouvaient en faire apparaitre de nouvelles plus fructueuses et surtout fournissant suffisamment d'éléments pour la construction du problème que cette contrainte de stockage ne permet pas de faire avancer.

Après avoir rappelé que le problème n'était plus le calcul ici, permettant de donner à ²IMaxime_1 (« on peut trouver le nombre de grains de riz qu'il faut ») et ²IMaxime_3 (« il est assez énorme ! ») le statut de données (²D1 et ²D2), deux conditions apparaissent ici. La nécessité d'une importante capacité de stockage construite avec ²IElsa_5 (« tout dépend de l'échiquier ») et précisée par ²IMaxime_6 (²C1) (« la taille de l'échiquier ») s'impose suite à ²IEvan_4 (« il n'y a pas assez de place ») déposée comme un fait ici ce qui permet de lui donner le statut de donnée (²D3). La seconde condition (²C2) révélée par ²IRomain_10 (« ce qui n`est pas écrit n'est pas écrit ») s'impose par le fait révélé par ²ICoralie_7 (« on n'a jamais dit qu'il fallait les poser sur le cadre ») et formulée différemment dans ²IDavid_8 (« c'est pas marqué ! ») déjà relevée dans le document 1 Coralie dans le paragraphe précédent (¹ICoralie_23).

La solution n'est ici que partielle, mais elle permet de poser le problème ²Pb1 (trouver les conditions pour pouvoir statuer sur la faisabilité de la requête). Nous proposons alors le losange de problématisation suivant :

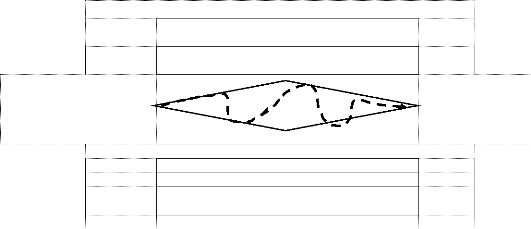
²IMaxime_6 :

²IRomain_10 : Ou ne pas tenir compte de ce qui n'est pas écrit 2C2

dans l'énoncé

Problème ²Pb1:
Est-ce que le problème de
stockage est à prendre en
compte ?

Données :

²IMaxime_1 : On peut calculer le nombre total de grains ²D1

²IMaxime_3 : La quantité de grains sera très importante ²D2

²IEvan_4 : Il n'y aura pas assez de place sur l'échiquier pour 2D3

stocker les grains de riz

²ICoralie_7 : Rien n'est précisé dans l'énoncé à ce sujet ²D4

²IElsa_5 et Tout dépend de l'échiquier...de la taille de l'échiquier ²C1

Conditions :

Hypothèse ²H1:

Si rien n'est écrit alors on fait abstraction de

la contrainte de

stockage

L'échange révèle également d'autres problèmes relevés par le questionnement des élèves.

Comment les élèves abandonnent la contrainte de la nécessité du temps à passer pour le comptage de la récompense finale :
36	Maxime	La taille de l'échiquier... l'échelle de l'échiquier. Donc il ne va pas s'amuser à compter un million de grains de riz non plus quoi !	(^2I17 =) ^2I19	^2IMaxime_11 ( ^2IMaxime_3)
37	PS (note)	Tout dépend de l'échiquier
38	Elsa	En pas mal de temps quoi !	^2I18	^2IElsa_12

Christelle Brémaud_E179552Q

[54]

39	PS	Ça met du temps
40	Elsa	.... C'est possible... c'est possible mais il va passer pas mal de temps !	^2I19	^2IElsa_13
41		(inaudible)
42	Inès	C'est clair
43	David	... mais c'est le souverain... (inaudible)
44	PS (note)	Ça met du temps mais c'est possible... que peut-on rajouter ?
91	Romain	Ce qui n'est pas écrit n'est pas écrit	(^2I20=) ^2I16	^2IRomain_10

Peut-on vraiment parler de problématisation ici sur ce point particulier de la contrainte de temps que cela peut prendre pour que la requête soit envisagée comme réalisable?

Alors qu'il y a questionnement, aucun cheminement clair n'apparait dans le raisonnement pour construire une hypothèse, voire une solution à ce problème sous-jacent. Il nous parait toutefois, important de faire apparaitre ce début de questionnement dans la mesure où il aurait pu faire émerger la nécessité de mesurer le nombre de grains de riz total (que les élèves semblent pouvoir calculer) dans une autre grandeur que la seule valeur cardinale envisagée. Avec la masse d'un grain de riz par exemple, il leur serait faisable de calculer la masse totale du résultat trouvé, ce qui aurait plus de sens et qui permettrait d'éviter ce comptage envisagé qui semble faire obstacle à ce que la requête soit réalisable même si l'élève balaie trop rapidement cette contrainte empêchant par là-même, la création de nouvelles données nécessaires pour l'avancée dans la résolution du problème posé et qui nécessitera par la suite de leur proposer un « coup de pouce ».

Comment les élèves abandonnent la contrainte de la nécessité que le souverain « soit riche » :
21	Romain	Il n'y aura pas assez de grains	^2I21	^2IRomain 14
25	Romain	Il n'y aura jamais assez de grains
26	PS (note)	Il n'y aura jamais assez de grains
27	Dorian	Bah, Ça dépend du nombre de grains qu'il a	^2I22	^2IDorian_15
28	Elsa	Bah non, s'il réunit toutes les rizicultures	^2I23	^2IElsa_16
30	PS	Il n'y aura jamais assez de grains
43	David	... mais c'est le souverain... (inaudible)	^2I24	^2IDavid_17
67	Dorian	(A Elsa) Non parce que tu peux connaître le nombre de grains de riz, mais tu seras incapable de dire s'il y en a assez ou pas.	^2I25 ^2I26	^2IElsa_18 ^2IElsa_19
68	Evan	Ah oui !
69	Maxime	Bah on peut trouver le nombre de grains de riz qu'il faut mais on ne peut pas savoir si... il est assez énorme	^2I27	(^2IMaxime_20=) ^2IMaxime_3
71	Maxime	On peut réussir à connaître le nombre de grains de riz qu'il faut mais on sait pas après s'il y en a assez ou pas
72		Bah si !
73	Elsa	Le roi on ne sait pas ce qu'il est capable de fournir	^2I28	^2IElsa_21
74	Dorian	Est-ce qu'il est capable de fournir ?... oh bah dis donc c'est français ça !
75	Maxime	(à son voisin) C'est le souverain qui donne des grains de riz	^2I29	^2IMaxime 22
76	Dorian	(à Maxime) oui oui
91	Romain	Ce qui n'est pas écrit n'est pas écrit	^2I30	(^2IRomain_23=) 2IRomain_10

Nous notons un certain abandon qui n'est que provisoire ici de cette condition que le souverain ait assez de grains à disposition. Il y aura une nécessité qui n'a pas émergé ici, de comparer le nombre total obtenu de grains de riz à une autre donnée, qui effectivement n'apparaît pas dans l'énoncé pour pouvoir prendre une décision sur la faisabilité de la requête.

La remarque de Romain ²IRomain_10 (tour de parole 91) qui apparait alors ici comme une nécessité (« ce qui n'est pas écrit, n'est pas écrit ! ») fait apparaitre un autre problème que les élèves ont à gérer :

Christelle Brémaud_E179552Q

[55]

« il n'y a pas assez d'informations » dans l'énoncé ce qui peut alors apparaitre paradoxal avec la condition de ne prendre que ce qui est écrit (²C2) pour pouvoir évacuer certains problèmes sous-jacents qui font obstacles.

Nous nous interrogeons sur le fait que les informations ¹IThéo_24 relevées dans document 1Théo n'apparaissent pas (« production de grains de riz par an : 429 200 000 000 kg » et « masse d'un grain de riz 0.020g ») alors même qu'elles auraient pu permettre de trouver cette contrainte que les élèves semblent chercher pour pouvoir conclure sur la faisabilité de la requête. Nous nous demandons ici si l'hypothèse faite par les élèves à ce stade (si rien n'est écrit alors on fait abstraction des problèmes de stockage, de temps et de la richesse du roi, réinterrogeant ce que nous avons appelées précédemment informations non explicites de l'énoncé) n'est pas en soi paralysant pour permettre qu'émerge la nécessité des données révélées dans document 1Théo.

Même si effectivement, comme précisé précédemment, nous ne voyons pas apparaitre la nécessité d'avoir recours à d'une ressource extérieure pour pouvoir répondre au problème, les élèves aboutissent tout de même à l'hypothèse qu'ils ne peuvent pas créer n'importe quelles nécessités (abandon du temps nécessaire à compter les grains, de celle de savoir si le souverain est riche, de celle d'avoir une capacité suffisante de stockage).

Cette phase 2 montre un réel questionnement mais ne permet pas de parler de problématisation. En effet, seule l'hypothèse qu' il ne faut pas prendre en compte certaines contraintes car elles ne sont pas explicitées dans l'énoncé, est vraiment formalisée. Le risque est alors de ne pas mobiliser la donnée extérieure (D6 : résultat 2 dans l'analyse a priori = la production mondiale de riz) et par suite ne pas construire la condition (C6 : comparer le nombre de grains trouvé à la production mondiale) à laquelle il faut avoir recours (comme envisagé dans l'analyse a priori), toutes deux non explicitées dans l'énoncé.

iii. Recherche de données non explicites : « on n'a pas assez d'informations »

Les élèves ont fait émerger des contraintes qui ont été en partie implicitement rejetées sous la forme sous laquelle ils les présentaient. Ces contraintes auraient pu apparaitre comme des conditions mais ayant été rejetées nous ne parlerons que de contraintes. Mais les élèves constatent un défaut d'information. ²IMaxime_2 (« on ne peut pas savoir... ») et ²IDorian_24 (« on n'a pas assez d'informations ») apparaissent comme des données permettant de voir que les élèves pressentent une nécessité qu'ils ne parviennent pas à formaliser et sont démunis pour certains, face à sa non explicitation dans l'énoncé :

61	PS	Bon alors, où est-ce que ça butte ? où est-ce que vous ne comprenez pas ?
62	Dorian	Bah, on n'a juste pas assez de ..... On n'a pas assez d'informations	^2I31	^2IDorian_24
63	Maxime	Il n'y a pas assez d'informations
69	Maxime	Bah on peut trouver le nombre de grains de riz qu'il faut mais on ne peut pas savoir si... il est assez énorme	2I32	(2IMaxime_25=) ^2IMaxime_2

Christelle Brémaud_E179552Q

[56]

Les élèves ne parviennent pas à formaliser cette nécessité (de mobiliser la donnée extérieure (D6) pour pouvoir conclure avec leur résultat 1 (qui semble leur paraître somme toute simple à obtenir) sur la faisabilité ou non de la requête (même si ce résultat n'a pas encore été déterminé). L'enseignant stagiaire (PS dans les transcriptions) tente sans grand succès de les interroger, pour les aider dans leur recherche, mais il ne peut que leur assurer qu'il y a d'autres contraintes (que celles discutées précédemment et que les élèves semblent accepter d'abandonner). Cette tentative de l'enseignant semble leur permettre, dans un premier temps de se dégager des « faux problèmes » afin de passer aux calculs. Mais les élèves ne réinterrogent pas le fait que « tu en as des contraintes, mais pas celles-ci » posé par les enseignants tour à tour (même si formalisé différemment) :

81	PS	Qu'est-ce qui nous manque comme donnée ?
82	David	De quoi ?
83	PS	Vous avez dit qu'il n'y avait pas assez d'informations... est-ce que c'est la seule info qui nous manque ?
91	Romain	Ce qui n'est pas écrit n'est pas écrit
92	David	Bah c'est obligatoirement possible
93	Ens.	Qu'est-ce qui est obligatoirement possible ?
94	David	Que chaque case, on peut toujours doubler si on n'a pas de contrainte...ça nous fait zéro contrainte
95	Ens.	Tu en as des contraintes mais pas celles-ci
97	David	Ah bon !?... parce que j'en vois pas

Nous pouvons alors envisager à ce stade de l'analyse que les élèves réinterrogeront peut-être ultérieurement ce défaut d'informations une fois le nombre de grains de riz trouvé.

L'extrait suivant montre clairement que les élèves passent à l'étape calculatoire sans avoir résolu le problème précédent et que les procédures de calcul ont déjà été réfléchies dans leur prémices ce qui corrobore le pressenti précédent que le calcul n'était pas ce qui les préoccupait en premier lieu. L'enseignant les conforte dans l'idée qu'ils vont obtenir un résultat chiffré mais les réinterroge sur la nécessité de confronter ce résultat (résultat 1) à une autre donnée pour faire apparaitre une condition dans la faisabilité de la requête. Malgré tout, les contraintes discutées précédemment sont tenaces pour les élèves, et même s'ils acceptent de ne pas les prendre en compte pour pouvoir engager un calcul, ils ne les abandonnent pas totalement, ce qui nous parait comme un réel obstacle pour envisager d'en chercher d'autres plus pertinentes :

100	David	Au pire on le fait à la calculette
101	Ens.	.. et comment tu vas faire avec la calculette ?
102	Elsa	Avec les puissances !
103	Ens.	Avec les puissances... c'est toutes ces questions-là qu'il faut que vous vous posiez
104	Elsa	(en même temps que l'Ens.) 2 puiss...1... plus 2 puissance 2 plus de 2 puissance 3
105	Ens.	C'est avec toutes ces questions-là que vous allez réussir à arriver à la solution... est-ce qu'il n'y a que la calculatrice ? Vous avez peut-être d'autres outils à disposition
107	Ens.	Les tableurs... vous pouvez tout imaginer... comment vous allez chercher à résoudre ce problème-là pour pouvoir y répondre ... et est-ce que la solution à laquelle vous allez arriver elle est plausible ? parce que l'idée c'est que « est-ce que la requête est réalisable ? » c'est-à-dire est-ce que la réponse à laquelle vous allez arriver est plausible ?... Au regard de quoi ?
108	Elsa	Bah du temps passé quoi!
109	Ens.	Et peut-être d'autres informations dont vous ne disposez pas, que vous allez avoir à aller chercher... pour comparer votre résultat à des données
110	Maxime	De toute façon, il n'arrivera jamais à compter exactement tout le nombre des grains de riz
113	Ens.	Ah bah le but, si on vous donne ça c'est qu'il y a quand même une possibilité d'y arriver !

Christelle Brémaud_E179552Q

[57]

115	Ens.	« Est-ce que c'est réalisable ? » ça ne veut pas dire que vous n'allez pas réussir à obtenir une réponse
117	Ens.	parce que le but du jeu, parce qu'on n'est pas pervers quand même, c'est que vous êtes censés pouvoir obtenir une réponse... maintenant pour savoir si c'est réalisable il va falloir que vous mettiez votre réponse au regard de certaines données que vous irez chercher... qui vous semblent pertinentes... pour pouvoir comparer et valider du coup la chose

Il n'y a pas de problématisation dans ces extraits. Malgré les tentatives des enseignants pour que les élèves se réinterrogent sur le défaut d'informations qui les met à mal, nous ne voyons pas dans la transcription de tours de parole élève construire le problème autour de cela. Nous voyons même une persistance (« on peut toujours doubler si on n'a pas de contrainte... ça nous fait zéro contrainte » tour de parole 94) à ne pas envisager d'autres données.

Même si apparaissent des semblants de données et/ou nécessités, le cheminement dans le questionnement est trop chaotique et surtout n'aboutit pas pour pouvoir parler de problématisation. Mais il nous semble important toutefois de ne pas passer sous silence ces différents échanges soulevant de nécessaires questions sachant qu'il n'y a pas de cheminement linéaire dans une résolution de problème que les élèves ont d'abord à construire avant de le résoudre.

5.3. Deuxième analyse (phase 3) : ce que révèlent les traces écrites des recherches de protocole de résolution lors du travail de groupe (documents 2)

Les documents 2 relevés suite aux travaux des 5 groupes révèlent encore peu de chose en termes de problématisation. La consigne avait été clairement donnée de ne pas chercher à obtenir de résultat

chiffré mais de rendre compte d'un protocole de résolution (pour obtenir un résultat et par la suite

conclure sur la faisabilité de la requête) comme rappelé par l'enseignant stagiaire (au tour de parole 21) dans l'extrait suivant de la transcription de la phase 3³⁶ : « Alors dans cette deuxième partie, on ne vous

demande pas de trouver la réponse, mais on vous demande de proposer une démarche qui peut conduire à la résolution, donc pour faire cela c'est toutes les ressources dont vous allez avoir besoin... que ce soit des informations... concernant le problème, que ce soit du matériel, des calculs. D'accord ?... c'est tout ça qui doit apparaitre dans votre trace écrite... »

La lecture des documents 2 laisse apparaitre que seul le problème 1 (de l'analyse a priori) relatif au calcul a été traité pendant cette phase de travail de groupe faisant suite au problème ¹Pb2 construit en phase 1. Au-delà de notre enquête pour savoir si les élèves problématisent, nous cherchons ici à repérer

- comment le savoir se construit

- comment les élèves vont parvenir au nombre total de grains de riz

- s'ils cherchent également à répondre au problème posé de la faisabilité de la requête

³⁶ Annexe 8

[58]

Sans vouloir faire l'analyse des erreurs repérées car tel n'est pas notre sujet d'étude, nous pointerons certaines erreurs tout de même pour mettre en perspective la difficulté à mobiliser à bon escient les outils mathématiques. Puisque, comme dans l'analyse précédente, nous pointons encore ici, à la première lecture de leurs traces écrites un réel défaut de problématisation, nous pourrons nous interroger sur les raisons de ce manque. Est-ce dû à une non maitrise des fondamentaux mathématiques ? A un problème à oraliser et/ou par suite à transcrire ? Au fait que la problématisation ne soit pas enseignée comme outil de raisonnement (si l'on considère qu'elle n'est pas naturellement mobilisable) ?

Nous retenons du corpus, quatre documents révélant chacun des singularités.

Groupe 1 : Les élèves ici ne semblent pas avoir compris la consigne et ne cherchent qu'à parvenir à un résultat sans vraiment savoir à quoi il correspond. Les égalités écrites sont fausses mais traduisent le fait que deux calculs ont été faits pour obtenir le nombre de grains sur les cases 32 et 64. 2 147 483 648 correspond au nombre de grains sur la case
	Figure 20: document 2_David (groupe 1)

n°32. L'écoute de l'échange entre les élèves³⁷ révèle que le groupe parvient laborieusement à ce résultat par multiplications successives par 2 construisant ainsi la suite terme par terme à partir du précédent alors qu'initialement l'utilisation des puissances étaient envisagées mais vite abandonnée car non maitrisée.

La seconde valeur écrite 1.844674407E+19 (que les élèves ne parviennent pas à interpréter comme étant 1.844674407×10¹⁹) présentée comme le 64^eme terme à déterminer (nombre de grains sur la dernière case) semble avoir pourtant été obtenue avec les puissances en calculant 2⁶⁴ (au lieu de 2⁶³ attendu révélant le problème d'indice).

La transcription de l'échange montre qu'ils envisagent de « tout additionner » mais ni la transcription ni leur trace écrite ne dit ce que le « tout » représente.

Groupe 2 :

Figure 21: document 2_Elsa (groupe 2)

Les élèves proposent ici un calcul détaillé qui indique que le nombre de grains de riz un de la case n (cases implicitement numérotées ici de 1 à 64 « car il y a 64 cases » ³Igroupe2_1), sera calculé à partir de n-1, selon la formule un=2^n-1 (avec

³⁷ Annexe 8

Christelle Brémaud_E179552Q

Christelle Brémaud_E179552Q

[59]

explicitement détaillé 1, 2¹, 2², , 264 (³Igroupe2_2) voire de façon littérale « soit 2 fois puissance le

nombre de la case » (³Igroupe2_Elsa_3) avant d'envisager la somme de ces 65 (!) termes (« et ensuite tout additionné » ³Igroupe2_Dorian_4).

Mais ils ne semblent pas se poser plus de question sur cet indice n et s'ils partent bien du terme u1 = 1, ils ne l'associent pas à 2⁰ pour envisager le dernier terme u64 = 2⁶³.

Même si ces informations correspondent en partie à certaines données de l'analyse a priori du problème 1, elles ne permettent pas ici de discuter pour leur donner un statut de donnée ou de nécessité dans la mesure où les élèves poursuivent ici la construction du problème ¹Pb2 engagé en phase 1 mais sans encore parvenir à formaliser le résultat. Nous notons par exemple que ³Igroupe2_Elsa_3 est littéralement identique à D4 (l'échiquier à 64 cases) mais que par exemple ³Igroupe2_Elsa_2 peut aussi bien être interprétée

- comme D2 (1 seul grain dans la case 1) et D3 (2 dans la case 2 et ainsi de suite) réunies

- que comme les conditions (récurrence du calcul) et C3 (les calculs doivent être organisés les

uns après les autres) réunies

selon le cadre explicatif d'une problématisation éventuelle qui n'a pas cours ici.

Nous ne relevons ces informations que dans la mesure où elles permettront peut-être de faire aboutir la construction du problème 1 en phase 4.

Les élèves n'expliquent pas ici comment ils se serviront de la calculatrice ou du tableur pour effectuer ce fastidieux calcul. Peut-être que lors de la phase 4 (résolution du problème donc inévitablement réalisation du calcul), ils pointeront ce problème d'indice et le résoudront.

Le groupe 1 n'a visiblement pas compris la consigne et ne cherche pas vraiment à la comprendre d'ailleurs comme peut le révéler la transcription. Quant au groupe 2, il semble se satisfaire d'un calcul rapidement trouvé, avec d'ailleurs une certaine aisance et qui lui garantit d'obtenir un résultat (voire LE résultat), sans vouloir plus s'engager dans la suite du travail demandé, à savoir, réfléchir à l'utilisation de la calculatrice ou du tableur qu'il propose d'utiliser. Cela aurait pu permettre que les élèves se questionnent afin de résoudre le problème d'indice mis en évidence précédemment.

Les échanges dans les groupes 1 et 2 lors de cette phase 3 ont été enregistrés mais seul celui du groupe 1 a été transcrit (même s'il ne nourrira pas l'analyse faite par la suite comme nous l'expliquerons plus tard) car celui du groupe 2 révèle un certain manque de sérieux dans le travail demandé malgré un réussite constatée dans leur traces écrites laissées dans les documents 2.

Groupe 3 : L'information « si on s'en suit à la consigne l'expérience est réalisable » ne nous donne que très peu d'indication sur ce que les élèves entendent du problème à traiter (« exercice » ?) et ce qu'ils extraient	[60]
	Figure 22: document 2_Gabin (groupe 3)

de « la consigne » et d'ailleurs même ce qu'ils désignent comme « consigne ». Sous entendent-ils ici que si le calcul est réalisable alors la requête l'est aussi créant une confusion entre faisabilité du calcul nécessaire dans ce problème et faisabilité de la requête ? Nous supposons alors (ce que confirmera la transcription) que le groupe répond au problème posé en stipulant que puisque le calcul est possible, la requête est réalisable mettant ainsi de côté tous les problèmes de contraintes non trouvées qui semblaient faire obstacle lors de la phase 2.

Ce qu'ils présentent ici comme ébauche de ce qu'ils envisagent d'effectuer sur tableur, ne prend pas en compte le nombre de grains sur la première case et ne commencent qu'à partir de la case n° 2 détaillant le calcul à effectuer pour la case n°3 alors même que sur chacun de leurs trois documents 1 de recherche individuelle, ils avaient pris en compte ces informations manquant ici.

La trace écrite ici ne rend pas vraiment compte de la richesse des échanges qui ont eu lieu dans ce groupe. La transcription nous permettra une seconde analyse plus fine dans le paragraphe suivant tant sur la construction du savoir en jeu que sur les nécessités s'imposant et qui prédisent une éventuelle problématisation. Nous pourrons alors voir de façon plus claire l'obstacle que constitue le passage à l'écrit dans la restitution des travaux de ces élèves.

Groupe 4 :

Le seul groupe qui ait réellement répondu à la consigne fait apparaitre clairement l'importance des numéros de chaque case, qui constitueront les indices dans la suite à construire (³Igroupe 4_5).

Figure 23: document 2_Jordan (groupe 4)

Cette information à elle seule résume les trois conditions C1 (63 calcul à envisager), C3 (les calculs sont organisés les uns après les autres) et C4 (à partir du nombre 1).

Christelle Brémaud_E179552Q

Sur la même ligne nous voyons apparaitre le calcul (qui laisse présager d'une formule du type « =2×cellule précédente », sur le côté droit des 2 colonnes utilisées dans le tableur pour construire terme à terme cette suite géométrique de premier terme u1 = 1 et de dernier u64 et de raison 2, par multiplications

Christelle Brémaud_E179552Q

[61]

successives du terme précédent par la raison 2 (³Igroupe 4_6). Ces informations laissent présager d'une utilisation pertinente du tableur envisagé comme outil pour ce calcul coûteux.

3I groupe 4_5 et 3I groupe 4_6 apparaissent alors ici comme des conditions pour pouvoir envisager un calcul. Mais rien ne permet encore ici de construire un losange de problématisation dans la mesure où la trace écrite ne renseigne pas sur de quelconques données prises en compte pour parvenir à ce protocole ni de plus de conditions que les deux relevées précédemment.

N'apparait toutefois pas ici la nécessité de la somme des 64 termes obtenus pour pouvoir envisager de répondre au problème posé, ni de la nécessité de comparer le résultat final obtenu à une donnée qui aurait du sens.

On note ici la non maitrise de la multiplication par 2 de l'élève rédacteur de cette trace écrite (2×2=6 !, 2×6=8 !...) qui additionne 2 plutôt que multiplier par 2 alors même que son détail de calcul est sans ambiguïté sur l'opération à effectuer. Nous pouvons nous interroger sur les conséquences de la non maîtrise des fondamentaux mathématiques sur la possibilité éventuelle de problématiser dans le cadre d'une situation mathématique.

5.4. Complément de la deuxième analyse (phase 3) : ce que révèlent les enregistrements lors du travail de groupe pour la recherche d'un protocole de résolution

Nous ne retiendrons ici qu'une seule des deux transcriptions faites pour cette phase 3, celle du groupe 3³⁸ (Evan, Gabin, Romain). L'échange qui a eu lieu dans le groupe 1 ne permet pas de trouver de traces de problématisation et révèle trop peu d'engagement des élèves dans le travail demandé.

Nous tenterons de dégager de cette transcription les informations nous renseignant sur la construction du problème 1 d'une part, mobilisant les élèves sur le calcul à mener pour obtenir le résultat 1, et la construction du problème 2 d'autre part, pour conclure sur la faisabilité de la requête posée dans la situation-problème.

Les informations relevées relatives au problème 1 pour obtenir le nombre total de grains de riz seront surlignées en jaune, celles relatives au problème 2 pour pouvoir conclure sur la faisabilité de la

requête seront surlignées en bleu. Et nous surlignerons en vert les

informations permettant de trouver la

donnée extérieure qui permettra d'aboutir à la conclusion car il nous semble que suite à l'analyse de la phase 2, pendant laquelle les élèves se sont interrogés sur les contraintes à prendre en compte, cette donnée à trouver semble constituer un réel problème que les élèves doivent résoudre.

Ce codage par couleurs fait apparaitre trois séquences dans cette transcription. Nous décidons de nommer séquences 1 et 2 celles construisant le problème 1 avec d'une part la recherche des calculs à effectuer et la seconde avec leur organisation afin de parvenir aux résultats. Ces deux séquences seront

³⁸ Annexe 8

Christelle Brémaud_E179552Q

[62]

analysées au regard du savoir à construire. La troisième séquence permet de construire le problème 2. Nous faisons remarquer que le numéro de séquence ne respecte pas la chronologie des échanges. En effet, chronologiquement la séquence 3 fait suite à la séquence 1. La séquence 2 n'apparaissant qu'en fin de cette phase 3, au moment où les élèves doivent rédiger la procédure de résolution (qui ne se limitera ici au final, qu'à l'organisation sur tableur des calculs à effecteur comme nous le verrons par la suite, donc uniquement à une partie de la résolution du problème 1).

i. Séquences 1 et 2 : construction du problème 1 et calculs envisagés par les élèves au regard du savoir à construire

Les extraits suivants de la transcription des échanges lors de cette phase 3 révèlent en fait bien plus de choses concernant les choix que font les élèves et la construction des problèmes 1 et 2 que ce que révèlent les documents 2.

Séquence1 :

Nous analysons la séquence 1 correspondant à la formalisation des calculs à effectuer afin de trouver le nombre de grains de riz au regard du savoir à construire et tentons de voir au-delà du questionnement des élèves comment ils poursuivent la construction du problème 1 déjà engagé en phase 1 même si leur trace écrite (documents 2) ne révèlent rien à ce sujet.

La première séquence relevée dans cette transcription et correspondant à la première partie des échanges, renseigne sur la construction que les élèves envisagent pour trouver LE résultat. Encore faut-il comprendre de quel résultat il s'agit, ce que ne révèlent pas les documents 2 des élèves de ce groupe (figure 2 : Gabin). Nous rappelons que leurs comptes rendus n'indiquent que 2 calculs permettant de voir que les élèves envisageaient la multiplication par 2 de façon récurrente pour passer du nombre de grains d'une case à celui de la suivante mais en partant de la case n°2 (avec 2 grains) et sans préciser combien de fois ils envisageaient ce calcul récurrent ni comment ils allaient clairement mobiliser les cellules du tableur avec en commentaire unique « le calcul total sera fait sur Excel » :

2	X	2	4
4	X	2	8

Nous rappelons la valeur chiffrée « 2×2⁶³ » et la conclusion « la requête est donc iréalisable » du document 1Romain³⁹ ainsi que la valeur « 2080 » correspondant à la somme des 64 premiers entiers naturels des documents 1Gabin⁴⁰ et document 1Evan⁴¹. Les échanges permettent de voir quels sont les problèmes rencontrés notamment concernant les premier et dernier termes de la suite à construire :

³⁹ Annexe 5 p.96

⁴⁰ Annexe 5 p.65

⁴¹ Annexe 5 p.94

Christelle Brémaud_E179552Q

[63]

Echanges entre les élèves du groupe 3 lors de la phase 3			Informations relevées	Construction du savoir en jeu
				Raisonnement élève
8	Romain	En formule ? Euh... Bah c'est 2 fois 2... euh.... Puissance 63	^3IRomain_1 3 IRomain_2	dernier terme envisagé = 2×263 (considéré comme le résultat 1 recherché ?)	Récurrence du calcul : multiplication par 2 un+1=un×2 (1=n=63) ? ou utilisation des puissances vn=2^n (0=n=63) ?
9	Evan	2 fois 2 puissance 63 ?			Premier terme : u1= 1 si un+1 = un×2 v0= 1 si vn=2^n Dernier terme : u64 = u63×2 si un+1 = un×2 v64= 263 si vn=2^n La suite aurait pu aussi se construire suivant un+1 = un + un (1=n=63) mais de façon beaucoup plus coûteuse car le calcul n'est alors plus récurrent et il ne s'agit alors plus de suite géométrique (ni arithmétique d'ailleurs)
10	Romain	Et puis t'as ton résultat
11	Evan	Non ! Puissance 64	^3IEvan_3
12	Romain	3	(^3IRomain_4=) ^3IRomain_2
16	Romain	Parce que 1 plus 1, 2... c'est là où tu pars de 2 fois 2	^3IRomain_5 ^3IRomain_6	terme 0 = 1 (évoqué mais occulté dans la construction de la suite) terme 1 = 1+1 = 2 (premier terme dans la suite envisagée)
19	Gabin	Et pourquoi t'as fait 2 fois 2 fois 2 fois 2?
20	Romain	Parce qu'en fait je ne me rappelais plus comment on faisait pour faire les exposants, enfin euh... pour les puissances avec la calculatrice...donc au moins là je suis sûr que c'est bon. Et après tu vois là regarde, tu fais le calcul simple... tu vois (passe sa calculatrice à Gabin)	^3IRomain_7		Choix fait : multiplication par 2 pour construire (un) : un+1 = un×2 (1=n=63) avec u1= 1 choix par défaut semble-t-il puisque les puissances (exposants ?) ne semblent pas maitrisées ou tout au moins pose un problème dans l'utilisation de la calculatrice.
25	Romain	En fait, la première case, la première case, c'est 1 plus 1, parce que la deuxième fois c'est 2 parce que tu prends une case de plus... fois 2 et tu peux exposant, euh puissance 63 parce que tu peux pas faire toutes les cases d'un coup	(^33 Romain_8=) 'Romain_5 ^3IRomain_9 3IRomain_10	Pour la « première case » : terme 1 = 1+1 = 2 (alors qu'en fait il s'agit de la case n°2 la case n°1 étant alors occultée ! Calcul du dernier terme à l'aide d'exposant * 663 mais avec 2 2 ou 2^63 ??	Premier terme u1= 1 Deuxième terme u2=u1×2 = 1×2=2 Calcul terme à terme de la suite. Intérêt d'une formule ne faisant intervenir que la raison 2 et l'indice n (utilisation des puissances vn=2^n (0=n=63)) pour s'affranchir des résultats précédents dans le calcul du nombre de grains sur la case n. L'élève obtient alors directement le nombre de grains sur la dernière case u64= 263
38	Romain	1, 2, 4, 8, 16, 32, 64, 128, 2 cents...euh... 256, 520... euh... mille vingt euh	3 IRomain_11	Calcul des 10 premiers termes en considérant la case n°1 ici avec les multiplications successives par 2
42	Gabin	On nous demande pas d'aller jusqu'à autant de nombres là ! On demande juste si la requête est réalisable
51	Gabin	Oui c'est réalisable, si on ne s'attarde vraiment qu'aux consignes c'est largement réalisable ! On nous dit 1 grain de riz sur la première case de l'échiquier, 2 pour la deuxième, et ainsi de suite, le nombre...	(^3IGabin_12=) ^3IRomain_11	L'élève réinterroge les premiers termes u1= 1 et u2= 2
55	Gabin	Parce que là en soi on a là 64	3IGabin_13	Et le rang du dernier n=64
56	Romain	Oui, y a 64 cases
57	Gabin	1, 2...
58	Romain	Je te rassure quand tu arrives à ... dans 7 cases tu t'arrêtes !	3IRomain_14
59	Evan	Pourquoi ?

Christelle Brémaud_E179552Q

[64]

		Tu vas voir... je me suis arrêté à pas très loin en fait... à partir d'un
60	Romain	moment tu commences à aller beaucoup trop loin
61	Evan	On est déjà à 16000...oh !
62	Romain	Ouais et après 32, 64, 128, 720...
		Moi je suis à un million.... Mais
79	Evan	c'est c'est... j'ai fait que trois lignes	^3IEvan_15
		Après, maintenant il reste plus
85	Gabin	qu'à mettre les résultats de nos calculs	^3IGabin_16

Cet extrait met en évidence la difficulté entre autre que pose le choix du premier terme.

Les élèves conçoivent qu'il y aura autant de résultats qu'il y a de cases avec une recherche de calcul récurrent (³IRomain_1 « la formule ») pour passer de la case n°2 (contenant « 1+1=2 » grains (³IRomain_5)) à la case n°3 (³IRomain_6 « c'est là où tu pars 2 fois 2 »). Le choix du calcul fait ici mobilise

- l'addition dans un premier temps pour obtenir le résultat sur la case n°2 d'où veut partir Romain,

- puis la multiplication par 2 pour passer d'une case à l'autre (pour les premières cases)

- puis pour envisager les résultats pour les cases se rapprochant de la dernière case n°64, les

puissances de 2 avec une discussion sur la valeur de cet exposant pour obtenir le résultat attendu pour la dernière case n°64 (tour de parole 8 avec ³IRomain_2 « c'est 2 fois 2... euh.... Puissance 63 » et tour de parole 11 avec ³IEvan_3 « Non ! Puissance 64 »). D'où la nécessité de déterminer d'où part le calcul récurrent.

Les calculs à effectuer se construisent peu à peu mais les élèves ne parviennent pas clairement à

choisir une formule de récurrence pressentie par Romain (³IRomain_1). Ces calculs d'ailleurs ne portent ici que sur les résultats relatifs à chaque case mais les élèves ne parlent pas de la nécessité d'additionner tous ces résultats pour obtenir le résultat 1 attendu.

Le savoir visé (colonne 6) se construit petit à petit (colonne 5) mais les échanges ici traduisent une explication sur la procédure de calcul à suivre, donnée par un élève (Romain) plus avancé dans le raisonnement que les autres (Evan et Gabin), sans remettre en question cette construction encore fragile.

Cet échange entre les trois élèves pourrait se résumer à une construction encore fragile du calcul à formaliser. Romain explique, les autres essaient de comprendre sans que cela ne donne de réelle problématisation malgré le questionnement certain dans cet échange qui nourrit le problème 1 à construire.

En fin de cette séquence 1, nous remarquons l'intervention de Gabin (tours de parole 51 (³IGabin_12) et 57 suite à celui de Romain (³IRomain_11)) pour repréciser les premiers termes u1=1 et u2=2, cette valeur « 1+1 = 2 » (³IRomain_5) étant précédemment prise à tort comme premier terme (³IRomain_6). Mais cela n'engage pas de discussion entre les élèves et ne sera d'ailleurs par retranscrit dans leur traces écrites documents 2 en fin de phase 3.

Christelle Brémaud_E179552Q

[65]

Certaines des informations relevées nous laissent tout de même entrevoir certains problèmes que les élèves vont avoir à résoudre dont celui de la gestion de ce coûteux calcul dont il est question dans la séquence 2 suivante. Nous pouvons espérer que la résolution de ce problème (que nous noterons ³Pb1) permettra aux élèves de faire aboutir leur résolution du problème 1.

Séquence 2 :

L'extrait suivant nous permet de voir comment se construit ce problème ³Pb1 pour lequel nous aurons certainement besoin de remobiliser les informations relevées dans la séquence 1 précédente :

Echanges entre les élèves du groupe 3 lors de la phase 3			Informations relevées	Construction du savoir
92	Romain	Tiens, Gabin, tu sais que tu as le menu TABLE ? Est-ce que tu sais comment on fait ?		Envisageable en mode TABLE avec la calculatrice à condition - de saisir Y=2^X donc à condition d'utiliser les exposants de 2 ce que les élèves semblent avoir abandonné à ce stade. - et de paramétrer 0<X<63 avec des pas de 1
98	Romain	Moi, tu vois,... tu vois je voudrais faire un peu la même chose qu'Evan mais sauf qu'avec cette version simple tu vois. Parce que bon, faire 2 fois 2 fois 2 fois 2	^3IRomain_17 ^3IRomain_18
102	Evan	Ho la vache, c'était long !	^3IEvan_19
103	Gabin	Mais non toi ce que tu veux c'est pas TABLE
104	Romain	Euh... Ah ouais, bah ouais !
105	Gabin	Attends... (inaudible)
106	Romain	Non moi en fait ce que je veux faire, c'est par exemple, tu vois,... on va être d'accord... tu veux faire 2 fois 2 fois 2 fois 2 fois 2... sauf qu'au lieu d'écrire et faire 2 fois 2 à chaque fois pour savoir le résultat que ça fait au total, tu fais le calcul et t' auras toute la ligne de tous les chiffres	^3IRomain_20
107	Gabin	Oui comme sur Excel	^3IGabin_21
108	Romain	Oui en bref, c'est Excel mais en... bah au pire on se met sur un ordi mais y aura pas le temps... Y a pas le time !
112	Gabin	Là, tu mets... le calcul... total....sera...fait sur Excel	^3IGabin_22
116	Romain	Bah euh.... Le truc c'est que je vois pas... je sais comment le... je sais, dans ma tête tout est déjà fait... mais le poser... j'ai toujours un défaut là-dessus...mmmmm... attends, imaginons que... Excel, Excel, Excel... ça voudrait dire qu'il faudrait transférer le résultat là et le remultiplier par 2...	3I Romain_23 3IRomain_24	Construction de (un) avec un+1 = unx2 Mais avec une erreur sur le premier terme que les élèves choisissent à 2 au lieu de u1= 1 et avec une erreur ici sur le rang du dernier terme que les élèves conviennent à 64 (au lieu de 63)
119	Gabin	Les premières valeurs	^3IGabin_25
120	Romain	Et on les transfère	^3IRomain_26
123	Gabin	Du coup sur Excel, tu sais, tu les élargis, tu vois ? (faisant le signe du copier glisser de haut en bas)	^3IGabin_27
124	Romain	Ouais... sauf que ça ne ferait pas la même chose, ça restera 2 fois 2 fois 2 fois 2 fois 2
125	Evan	Bah oui !
126	Gabin	.... Tu sais faut mettre égal somme et truc...	^3IGabin_28
127	Romain	Donc, tu vois, regarde, je t'ai mis sur ta feuille...là tu vois c'est Excel.... Tu le mets 2 fois 2... et là t'as ton résultat... c'est 4. Tu prends ça, ton 4 là, et y aura toujours fois 2 ici. 8 fois 2... 16. Ça donnera un truc comme ça mais à l'infini... jusqu'à 64	^3IRomain 29 -
130	Evan	Voilà... c'est... le total (montrant le même schéma à la caméra)
131	Romain	Non, il te manque des chiffres !	^3IRomain_30
133	Gabin	Les multiplications
134	Romain	Les calculs
135	Gabin	Sur le tableur... en fait, tu mets exemple entre parenthèses, et tu mets... bah deux trois calculs
136	Romain	Ouais j'avoue que ce système de puissances c'est la merde ! Voilà, moi, j'ai mis ça comme ça ! Hein Gabin

Christelle Brémaud_E179552Q

[66]

Là encore aucune mention n'est faite de la somme à effectuer pour obtenir le résultat final. Les élèves cherchent uniquement une solution pour gérer un calcul coûteux des 64 termes (s'ils démarrent leurs calculs de la valeur 1) ce qui nécessite qu'ils organisent leur réflexion précédente concernant la formalisation des calculs.

Nous remarquons encore ici que les élèves ne partent que du terme 2 « c'est là où tu pars de 2 fois 2 » (³IRomain_6) et « .... Tu le mets 2 fois 2... et là t'as ton résultat... c'est 4 » (³IRomain_28) pour obtenir le troisième en occultant le premier terme de la suite à construire (alors même que cela a été évoqué à plusieurs reprises dans cet extrait) en espérant que la phase 4 de réalisation lors de la séance suivante leur permettra de se réinterroger sur ce point. Ce « décalage » (que nous verrons en phase 4) nécessitera de bien préciser le nombre de calculs à effectuer sur tableur qui sera fonction du terme de départ donné ce qui leur posera problème lors de la phase 4 car non résolu dans cette phase 3.

Ils semblent se satisfaire de la valeur du ^64ième terme comme résultat et confirment ici un choix d'utiliser les multiplications par 2 plutôt que les puissances de 2 pour lesquelles il semble que la non maitrise des commandes de saisies (=2^X) pour utiliser la calculatrice en mode TABLE ou le tableur soit paralysante. En effet, nous relevons dans la séquence 1, «Parce qu'en fait je ne me rappelais plus comment on faisait pour faire les exposants, enfin euh... pour les puissances avec la calculatrice...donc au moins là je suis sûr que c'est bon. Et après tu vois là regarde, tu fais le calcul simple... tu vois (passe sa calculatrice à Gabin) » (³IRomain_7) même si l'élève malgré tout utilise les puissances de 2 pour calculer ce qui semble être le dernier terme et l'obtenir sans les calculs précédents nécessaires avec les multiplications successives par 2 pour passer d'un terme à l'autre : « et tu peux exposant, euh puissance 63 parce que tu peux pas faire toutes les cases d'un coup » (³IRomain_10).

Nous regardons alors plus précisément comment se construit le choix d'utiliser le tableur qui construira en partie le problème ³Pb1.

Les élèves se sont peu à peu accordés sur le fait que les calculs étaient coûteux (³IRomain_11 : « 1, 2, 4, 8, 16, 32, 64, 128, 2 cents...euh... 256, 520... euh... mille vingt euh » et ³IEvan_18 : « Ho la vache c'est long ! »). Et que très vite les résultats obtenus étaient importants de l'ordre de 10⁶ (pour information : 223 = 8 388 608) dès la ^22ième case (³IEvan_15 : « Moi je suis à un million.... Mais c'est c'est... j'ai fait que trois lignes (sous-entendu pour les 3×8=24 premières cases de l'échiquier)»).

Les élèves conviennent que le calcul ne pourra pas aboutir avec cette procédure (³IRomain_14 : « Je te rassure quand tu arrives à ... dans 7 cases tu t'arrêtes ! »). Les informations ³IRomain_11 et ³IRomain_14 apparaissent alors comme des faits (³D1) : le calcul est possible pour générer la suite terme à terme mais on peut faire autrement.

Nous relevons ³IRomain_17 : « tu vois je voudrais faire un peu la même chose qu'Evan (calculs successifs avec multiplication par 2 du résultat précédent) » qui annonce la recherche d'une procédure moins coûteuse qui apparait alors dans ³IRomain_18 comme une alternative nécessaire (³C1) pour la réalisation de ces calculs longs et

Christelle Brémaud_E179552Q

[67]

répétitifs : « mais sauf qu'avec cette version simple tu vois (l'utilisation de calculatrice en mode TABLE étant proposée ici). Parce que bon, faire 2 fois 2 fois 2 fois 2 ».

Un élève propose alors d'utiliser le tableur ce qui apparait ici comme la solution pour gérer cette succession de calculs répétitifs mais que nous considérerons comme un fait dans la construction du problème ³Pb1 avec ³IGabin_21 « Oui comme sur Excel » (³D2). ³IGabin_25 propose de partir des premières valeurs connues (à redéfinir ultérieurement) apparaissant comme des données (³D3). Ces valeurs, et par suite les résultats des calculs ultérieurs, devront être transférées, donnant à ³IRomain_26 le statut de condition pour le calcul itératif à faire sur tableur (³C2). ³IRomain_20 rappelle le calcul itératif envisagé qui est alors une donnée à considérer (³D4) aux conditions précisées par Gabin (³IGabin_28) qu'il faudra saisir une formule de calcul avant de faire un copier glisser (³IGabin_27) pour réitérer la procédure de calcul conférant à ces deux informations alors le statut de conditions (³C3 et ³C4).

Nous remarquons au travers de ces échanges un vocabulaire parfois très approximatif et, ce qui semble être, une maîtrise fragile des fonctionnalités d'un tableur :

- « ... égal somme truc » (³IGabin_28) pour évoquer la nécessité de saisir une formule dans la cellule
du tableur pour qu'il puisse réitérer la procédure ;

- « ... tu les élargis, tu vois ? » (³IGabin_27) pour préciser qu'il faudra faire un copier glisser de
cellules préalablement sélectionnées.

Malgré tout, les élèves avancent dans leur raisonnement et font des choix, mobilisant certaines de leurs connaissances souvent incertaines qui ne leur permettent pas toujours d'obtenir le cheminement le plus simple pour parvenir à leurs fins.

Nous présageons que les élèves du groupe 3 finiront de construire ce problème ³Pb1_groupe3 (non résolu en phase 3) lors de la séance suivant (phase 4) quand ils seront « en action » sur tableur pour la réalisation de leurs calculs et la finalisation de la résolution de la situation-problème qui leur a été soumise.

Nous proposons le losange de problématisation suivant dans lequel la solution ³S1 n'est alors que provisoire :

[68]

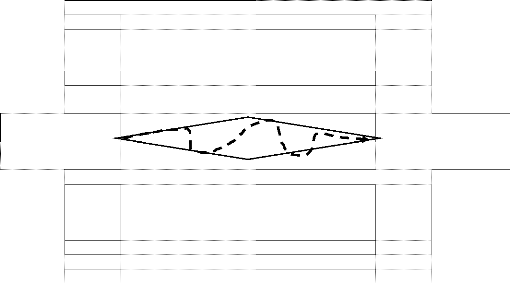
Problème ³Pb1 :
Organiser le calcul
pour obtenir le résultat

³IRomain_11 ³IRomain_14

Conditions :

³IRomain_18 « mais sauf qu'avec cette version simple tu vois » ³C1

³IRomin_24

³IGabin_28 « .... Tu sais faut mettre égal somme et truc... » ³C3

3IRomin_27 « Du coup sur Excel, tu sais, tu les élargis, tu

vois ? »

³IGabin_21 « Oui comme sur Excel » ³D2

³IGabin_25 « Les premières valeurs » ³D3

³IRomin_20 « ... tu veux faire 2 fois 2 fois 2 fois 2 fois 2...» ³D4

« ça voudrait dire qu'il faudrait transférer le résultat

là

et le remultiplier par 2... »

« 1, 2, 4, 8, 16, 32, 64, 128, 2 cents...euh... 256,
520... euh... mille vingt euh »
« Je te rassure quand tu arrives à ... dans 7 cases tu
t'arrêtes ! »

Données :

Solution ³S1 :
Organiser le calcul sur
tableur pour obtenir le
résultat 1

³C2

³C4

³D1

Christelle Brémaud_E179552Q

ii. Séquence 3 : Construction du problème 2

Jusqu'alors pour conclure sur la faisabilité de la requête (problème 2) aucun raisonnement mathématique n'a vraiment émergé. Dans cette séquence, nous illustrons cet état de fait par les extraits de transcription suivant, mais nous ne relèverons aucune information dans la mesure où rien ne semble ici construire le problème 2 (qu'il faudra bien alors envisager de construire dans la dernière phase 4). Les élèves se contredisent même « Bah ouais c'est irréalisable mais sinon dans l'ensemble c'est réalisable » (tour de parole 48).

Mais assez rapidement, comme le montre l'extrait suivant, les élèves concluent que puisque le calcul est faisable, la requête est réalisable « On a juste à calculer... oui la quête est réalisable. Et voilà ! Oui la requête est réalisable, il suffit juste de le calculer » (tour de parole 52), ne s'encombrant ainsi pas des contraintes à prendre en compte, non trouvées en phase 2, pour pouvoir répondre autrement au problème posé et donc ne pas avoir à résoudre ce problème 2 envisagé dans l'analyse a priori. Une confusion entre la faisabilité des calculs à effectuer et la faisabilité de la requête apparait clairement « Si on suit l'exercice, la question est de savoir si c'est réalisable et que le problème est réalisable « (tour de parole 76).

Nous notons toutefois que les élèves pressentent que le raisonnement est un peu léger « Bah en fait, tu ne peux pas vraiment le prouver » (tour de parole 86).

Echanges entre les élèves du groupe 3 lors de la phase 3
26	Gabin	Ha ok ! Et du coup, maintenant la question c'est est-ce que la requête est réalisable ? ... Ouais mais du coup il y a plein de facteurs différents
28	Gabin	Déjà il faut bien relire l'énoncé, le texte
30	Romain	C'est quoi que tu lis ?

Christelle Brémaud_E179552Q

[69]

31	Gabin	Ca ! (en montrant l'énoncé en vidéo projection) Mais en fait le problème... euh... c'est qu'on a trop de ... on a trop de... euh... des choses différentes
33	Gabin	Faut prendre les principales
42	Gabin	On nous demande pas d'aller jusqu'à autant de nombres là ! On demande juste si la requête est réalisable
43	Romain	Non là... Evan, Evan... on ne nous demande pas de résoudre
44	Evan	Ah d'accord !
45	Gabin	On nous demande juste si euh
46	Romain	Ouais mais ça dépend... Ça dépend de beaucoup de facteurs qu'on ne sait pas
47	Gabin	Oui mais si on le fait sur... (inaudible)
48	Romain	Bah ouais c'est irréalisable mais sinon dans l'ensemble c'est réalisable.
49	Gabin	Ce qu'on nous demande c'est la base de la base en soit on nous demande pas
50	Romain	Mais dans l'ensemble c'est réalisable
51	Gabin	Oui c'est réalisable, si on ne s'attarde vraiment qu'aux consignes c'est largement réalisable ! On nous dit 1 grain de riz sur la première case de l'échiquier, 2 pour la deuxième, et ainsi de suite, le nombre...
52	Romain	On a juste à calculer... oui la quête est réalisable. Et voilà ! Oui la requête est réalisable, il suffit juste de le calculer
53	Evan	Bah non...
54	Romain	Bah si !
76	Romain	Si on suit l'exercice, la question est de savoir si c'est réalisable et que le problème est réalisable
77	Gabin	Si on s'en suit à la consigne, l'expérience est réalisable
78	Romain	Voilà
86	Romain	Bah en fait, tu ne peux pas vraiment le prouver

Retenir de cette phase 3 :

Lors de cette phase 3 de recherche d'un protocole de résolution, même si les échanges entre les trois élèves, s'avèrent riches, nous constatons que seul le problème 1 se construit avec un sous problème de l'ordre de l'organisation des calculs (³Pb1) qui permet aux élèves d'envisager l'utilisation d'un tableur mais ce problème ne permet pas de voir clairement comment vont s'organiser ces calculs avec un tel logiciel ce que nous imaginons que les élèves auront à résoudre en phase 4 de résolution. La situation-problème est encore loin d'être résolue faisant même réapparaitre les contraintes paralysantes que nous aurions pu imaginer comme abandonnées suite à la phase 2 « Ça dépend de beaucoup de facteurs qu'on ne sait pas » (tour de parole 46).

Reste à voir comment les élèves lors de la séance suivante, alors qu'ils doivent mettre en oeuvre leur protocole de résolution, se réinterrogeront sur ces deux problèmes lors de la phase 4.

5.5. Troisième analyse (phase 4) : comment les élèves doivent revenir sur des problèmes soulevés précédemment mais non résolus pour répondre à la situation-problème

i. Analyse des traces écrites (documents 3)

Nous rappelons que les élèves disposaient d'une séance complète pour cette phase de résolution alors qu'ils n'avaient qu'une seule séance pour les 3 phases précédentes au cours desquelles nous rappelons que le problème 1 a été construit même si les élèves ne sont pas encore parvenu au résultat 1 attendu alors que le problème 2 n'en est qu'à ce que nous avons appelé ces prémices.

Christelle Brémaud_E179552Q

[70]

Dans tous les documents 3, les résultats chiffrés apparaissent avec le nombre de grains total et/ou son équivalent en masse, ainsi que la production mondiale de riz pour pouvoir faire une comparaison et conclure sur la faisabilité de la requête, même si les comptes rendus sont pour certains pauvres en informations sur le raisonnement suivi.

Groupe 1 : Dans le document ci-contre, les élèves se dispensent même de tout argument explicatif avec « vous pouvez comprendre qu'il n'est pas possible de résoudre votre exercice » en guise de seule conclusion. Nous notons au passage qu'ils ont « réalisé » l'exercice (contrairement à ce qu'ils rédigent) et qu'il y a une certaine
	Figure 24: document 3_Inès (groupe 1)

confusion entre résoudre « l'exercice » et la faisabilité de la requête questionnée dans le problème.

Groupe 2 :

Seuls les documents 3 du groupe 2⁴², détaillent la procédure suivie pour le calcul et renseignent sur le raisonnement que les élèves ont suivi.

Nous rappelons que les documents 2 du groupe 3 n'indiquaient, pour protocole de procédure de résolution, que le calcul 1+2¹+ 2²+2³+2⁴+2⁵+2⁶+2⁷+2⁸+2⁹+2¹⁰...2⁶⁴ (³Igroupe2_2 et ³Igroupe2_Dorian_4), avec la justification « car il y a 64 cases sur l'échiquier » (³Igroupe2_1), en rajoutant qu'ils le feraient « sur la calculatrice ou un tableur » (document 2_Elsa) sans plus d'explication sur la manière dont ils l'envisageaient techniquement parlant. Nous avions alors relevé lors de l'analyse de cette phase, que la somme étant constituée de 65 termes avec le premier terme=1 (non considéré par les élèves comme 2⁰). Ce dernier ne paraissait alors pas comptabilisé par les élèves dans le nombre total de termes qu'ils semblaient vouloir être de 64 (comme le nombre de cases de l'échiquier). Nous avions alors pointé le problème de l'utilisation d'indices de 1 à 64 pour l'organisation des calculs.

Les documents 3 font ici apparaitre que les deux problèmes 1 et 2 de l'analyse a priori ont été résolus.

⁴² Annexe 10 pp. 131-134

Christelle Brémaud_E179552Q

[71]

Résolution par le groupe 2 du problème 1 :

Figure 25: document 3_Maxime (groupe 2)

L'impression de la feuille de calcul sur tableur (Annexe 10 p. 134) permet de voir que le problème de l'organisation des calculs sur tableur, codé ⁴Pb1 (=³Pb1), a été résolu.

La façon dont ce problème a été résolu est en partie révélée par les comptes rendus écrits détaillés des élèves dans les documents 3.

Nous relèverons ici 5 nouvelles informations qui nous semblent poursuivre la construction du problème ³Pb1 précédemment posé par le groupe 3. Nous remarquons alors que les informations relevées en phase 3 dans les documents 2 du groupe2, auxquelles nous ne pouvions alors pas clairement attribuer de statut de données ou de conditions apparaissent ici également construire ce problème en tant que données.

Dans cette phase 3, les élèves rappelaient que l'échiquier comportait 64 cases (³Igroupe2_1), cette information apparaissant comme un fait (⁴D1) maintenant avéré, impose une nécessité de calculer 64 termes qui seront organisés sur les 64 lignes du tableur (⁴Igroupe2_1) et pour plus de clarté les élèves ont besoin de rappeler dans les cellules d'A1 à A64 les numéros des cases de l'échiquier. Cette information apparaissant alors comme une condition pour l'organisation des calculs sur le tableur (⁴C1). Nous voyons alors apparaitre une distinction faite entre les cases de l'échiquier et les cellules du tableur. L'information ³Igroupe2_2 clarifiant le calcul à effectuer, permet alors d'envisager en tant que donnée (⁴D2), les formules à saisir comme des conditions de réalisation de ces calculs sur tableur attribuant à ⁴Igroupe2_Elsa_2 et ⁴Igroupe2_Maxime_3, le statut de condition (⁴C2). Reste alors à rappeler ³Igroupe2_Dorian_4 qui n'est plus à discuter et prend le statut de fait ici (⁴D3) pour envisager la nécessité d'utiliser la fonction SOMME du tableur donnant alors à ⁴Igroupe2_Maxime_5 le statut de condition (⁴C3) pour obtenir le résultat attendu, solution du problème ⁴Pb1_groupe2. Nous notons au passage que les élèves n'ont plus à gérer le problème du dernier terme qui apparait ici résolu avec =B63×2 saisi en B64 leur permettant d'obtenir leur 64ième terme. Nous pouvons alors résumer la résolution du problème ⁴Pb1 par le losange suivant. Nous remarquons que ce problème fini de construire le problème 1 (analyse a priori) permettant enfin de trouver la valeur chiffrée du résultat 1 correspond au nombre total de grains de riz que contiendra l'échiquier.

[72]

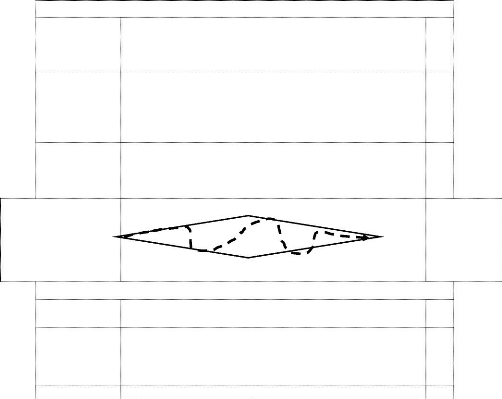
Problème ⁴Pb1 :
Organiser le calcul
pour obtenir le résultat

⁴Igroupe2_Elsa_2
⁴Igroupe2_Maxime_3

⁴Igroupe2_Maxime_4

³Igroupe2_Dorian_4 « et ensuite tout additionné » ⁴D3

⁴Igroupe2_1

Données :

3Igroupe2_1 « il y a 64 cases sur l'échiquier » pouvant être numérotées de 4D1

1 à 64

³Igroupe2_2

« nous calculons la somme de toute les case en utilisant l'outil
somme »
Nécessité de la formule de calcul =somme (B1 :B64) saisi
en B65

Chaque terme dépend - soit du numéro de la case sur l'échiquier

(1,2¹, 2²,...2⁶³

- soit du terme précédent

« nous avons crée la formule =celluleprécédenteX2 »
« nous mettons la même formule que l'on étire : célule du
dessu X2 »
Nécessité de la formule de calcul =B1×2 saisi en B2 puis
copié glissé jusqu'en B64

64 termes à calculer
Nécessité des numéros de lignes (de 1 à 64) pour
l'organisation des calculs
Les entiers de 1 à 64 sont affectés aux cellules de A1 à A64

Conditions :

⁴C1

⁴C2

⁴C3

Solution ⁴S1 :
résultat 1 =
nombre de
grains de riz
total sur
l'échiquier

⁴D2

Christelle Brémaud_E179552Q

Résolution par le groupe 2 du problème 2 :

Les élèves du groupe 2 sont parvenus à résoudre le problème 1 et ont obtenu le nombre total de grains de riz sur l'échiquier (18 446 744 073 709 600 000 (⁴Igroupe2_5)), solution (résultat 1) du problème 1 de l'analyse a priori. Il ne leur reste plus qu'à conclure, mais pour cela doivent résoudre le problème 2 envisagé dans l'analyse a priori. Nous coderons par ⁴Pb2, ce nouveau problème qu'ils ont à construire pour parvenir à partir de leur résultat précédent à conclure sur la faisabilité de la requête.

Figure 26:document 3_Maxime (groupe 2)

Christelle Brémaud_E179552Q

[73]

Cette information (⁴Igroupe2_5) apparaissant alors comme un fait, une donnée (⁴D4), les élèves constatent qu'il faudrait beaucoup de temps pour le comptage (« compter autant de grains de riz et trop long » ⁴Igroupe2_Maxime_6). Cette évidence présente alors cette information comme également un fait, conférant à ⁴Igroupe2_Maxime_6 le statut de donnée également (⁴D5).

Elsa annonce alors la condition qu'il faudra passer par la masse: « nous allons trouver une solution alternative pour gagner du temps » (⁴Igroupe2_Elsa_7) cette information apparait alors comme une nécessité (⁴C4) pour envisager la suite de la résolution de cette situation. La masse d'un grain (« 0.020 g » (⁴Igroupe2_Maxime_8)) est alors utilisée comme une donnée extérieure au problème (⁴Igroupe2_Maxime_8 = ⁴D6) pour calculer cette masse totale de « 368 934 881 474 191 000 gramme » (⁴Igroupe2_9) qui apparait comme une nouvelle donnée (⁴D7).

Il leur faut alors convertir nécessairement cette quantité en tonne (⁴Igroupe2_11 = ⁴C5) pour pouvoir la comparer à leur nouvelle donnée qui est la « production annuelle (mondiale) de riz en 2013-2014 est de 479.2 million de tonne » (⁴Igroupe2_10 = ⁴D8).

Nous n'avons aucune information nous éclairant sur le cheminement entre ces données chiffrées et la conclusion à laquelle parviennent les élèves ici « ce n'est pas possible car il faudrait garder la production mondiale pendant plusieurs années » (⁴Igroupe2_12). Nous supposons qu'ils n'ont fait qu'une estimation comparative approximative et ont jugé que « 368 934 881 474.191 Tonne » = 368 934 millions de tonnes était beaucoup plus grand que « 479.2 million de tonne » (⁴Igroupe2_13 = ⁴D9) et que cette estimation ne remplissait pas la condition (⁴I12=⁴C3) de faisabilité.

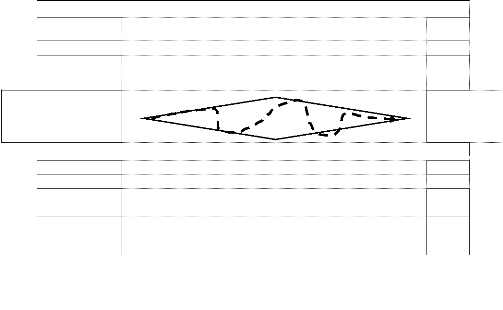
⁴C4

Problème ⁴Pb2_groupe2 :
La requête est-elle réalisable

Données :

⁴Igroupe2_5 18 446 744 073 709 600 000 ⁴D4

⁴Igroupe2_Maxime_6 « compter autant de grains de riz et trop long » ⁴D5

⁴Igroupe2_Maxime_8 « 0.020 g » = masse d'un grain ⁴D6

⁴Igroupe2_9 « 368 934 881 474 191 000 gramme » = masse totale ⁴D7

« production annuelle (mondiale) de riz en 2013-2014 est de 479.2 million

⁴Igroupe2_10 ⁴D8

de tonne »

⁴Igroupe2_13 masse totale de riz sur l'échiquier >> production mondiale de riz ⁴D9

Conditions :

4Igroupe2_Elsa_7 « nous allons trouver une solution alternative pour gagner du temps » en

calculant la masse totale de cette quantité

⁴Igroupe2_11 Convertir la masse totale en tonnes « 368 934 881 474.191 Tonne » ⁴C5

⁴I12 SI masse totale de riz sur l'échiquier << production mondiale de riz ⁴C3

Requête réalisable

Solution

⁴S2 (=⁴Igroupe2_12): Non elle n'est pas réalisable

Ce cheminement peut alors être résumé par le losange de problématisation suivant :

[74]

Groupe 3 : Comme dans le paragraphe 5.3 (analyse documents 2 de la phase 3), les documents 3 des élèves du groupe 3^43 ne renseignent que sur les résultats obtenus sans plus d'informations sur la manière dont ils ont été obtenus et comment les élèves ont dû raisonner pour y parvenir.
	Figure 27:document 3_Evan (groupe

Figure 28: impression travail phase 4 sous Excel

Les comptes rendus de chacun des trois élèves du groupe 3 sont accompagnés de l'impression de leur travail sur Excel mais ne renseignent pas sur les démarches effectuées pour parvenir à ces résultats (qui sont ceux attendus). Il aurait pour cela fallu, en partie, connaitre les formules saisies dans les cellules contenant les valeurs chiffrées dans la colonne de droite. La transcription des échanges pourra nous renseigner sur le processus engagés pour atteindre cette performance.

Groupe 4 :

Nous notons ici comme dans le groupe 2, des traces de problématisation mais les élèves ici ne donnent pas assez d'informations permettant de construire le problème 2 même s'ils parviennent à la conclusion attendue en argumentant.

Figure 29:document3_Rozen (groupe4)

Nous notons au passage que le résultat trouvé ici

Christelle Brémaud_E179552Q

« 92 3337 2036 854 780 000 grains de riz » ne correspond pas à ce qui est attendu (18 446 744 073 709 600 000 grains de riz au total). Le résultat proposé par les élèves ici, représente le nombre de grains de riz sur la ^63ième case de l'échiquier.

⁴³ Annexe 10 pp. 135-137

Christelle Brémaud_E179552Q

[75]

ii. Analyse non formalisée de la transcription⁴⁴

Dans la transcription pour l'analyse envisagée de cette phase 4, nous voyons apparaitre régulièrement des informations apportées par l'enseignante (auteure de ce travail de recherche) lors de 38 tours de parole sur un total de 225 (ce qui représente presque 17% des échanges de cette transcription).

Dans les extraits utilisés pour cette analyse (en annexes 12, 12 bis et 12 ter), ces prises de parole sont en caractères violets pour les distinguer de ceux des élèves et nous faisons remarquer que beaucoup de ces interventions consistent à interroger les élèves sur leur raisonnement mais aussi, parfois, à leur donner plus d'informations pour les guider. Nous avons précisé en caractères gras celles qui vont au-delà d'une simple interrogation en délivrant des informations considérées comme des coups de pouce voire, pour certaines, comme des inducteurs de problématisation (FABRE M. et MUSQUER A., 2009). Si les échanges précédents lors des deux dernières phases n'ont pas toujours permis de voir de problématisation pour ce groupe 3 (ainsi que parfois dans les traces écrites), nous pouvons envisager que la contribution de l'enseignante pourra ici aider les élèves à problématiser pour faire aboutir leur recherche.

Plusieurs lectures de cette transcription en vue de l'analyse ici a permis de décomposer la transcription en 3 séquences :

- Séquence 1⁴⁵ dans laquelle les élèves mettent en forme le calcul à effectuer sur tableur pour obtenir
le nombre de grains de riz par case pour finir de construire le problème ³Pb1_groupe3 (voir phase 3)

- Séquence 2⁴⁶ dans laquelle les élèves réalisent que cela ne suffit pas pour répondre au problème

- Séquence 3⁴⁷ où les élèves ayant trouvé le nombre total de grains et la donnée à utiliser pour

pouvoir comparer leur résultat, vont pouvoir construire le problème ⁴Pb2_groupe3 leur permettant de conclure.

Le temps imparti à cette recherche ne permet pas d'aller plus loin dans l'analyse de cette transcription qui pourtant présageait d'un éclairage supplémentaire sur le processus de résolution de la situation que les élèves avaient à résoudre dans cette étude. Nous considérons malgré tout que ce travail de recherche a permis de relever et d'analyser suffisamment d'éléments pour pouvoir discuter des résultats obtenus et conclure sur notre question de recherche qui s'intéressait à ce que la problématisation pouvait renseigner sur les processus engagés par des élèves de lycée professionnel, dans leur résolution d'une situation-problème en mathématiques.

⁴⁴ Annexe 11

⁴⁵ Annexe 12

⁴⁶ Annexe 12 bis

⁴⁷ Annexe 12 ter

Christelle Brémaud_E179552Q

[76]

6. DISCUSSION, LIMITES DE LA RECHERCHE ET PERSPECTIVES

En posant notre objet d'étude relatif à l'Approche Par Compétences, nous nous étions fixés comme objectif, en préambule de ce travail, de ne nous intéresser qu'aux démarches et processus engagés par un élève pour résoudre un problème, ce qui nous semblait être une « condition indispensable pour pouvoir, dans l'enseignement... aider le sujet à construire ses compétences » (REY, 2014).

Mais pour rappel, nous nous étions interrogés également sur un certain nombre d'autres points portant principalement sur l'aspect évaluatif de l'APC :

- avec une distinction non exhaustive à faire entre l'évaluation DES compétences et l'évaluation
PAR compétences

- et un certain nombre d'interrogations concernant les épreuves certificatives demandées par
l'Institution (Contrôles en Cours de Formation) mettant en perspective les tensions entre le prescrit et le réalisé dans la réalité des classes avec ce que l'APC semble signifier et/ou impliquer.

Après avoir discuté des résultats de notre analyse et tenté de répondre en partie à notre sujet de recherche, nous pointerons certaines limites de ce travail et élargirons le cadre de notre réflexion avec ce qui pourrait apparaitre comme des réponses aux questions soulevées en début de recherche voire des perspectives qui nous paraissent complémentaires.

6.1. Discussion

Dans cette étude nous voulions voir quand et comment certaines compétences se mettaient au travail dans le cadre de l'apprentissage par situations-problèmes en mathématiques. Nous envisagions que ce travail permette de discuter des conditions pour que s'engagent les processus en jeu et le cas échéant, d'en préciser certains mécanismes dans la construction du savoir visé qui nous semble indissociable des compétences à développer dans le cadre de l'enseignement des mathématiques.

Sans parler de performance, il s'agissait ici que l'élève parvienne à une certaine réussite pour que l'on puisse avoir suffisamment d'éléments sur lesquels s'appuyer pour attester qu'il y a compétence, ou non, au regard de son questionnement, des savoirs et capacités qu'il mobilisait pour résoudre le problème et de la façon dont il s'était approprié les coups de pouce ou « inducteurs de problématisation » (FABRE M. et MUSQUER A., 2009) en phases 3 et 4 notamment.

Nous voulions voir comment l'élève « s'approprie » une situation-problème donnée en mathématiques, l'« analyse et raisonne » pour engager une résolution et trouver une solution au problème posé et plus précisément chercher s'il problématisait et comment se faisait cette problématisation le cas échéant.

Christelle Brémaud_E179552Q

[77]

Analyse de la grille et quelques conclusions :

Deux problèmes apparaissaient dans l'analyse a priori de la situation-problème proposée aux élèves, comme autant d'obstacles à surmonter, que les élèves avaient à résoudre pour parvenir à s'approprier le problème, proposer un protocole de résolution, organiser les calculs et obtenir un résultat, et enfin interpréter ce résultat pour répondre au problème initial posé. Le problème 1 identifié dans l'analyse a priori, était de calculer le nombre total de grains de riz posés sur un échiquier sachant que les le nombre était doublé d'une case à l'autre. Le problème 2 consistait à conclure sur la faisabilité de la requête du souverain de donner la totalité des grains de l'échiquier à l'inventeur du jeu.

L'analyse des travaux d'élèves nous a permis de relever un certain nombre d'informations nous renseignant sur la construction de leur raisonnement. Ces dernières, répertoriés dans une grille⁴⁸, se sont révélées pour certaines comme de vrais indices de problématisation. Ces indices ont alors été catégorisés en données D et conditions C construisant des problèmes posés par les élèves. Nous résumons dans le tableau suivant, ces différents problèmes ainsi que leurs solutions respectives. Pour rappel, nous avions codé ^n°phasePbn°ordre ces problèmes avec 1, 2, 3 ou 4 le numéro de la phase de travail au cours de laquelle le problème avait été construit et n° d'ordre indiquant l'ordre dans lequel apparaissait le problème dans cette phase :

Problème n°phasePbn°ordre		Solution ^n°p^haseSn°ordre ° ou hypothèse ^n phaseHn°ordre
1Pb1	Quelles contraintes impose le plateau de jeu ?	1S1	Il y a 64 à remplir de grains de riz les unes après les autres
1Pb2	Comment obtenir le nombre total de grains de riz ?	1 S2	Proposition de calcul pour obtenir résultat 1 (non encore finalisé)
2 Pb1	Est-ce que le problème de stockage est à prendre en compte ?	2 H1	Si rien n'est écrit alors on fait abstraction de la contrainte de stockage
3Pb1	Comment organiser le calcul pour obtenir le résultat ?	3S1	Organiser le calcul sur tableur pour obtenir le résultat 1
4Pb1	Organiser le calcul sur tableur pour obtenir le résultat ?	^4S1	Résultat 1
^4Pb2	Est-ce que la requête est réalisable ?	^4S2	Non

L'extrait suivant de la grille élaborée pendant l'analyse du corpus, permet de répertorier les informations relevées, ayant permis aux élèves de problématiser (et donc ayant le statut de données D ou de conditions C) pour construire les problèmes 1 et 2 envisagés dans l'analyse a priori. Le codage ^n°phaseDn°ordre ou ^n°phaseCn°ordre est à lire comme pour les problèmes Pb précédemment. Nous avons mis en caractères rouges les données et conditions correspondant à celles construites dans l'analyse a priori et ayant le même statut.

Nous notons que rien n'ayant permis de mettre en évidence de problématisation pendant la phase 2 pour la construction des problèmes 1 et 2, nous n'avons pas mentionné la colonne correspondant. Nous

⁴⁸ Annexe 13

Christelle Brémaud_E179552Q

[78]

reviendrons ultérieurement sur cette phase ainsi que la phase 3 dans laquelle apparaissent des informations remobilisées en phase 4 (même si leur statut est différent).

	Analyse a priori		Phase 1 Analyse 1	Phase 1 Analyse 1 bis	Phase 3 Analyse 3	Phase 4 Analyse 4
Analyse a priori	Problème 1	D1	^1C1	^1D5	^4D1
		D2	^1D4	^1D7
		D3	^1D3	^1D8
		D4		^1D9	^4D3
		C1		^1C5		^4C1
		C2		^1C7	^4D2	^4C2
		C3				^4C1
		C4		^1C9		^4C2
		C5		^1C10	^4D3	^4D3 et^4C3
	Problème 2	D5				^4D5
		D6				^4D8
		D7
		D8				^4D9
		C6				^4C4
		C7				^4C5,^4D6 et ^4D7
		C8
		C9				^4C3

Cette grille révèle que les éléments nécessaires à la construction du problème dévolu aux élèves ont été évoqués voire discutés et formalisés (consciemment ou non par les élèves) et leur ont permis de résoudre la situation-problème pour parvenir aux résultats attendus.

La réflexion engagée ne s'est pas faite de façon linéaire comme le montre cette grille. Il aura fallu aux élèves un certain temps pour qu'ils puissent poser et construire les deux problèmes envisagés dans l'analyse a priori.

Il faut du temps et des allers retours dans les raisonnements des élèves pour parvenir à une solution acceptable. Notamment, pour le problème 1, où l'analyse a mis en évidence que parvenir à un résultat chiffré (le nombre de grains de riz total) nécessitait la construction d'un savoir (suites numériques) et l'organisation d'un calcul (ce qu'ont construit les problèmes ¹Pb1, ¹Pb2, ³Pb1 et ⁴Pb1), pour lesquels les 4 phases de travail étaient nécessaires.

Quant au problème 2 (pour conclure sur la faisabilité de la requête), il s'est construit en parallèle du problème 1 (avec les problèmes ²Pb1 et ⁴Pb2), dans des conditions différentes, voire en parasitant parfois la construction de ce dernier (²Pb1), mais n'a vraiment été construit qu'en phase 4 (⁴Pb2) une fois le problème 1 résolu.

Rien n'apparait dans cette grille quant à ce qui s'est travaillé pendant la phase 2 (synthèse de classe post-recherche individuelle) alors même que le problème ²Pb1 se posait, nourrissant le problème 2 mais sans le construire.

Christelle Brémaud_E179552Q

[79]

De même, très peu de chose propre à la phase 3 (proposition de protocole de résolution lors de travail en trinôme) apparait dans cette grille, les quelques informations relevées en phase 3 ayant servi à construire le problème ³Pb1 (nourrissant ⁴Pb1) qui n'a réellement abouti qu'en phase 4.

L'analyse du corpus a cependant révélé l'importance de ces deux phases qui malgré un manque de problématisation avéré, a permis aux élèves d'échanger, de discuter des données du problème voire de poser les problèmes que soulevait la résolution demandée et mettre en forme un cheminement dans leur(s) raisonnement(s).

Nous voyons que la construction du problème 1 engagée dans la phase 1 a nécessité les deux séances pour n'aboutir qu'en dernière phase 4 de résolution lorsque les élèves devaient « réaliser », formaliser sur tableur ce qu'ils avaient envisagé précédemment de façon abstraite sans avoir alors concrètement à formaliser leur raisonnement pour aboutir à un résultat chiffré. Nous pourrions alors nous interroger sur la nécessité de ces deux phases 2 et 3 s'il apparait finalement que la « manipulation » (phase 4) reste un facteur essentiel pour aider les élèves à formaliser leur raisonnement et le faire aboutir. Une étude plus approfondie sur le sujet permettrait de voir avec des séquences forcées, comment, avec ou sans ces phases, les élèves avancent sur la résolution d'un problème ouvert. Il n'en demeure pas moins que nous pensons, dans ce que nous avons appelé le « paradigme » des compétences, que ces deux phases sont essentielles pour conceptualiser un raisonnement et communiquer pour le faire aboutir avant de passer à une réalisation (concrète et/ou matérielle).

Bilan sur l'activité de problématisation des élèves :

Nous rappelons, pour pouvoir relativiser ce bilan sur l'activité de problématisation que nous avons tentée d'analyser dans ce travail de recherche, que la séquence observée était une séquence ordinaire et que les élèves n'ont jamais été sensibilisés à ce que signifie la problématisation comme ce qui pourrait apparaitre un outil potentiel de résolution de problème.

L'analyse montre que les élèves se sont engagés dans l'activité proposée, qu'ils se sont questionnés et que l'organisation de leur questionnement, parfois laborieux, a malgré tout, pris forme pour aboutir à une certaine réussite dans la résolution du problème.

La recherche d'une éventuelle activité de problématisation a nécessité des relevés nombreux et variés pour pouvoir à partir de quelques-uns de ces éléments (relevés comme autant de preuves d'un questionnement), mettre en évidence une réelle problématisation.

Différentes phases et modalités de travail, ont été proposées pour permettre aux élèves d'avoir plusieurs supports et cadres de réflexion pour poser, construire et résoudre les problèmes que soulevait la situation proposée. Ceci apparaissant alors comme des conditions nécessaires à la problématisation pour des élèves de lycée professionnel qui, malgré très souvent une bonne volonté, ne parviennent pas toujours à faire aboutir leurs raisonnements. L'enquête menée dans cette recherche, a été parfois

Christelle Brémaud_E179552Q

[80]

laborieuse car les éléments révélant cette problématisation apparaissent souvent de façon décousue dans la séquence, de manière pas toujours significative et avec souvent une nécessité de les interpréter pour en tirer une certaine signification dans le cadre d'une problématisation pressentie qu'a tenté de formaliser cette analyse.

Bilan de l'activité au regard des compétences et les questions soulevées a posteriori :

A propos du questionnement des élèves, doit-on parler d'aptitude, de capacité, de facilité ou de compétences? Préalablement à ces questions, nous avons tenté de voir quels étaient les processus engagés par l'élève dans son raisonnement pour résoudre un problème mais au-delà de cela, nous voulions observer d'une certaine manière un processus d'apprentissage en prenant le temps nécessaire qui n'est pas toujours donné à l'enseignant en classe.

Bien au-delà des questions qui se posent encore et auxquelles cette recherche n'a pas répondu clairement, nous pouvons tout de même, avec une certaine certitude, mettre en corrélation la pertinence de la problématisation dans le cadre de la mise au travail des compétences et la construction des savoirs. Nous sommes tentés d'envisager pour éclairer l'APC certaines conditions pour qu'il y ait mise au travail des compétences :

- approcher un savoir visé par une situation de recherche (ce sur quoi il n'y avait déjà aucun doute),

- pour permettre aux élèves de construire ce savoir avant toute forme d'institutionnalisation,

- et les accompagner dans leur recherche par un étayage de leur questionnement pour qu'ils

parviennent à problématiser. Les compétences (principalement s'approprier et analyser/raisonner observées ici) apparaissent alors comme inconditionnellement liées à la capacité à problématiser et donc à faire aboutir leur(s) raisonnement(s), voire mieux identifier leurs difficultés pour y remédier. Ce dernier point allant bien au-delà de ce qui peut s'engager dans seulement une simple activité à résoudre en mathématiques.

Nous faisons une parenthèse ici, pour interroger ce que signifie « proposer une activité qui a du sens »⁴⁹... De quoi parle-t-on ici ! Cela n'aurait alors pas de sens de mettre les élèves au travail sur une activité qui proposerait un énoncé hors cadre professionnel et question de société, dans le seul but de faire des maths alors même qu'il s'agit de parler de développer des compétences chez les élèves de lycée professionnel ?

49 « Les situations choisies permettent d'approcher les grands débats de société, par exemple autour du développement durable, et de traiter des problématiques parfaitement identifiées. Elles sont, autant que possible, adaptées aux métiers préparés afin de donner du sens aux notions étudiées. » (Document d'accompagnement du programme de mathématiques en classe de seconde professionnelle p.9/18) https://cache.media.education.gouv.fr/file/SP5-MEN-11-4-2019/26/8/spe628 annexe 1105268.pdf

Christelle Brémaud_E179552Q

[81]

D'ailleurs, en partie pour répondre à cette question, et de façon anecdotique, nous pensons qu'il est significatif de relater une séance à laquelle les élèves (dont il est question dans cette recherche, alors en classe de première l'année dernière, lors de la constitution de ce corpus) ont participé cette année en terminale. Et surtout d'évoquer leur réaction quand le thème des suites numériques a été à nouveau abordé. Il s'agissait alors d'introduire la formule permettant de calculer la somme des n premiers termes d'une suite numérique. La simple vidéo projection du tableur⁵⁰ (qui aurait pu être un de ceux qu'ils avaient réalisés lors de la résolution de la situation-problème grains de riz l'année précédente) a déclenché un véritable brouhaha dans la classe, avec des commentaires particulièrement significatifs. Un rapide rappel de l'activité et des résultats alors attendus pour se remettre en mémoire l'organisation des données vidéo projetées, a permis de voir que les élèves avaient encore en mémoire leurs démarches et qu'ils les remobilisaient avec une certaine aisance et une certaine fierté... alors qu'ils avaient « galéré » !

6.2. Limites de cette recherche :

La transcription des échanges pendant la phase 4_groupe3⁵¹ a été l'élément déclencheur des intentions de cette recherche. Elle n'a pourtant pas pu être analysée même si une étude très partielle a permis de vérifier qu'il était bien question de finir de construire les problèmes soulevés par les élèves lors des phases de recherches antérieures. Le temps a fait défaut dans ce travail de recherche pour permettre de finir cette analyse mais nous pensons que les éléments que nous en aurions tirés n'auraient fait que confirmer ce que le reste de l'analyse avait déjà permis de mettre à jour.

Nous notons que la situation proposée dans cette étude était un problème ouvert qui n'est pas le type de situation le plus souvent proposé en classe. Son analyse a nécessité beaucoup de temps, et tout l'espace de cette recherche. Peut-être que des situations moins robustes auraient permis de faire l'analyse de plusieurs situations pour croiser des résultats et permettre d'en tirer des conclusions plus fiables avec plus de certitude. Qu'en serait-il sur des situations de recherche avec des énoncés moins ouverts (le plus souvent proposés en classe) ? Il serait intéressant de voir comment les élèves de lycée professionnel organisent leur(s) raisonnement(s) sur des situations moins complexes et voir si la problématisation se fait plus naturellement avec des éléments d'observations plus évidents pour l'enseignant.

Cette recherche a révélé certaines conditions pour que les élèves problématisent mais elles s'avèrent différentes des conditions des évaluations qu'imposent les CCF (entre autre) ! On peut alors interroger certains points qui n'ont pas permis de répondre à des questions que pose l'APC, objet d'étude

⁵⁰ Extrait dans l'étape 4 de l'annexe 4

⁵¹ Annexe 11

Christelle Brémaud_E179552Q

[82]

initial. Entre autre celui portant sur la corrélation entre les phases de travail de groupe et le phases de travail individuel pour pouvoir juger s'il y a compétence ou pas. En effet, est-ce que les phases de travail collectif permettent de développer les compétences de façon individuelle ? Les phases d'échanges et de recherche en groupe sont des éléments apparaissant comme essentiels pour permettre de problématiser.

Sachant que nous avons d'une certaine façon conclu qu'il y avait problématisation dans la résolution d'un problème que faisait un élève, comment peut-on alors envisager d'observer les compétences au travail en isolant l'élève de toute interaction possible en vue d'une évaluation individuelle qui ne porterait que sur les processus et résultats issus de son travail ? Et par conséquent comment peut-on imaginer que seul en évaluation certificative, un élève puisse reproduire un tel travail ? A moins d'imaginer que cet exercice permettra d'équiper l'élève pour des situations moins complexes à traiter lors d'évaluations individuelles. Ce qui réinterroge les familles de situations discutées en préambule de ce travail, ainsi que les compétences qui ne peuvent être mises au travail que lors de résolution de tâches complexes et inédites.

Ce que ne révèle pas cette recherche sur les critères d'observation et/ou d'évaluation :

Les tentatives d'évaluation faites dans le prolongement de cette recherche avec les deux grilles

d'évaluation, l'une (grille 1) relative à une évaluation DES compétences⁵² et l'autre (grille 3), relative à une évaluation PAR compétences⁵³ (axée sur le savoir à construire), posent question. En effet, la traduction chiffrée des acquis relativement à une évaluation des compétences dans la première grille interroge car

- Les élèves du groupe 2 obtiennent une note chiffrée moindre que les élèves du groupe 3, alors

même qu'ils ont été plus « efficaces » dans leur raisonnement, plus rapides pour atteindre les résultats attendus avec semble-il un raisonnement qui s'est construit plus vite et de façon plus sûre comparativement aux élèves du groupe 3. Nous interrogeons les conséquences de cette rapidité et cette efficacité pour l'évaluation DES compétences et par voie de fait nous interrogeons également les critères d'observation : les phases d'échanges ont été tellement rapides qu'elles apparaissent comme inexploitables avec beaucoup d'amusements et/ou propos hors sujet ici ce qui n'a pas toujours permis de relever les éléments permettant d'apprécier le niveau de performance relatif aux critères d'observation fixés ;

- La grille 3 pensée dans le cadre d'une évaluation PAR compétences prouve que cette interrogation
est légitime. Elle explicite ce qui a été observé phase par phase dans les écrits des élèves au regard de la construction du savoir en jeu dans cette activité. Elle montre plus d'éléments de réponse

⁵² Annexe 14 p.162

⁵³ Annexe 14 ter p. 164

Christelle Brémaud_E179552Q

[83]

explicites et/ou pertinents pour les élèves du groupe 2 que pour ceux du groupe 3 alors même que la note chiffrée qu'ils obtiennent dans le cadre de l'évaluation des compétences est moindre.

Cette recherche ne permet que de poser la question sur ce qui peut être, ou ce qui est effectivement réellement observé, pour pouvoir porter un avis sur l'appréciation des compétences mises au travail dans une activité de problématisation en mathématiques. Elle a montré que les compétences étaient effectivement mises au travail mais elle ne permet pas d'aller plus loin sur la question de leur évaluation.

6.3. Perspectives :

Si nous avons insisté en préambule de cette recherche, sur la nuance faite ici entre « évaluer LES compétences » et « évaluer PAR compétences », c'est qu'il nous semble que nous n'observerons pas l'activité de l'élève de la même manière selon si l'évaluation porte sur les compétences ou si l'on évalue par compétences. Ce que nous voulons mettre en perspective ici, c'est la nécessité de différencier les critères d'observation et/ou d'appréciation et donc de différencier les objectifs selon si l'on évalue LES compétences ou les savoirs par le biais des compétences (évaluer PAR compétences). Aucun document institutionnel ne renseigne sur cette nuance voire ils contribuent même au flou autour de ce point. Cette nuance pourtant ne nous parait pas négligeable car elle parait pouvoir éclairer l'APC, lever dans une certaine mesure le flou autour des compétences dans l'enseignement et par voie de fait contribuer très largement à ce que nous avions évoqué comme tension entre le prescrit par l'Institution et le réalisé en classe par les enseignants.

En posant notre objet d'étude, nous évoquions d'autres points paraissant contribuer à certaines polémiques autour de l'APC. Entre autre, nous nous interrogions sur les raisons qui mettent parfois en contradiction savoirs et compétences quand il s'agit de l'APC. Il nous semble que l'analyse de notre corpus a prouvé notre conviction de départ que compétences et savoirs, loin d'être antinomiques, se nourrissent l'un de l'autre et ne peuvent se penser l'un sans l'autre.

Notre étude a également répondu en partie à nos interrogations sur ce que les traces écrites des élèves renseignent (ou pas) quant à la problématisation. En corrélant ces résultats aux questions que soulève la nuance entre « évaluer LES ou PAR compétences », nous avons un certain éclairage sur le manque de cohérence que nous soulevions en préambule. En effet lorsqu'il s'agit d'évaluer PAR compétences, il nous semble que les critères d'évaluation portant sur les savoirs à construire (les résultats à atteindre comme preuve de la résolution du problème posé) ne peuvent prendre en compte les processus mis en jeu dans la résolution que l'élève a fait du problème. Ceci même si paradoxalement, les compétences ont été mises au travail dans le cadre de cette résolution. Il ne s'agit pas alors d'évaluer LES compétences ici, ce qui permet de répondre en partie à une certaine incohérence lorsqu'un élève ayant produit un résultat considéré comme pertinent, n'a renseigné en rien dans sa trace écrite sur ses procédures de résolution. Et les critères d'évaluation portant sur les résultats à obtenir avec

Christelle Brémaud_E179552Q

[84]

éventuellement une échelle descriptive (précisant les critères de réussite avec les niveaux d'exigence) permettant de juger du degré de pertinence de la réponse, paraissent alors adaptés et ne doivent plus mettre mal à l`aise quand on pense évaluation PAR compétence.

Nous pouvons tenir le même raisonnement quant aux évaluations DES compétences avec bien entendu des critères d'évaluation ne portant que sur les processus et des résultats ou plutôt des actions observables. Se posent alors la question des critères d'évaluation qui ne doivent alors être relatifs qu'aux résultats d'un processus. Nous nous demandons alors quelle serait la cohérence d'une telle évaluation non corrélée aux résultats attendus relatifs aux savoirs ?... Mais il s'agit ici d'une recherche à part entière nous semble-t-il.

Concernant les tensions que peuvent représenter les CCF en mathématiques, leur élaboration et l'évaluation des élèves dans le cadre de cette épreuve, une fois la clarification faite sur l'évaluation DES ou PAR compétences, reste à s'interroger sur le type de situations à proposer dans ce cadre.

En effet, les contraintes de ce type d'évaluation nous éloignent des conditions d'une activité mettant au travail les compétences :

- les élèves sont seuls (alors même que le travail en groupe favorise la problématisation),

- dans un temps très limité pour résoudre le problème donné (alors même que les élèves ont besoin

de temps pour construire les problèmes avec des allers retours dans leurs raisonnements),

- avec des compétences incertaines pour « communiquer » même si cela ne présage pas forcément
d'une incompétence d'analyse d'où la nécessité d'une part d'oralité pour mieux percevoir le travail de l'élève (difficile de l'envisager pendant les épreuves certificatives).

Au risque de ne pas aller dans le sens de ce que l'Institut préconise, ce qui paraissait en début d'étude comme un point de tension, l'évaluation certificative nous parait alors plus simple à penser si nous acceptons que l'objectif d'un CCF n'est pas de mettre au travail les compétences, mais bien de proposer aux élèves de résoudre une situation permettant de mobiliser des savoirs et savoir-faire déjà travaillés en classe pour évaluer ces derniers par le prisme des compétences qui ne sont en fait alors pas l'objet d'évaluation. Nous ne pouvons pas percevoir les épreuves de CCF autrement, après avoir regardé de plus près ce à quoi doit correspond réellement une activité qui permet de mettre les compétences au travail.

Les compétences ne peuvent s'enseigner mais enseigner par compétences prend tout son sens une fois que l'on a clarifié ce qui parait être les conditions pour les mettre au travail, les construire, les développer. Dans ce cadre, nous pouvons penser que la problématisation permet de mieux percevoir ce que l'on attend de l'APC voire même affirmer qu'il y a nécessité d'enseigner la problématisation pour que la mise au travail des compétences soit pertinente et que l'APC soit une pratique pédagogique viable.

S'engagent alors d'autres axes de réflexion avec entre autre celui de l'ingénierie didactique et des choix pédagogiques de l'enseignant pour voir comment enseigner la problématisation.

Christelle Brémaud_E179552Q

[85]

CONCLUSION

Le temps de l'enseignement n'étant pas celui de la recherche, nous nous sommes indirectement interrogés, dans cette étude, sur les moyens dont disposent les enseignants pour s'emparer de ce que les textes officiels suggèrent. Nous avons mis en perspective la nécessité de certains apports de la didactique pour pouvoir mieux s'emparer de ces textes et tenter de comprendre ce que certains concepts parfois obscurs dans leur complexité, peuvent avoir comme implications afin d'opérer en raison des choix didactiques et pédagogiques.

Nous pouvons par exemple, lire dans les dernières instructions officielles, que « les évaluations doivent être conçues comme un moyen de faire progresser les élèves, d'analyser leurs apprentissages et de réguler ainsi l'enseignement dispensé »⁵⁴. Cette courte phrase porte en elle-même beaucoup d'axes de réflexion et de travail sur des sujets certes complémentaires mais qui nécessitent chacun d'être réfléchi à part entière.

Au-delà des tensions entre le prescrit par l'Institution et le réalisé en classe, nous avons porté, dans cette recherche, un regard didactique pour mieux observer la corrélation entre compétences et savoirs et pouvoir de façon plus systémique comprendre ce que cela impose dans l'ingénierie de l'enseignant.

Même si rien dans ce travail n'évoque ce point, les élèves de lycée professionnel, avec des profils souvent complexes et difficiles à appréhender, imposent aux enseignants de se pencher en premier lieu sur la question de la gestion de classe. Pourtant, il nous semble que la didactique très souvent mise de côté, car pouvant apparaître un peu nébuleuse dans sa complexité théorique et chronophage dans l'acquisition de ses apports (il faut du temps pour lire, comprendre, s'en emparer et expérimenter), apporte certaines réponses voire solutions.

Notre recherche nous a permis de prendre « un peu de temps » pour mieux « analyser » les apprentissages des élèves, sous prétexte d'observer de plus près la mobilisation de certaines compétences en mathématiques dans le cadre d'une résolution de problème faite par des élèves de lycée professionnel.

Bien au-delà de la certitude que l'approche par compétences ne se limite pas qu'à tenter de « faire réfléchir les élèves », et donner aux enseignants bonne conscience vis-à-vis des textes officiels, l'étude met en évidence certains éléments clés pour donner du sens au travail effectué en classe.

En effet, elle montre que les élèves peuvent se mobiliser pour entrer dans une activité mathématique, qui plus est ici, pas facile d'accès, mobiliser les compétences d'appropriation et d'analyse, se poser des questions et parvenir à résoudre le problème qui leur est donné.

54 https://cache.media.eduscol.education.fr/file/Consultations2018-2019/41/6/PPLP19_mathematiques_2ePro_1077416.pdf

[86]

Christelle Brémaud_E179552Q

Le cadre théorique de la problématisation permet de suivre leur réflexion et d'en éclairer son organisation. Il met en perspective que les élèves de lycée professionnel problématisent même si le cheminement de leur raisonnement est parfois confus et laborieux.

Cela peut réinterroger certains des choix didactiques et, par voie de fait, pédagogiques. S'il s'avère que la mobilisation de la problématisation permet à l'enseignant de mieux appréhender les apprentissages des élèves, d'observer de façon plus clairvoyante les compétences qu'ils mobilisent et que ce processus peut en plus aider les élèves à surmonter les obstacles rencontrés, nous pouvons maintenant réfléchir aux moyens d'aider les élèves à mieux problématiser ou tout au moins de façon plus consciente.

Christelle Brémaud_E179552Q

[87]

BIBLIOGRAPHIE

i. Ouvrages :

DEL REY A. (2009). « À l'école des compétences - De l'éducation à la fabrique de l'élève performant ».

Paris : La Découverte.

FABRE M. (2016). « Le sens du problème ». Louvain-la-Neuve : de Boeck.

FABRE M. (2017). « Qu'est-ce que problématiser ? ». PARIS : VRIN chemins philosophiques.

JONNAERT Ph., ETTAYEBI M., DEFISE R. (2009). « Curriculum et compétences ». Bruxelles : de Boeck.

ORANGE C. (2012). « Enseigner les sciences ». Bruxelles : de Boeck.

REY B. (1996). « Les compétences transversales en question ». Paris : ESF.

REY B. (2014). « La notion de compétence en éducation et formation ». Louvain-la-Neuve : de Boeck.

ii. Articles :

BENOIT J.P. (2005). « L'émergence des « mots de la problématisation » dans les sources universitaires et les

dictionnaires spécialisés et généraux : constats et analyses ». Les Sciences de l'éducation : Pour l'Ère nouvelle, Vol. 38, n°3, pp. 33-51.

BOUTIN G. (2004). « L'approche par compétences en éducation : un amalgame paradigmatique ». Eres :
Connexions, n°81, pp. 25-41.

BROUSSEAU G. (1990). « Le contrat didactique : le milieu ». Recherche en didactique des maths, La Pensée Sauvage, Vol. 9, n°3, pp. 309-336.

BROUSSEAU G. (2007). « Théorie des situations didactiques en maths ». Éducation et didactique, vol. 5, n°. 1, 2011.

CHARNAY R. (2003). « L'analyse a priori : un outil pour l'enseignant ». Math-école, n°209, décembre 2003, pp. 19-26.

CRAHAYE M. (2006). « Dangers, incertitudes et incomplétude de la logique de compétence en éducation ». Revue française de pédagogie, n°154, pp.97-110.

DE KETELE J.-M., GERARD F.-M., ROEGIERS X. (1997). « L'évaluation et l'observation scolaires : deux démarches complémentaires ». Éducations : Revue de diffusion des savoirs en éducation, n°12, pp. 33-37.

DE KETELE J.-M. et GERARD F.-M. (2005). « La validation des épreuves d'évaluation selon l'approche par les compétences ». Mesures et évaluation en éducation, Vol.28, n°3, pp. 1-26.

FABRE M. (1997). « Pensée pédagogique et modèles philosophiques : le cas de la situation-problème ».
Revue française de pédagogie, Vol. 120, penser la pédagogie, pp. 49-58.

FABRE M., ORANGE C. (1997). « Construction des problèmes et franchissements d'obstacles ».

ASTER : obstacles : travail didactique, N° 24. 1997.

FABRE M. et MUSQUER A. (2009). « Les inducteurs de problématisation ». Les sciences de l'éducation - Pour l'ère nouvelle, vol. 42, n°3, pp. 111-129.

Christelle Brémaud_E179552Q

[88]

JONNAERT Ph. (2010). « Approche par situation - Matrice du traitement compétent d'une situation ». Cahier de la CUDC/UQAM (Chaire Unesco pour le développement curriculaire/Université de Québec A Montréal), Cahier 5 : octobre 2010.

JONNAERT Ph. (2011). « Sur quel objet évaluer les compétences ? ». Education & Formation. N° e-296, Décembre 2011.

JONNAERT Ph., FURTUNA D., AYOTTE-BEAUDET J.-P., SAMBOTE J. (2015). Cahier de la CUDC/UQAM (Chaire Unesco pour le développement curriculaire/Université de Québec A Montréal), Cahier 34 : décembre 2015.

MARGOLINAS C. (2014). « Connaissance et savoir. Concepts didactiques et perspectives sociologiques ? ». Revue française de pédagogie, n° 188, pp. 13-22.

NONNON E. (2002). « Formulation de problématiques et mouvements de problématisation dans les textes
réflexifs : un point aveugle pour l'enseignant ? ». Spirale - Revue de recherches en éducation, n°29 (Lire-écrire dans le supérieur), 2002, pp. 29-74.

ORANGE C. (2005). « Problématisation et conceptualisation en sciences et dans les apprentissages
scientifiques ». Les Sciences de l'éducation - Pour l'Ère nouvelle, Vol. 38, n°3, pp. 6994.

ORANGE C. (2005). « Problème et problématisation dans l'enseignement scientifique ». ASTER : Problème
et problématisation coordonné par ORANGE C., N° 40. 2005, pp. 3-11.

PERRENOUD P. (1998). « La transposition didactique à partir de pratiques : des savoirs aux compétences ».

Revue des sciences de l'éducation (Montréal), Vol. XXIV, n° 3, 1998, pp. 487-514. ROEGIERS X. (1999). « Savoirs, capacités et compétences à l'école : une quête de sens ». BIEF : Forum-

pédagogies, pp : 24-31.

ROYE L. (1993). « Acquisition de compétences à l'Ecole par la résolution de problèmes mathématiques
au quotidien : analyse et critères de situations ». SPIRALE - Revue de Recherches en Éducation - N° 10 (124-164)

SCHNEIDER M. et MERCIER A. (2014). « Approche par compétences, définition et désignation des savoirs mathématiques : peut-on envisager la disparition d'une organisation disciplinaire des savoirs ? ». Education et didactique, vol. 8 n°2, pp. 109-124.

REFERENCES ELECTRONIQUES

BROUSSEAU G. (1976). La problématique et l'enseignement de la mathématique. Comptes rendus de la XXVIIIe rencontre organisée par la Commission Internationale pour l'Etude et l'Amélioration de l'Enseignement des Mathématiques. Louvain-la-Neuve. https://hal.archives-ouvertes.fr/hal-00516569v1/document

BROUSSEAU G. (1983) : « Les « effets » du « contrat didactique » ». ^2ième école d'été de didactique des mathématiques (Olivet).

http://guy-brousseau.com/wp-content/uploads/2012/02/82-83-effet-de-contrat.pdf

Christelle Brémaud_E179552Q

[89]

BROUSSEAU G. (1997). Didactique des maths. http://guy-brousseau.com/1694/la-theorie-des-situations-didactiques-le-cours-de-montreal-1997/

DE KETELE J.-M. (2016). Conférence « L'évaluation des compétences : passer d'une posture de contrôle à une posture de la reconnaissance ». Neuchâtel, 18 janvier 2016. https://portail.rpn.ch/actualites/Documents/Conf_JMdK/JMdK.pdf

DELL'ANGELO M. (2011). « Les tâches complexes et l'évaluation de compétences dans l'investigation ». Bulletin pédagogique trimestriel de l'association des professeurs de biologie et géologie, pp.131-147).

https://hal.archives-ouvertes.fr/hal-

01138576/file/DellAngeloTaches%20complexes.pdf

DEL REY A. (2009). « À l'école des compétences - De l'éducation à la fabrique de l'élève performant ».
Paris : La Découverte. Entretien avec Guillermo KOZLOWSKI. https://www.cesep.be/index.php/72-publications/analyses/enjeux-de-societe/190-entretien-avec-angelique-del-rey

IREM (2013). « Enseignement par compétences ». Résumé de l'exposé lors du séminaire IREM de
l'académie de la Réunion du 27 02 2013.

http://irem.univ-reunion.fr/IMG/pdf/1.1_competences.pdf

PERRENOUD P. (1997). « Construire des compétences dès l'école ». Paris, ESF, 3^e éd. 2000.

http://www.unige.ch/fapse/SSE/teachers/perrenoud/php_main/php_livres/php_construi re.html#INTROO

PERRENOUD P. (2000). « Du curriculum aux pratiques : question d'adhésion, d'énergie ou de compétence ? ». Texte d'une conférence présentée à Québec le 10 octobre 2000. https://www.unige.ch/fapse/SSE/teachers/perrenoud/php_main/php_2000/2000_28.ht ml

ROEGIERS X. (2010). « Approche par compétences ».

https://www.youtube.com/watch?v=u7dK_rMWXdI

SORBE X. (2009). « Evaluer des compétences : pourquoi et comment ? ». Intervention du 4 décembre 2009
au colloque des 10 ans de l'IREM de l'académie de la Réunion. http://irem.univ-reunion.fr/spip.php?article307

TARDIF J. (2013). « L'approche par compétences : un changement de paradigme ».
https://www.youtube.com/watch?v=PR6N6-dJvzU

VERGNAUD G. (2004). « Didactique professionnelle et didactique des disciplines : la notion de compétences ». Fondation maison des sciences de l'homme. Entretiens 2002-2015. https://www.canal-u.tv/video/fmsh/didactique professionnelle et didactique des disciplines.28357

Christelle Brémaud_E179552Q

[90]

ANNEXES

ANNEXE 1: GRILLE NATIONALE D'ÉVALUATION en mathématiques et en sciences physiques et

chimiques

ANNEXE 1 bis : DOCUMENT D'ACCOMPAGNEMENT de la grille nationale d'évaluation en
mathématiques et en sciences physiques et chimiques

ANNEXE 2 : Extrait du REFERENTIEL DES ACTIVITES PROFESSIONNELLES du baccalauréat
professionnel MELEC (Métiers de l'Electricité et de ses Environnements Connectés)

ANNEXE 3 : GRILLE DETAILLEE DES COMPETENCES conçue par l'auteure de cette recherche et
distribuée aux élèves en début de formation

ANNEXE 4 : DOCUMENTS DE PREPARATION de l'enseignante pour la mise en oeuvre de l'activité
« grains de riz »

ANNEXE 5 : Relevés des TRACES ECRITES_RECHERCHE INDIVIDUELLE_ phase 1

ANNEXE 6 : TRANSCRIPTION synthèse de classe_ phase 2

APPROPRIATION DE LA SITUATION PROBLEME grains de riz

ANNEXE 7 : Relevés de TRACES ECRITES_PROPOSITION DE PROTOCOLE DE RESOLUTION_
phase 3

ANNEXE 8 : TRANSCRIPTION travail de groupe

PROPOSITION DE PROTOCOLE DE RESOLUTION_ phase 3

Transcription investigation 1 TEB_ phase 3 Groupe 1 : David Erwan Inès

ANNEXE 9 : TRANSCRIPTION travail de groupe

PROPOSITION DE PROTOCOLE DE RESOLUTION_ phase 3

Transcription investigation 1 TEB_ phase 3 Groupe 3 : Gabin Evan Romain

ANNEXE 10 : Relevés de TRACES ECRITES_RESOLUTION_ phase 4

ANNEXE 11 : TRANSCRIPTION travail de groupe

RESOLUTION DE LA SITUATION PROBLEME grains de riz Transcription investigation 1 TEB_ phase 4 groupe 3 : Gabin Evan Romain

ANNEXE 12 : ANALYSE de la transcription investigation 1 TEB_phase 4 groupe 3_séquence 1
ANNEXE 12 bis : ANALYSE de la transcription investigation 1 TEB_phase 4 groupe 3_séquence 2

ANNEXE 12 ter : ANALYSE de la transcription investigation 1 TEB_phase 4 groupe 3_séquence 3

ANNEXE 13 : RECAPITULATIF de l'ANALYSE DU CORPUS : informations recueillies, données et

conditions construites

ANNEXE 14 : GRILLES 1 D'EVALUATION des compétences

ANNEXE 14 bis: GRILLE 2 D'EVALUATION CHRONOLOGIQUE par compétences

ANNEXE 14 ter: GRILLE 3 D'EVALUATION CHRONOLOGIQUE par compétences dans le cadre de
l'analyse du corpus

[91]

ANNEXE 1 : GRILLE NATIONALE D'ÉVALUATION EN MATHÉMATIQUES ET EN SCIENCES PHYSIQUES ET CHIMIQUES
NOM et Prénom :	Diplôme préparé :	Séquence d'évaluation^55 n°

1. Liste des capacités, connaissances et attitudes évaluées

Capacités

Connaissances

Attitudes

Christelle Brémaud_E179552Q

2. Évaluation⁵⁶

Compétences^57	Capacités	Questions	Appréciation du niveau d'acquisition^58
S'approprier	Rechercher, extraire et organiser l'information.
Analyser Raisonner	Émettre une conjecture, une hypothèse. Proposer une méthode de résolution, un protocole expérimental.
Réaliser	Choisir une méthode de résolution, un protocole expérimental. Exécuter une méthode de résolution, expérimenter, simuler.
Valider	Contrôler la vraisemblance d'une conjecture, d'une hypothèse. Critiquer un résultat, argumenter.
Communiquer	Rendre compte d'une démarche, d'un résultat, à l'oral ou à l'écrit.
			/ 10

55 Chaque séquence propose la résolution de problèmes issus du domaine professionnel ou de la vie courante. En mathématiques, elle comporte un ou deux exercices ; la résolution de l'un d'eux nécessite la mise en oeuvre de capacités expérimentales.

⁵⁶ Des appels permettent de s'assurer de la compréhension du problème et d'évaluer le degré de maîtrise de capacités expérimentales et la communication orale. Il y en a au maximum 2 en mathématiques et 3 en sciences physiques et chimiques.

En mathématiques : L'évaluation des capacités expérimentales - émettre une conjecture, expérimenter, simuler, contrôler la vraisemblance d'une conjecture - se fait à travers la réalisation de tâches nécessitant l'utilisation des TIC (logiciel avec ordinateur ou calculatrice). Si cette évaluation est réalisée en seconde, première ou terminale professionnelle, 3 points sur 10 y sont consacrés.

En sciences physiques et chimiques : L'évaluation porte nécessairement sur des capacités expérimentales. 3 points sur 10 sont consacrés aux questions faisant appel à la compétence « Communiquer ».

⁵⁷ L'ordre de présentation ne correspond pas à un ordre de mobilisation des compétences. La compétence « Être autonome, Faire preuve d'initiative » est prise en compte au travers de l'ensemble des travaux réalisés. Les appels sont des moments privilégiés pour en apprécier le degré d'acquisition.

⁵⁸ Le professeur peut utiliser toute forme d'annotation lui permettant d'évaluer l'élève (le candidat) par compétences.

Christelle Brémaud_E179552Q

[92]

ANNEXE 1 bis :

DOCUMENT D'ACCOMPAGNEMENT

De la grille nationale d'évaluation en mathématiques et en sciences physiques et chimiques

Elaboré par les Inspecteurs de l'Education Nationale C. Orven et S. Garnung de l'académie de Caen.

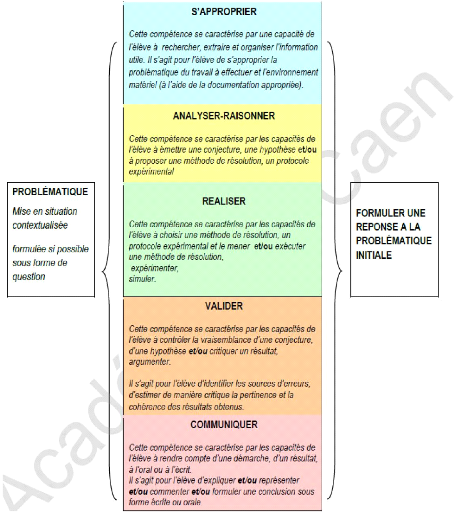
[93]

Ce même document d'accompagnement conseillant pour mieux communiquer avec l'élève d'utiliser le tableau suivant :

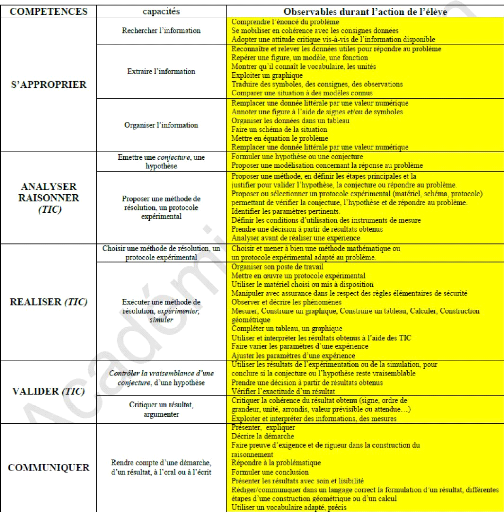
Christelle Brémaud_E179552Q

[94]

ANNEXE 2 :
Extrait du référentiel des activités professionnelles
du baccalauréat professionnel MELEC
(Métiers de l'Electricité et de ses Environnements Connectés)

Christelle Brémaud_E179552Q

[95]

ANNEXE 3 :

GRILLE DETAILLEE DES COMPETENCES

Conçue par l'auteure de cette recherche et distribuée aux élèves en début de formation

Inspirée du manuel scolaire Mathématiques CAP groupement A et Editions Foucher, 2016, pp.5 et 6.

Durant chaque évaluation, le professeur analyse votre travail à travers 5 compétences : s'approprier, analyser/raisonner, réaliser, valider, communiquer.

Quel est le sens de ces verbes? Quel est le travail attendu? Comment s'y prendre?

Voici quelques conseils et explications pour travailler efficacement.

ATTITUDES (savoir-être) : c'est une prédisposition à l'action indispensable pour s'engager dans le travail

Le sens de l'observation

La curiosité, l'imagination raisonnée, la créativité, l'ouverture d'esprit

L'ouverture à la communication, au dialogue et au débat argumenté

Le goût de chercher et de raisonner

La rigueur et la précision ; l'esprit critique vis-à-vis de l'information disponible

La persévérance

L'esprit critique vis-à-vis de l'information disponible

COMPETENCES : capacité à mobiliser et à réinvestir des connaissances, des capacités et des attitudes afin d'atteindre un objectif donné dans une situation de résolution d'un problème

Que doit faire l'élève?

Qu'attend le professeur?

S'APPROPRIER

ANALYSER RAISONNER

REALISER

VALIDER

Prendre connaissance de la situation et la comprendre

Bien lire la situation et la problématique

Repérer les informations qui semblent utiles, en les surlignant par exemple

S'interroger : Quel est le problème? Que cherche-t-on? Indications des données ou informations recensées

Classement des informations si cela est demandé ou nécessaire

Eventuellement explication orale de ce qu'il faut chercher

Proposer une méthode de résolution ou faire une proposition de réponse avec les éléments à disposition

Lire avec attention la consigne qui donne des indications sur les hypothèses à émettre :

- Émettre des conjectures, formuler des hypothèses.

- Proposer une méthode de résolution. - Élaborer un algorithme.

Choisir, élaborer un protocole. Proposition de méthode de résolution en nommant les outils mathématiques à utiliser

Formulation d'une proposition qui permet de répondre à la question posée

Détail des étapes de la méthode de résolution

Effectuer des calculs, lire un graphique, utiliser une simulation
	Mettre en oeuvre une démarche validée par le professeur Effectuer les calculs nécessaires en étant très attentif (pour éviter faute de frappe...)		L'unité de mesure et/ou les symboles sont indiqués Toutes les étapes des calculs sont indiquées
	Utiliser la simulation informatique si elle est proposée ou si elle parait pertinente dans la recherche		Les calculs sont justifiés par une formule, une propriété...

Vérifier la vraisemblance des résultats ou indiquer si une proposition de réponse est vraie ou fausse

Rendre compte d'une démarche, d'un résultat à l'écrit ou à l'oral

Comparer les résultats avec les données et/ou informations recueillies pour en vérifier la cohérence

Vérifier si l'ordre de grandeur des résultats semble possible

Analyser les résultats trouvés aux différentes questions et réfléchir à leur utilisation pour répondre à la problématique

COMMUNIQUER

Bien s'assurer de répondre à la question posée

Organiser ses réponses

Réfléchir à bien justifier ses réponses Validation (ou non) de la proposition de réponse de départ

Justification des conclusions en utilisant les résultats et/ou les données

Rédaction d'une conclusion qui répond bien à la problématique de départ

Utilisation d'un vocabulaire mathématique adapté

Présentation d'un travail soigné, clarté de l'expression (orale et/ou écrite)

Christelle Brémaud_E179552Q

Christelle Brémaud_E179552Q

[96]

ANNEXE 4 :

Documents de préparation de l'enseignante pour la mise en oeuvre de l'activité « grains de riz »

INVESTIGATION grains de riz : mise en oeuvre Document prof

Séance 1 :

5 min : En vidéo projection l'énoncé de l'investigation1.

Distribution du document 1 « recherche individuelle investigation ».

15 min : Les élèves seuls

- Cherchent à s'approprier la situation

- Doivent produire une trace écrite « brouillon » des questions qu'ils se posent, des

éléments dont ils disposent pour cette appropriation et la compréhension de ce qui est demandé...

- Envisagent une méthode de résolution (trace écrite de leur(s) recherche(s)).
Le document 1 « recherche individuelle investigation » est ramassé.

10 min : Synthèse collective des recherches individuelles, discutions, débat sur les méthodes engagées... Distribution du document 2 « protocole de résolution envisagé _ investigation ».

5 min : Constitution de groupes de travail.

15 min : Mise en commun par groupes des réflexions individuelles.

Sur le document 2 distribué « protocole de résolution envisagé _ investigation », chaque élève du groupe doit, après concertation avec les autres du groupe, o rédiger à l'écrit la démarche de résolution engagée (sur doc.2 « protocole de résolution envisagé _ investigation ») afin d'être « opérationnels » à la séance suivante pour la réalisation de leur protocole et la résolution du problème avec rédaction du compte rendu.

- Lister l'ensemble des ressources dont le groupe aura besoin (ordinateur, calculatrice, ...) Le document 2 « recherche individuelle investigation » est ramassé.

Séance 2 :

Distribution du document 3 « compte rendu de la résolution du problème d'investigation ». Il sera ramassé en fin de séance.

Les documents supports ramassés séance 1, sont distribués nominativement aux élèves : Doc.1

« recherche individuelle investigation » et Doc.2 « protocole de résolution envisagé »

55 min : Les élèves reconstituent les groupes de travail mis en place séance 1.

Les ordinateurs sont à disposition (6 ordinateurs pour 18 élèves) et l'enseignant est disponible pour répondre à leurs besoins matériels.

L'enseignant ne répondra à leur question que par des feedbacks afin de guider les élèves dans leur réflexion sans la piloter.

Christelle Brémaud_E179552Q

[97]

INVESTIGATION : éléments de correction Document prof

!!! VIGILANCE RECHERCHE INTERNET : les élèves ne doivent pas ouvrir les pages concernant

la résolution du problème !!!!

Etape 1 : recherche du nombre total de grains de riz

Utilisation du tableur pour simulation :

Information relevée : nombre de grains de riz = 18 446 744 073 709 600 000

Etape 2 : masse correspondant

Ressource 1 :

https://www.ilephysique.net/sujet-masse-d-un-grain-de-riz-190277.html Information relevée : Un grain de Riz a une masse de 0.020 g

Calcul de la masse totale de grains de riz obtenus :

0.020 * 18 446 744 073 709 600 000 = 368 934 881 474 191 000 grammes
= 368 934 881 474 tonnes

Etape 3 : recherche d'éléments de comparaison pour répondre à la problématique Ressource 2 : http://www.fao.org/worldfoodsituation/csdb/fr/

Site de l'organisation des Nations Unies pour l'alimentation et l'agriculture (Food and Agriculture Organization of the United Nations).

Information relevée : Production mondiale de riz en 2017 = 500.9 tonnes

Etape 4 : interprétation et conclusion

Calcul du rapport entre la masse obtenue sur l'échiquier et la production mondiale en 2017 = 368 934 881 474 / 500.9 = 736 543 984

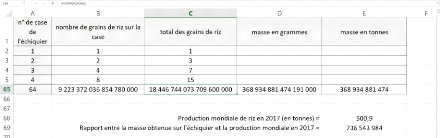
Christelle Brémaud_E179552Q

[98]

INVESTIGATION grains de riz: SCENARIO A PRIORI et éléments de correction				Document prof
compétences	capacités	observable durant l'action de l'élève	Attendus
s'approprier	rechercher, extraire et organiser l'information	comprendre l'énoncé du problème se mobiliser en cohérence avec les consignes données, reconnaître et relever des données utiles pour répondre au problème organiser les données dans un tableau/faire un schéma	1 grain de riz pour la première case de l'échiquier, 2 pour la deuxième et ainsi de suite, le nombre de grains étant doublé d'une case à l'autre.
analyser	émettre une conjecture	formuler une hypothèse ou une conjecture, proposer une modélisation concernant la réponse au problème	pour pouvoir répondre à la question "requête réalisable?" on cherche si - le calcul est possible pour connaitre le nombre total de grains de riz - si le résultat éventuel a du sens
analyser	émettre une conjecture, proposer une méthode de résolution	proposer une méthode, en définir les étapes principales et la justifier pour valider l'hypothèse, la conjecture ou répondre au problème identifier les paramètres pertinents	il y a 63 calculs (64 résultats en partant de 1) à effectuer les uns après les autres, le résultat étant le produit par 2 du résultat précédent en partant de 1 (le nombre de grains dans la case 1)
			il faudra comparer la somme de ces 64 résultats obtenus à une donnée qui a du sens (production mondiale de riz en 2017)
			on utilise un tableur avec - colonne A les n° de cases de 1 à 64, - colonne B, en Bn les produits par 2 du résultat précédent en Bn-1, avec en B1 la valeur de départ 1, - en B65 le résultat de la somme des 64 résultats intermédiaires pour le nombre total de grains.
réaliser	choisir une méthode de résolution	choisir et mener à bien une méthode mathématique	apparait le nombre de grains de riz sur chaque case
			apparait le nombre de grains de riz total avec - le calcul "=SOMME(B1:B64)" - le résultat (= 18 446 744 073 709 600 000)
s'approprier	rechercher l'informatio n	reconnaître et relever (trouver) des données utiles pour répondre au problème	avec masse d'un grain de riz = 0,020 g
analyser	proposer une méthode de résolution	identifier les paramètres pertinents	détail du calcul pour obtenir la masse totale des grains de riz 0,020×18 446 744 073 709 600 000

[99]

réaliser	exécuter une méthode de résolution	calculer	masse totale des grains de riz = 368 934 881 474 191 000 (grammes)
communiquer	rendre compte d'un résultat	utiliser un vocabulaire adapté, précis (ici les unités de mesure sont précisées et correctes)	en grammes
s'approprier	rechercher l'information	reconnaître et relever (trouver) des données utiles pour répondre au problème	Production mondiale de riz en 2017 = 500,3 millions de tonnes
Analyser.	proposer une méthode de résolution	identifier les paramètres pertinents	conversion en tonnes de la masse totale de riz trouvée = 368 934 881 474 tonnes
		identifier les paramètres pertinents	comparaison des deux masses, 368 934 881 474 / 500 300 000 = 737
s'approprier	Extraire l'information	traduire une observation	interprétation du quotient des 2 masses (justification de la conclusion)
valider	contrôler la vraisemblance d'une hypothèse	prendre une décision à partir de résultats obtenus	conclusion: la requête n'est pas réalisable

Christelle Brémaud_E179552Q

Christelle Brémaud_E179552Q

[100]

ANNEXE 5 :

Relevés de TRACES ECRITES pour la résolution de la situation-problème RECHERCHE INDIVIDUELLE_ phase 1

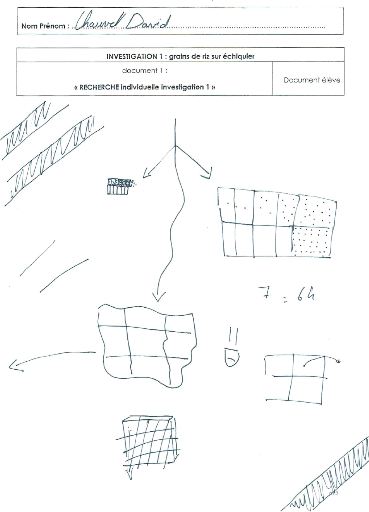
Christelle Brémaud_E179552Q

[101]

[102]

Nom Prénom : `

INVESTIGATION 1 : grains de riz sur échiquier

document 1

Document élève

cc RECHERCHE individuelle investigation 1 n

t

t

Lat

Qat ,te pla Q cat .l^- Cc>i d ch Îta

ca c. L! ci ds .-64A Cf c ?r C .

I' ~

_,3 L.04 A0_

}w:S -( c`i-! c0, dee{ f fvi oti. -rev f ) _ 3

Christelle Brémaud E179552Q

[103]

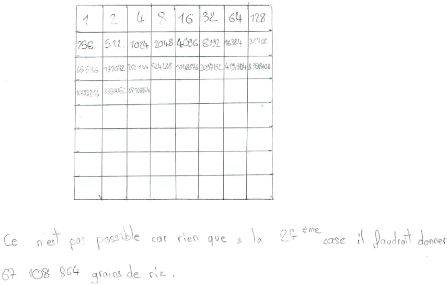
Christelle Brémaud_E179552Q

[ 104]

tI

Nom Prénom :

a

INVESTIGATION 1 : grains de riz sur échiquier

document 1 :

Document élève

u RECHERCHE individuelle investigation 1 »

4,34^\

Christelle Brémaud E179552Q

P.3

[105]

Christelle Brémaud_E179552Q

Christelle Brémaud E179552Q

[106]

Nom Prénom : ⁶⁷ Yom--

INVESTIGATION 1 : grains de riz sur échiquier

document 1 :

Document élève

rr RECHERCHE individuelle investigation 1 n

e,,`,Z c3

c	,)		)	-s&	co	i8d	z3
Sig.	loZL;	if..I	)109c	8iyz	aiseh

cw.

[107]

Christelle Brémaud_E179552Q

Christelle Brémaud_E179552Q

[108]

Christelle Brémaud_E179552Q

[109]

Christelle Brémaud_E179552Q

[110]

Christelle Brémaud_E179552Q

[111]

[112]

Christelle Brémaud_E179552Q

Christelle Brémaud_E179552Q

[113]

ANNEXE 6 : TRANSCRIPTION synthèse de classe_ phase 2 APPROPRIATION DE LA SITUATION PROBLEME grains de riz
Tour de parole	intervenant	intervention
1	Enseignant stagiaire ES	Vous avez aussi le droit de noter euh là où vous hésitez, ce que vous ne comprenez pas. Si ça vous avez besoin de le mettre, n'hésitez pas aussi à le mettre.
2		Tu doubles
3		...
4		Moi je ne comprends pas
5	ES	Bah tu expliques pourquoi.... ce que tu ne comprends pas
6		...
7	Romain	On ne la rend pas comme ça
8	Dorian	Oh là toutes les cases, tu ne t'es pas embêté !
9	Maxime	Bah c'est un damier blanc
10	Elsa	Bah non après faut additionner toutes les cases
11	Evan	Bah non, faut pas additionner toutes les cases
12	Elsa	Bah si parce qu'il faut savoir combien de grains de riz... après faut savoir...
13	Enseignante Ens.	Attention c'est une recherche qui se veut personnelle pour l'instant, vous aurez l'occasion après de mettre en commun. D'accord ?
14	ES	Temps écoulé, on va ramasser vos feuilles
15	Elsa	Faudrait quand même que je fasse...
16	Evan	Tout ça ? Je ne sers à rien dans la vie !
17	Ens.	Je vous ramasse votre feuille ?... s'il y a du recto verso, faites une petite flèche.
18		...
19	ES	Alors ? ... il en ressort quoi de tout ça ?
20	Evan	2080
21	Romain	Il n'y aura pas assez de grains
22	Maxime	(Tout bas à son voisinage) Bon bah c'est 2 puissance 64
23	Ens.	Vous levez la main pour prendre la parole, ce serait parfait et vous essayez de ne pas parler à deux en même temps
24	Elsa	(tout bas en réponse à Maxime) Bah non, bah non, c'est 2 plus 2 puissance 3 plus 2 puissance 3....
25	Romain	Il n'y aura jamais assez de grains
26	ES (note)	Il n'y aura jamais assez de grains
27	Dorian	Bah, Ça dépend du nombre de grains qu'il a
28	Elsa	Bah non, s'il réunit toutes les rizicultures
29		Il n'y aura jamais assez de place
30	ES	Il n'y aura jamais assez de grains
31	Maxime	Il ne va jamais compter...
32	Evan	Il n'y a pas assez de place
33	Maxime	... même pour euh
34	ES (note)	Il n'y a pas assez de place
35	Elsa	Bah ça dépend de l'échiquier ! Tout dépend de l'échiquier...
36	Maxime	La taille de l'échiquier... l'échelle de l'échiquier. Donc il ne va pas s'amuser à compter un million de grains de riz non plus quoi !
37	ES (note)	Tout dépend de l'échiquier
38	Elsa	En pas mal de temps quoi !

Christelle Brémaud_E179552Q

[114]

39	ES	Ça met du temps
40	Elsa	.... C'est possible... c'est possible mais il va passer pas mal de temps !
41		(inaudible)
42	Inès	C'est clair
43	David	... mais c'est le souverain... (inaudible)
44	ES (note)	Ça met du temps mais c'est possible... que peut-on rajouter ?
45	Coralie	On n'a jamais dit qu'il fallait les poser sur le cadre
46	ES	(Relecture à voix haute de l'énoncé) ...de lui donner un grain pour la première case de l'échiquier, 2 pour la deuxième, et ainsi de suite, et on ne demande jamais de le poser
47		... (inaudible)
48	Erwan	C'est pas marqué !
49	David	Voilà... en gros c'est obligé !
50	ES	Est-ce qu'on peut rajouter autre chose... rien d'autre ?...
51	Elsa	(tout bas à ses voisins) 2 puissance 4 pfffff
52	ES	Alors qui n'a pas compris l'énoncé dans ce cas-là ?!... allez, on n'hésite pas hein !
53	Inès	Bah il n'est pas détaillé, alors !
54	ES	Euh non mais... (inaudible)
55	Inès	Ah nan... mais moi je...
56	ES	Alors il n'y a qu'une seule personne qui n'a pas compris, donc tous les autres sont capables de résoudre le problème d'un seul coup ?
57		Ouais
58		Non
59	Elsa	Bah avec les puissances !
60	David	Ca on peut le dire avec un dessin
61	ES	Bon alors, où est-ce que ça butte ? où est-ce que vous ne comprenez pas
62	Dorian	Bah, on n'a juste pas assez de ..... On n'a pas assez d'informations
63	Maxime	Il n'y a pas assez d'informations
64	ES (note)	Il n'y a pas assez d'informations
65	Evan	Ouais
66	Elsa	Bah si !
67	Dorian	(A Elsa) Non parce que tu peux connaître le nombre de grains de riz, mais tu seras incapable de dire s'il y en a assez ou pas.
68	Evan	Ah oui !
69	Maxime	Bah on peut trouver le nombre de grains de riz qu'il faut mais on ne peut pas savoir si... il est assez énorme
70	Ens.	Ce serait bien que tout le monde s'écoute !... tu peux redire Maxime
71	Maxime	On peut réussir à connaître le nombre de grains de riz qu'il faut mais on sait pas après s'il y en a assez ou pas
72	Erwan	Bah si !
73	Elsa	Le roi on ne sait pas ce qu'il est capable de fournir
74	Dorian	Est-ce qu'il est capable de fournir ?... oh bah dis donc c'est français ça !
75	Maxime	(à son voisin) C'est le souverain qui donne des grains de riz
76	Dorian	(à Maxime) oui oui
77		La taille de l'échiquier
78	ES (note)	Alors... On ne connait pas la quantité de riz...
79	Dorian	que possède le souverain
80	ES	... dont dispose le souverain
81	ES	Qu'est-ce qui nous manque comme donnée ?
82	David	De quoi ?
83	ES	Vous avez dit qu'il n'y avait pas assez d'informations... est-ce que c'est la seule info qui nous manque ?

Christelle Brémaud_E179552Q

[115]

84	David	Est-ce que, non... est-ce que les grains de riz doivent rester absolument sur les cases ou euh
85		Non !
86	ES	On a déjà posé la question... on ne demande jamais de poser les grains de riz sur l'échiquier...
87	David	Vous n'avez pas de réponse alors
88	ES	je n'ai pas de réponse là-dessus non
89	Ens.	Est-ce que c'est écrit ? Quelqu'un a dit tout à l'heure « ce n'est pas écrit »
90	David	Bah oui
91	Romain	Ce qui n'est pas écrit n'est pas écrit
92	David	Bah c'est obligatoirement possible
93	Ens.	Qu'est-ce qui est obligatoirement possible ?
94	David	Que chaque case, on peut toujours doubler si on n'a pas de contrainte...ça nous fait zéro contrainte
95	Ens.	Tu en as des contraintes mais pas celles-ci
96		(rire d'un élève)
97	David	Ah bon !?... parce que j'en vois pas
98	Ens.	Au pire
100	David	Au pire on le fait à la calculette
101	Ens.	.. et comment tu vas faire avec la calculette ?
102	Elsa	Avec les puissances !
103	Ens.	Avec les puissances... c'est toutes ces questions-là qu'il faut que vous vous posiez
104	Elsa	(en même temps que l'Ens.) 2 puiss...1... plus 2 puissance 2 plus de 2 puissance 3
105	Ens.	C'est avec toutes ces questions-là que vous allez réussir à arriver à la solution... est-ce qu'il n'y a que la calculatrice ? Vous avez peut-être d'autres outils à disposition
106	Elsa	Bah les tableurs
107	Ens.	Les tableurs... vous pouvez tout imaginer... comment vous allez chercher à résoudre ce problème-là pour pouvoir y répondre ... et est-ce que la solution à laquelle vous allez arriver elle est plausible ? parce que l'idée c'est que « est-ce que la requête est réalisable ? » c'est-à-dire est-ce que la réponse à laquelle vous allez arriver est plausible ?... Au regard de quoi ?
108	Elsa	Bah du temps passé quoi!
109	Ens.	Et peut-être d'autres informations dont vous ne disposez pas, que vous allez avoir à aller chercher... pour comparer votre résultat à des données
110	Maxime	De toute façon, il n'arrivera jamais à compter exactement tout le nombre des grains de riz
111	Ens.	Je n'ai pas entendu Maxime
112	Maxime	Il n'arrivera jamais à compter exactement le nombre de grains de riz qu'il a
113	Ens.	Ah bah le but, si on vous donne ça c'est qu'il y a quand même une possibilité d'y arriver !
114		(Brouhaha)
115	Ens.	Est-ce que c'est réalisable ça ne veut pas dire que vous n'allez pas réussir à obtenir une réponse
116	Elsa	Ah !
117	Ens.	parce que le but du jeu, parce qu'on n'est pas pervers quand même, c'est que vous êtes censés pouvoir obtenir une réponse... maintenant pour savoir si c'est réalisable il va falloir que vous mettiez votre réponse au regard de certaines données que vous irez chercher... qui vous semblent pertinentes... pour pouvoir comparer et valider du coup la chose

Christelle Brémaud_E179552Q

[116]

ANNEXE 7 :

Relevés de TRACES ECRITES

PROPOSITION DE PROTOCOLE DE RESOLUTION_ phase 3

Groupe 1 : David, Erwan (document 2 non rendu), Inès

Christelle Brémaud_E179552Q

[117]

Groupe 2 : Dorian, Elsa, Maxime

[118]

Christelle Brémaud E179552Q

Nom Prénom de l'élève :...ClGSA1V Noms des autres élèves du groupe :	ç^'.1q1;'litke
INVESTIGATION 1 : grains de riz sur échiquier
document 2 : « PROTOCOLE de résolution envisagé _ investigation 1 »		Document élève

1`00\1Dce_ Ae. CASe

1Vocs ad ,,,,oi\

Christelle Brémaud_E179552Q

[119]

Groupe 3 : Evan, Gabin, Romain

[ 120]

Nom Prénom de l'élève :.:~..~~~~.°.t Noms des autres élèves du groupe :
INVESTIGATION 1 : groins de riz sur échiquier
document 2 : « PROTOCOLE de résolution envisagé _ investigation 1 D	Document élève

men tal^'exilent'nea eht. r c usabl.

culcut E,otale. :e(A -p.t w(

tab Cu(

:su( I

b1 ,narç, le rm1.8¹.61^.1ci;.hm_s

z

Li F 2

e.r n J, t,C' I &y&(

eai2x4)-$

Christelle Brémaud E179552Q

[121]

Nom Prénom de l'élève :			13J

Noms des autres élèves du groupe :

Ixtv

INVESTIGATION 1 : grains de riz sur échiquier
document 2 : « PROTOCOLE de résolution envisagé _ investigation 1 »	Document élève

Christelle Brémaud E179552Q

g IC

32

P. 4

Christelle Brémaud_E179552Q

[122]

Groupe 4 : Coralie, Jordan, Léa

[123]

Christelle Brémaud_E179552Q

[124]

Christelle Brémaud_E179552Q

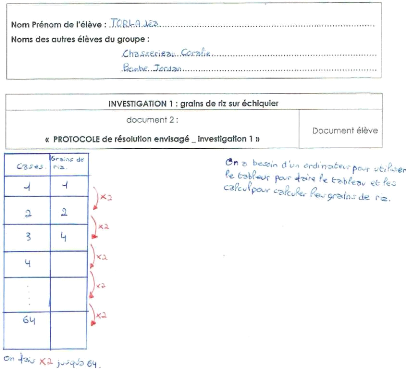
[125]

Groupe 5 : Hugo, Marie, Rozenn

Christelle Brémaud_E179552Q

Christelle Brémaud_E179552Q

[126]

Groupe 6 : Axel et Théo n'ont pas remis leur document 2

Christelle Brémaud_E179552Q

[127]

ANNEXE 8 :

TRANSCRIPTION travail de groupe PROPOSITION DE PROTOCOLE DE RESOLUTION_ phase 3

Transcription investigation 1 TEB_phase 3 Groupe 1 : David Erwan Inès

Tour de parole	intervenant	intervention
1	Erwan	Tu l'as fait 7 fois, il faut le faire 64 fois !
2	David	Merci Erwan pour ton coup de pouce ! Waouah !
3	Inès	Je l'ai fait 2 fois
4	David	Vas-y, continue, continue.... Et tu calcules par contre faut pas que tu sois perdue, faut que tu t'arrêtes à 64, donc 2 puiss.....euh...oh...
5	Erwan	64 au carré
6	Inès	Ça fait beaucoup !
		Brouhaha
7	Ens	Vous êtes censés discuter dans vos binômes pour éviter de parasiter le son
8	David	Tu es enregistré toi aussi ?...oh moi aussi je suis enregistré !
9	David	Erwan ?
10	Erwan	Ouais !
		(aparté inintéressante)
11	Inès	C'est la 32eme fois
12	David	Oh t'es trop forte tu sais ! tu as calculé ?
13	Erwan	Bah tu mets tout au carré
14	Inès	Bah vas-y fais-le ! ferme ta gueule !
15	Erwan	Genre, là en fait, tu mets 64 au carré
16	Inès	ok
17	David	Attends attends nan nan déjà on va faire 32
18	Erwan	Ha non non non là je dis de la merde !
19	Inès	Bah alors vas-y
20	Inès	Bah je crois que c'est 32.... Mais pourquoi tu marques trente...ha oui ! d'accord... je ne suis pas sure que ce soit 32
21	Ens	Si vous avez besoin de choses dont vous ne disposez pas aujourd'hui, par exemple un ordinateur ou je ne sais pas...euh... des bouquins... il faut que vous le précisiez clairement. C'est-à-dire que ce qu'on va ramasser là sur cette feuille c'est votre décision collective de groupe... « on pense faire ça »...
22	Inès	On pense faire quoi ?
23	Ens	si vous dites on a besoin de la calculatrice vous expliquez pour faire quoi, si vous dites on a besoin de bouquins, pourquoi,
24	David	Tiens on fait ça, on trouve le résultat et après on dit calculateur
25	Ens	si vous dites que vous avez besoin d'un tableur comment vous allez l'utiliser et pour faire quoi...
26	Inès	Calculateur ??
27	David	Tu sais le truc sur ordi
28	Inès	Tableur (rires)
29	David	Ça fait longtemps qu'on ne l'a pas fait !
30	Inès	T'es vraiment bizarre toi !
31	David	calculateur

Christelle Brémaud_E179552Q

[128]

32	Inès	Ha non je ne continue pas moi, je suis perdue
33	David	S'te plait
34	Inès	non
35	David	Inès ! Pour le bien de l'équipe !
36	Inès	Faut faire des sacrifices !
37	David	Vous entendez, elle ne veut pas travailler !... et mais Erwan travaille aussi ! Moi j'écris tout !
38	Inès	He mais quand on fait ça c'est le double ?
39		...
40	David	Mais calcule comment tu cliques !!
41	Inès	Oh
42	David	Mais calcule comment tu cliques
43	Inès	Oh mais c'est pas possible regarde !
44	David	Mais on s'en fout ! Moi je vais avoir (inaudible)
45		(échanges inintéressants, insultes)
46	Ens	D'un groupe à l'autre vous ne communiquez pas ! Vous devez tous impérativement arriver à une solution, et à partir de votre solution... vous n'allez pas trouver forcément aujourd'hui.... Aujourd'hui vous mettez en place la stratégie pour y arriver...
47	David	Ah non, attends tends tends...1...2...3...4...5...6...
48	Inès	Ouais mais ça donne quoi ?
49	David	...11...12...
50	Ens	Maxime vous êtes enregistrés, alors un peu de sérieux !
51	David	(jusqu'à 32)
52	Erwan	Mais on travaille sur quoi ?
53	David	C'est bon !
54	Erwan	Non mais faut nous aider !
55	David	non mais c'est bon ! on a trouvé ! on a trouvé un résultat
56	Ens	Oui mais faut peut-être répondre à Erwan
57	David	Oui mais Erwan il ne veut pas comprendre
58	Erwan	On travaille sur quoi ? Vas-y !
59	David	On travaille on travaille
60	Erwan	On travaille sur quoi ?
61	David	Eh, t'avais qu'à travailler avec moi
62	Inès	On travaille sur les grains de riz
63	David	Faut tout vous expliquer maintenant !
64	Inès	Alors c'est combien le résultat ?
65	David	Je vous dirai pas... je vous le dirai après
66	Inès	Plus e....C'est ça !
67	David	C'est pour ça que je préfère pas le dire !
68	David	J'arrive même pas à le dire !
69	ES (à Erwan)	Regarde tu dois poser sur chaque case, sur la première tu poses grain de riz, sur la deuxième tu doubles, sur la troisième tu en poses le double de la deuxième et ainsi de suite...d'après toi quand on fait tout ça on va obtenir quoi au final ?
70	Inès	Bah le nombre de grains de riz
71	ES	Le nombre de grains de riz...d'accord
72	Inès	Non mais sérieux
73	David	C'est long hein !
74	Inès	C'est quoi e plus 19 ?

Christelle Brémaud_E179552Q

[129]

75	David	C'est euh..... Le e je ne pourrais pas te dire mais le plus c'est comme si tu multipliais par euh...
76	ES	Alors ça du coup c'est quoi ? le résultat ?
77	David	C'est le nombre de grains de riz qu'il y a sur la dernière case
78	ES	Ça faut que tu le mettes alors !????
79	ES	Faut que tu le mettes alors, parce que... et tu mets 64 égale 1.8 fois
80	David	C'est la case ça, c'est la case ça, mais j'ai tout marqué
81	ES	Mais il faut il faut il faut
82	Inès	Et puis en plus, c'est pas (inaudible)
83	David	Quoi ?
84	Inès	Bah oui mais le e, ça ne s'écrit pas comme ça !
85	David	Tu crois que je sais moi ?
86	PS	Donc là le principe c'est qu'on a déjà la réponse dans l'énoncé de ce qu'on a étudié
87	David	On a déjà la réponse dans l'énoncé?
88	PS	Non pas de ça, vous n'avez pas la solution dans l'énoncé mais de ce qu'on étudie vous l'avez dans l'énoncé en fait
89	David	Ha ouais
90	David	Et e c'est quoi déjà ?
91	David	Et ainsi de suite...oh moi je sens que je vais
92	David	Du coup moi j'ai marqué le brouillon, Inès va marquer le propre
93	Inès	Mais tais-toi !
94	PS	Dans tous les cas on ramasse toutes les feuilles
95		(échanges inintéressants)
96	Inès (à Erwan)	Nous on est là, on travaille et toi tu ne fais rien du tout!
97	Erwan	C'est normal !
98	David	En gros j'ai fait xxxx...jusqu'à 64 si Inès ne s'est pas trompée
100	Inès	Non je ne me suis pas trompée
101	David	Ho la provoque laisse tomber
102	Inès	Je me suis pas trompée je te dis
103	Erwan	T'as trouvé un nombre comme ça ?...t'as pas trouvé genre.... avec des puissances derrière ?
104	David	Bah tu crois que c'est quoi ça ?
105	Inès	C'est quoi une puissance ?
106	David	C'est ça les puissances !
107		(rires)
108	Erwan	Non ...tu ne sais pas ce que c'est une puissance ?
109		(rires)
110	David	Ho quel génie yes ! Si la prof de maths écoute ça, ça craint pour vous là!
111	Erwan	Ta puissance elle pas additionnée là...faut que tu l'additionnes
112	David	En tout cas moi j'avais cru entendre...Après c'est le résultat, cherche pas à comprendre hein!
113	Inès	Ensuite on a trouvé ça, et ensuite on fait quoi ?
114	David	Bah, en gros, après faut les (inaudible) et faut voir si les sachets de beaucoup de grains de riz...moi je ne sais rien de toute façon !
115	PS	Qu'est-ce que ça signifient ces valeurs là que tu as trouvées?
116	David	Ça veut dire qu'il y a beaucoup beaucoup de grains de riz
117	Inès	Et là pourquoi y a un e ?
118	PS	Pourquoi il y a un e ici ? Ça veut dire quoi ? Le e, tu l'as recopié de ta calculatrice ? Ça veut dire puissance !
119	Erwan	He mais non !

Christelle Brémaud_E179552Q

[130]

120	PS	Parce que e plus quelque chose ça veut dire puissance...
121	Erwan	He là faut toutes les sommes avant !
122	PS	Donc du coup, là sur 64 cases.... cela donne...ça ! bon bah alors ?
123	David	Là ce n'est pas terminé
124	PS	Alors est-ce que la requête est réalisable dans ce cas-là ? est-ce que ça signifie que la requête est réalisable ?
125	David	Bah si on a....ooooonnnnn....
126	Erwan	Bah oui elle est réalisable !
127	David	Si on a un nombre compréhensible par toute personne... parce que moi je ne le comprends pas !... mais si on fait... en gros si on calcule ce nombre, on le met puissance...euh...je ne sais même pas si c'est vraiment puissances là
128	Inès	Si c'est la puissance
129	David	Si on met puissance 19 et tout, on fait le calcul correctement...on pourrait essayer de le faire.... Après faut additionner tout ce qu'on a fait !
130	Erwan	Mais oui faut additionner toutes...là en fait, ce n'est que la 64eme case !
131	Inès	Ah ouais
132	Erwan	Faut additionner toutes les autres cases !
133	Inès	Ah ouais...là je n'ai fait que la 32 et la 64 !
134	PS	Et quel est l'intérêt de tout additionner ?
135	David	Bah savoir le nombre de grains de riz qu'il va nous falloir !
136	PS	Le nombre de grains ? Pardon ?
137	David	Qu'il va nous falloir !
138	PS	Qu'il vous faudra au total... D'accord ?... OK
139	Inès	Toi tu fais le total....
140	David	Alors moi j'ai déjà fait tout tout tout
141	Inès	Pardon ?... moi je suis à fond
142	David	Tu additionnes, tu additionnes...tout tout à la calculatrice...tu additionnes....non mais ça va 5 minutes, faut que tu travailles un peu aussi
143	Erwan	C'est impossible !
145	David	De quoi ?
146	Inès	Ça, ça c'est impossible
147	Erwan	Non mais il y a un calcul spécifique pour le faire
148	David	Non mais c'est bon connard
149	Inès	Un calcul spécifique
150	Erwan	Bah si mec
151	David	Comme une des fonctions par exemple
152	Erwan	Je ne sais pas du tout ! Il m'a dit qu'il y avait le truc dans le (inaudible)
153	David	Non j'avais fait un super dessin...ça c'est mes grains de riz qu'il va falloir
154	Ens	Maintenant vous nous remettez vos feuilles
155	David	Au pire c'est ça le résultat
156	Erwan	Bah voilà
157	David	On ne se fait pas chier

Christelle Brémaud_E179552Q

[131]

ANNEXE 9 :

TRANSCRIPTION travail de groupe

PROPOSITION DE PROTOCOLE DE RESOLUTION_ phase 3

Transcription investigation 1 TEB_ phase 3 Groupe 3 : Gabin Evan Romain

Tour de parole	intervenant	intervention
1	Maxime	madame, est-ce qu'on a droit à l'ordinateur ?
2	Ens (à la classe)	vous avez droit à tout ce que vous voulez... Sauf que, dans cette phase-là, très clairement, vous allez vous coordonner et vous mettre d'accord...(brouhaha)... He, les consignes !...de manière à ce que mercredi, selon ce dont vous avez besoin, on vous le mette à disposition. C'est-à-dire que là, on va vous demander, de mettre sur papier les stratégies que dans le groupe vous envisagez pour aller chercher la solution
3	Ens (à la classe)	Vous vous dépêchez, il ne vous reste que 15 minutes. ...
4	Gabin	1 Virgule.... (inaudible) (pendant qu'Evan s'installe en regardant sur la calculatrice de Gabin)
5	Evan	Bah ça fait beaucoup moi je dis !
6		Bah ça fait plus que des trilliards et des trilliars et des trilliards !
7	Evan	Combien t'as trouvé ?
8	Romain	En formule ? Euh... Bah c'est 2 fois 2... euh.... Puissance 63
9	Evan	2 fois 2 puissance 63 ?
10	Romain	Et puis t'as ton résultat
11	Evan	Non ! puissance 64
12	Romain	3
13	Evan	64
14	Romain	3
15	Evan	Pourquoi ?
16	Romain	Parce que 1 plus 1, 2... c'est là où tu pars de 2 fois 2
17	Evan	Ouais
18		(réglage caméra prof)
19	Gabin	Et pourquoi t'as fait 2 fois 2 fois 2 fois 2?
20	Romain	Parce qu'en fait je ne me rappelais plus comment on faisait pour faire les exposants, enfin euh... pour les puissances avec la calculatrice...donc au moins là je suis sûr que c'est bon. Et après tu vois là regarde, tu fais le calcul simple... tu vois (passe sa calculatrice à Gabin)
21	ES (à la classe)	Alors dans cette deuxième partie, on ne vous demande pas de trouver la réponse, mais on vous demande de proposer une démarche qui peut conduire à la résolution, donc pour faire cela c'est toutes les ressources dont vous allez avoir besoin... que ce soit des informations... concernant le problème, que ce soit du matériel, des calculs. D'accord ?... c'est tout ça qui doit apparaitre dans votre trace écrite...
22	Gabin	(examine l'affichage de la calculatrice... inaudible car couvert par la voix du prof qui rappelle les consignes de cette phase de travail en groupe) ...
23	Romain	C'est ça ! En fait... regarde en reprenant la calculatrice
24	Gabin	Et du coup pourquoi tu as mis 6 fois 2 en fait ?

Christelle Brémaud_E179552Q

[132]

25	Romain	En fait, la première case, la première case, c'est 1 plus 1, parce que la deuxième fois c'est 2 parce que tu prends une case de plus... fois 2 et tu peux exposant, euh puissance 63 parce que tu peux pas faire toutes les cases d'un coup
26	Gabin	Ha ok ! Et du coup, maintenant la question c'est est-ce que la requête est réalisable ? ... Ouais mais du coup il y a plein de facteurs différents
27	Romain	Y en a trop là.
28	Gabin	Déjà il faut bien relire l'énoncé, le texte
29		(... Gabin relit, Evan note quelque chose sur sa feuille, Romain discute)
30	Romain	C'est quoi que tu lis ?
31	Gabin	Ca ! (en montrant l'énoncé en vidéo projection) Mais en fait le problème... euh... c'est qu'on a trop de ... on a trop de... euh... des choses différentes
32	Romain	(inaudible)
33	Gabin	Faut prendre les principales
34	Romain	Là tu vois, là regarde
35	Evan	Quoi
36	Romain	Relis, relis l'énoncé
37	Evan	Ah oui mince !
38	Romain	1, 2, 4, 8, 16, 32, 64, 128, 2 cents...euh... 256, 520... euh... mille vingt euh
39	Evan	Chut chut chut
40	Romain	Tu sais que tout à l'heure, je les ai fait jusqu'à....
41	Evan	Oui, moi je t'ai entendu faire
42	Gabin	On nous demande pas d'aller jusqu'à autant de nombres là ! On demande juste si la requête est réalisable
43	Romain	Non là... Evan, Evan... on ne nous demande pas de résoudre
44	Evan	Ah d'accord !
45	Gabin	On nous demande juste si euh
46	Romain	Ouais mais ça dépend... Ca dépend de beaucoup de facteurs qu'on ne sait pas
47	Gabin	Oui mais si on le fait sur... (inaudible)
48	Romain	Bah ouais c'est irréalisable mais sinon dans l'Ens.emble c'est réalisable.
49	Gabin	Ce qu'on nous demande c'est la base de la base en soit on nous demande pas
50	Romain	Mais dans l'Ens.emble c'est réalisable
51	Gabin	Oui c'est réalisable, si on ne s'attarde vraiment qu'aux consignes c'est largement réalisable ! On nous dit 1 grain de riz sur la première case de l'échiquier, 2 pour la deuxième, et ainsi de suite, le nombre...
52	Romain	On a juste à calculer... oui la quête est réalisable. Et voilà ! Oui la requête est réalisable, il suffit juste de le calculer
53	Evan	Bah non...
54	Romain	Bah si !
55	Gabin	Parce que là en soi on a là 64
56	Romain	Oui, y a 64 cases
57	Gabin	1, 2...
58	Romain	Je te rassure quand tu arrives à ... dans 7 cases tu t'arrêtes !
59	Evan	Pourquoi ?
60	Romain	Tu vas voir... je me suis arrêté à pas très loin en fait... à partir d'un moment tu commences à aller beaucoup trop loin
61	Evan	On est déjà à 16000...oh !
62	Romain	Ouais et après 32, 64, 128, 720...
63	Gabin	On rédige sur quelle feuille ?
64	Romain	Bah les 3

Christelle Brémaud_E179552Q

[133]

65	Gabin	OK, euh...
66	Romain	Gabin Facquet
67	Gabin	Naudet ça prend bien un t à la fin ?
68	Romain	ouais
69	Evan	Poyard ça prend un d
70	Gabin	Je sais
71	Evan	Bien
72	Romain	Protocole de résolution envisagé par le groupe
73		(vérification orthographe des noms à indiquer sur chaque copie)
74	Romain	Ha je ne m'attendais pas à le faire aussi merdique ce truc-là !
75	Gabin	Sinon, on écrit quoi ?
76	Romain	Si on suit l'exercice, la question est de savoir si c'est réalisable et que le problème est réalisable
77	Gabin	Si on s'en suit à la consigne, l'expérience est réalisable
78	Romain	Voilà
79	Evan	Moi je suis à un million.... Mais c'est c'est... j'ai fait que trois lignes (sur sa calculatrice)
80	Romain	Ouais je sais
81	Evan	T'es sûr ?
82	Romain	Relis, euh, relis le truc. T'as juste la dernière phrase à relire. Si on s'en suit à l'exercice ? Gabin ! si on s'en suit à l'exercice ?
83	Gabin	L'expérience est réalisable
84	Evan	C'est ça en plus (après avoir relu l'énoncé)
85	Gabin	Après, maintenant il reste plus qu'à mettre les résultats de nos calculs
86	Romain	Bah en fait, tu ne peux pas vraiment le prouver
87	Evan	Vous avez écrit quoi ? Si... ?
88	Romain	Hein ?
89	Gabin	(inaudible)
90	Romain	La franchement il y a deux solutions... soit on écrit toutes les rép....
91	Evan	(Inaudible)
92	Romain	TiEns., Gabin, tu sais que tu as le menu table ? Est-ce que tu sais comment on fait ?
93	Gabin	Quoi ?
94	Evan	Je sais faire moi
95	Romain	Oui mais tu ne sais pas exactement ce que je veux faire
96	Evan	Bah non, si tu ne me dis pas je ne sais pas faire
97	Gabin	(se déplace pour aller derrière Romain et sa calculatrice)
98	Romain	Moi, tu vois,... tu vois je voudrais faire un peu la même chose qu'Evan mais sauf qu'avec cette version simple tu vois. Parce que bon, faire 2 fois 2 fois 2 fois 2
100	Gabin	Attends je vais prendre ma calculatrice
101	Romain	Vas-y
102	Evan	Ho la vache, c'était long !
103	Gabin	Mais non toi ce que tu veux c'est pas Table
104	Romain	Euh... Ah ouais, bah ouais !
105	Gabin	Attends... (inaudible)
106	Romain	Non moi en fait ce que je veux faire, c'est par exemple, tu vois,... on va être d'accord... tu veux faire 2 fois 2 fois 2 fois 2 fois 2... sauf qu'au lieu d'écrire et faire 2 fois 2 à chaque fois pour savoir le résultat que ça fait au total, tu fais le calcul et t' auras toute la ligne de tous les chiffres
107	Gabin	Oui comme sur Excel
108	Romain	Oui en bref, c'est Excel mais en... bah au pire on se met sur un ordi mais y aura pas le temps... Y a pas le time !

Christelle Brémaud_E179552Q

[134]

109	Evan (qui rédige)	Si on s'en suit à l'exercice
110	Gabin	Du coup, là, on en est... le reste du raisonnement, on le met sur euh, ...
111	Romain	Le calcul... le calcul total on aura besoin... elle est où ma feuille ?
112	Gabin	Là, tu mets... le calcul... total....sera...fait sur Excel
113	Evan	Qu'est-ce que vous notez ?... oui, non... mais là, on fait ça sur calculette ou sur Excel ?
114	Romain	Sur Excel
115	Gabin	Après on met une petite flèche en bas... du coup tu veux faire quoi ? tu veux mettre les valeurs en bas... (inaudible)
116	Romain	Bah euh.... Le truc c'est que je vois pas... je sais comment le... je sais, dans ma tête tout est déjà fait... mais le poser...j'ai toujours un défaut là- dessus...mmmmm... attends, imaginons que... Excel, Excel, Excel... ça voudrait dire qu'il faudrait transférer le résultat là et le remultiplier par 2...
117	Gabin	Ok ! Donc en fait.... On....
118	Romain	Putain, ça va faire faire un changement de fou
119	Gabin	Les premières valeurs
120	Romain	Et on les transfère
121	Gabin	Et on les élargit ?.... Du coup sur Excel, on les élargit, tu sais
122	Romain	?
123	Gabin	Du coup sur Excel, tu sais, tu les élargis, tu vois ? (faisant le signe du copier glisser de haut en bas)
124	Romain	Ouais... sauf que ça ne ferait pas la même chose, ça restera 2 fois 2 fois 2 fois 2 fois 2
125	Evan	Bah oui !
126	Gabin	.... Tu sais faut mettre égal somme et truc...
127	Romain	Donc, tu vois, regarde, je t'ai mis sur ta feuille...là tu vois c'est Excel.... Tu le mets 2 fois 2... et là t'as ton résultat... c'est 4. Tu prends ça, ton 4 là, et y aura toujours fois 2 ici. 8 fois 2... 16. Ca donnera un truc comme ça mais à l'infini... jusqu'à 64
128	Gabin	Ah d'accord ! Ça c'est des fois ça ?
129	Romain	Ouais... attends, attends, regarde, je vais le résoudre... Alors en fait on veut résoudre le truc, vous voyez madame on veut faire ça au final (montrant un schéma à la caméra)
130	Evan	Voilà... c'est... le total (montrant le même schéma à la caméra)
131	Romain	Non, il te manque des chiffres !
132	Evan	Mais euh, dites-moi quand vous voulez écrire quelque chose, je sais pas
133	Gabin	Les multiplications
134	Romain	Les calculs
135	Gabin	Sur le tableur... en fait, tu mets exemple entre parenthèses, et tu mets... bah deux trois calculs
136	Romain	Ouais j'avoue que ce système de puissances c'est la merde ! Voilà, moi, j'ai mis ça comme ça ! Hein Gabin
137	Gabin	Oui t'as raison
138	Romain	Bon après celui qui arrive à me relire vu comment j'écris !
139	Evan	Si si
140	Romain	J'ai fait mon écriture de médecin

[135]

ANNEXE 10 :

Relevés de TRACES ECRITES
RESOLUTION_ phase 4

Groupe 1 : David (document 3 non remis), Erwan (absent), Inès

Christelle Brémaud_E179552Q

Christelle Brémaud_E179552Q

[136]

Groupe 2 : Dorian, Elsa, Maxime

Christelle Brémaud E179552Q

[137]

Nom Prénom de l'élève : Noms des autres élèves du groupe :
INVESTIGATION 1 : grains de riz sur échiquier
document 3 : « COMPTE RENDU de la résolution du problème _ investigation 1 »	Document élève

auttruzticcolti x Z '' plu)) ,ta Aerrrvm_f_ c(aA 6 G Cc

(lao cl-0^,971)N 0-e)4607l..c,0 /15 il cl c:7 LOA 04 34 0 g ⁶⁰ 0r , CID gtcuiv

C A. ,cem pwLC me7 r .cna Q,W .

N Cvt orv, ^-tnc .

^64- tk pLQ n_vi d avr,h pari - ®m m2

aitzcOitz ,ccv. -4uctkcio (lito c_vy-_vraih^- .J2k^-

t_` o(x i.5^,4 rl, cn-b4, dc .k rrn

[138]

Nom Prénom de l'élève : _C t i~ ° x'ame Noms des autres élèves du groupe : . Le,roy
INVESTIGATION 1 : grains de riz sur échiquier
document 3 : w COMPTE RENDU de la résolution du problème _ investigation 1 »						Document élève
NooS	ye.\\ ca1c\lec le c oct e 8e....3 c0;. I~ ci, vit				e, e
CCASe CTDVS mean_5		1, EhE0\G Siot	5 cive p ', (e	Lélu `C C\u			ce.SSV k2. .

CACOL T \a Sornme

-i & ç, WN 03 @O (1 trA^.%0' cie

aU^-ka de- ₃1-0,,r,

ti

Ae Ov`e
^·J\eS

re f i .. _cè ~(Ot

ae rue

( 0 2-0_.__..t) op e_

^{f 36}'⁸ "34SM 4 G' coevamme'

53L\ 821 4T ^t-k , 15' T

Or_J

case.~.(\ ulilsvltl ett^-h; mmL, s)ousituye,

Ce- nⁱe

YrtU `\-; Pi60S

^,malls

co1 ory es

\Q clyrntse.

Sa CI) ai~ cl^1/43e 1 DL Vaauc or avwe..)\f. Mar ctç (20¹3^--ZeA4) ,.sv de

Ce. V,

~04 f3.7w 1e

Ca(

0( 0040cl',oi^,Ac.. (^,;L m,ot ~'ole n~Gir~

Christelle Brémaud E179552Q

p,5

[139]

ivestigetion grains de riz .

maxime darian

	1	1
	2	2
	3	4
	4	8
	5	16
	6	32
	7	64
	8	128
	9	256
	10	5.12
	11	1 024
	12	2 048
	13	4 096
	14	8 19 2
	15	16 384
	16	32 768
	17	65 536
	18	1.31 072
	19	262 144
	20	524 288
	21	1 048 576
	22	2 097 152
	23	4 194 304
	24	8 388 608
	25	16777216
	26	33 554 432
·	27	67 108 864
	28	134 217 728
	29	258 435 456
	30	536 870 912
	31	1073 741824
	32	2 147 483 648
	33	4 294 967 296
	34	8 589 934 592
	35	17 179 869184
	35	34 359 738 368
	37	68 719 476 736
	38	137 438 953 472
	39	274 877 906 944
		40549 755 813 888
	41	1 099 511 627 776
	42	2 199 023 255 552
	43	4 398 046 511104
	44	8 796 093 022 208
	45	17 592 186 044 416
	46	35 184 372 088 832
	47	70 368 744177 664
	48	140 737 488 355 325
	49	281474 976 710 658
	50	562 949 953 421 312
	51	1 125 899 906 842 62C
	82	2 251 799 813 685 25C
	93	4 503 599 627 370 500
	54	9 007 199 254 740 99C
	55	18 014 398 509 482 00C
	56	36 028 797 018 964 000
	57	72 057 594 037 927900
	58	144 115 188 075 856 00C
	59	288 230 376 151 712 DOC
	50	576 460 752 303 423 00C
	51	1 152 921504 606 850 001
	62	2 305 843 009 213 690 00C
	63	4 511 686 018 427 390 001
	64	9 223 372 036 854 780 00C
Somme		18-446 744 073 709 600.000

C

368 934.881 474 191 00C1

Christelle Brémaud E179552Q

Christelle Brémaud E179552Q

[ 140]

Groupe 3 : Evan, Gabin, Romain

Nom Prénom de l'élève :.E°'/.¹..R.D... ~Y= Noms des autres élèves du groupe :

t,-64.44-0 l

INVESTIGATION 1 : grains de riz sur échiquier
document 3 : « COMPTE RENDU de la résolution du problème _ investigation 1 u		Document élève
6Î.e -toi-4 7 r~_. rne c9-`_*r e ^.44-1 e- ~ ^cJ`~m rrox,-, 4Vcs,~e 4I- ~,? 9.?0a

3⁶i13^,1 3^,1 4^,?ei

42^,EA-N ,

Christelle Brémaud_E179552Q

[141]

[142]

Christelle Brémaud_E179552Q

Christelle Brémaud_E179552Q

[143]

Groupe : Coralie (absente à la séance 2), Jordan, Léa

[144]

Christelle Brémaud_E179552Q

Christelle Brémaud E179552Q

[145]

Groupe 5 : Hugo, Marie, Rozenn

Nom Prénom de l'élève : P ~ Noms des autres élèves du groupe :
INVESTIGATION 1 : grains de riz sur échiquier
document 3 : « COMPTE RENDU de la résolution du problème _ investigation 1 »	Document élève

m^'e Pa.) ~ CO" I).-

?(AL#177;:_is, .Q

2⁰0 Cg) goo k^,:^,0 acents

Tv\. c.i.J\i\ikz)_. ecuY2- csack,_

NQ)-\ki (:)1 ^c?3⁽c) TN21,

\\T34 Q>J& ÇAN c)^sv₉. ola

cKL g 223 34t o36 ~5`f^{, -}11)⁶ ')t0 (\j:.L,

0^-
· (\eNgir-Lt cro----eck\ ~ !~~-~...~. o~ c

k ,J

00D

[ 146]

Nom Prénom de l'élève : - Î`tliTt

Noms des autres élèves du groupe :

INVESTIGATION 1 : grains de riz sur échiquier

document 3 :

Dgcun^-lent élève

« COMPTE RENDU de la résolution du problème investigation 1 »

off cc '- _D 31e;'&A.0a..- cav\_

c& G ub-r . c&-- da--

^(3°N

P' a 33^-q 6$S R$o 0₁,
4-ao 44

_u Qa

8Y\P'^jl- _n ~ maw) ran)eno

xa,veA mow wueT\D c9tiMAw iwn vNk-e.kk- c'Y` Q3.0 a ccm~^-~

Christelle Brémaud E179552Q

[147]

Christelle Brémaud_E179552Q

Christelle Brémaud_E179552Q

[148]

Groupe 6 : Axel et Théo (absents à la séance 2)

Christelle Brémaud_E179552Q

[149]

ANNEXE 11 :

TRANSCRIPTION travail de groupe RESOLUTION DE LA SITUATION PROBLEME grains de riz

Transcription investigation 1 TEB_ phase 4 groupe 3 : Gabin Evan Romain

Tour de parole	Intervenant	Intervention
1	Romain	Ça fois ça...
2	Gabin	Ha, ok ! Ouais mais du coup ouais c'est infini
3	Romain	Regarde, là si tu fais ça égale ça...ça marche
4	Gabin	Ok... Du coup on va jusqu'à combien de...
5	Romain	Fois ça
6	Gabin	Attends On va jusqu'à 1000 ?
	Romain	Euh... on va voir si ça marche déjà... noooon !
7	Ens.	Parce que là vous voulez faire quoi en fait ?
8	Romain	Ça fois ça égale ça, et mettre ce chiffre-là, le caler ici
9	Ens	Ah, donc en fait, ça vous donne le nombre de grains de riz... sur quelle case ?
10	Romain	Euh là c'est....
	Ens	Une deux trois
11	Romain	Là c'est la troisième
12	Ens	Donc sur votre première case vous avez combien ?
13	Romain	Euh, sur la première on a 1, après 2, 4, 8, 16, 32
14	Esn	Est-ce que ce ne serait pas plus simple du coup de faire de 1 à 64... et à côté, vous partez sur la première donnée, sur la deuxième vous dites à Excel de faire votre calcul, c'est lui qui va vous le faire
15	Gabin	Oui en fait, tu vas jusqu'à 64
16	Romain	Hein ?
17	Evan	Là tu descends jusqu'à 64...
18	Romain	Bah
19	Gabin	Tu vas deux par deux
20	Evan	tu mets tous les chiffres
21	Ens	Pourquoi deux par deux ? Vous avez 64 cases !
22	Gabin	Bah non
23	Evan	regarde, là tu, tu descends... tu vas jusqu'à la 63eme case
24	Ens	Faut les numéroter peut-être vos cases ? non ?
25	Romain	bah elles sont déjà numérotées, (référence aux numéros de lignes)
26	Ens	Tu n'as pas la case 3...5
27	Romain	Oui mais on sait quelle case, on sait que la case 1 c'est la une, la case 2 c'est la 2
28	Ens	Bah et la case 3 alors ?
29	Gabin	Ouais j'avoue là
30	Romain	Ah ouais !...
31	Gabin	Ouais du coup ça sert plus à rien
32	Romain	Mais enfin c'est juste un décalage, il n'y a pas...
33	Ens	Réfléchissez
34	Romain	Y a pas la case 1
35	Gabin	Bah si elle est là la case une
36	Romain	Non mais faut qu'on aille jusqu'à 63

Christelle Brémaud_E179552Q

[150]

37	Gabin	Oui mais là ?
38	Romain	Non parce que la case une en fait c'est 1... donc la 1 on ne l'a pas vraiment posée on va dire
39	Gabin	Oui mais de toute façon là faut faire 1, 2, 3, 4, 5, 6, 7
40	Romain	Regarde là case 2, case 3, case 4, case 5, case 6, 7 et cetera
41	Evan	Là tu vas jusqu'à 62 là, tu vas pas jusqu'à....
42	Ens	Et là ? Du coup tu as quoi dans la colonne A ?
43	Romain	Le premier chiffre... enfin moi je sais pas...je sais...
44	Gabin	Vas y fais, fais et on verra si c'est bon ! Là tu mets ce que tu penses
45	Romain	Hop, voilà !
46	Gabin	Vas y...Ok c'est pas le même résultat
47	Evan	Non c'est pas bon... c'est pas bon ! c'est ce que j'allais dire
48	Gabin	T'es à combien là, t'es à... en dessus de 24
49	Evan	24...ça fait 96
50	Gabin	Là on avait 25
51	Evan	Mais si on regarde d'en haut regarde remonte en haut... 24 par 4 ça fait 96 donc nous on a seulement 32 donc normalement (inaudible)
52	Romain	Ouais mais je sais ce qui change... parce que ça c'est beaucoup trop grand... attends... là on va faire plutôt
53	Gabin	A y est
54	Romain	Non non ça c'est....
55	Gabin	Et là, pourquoi tu mets jusqu'à 96 ( ? pas très audible)... là faudra quand même aller jusqu'à 64 ce serait plus simple non ?
56	Romain	oui si on va jusqu'à 64...
57	Ens	Je ne comprends pas, c'est quoi ? pourquoi vous ne demandez pas... donc 2,... ça c'est sur la première case ? y a 2 grains de riz sur la première case ?
58	Romain	Ça, C'est la... enfin là c'est la deuxième, la première en fait, vu qu'il n'y en a qu'une on ne la pas mise, on s'arrête à 63
59	Ens	Donc du coup ça c'est le nombre de grains de riz sur chaque case
60	Romain	Vu que c'est demandé de doubler à chaque fois
61	Ens	Et pourquoi vous faites cette opération ? parce que si vous doublez à chaque fois...
62	Gabin	Oui mais du coup...
63	Ens	... si vous doublez à chaque fois, c'est ça fois 2... c'est à la case précédente fois 2
64	Romain	Mmm mmm
65	Gabin	Bah c'est pas ce qu'on veut en fait
66	Romain	Non
67	Ens	Bah c'est ce que vous avez. Non ? Bah si !
68	Evan	Si c'est ça. On a
69	Romain	2 fois 8, 16, 2 fois 16
70	Ens	Et pourquoi vous prenez ces 3, pourquoi vous mettez du 2 partout ? Si vous dites ici, tu fais la case précédente... c'est-à-dire le résultat que j'avais fois 2...Vous n'avez pas besoin ici de mettre fois 2 partout
71	Gabin	Ah d'accord
72	Romain	Ah c'est juste qu'il multiplie... Ah ouais
73	Ens	Je sais pas, on imagine, je ne vous l'efface pas, je le masque juste... d'accord... ici, vous partez... vous m'avez dit sur la première case il y en a combien ?
74	Gabin	1
75	Ens	... ça c'est votre valeur initiale, d'accord ? La deuxième a priori vous me dites que vous doublez... Excel il le fait très bien... il va vous faire le calcul de ce que vous av

Christelle Brémaud_E179552Q

[151]

76	Romain	Ah ouais, ah ouais d'accord !
77	Ens	Bah ouais
78	Gabin	On étire, ça va le faire pour tout
79	Ens	Et après, vous faites un copier-coller jusqu'en bas et puis vous allez obtenir normalement
80	Romain	Normalement ce sera bon
81	Ens	Vous allez obtenir la même chose mais c'est plus clean
82	Gabin	Oui ça remplace
83	Ens	Si vous voulez vous débarrasser ici des puissances de 10, dans format de cellule vous lui dites que c'est un nombre... vous séparez avec les milliers... comme ça vous avez le nombre
84	Gabin	D'accord
85	Ens	Ça, ça correspond à quoi du coup ce résultat ?
86	Gabin et Evan	Bah le nombre de grains de riz sur la dernière case
87	Romain	Sur la 64eme
88	Ens	Sur la dernière case ?
89	Gabin	Du coup c'est pas possible
90	Romain	bah
91	Ens	Qu'est-ce qui vous fait dire que ce n'est pas possible ?
92	Romain	Si, mais si, t'as intérêt à avoir un peu de temps devant toi
93	Evan	Ça en fait un de trop
94	Ens	Réfléchissez
95	Romain	Non non non
96	Gabin	Ca, mettre ça sur une case c'est pas possible ça
97	Ens	Réfléchissez ! C'est le résultat sur une case qui vous intéresse ?
98	Romain	Non
100	Gabin	Non, nous ce qui nous intéresse c'est « est-ce que la requête est réalisable ? »
101	Romain	C'est le total
102	Ens	Le total. Oui mais ça veut dire quoi « la requête est réalisable » ? Ce n'est pas parce que tu as réussi à faire le calcul que c'est réalisable
103	Gabin	Non, c'est ce que je dis, c'est que là du coup il y a beaucoup trop de grains de riz
104	Romain	Oui mais là, c'est réalisable quand même parce que ou... tu peux en avoir quand même autant mais bon, tu as le temps il faut prendre son temps
105	Ens	Sauf que... Il va peut-être falloir aller trouver
106	Romain	On n'a pas dit qu'il fallait tout mettre sur une même case
107	Ens	Bah oui mais il va peut-être falloir aller trouver... d'accord ?... des valeurs chiffrées auxquelles vous allez pouvoir comparer en sachant que vous, pour vous c'est la somme de tout ça... d'accord ?
108	Romain	La somme de tout ça ?....
109	Gabin	Du coup, là tu fais tu fais la cellule et ça tu fais ça plus
110	Ens	Vous connaissez la valeur de la production mondiale du riz ?
111	Romain	Non
112	Ens	Bah, Comparez peut-être à des valeurs de ce style là ! Est-ce que ça a du sens ce qu'on vous demande
113	Romain	Ah d'accord !
114	Gabin	Ça, ça pourrait nous indiquer si c'est possible de faire cette requête
115	Evan	Ecarte met g et tu écartes. Tu sais normalement on a doublé pour que ce soit
116	Romain	attend
117	Gabin	En fait tu restes euh
118	Romain	internet

Christelle Brémaud_E179552Q

[152]

119	Gabin	Ensuite tu iras sur google pour voir la quantité de grains de riz qu'ils font sur chaque euh... (à l'Enseignante) c'est chaque jour ou chaque année?
120	Ens	Bah je n'en sais rien, je ne sais pas... déjà vous, votre résultat final, est-ce que vous l'avez ?
121	Evan	ouais
122	Romain	Non
123	Evan	Non ?
124	Gabin	Et là, il faut additionner tout ça en fait
125	Ens	Du coup vous allez comparer ça à la production mondiale, sauf que là c'est le nombre de grains de riz, la production mondiale... vous regarderez ils ne vous la donneront peut-être pas en grains de riz
126	Evan	On va avoir toutes les couleurs de l'arc en ciel ! Allez c'est parti !
127	Romain	Je l'ai fait 63 fois ! je suis parti là ! ... c'est joli
128	Gabin	Bah ça va en fait
129	Evan	En plus t'as mis un plus à la fin
130	Romain	Faut peut-être mettre des parenthèses non ?
131	Romain	C'est normal ! regarde !
132	Romain	Alors maintenant protection internationale de riz !
133	Gabin	Oui mais là elle a dit que ça n'allait pas nous donner la quantité en grains de riz, je pense que ça va nous donner la quantité en
134	Romain	En tonnes
135	Gabin	En sacs ou
136	Romain	En tonnes... oui mais après la tonne tu peux la calculer
137	Gabin	Ouais mais
138	Evan	Tu calcules combien fait un grain de riz environ et après bah...tu multiplies et
139	Gabin	De toute façon on va bien voir... si... si là le nombre qu'on a obtenu est supérieur à la quantité de grains, enfin ... à la quantité de production de grains de riz, ça dira ce que ça veut dire...
140	Gabin	Au premier janvier (lecture informations recherche internet)
141	Romain	(rire étonné)
142	Evan	Putain
143	Gabin	Non mais tu vois hein !? nous on est supérieur... on est largement supérieur, c'est pas possible.... C'est quoi ça ?
145	Romain	Faut que je fusionne deux cases
146	Gabin	Non c'est pas possible
147	Evan	Bah on s'arrête à
148	Romain	Non regarde on s'arrête...ça voudrait dire qu'il faudrait 38 millions 494 mille 874 virgule 85
149	Evan	95
150	Romain	Pour avoir le total
151	Gabin	Bah du coup c'est bon
152	Romain	C'est bon je crois qu'on a la réponse (en rigolant)
153	Gabin	On a la réponse
154	Romain	Ah non... en kilos kilos kilos
155	Gabin	Oui kilos de riz par an
156	Romain	Oui sauf que nous on n'est pas en kilos
157	Gabin	Nous on est en grains de riz... donc en soit là faut qu'on converse tous les grains de riz en kilos ?
158	Romain	Voilà... fois les grains de riz... putain c'est pas possible ! on se fait vraiment chier pour rien
159	Evan	1000 grains 28 grammes
160	Romain	1 grain de riz 0.20

Christelle Brémaud_E179552Q

[153]

161	Ens	Oui c'est à peu près ça 20 milligrammes
162	Romain	Donc il y en avait 420 millions de t...de kilos... oh putain 479 milliards 200 mille euh
163	Evan	200 millions
164	Ens	Ecrivez-le votre calcul
165	Gabin	En fait on l'a mis là
166	Romain	Non là c'est autre chose
167	Gabin	En fait on n'avait pas
168	Ens	Mettez-le sur votre tableur
169	Romain	J'avais mis autre chose... en fait je me suis trompé dans le calcul, j'ai oublié que c'était en poids, donc... moi je suis en grains de riz et là c'est en poids
170	Ens	Et donc tu as fait quel calcul pour passer du nombre de grains de riz au
171	Romain	Je ne l'ai pas fait
172	Gabin	Justement on va le faire
173	Romain	Je vais le faire là
174	Romain	On a dit 0.20... ça va faire un léger changement
175	Evan	Non 0.02
176	Romain	Bah après... hé il suit le petit
177	Evan	Ah bah je sais quand même ce que je dis !
178	Romain	Alors... égal... j'ai pas envie de poser ce calcul ! je veux juste vérifier quelque chose... oh putain ça craint ! fait chier c'est en grammes ! Oh faut faire une conversion
179	Evan	Tu veux mettre ça en kilo ?
180	Gabin	Ah bah oui parce que le chiffre qu'on voit c'est en kilos
181183	Romain	Alors que nous on est en grammes
182184	Gabin	Ah là c'est une erreur con
185	Evan	Attends je fais ça. Je peux le faire ?
186	Romain	Ouais ouais vas y parce que là j'ai la flemme
187	Gabin	Sinon on garde en grains de riz
188	Romain	On peut mais vas-y ça l'amuse
189	Gabin	Mec fais-le au cas où
190	Romain	Bah si, si, s'il sait pas poser un kilogramme, le zéro il met dans gramme et après il mute
191	Evan	0 virgule 00002
192	Gabin	Tu mets 4 zéros après la virgule
193	Evan	0 virgule 00002, 4 zéros après la virgule... ... Non c'est multiplier !
194	Romain	oui
195	Gabin	Et déjà, D'abord là t'aurais dû
196	Evan	Oui t'aurais dû
197	Romain	Est-ce, est-ce que j'appuie ?
198	Gabin	Vas-y
199	Romain	Voilà, t'as fait planter l'ordi... euh, ça multiplié par ça...
200	Gabin	Non là, t'aurais, c'est complètement con ! là t'aurais dû élargir tout ça pour savoir, euh, quelle quantité en kilos ça fait à la fin. T'es bête ou quoi ?
201	Romain	Mais on s'en fout !
202	Gabin	Bah non, non justement, on veut le comparer avec la quantité de kilos par an
203	Romain	Mais regarde, ça c'est la quantité par an... non tu t'es trompé Evan
204	Evan	Non, je ne trompe jamais sur un calcul
205	Romain	Regarde... le total...
206	Evan	Ça fait beaucoup de grains de riz quand même hein !

[154]

207	Romain	Entre nous !
208	Gabin	Non là c'est en kilos qu'on l'a obtenu
209	Romain	On va mettre notre poids à nous.... Ouiiiiiii le vieux décalage.... On a quand même un peu plus de poids !
210	Gabin	Donc la requête n'est pas réalisable !
211	Romain	C'est ça !
212	Gabin	Là c'est en kilos qu'on met ça ?... on met quoi alors ?... non en fait elle n'est pas réalisable car on a une quantité de (inaudible)... et on a vu sur internet que
213	Evan	1 grain de riz c'est 0.02 gramme et du coup, bah on a mis ça en kilo du coup ça fait 0.0000...
214	Romain	Non on va faire encore plus simple, ça c'est la production en kilos par an et ça c'est ce qu'il voudrait au total... en kilos bien sûr !
215	Gabin	Donc en fait c'est pas possible !?
216	Romain	Si... Si c'est possible mais y a plusieurs années devant soi
217	Gabin	Oui mais en soit là
218	Romain	368...
219	Evan	365
220	Romain	Fois 2
221	Gabin	Il faut combien d'années
222	Romain	C'est pas très compliqué
223	Romain	Ouais mais 736 ans...ouais environ
224	Evan	Moi je dis c'est réalisable hein ! Mais faut avoir 736 ans à perdre
225	Romain	Ouais euh, tu veux dire quatre générations facile !
226		(rédaction compte rendu individuel)

Christelle Brémaud_E179552Q

Christelle Brémaud_E179552Q

[155]

ANNEXE 12 :

ANALYSE de la transcription investigation 1 TEB_ phase 4 groupe 3_séquence 1

Séquence 1 : formalisation de la construction du ³Pb1_groupe3 : organisation sur tableur des calculs à effectuer pour trouver le nombre de grains sur chaque case

Nous remarquons les 24 tours de parole de l'enseignante sur un total de 88 ce qui représente 27% des échanges extraits ci-dessous :

Tour de parole	Intervenant	Intervention	Informations relevées	Construction du problème
1	Romain	Ça fois ça...
2	Gabin	Ha, ok ! Ouais mais du coup ouais c'est infini	^4IGabin_1
3	Romain	Regarde, là si tu fais ça égale ça...ça marche
4	Gabin	Ok... Du coup on va jusqu'à combien de...
5	Romain	Fois ça
6	Gabin	Attends On va jusqu'à 1000 ?
	Romain	Euh... on va voir si ça marche déjà... noooon !
7	Ens.	Parce que là vous voulez faire quoi en fait ?
8	Romain	Ça fois ça égale ça, et mettre ce chiffre-là, le caler ici	^4IRomain_2	Essai 1 :
9	Ens.	Ah, donc en fait, ça vous donne le nombre de grains de riz... sur quelle case ?		Confusion entre cases (de l'échiquier) et cellules (du tableur) dont le contenu n'est pas encore clairement défini
10	Romain	Euh là c'est....
	Ens	Une deux trois
11	Romain	Là c'est la troisième
12	Ens.	Donc sur votre première case vous avez combien ?
13	Romain	Euh, sur la première (sous-entendu de l'échiquier) on a 1, après 2, 4, 8, 16, 32	4IRomain_3
14	Ens.	Est-ce que ce ne serait pas plus simple du coup de faire de 1 à 64... et à côté, vous partez sur la première donnée, sur la deuxième vous dites à Excel de faire votre calcul, c'est lui qui va vous le faire	^4I4	Proposition 1 de l'enseignante (à l'oral mais non formalisée sur le tableur des élèves):
15	Gabin	Oui en fait, tu vas jusqu'à 64	4IGabin_5	En partant de u1=1 les élèves obtiendront u64 à la ligne 64
16	Romain	Hein ?
17	Evan	Là tu descends jusqu'à 64...
18	Romain	Bah
19	Gabin	Tu vas deux par deux		Essai 2 :
				Les élèves font un copier glisser de A1à D2 alors qu'aucune formule n'a été saisie dans la colonne D jusqu'à la ligne 64
20	Evan	tu mets tous les chiffres		Confusion entre « chiffres », nombre, résultats, ...
21	Ens.	Pourquoi deux par deux ? Vous avez 64 cases !
22	Gabin	Bah non
23	Evan	regarde, là tu, tu descends... tu vas jusqu'à la 63eme case	4IEvan_6	En partant de u2=2 les élèves obtiendront u64 à la ligne 63

Christelle Brémaud_E179552Q

[156]

24	Ens.	Faut les numéroter peut-être vos cases ? non ?		Essai 2 :
25	Romain	bah elles sont déjà numérotées, (référence aux numéros de lignes)	4IRomain_7
				de dans
26	Ens.	Tu n'as pas la case 3...5
27	Romain	Oui mais on sait quelle case, on sait que la case 1 c'est la une, la case 2 c'est la 2	4IRomain_8
					Confusion entre n° de ligne (donc case de l'échiquier) et valeur les cellules de la colonne 1
28	Ens.	Bah et la case 3 alors ?
29	Gabin	Ouais j'avoue là
30	Romain	Ah ouais !...
31	Gabin	Ouais du coup ça sert plus à rien
32	Romain	Mais enfin c'est juste un décalage, il n'y a pas...	^4IRomain_9
33	Ens.	Réfléchissez
34	Romain	Y a pas la case 1	^4IRomain_10
35	Gabin	Bah si elle est là la case une
36	Romain	Non mais faut qu'on aille jusqu'à 63
37	Gabin	Oui mais là ?
38	Romain	Non parce que la case une en fait c'est 1... donc la 1 on ne l'a pas vraiment posée on va dire	4IRomain_11	Confusion entre n° de case et nombre de grains qu'elle contient
39	Gabin	Oui mais de toute façon là faut faire 1, 2, 3, 4, 5, 6, 7
40	Romain	Regarde là case 2, case 3, case 4, case 5, case 6, 7 et cetera
41	Evan	Là tu vas jusqu'à 62 là, tu vas pas jusqu'à....	^4IEvan_12
42	Ens.	Et là ? Du coup tu as quoi dans la colonne A ?		Importance de clarifier le contenu des cellules (colonne A dans l'essai 2 correspond au nombre de grains dans les cases de l'échiquier à partir de la case n°2)
43	Romain	Le premier chiffre... enfin moi je sais pas...je sais...
44	Gabin	Vas y fais, fais et on verra si c'est bon ! Là tu mets ce que tu penses
45	Romain	Hop, voilà !
46	Gabin	Vas y...Ok c'est pas le même résultat
47	Evan	Non c'est pas bon... c'est pas bon ! c'est ce que j'allais dire		Les élèves ont fait un copier glisser des lignes 1 et 2 sans qu'aucune formule de calcul n'ait été saisie comme proposé dans proposition 1 d'où une incidence sur les résultats à obtenir Essai 2 :
48	Gabin	T'es à combien là, t'es à... en dessus de 24
49	Evan	24...ça fait 96
50	Gabin	Là on avait 25
51	Evan	Mais si on regarde d'en haut regarde remonte en haut... 24 par 4 ça fait 96 donc nous on a seulement 32 donc normalement (inaudible)
52	Romain	Ouais mais je sais ce qui change... parce que ça c'est beaucoup trop grand... attends... là on va faire plutôt
53	Gabin	A y est
54	Romain	Non non ça c'est....
55	Gabin	Et là, pourquoi tu mets jusqu'à 96 ( ? pas très audible)... là faudra quand même aller jusqu'à 64 ce serait plus simple non ?
56	Romain	oui si on va jusqu'à 64...
57	Ens.	Je ne comprends pas, c'est quoi ? pourquoi vous ne demandez pas... donc 2,... ça c'est sur la première case ? y a 2 grains de riz sur la première case ?		Essai 3 :
58	Romain	Ça, C'est la... enfin là c'est la deuxième, la première en fait, vu qu'il n'y en a qu'une on ne la pas mise, on s'arrête à 63	^4IRomain_13
59	Ens.	Donc du coup ça c'est le nombre de grains de riz sur chaque case (sous-entendu les résultats dans la colonne A)
60	Romain	Vu que c'est demandé de doubler à chaque fois
61	Ens.	Et pourquoi vous faites cette opération ? parce que si vous doublez à chaque fois...
62	Gabin	Oui mais du coup...

[157]

Christelle Brémaud_E179552Q

63

	Ens.	... si vous doublez à chaque fois, c'est ça fois 2... c'est à la case précédente fois 2	^4I14
64	Romain	Mmm mmm
65	Gabin	Bah c'est pas ce qu'on veut en fait
66	Romain	Non
67	Ens.	Bah c'est ce que vous avez. Non ? Bah si !
68	Evan	Si c'est ça. On a
69	Romain	2 fois 8, 16, 2 fois 16
70	Ens.	Et pourquoi vous prenez ces 3 (sous-entendu colonnes A, B et C), pourquoi vous mettez du 2 partout ? Si vous dites ici, tu fais la case précédente... c'est-à-dire le résultat que j'avais fois 2...Vous n'avez pas besoin ici de mettre fois 2 partout		Proposition 2 :
71	Gabin	Ah d'accord
72	Romain	Ah c'est juste qu'il multiplie... Ah ouais	^4IRomain 15
73	Ens.	Je sais pas, on imagine, je ne vous l'efface pas, je le masque juste... d'accord... ici, vous partez... vous m'avez dit sur la première case il y en a combien ?
74	Gabin	1	^4IGabin_16
75	Ens.	... ça c'est votre valeur initiale, d'accord ? La deuxième a priori vous me dites que vous doublez (sous-entendu en D2)... Excel il le fait très bien... il va vous faire le calcul de ce que vous av	^4I17
76	Romain	Ah ouais, ah ouais d'accord !
77	Ens.	Bah ouais
78	Gabin	On étire, ça va le faire pour tout		Essai 4 :
79	Ens.	Et après, vous faites un copier-coller jusqu'en bas et puis vous allez obtenir normalement	^4I18
80	Romain	Normalement ce sera bon
81	Ens.	Vous allez obtenir la même chose mais c'est plus clean	^4I19
82	Gabin	Oui ça remplace	^4IGabin_20
83	Ens.	Si vous voulez vous débarrasser ici des puissances de 10, dans format de cellule vous lui dites que c'est un nombre... vous séparez avec les milliers... comme ça vous avez le nombre
84	Gabin	D'accord
85	Ens.	Ça, ça correspond à quoi du coup ce résultat ?
86	Gabin et Evan	Bah le nombre de grains de riz sur la dernière case
87	Romain	Sur la 64eme	^4IRomain_21
88	Ens.	Sur la dernière case ?

Christelle Brémaud_E179552Q

[158]

ANNEXE 12 bis :

ANALYSE de la transcription investigation 1 TEB_ phase 4 groupe 3_séquence 2

Séquence 2 : Calcul du nombre total et faisabilité de la requête :

Remarque : 9 tours de parole enseignante soit 9 sur 35 = 26% des échanges extraits ci-dessous :

Tour de parole	Intervenant	Intervention	Informations relevées
89	Gabin	Du coup c'est pas possible
90	Romain	Bah
91	Ens.	Qu'est-ce qui vous fait dire que ce n'est pas possible ?
92	Romain	Si, mais si, t'as intérêt à avoir un peu de temps devant toi
93	Evan	Ça en fait un de trop
94	Ens.	Réfléchissez
95	Romain	Non non non
96	Gabin	Ca, mettre ça sur une case c'est pas possible ça
97	Ens.	Réfléchissez ! C'est le résultat sur une case qui vous intéresse ?
98	Romain	Non
100	Gabin	Non, nous ce qui nous intéresse c'est « est-ce que la requête est réalisable ? »
101	Romain	C'est le total
102	Ens.	Le total. Oui mais ça veut dire quoi « la requête est réalisable » ? Ce n'est pas parce que tu as réussi à faire le calcul que c'est réalisable
103	Gabin	Non, c'est ce que je dis, c'est que là du coup il y a beaucoup trop de grains de riz
104	Romain	Oui mais là, c'est réalisable quand même parce que ou... tu peux en avoir quand même autant mais bon, tu as le temps il faut prendre son temps
105	Ens.	Sauf que... Il va peut-être falloir aller trouver
106	Romain	On n'a pas dit qu'il fallait tout mettre sur une même case
107	Ens.	Bah oui mais il va peut-être falloir aller trouver... d'accord ?... des valeurs chiffrées auxquelles vous allez pouvoir comparer en sachant que vous, pour vous c'est la somme de tout ça... d'accord ?
108	Romain	La somme de tout ça ?....
109	Gabin	Du coup, là tu fais tu fais la cellule et ça tu fais ça plus
110	Ens.	Vous connaissez la valeur de la production mondiale du riz ?
111	Romain	Non
112	Ens.	Bah, Comparez peut-être à des valeurs de ce style là ! Est-ce que ça a du sens ce qu'on vous demande
113	Romain	Ah d'accord !
114	Gabin	Ça, ça pourrait nous indiquer si c'est possible de faire cette requête
115	Evan	Ecarte met g et tu écartes. Tu sais normalement on a doublé pour que ce soit
116	Romain	Attend
117	Gabin	En fait tu restes euh
118	Romain	Internet
119	Gabin	Ensuite tu iras sur google pour voir la quantité de grains de riz qu'ils font sur chaque euh... (à l'enseignante) c'est chaque jour ou chaque année?
120	Ens.	Bah je n'en sais rien, je ne sais pas... déjà vous, votre résultat final, est-ce que vous l'avez ?
121	Evan	Ouais
122	Romain	Non
123	Evan	Non ?
124	Gabin	Et là, il faut additionner tout ça en fait

Christelle Brémaud_E179552Q

[159]

ANNEXE 12 ter :

ANALYSE de la transcription investigation 1 TEB_ phase 4 groupe 3_séquence 3

Séquence 3 : Construction du problème 2 :

Remarque : 4 tours de parole enseignante soit 4 sur 100 = 4% des échanges extraits ci-dessous :

Tour de parole	Intervenant	Intervention	Informations relevées
125	Ens.	Du coup vous allez comparer ça à la production mondiale, sauf que là c'est le nombre de grains de riz, la production mondiale... vous regarderez ils ne vous la donneront peut-être pas en grains de riz
126	Evan	On va avoir toutes les couleurs de l'arc en ciel ! Allez c'est parti !
127	Romain	Je l'ai fait 63 fois ! je suis parti là ! ... c'est joli
128	Gabin	Bah ça va en fait
129	Evan	En plus t'as mis un plus à la fin
130	Romain	Faut peut-être mettre des parenthèses non ?
131	Romain	C'est normal ! regarde !
132	Romain	Alors maintenant protection internationale de riz !
133	Gabin	Oui mais là elle a dit que ça n'allait pas nous donner la quantité en grains de riz, je pense que ça va nous donner la quantité en
134	Romain	En tonnes
135	Gabin	En sacs ou
136	Romain	En tonnes... oui mais après la tonne tu peux la calculer
137	Gabin	Ouais mais
138	Evan	Tu calcules combien fait un grain de riz environ et après bah...tu multiplies et
139	Gabin	De toute façon on va bien voir... si... si là le nombre qu'on a obtenu est supérieur à la quantité de grains, enfin ... à la quantité de production de grains de riz, ça dira ce que ça veut dire...
140	Gabin	Au premier janvier (lecture informations recherche internet)
141	Romain	(rire étonné)
142	Evan	Putain
143	Gabin	Non mais tu vois hein !? nous on est supérieur... on est largement supérieur, c'est pas possible.... C'est quoi ça ?
145	Romain	Faut que je fusionne deux cases
146	Gabin	Non c'est pas possible
147	Evan	Bah on s'arrête à
148	Romain	Non regarde on s'arrête...ça voudrait dire qu'il faudrait 38 millions 494 mille 874 virgule 85
149	Evan	95
150	Romain	Pour avoir le total
151	Gabin	Bah du coup c'est bon
152	Romain	C'est bon je crois qu'on a la réponse (en rigolant)
153	Gabin	On a la réponse
154	Romain	Ah non... en kilos kilos kilos
155	Gabin	Oui kilos de riz par an
156	Romain	Oui sauf que nous on n'est pas en kilos
157	Gabin	Nous on est en grains de riz... donc en soit là faut qu'on converse tous les grains de riz en kilos ?
158	Romain	Voilà... fois les grains de riz... putain c'est pas possible ! on se fait vraiment chier pour rien
159	Evan	1000 grains 28 grammes
160	Romain	1 grain de riz 0.20
161	Ens.	Oui c'est à peu près ça 20 milligrammes
162	Romain	Donc il y en avait 420 millions de t...de kilos... oh putain 479 milliards 200 mille euh
163	Evan	200 millions
164	Ens.	Ecrivez-le votre calcul
165	Gabin	En fait on l'a mis là
166	Romain	Non là c'est autre chose
167	Gabin	En fait on n'avait pas
168	Ens.	Mettez-le sur votre tableur
169	Romain	J'avais mis autre chose... en fait je me suis trompé dans le calcul, j'ai oublié que c'était en poids, donc... moi je suis en grains de riz et là c'est en poids
170	Ens.	Et donc tu as fait quel calcul pour passer du nombre de grains de riz au

Christelle Brémaud_E179552Q

[160]

171	Romain	Je ne l'ai pas fait
172	Gabin	Justement on va le faire
173	Romain	Je vais le faire là
174	Romain	On a dit 0.20... ça va faire un léger changement
175	Evan	Non 0.02
176	Romain	Bah après... hé il suit le petit
177	Evan	Ah bah je sais quand même ce que je dis !
178	Romain	Alors... égal... j'ai pas envie de poser ce calcul ! je veux juste vérifier quelque chose... oh putain ça craint ! fait chier c'est en grammes ! Oh faut faire une conversion
179	Evan	Tu veux mettre ça en kilo ?
180	Gabin	Ah bah oui parce que le chiffre qu'on voit c'est en kilos
181	Romain	Alors que nous on est en grammes
182	Gabin	Ah là c'est une erreur con
185	Evan	Attends je fais ça. Je peux le faire ?
186	Romain	Ouais ouais vas y parce que là j'ai la flemme
187	Gabin	Sinon on garde en grains de riz
188	Romain	On peut mais vas-y ça l'amuse
189	Gabin	Mec fais-le au cas où
190	Romain	Bah si, si, s'il sait pas poser un kilogramme, le zéro il met dans gramme et après il mute
191	Evan	0 virgule 00002
192	Gabin	Tu mets 4 zéros après la virgule
193	Evan	0 virgule 00002, 4 zéros après la virgule... Non c'est multiplier !
194	Romain	Oui
195	Gabin	Et déjà, D'abord là t'aurais dû
196	Evan	Oui t'aurais dû
197	Romain	Est-ce, est-ce que j'appuie ?
198	Gabin	Vas-y
199	Romain	Voilà, t'as fait planter l'ordi... euh, ça multiplié par ça...
200	Gabin	Non là, t'aurais, c'est complètement con ! là t'aurais dû élargir tout ça pour savoir, euh, quelle quantité en kilos ça fait à la fin. T'es bête ou quoi ?
201	Romain	Mais on s'en fout !
202	Gabin	Bah non, non justement, on veut le comparer avec la quantité de kilos par an
203	Romain	Mais regarde, ça c'est la quantité par an... non tu t'es trompé Evan
204	Evan	Non, je ne trompe jamais sur un calcul
205	Romain	Regarde... le total...
206	Evan	Ça fait beaucoup de grains de riz quand même hein !
207	Romain	Entre nous !
208	Gabin	Non là c'est en kilos qu'on l'a obtenu
209	Romain	On va mettre notre poids à nous.... Ouiiiiiii le vieux décalage.... On a quand même un peu plus de poids !
210	Gabin	Donc la requête n'est pas réalisable !
211	Romain	C'est ça !
212	Gabin	Là c'est en kilos qu'on met ça ?... on met quoi alors ?... non en fait elle n'est pas réalisable car on a une quantité de (inaudible)... et on a vu sur internet que
213	Evan	1 grain de riz c'est 0.02 gramme et du coup, bah on a mis ça en kilo du coup ça fait 0.0000...
214	Romain	Non on va faire encore plus simple, ça c'est la production en kilos par an et ça c'est ce qu'il voudrait au total... en kilos bien sûr !
215	Gabin	Donc en fait c'est pas possible !?
216	Romain	Si... Si c'est possible mais y a plusieurs années devant soi
217	Gabin	Oui mais en soit là
218	Romain	368...
219	Evan	365
220	Romain	Fois 2
221	Gabin	Il faut combien d'années
222	Romain	C'est pas très compliqué
223	Romain	Ouais mais 736 ans...ouais environ
224	Evan	Moi je dis c'est réalisable hein ! Mais faut avoir 736 ans à perdre
225	Romain	Ouais euh, tu veux dire quatre générations facile !

Christelle Brémaud_E179552Q

[161]

ANNEXE 13 :

RECAPITULATIF de l'ANALYSE DU CORPUS : Informations recueillies, données et conditions construites

Nous indiquons en rouge les informations qui ont été relevées à plusieurs stades de l'analyse en les faisant correspondre à celles qui les précèdent (déjà relevées et mentionnées dans le tableau). Par exemple, la quatrième information relevée dans l'analyse de la phase 1 (¹I4 considérée comme première condition apparaissant dans le problème à résoudre dans cette phase ¹C1) correspond à la donnée D1 de l'analyse faite a priori, elle est alors notée comme indiqué dans le tableau ci-dessus en noir sur la ligne correspondant au relevé de l'information puis surlignée en jaune et en rouge sur la ligne correspondant à D1. Les cases coloriées en bleu correspondent à des informations qui ont permis de construire un losange de problématisation suite aux analyses des productions et/ou enregistrements des élèves.

Analyse a Phase 1 Phase 1 Phase 2 priori Analyse 1 Analyse 1 bis Analyse 2

Phase 3 Analyse 3

Phase 4 Analyse 4

Analyse a priori

Problème 1

D1

^1I4

^1C1

(^1I9=) ^1I4

^1D5

^3Igroupe2_1

^4D1

D2

^1I7

^1D4

(^1I12=) ^1I7

^1D7

D3

^1I6

^1D3

(^1I11=) ^1I6

^1D8

D4

^1I18

^1D9

^3Igroupe2_Dorian_4

^4D3

C1

^1I17

1C5

3I groupe 4_5

^4Igroupe2_1

^4C1

C2

^1I16

^1C7

^3Igroupe2_2 3I groupe 4_6

^4D2

^4Igroupe2_Elsa_2 ^4Igroupe2_Maxime_3

^4C2

C3

3I groupe 4_5

^4Igroupe2_1

^4C1

C4

^1I15

^1C9

^4Igroupe2_Elsa_2 ^4Igroupe2_Maxime_3

^4C2

C5

^1I19

^1C10

^3Igroupe2_Dorian_4 3I groupe 4_5

^4D3

^3Igroupe2_Dorian_4 ^4Igroupe2_Maxime_4

^4D3 ^4C3

Problème 2

D5

^4Igroupe2_Maxime_6

^4D5

D6

^1IThéo_24

^2I6

^4Igroupe2_10

^4D8

D7

D8

^4Igroupe2_13

^4D9

C6

^4Igroupe2_Elsa_7

^4C4

C7

^4Igroupe2_11 ^4Igroupe2_Maxime_8 ^4Igroupe2_9

^4C5 ^4D6 ^4D7

C8

C9

^4I12

^4C3

Christelle Brémaud_E179552Q

[162]

Phase 1 analyse des documents 1

^1Pb1

^1I1

^1D1

^1I2

^1C2

^1ILéa_3

^1D2

^1I4

^1C1

^1I9

^1D5

^1I5

^1C3

^1I10

^1C8

^1I6

^1D3

^1I11

^1D8

^1I7

^1D4

^1I12

^1D7

^1I8

^1C4

^1I13

^1D6

^1Pb2

(^1I9=) ^1I4

^1D5

(^1I10=) ^1I5

^1C8

(^1I11=) ^1I6

^1D8

(^1I12=) ^1I7

^1D7

(^1I13=) ^1I8

^1D6

^1I14

^1C6

^1I15

^1C9

^1I16

^1C7

^2I1

^1I17

^1C5

^1I18

^1D9

^1I19

^1C10

^1I20

^1IDorian_21

^2I6

^1IDavid_22

^2I2

^1ICoralie_23

^2I3

^1IThéo_24

^2I6

Phase 2 traces écrites tableau

^2I1

^2I2

^2I3

^2I4

^2I5

^2I6

Phase 2 transcription des échanges

2Pb1

(^2I7=)

^2IMaxime_1

^2D1

(^2I8=)

^2IMaxime 2

(^2I9=)

^2IMaxime_3

^2D2

(^2I10=)

^2IEvan_4

^2D3

(2I11=)

(2IElsa_5=) ^1IDavid_22

(^2I12=)

^2IMaxime_6

^2C1

(^2I13=

(^2ICoralie_7=) ^1ICoralie_23

^2D4

(^2I14=)

^2IDavid_8

(^2I15=)

^2IDavid_9

(^2I16=)

^2IRomain_10

^2C2

Christelle Brémaud_E179552Q

[163]

(2I17=` 1

(22Maxime_11) IMaxime_3

(^2I18=)

^2IElsa_12

(^2I19=)

^2IElsa_13

(2I20=2 I16=)

2 IRomain 10

2 C2

(^2I21=)

^2IRomain_14

(^2I22=)

^2IDorian_15

(^2I23=)

^2IElsa 16

(^2I24=)

^2IDavid 17

(^2I25=)

^2IElsa_18

(^2I26=)

^2IElsa_19

(2I27=)

(2IMaxime_20=) ^2IMaxime_3

2D2

(^2I28=)

^2IElsa_21

(^2I29=)

^2IMaxime_22

(2I30=

(2IRomain_23=) ^2IRomain_10

2C2

(^2I31=)

^2IDorian_24

(2I32=)

(2IMaxime_25=) ^2IMaxime_2

^3Igroupe2_1

^4D1

^3Igroupe2_2

^4D2

^3Igroupe2_Elsa_3

Doc^23Igroupe2_Dorian_4

^4D3

3I groupe 4_5

3I groupe 4_6

Phase 3 transcription groupe 3

3Pb1

^3IRomain_1

^3IRomain_2

^3IEvan_3

(^3IRomain_4=) ^3IRomain_2

^3IRomain_5

^3IRomain_6

^3IRomain_7

(^3IRomain_8=) ^3IRomain_5

^3IRomain_9

Christelle Brémaud_E179552Q

[164]

résolution 4Phase

^3IRomain_10

^3IRomain_11

(^3IGabin_12=) ^3IRomain_11 ^3IGabin_13

^3D1

^3IRomain_14

^3D1

^3IEvan_15

^3IGabin 16

^3Pb1

^3IRomain_17

^3IRomain_18

^3C1

^3IEvan_19

^3IRomain_20

^3D4

^3IGabin_21

^3D2

^3IGabin_22

^3IRomain_23

^3IRomain_24

^3C2

^3IGabin_25

^3D3

^3IRomain_26

^3IGabin_27

^3C4

^3IGabin_28

^3C3

^3IRomain_29

^3IRomain_30

Doc 3

^3Pb1_= ^4Pb1

^4Igroupe2_1

^4C1

4Igroupe2_Elsa_2 ^4Igroupe2_Maxime_3

4C2

^4Igroupe2_Maxime_4

^4C3

4Pb2

^4Igroupe2_5

^4D4

^4Igroupe2_Maxime_6

^4D5

^4Igroupe2_Elsa_7

^4C4

^4Igroupe2_Maxime_8

^4D6

^4Igroupe2_9

^4D7

^4Igroupe2_10

^4D8

^4Igroupe2_11

^4C5

^4Igroupe2_12

^4C3

^4Igroupe2_13

^4D9 transcription

Christelle Brémaud_E179552Q

[165]

ANNEXE 14 :

GRILLES 1 D'EVALUATION DES compétences

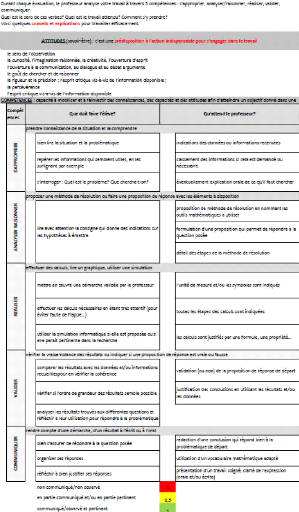
[166]

Christelle Brémaud_E179552Q

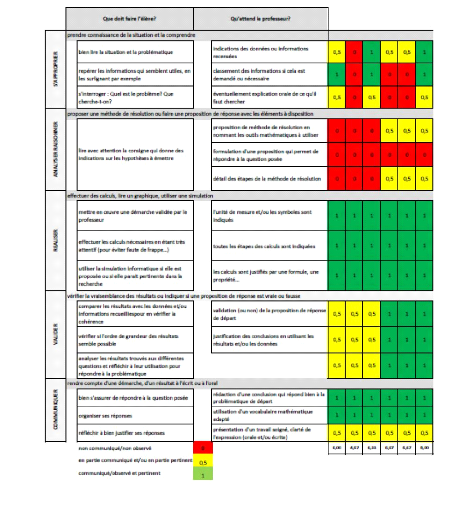
pôrrrlotlm sr= Irrri oaiwiL drik do I oap roma on Imam Wow icrIY}

4S OA 45 45 45 41

411

f]

w

YrliarEori dos Lrrorrralo clan rim co aro	~h			u!	J h
nooaib
d · Irllorn awn a cbrrwll via .1	t	8	1	8	ü	_
dr rrrali cal Ms main
i`rrb 1hrrolL do opMyLol coml. cm q,ill	's			0
Fouidly dtif

Qup rridodr dr ridiltrl au ilIra Low pvpvatlor nfmrrom rii i ,i I L: r

in mom Mimeon In oaroyQr q,l dm r
· trio taxa ao la kRpalhdta I inai7n

FrapsMun dr mithair do rfooYlLtrl aro lo l ro warm!" aAlo rM}rirrrlprar ri1li ·	4	0		8,5	45	8,i
Formal 4Wn dor l_on*Al papoa poi mit.	4	u	If 0		6	d
r ipmd r i Ir coldl m paa"o
irlIId.ia am. daIonrllododr rind uU,	4	U		qS	'Rh	LIZ

rfFrrbrfr do okru ko unroplIcentslr Mbar ism ol m,i Mon

I m lli do rroia 01,1al Id amt.= ma-..	7	1	1	]	^le 1	'
Lay I. fho po do c o%A. o rt Lrd4,rca	1	1	t	]	1	'
I. cobrk born lusllcn w_ ·r :s ·-Jr _rrr ppail_	L	]	1			'

rllt:i rolonililro do rb,le.b I rcligana rl'ara Fro pJüm dr riporr a xW ou Fraao

.Iid Kim !au r,ail dr l propsoltio r dr riperor dr d}rt	AS	IV	A5			·
kr rem olm cord ,alao. on .Athrrl m-. ridt.h Woo In darn".	U. h	CO	Q S		t	_
	45	4E	15	]	t	_

Earn iaaor do ripari
·o i a colalkn pv io

room.. ao nfrperm

rü{kYY 16ir, jalfrr oar riporm

roan crn nal nlgaEj roan morvi -

m pew curnunqui ri ou aro por! por!non'. i

:am rnr riaF, i; alo IA ar! pre In ml

ormia =owl= d,a diard . doom r#ax va Ibral

ida ti n d5rrr cord ,alm qui rfipod hlo n i lo pahlknotgla do dimr1

bblm Ion dRalroaa6rLn mod^-Nina lkuc

n dopy

12

~d Itiiur dime

Clair Nrd I. prrksm.

word ro oanbabo ro do IN rErilm rlln con pnrdn

lam Ira L. ralualso EL La prvElimolqu

rooi^-rr. Io I Ann rloo q1 1.1.1uni. uuEx, on loa >a ri _M molt pr orrpir

i Lrd
·ro~ : Qua! d La poblirnri 6.M. ohrdt Lali

ntWr in anry m ddrnordlr ridir pr. I. ps(mu i

rfirrhwr . obritMona lra
·n alma h
·i. rtLrtif I par .6~ hum. dr hnrpa_}

u7I law I o u1 rru lebn Ldom.Ucoa al NI IN 01 pup.ui ou ol .1. pa mi. pll rrn d dorm lo rm:1r!

mnpor Ir nfslha!arm. a iv mirai Yfvrtalicrarraurillnpaoa on tiiricr a dltro

ArMor u rordn dr Anrdrr do rilirrn wrrblo pcuab IN

on rpm Iari hala Irawlio mum dll~rrrha

quo Llo, o nt r#Rih I r i Far ul p., r
ripmdn i lo Froblirrllcentsa

Christelle Brémaud E179552Q

[ 167]

#a iralm dd ca pMnc.
Im.7rrlbnrarcents d
· rlr 1.1E15

[168]

ANNEXE 14 bis:

GRILLE 2 D'EVALUATION chronologique PAR compétences

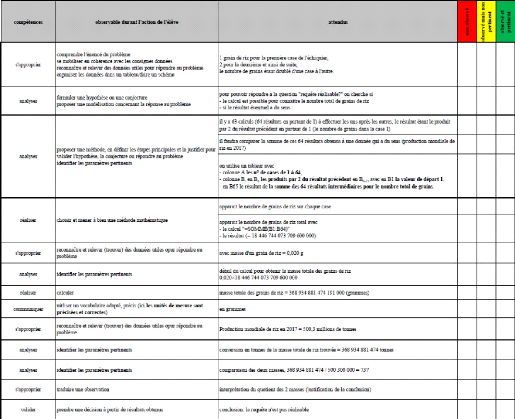
Christelle Brémaud_E179552Q

Christelle Brémaud_E179552Q

[169]

ANNEXE 14 ter:

GRILLE 3 D'EVALUATION chronologique PAR compétences
Dans le cadre de l'analyse du corpus

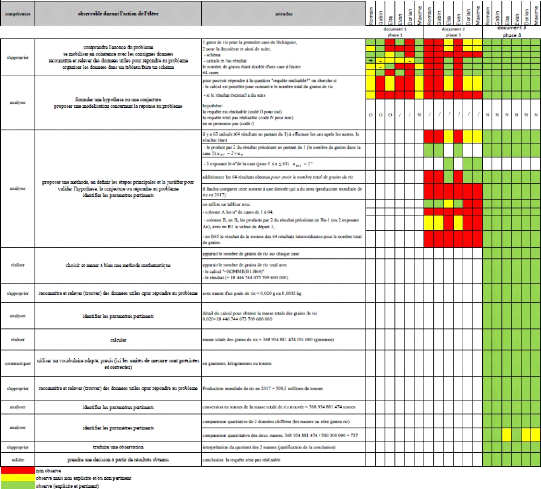
Christelle Brémaud_E179552Q

[170]

4ème de couverture

5 mots clés : mathématiques, situation-problème, compétences, problématisation, évaluation.

Résumé en Français :

Cette étude interroge la notion de compétences en mathématiques sachant qu'il s'agit, depuis la rénovation de la voie professionnelle en 2009, d'évaluer les élèves de lycée professionnel en Contrôle en Cours de Formation. L'analyse didactique de l'activité des élèves dans le travail qu'ils engagent pour la résolution d'une situation-problème, permet dans le cadre théorique de la problématisation d'observer le cheminement de leur questionnement et d'observer le processus de construction d'un apprentissage autour des suites numériques. Dans le prolongement de ce travail, nous nous sommes interrogés sur l'évaluation demandée par l'Education Nationale avec une nuance faite entre l'évaluation des compétences et l'évaluation par compétences, nuance qui semble être une condition pour mieux appréhender la nécessaire Approche Par Compétences et d'une certaine manière éclairer de façon plus systémique certaines injonctions ministérielles.

5 keywords : mathematics, «situation-problem (fr)», skills, «problématisation (fr)» assessment.

Summary in English :

This study questions the notion of math skills since vocational schools were renovated in 2009 and students have been tested through continuous assessment ever since. The didactic analysis of students' work when it comes to problem solving («problematisation»), allows to observe how students build their investigation and how they manage to learn numerical sequences. As a continuation of this work, this study also deals with the assessment requested by The French ministry of National Education and focuses on the slight difference which has to be made between «l'évaluation des competences» and «l'évaluation par compétences». It is necessary to understand this slight difference in order to apprehend the skill-based approach and in some way, shed a more systemic light on some ministerial instructions.