III.1.2. Les Tâches Du Datamining
Contrairement aux idées reçues, le Data Mining
n'est pas le remède miracle capable de résoudre toutes les
difficultés ou besoins de l'entreprise cependant, une multitude de
problèmes d'ordre intellectuel, médical, économique
peuvent être regroupés, dans leurs formalisations, dans l'une des
tâches suivantes :
1. Classification ;
2. Estimation ;
3. Prédiction ;
4. Discrimination ;
5. Segmentation.
III.I.2.1. Les Tâches Et Technique Du
Datamining
|
TACHES
|
TECHNIQUE
|
|
Classification
|
L'arbre de décision
|
|
Le raisonnement par cas
|
|
L'analyse de lien
|
|
Estimation
|
Le réseau de neurones
|
|
Prédiction
|
L'analyse du panier de la ménagère
|
|
Le raisonnement base sur le mémoire
|
|
L'arbre de décision
|
|
Les réseaux de neurones
|
|
Extraction de connaissance
|
L'arbre de décision
|
Tableau 4: les taches et
technique du datamining.
En outre, hormis ces quelques techniques et tâches du
datamining, nous signalons qu'il existe d'autres que nous n'avons pas
énumérez dans notre travail.
44
III.2. Arbre de décision
III .2.1. Introduction à l'arbre de
décision
Un arbre de décision est une structure qui permet de
déduire un résultat à partir de décisions
successives. Pour parcourir un arbre de décision et trouver une
solution, il faut partir de la racine. Chaque noeud est une décision
atomique.24
Proche en proche, on descend dans l'arbre jusqu'à
tomber sur une feuille. La feuille représente la réponse
qu'apporte l'arbre au cas où l'on vient de tester.
a) Début à la racine de l'arbre
Descendre dans l'arbre en passant par les noeuds de test, la
feuille atteinte à la fin permet de classer l'instance testée.
Très souvent on considère qu'un noeud pose une question sur une
variable, la valeur de cette variable permet de savoir sur quels fils
descendre. Pour les variables énumérées, il est parfois
possible d'avoir un fils par valeurs, on peut aussi décider que
plusieurs variables différentes mènent au même sous
arbre.
Pour les variables continues, il n'est pas imaginable de
créer un noeud qui aurait potentiellement un nombre de fils infini, on
doit discrétiser le domaine continu (arrondis, approximation), donc
décider de segmenter le domaine en sous-ensembles. Plus l'arbre est
simple, et plus il semble techniquement rapide à utiliser.
En fait, il est plus intéressant d'obtenir un arbre qui
est adapté aux probabilités des variables à tester. La
plupart du temps un arbre équilibré sera un bon
résultat.
Si un sous arbre ne peut mener qu'à une solution
unique, alors tout ce sous arbre peut être réduit à sa
simple conclusion, cela simplifie le traitement et ne change rien au
résultat final.
III.2.2. Définition
Un arbre de décision est un outil d'aide à la
décision et à l'exploration de données. Il permet de
modéliser simplement, graphiquement et rapidement un
phénomène mesuré plus ou moins complexe. Sa
lisibilité, sa rapidité d'exécution et le peu
d'hypothèses nécessaires a priori expliquent sa popularité
actuelle.25
III.2.3. Caractéristiques et
Avantages
La caractéristique principale est la lisibilité
du modèle de prédiction que l'arbre de décision fourni, et
de faire comprendre ses résultats afin d'emporter l'adhésion des
décideurs.
24 VINCENT GUIJARRO, Les Arbres de Décisions
L'algorithme ID3, lile, 2006, p.16
25 RAKOTOMALALA. : Graphes d'induction apprentissage et data
mining, hermès, 2000.THESE, p.43
26 KANGIAMA LWANGI Richard : Extraction des connaissances
a partir d'un entrepôt des données à l'aide de l'arbre de
décision application aux données médicales, UNIKIN
2010-2011.
45
Cet arbre de décision a également la
capacité de sélectionner automatiquement les variables
discriminantes dans un fichier de données contenant un très grand
nombre de variables potentiellement intéressantes. En ce sens, constitue
aussi une technique exploratoire privilégiée pour
appréhender de gros fichiers de données.
III.2.4. Algorithme ID3
L'algorithme ID3 a été développé
à l'origine par ROSS QUINLAN. C'est un algorithme de classification
supervisé. C'est-à-dire il se base sur des exemples
déjà classés dans un ensemble de classes pour
déterminer un modèle de classification. Le modèle que
produit ID3 est un arbre de décision. Cet arbre servira à classer
de nouveaux échantillons. Il permet aussi de générer des
arbres de décisions à partir de données. Imaginons que
nous ayons à notre disposition un ensemble d'enregistrements ayant la
même structure, à savoir un certain nombre de paires attribut ou
valeur. L'un de ses attributs représente la catégorie de
l'enregistrement. Le problème consiste à construire un arbre de
décision qui sur la base de réponses à des questions
posées sur des attributs non cible peut prédire correctement la
valeur de l'attribut cible. Souvent l'attribut cible pend seulement les valeurs
vrai, faux ou échec, succès.
III.2.5. Principes
Les principales idées sur lesquels repose ID3 sont les
suivantes :
Dans l'arbre de décision chaque noeud correspond
à un attribut non cible et chaque arc a une valeur possible de cet
attribut. Une feuille de l'arbre donne la valeur escomptée de l'attribut
cible pour l'enregistrement testé décrit par le chemin de la
racine de l'arbre de décision jusqu'à la feuille.
(Définition d'un arbre de décision). Dans l'arbre de
décision, à chaque noeud doit être associé
l'attribut non cible qui apporte le plus d'information par rapport aux autres
attributs non encore utilisés dans le chemin depuis la racine.
(Critère d'un bon arbre de décision). L'entropie est
utilisée pour mesurer la quantité d'information apportée
par un noeud. (Cette notion a été introduite par Claude Shannon
lors de ses recherches concernant la théorie de l'information qui sert
de base à énormément de méthodes du
datamining).26
Algorithme
Entrées : ensemble d'attributs A; échantillon E;
classe c
Début
Initialiser à l'arbre vide;
Si tous les exemples de E ont la même classe c
46
Alors étiqueter la racine par c;
Sinon si l'ensemble des attributs A est vide
Alors étiqueter la racine par la classe majoritaire
dans E;
Si non soit a le meilleur attribut choisi dans A;
Étiqueter la racine par a;
Pour toute valeur v de a
Construire une branche étiquetée par v;
Soit Eav l'ensemble des exemples tels que e(a) = v;
ajouter l'arbre construit par ID3 (A-{a}, Eav, c);
Fin pour Fin sinon
Fin sinon
Retourner racine;
Fin
III.2.6. Exemple Pratique d'un Algorithme
ID3
Pour introduire et exécuter "à la main"
l'algorithme ID3 nous allons tout d'abord considérer l'exemple
ci-dessous: Une entreprise possède les informations suivantes sur ses
clients et souhaite pouvoir prédire à l'avenir si un client
donné effectue des consultations de compte sur Internet.
|
Client
|
Moyenne des
montants
|
Age
|
Lieu de
Résidence
|
Etudes
supérieures
|
Consultation par
internet
|
|
1
|
Moyen
|
Moyen
|
Village
|
Oui
|
Oui
|
|
2
|
Elevé
|
Moyen
|
Bourg
|
Non
|
Non
|
|
3
|
Faible
|
Age
|
Bourg
|
Non
|
Non
|
|
4
|
Faible
|
Moyen
|
Bourg
|
Oui
|
Oui
|
|
5
|
Moyen
|
Jeune
|
Ville
|
Oui
|
Oui
|
|
6
|
Elevé
|
Agé
|
Ville
|
Oui
|
Non
|
|
7
|
Moyen
|
Agé
|
Ville
|
Oui
|
Non
|
|
8
|
Faible
|
Moyen
|
Village
|
Non
|
Non
|
Tableau 5: exemples pratiques
Log (P (C[ville)))
47
Ici, on voit bien que la procédure de classification
à trouver, qui à partir de la description d'un client, nous
indique si le client effectue la consultation de ses comptes par Internet,
c'est-à-dire la classe associée au client.
o Le premier client est décrit par (M : moyen, Age :
moyen, Résidence : village, Etudes : oui) et a pour classe Oui.
o Le deuxième client est décrit par (M :
élevé, Age : moyen, Résidence : bourg, Etudes : non) et a
pour classe Non.
Pour cela, nous allons construire un arbre de décision qui
classifie les clients. Les arbres sont construits de façon descendante.
Lorsqu'un test est choisi, on divise l'ensemble d'apprentissage pour chacune
des branches et on
Réapplique récursivement l'algorithme.
H(C[Lieu) = -P (bourg). (P (C[bourg) log (P (C[bourg)) + P (C
[bourg)
a) Choix du meilleur attribut :
Pour cet algorithme deux mesures existent pour choisir le meilleur
attribut : la mesure d'entropie et la mesure de fréquence:
b) L'entropie : Le gain (avec pour
fonction il'entropie) est également appelé l'entropie de
Shannon et peut se réécrire de la manière suivante :
Pour déterminer le premier attribut test (racine de
l'arbre), on recherche l'attribut d'entropie la plus faible. On doit donc
calculer H(C[Solde), H(C[Age), H(C[Lieu), H(C[Etudes), où la classe C
correspond aux personnes qui consultent leurs comptes sur Internet.
H(C[Solde) = -P (faible).(P (C[faible) log(P (C[faible)) + P (C
[faible) log(P (C[faible)))-P (moyen).(P (Cmoyen) log(P (Cmoyen)) + P (Cmoyen)
log(P (Cmoyen)))-P (eleve).(P (C[eleve) log(P (C[eleve)) + P (C[eleve)
log(P(C[eleve)))H(C[Solde)
H(CSolde) = -3/8(1/3.log(1/3) + 2/3.log(2/3)-3/8(2/3.log(2/3) +
1/3.log(1/3) -2/8(0.log (0) + 1.log(1)
H (C[Solde) = 0.20725
H(C[Age) = -P (jeune).(P (C[jeune) log(P (C[jeune)) + P (C
[jeune) log(P (C[jeune)))-P (moyen).(P (C[moyen) log(P (C[moyen)) + P (C
[moyen) log(P (C[moyen)))-P (age).(P (C[age) log(P (C[age)) + P (C[age) log(P
(C[age)))
H(C[Age) = 0.15051
Log (P (C[bourg)))-P (village).(P (C[village) log(P (C[village))
+ P (C [village) log(P (C[village)))-P (ville).(P (C[ville) log(P (C[ville)) +
P (C[ville)
48
H(C[Lieu) = 0.2825
H(C[Etudes) = -P (oui).(P (C[oui) log(P (C[oui)) + P (C [oui)
log(P (C[oui)))
-P (non).(P (C[non) log(P (C[non)) + P (C[non) log(P (C[non)))
H(C[Etudes) = 0.18275 Le premier attribut est donc l'âge (attribut dont
l'entropie est minimale). On obtient l'arbre suivant :
Age
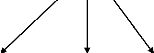
Jeune moyen âgé
Consultation ? Consultation
Figure 9: Arbre de décision construit à partir de
l'attribut âge
Pour la branche correspondant à un âge moyen, on ne
peut pas conclure, on doit donc recalculer l'entropie sur la partition
correspondante.
H(C|Solde) = -P (faible).(P (C|faible) log(P (C|faible)) + P (C
|faible) log(P
(C|faible)))-P (moyen).(P (C|moyen) log(P (C|moyen)) + P
(C|moyen)
Log (P (C|moyen)))-P (eleve). (P (C|eleve) log(P (C|eleve)) + P
(C|eleve) log(P
(C|eleve)))
H(C|Solde) = -2/4(1/2.log(1/2) + 1/2.log(1/2)-1/4(1.log(1) +
0.log(0)
-1/4(0.log (0) + 1.log (1)
H (C|Solde) = 0.15051
H(C|Lieu) = -P (bourg).(P (C|bourg) log(P (C|bourg)) + P (C
|bourg) log(P
(C|bourg)))-P (village).(P (C|village) log(P (C|village)) + P (C
|village) log(P
(C|village)))-P (ville).(P (C|ville) log(P (C|ville)) + P
(C|ville) log(P (C|ville)))
H (C|Lieu) = 0.30103
H (C|Etudes) = -P (oui).(P (C|oui) log(P (C|oui)) + P (C |oui)
log(P (C|oui)))
-P (non). (P (C|non) log(P (C|non)) + P (C|non) log(P (C|non)))
H(C|Etudes) = 0
L'attribut qui a l'entropie la plus faible est « Etudes
».
49
L'arbre devient alors :
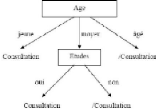
Figure 10 : Arbre de décision
finale
L'ensemble des exemples est classé et on constate que sur
cet ensemble d'apprentissage, seuls deux attributs sur les quatre sont
discriminants.
III.3 Concepts Théoriques Sur Le
Graphe
III.3.1. Définition : Un graphe
G est un couple G=(X, U), X est un ensemble non vide et au plus
dénombrable.
Nota : X est un ensemble fini, les éléments de x X
sont appelés les sommets ou noeuds. U = une famille
d'éléments du produit cartésiens X€X .
Les éléments de U=(x,y) , x,y X, sont
appelés : soit des arcs lorsqu'on tient compte de l'orientation, soit
les arêtes lorsqu'on ne tient pas compte de
l'orientation.27
III.3.2. Graphe connexe a) Définition
:
Un graphe est connexe si l'on peut atteindre n'importe quel
sommet à partir d'un sommet quelconque en parcourant les
différentes arêtes.
Exemple : soit G=(X, U) qui est un
graphe connexe

Figure 11 : graphe connexe
27 MANYA NDJADI, Recherche opérationnelle, G3
informatique option Gestion, cours inédit, U.K.A 2013-2014.
Figure 13 : arborescence
50
U6 U5
U7
U8
EX :
U4
U3
U1 U2
III.3.2. Arbres et arborescence
1. Arbres
a) Définition : Un arbre est un
graphe connexe sans cycle. C'est-à-dire dont on peut atteindre n'importe
quel sommet à partir d'un sommet quel- conque en parcourant
différents arêtes et ses arêtes ne coïncide pas.
EX :
Figure 12 : Arbre
2) Arborescence
a) Définition : une structure
qui permet de déduire un résultat à partir de
décision successive.
Soit G=(X, U) on dit que le sommet rX est une racine de G si V
X, (avec xr) un chemin de r à x .c'est -à -dire un arbre ayant
une racine.
51
| 


