1.1.1.1. VARIABLE TAUX DE DOLLARISATION (Y)
CONCEPTS
Le taux dollarisation est annuel est la variable retenue
pour évaluer la stabilité monétaire qui est l'objectif
majeur de la politique monétaire de la BCC en RDC, noté
« y », il traduit l'évolution du taux de
dollarisation au cours de la période d'étude. Tenant compte de
l'extraversion de l'économie congolaise le taux d'inflation et le taux
de change jouent un rôle déterminant en ce concerne le taux de
dollarisation dans la mesure où lorsque le taux de l'inflation est
à la hausse cela a des effets négatifs sur le taux de
dollarisation. En revanche le taux de change explique le taux de dollarisation
dans une faible proportion.
Ø STATIONNARISATION DE LA SERIE Y
La stationnarisation consiste à enlever l'effet du
temps sur une série statistique. À chaque processus, selon qu'il
est de type trend stationary (TS) ou differency stationary (DS) correspond la
méthode appropriée de stationnarisation. Le seuil retenu est de
5%.
La probabilité trend et intercept associée
à la statistique t est de 0.000% ; inférieure à 5%.
Le trend est statistiquement significatif. Ensuite le test de la statistique
ADF nous donne une probabilité égale à 0.000%,
inférieur à 5%. La série Y est donc stationnaire en niveau
avec un modèle avec trand et intercept. (Voir Annexe 1)
Par ailleurs, YC est la variable endogène retenue dans
la présente étude. Ses valeurs dépendent des variables
exogènes.
1.1.1.2. LES VARIABLES TAUX D'INFLATION (X1c), TAUX DE CHANGE
(SX2C)
CONCEPTS
Le taux de dollarisation peut être expliquée par
les variables taux d'inflation X1C et le taux de change SX2C, nous avons retenu
ces variables pour capter le taux de dollarisation ayant des effets sur la
stabilité monétaire en RDC. Le taux de dollarisation est la
variable endogène. Plusieurs autres variables peuvent expliquer le
taux de dollarisation, dans le cadre de notre étude, nous avons
ciblé uniquement le taux d'inflation et le taux de change. Les
informations qui vont échapper à notre modèle seront
prises en compte par le terme de l'erreur.
Ø STATIONNARISATION DE LA SERIE YC
TABLEAU DE STATIONNARISATION DE LA VARIABLE
YC
|
Null Hypothesis: YC has a unit root
|
|
|
Exogenous: Constant
|
|
|
|
Lag Length: 0 (Automatic based on SIC, MAXLAG=1)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic
|
Prob.*
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic
|
-7.372717
|
0.0003
|
|
Test critical values:
|
1% level
|
|
-4.420595
|
|
|
5% level
|
|
-3.259808
|
|
|
10% level
|
|
-2.771129
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
Warning: Probabilities and critical values calculated for 20
observations
|
|
and may not be
accurate for a sample size of 9
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation
|
|
|
Dependent Variable: D(YC)
|
|
|
|
Method: Least Squares
|
|
|
|
Date: 06/30/19 Time: 14:15
|
|
|
|
Sample (adjusted): 2010 2018
|
|
|
|
Included observations: 9 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
YC(-1)
|
-1.197133
|
0.162373
|
-7.372717
|
0.0002
|
|
C
|
103.4385
|
14.19980
|
7.284500
|
0.0002
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.885914
|
Mean dependent var
|
-1.111111
|
|
Adjusted R-squared
|
0.869615
|
S.D. dependent var
|
6.132790
|
|
S.E. of regression
|
2.214477
|
Akaike info criterion
|
4.621040
|
|
Sum squared resid
|
34.32736
|
Schwarz criterion
|
4.664867
|
|
Log likelihood
|
-18.79468
|
Hannan-Quinn criter.
|
4.526460
|
|
F-statistic
|
54.35695
|
Durbin-Watson stat
|
1.042753
|
|
Prob(F-statistic)
|
0.000153
|
|
|
|
La probabilité du trend associée à la
statistique t est de 0.0003% ; inférieure à 5%. Le trend est
statistiquement significatif. Ensuite le test de la statistique ADF nous donne
une probabilité égale à 0.0002%, inférieur à
5%. La série YC est donc stationnaire en niveau avec un modèle
intercept.
Ø STATIONNARISATION DE LA SERIE X1C
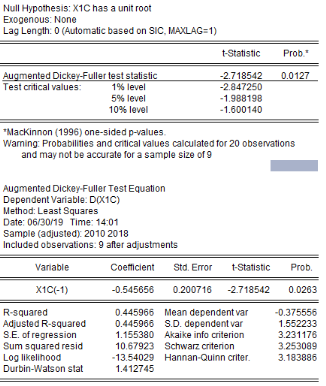
La probabilité de none (C) associée à la
statistique t est de 0.01% ; inférieure à 5%. L'intercept
est statistiquement significatif. Ensuite le test de la statistique ADF nous
donne une probabilité égale à 0.02%, inférieur
à 5%. La série X1C est donc stationnaire en niveau avec un
modèle avec none.
Ø STATIONNARISATION DE LA SERIE SX2C
|
Null Hypothesis: D(SX2C) has a unit root
|
|
|
Exogenous: None
|
|
|
|
Lag Length: 1 (Automatic based on SIC, MAXLAG=1)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic
|
Prob.*
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic
|
-3.114596
|
0.0085
|
|
Test critical values:
|
1% level
|
|
-3.007406
|
|
|
5% level
|
|
-2.021193
|
|
|
10% level
|
|
-1.597291
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
Warning: Probabilities and critical values calculated for 20
observations
|
|
and may not be
accurate for a sample size of 6
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation
|
|
|
Dependent Variable: D(SX2C,2)
|
|
|
|
Method: Least Squares
|
|
|
|
Date: 07/06/19 Time: 14:09
|
|
|
|
Sample (adjusted): 2013 2018
|
|
|
|
Included observations: 6 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
D(SX2C(-1))
|
-2.002052
|
0.642797
|
-3.114596
|
0.0357
|
|
D(SX2C(-1),2)
|
1.202245
|
0.532730
|
2.256763
|
0.0870
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.691319
|
Mean dependent var
|
-57.65833
|
|
Adjusted R-squared
|
0.614148
|
S.D. dependent var
|
243.3815
|
|
S.E. of regression
|
151.1811
|
Akaike info criterion
|
13.13604
|
|
Sum squared resid
|
91422.96
|
Schwarz criterion
|
13.06662
|
|
Log likelihood
|
-37.40811
|
Hannan-Quinn criter.
|
12.85817
|
|
Durbin-Watson stat
|
1.965337
|
|
|
|
|
|
|
|
|
|
|
|
|
|
La probabilité de l'intercept (C) associée
à la statistique t est de 0.03% ; inférieure à 5%.
L'intercept est statistiquement significatif. Ensuite le test de la
statistique ADF nous donne une probabilité égale à 0.02%,
inférieur à 5%. La série SX2C est donc stationnaire en
niveau avec un modèle avec none. (Voir Annexe 3)
| 


