II.4. Harmoniques (Ordres)
Les signaux vibratoires sont difficiles à analyser du fait
de leur contenu riche en pics.
Cependant un signal périodique complexe peut toujours
être décomposé en une somme de signaux sinusoïdaux
appelés harmoniques ou ordres.
Le but est de faire apparaître le fondamental et les
harmoniques qui ont une fréquence multiple de ce dernier. harmoniques:
relation entre une fréquence et la fréquence de rotation.
Exemple : pour 1500 tr/min , donc H= 1500/60 = 25 Hz

Fig.II.18. Harmoniques pour 1500 tr/min.
[44]
Analyse Vibratoire des Machines sur un Banc d'Essai - Cas
d'un Disque Tournant - 45
II.5. Spectre FFT (Fast Fourier Transform)
L'invention de l'algorithme FFT (transformée de Fourier
rapide) au milieu des années 1960 a rendu possible l'analyseur de
spectre moderne en temps réel, qui transforme les signaux variant dans
le temps du domaine temporel au domaine fréquentiel et fournit ainsi une
image actualisée en permanence de la composition fréquentielle
d'un signal. Avant l'apparition des analyseurs de spectre FFT, la principale
visualisation en temps réel sur place des signaux de vibration se
faisait dans leur domaine temporel naturel, généralement à
l'aide d'un oscilloscope.
La base mathématique de l'analyse spectrale est
l'intégrale de Fourier, qui a été fournie par le
mathématicien Joseph Fourier au début des années 1800,
bien avant les machines rotatives modernes. Cependant, avant l'algorithme FFT,
qui utilise les méthodes de calcul numérique modernes, la
transformation d'un signal mesuré dans le domaine temporel en un signal
dans le domaine fréquentiel nécessitait un traitement "hors
ligne" coûteux et lent. Plus précisément, un enregistrement
du signal analogique était traité à travers plusieurs
filtres analogiques à bande étroite dont les fréquences de
la bande centrale couvraient la gamme de fréquences concernée.
Les analyseurs de spectre pré-FFT étaient des équipements
électroniques encombrants à utiliser avec succès,
nécessitant un technicien expérimenté dans la façon
d'accorder et d'ajuster les filtres de largeur de bande pour obtenir des
résultats optimaux pour un enregistrement de signal de base de temps
donné. Il est compréhensible que l'analyse spectrale
pré-FFT ait été très peu utilisée. Les
détails mathématiques des séries de Fourier, des
intégrales de Fourier et des FFT font désormais partie
intégrante de la composante mathématique des programmes
universitaires d'ingénierie et sont bien traités dans de nombreux
manuels et guides d'analyse mathématique et technique. Dans
l'intérêt de l'espace et de la brièveté, ces
détails mathématiques ne sont pas couverts ici. Au lieu de cela,
une explication plus heuristique de l'analyse spectrale est donnée ici
pour aider le praticien de la vibration des machines à comprendre la
connexion directe entre un signal de base de temps et son spectre de
fréquence.
L'idée pratique sous-jacente de la transformée
de Fourier est qu'une fonction (par exemple, un signal de base de temps) peut
être construite à partir d'une somme de fonctions
sinusoïdales avec une distribution continue de la fréquence de
zéro à une fréquence de coupure appropriée.
Pour un signal se répétant périodiquement
ou une période définie, une version plus simple et plus
restrictive de ceci (la série dite de Fourier) est applicable et
additionne les composantes
Chapitre II l'Analyse Vibratoire, Captures et Identification
des Défauts
Analyse Vibratoire des Machines sur un Banc d'Essai - Cas
d'un Disque Tournant - 46
sinusoïdales uniquement à un ensemble discret de
fréquences qui sont les multiples entiers (n_1, 2, ...) d'une
fréquence de base désignée Ù1 = 2ð/t, où
t durée d'une période. Bien que les signatures de vibrations de
machines ne contiennent souvent qu'un nombre limité de composantes
harmoniques significatives, leurs fréquences ne sont souvent pas toutes
des multiples entiers d'une seule fréquence de base, et par
conséquent la transformée de Fourier, et non la série de
Fourier, est l'outil approprié pour cartographier les signaux de
vibrations de machines tournantes du domaine temporel au domaine
fréquentiel.
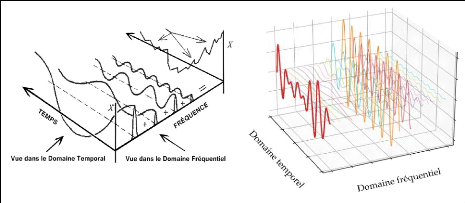
La figure II.19 fournit un lien visuel entre une fonction du
temps, X(t), et sa transformée de Fourier ou spectre de
fréquence. Comme l'illustre la figure, quelques harmoniques
additionnées produisent facilement une trace temporelle à partir
de laquelle il est difficile de visualiser ou d'identifier directement les
composants individuels qui y contribuent. En transformant le signal dans le
domaine des fréquences, les composantes contributives sont facilement
identifiées.[45]
?
X(t)
Fig.II.19. Illustration temporal-fréquentiel d'un
signal oscillant. [45][46] II.6. Tendances et lignes de base
en matière de vibrations
Même dans les machines les plus saines, les signaux de
vibration surveillés peuvent avoir tendance à migrer en amplitude
et en angle de phase, tout en restant dans une "enveloppe" de base de niveaux
de vibration acceptables. Ces changements bénins sont des effets normaux
des changements des conditions de fonctionnement, par exemple, les transitoires
thermiques, les changements de charge, l'usure normale et les fluctuations de
l'environnement global de la machine. D'autre part, lorsque les signaux de
vibration surveillés
Chapitre II l'Analyse Vibratoire, Captures et Identification
des Défauts
Analyse Vibratoire des Machines sur un Banc d'Essai - Cas
d'un Disque Tournant - 47
commencent à augmenter en amplitude au-delà des
niveaux de base établis pour une machine donnée, cette tendance
doit être suivie attentivement par les opérateurs de l'usine afin
d'évaluer en permanence la nécessité potentielle de :
? Modifier temporairement les conditions de fonctionnement de la
machine.
? Programmer un arrêt anticipé de la machine pour
des actions correctives.
? Procéder à un arrêt immédiat
dicté par une augmentation rapide des amplitudes de
vibration.
Lorsque les niveaux de vibration d'une machine commencent
à augmenter au-delà des niveaux de base établis, un
problème à l'intérieur de la machine commence à
émerger et l'augmentation des niveaux de vibration n'est souvent pas le
seul symptôme du problème sous-jacent. Une fois que l'attention
est portée sur une machine qui commence à montrer une tendance
à la hausse des niveaux de vibration, divers outils d'analyse des
signaux de vibration sont maintenant couramment utilisés pour chercher
à identifier la ou les causes profondes.[45]
| 


