II.1.2 : Méthode
d'estimation et test de robustesse
a) Principe de
l'estimation
La spécification en panel dynamique voudrait que l'on
introduise parmi les variables explicatives, la variable expliquée
retardée d'une période au moins. Nous utilisons les estimateurs
de la Méthode des Moments Généralisés (GMM) comme
Farhadiet al. (2015). En effet, en introduisant parmi les variables
explicatives la variable dépendante retardée, l'une des six
hypothèses des méthodes des Moindres Carrés Ordinaire
(MCO) se retrouve violée. Ceci crée donc le problème
d'omission de variables explicatives pertinentes dans la spécification
du modèle ; de la simultanéité qui apparaît lorsque
la variable dépendante et certaines variables explicatives sont
déterminées au même moment, ou encore des erreurs de
mesures sur les variables indépendantes et ou de la variable
dépendante. Ainsi donc l'utilisation des MCO n'est plus convenable
puisqu'elle donne des estimateurs biaisés et non convergents à
cause de la corrélation entre la variable endogène
retardée et le terme d'erreur, lorsque les résidus sont
autorégressifs.
Nous utilisons donc la méthode des moments
généralisés (GMM) développée par
(Holtz-Eakin et al.(1988) et (Arellano et Bond, 1991).En effet, Arellano et
Bond (1991) ont mis au point des estimateurs efficaces sous contraintes et
construits à partir des instruments basés sur
l'orthogonalité entre les valeurs retardées de la variable
endogène et le terme d'erreur. Les variables en niveau
décalées sont de bons instruments de l'équation en
différence dans la mesure où elles sont corrélées
avec les variables explicatives et ne le sont pas avec les termes d'erreurs.
L'estimateur ainsi obtenu, est appelé l'estimateur en
différence.
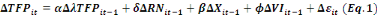
Toutefois, il est à noter que cet
estimateursoulève un nouveau problème puisque les variables
dépendantes retardées sont par construction
corrélées avec le terme d'erreur. Aussi, il a une faible
précision et présente des biais importants lorsqu'il est
appliqué aux petits échantillons, conduisant à les
compléter par des régressions sur les variables en niveau. Pour
résoudre ce problème, les auteurs proposent deux
hypothèses. L'absence d'autocorrélation des termes d'erreurs et
la faible exogénéité des variables explicatives (les
variables explicatives sont non corrélées avec les
réalisations futures des termes d'erreurs). Dès lors, Arellano et
Bond (1991) proposent les conditions des moments suivantes :
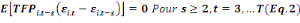
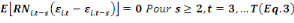
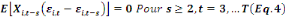
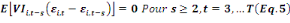
Les conditions (Eq.2) (Eq.3) (Eq.4) et (Eq.5) soulignent
l'absence de corrélation entre les variables explicatives
retardées ainsi que les variables endogènes retardées avec
les variations du terme d'erreur. De ce fait, les conditions (Eq.2) (Eq.3)
(Eq.4) et (Eq.5) permettent l'utilisation des variables retardées en
niveau comme instruments pour estimer les modèles (1a) (1b) (1c) et
(1d)
| 


