Stabile de la pression de fond et maintien de l'état d'underbalance des puits en UBD.

4.4 Analyse de stabilité des parois pour puits déviés

Contraintes déviées. Avant d'entamer l'étude de stabilité des parois pour les puits déviés, on doit tout d'abord définir la notion de contrainte déviée. Ces dernières sont le produit de la transformation par matrice de passage des contraintes déjà connus (2 horizontales et une verticale) à des contraintes équivalentes dans un autre système de coordonnées. (Figure-4.5)

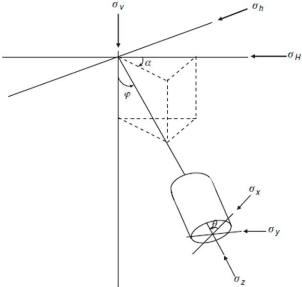
Figure 4.5 : Orientation des contraintes déviées. (Mitchell, 2011)

On définit les contraintes orientées :			6x = (6Hcos^2a + 6hsin^2a)cos^2a + 6sin^2Cp
(4.7)		6y = (6Hsin^2a + 6hcos^2a)
(4.8)		6z = (6Hcos^2a + 6hsin^2a)sin^2a + 6cos^2Cp
(4.9)

En plus des contraintes de cisaillement :			ixy = 0.5(6h -- 6H)sin2a cosCp (59)
(4.10)		iyz = 0.5(6h -- 6H)sin2a sinCp (60)
(4.11)		ixz = 0.5(6Hcos^2a + 6hsin^2a -- 6)sin2Cp (61)
(4.12)

58

Chapitre4-Initiation à la geomécanique en Forage

On définit les contraintes agissant sur le puits :

Contrainte radial 6_r = P_w (4.13)

Contrainte tangentielle 6 = 6_x + 6_y -- P_w -- 2(6_x -- 6_y)cos28 - 4T_xysin28 (4.14)

Contrainte axiale a_z = 6_z -- 2v(6_x -- 6_y)cos28 - 4VT_xysin28 (4.15)

Contrainte de cisaillement iez = 2(T_yzcosG -- T_xzsinG) (4.16)

avec les contraintes sur les autres plans considérées nulles.

Analyse pour le Collapse. Les contraintes dans le cas d'un puits dévié deviennent :

6_i = 0.5(a9 + a_z) + 0.5/(69 - a_z)² + ⁴1-9z (4.17)

6₃ = P_w (4.18)

Le résultat du calcul de la pression de collapse pour le cas d'étude est présenté dans le chapitre 8, le principe de calcul est le même que pour un puits vertical. Les étapes de calcul étant trop fastidieuses et n'entrant pas dans le but de ce mémoire il a été préféré les négliger.

4.5 Estimation des contraintes in-situ1

Le but de cette partie est d'estimer les contraintes horizontales pour un puits quelconque, pour cela l'algorithme suivant est proposé :

Si c_y < a_x

Pwf+Ppore			+ sin^2(p = (3sin^2a - cos^2a cos2(p) QH Qv		+ (3cos^2a - sin^2a cos^2(p)^Qh Qv (4.19)
Qv

Pwf+Ppore			3sin^2(p = (3cos^2a cos^2(p - sin2a )QH Qv		+ (3sin^2a cos^2(p - cos2a )Qh Qv
Qv
					(4.20)

Dans les deux cas elle peut s'écrire sous la forme :

P' = a QH Qv P', a et b étant des termes adimensionnels.

+ b Qh (4.21) Qv

En insérant les données d'un puits comme sont azimuth, inclinaison, on obtient les matrices suivantes :

¹ Aiyeru, 2014.

59

Chapitre4-Initiation à la geomécanique en Forage

~~/&/ O/ ~~ ~~

~~+ &+ O+ U

P S = P S T ?? ~~ ~~ V (4.22)

? U

P R &_R O_R

Qui peut s'exprimer comme suit :

WP'X = WYXWQX (4.23)

Cette équation peut se résoudre avec autant de données que ce soit, avec un minimum de 2. Cependant un grand nombre de données risque d'entrainer des erreurs de calcul, et donc pour cela il faut minimiser l'erreur e :

WeX = WYXWaX - WP'X (4.24)

On utilise la méthode des moindres carrés et on minimise le carré de l'erreur :

e+ = WeX^ZWeX (4.25)

Pour le minimiser, on le dérive par rapport à WaX et on prend la dérivée égale à 0 pour chercher un extrema.

[ e² [WJX

= 0 (4.26)

En substituant l'équation (4.24) dans (4.26) on obtient :

W0X = \WYX^ZWYX]^^/WYX^ZWP'X (4.27)

Le résultat donne toujours deux valeurs, on prend la plus grande comme étant a_H et la plus petite ah.

Chapitre5-Effet d'Accumulateur : définition et expliquation