Collapse. Prend place habituellement
dans les cas de pression de fond faibles, le contraste élevé
entre la contrainte tangentielle et la pression appliquée au fond par le
fluide de forage va engendrer une contrainte de cisaillement. En
conséquence, le collapse est définit comme étant une
rupture par cisaillement.
Parfois au lieu d'une rupture on a un resserrement des parois,
phénomène dit « Tight hole », ce
phénomène nécessite plusieurs passes de reforage.
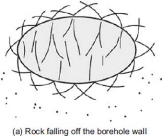
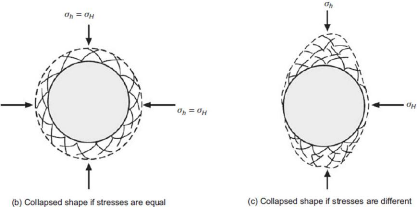
La Figure 4.3 illustre des ruptures par cisaillement typiques,
les plans de cisaillement sont courbés du fait de la
géométrie circulaire du trou, la première illustration
montre le cas où les plans de cisaillement se connectent,
résultant une fragmentation des roches qui vont tomber dans le trou.
55
Figure 4.3 : Modes de collapse du trou. (Mitchell,
2011)
Analyse de la rupture par collapse. Le
mécanisme de la rupture a été définit comme
étant une rupture par cisaillement, les résistances de la roche
sont estimées à partir des essais sur carottes avec une pression
de confinement constante. La discussion sur les tests sur échantillons
ne fait pas l'objet de ce mémoire, le lecteur est dirigé vers un
cours sur l'essai triaxial pour plus de détails.
Chapitre4-Initiation à la geomécanique en
Forage
Plusieurs modèles de ruptures ont été
élaborés pour décrire les mécanismes de rupture de
la roche, il est cité les plus utilisés : Critère de Von
Mises, Critère de Mogi-Coulomb et aussi Critère de Lade
modifié. Cependant la description classique du modèle de
Mohr-Coulomb donne de très bons résultats dans l'estimation de la
pression de collapse.
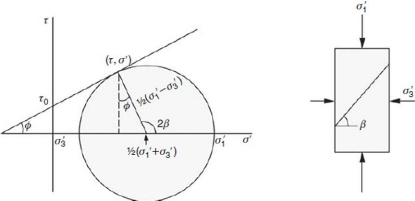
Modèle de Mohr-Coulomb. En 2 dimensions, les
contraintes peuvent être estimées par le biais du cercle de Mohr.
Ceci est fait par la construction d'un cercle dont le diamètre est
égal à la différence entre la contrainte maximale et
minimale à la rupture. (Figure-4.4)
Le modèle de rupture de Mohr-Coulomb est cette ligne de
rupture, est décrite mathématiquement comme suit :
# = #$ + a't&'( (4.3)
Où ( est définit comme étant l'angle de
friction interne de la roche.
La courbe est obtenue avec des données de laboratoire,
pour appliquer ce modèle au puits, il faut dériver les
expressions pour les contraintes agissant sur le trou.
56
Figure 4.4 : Illustration des contraintes pour le
modèle de Mohr-Coulomb (Mitchell, 2011)
Avec ) = * + + 45° (4.4)
Les coordonnées à la rupture sont définies
comme suit :
I = + / 0,/ 12 ~ + /
0/ --a'1256'( (4.6)
La pression de collapse est directement tirée de
l'expression de l'équation (4.3) égal (4.5), en y insérant
l'équation (4.6), on cherche Pw pour que l'égalité soit
correcte.
La contrainte a'/ étant égale
à la contrainte tangentielle effective, et a1 à la
contrainte radiale effective.
57
Chapitre4-Initiation à la geomécanique en
Forage



