Synthèse
On a pu voir à quel point la numération
était un domaine important lors des apprentissages fondamentaux des
élèves. En effet, ce thème fait partie intégrante
des savoirs indispensables que l'école doit pouvoir transmettre à
ses élèves. Chaque enseignement doit être compris par les
élèves et doit être amené de façon à
ce qu'il ait du sens. C'est la grande difficulté de l'école.
Afin que les élèves puissent avoir une
compréhension optimale de la numération, on a pu voir que les
enseignants, les programmes et les manuels mettaient en place des aides
à cette assimilation. En effet, la stratégie de groupement
constitue un véritable tremplin pour que l'élève puisse
donner du sens à notre système positionnel de numération
décimale.
Grâce à la lecture de différents articles
et aux apports directement prélevés en classe, j'ai pu constater
qu'il existait différentes techniques concernant le groupement, pouvant
permettre à l'élève de comprendre la numération
dans son sens le plus profond.
Certains privilégient les méthodes de
groupements à l'écrit, qui vont permettre de mettre en avant une
organisation spatiale qui fera sens au dénombrement (exemple :
bâtonnets) mais ne pourra pas être transposée
automatiquement à l'écriture chiffrée (Cf. disposition
spatiale de Hilli et Ruellan-Le-Coat). En effet, les apprentissages de
l'écriture chiffrée au cours préparatoire peuvent toujours
entraîner des erreurs de la part des élèves. Lors d'un
dénombrement et afin d'être compris par tous les
élèves de la classe, quel que soit leur niveau, les
élèves vont être amenés à grouper pour
communiquer de façon écrite. Cela passe souvent à travers
l'élaboration d'un bon de commande. Favoriser le groupement dans
l'écriture va également permettre aux élèves de
comprendre le sens de l'écriture chiffrée du système
positionnel français. En effet, grâce à une première
symbolisation écrite, les élèves vont pouvoir
appréhender les notions d'unités, dizaines, centaines, et
comprendre la position d'un chiffre dans un nombre.
D'autres vont privilégier l'absence de l'oral («
Freddy la grenouille ») qui va obliger l'élève à
trouver une autre stratégie de communication (sous entendue
l'écrit). Dans les articles que j'ai pu lire, l'oral n'est pas toujours
mis en avant. Il serait intéressant, lors d'une éventuelle
recherche, de s'attarder sur l'aspect oral des nombres et sur le sens qu'il
peut transmettre. En effet, les nombres sont constitués
généralement grâce aux groupements auxquels ils
appartiennent, mais dans le système français, il existe
énormément d'exceptions des mots-nombres pouvant engendrer une
difficulté de compréhension du système en lui-même
par les élèves (exemple : le mot « dix-sept » peut
être perçu comme une dizaine et sept unités par les
élèves, après un apprentissage. Mais le mot « douze
» ne peut pas être associé facilement à une dizaine et
deux unités.). L'apprentissage de la numération à travers
les groupements oraux me semble être plus difficile que l'écrit
à transmettre aux élèves, bien qu'il soit très
intéressant.
La symbolisation des groupements par les objets et la
manipulation sont des atouts majeurs dans la compréhension de la
numération. Il est en vrai que c'est en manipulant que les
élèves arrivent à donner du sens à leurs
apprentissages. Utiliser du matériel et privilégier la
manipulation va rendre la situation plus concrète. Mais attention, il ne
s'agit pas juste de manipuler des objets et de passer ensuite aux groupements.
Manipuler ces objets doit permettre de faire un lien avec les groupements. Les
enseignants doivent faire comprendre aux élèves que le but de la
symbolisation grâce au matériel est la compréhension de
l'écriture décimale des nombres (exemple : si
l'élève manipule 10 paquets de 3, ils symboliseront trois
dizaines). La manipulation permet de rendre une situation réelle et est
très importante puisqu'elle permettra une meilleure compréhension
si le lien entre celle-ci et l'écriture des nombres est bien fait. On ne
doit pas seulement manipuler pour écrire, on doit manipuler pour donner
du sens et écrire grâce à ce que l'on a compris de la
manipulation.
Lors des expériences, les auteurs des différents
textes ont parfois provoqué le groupement ou ont laissé
l'élève choisir seul sa stratégie. C'est lorsque
l'élève tâtonne afin de trouver une stratégie qu'il
va offrir plusieurs possibilités de réponses à sa
situation problème. Les auteurs ont voulu faire émerger la
stratégie de groupement par les élèves, sans pour autant
s'être attardés sur l'aspect numéral de ces groupements. En
effet, les expériences ont permis aux élèves de
créer des groupements, mais pas souvent
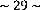
des groupements de 10. Il ne s'agit pas de quelque chose de
très grave, puisque, par la suite, les enseignants pourront aider les
élèves à comprendre que la stratégie de groupements
par 10 est la plus simple à utiliser. Il est vrai que l'enseignant doit
faire comprendre aux élèves que créer des groupements
irréguliers (tels que 3-5-7-9-2) ne va pas permettre une addition
facile. De plus, il est plus utile que les élèves comprennent que
créer des groupements de même quantité va leur permettre de
comparer deux quantités très rapidement (exemple : cinq
groupements de dix d'un côté, quatre groupements de dix de l'autre
; on peut repérer directement qui en a le plus). En revanche, si l'on
regroupe par 10, on pourra, grâce à la comptine numérique,
aux calculs ou encore aux apprentissages de 10 en 10, prouver aux
élèves qu'il est plus stratégique d'effectuer des
groupements de 10, bien qu'à ce stade de l'apprentissage de la
numération, ils pourront préférer d'autres
stratégies (2 en 2, 20 en 20). La capacité du groupement n'est
pas très importante puisqu'elle permet tout de même aux
élèves de grouper et cela constituera une bonne introduction pour
la numération décimale.
Bien que la numération et les opérations soient
deux apprentissages différents, ils peuvent et doivent être
reliés entre eux. C'est grâce à cela que les
élèves comprendront le véritable sens des
opérations dès le plus jeune âge. En effet, pour les quatre
opérations, on a recours à la notion de groupement. L'addition et
la soustraction étant les deux opérations ayant des règles
de groupements décimaux, il est important pour les élèves
de comprendre pourquoi on additionne (ou soustrait) tel chiffre avec tel
chiffre. Les problèmes de multiplication et de division font
également appel aux groupements, mais les groupements semblent moins
évidents puisque moins visibles directement lors de
l'opération.
~ 31 ~
| 


