Chapitre Troisième : APPROCHES
METHODOLOGIQUES
Dans ce travail nous traitons un problème
d'optimisation combinatoire appliqué au problème concret
d'entreposage d'objets 3D dans un espace de stockage. De ce fait, nous aurons
besoin d'au moins un algorithme pouvant nous permettre d'atteindre notre
objectif, celui d'utiliser de la meilleure façon possible l'espace de
stockage disponible.
Ce chapitre est consacré à la
représentation et l'analyse des algorithmes pouvant résoudre le
problème de 3DBP. De prime à bord, nous avons
procédé à la présentation des algorithmes qui ont
constitués notre objet de recherche, nous avons commencé par la
présentation d'un algorithme exacte du problème de remplissage de
paniers puis les algorithmes d'approximations qui nous ont permis de
résoudre ce problème en donnant une solution acceptable en un
temps convenable.
III.1. Modélisation algorithmique du
problème de 3DBP
III.1.1. Formulation du problème
Le problème de 3D bin packing relève de la
recherche opérationnelle et de l'optimisation combinatoire. Il s'agit de
trouver le rangement le plus économique possible pour un ensemble
d'articles dans des boîtes. Le problème classique se
définit en une dimension, mais il existe de nombreuses variantes en deux
ou trois dimensions.
Le problème de chargement d'entrepôts que nous
tentons de modéliser est une variante du problème en trois
dimensions. En fait, dans ce travail nous ne faisons
23
allusion qu'aux articles possédant chacun une largeur,
une longueur (ou profondeur) et une hauteur c'est de là d'ailleurs que
vient de concept 3D (figure 4).
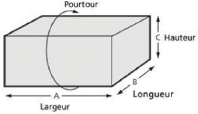
Figure 4 : Dimensions d'articles commerciaux qui nous
intéressent.
Dans le problème classique, les données sont : Un
nombre infini de paniers de taille C
Une liste 1,2,.......,n d'objets i de taille
ci
On cherche à trouver le rangement valide pour tous ces
objets de façon à minimiser le nombre de paniers à
utiliser. Pour qu'un rangement soit valide, la
somme des tailles des objets affectés à un panier
doit être inférieure ou égale à C.
Pour décrire une solution, on peut utiliser un codage
binaire pour indiquer dans quel panier un objet est rangé.
La variable vaudra si l'article est rangé dans le panier ,
et sinon.
La variable binaire est égale à si la boîte
est utilisée, sinon.
On cherche donc à minimiser le nombre de
panier :
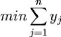
Sous les contraintes suivantes :
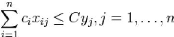
24
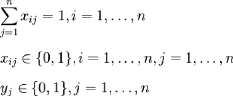
Source : Wikimedia Foundation (2013).
La première inégalité signifie qu'on ne peut
dépasser la taille d'un panier pour un
rangement. À noter que la partie droite de
l'inégalité oblige à prendre la valeur
dès qu'un article est rangé dans le panier . La
deuxième inégalité impose à chaque objet
d'être rangés dans une boîte et une seule. Toute solution
pour laquelle la famille d'équations précédente est
vérifiée est dite réalisable. (Kantorovitch,
1960).
Le problème de bin packing a été
largement étudié dans la communauté de recherche
opérationnelle. Il existe des heuristiques
très efficaces pour le résoudre, et des
méthodes exactes utilisant l'optimisation
linéaire en nombre entiers, la formulation de Kantorovich, une
résolution par génération de colonnes, la procédure
par séparation et évaluation,... Les méthodes exactes
permettent d'obtenir la solution optimale à chaque fois, mais le temps
de calcul peut être long si le problème est compliqué
à résoudre. Les méthodes approchées, encore
appelées heuristiques, permettent d'obtenir rapidement une solution
approchée, donc pas nécessairement optimale. Nous n'allons pas
vraiment parler de toutes ces méthodes car ce qui nous intéresse
dans ce travail c'est plutôt trouver une heuristique qui donne une
solution acceptable en un temps convenable.
| 


