Chapitre 3
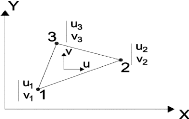
Figure 3.4 : Elément triangulaire plan à
trois noeuds.
3.2.2. Matrice de rigidité
élémentaire
Cet élément possède deux degrés de
liberté en déplacement par noeuds.
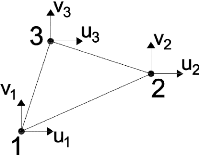
Figure 3.5 : Elément triangulaire plan avec deux
degrés de liberté par noeuds.
La matrice de rigidité élémentaire
utilisée dans les calculs est :
eE
[K l 4A( 1 -- v2)
Sym
x11 + Cyiz
Avec :
66 /176
Chapitre 3
3.3. Elément fini tétraédrique
à quatre noeuds 3.3.1. Définition
Le tétraèdre à champ
linéaire est l'élément tridimensionnel le plus
simple, son élément de référence se présente
comme suit :
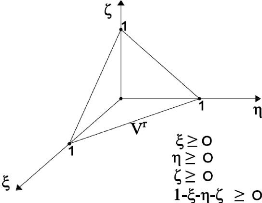
Figure 3.6 : Elément de référence de forme
tétraédrique.
Celui-ci est construit par extension du triangle
isoparamétrique à trois noeuds. Il possède trois
degrés de liberté en déplacement par noeud, ce
qui correspond à un total de douze degrés de
liberté (DDL).
3.3.2. Construction de la matrice des fonctions
d'interpolation
Choix de la base polynomiale (P())
La base polynomiale utilisée est celle-ci : (P())
= ( 1 f i 0 Evaluation de la matrice nodale [Pa]
Calcul de la matrice [Pa] :
[ ]
67 /176
Chapitre 3
|
, -
|
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
< >
< >
< >
< >
|
Le calcul de , - donne :
, -
[
]
Inversion de la matrice nodale , -
Le calcul de , - donne :
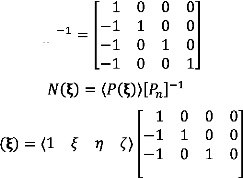
, -
( ) < ( )>, -]
( ) < > [
10 0
--1 1
--1 0 0
< ( )> < >
| 


