Chapitre 2
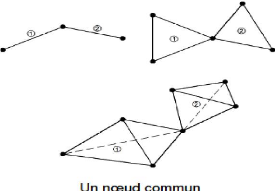
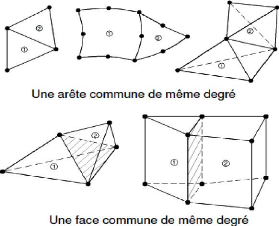
Figure 2.10 : Connexions adéquates entre
éléments
? L'ensemble de tous les éléments
Ve doit constituer un domaine aussi proche que possible du
domaine donné V, nous excluons en particulier les
« trous » entre éléments
[5]:
38 /176
Chapitre 2
1
2
Trou inadmissible entre éléments
Figure 2.11 : Exemple de maillage à exclure
Lorsque la frontière du domaine V est
constituée par des courbes ou des surfaces plus complexes que celles qui
définissent les frontières des éléments, une erreur
est inévitable. Cette erreur est appelée
erreur de discrétisation géométrique,
elle peut être réduite en diminuant la taille des
éléments, ou en utilisant des éléments à
frontières plus complexes :
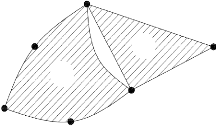
Erreur
de
discrétisation
géométrique
Augmentation du
nombre
d'éléments
Utilisation d'éléments à frontières
courbées
Figure 2.12 : Discrétisation géométrique
des frontières courbes
Les deux règles précédentes sont
respectées si les éléments sont construits de la
manière suivante :
- Chaque élément est défini de
manière unique à partir des coordonnées des noeuds
géométriques situés sur cet élément. Le plus
souvent ces noeuds géométriques sont situés sur les
frontières de l'élément et sont communs à plusieurs
éléments ;
- La frontière d'un élément à deux
ou trois dimensions est formée par un ensemble de courbes ou de
surfaces. Chaque portion de
Chapitre 2
frontière doit être définie de
manière unique à partir des coordonnées des seuls noeuds
géométriques situés sur cette portion de frontière.
Ainsi les portions de frontière communes à deux
éléments sont définies de manière identique pour
l'un ou l'autre élément.
2.3. Approximation nodale
Un modèle mathématique d'un système physique
fait intervenir plusieurs
variables ou fonctions dites exactes ( ) :
températures, vitesses,
épaisseurs,
déplacements, etc.
Celles-ci sont représentées par des fonctions
« approchées» ( ) telles que la différence :
( ) ( )
soit assez « petite» pour l'objectif
visé.
La fonction approchée u est le plus souvent
linéaire en ái :
( ) ( ) ( ) ( )
( ) < ( ) ( ) ( )> { }
où : P1,P2,...,Pn sont des fonctions
connues linéairement
indépendantes (chaque fonction ne peut
pas être construite par combinaison linéaire des autres
fonctions), telles que des polynômes ou des fonctions
trigonométriques, ces fonctions sont indépendantes des
ái
á1, á 2, ..., á n
sont les paramètres de l'approximation.
39 /176
Les paramètres á1, á 2,
..., á n n'ont pas en général de sens
physique.
40 /176
Chapitre 2
Cependant nous pouvons choisir comme paramètres
á, les valeurs de la fonction ( ) en n
points appelés noeuds de coordonnées
Imposons de plus que la fonction approchée coïncide
avec la fonction exacte ( ) en ces noeuds:
( ) ( )
( ) ( )
( ) ( )
La fonction approchée s'écrit alors:
( ) ( ) ( ) ( )
un
( ) < ( ) ( ) ( )> { }
ü La relation ci-dessus définit une
approximation nodale ;
ü Les paramètres ái, sont les
paramètres généraux de l'approximation
;
ü Les paramètres ui, sont les
paramètres nodaux ou variables nodales
de l'approximation ;
ü Les fonctions N(x) sont les fonctions
d'interpolation.
L'approximation nodale possède les deux
propriétés suivantes :
Comme ( ) les fonctions Ni vérifient
( ) {
L'erreur d'approximation définie par:
| 


