CHAPITRE 3. ÉTAT DE L' ART
18
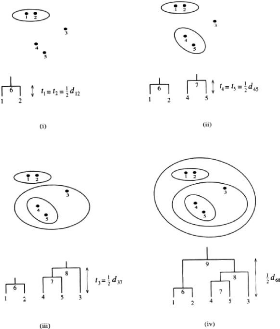
FIGURE 3.1 - Application de UPGMA
de l'arbre. La prise en compte des vitesses d'évolution
utilise la notion d'arbre additif.
Un arbre phylogénétique non-enraciné sur
n gènes est additif pour une matrice de distance D
symétrique entre les n gènes si les arcs de l'arbre
sont étiquetés avec des distances de sorte que pour chaque paire
de feuilles (i, j) dans l'arbre, la somme des distances des
arêtes du chemin de i à j est égale
à D(i, j).
La méthode NJ se base sur l'hypothèse qu'il
existe un arbre additif pour la matrice de distance donnée comme
entrée, et produit un tel arbre non enraciné.
Les principales étapes de NJ sont :
1. Initialiser l'ensemble des noeuds (groupes) de l'arbre
à l'ensemble des gènes
2. De façon itérative, jusqu'à ce qu'il ne
reste plus qu'un groupe : ~ Créer un nouveau groupe Ck
regroupant deux groupes Ci et Cj minimisant
19
CHAPITRE 3. ÉTAT DE L' ART
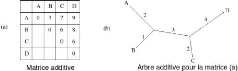
FIGURE 3.2 - Matrice et graphe additif
1 P
la formule d(i,j) - (ri +rj) avec ri =
k?L dik, et retirer ces deux
|L| - 2
groupes de la liste des groupes.
~ Ajouter dans l'arbre un nouveau noeud correspondant au
nouveau groupe Ck, comme parent des deux noeuds correspondant aux
groupes retirés, de sorte que les nouvelles arêtes de l'arbre sont
étiquetés dik = 1 2(dij +ri -rj)
et djk = dij - dik.
~ Pour chaque autre groupe Cm, recalculer
la distance entre Cm et Ck suivant la formule:
dkm = 1 2(dim + djm - dij)
La méthode NJ construit un arbre non-enraciné.
Pour enraciner cet arbre, il suffit d'ajouter un gène très
éloigné des autres gènes considérés
(outgroup). La position du branchement de ce gène sur l'arbre indique la
position de la racine de l'arbre.
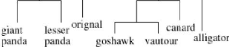
FIGURE 3.3 - Enraciner un arbre à l'aide d'un
outgroup.
Une autre stratégie d'enracinement d'arbre est de
considérer comme racine le milieu d'un plus long chemin dans l'arbre
(hypothèse de l'horloge moléculaire).
20
CHAPITRE 3. ÉTAT DE L' ART
3.1.3 Les méthodes de parcimonie
L'approche par parcimonie consiste à rechercher un
arbre qui minimise le nombre de modifications évolutives (mutations,
délétions, ou insertions) pour passer d'une séquence
à l'autre sur les branches de l'arbre. Les deux principaux algorithmes
permettant de calculer le nombre de modifications évolutives induites
par un arbre donné sont celui de Fitch [13] et Sankoff [6].
Le principe de l'algorithme classique de Fitch est le
suivant :
1. Initialiser le nombre de modifications C à
0.
2. Pour chaque noeud k de l'arbre, en allant des
feuilles vers la racine (parcours
postfixe des noeuds)
~ Si k est une feuille, poser Rk =
{étiquette de k}
~ Si k n'est pas une feuille,
~ Calculer Inters = Ri n R ,
où i, j sont des enfants de k ;
~ Si Inters == Ø, poser Rk = Ri
U R et incrémenter C de 1
~ Sinon, poser Rk = Inters
L'algorithme de parcimonie pondérée de Sankoff
est plus général que celui de Fitch. Il ne calcule pas juste le
nombre de modifications, mais considère un poids S(a;
b) pour la substitution d'une lettre a en b. Il
étiquette les noeuds internes de l'arbre de sorte à minimiser le
poids total de l'arbre. L'étiquetage des noeuds est déduit par
récurrence, en calculant l'étiquette d'un noeud à partir
des étiquettes de ses noeuds enfants.
Les principales étapes des méthodes de
parcimonie sont :
1. Calculer un alignement multiple des séquences
(gènes)
2. Pour chaque colonne de l'alignement, trouver un arbre
minimisant le nombre de modifications évolutives pour cette colonne sur
les branches de l'arbre. La recherche de l'arbre se fait par
énumération des arbres, ou en utilisant des heuristiques
d'exploration de l'espace de recherche qui évite
d'énumérer tous les arbres.
3. À partir de l'ensemble des arbres obtenus, trouver
un super-arbre qui minimise la somme totale des nombres de modifications
évolutives pour toutes les colonnes de l'alignement.
| 


