Développement d'un modèle d'évolution de gènes.

Mémoire présenté en vue de l'obtention du diplôme d'Ingénieur de Conception de Génie Informatique

Développement d'un modèle

d'évolution de l'architecture

des gènes

PAR: Esaie KUITCHE KAMELA

Sous la direction de AïDA OUANGRAOUA, Professeur

MEMBRES DU JURY:

Président: CREPIN TIMOLEON KOFANE, Professeur Rapporteur: THOMAS BOUETOU BOUETOU, Professeur Examinateur: GEORGES KOUAMOU, Docteur

Date de soutenance : 26 septembre 2016

ii

DÉDICACE

Je dédie ce travail :

-- À ma très chère et tendre maman, Mme KAMELA née MAFOKAM Maria et à mon papa KAMELA Martin, qui grâce à leur concours ont toujours su me soutenir au prix de sacrifices incommensurables.

iii

REMERCIEMENTS

La réalisation de ce mémoire a été possible grâce au concours de plusieurs personnes à qui je voudrais témoigner toute ma reconnaissance. Il s'agit notamment :

-- de mes encadreurs, les professeurs Aïda OUANGRAOUA et Thomas BOUETOU BOUETOU, pour leurs disponibilité, indications, supports et surtout leurs judicieux conseils, qui ont contribué à alimenter de manière soutenue ma réflexion.

-- du professeur Crepin TIMOLEON KOFANE et docteur Georges Edouard
KOUAMOU, pour avoir accepté de faire partie de notre jury d'évaluation.

-- des enseignants de l'ENSPY en particulier ceux du Génie Informatique pour m'avoir fourni les outils nécessaires à la réussite de mes études d'ingénierie.

-- également de mes collègues du laboratoire CoBIUS : Safa JAMMALI, Jean-David AGUILAR, Sarah BELHAMITI, Nilson COIMBRA, et Michael LUCE pour nos discussions enrichissantes et constructives qui ont permis à l'amélioration de la qualité de mon travail.

-- de tous mes frères et soeur dont Livane MAMOUBÉ KAMELA, Thierry NGATEU KAMELA, Armand FOTSING KAMELA, Valery Martial TANKOU KAMELA ainsi qu'à mes parents papa Martin KA-MELA et maman Maria MAFOKAM.

-- de toute la communauté estudiantine de l'ENSPY, en particulier ceux de la Promotion 2016 du Génie Informatique dont leur dynamisme et humour indubitables ont été pour moi une source continue de courage.

-- de mes amis Floriane MEPOUBONG, Jean BIEMEWOU, Pascal

DONGMO, Alain TSAYO, vous tous qui ne cessez de me motiver. -- de la communauté camerounaise du Canada et spécialement celle de Sher-

brooke pour leur accueil et hospitalité.

-- de tous(tes) ceux et (celles) qui de près ou de loin, d'une manière comme d'une autre, pensent toujours à moi et que j'ai oublié de citer.

iv

RÉSUMÉ

Les analyses génomiques récentes ont révélé la capacité des gènes eucaryotes de produire plusieurs ARN et protéines. Ce mécanisme joue un rôle majeur dans la diversification fonctionnelle des gènes [1]. Cependant, les modèles de reconstruction actuelles de la phylogénie de famille de gènes sont basés sur une seule protéine de référence par gène, négligeant ainsi toutes les autres protéines alternatives produites par les gènes [31]. Ensuite, la réconciliation de l'arbre de gènes dans l'arbre d'espèces est utilisée pour déduire l'histoire évolutive des familles de gènes [12].

Le problème de la reconstruction de l'évolution de l'expression du gène a été introduit dans [2], où un modèle et un algorithme pour la reconstruction de la phy-logénie des transcipts, ayant pour entrée l'arbre de gènes et les structures des gènes. Ici, nous explorons une approche différente en utilisant la réconciliation. Nous proposons une extension de la réconciliation afin de reconstruire à la fois l'arbre des gènes et l'histoire de l'évolution de toutes les protéines produites par les gènes d'une famille de gènes, compte tenu de l'arbre d'espèces. Nous proposons un modèle d'évo-lution des protéines impliquant deux nouveaux types d'événements évolutif appelé "création de protéines" et "perte de protéines", en plus des événements classiques de spéciation, duplication et de perte de gènes.

Ce mémoire présente également les limites des méthodes actuelles et propose une méthode heuristique pour la reconstruction des arbres de gènes et d'arbres de protéines. Cette méthode est résumée dans un processus à sept étapes et vise à minimiser le coût de la réconciliation. Aussi, nous avons implémenté et appliqué ce modèle pour les familles de gènes de la base de données Ensembl, montrant que notre modèle permet de réduire le coût de la réconciliation des arbres de gènes reconstruits avec des arbres d'espèces, par rapport aux arbres de gènes Ensembl correspondants.

v

ABSTRACT

Recent genome analyses have revealed the ability of eukaryotic genes to produce multiple transcripts and proteins. This mechanism plays a major role in the functional diversification of genes [1]. Still, current reconstructions of gene family phylogenies are based on a single reference protein per gene, thus neglecting all other alternative products of genes [31].

The problem of reconstructing gene product evolution was first introduced in [2], where a model and an algorithm for transcript phylogeny reconstruction, given the gene tree and the gene exon structures, were introduced. Here, we explore a different approach using reconciliation. Gene trees reconciliation with species trees is used to infer the evolutionary history of gene families [12]. We propose an extension of the framework of reconciliation in order to reconstruct both the gene tree and the evolutionary history of all the proteins produced by the genes of a gene family, given the species tree. We propose a model of protein evolution involving two types of evolutionary event called "protein creation" and "protein loss", in addition to the classical speciation, gene duplication and gene loss events.

In this report, we introduce new reconciliation problems derived from the protein evolutionary model. We present some preliminary algorithmic results and a heuristic method for the joint reconstruction of gene trees and proteins trees. We applied this algorithm to gene families of the Ensembl database, showing that our framework allows to lower the reconciliation cost of the reconstructed gene trees with species trees, as compared to the corresponding Ensembl gene trees.

vi

Table des figures

2.1 Structure de la cellule chez les Eucaryotes 5

2.2 Illustration d'une molécule d'ADN d'une cellule d'eucaryote 6

2.3 Illustration des deux brins de l'ADN et de la relation de complémen-

tarité des différentes bases 7

2.4 Chaque chromosome contient plusieurs gènes. 7

2.5 Épissage alternatif d'un gène chez les eucaryotes 8

2.6 Code génétique 9

2.7 Exemple de deux séquences de nucléotides à aligner 11

2.8 Résultat d'alignement possible des deux séquences 11

2.9 Exemple d'alignement multiple de neuf séquences protéiques. Les colonnes d'acides aminés conservés dans l'alignement sont surlignées en

vert et bleu. Crédit : wikipedia. 11
2.10 Arbre d'espèce enraciné, montrant les trois domaines de vivant : bactéries, archées et eucaryotes, reliant les trois branches d'organismes

au dernier ancêtre universel (le tronc noir en bas de l'arbre) 12

2.11 Arbre d'espèces 13

2.12 Arbre de gènes non étiqueté 14

2.13 Résultat de la réconciliation de l'arbre de gène 2.14 avec l'arbre d'es-

pèce 2.11 14
2.14 Arbre de gènes étiquetés extrait de la réconciliation de l'arbre de gène

dans l'arbre d'espèce 15

3.1 Application de UPGMA 18

3.2 Matrice et graphe additif 19

3.3 Enraciner un arbre à l'aide d'un outgroup. 19

3.4 Méthode de Ensembl-Compara pour la construction des arbres de gènes 22

3.5 Produit de l'épissage alternatif 24

vii

TABLE DES FIGURES

4.1 Arbre de protéines étiqueté avec les événements de spéciation, dupli-

cation, création et perte 26

4.2 Exemple de réconciliation d'arbres de protéines avec arbre de gènes 28

4.3 Arbre de gènes étiqueté 29

4.4 arbre d'espèces 29

4.5 Processus de construction d'arbre de gènes à sept étapes 31

4.6 Extrait d'arbre de protéines 34

4.7 Les trois principales catégories d'algorithmes utilisées pour le regrou-

pement des séquences de protéines 35
4.8 Illustration présentant la différence entre le regroupement avec che-

vauchement et le regroupement sans chevauchement 36
4.9 Exemple d'application de l'algorithme de regroupement avec chevauchement sur sept protéines de cinq gènes. Les cinq gènes sont p1, p2 et p4 ayant chacun une protéine, et p3 et p5 ayant chacun deux

protéines. 37
4.10 Application de l'algorithme glouton de fusion de 6 arbres. Les arbres sont greffés à l'arbre de référence par des créations matérialisées sur

la figure par des triangles au fond noir. 42

5.1 Arbre de gènes de la famille MAG obtenu avec notre méthode . . . 44

5.2 Arbre de gène de la famille MAG obtenu de Ensembl 45

5.3 Arbre de gène de la famille FAM86 obtenu de notre modèle 46

5.4 Arbre de gène de la famille FAM86 obtenu de Ensembl 47

viii

Table des Matières

DÉDICACE ii

REMERCIEMENTS iii

RÉSUMÉ iv

ABSTRACT v

LISTE DES FIGURES vii

GLOSSAIRE xi

1	INTRODUCTION		1
	1.1	Problématique	2
	1.2	Hypothèses	2
	1.3	Objectif général	2
	1.4	Objectifs spécifiques	2
	1.5	Résumé des contributions	3
	1.6	Plan du mémoire	3
2	GÉNOMIQUE		4
	2.1	Bio-informatique et biologie computationnelle	4
		2.1.1 Cellule	4
		2.1.2 Chromosome	5
		2.1.3 Acide désoxyribonucléique (ADN)	5
		2.1.4 Gène	6
		2.1.5 Acide ribonucléique (ARN)	6
		2.1.6 Protéine	7
	2.2	Bases de données	8

ix

TABLE DES MATIÈRES

	2.3 2.4	2.2.1 Bases de données existantes 2.2.2 Accès aux bases de données Évolution des séquences biologiques 2.3.1 Recherche de similarités entre séquences 2.3.2 Construction d'arbres phylogénétiques Conclusion sur la génomique	8 9 10 10 10 14
3	ÉTAT DE L' ART		16
	3.1	Méthodes de construction d'arbres phylogénétiques	16
		3.1.1 Énumération des arbres	16
		3.1.2 Construction d'arbres à partir des distances entre feuilles . . .	17
		3.1.2.1 UPGMA	17
		3.1.2.2 Neighbour Joining	17
		3.1.3 Les méthodes de parcimonie	20
		3.1.4 Méthodes de maximum de vraisemblance	20
	3.2	Construction des arbres de gènes	21
		3.2.1 Exemple de construction d'arbres de gènes - EnsemblCompara	21
		3.2.2 Limites des arbres de gènes actuels	23
	3.3	Conclusion sur l'état de l'art	23
4	MÉTHODOLOGIE ET IMPLÉMENTATION		25
	4.1	Modèle d'évolution des protéines et problème de réconciliation . . . .	25
		4.1.1 Idée de base	25
		4.1.2 Définitions formelles	26
	4.2	Méthodologie : Processus à sept étapes	30
		4.2.1 Étape 1 : Définition du jeu de données	30
		4.2.2 Étape 2 : Alignement multiple de toutes les séquences codantes	32
		4.2.3 Étape 3 : Calcul de la matrice de similarité	32
		4.2.4 Étape 4 : Regroupement avec chevauchement des séquences
		codantes	32
		4.2.4.1 Définition du regroupement	33
		4.2.4.2 Problème de regroupement dans le cas présent . . . .	33
		4.2.4.3 Regroupement avec chevauchement hiérarchique . . .	35
		4.2.5 Construction d'un groupe de référence	36
		4.2.6 Étape 6 : Création des arbres de protéines pour les groupes . .	40
		4.2.7 Étape 7 : Construction de l'arbre de protéines et de l'arbre
		des gènes	41
	4.3	Implémentation	41

X

TABLE DES MATIÈRES

5	ÉTUDE DE CAS		43
	5.1	Étude de cas de la famille The Myelin-Associated Glycoprotein (MAG) 43
	5.2	Étude de cas de la famille FAM86 46
6	CONCLUSION GÉNÉRALE		48

xi

Glossaire

ADN Acide Désoxyribonucléique.

API Application Programming Interface. ARN Acide Ribonucléique.

BLAST Basic Local Alignment Search Tool.

CoBIUS Complexité Biologique & Informatique de l'Université de Sherbrooke. FTP File Transfer Protocol.

MACSE Multiple Alignment of Coding SEquences. MUSCLE Multiple Sequence Alignment by log-Expectation.

NJ Neighbour joining.

TreeBest Tree Building guided by Species Tree.

UPGMA Unweighted Pair Group Method with Arithmetic Mean.

1

CHAPITRE UN

INTRODUCTION

L'aboutissement du projet d'annotation du génome humain en 2003 a permis aux scientifiques de mieux comprendre les processus biologiques qui se déroulent dans les cellules des êtres vivants au travers de l'Acide Désoxyribonucléique (ADN). Cet ADN est l'entité qui contient toutes les informations régissant le développement, le fonctionnement et la reproduction des êtres vivants. Ces nouvelles connaissances ont eu le mérite de susciter un regain d'attention de la part du public et des chercheurs.

L'ADN est composé de gènes, supports de l'information, qui sont la base de la structure et du fonctionnement des génomes. Il est donc naturel que nous nous intéressions tout particulièrement à ce programme génétique qui détermine notre fonctionnement.

Une bonne caractérisation et compréhension du fonctionnement des gènes sera d'un apport considérable dans des domaines tels que l'industrie pharmaceutique ou encore des traitements contre les cancers. Les recherches dans ces domaines constituent une tâche collective faisant appel à des collaborations multidisciplinaires.

De nombreux travaux en bio-informatique ont été réalisés dans le but de proposer des modèles d'évolution des gènes, tenant de diverses caractéristiques séquentielles ou structurales des gènes. Ce mémoire se focalise principalement à l'analyse des limites de ces modèles et propose un nouveau modèle d'évolution basé sur l'expression des gènes, suivi d'un algorithme pour la reconstruction de l'histoire évolutive des gènes.

Ce mémoire qui décrit des approches computationnelles pour résoudre une problématique issue des sciences de la vie aura la particularité de marquer des temps d'arrêt pour introduire les notions biologiques sous-jacentes.

2

CHAPITRE 1. INTRODUCTION

1.1 Problématique

Chez les eucaryotes¹, il est maintenant reconnu que chaque gène de l'ADN d'une espèce peut produire plusieurs protéines et que les gènes des organismes eucaryotes peuvent être classés en familles de gènes homologues ². La problématique soulevée par ce mémoire est de définir un modèle d'évolution et un algorithme associé pour reconstruire l'histoire évolutive d'une famille de gènes (un ensemble de gènes homologues) en prenant en compte toutes les protéines issues de chacun de ces gènes. Cette approche diffère de celle des méthodes actuelles qui ne considèrent qu'une seule protéine par gène, conduisant ainsi souvent à des arbres (phylogénies) de gènes erronés.

1.2 Hypothèses

Nous admettons dans nos travaux:

~ L'hypothèse de la théorie de l'évolution [5], qui stipule que tous les êtres vivants sont issus d'un ancêtre commun;

~ Les arbres d'espèces utilisés dans les applications de nos algorithmes sont corrects.

1.3 Objectif général

L'objectif général est de proposer un modèle d'évolution, un algorithme associé, ainsi qu'une implémentation de l'algorithme pour la reconstruction de l'évolution d'une famille de gènes en tenant compte de toutes les protéines de chaque gène.

1.4 Objectifs spécifiques

~ Modéliser le mécanisme de production de plusieurs protéines par un même gène;

~ Modéliser l'évolution de l'ensemble des protéines au sein d'une famille de gènes;

1. les eucaryotes sont un domaine du vivant regroupant toutes les espèces, unicellulaires ou pluricellulaires, qui se caractérisent par la présence d'un noyau dans leurs cellules. Il s'oppose aux domaines des procaryotes.

2. les gènes homologues sont des gènes qui sont issus d'un gène ancêtre commun qui a divergé par la suite. Ces gènes peuvent appartenir à la même espèce ou non.

3

CHAPITRE 1. INTRODUCTION

-- Proposer une modélisation globale suivie d'un algorithme de reconstruction de l'évolution;

-- Étudier un cas et comparer les résultats obtenus avec ceux issus de méthodes existantes.

1.5 Résumé des contributions

Nous avons proposer un modèle d'évolution des protéines dans les arbres de gènes avec nouveaux événements (création et pertes de protéines), puis définit du problème d'optimisation (Entrée : sous-arbres de protéines (groupes); arbre d'espèces; Sortie: arbre global des protéines, et arbre des gènes), par la suite nous avons proposer une heuristique pour résoudre le problème et enfin nous avons réaliser une implémentation et effectuer une étude de cas.

1.6 Plan du mémoire

Le mémoire est structuré autour de six chapitres. Le premier chapitre introduit le problème de construction des arbres de gènes et présentera les objectifs à atteindre. Le chapitre 2 décrit les notions biologiques et bio-informatiques nécessaires à la compréhension du sujet. Le chapitre 3 est l'état de l'art, et présente les différents modèles, méthodes existantes pour la construction des arbres phylogénétiques. Le chapitre 4 quant à lui présente les modèles et méthodes que nous avons développés, ainsi que l'implémentation que nous avons réalisée. Le chapitre 5 est dédié à l'étude de cas et le chapitre 6 conclut le mémoire et pose des axes d'amélioration.

4

CHAPITRE DEUX

GÉNOMIQUE

Ce chapitre a pour but de fournir les notions biologiques et bio-informatiques de base nécessaires pour mieux appréhender le problème d'optimisation que nous considérons dans ce mémoire. On commercera par définir la bio-informatique et la biologie computationnelle. Ensuite on définira, par ordre d'inclusion, les notions de cellules, chromosomes, ADN, gènes et protéines. On finira en présentant quelques usages fréquents de ces types d'objets biologiques en biologie computationnelle.

2.1 Bio-informatique et biologie computationnelle

La biologie est la science du vivant s'intéressant en particulier à l'origine, la croissance, la reproduction, la structure et le comportement des êtres vivants.

La bio-informatique se définit comme l'application de l'informatique à la biologie. Notamment, il s'agit d'utiliser des notions et ressources informatiques pour faciliter la compréhension et la manipulation de données biologiques.

La biologie computationnelle quant à elle vise le développement de modèles et algorithmes s'inspirant des processus biologiques afin de répondre à des questions issues de la biologie.

2.1.1 Cellule

La cellule est l'unité structurale, fonctionnelle et reproductive constituant toute ou partie des êtres vivants, à l'exception des virus. On distingue deux types d'orga-nisme. D'une part, il y a les organismes unicellulaires qui sont constitués d'une seule cellule. C'est le cas des bactéries ou des levures. D'autre part, il y a les organismes multicellulaires composés de plusieurs cellules tels que l'humain. Tout être vivant

5

CHAPITRE 2. GÉNOMIQUE

est composé de cellules dont la structure fondamentale est commune [22, 26]. La figure 2.1 illustre une cellule d'eucaryote.

Crédit :fr.bio.wikia.com/wiki/Cellule_Eucaryote

FIGURE 2.1 - Structure de la cellule chez les Eucaryotes

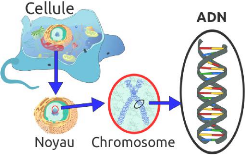
2.1.2 Chromosome

Le chromosome est une structure cellulaire microscopique représentant le support physique du matériel génétique. Tous les êtres vivants disposent des chromosomes en nombre variable propre à chaque espèce. Par exemple, chaque cellule humaine possède 22 paires de chromosomes homologues numérotés de 1 à 22, et une paire de chromosomes sexuels, soit un total de 23 paires. La figure 2.2 présente de manière explicite la relation entre cellule, chromosome, ADN et gène, chez les eucaryotes. [22, 26]

2.1.3 Acide désoxyribonucléique (ADN)

L'ADN est une macromolécule biologique constituant les chromosomes des cellules. L'ADN contient toute l'information génétique, appelée génome, permettant le développement, le fonctionnement et la reproduction des êtres vivants.

Les molécules d'ADN sont formées de deux brins antiparallèles enroulés l'un autour de l'autre pour former une double hélice comme présentée sur la figure 2.2. Chacun de ces brins est un polymère constitué d'une succession d'acides nucléiques. Chaque nucléotide est caractérisé par une base azotée, adénine (A), cytosine (C), guanine (G) ou thymine (T). L'ADN est représenté sous la forme d'une séquence sur un alphabet de quatre lettres correspondant à l'un de ses brins. Exemple : ATTCCGATCGGAAATTGC.

6

CHAPITRE 2. GÉNOMIQUE

Crédit :fr.wikipedia.org/wiki/Acide_desoxyribonucleique

FIGURE 2.2 - Illustration d'une molécule d'ADN d'une cellule d'eucaryote

2.1.4 Gène

La définition de gène a évolué au cours des dernières années. La définition générale repose sur les trois aspects ci-dessous [14] :

1. Le gène est une portion de séquence d'ADN générant des produits fonctionnels (ARNs ou protéines).

2. Le gène est la principale composante utile de l'ADN.

3. Les gènes sont le support de l'évolution, transmis aux générations suivantes avec l'ensemble de mutations qu'ils subissent.

2.1.5 Acide ribonucléique (ARN)

L'acide ribonucléique (ARN) est une copie d'un gène composée d'un seul brin d'acides nucléiques. Il existe deux principaux types d'ARN. Les ARNs codants destinés à être lus par des ribosomes pour permettre la synthèse de protéines. Les ARNs non-codants sont directement impliqués dans des fonctions au sein de la cellule.

Chez les eucaryotes, l'épissage [3, 15] est un processus par lequel, les ARNs transcrits à partir des gènes subissent des étapes de coupure et ligature qui conduisent à l'élimination de certains segments pour aboutir à un ARN final dit mature (ARNm). Les segments d'ARN conservés s'appellent des exons et ceux qui sont éliminés s'ap-pellent des introns. Un gène eucaryote peut donc être redéfini comme une suite d'exons et d'introns alternés. L'épissage alternatif est un mécanisme qui permet à un gène de produire plusieurs ARNm en générant différentes combinaisons des exons [3, 15, 4].

7

CHAPITRE 2. GÉNOMIQUE

Crédit :https : // www.bioutils.ch/protocoles/9extractiondadn

FIGURE 2.3 - Illustration des deux brins de l'ADN et de la relation de complémentarité des différentes bases.

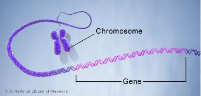
FIGURE 2.4 - Chaque chromosome contient plusieurs gènes.
Crédit : U.S. National Library of Medicine

2.1.6 Protéine

Un des enjeux majeurs de l'ère postgénomique ¹ est la description et la caractérisation fonctionnelle de l'ensemble des protéines exprimées par les gènes d'un

1. Le projet d'annotation du génome humain débute en 1993 et voit la participation de milliers de chercheurs de par le monde, dix ans après il est arrivé au terme et l'ère postgénomique débute.

8

CHAPITRE 2. GÉNOMIQUE

Crédit :https : // fr.wikipedia.org/wiki/Epissage

FIGURE 2.5 - Épissage alternatif d'un gène chez les eucaryotes

organisme.

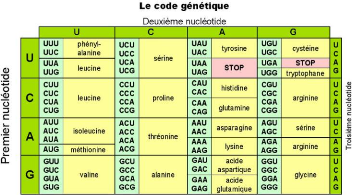
Une protéine est un polymère constitué d'une succession d'acides aminés. La traduction [16] est le processus biologique permettant de traduire une séquence d'ARNm en séquence d'acides aminés suivant le code génétique présenté à la figure 2.6. Ce code universel (identique pour tous les êtres vivants) spécifie 20 acides aminés, et permet d'associer à tout triplet de nucléotides, un acide aminé. Une protéine est représentée sous la forme d'une séquence sur un alphabet de 20 lettres correspondant aux acides aminés du code génétique. Par exemple, la séquence d'ARNm ci-après est traduite en la séquence d'acides aminés ci-dessous.

>ARNm

ATGTTCCTGCCGCTGTTCTTGGCCATGCTGTGGGGCGGGTCGCAGGCTCTGGACTCATTC >Protéines

MFLPLFLAMLWGGSQALDSF

2.2 Bases de données

2.2.1 Bases de données existantes

Des bases de données biologiques ont été développées pour faciliter le stockage et l'accès aux données biologiques de taille volumineuse. Ces bases de données sont de deux grands types, les bases de données primaires qui contiennent les données provenant des résultats expérimentaux et les bases de données secondaires qui contiennent

9

CHAPITRE 2. GÉNOMIQUE

Crédit :http : // raymond.rodriguez1.free.fr/Textes/1s13.htm

FIGURE 2.6 - Code génétique

les résultats de l'analyse des bases de données primaires. On distingue trois principales bases de données primaires à avoir :

1. DNA Data Bank of Japan (National Institute of Genetics) Site web : http://www.ddbj.nig.ac.jp/

2. EMBL (European Bioinformatics Institute) Site web : http://www.ebi.ac.uk/

3. GenBank (National Center for Biotechnology Information) Site web : http://www.ncbi.nlm.nih.gov/genbank/

Il existe une panoplie de bases de données secondaires qui diffèrent suivant l'usage auquel elles sont destinées. Pour nos travaux, nous avons utilisé Ensembl, qui est l'une des base de données génomique secondaire la mieux annotée pour les eucaryotes.

2.2.2 Accès aux bases de données

Afin de faciliter la récupération et la manipulation des données répertoriées dans les bases de données, différentes méthodes d'accès sont généralement proposées :

1. via des interfaces web (navigateurs)

10

CHAPITRE 2. GÉNOMIQUE

2. via des Datamart²

3. via des accès directs aux bases de données en lecture

4. via FTP

5. via des API spécialisées

La section suivante présente différents modèles, algorithmes et notions de biologie computationnelle, liées aux objets biologiques précédemment décrits.

2.3 Évolution des séquences biologiques

Après acquisition des séquences biologiques (gènes, ADN, ARN, protéines), ces données biologiques sont ensuite traitées pour en extraire des informations et des connaissances.

2.3.1 Recherche de similarités entre séquences

Une opération fréquente en bio-informatique est la recherche de similarité entre séquences dans le but de déterminer les régions conservées entre ces séquences. Plusieurs techniques de recherche de similarité existent parmi lesquelles on peut citer l'alignement des séquences qui est une façon d'agencer les séquences d'acides nucléiques ou d'acides aminés afin d'identifier des régions de similarité qui peuvent être une conséquence de relations fonctionnelles, structurales ou d'évolution entre les séquences. Il s'agit d'un problème d'optimisation consistant à trouver la meilleure combinaison des nucléotides ou des acides aminés de chacune des séquences qui va maximiser la similarité entre elles. Les figures 2.7 et 2.8 montrent un exemple d'ali-gnement de deux séquences nucléiques. La figure 2.9 montre un exemple d'aligne-ment multiple de neuf séquences protéiques.

2.3.2 Construction d'arbres phylogénétiques

Phylogénie. Charles Darwin a posé les bases de la théorie de l'évolution [5]. La phylogénie se définit comme l'étude de l'histoire de l'évolution d'un groupe de gènes ou d'espèces. L'analyse phylogénétique est fréquemment réalisée pour découvrir comment des groupes d'organismes ont évolué au fil du temps depuis un ancêtre commun. De nombreux modèles ont été proposés pour reconstruire l'histoire évolutive des êtres vivants [25]. On peut citer entre autres :

2. Un datamart est un sous-ensemble d'un data warehouse destiné à fournir des données aux utilisateurs, et souvent spécialisé vers un groupe ou un type d'affaires.

11

CHAPITRE 2. GÉNOMIQUE

FIGURE 2.7 - Exemple de deux séquences de nucléotides à aligner

FIGURE 2.8 - Résultat d'alignement possible des deux séquences

FIGURE 2.9 - Exemple d'alignement multiple de neuf séquences protéiques. Les colonnes d'acides aminés conservés dans l'alignement sont surlignées en vert et bleu. Crédit : wikipedia.

-- Les modèles basés sur les réseaux phylogénétiques [24, 18, 19] dans lesquels on suppose que l'évolution peut-être, représentée par un graphe;

-- Les modèles basés sur les arbres phylogénétiques qui s'appuient sur le concept de base de la descendance avec modification [11, 17, 28]. Cette représentation est la plus répandue et est celle considérée dans ce mémoire. Un arbre phylogénétique est un arbre enraciné, étiqueté tel que :

-- ses feuilles représentent les espèces ou gènes étudiés;

-- ses noeuds internes représentent les ancêtres virtuels ayant divergé;

-- ses arêtes représentent les liens de descendance entre les espèces (ou gènes).

Un arbre phylogénétique représente les relations évolutives d'un ensemble d'espèces ou de gènes. Il permet, de représenter comment à partir d'un ancêtre

12

CHAPITRE 2. GÉNOMIQUE

commun qui est la racine de l'arbre, on a obtenu toutes les espèces (ou gènes) qui sont aux feuilles de l'arbre.

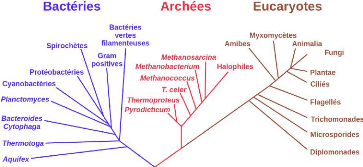
Les arbres d'espèces. L'arbre d'espèces est un arbre phylogénétique qui présente les relations évolutives d'un ensemble d'espèces. L'évolution des espèces depuis une espèce ancestrale commune se fait par un événement appelé la spéciation ³. La figure 2.10 présente l'arbre d'espèces, communément accepté, des trois grandes familles du vivant.

Crédit :https : // fr.wikipedia.org/wiki/Arbre_phylogenetique

FIGURE 2.10 - Arbre d'espèce enraciné, montrant les trois domaines de vivant : bactéries, archées et eucaryotes, reliant les trois branches d'organismes au dernier ancêtre universel (le tronc noir en bas de l'arbre)

Les arbres de gènes. L'arbre de gènes est un arbre phylogénétique qui décrit comment un gène particulier appartenant à une espèce ancestrale commune a évolué au fil du temps. L'évolution d'un gène se fait notamment à travers trois événements: la duplication de gènes ⁴, la spéciation de gènes qui résulte de la spéciation d'espèces et la perte de gènes.

3. La spéciation est le processus évolutif par lequel deux nouvelles espèces vivantes apparaissent à partir d'une espèce ancestrale.

4. La duplication est une mutation génétique aboutissant au dédoublement d'un gène dans le génome d'une espèce.

13

CHAPITRE 2. GÉNOMIQUE

Réconciliation d'arbre de gènes avec arbre d'espèces. La réconciliation d'un arbre de gènes avec un arbre d'espèces est une imbrication de l'arbre des gènes dans l'arbre d'espèces qui permet de représenter l'histoire évolutive d'une famille de gènes à l'intérieur de l'arbre d'espèces. La réconciliation permet d'étiqueter les noeuds de l'arbre de gènes comme duplication ou spéciation. Les gènes d'une famille de gènes sont tous homologues (descendants d'un même gène ancestral). Deux gènes d'une famille sont soit paralogues⁵ ou orthologues. Par définition, deux gènes orthologues appartiennent toujours à deux espèces différentes.

Le problème de réconciliation est un problème d'optimisation qui consiste, à trouver une réconciliation de l'arbre des gènes dans l'arbre d'espèces qui minimisent les différences entre les deux arbres, étant donnés un arbre de gènes et un arbre d'espèces. Ces différences sont évaluées comme le nombre de duplications et de pertes de gènes induits par la réconciliation dans l'arbre des gènes, les spéciations étant communes aux deux arbres.

Une réconciliation optimale de l'arbre de gènes décrit à la figure 2.12 avec l'arbre d'espèces décrit à la figure 2.11 est présentée à la figure 2.13. Après cette réconciliation on obtient l'arbre de gènes étiqueté présenté à la figure 2.14.

FIGURE 2.11 - Arbre d'espèces

5. Deux gènes sont paralogues (resp. orthologues) lorsque leur plus proche ancêtre commun dans l'arbre des gènes a subi une duplication (resp. spéciation).

14

CHAPITRE 2. GÉNOMIQUE

FIGURE 2.12 - Arbre de gènes non étiqueté

FIGURE 2.13 - Résultat de la réconciliation de l'arbre de gène 2.14 avec l'arbre d'espèce 2.11

2.4 Conclusion sur la génomique

Ce chapitre a défini la bio-informatique et la biologie computationnelle, puis a poursuivi en introduisant les notions de biologie et biologie computationnelle né-

15

CHAPITRE 2. GÉNOMIQUE

FIGURE 2.14 - Arbre de gènes étiquetés extrait de la réconciliation de l'arbre de gène dans l'arbre d'espèce

cessaires pour la compréhension du sujet. La dernière partie du chapitre a présenté deux grands types de traitement informatique sur les objets biologiques qui sont la recherche de similarité entre séquences et l'évolution des séquences biologiques.

Les concepts de base étant présentés, le chapitre suivant va s'atteler à présenter un état de l'art des méthodes computationnelles actuelles pour la construction des arbres phylogénétiques, en présentant les limites de ces approches pour lesquelles nous allons proposer de nouvelles solutions.

16

CHAPITRE TROIS

ÉTAT DE L' ART

Les différents processus biologiques sur lesquels s'appuie la phylogénie ont été introduits au chapitre précédent. Ce présent chapitre a pour objectif de faire un état des lieux de l'art des solutions qui sont actuellement utilisées pour reconstruire la phylogénie des gènes.

Nous commencerons par présenter les approches générales de construction d'arbres phylogénétiques puis, plus spécifiquement, celles de construction des arbres de gènes. Nous relèverons les limites des méthodes actuelles qui seront corrigées par la suite.

Il faut cependant noter que dans ce chapitre, tous les arbres phylogénétiques considérés seront binaires, c'est-à-dire que tous les noeuds internes d'un arbre possèdent deux enfants. Cette propriété ne constitue pas une limitation, car, tout arbre non binaire pourra être approximé par un arbre binaire.

3.1 Méthodes de construction d'arbres phylogénétiques

Il existe plusieurs techniques de construction d'arbres phylogénétiques. Ces méthodes basées sur des problèmes d'optimisation reposent sur plusieurs critères à savoir : (i) la distance entre les séquences, (ii) la parcimonie et (iii) vraisemblance. Nous commencerons par présenter la méthode naïve consistant à énumérer toutes les topologies d'arbre possible, puis nous décrirons les trois méthodes basées sur les critères ci-dessus.

3.1.1 Énumération des arbres

Cette méthode consiste à générer toutes les topologies d'arbre possibles étant donné un ensemble de gènes qui sont les feuilles de l'arbre, pour ensuite choisir parmi ces topologies, un arbre minimisant un critère donné. Par récurrence, on peut

17

CHAPITRE 3. ÉTAT DE L' ART

démontrer que pour n gènes, il existe C(n) = (2n-3)!

22n-2(n-2)! topologies d'arbre binaire

possibles.

Cette méthode a le mérite de générer tous les arbres possibles pour un ensemble de gènes donné. Néanmoins, son utilisation demeure limitée à cause de sa complexité qui croit à un rythme exponentiel en fonction du nombre de feuilles (C(30)estsuprieur10³⁸). Conséquemment, la recherche exhaustive ne peut se faire sur des données de grandes tailles.

3.1.2 Construction d'arbres à partir des distances entre feuilles

Cette approche prend en entrée une matrice de distance donnant les distances entre les gènes deux à deux, puis construit progressivement l'arbre phylogénétique des feuilles de l'arbre vers la racine. Nous décrivons ci-après deux méthodes basées sur cette approche [11] : la méthode Unweighted Pair Group Method with Arithmetic Mean (UPGMA) et la méthode Neighbour Joining (NJ).

3.1.2.1 UPGMA

UPGMA est un algorithme permettant, à partir d'une matrice de distance de construire un arbre enraciné en un sommet qui est le plus distant des feuilles. Cette méthode est simple et intuitive.

Les principales étapes de UPGMA sont:

1. Initialiser l'ensemble des noeuds (groupes ¹) de l'arbre à l'ensemble des gènes

2. De façon itérative, jusqu'à ce qu'il ne reste plus qu'un groupe :

~ Créer un nouveau groupe regroupant deux groupes les plus proches et retirer ces deux groupes de la liste des groupes.

~ Ajouter dans l'arbre un nouveau noeud correspondant au nouveau groupe, comme parent des deux noeuds correspondant aux groupes retirés.

L'arbre est construit des feuilles vers la racine, en ajoutant un noeud à chaque itération. À chaque étape, on définit la distance entre deux groupes Ci et Cj comme >

suit : dij = 1 pECi,qECj dpq. Si Ck = Ci ? Cj la distance entre Ck et un autre

|Ci||Cj|

groupe Cl est donnée par la formule récursive suivante : dklj = dil|Ci|+djl|Cj|

|Ci|+|Cj| .

La figure 3.1 montre un exemple d'application de UPGMA 3.1.2.2 Neighbour Joining

Neighbour Joining est un autre algorithme dédié à la construction des d'arbres phylogénétiques tenant compte des différences de vitesse d'évolution sur les branches

1. Un groupe est un ensemble de données partageant des caractéristiques communes.

CHAPITRE 3. ÉTAT DE L' ART

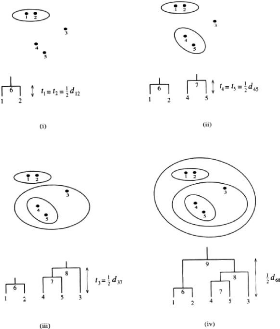
18

FIGURE 3.1 - Application de UPGMA

de l'arbre. La prise en compte des vitesses d'évolution utilise la notion d'arbre additif.

Un arbre phylogénétique non-enraciné sur n gènes est additif pour une matrice de distance D symétrique entre les n gènes si les arcs de l'arbre sont étiquetés avec des distances de sorte que pour chaque paire de feuilles (i, j) dans l'arbre, la somme des distances des arêtes du chemin de i à j est égale à D(i, j).

La méthode NJ se base sur l'hypothèse qu'il existe un arbre additif pour la matrice de distance donnée comme entrée, et produit un tel arbre non enraciné.

Les principales étapes de NJ sont :

1. Initialiser l'ensemble des noeuds (groupes) de l'arbre à l'ensemble des gènes

2. De façon itérative, jusqu'à ce qu'il ne reste plus qu'un groupe : ~ Créer un nouveau groupe Ck regroupant deux groupes Ci et Cj minimisant

19

CHAPITRE 3. ÉTAT DE L' ART

FIGURE 3.2 - Matrice et graphe additif

1 _P

la formule d(i,j) - (ri +rj) avec ri = k?L dik, et retirer ces deux

|L| - 2

groupes de la liste des groupes.

~ Ajouter dans l'arbre un nouveau noeud correspondant au nouveau groupe Ck, comme parent des deux noeuds correspondant aux groupes retirés, de sorte que les nouvelles arêtes de l'arbre sont étiquetés dik = 1 2(dij +ri -rj) et djk = dij - dik.

~ Pour chaque autre groupe C_m, recalculer la distance entre C_m et Ck suivant la formule: dkm = 1 2(dim + djm - dij)

La méthode NJ construit un arbre non-enraciné. Pour enraciner cet arbre, il suffit d'ajouter un gène très éloigné des autres gènes considérés (outgroup). La position du branchement de ce gène sur l'arbre indique la position de la racine de l'arbre.

FIGURE 3.3 - Enraciner un arbre à l'aide d'un outgroup.

Une autre stratégie d'enracinement d'arbre est de considérer comme racine le milieu d'un plus long chemin dans l'arbre (hypothèse de l'horloge moléculaire).

20

CHAPITRE 3. ÉTAT DE L' ART

3.1.3 Les méthodes de parcimonie

L'approche par parcimonie consiste à rechercher un arbre qui minimise le nombre de modifications évolutives (mutations, délétions, ou insertions) pour passer d'une séquence à l'autre sur les branches de l'arbre. Les deux principaux algorithmes permettant de calculer le nombre de modifications évolutives induites par un arbre donné sont celui de Fitch [13] et Sankoff [6].

Le principe de l'algorithme classique de Fitch est le suivant :

1. Initialiser le nombre de modifications C à 0.

2. Pour chaque noeud k de l'arbre, en allant des feuilles vers la racine (parcours

postfixe des noeuds)

~ Si k est une feuille, poser Rk = {étiquette de k}

~ Si k n'est pas une feuille,

~ Calculer Inters = Ri n R , où i, j sont des enfants de k ;

~ Si Inters == Ø, poser Rk = Ri ^U R et incrémenter C de 1

~ Sinon, poser Rk = Inters

L'algorithme de parcimonie pondérée de Sankoff est plus général que celui de Fitch. Il ne calcule pas juste le nombre de modifications, mais considère un poids S(a; b) pour la substitution d'une lettre a en b. Il étiquette les noeuds internes de l'arbre de sorte à minimiser le poids total de l'arbre. L'étiquetage des noeuds est déduit par récurrence, en calculant l'étiquette d'un noeud à partir des étiquettes de ses noeuds enfants.

Les principales étapes des méthodes de parcimonie sont :

1. Calculer un alignement multiple des séquences (gènes)

2. Pour chaque colonne de l'alignement, trouver un arbre minimisant le nombre de modifications évolutives pour cette colonne sur les branches de l'arbre. La recherche de l'arbre se fait par énumération des arbres, ou en utilisant des heuristiques d'exploration de l'espace de recherche qui évite d'énumérer tous les arbres.

3. À partir de l'ensemble des arbres obtenus, trouver un super-arbre qui minimise la somme totale des nombres de modifications évolutives pour toutes les colonnes de l'alignement.

3.1.4 Méthodes de maximum de vraisemblance

Le maximum de vraisemblance est une méthode probabiliste permettant de trouver la séquence de noeuds internes la plus probable. Les hypothèses de cette méthode sont : Le processus de substitution d'une séquence en une autre suit un modèle

21

CHAPITRE 3. ÉTAT DE L' ART

probabiliste dont on connaît l'expression mathématique. Les sites évoluent indépendamment les uns des autres; Les sites évoluent selon la même loi. Les taux de substitution ne changent pas au cours du temps le long d'une branche. Ils peuvent varier entre branches.

3.2 Construction des arbres de gènes

Les arbres de gènes présentés dans la littérature sont tous des approximations de la réalité car la modélisation qui conduit à leur construction ne prend pas en compte toute la structure des gènes. En particulier, les méthodes de construction d'arbres de gènes actuelles ne prennent en compte qu'une seule des protéines (généralement la plus longue) de chaque gène. Une partie des informations contenues dans les gènes est ainsi négligée.

3.2.1 Exemple de construction d'arbres de gènes - Ensembl-Compara

Les arbres de gènes de la base de données Ensembl sont construits suivant une méthode décrite dans [31]. La figure 3.4 décrit cette méthode composée de sept étapes pour la construction des arbres de gènes.

Nous détaillons ci-après le principe des sept étapes de la méthode de Ensembl-Compara pour la construction des arbres de gènes.

1. Définition des données de protéines : Pour chaque gène codant dans une espèce, considérer la plus longue protéine produite par le gène.

2. Basic Local Alignment Search Tool Protein (BLASTP)² : Chaque protéine est interrogée à l'aide de WU BLASTP contre la base de données de protéines de chaque espèce, y compris celle de l'espèce à laquelle la protéine appartient.

3. Construction du graphe : La relation entre deux protéines est conservée si elle satisfait soit à un meilleur partenaire réciproque par BLASTP ou à un score de BLASTP supérieur à 0.33. On construit alors un graphe dans lesquels, les noeuds correspondent aux protéines et les arêtes aux relations conservées.

4. Regroupement : On extrait à partir du graphe, les composantes connexes. Chaque composante connexe représente une famille de gènes. Si une famille

2. BLASTP est un programme d'alignement de protéines permettant, étant donnée une séquence protéique, d'autres séquences similaires à elle dans une base de données de séquences protéiques.

22

CHAPITRE 3. ÉTAT DE L' ART

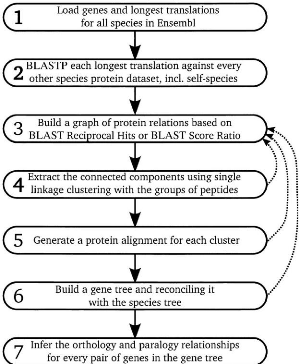
FIGURE 3.4 - Méthode de Ensembl-Compara pour la construction des arbres de gènes

23

CHAPITRE 3. ÉTAT DE L' ART

de gènes a plus de 750 membres, les étapes 3 et 4 sont répétées en augmentant le seuil de conservation de relation entre deux protéines.

5. Alignements multiples : Les protéines d'une même famille de gènes sont alignées à l'aide du programme "Multiple Sequence Comparison by Log-Expectation" (MUSCLE) [8, 9] pour obtenir un alignement multiple.

6. Arbre de gène et réconciliation : L'alignement multiple des protéines d'une famille de gènes et l'arbre des espèces sont donnés en entrée au programme de construction d'arbres "Tree Building guided by Species Tree" (TreeBeST) ⁴, pour construire l'arbre des gènes de la famille. L'arbre de gènes est alors réconcilié avec l'arbre d'espèces afin d'étiqueter comme duplication ou spéciation.

7. Inférence des orthologues et paralogues : Les arbres de gènes obtenus sont finalement aplatis en des tables d'orthologues et de paralogues décrivant les relations d'homologie entre paires de gènes.

De manière générale, tous les arbres de gènes disponibles dans les bases de données et dans la littérature sont construits sur ce modèle.

3.2.2 Limites des arbres de gènes actuels

Dans cette section, nous illustrons les limites des arbres de gènes construits par la méthode d'Ensembl Compara. Suivant cette méthode, seule la protéine 3 du gène décrit dans la figure 3.5 devrait être considérée pour la construction de l'arbre des gènes de la famille à laquelle le gène appartient. En effet, cette protéine est la plus longue. Elle possède quatre exons sur les six que compte le gène. Cependant, bien qu'étant la plus longue, elle ne couvre pas les exons E2 et E3 qui ne seront jamais considérés par la suite, alors qu'ils sont présents dans les protéines 1 et 2 qui sont produites par le même gène.

3.3 Conclusion sur l'état de l'art

En résumé, nous avons passé en revue les méthodes les plus utilisées pour la construction d'arbres phylogénétiques. En particulier, pour les arbres de gènes, nous

3. MUSCLE est un programme d'alignement multiple de séquences. MUSCLE peut aligner des centaines de séquences en quelques secondes. http://www.drive5.com/muscle/

4. TreeBeST est un programme polyvalent qui construit, manipule et affiche des arbres phylogénétiques. Il est particulièrement destiné à la construction d'arbres de gènes avec un arbre d'espèce connu.

CHAPITRE 3. ÉTAT DE L' ART

24

FIGURE 3.5 - Produit de l'épissage alternatif

avons expliqué les limites des méthodes de construction actuelles qui font abstraction d'informations importantes portant sur la structure des gènes. Dans le chapitre suivant, nous allons proposer une approche qui permet d'adresser ce problème.

25

CHAPITRE QUATRE

MÉTHODOLOGIE ET

IMPLÉMENTATION

Ce chapitre présente la méthodologie que nous proposons pour la construction des arbres de gènes en tenant compte de toutes les protéines issues des gènes. D'abord, nous introduisons formellement un nouveau modèle d'évolution de protéines à l'intérieur d'un arbre de gènes. Ensuite, nous étendons la notion de réconciliation afin de définir un problème d'optimisation qui consiste à reconstruire un arbre de protéines et un arbre de gène optimal, étant donné l'arbre des espèces. Nous terminons, en proposant une heuristique pour la résolution de ce problème, et une implémentation de cette heuristique.

4.1 Modèle d'évolution des protéines et problème de réconciliation

Dans un premier temps, nous commençons par introduire l'idée de base du nouveau modèle d'évolution de protéines que nous proposons. Puis, dans un second temps, nous décrirons formellement le modèle et les problèmes d'optimisation associés.

4.1.1 Idée de base

Le modèle d'évolution de protéines que nous proposons s'appuie sur l'hypothèse selon laquelle toutes les protéines sont issues d'un ancêtre commun et ont évolué au fil du temps au travers de quatre types d'événements qui sont : duplication 1,

1. Duplication: une protéine a donné naissance à deux protéines par le biais d'une duplication de gènes

26

CHAPITRE 4. MÉTHODOLOGIE ET IMPLÉMENTATION

spéciation ², création ³, et perte ⁴ de protéines. La figure 4.1 montre un exemple d'arbre d'évolution d'un ensemble de protéines. On observe qu'il y a deux créations et trois pertes de protéines dans cet arbre.

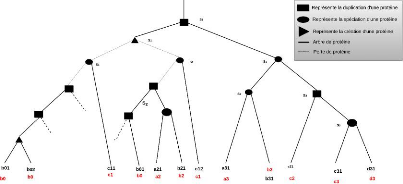
FIGURE 4.1 - Arbre de protéines étiqueté avec les événements de spéciation, duplication, création et perte

4.1.2 Définitions formelles

Dans cette section, 8 représente, l'ensemble des espèces, g représente l'ensemble des gènes d'une famille de gènes et P représente l'ensemble de protéines produites par les gènes d'une famille. On définit sur ces ensembles des fonctions de correspondance : s : g - 8 qui à tout gène fait correspondre l'espèce à laquelle il appartient et g : P - g qui à toute protéine fait correspondre le gène qui l'a produit. Les trois ensembles 8, g et P sont tels que 8 = {s(x) : x E g} et g = {g(x) : x E P}, c'est à dire que les fonctions s et g sont surjectives.

Arbres phylogénétiques : Tous les arbres phylogénétiques considérés sont enracinés et binaires. Un arbre T pour un ensemble L est un arbre binaire enraciné dont l'ensemble des feuilles est L. L'ensemble des feuilles d'un arbre T est notée G(T)

2. Spéciation : une protéine a donné naissance à deux protéines par le biais d'une spéciation d'espèce.

3. Création : une protéine est apparue à un certain moment dans un gène

4. Perte : un gène a perdu la fonctionnalité de produire une protéine à un certain moment

27

CHAPITRE 4. MÉTHODOLOGIE ET IMPLÉMENTATION

et l'ensemble des sommets de T est noté V(T). Étant donné un noeud x E V(T), le sous-arbre complet⁵ de T enracinée en x est notée T[x]. Le plus proche ancêtre commun (en anglais, least common ancestor (lca)) d'un sous-ensemble L^' de £(T) dans T, notée lcaT(L^'), est l'ancêtre commun à toutes les feuilles L^' qui est le plus éloigné de la racine de T. Étant donné un noeud interne x de T, les deux enfants de x sont arbitrairement désignés par xl et x_r (pour left et right, en anglais).

Arbres de protéines, gènes, et espèces : Nous notons S un arbre des espèces pour l'ensemble S, G est un arbre des gènes pour l'ensemble G, et P un arbre des protéines pour l'ensemble P.

La fonction de correspondance s est étendue pour devenir une fonction de V(G) E G vers V(S) comme suit : si x est un noeud interne de G, alors s(x) = lcaS({s(x^') : x' E £(G[x])}), c'est à dire que l'image d'un noeud x E V(G) dans V(S) est le plus proche ancêtre commun, dans l'arbre S, de toutes les images des feuilles du sous-arbre G[x].

De même, nous étendons la fonction de correspondance g pour qu'elle devienne une fonction de V(P) vers V(G) : si x est un noeud interne de P, alors g(x) = lcaG({g(x^') : x^' E £(P[x])}).

Réconciliation par LCA : Chaque noeud interne de l'arbre G représente un gène ancestral au moment d'un événement de spéciation (Spec) ou de duplication (Dup) de gènes. La réconciliation par LCA de G avec S est une fonction d'étiquetage lG : V(G) - £(G) ? {Spec, Dup} tels que l'étiquette d'un noeud interne x de G est lG(x) = Spec si s(x) =6 s(xl) et s(x) =6 s(x_r), et sinon lG(x) = Dup.

Nous étendons la notion de réconciliation aux arbres de protéines comme suit : chaque noeud interne de l'arbre P représente une protéine ancestrale au moment d'un événement de spéciation (Spec), de duplication (Dup) ou de création (Creat) de protéines. La réconciliation par LCA de P avec G est une fonction d'étiquetage lP : V(P) - £(P) ? {Spec, Dup, Creat} tels que l'étiquette d'un noeud interne x de P est lP (x) = Spec si g(x) =6 g(xl) et g(x) =6 g(x_r) et lG(g(x)) = Spec, sinon lP (x) = Dup si g(x) =6 g(xl) et g(x) =6 g(x_r) et lG(g(x)) = Dup, et sinon lG(x) = Creat .

La figure 4.2 illustre la réconciliation de l'arbre des protéines de la figure 4.1 (à considérer comme non-étiqueté) avec l'arbre de gènes de la figure 4.3, ce dernier ayant été réconcilié avec l'arbre d'espèces illustré à la figure 4.4. Sur la figure 4.1, on peut noter que, d'une part les créations de protéines correspondent uniquement aux noeuds placés sur les branches de l'arbre de gènes et d'autre part il n'y a que

5. Un sous-arbre enraciné en un noeud x d'un arbre T est complet si il contient toutes les feuilles descendantes de x dans T.

28

CHAPITRE 4. MÉTHODOLOGIE ET IMPLÉMENTATION

les arbres enracinés en un noeud de création qui peuvent contenir deux protéines du même gène.

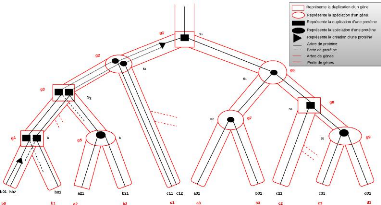
FIGURE 4.2 - Exemple de réconciliation d'arbres de protéines avec arbre de gènes

Coût de réconciliation : Le coût de réconciliation par LCA de l'arbre G avec l'arbre S est le nombre de noeuds de duplication et d'événements de perte de gènes dans G résultant de la réconciliation par LCA de G avec S.

Par extension, le coût de réconciliation par LCA de l'arbre P avec l'arbre G est le nombre de noeuds de création et d'événements de perte de protéines dans P résultant de la réconciliation par LCA de P avec G.

Le coût de double réconciliation de G avec P et S est la somme du coût de réconciliation par LCA de G avec S et du coût de réconciliation par LCA de P avec G.

Les définitions précédentes nous permettent maintenant d'introduire le problème d'optimisation dont l'objectif est de reconstruire un arbre de gènes optimal G, étant donné l'arbre des protéines P et l'arbre d'espèces S.

Problème: MINDRGT (POUR "MINIMUM DOUBLE RECONCILIATION GENETREE" EN ANGLAIS) :

Entrées : Un arbre d'espèce S pour un ensemble d'espèces S ; un arbre de protéines P pour un ensemble de protéines P

Sortie : Un arbre de gènes G pour G = {g(x) : x E L(P)} tel que le coût de double

29

CHAPITRE 4. MÉTHODOLOGIE ET IMPLÉMENTATION

FIGURE 4.3 - Arbre de gènes étiqueté

FIGURE 4.4 - arbre d'espèces

30

CHAPITRE 4. MÉTHODOLOGIE ET IMPLÉMENTATION

réconciliation de P vers G et S est minimum.

Le problème d'optimisation MinDRGT suppose que l'arbre des protéines P est connu. Dans le cas où l'arbre des protéines n'est pas entièrement connu, mais un ensemble de sous-arbres partiels P1. . . P, couvrant tout l'ensemble P est connu, le problème devient :

Problème: MINDRPGT (POUR "MINIMUM DOUBLE RECONCILIATION PROTEIN AND GENE TREES" EN ANGLAIS) :

Entrées : Un arbre d'espèce S pour un ensemble d'espèces S ; un ensemble de sous-arbres de protéines P1 . . . P, couvrant l'ensemble des protéines P

Sortie : Un arbre de protéines P tel que chaque Pi, 1 = i = k, est un sous-arbre de P, et un arbre de gènes G pour G = {g(x) : x E L(P)} tel que le coût de double réconciliation de P vers G et S est minimum.

La méthodologie de construction d'arbre de gènes présentée dans la section suivante consiste à construire un ensemble de sous-arbres P1 . . . P, couvrant l'ensemble des protéines P, puis à utiliser une solution heuristique⁶ du problème MinDRPGT pour reconstruire l'arbre de protéines P et l'arbre de gènes G.

4.2 Méthodologie : Processus à sept étapes

L'approche méthodologique utilisée pour la construction des arbres de gènes en tenant compte de toutes les protéines de chaque gène est basée sur une solution heuristique gloutonne pour résoudre le problème MinDRPGT. L'approche méthodologique est résumée dans un processus à sept étapes illustrées à la figure 4.5.

4.2.1 Étape 1 : Définition du jeu de données

La première étape consiste à définir l'ensemble des protéines de la famille de gènes dont on veut reconstruire l'arbre. Par définition, une famille de gène est composée d'un gène donné, tous ses orthologues, ses paralogues intra-spécifiques (au sein de la même espèce) et ses paralogues inter-spécifiques (dans des espèces différentes). Puis, dans la famille de gène, nous retenons uniquement les gènes produisant au moins une protéine. Pour chaque protéine produite par un gène de la famille, nous

6. L'analyse de la complexité des problèmes MinDRPT et MinDRPGT, et la conception de solution algorithmique exacte, le cas échéant, seront approfondie dans le cadre d'une thèse de doctorat.

3

4

CHAPITRE 4. MÉTHODOLOGIE ET IMPLÉMENTATION

Définition du jeu de donnée (génes et séquences codantes)

NJ'

2 r Alignement multiple de toutes les séquences codantes A l'aide de MACSE

Calcul d'une matrice de similarité â l'aide de FsePA

Regroupement avec chevauchement des

--)

séquences codantes

C'oustructiou du groupe de référence

Création des sous-arbres A l'aide de TreeBest

Construction de l'arbre de gènes et de protéines

31

FIGURE 4.5 -- Processus de construction d'arbre de gènes à sept étapes

32

CHAPITRE 4. MÉTHODOLOGIE ET IMPLÉMENTATION

retenons sa séquence codante, c'est-à-dire la séquence d'ARNm qui a été traduite pour obtenir la protéine.

4.2.2 Étape 2 : Alignement multiple de toutes les séquences codantes

Afin de pouvoir avoir une mesure de similarité entre les séquences codantes, nous procédons à un alignement multiple des séquences. Pour ce faire, nous utilisons le programme MACSE (Multiple Alignment of Coding SEquences Accounting for Frameshifts and Stop Codons) [29], qui est actuellement l'unique programme d'alignement multiple de séquences codantes prenant en compte les décalages de cadre de lecture dans la traduction⁷ en protéine. Contrairement à l'approche des méthodes actuelles de construction d'arbre de gènes, nous avons choisi d'aligner les séquences codantes plutôt que les protéines elles-mêmes, afin de tenir compte des phénomènes de décalage de cadre de lecture qui induisent des alignements erronés des séquences protéiques.

4.2.3 Étape 3 : Calcul de la matrice de similarité

Une fois les alignements effectués, nous calculons le score de similarité de chaque paire de séquences. On obtient comme résultat une matrice de similarité. Pour le calcul du score de similarité, nous utilisons un schéma de score tenant compte simultanément de l'échelle des nucléotides et celle des protéines définies dans [20]. Le but est de tenir compte à la fois des décalages de cadre de lecture, et des longueurs des différences, entre les protéines, issues de ces décalages. Les scores de similarités sont normalisés en les divisant par les longueurs des alignements.

4.2.4 Étape 4 : Regroupement avec chevauchement des séquences codantes

NB : il existe une bijection entre l'ensemble des protéines et l'ensemble des séquences codantes. Par la suite on utilisera le terme protéine par souci de simplification.

7. Les séquences codantes sont traduites en protéines en considérant un cadre de lecture des triplets de nucléotides consécutifs (codons) dans la séquence pour les traduire en acides aminés. Le décalage du cadre de lecture résulte d'un changement du positionnement du cadre de lecture d'un nombre de nucléotides non multiple de 3 conduisant à un changement de traduction des codons, et à des séquences protéiques différentes.

33

CHAPITRE 4. MÉTHODOLOGIE ET IMPLÉMENTATION

4.2.4.1 Définition du regroupement

Le regroupement appelé en anglais clustering [21] est une méthode de classification non supervisée, l'objectif étant de découvrir les regroupements naturels d'un ensemble de motifs, de points ou d'objets quelconques, ou dans notre cas des protéines. En pratique, la plupart des scientifiques décrivent un groupe en tenant compte de son homogénéité interne et de son hétérogénéité externe. En d'autres termes, les motifs au sein du même groupe devraient être similaires, tandis que les motifs dans différents groupes ne le devraient pas. Le regroupement est utilisé pour grouper les séquences de protéines en sous-familles en fonction de leurs similarités, ce qui fournira par ailleurs des indices importants sur les caractéristiques générales des familles de protéines. Cette approche de regroupement est également utile pour inférer la fonction biologique des protéines en déterminant leur appartenance à des familles de protéines bien connues et annotées.

4.2.4.2 Problème de regroupement dans le cas présent

Le modèle de regroupement que nous proposons s'appuie sur le modèle d'évolu-tion de protéines présenté dans la section précédente. Nous construisons un ensemble de groupes de protéines, tel que pour tout groupe C, le plus proche ancêtre commun de deux protéines du groupe ne doit jamais correspondre à une création dans l'arbre des protéines étiqueté.

La figure 4.6 illustre un exemple d'arbre de protéines étiqueté dans lequel le noeud 6 est une création de protéines qui conduit à deux protéines (1 et 2) appartenant au même gène A. À l'inverse, la création au niveau du noeud 9 va produire des protéines qui appartiennent dans un premier temps au même gène ancestral, mais par la suite de l'évolution, à des gènes différents à cause de la spéciation et de la duplication qui ont mené à trois gènes différents. Les protéines 1, 2, 4 appartiennent donc au même gène A, la protéine 3 au gène B, et les protéines 5, 11 au gène C.

L'ensemble des groupes de taille maximum en termes d'inclusion que l'on voudrait obtenir est {(1, 3, 11), (2, 3, 11), (4, 5)} dans lequel chaque groupe contient au plus une protéine par gène.

Cependant, dans notre cas, l'arbre des protéines et son étiquetage ne sont pas connus et nous cherchons à les reconstruire, en même temps que l'arbre des gènes. Par conséquent, nous simplifions le problème de regroupement des protéines au problème qui consiste à former un ensemble de groupes dans lesquels chaque groupe contient une seule protéine par gène, tout en permettant qu'une protéine puisse se retrouver dans plusieurs groupes. Ceci nous amène donc à définir une méthode de regroupement avec chevauchement ⁸ pour créer des groupes

8. le regroupement avec chevauchement est une technique de regroupement qui permet qu'un

34

CHAPITRE 4. MÉTHODOLOGIE ET IMPLÉMENTATION

FIGURE 4.6 - Extrait d'arbre de protéines

qui respectent nos contraintes.

Les principales méthodes de regroupement de protéines présentes dans la littérature sont décrites à la figure 4.7. Elles sont basées sur les méthodes par partition-nement [23], les méthodes hiérarchiques [7] et les méthodes utilisant des graphes [30]. Toutes ces méthodes approchent le problème posé en 4.2.4.2, mais présentent des limites majeures qui nous ont conduits à développer notre propre méthode de regroupement.

D'abord, les méthodes de regroupement hiérarchique, bien qu'étant les plus utilisées en bio-informatique du fait de leur complexité quadratique, conduisent automatiquement à des regroupements sans chevauchement. Ensuite, les approches par partitionnement quant à elles sont très efficaces, car chaque élément à classer est mis dans la meilleure classe préexistante. Mais leur principale limite est qu'elles exigent

élément puisse appartenir à plus d'un groupe, par opposition au regroupement sans chevauchement qui ne le permet pas

35

CHAPITRE 4. MÉTHODOLOGIE ET IMPLÉMENTATION

FIGURE 4.7 - Les trois principales catégories d'algorithmes utilisées pour le regroupement des séquences de protéines

de connaître au préalable le nombre de groupes, alors que dans notre cas ce nombre doit être découvert. Enfin, les approches basées sur la théorie de graphe conduisent également à des regroupements sans chevauchement. Bien qu'il existe des cas rares où l'on peut obtenir des regroupements avec chevauchement.

4.2.4.3 Regroupement avec chevauchement hiérarchique

Idée de base. L'idée de base de notre méthode de regroupement avec chevauchement est de proposer une version modifiée du regroupement hiérarchique (qui est à la base du regroupement sans chevauchement) pour créer des regroupements avec chevauchement. Tel que chaque groupe contient au plus une protéine par gène tout en permettant qu'une protéine puisse appartenir à plus d'un groupe. La figure 4.8 illustre graphiquement la différence majeure entre le regroupement sans chevauchement et le regroupement avec chevauchement que nous choisissons comme approche.

Présentation globale du modèle Soit n le nombre de protéines et á un seuil de similarité. Initialement, chaque protéine forme un groupe. La méthode va, de manière récursive, choisir à chaque étape les deux groupes les plus proches, les fusionner afin d'en former un nouveau. On choisit deux groupes à fusionner si et seulement si le score de similarité entre eux est inférieur au seuil á. Le score de similarité pour deux groupes A et B est calculé ainsi comme suit (D étant la matrice de similarité calculé à l'étape 3) :

A' ? A - B

36

CHAPITRE 4. MÉTHODOLOGIE ET IMPLÉMENTATION

FIGURE 4.8 - Illustration présentant la différence entre le regroupement avec chevauchement et le regroupement sans chevauchement

B' B - A

Si Card(A^') == 0 or Card(B^') == 0 Alors

D(A^',B^') oc

Sinon _{>I >I}

1

D(A^', B') yEB D(x, y)

Card(A').Card(B') xEA

La figure 4.9 présente un exemple d'application de l'algorithme de regroupement avec chevauchement sur sept protéines de cinq gènes.

Algorithme détaillé de regroupement avec chevauchement hiérarchique Définition des entrées

DistanceMatrix D : est une matrice de similarité qui contient les mesures de similarité entre chaque paire de séquences. C'est donc une matrice symétrique. Les valeurs de cette matrice sont normalisées entre 0 et 1, avec 1 représentant la plus grande similarité;

SimilarityLevel á : est une valeur de similarité comprise entre 0 et 1;

Header h : est un tableau associatif, qui associe à chaque gène la liste de ses protéines. Il est utile pour satisfaire la contrainte que chaque groupe doit contenir au plus une protéine de chaque gène.

L'algorithme 4.1 décrit formellement la méthode.

4.2.5 Construction d'un groupe de référence

Une fois les groupes obtenus, on choisit un groupe de référence de cardinalité maximale. Si la cardinalité de ce cluster est strictement inférieure au nombre de

CHAPITRE 4. MÉTHODOLOGIE ET IMPLÉMENTATION

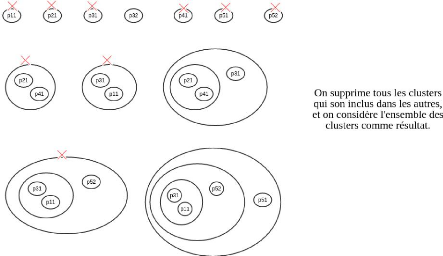
37

FIGURE 4.9 - Exemple d'application de l'algorithme de regroupement avec chevauchement sur sept protéines de cinq gènes. Les cinq gènes sont p1, p2 et p4 ayant chacun une protéine, et p3 et p5 ayant chacun deux protéines.

38

CHAPITRE 4. MÉTHODOLOGIE ET IMPLÉMENTATION

Algorithm 4.1 Soft Clustering

1: procedure CLuTTERING(DistanceMatrix D, SimilarityLevel á, ListeDesClus-ters listeCluster h)

2: groupeBanis ? []

3: loop :

4: i, j, min ? ChoisirPlusPetitEltV alide(D, groupeBanis, listeCluster, á)

5: if (i == -1 or j == -1 or min == +8) then

6: ConsiliderGroupe.

7: else

8: listeCluster ? listeCluster ? [listeCluster(i), listeCluster(j)]

9: groupeBanis ? groupeBanis ? [i,j]

10: Ajouter une ligne et une colonne à la matrice D

11: n ? nombreLinge(D) + 1

12: miseAJourValeur(i, j, n).

13: goto loop.

14: end if

15: ChoisirPlusPetitEltValide(D, groupeBanis, listeCluster, á) :

16: for i = 1 to nombreDeLigne(D) do

17: for j = i + 1 to nombreDeColonne(D) do

18: if (listerCluster[i] ? listeCluster[j] ?/ groupeBanis) then

19: if ((? p1 ? listeCluster[i] and ? p2
? listeCluster[j]) tel que gene(p1) =6 gene(p2)) and V aleurDeSimilarite(listeCluster[i], listeCluster[2], á)) then

20: Return (i,j,D[i,j])

21: else

22: Continue

23: end if

24: else

25: Continue

26: end if

27: end for

28: end for

29: Return (-1, -1, +8)

39

CHAPITRE 4. MÉTHODOLOGIE ET IMPLÉMENTATION

30: ValeurDeSimilarite(clusterI, clusterJ, á) :

31: clusterI^' ? clusterI - ClusterJ

32: clusterJ^' ? clusterJ - ClusterI

33: flag ? TRUE

34: for i = 1 to longeur(clusterI^') do

35: for j = i + 1 to longeur(clusterJ^') do

36: if (D[i,j] >= á) then

37: flag = FALSE

38: end if

39: end for

40: end for

41: Return flag

42: miseAJourValeur(i,j, n) :

43: B ? sequence(n) //

44: for i = 1 to n do

45: A ? sequence(i)

46: A^' ? A - B

47: B^' ? B - A

48: if (Card(A) == 0 or Card(B) == 0) then

49: D(A^', B^') ? 8

50: else _{>I >I}

51: D((A^', B^') ? 1 y?B D(x, y)
Card(A).Card(B) x?A

52: end if

53: end for

54: Return D

55: ConsiliderGroupe :

56: for i = 1 to longeur(listeCluster) do

57: if (?k ? [1, longeur(listeCluster)] avec k =6 i) and listeCluster[i] ? listeCluster[k] then

58: listeCluster ? listeCluster - listeCluster[i]

59: end if

60: end for

61: end procedure

CHAPITRE 4. MÉTHODOLOGIE ET IMPLÉMENTATION

gènes, on le complète en lui ajoutant une protéine de chaque gène non représenté dans ce groupe. La protéine d'un gène non représenté dans le groupe est choisie de sorte à minimiser le coût moyen de similarité entre cette protéine et les protéines présentes dans le groupe. L'algorithme 4.2 décrit le processus de construction du groupe de référence le cas échéant.

Algorithm 4.2 AugmenterGroupe

1: procedure AUGMENTERGROUPE(C_ref, G)

2: Entrées : Cref groupe de référence, G = {G1, ..., Gl} Collection des ensembles de protéines des l gènes non représentés dans Cref

3: if (E = Ø) then

4: Terminer

5: else

P = argmax{D(C_ref ,P )}

6: P _{??i?{1,...,l}} Gi . D étant la distance entre p et le groupe Cref

7: G_p = gène auquel p appartient

8: Cref = Cref U {P}

9:

G = G \ {GP }

1: AugmenterGroupe(C_ref, G)

2: end if

3: end procedure

40

À la fin de cette procédure, on obtient une liste de groupes, dans laquelle un groupe, le groupe de référence, contient une protéine de chaque gène et chaque protéine du groupe de référence n'appartient à aucun autre groupe, et les groupes sont tous deux à deux disjoints. L'étape suivante consiste à créer un arbre de protéines par groupe et de fusionner tous les arbres en un seul super-arbre de protéines.

4.2.6 Étape 6 : Création des arbres de protéines pour les groupes

Rendu à cette étape, on dispose d'un ensemble de groupes, il s'agit de créer un arbre par groupe. Pour ce faire, on utilise le programme TreeBest[10]. L'entrée de ce programme doit être un ensemble de séquences alignées. Pour ce faire, on utilise encore MACSE pour aligner les séquences codantes du groupe avant de passer l'alignement multiple obtenu à TreeBest. La sortie du programme est un arbre au format Newick⁹

9. Newick est le nom d'un format de fichier utilisé en bio-informatique pour décrire un arbre phylogénétique.

41

CHAPITRE 4. MÉTHODOLOGIE ET IMPLÉMENTATION

4.2.7 Étape 7 : Construction de l'arbre de protéines et de l'arbre des gènes

Disposant d'une forêt de l arbres pour l groupes telle que l'un des arbres est considéré comme l'arbre de référence (celui contenant une protéine pour chacun des gènes), l'objectif de cette étape est de fusionner les arbres en un seul arbre.

Les principales phases de l'algorithme de cette étape sont :

1. Définir l'arbre de gènes G comme égal à l'arbre de référence (contenant une protéine pour chacun des gènes)

2. Initialiser le super-arbre de protéines P comme égal à l'arbre de référence

3. De façon itérative jusqu'à fusionner tous les arbres

~ Choisir l'arbre Tk avec k E [1, l] tel que .C(Tk) n .C(P) est maximal.

~ Construire l'arbre induit T = Tk|L(Tk)\L(P

~ Calculer le noeud de P, x = lcaP{P1 E .C(P) | ?P2 E (.C(Tk)\.C(P)),g(p1) =

g(p2)}

La figure 4.10 montre un exemple d'application de l'algorithme glouton de concaténation d'une forêt d'arbres. L'arbre de référence étant l'arbre ayant pour racine étiqueté par 1.

4.3 Implémentation

Afin d'implémenter le modèle précédent, le langage python à été choisi pour deux raisons. D'une part, c'est un excellent langage de script et d'autre part, c'est l'un des langages les plus utilisés en bio-informatique, pour lequel de nombreuses bibliothèques sont disponibles. Chacune des sept étapes a été implémentée séparément, mais de telle sorte que chaque étape rende des résultats sous format réutilisable pour les étapes suivantes.

Les données ont été récupérées de la base de données de EnsemblCompara, version 84 et de NCBI, nous avons utilisé PyCongent, une API Python pour la récupération de données de la base de données Ensembl. Nous avons utilisé la bibliothèque numpy pour la manipulation des structures de données optimisées pour les tableaux et matrices.

42

CHAPITRE 4. MÉTHODOLOGIE ET IMPLÉMENTATION

FIGURE 4.10 - Application de l'algorithme glouton de fusion de 6 arbres. Les arbres sont greffés à l'arbre de référence par des créations matérialisées sur la figure par des triangles au fond noir.

43

CHAPITRE CINQ

ÉTUDE DE CAS

Afin de tester le modèle, les méthodes et les implémentations décrits précédemment, nous avons fait des études de cas. Pour nos tests, nous avons retenu les espèces suivantes : la vache, l'humain, la souris, le fugu, le zebrafich et le poulet, représentatives de l'ensemble des espèces vertébrés.

5.1 Étude de cas de la famille The Myelin-Associated Glycoprotein (MAG)

Le premier cas d'étude est réalisé sur la famille de gène MAG [27, 3]. Elle a été largement étudiée dans la littérature [3]. En raison du fait que les gènes de cette famille subissent l'épissage alternatif, ce cas constitue un candidat parfait pour tester notre algorithme. Le tableau 5.1 récapitule les informations sur cette famille MAG.

	Nom de la famille	Source de données	Nombre de gènes	Nombre de protéines
1	MAG	Ensembl	28	70

TABLE 5.1 - Données utilisées pour l'étude de cas de la famille MAG

La figure 5.1 présente l'arbre de référence (arbre de gènes) sur lequel viendront se greffer les arbres provenant des groupes restants. Notre arbre de gène partage 18 protéines sur les 28 au total avec celui de Ensembl et a un plus petit coût de réconciliation plus faible. Après réconciliation avec l'arbre d'espèce, l'arbre de gène obtenu comporte 5 pertes de gènes et 14 duplications. La figure 5.2 présente l'arbre de gènes construit par Ensembl-Compara, qui compte 12 pertes et 20 duplications. Ce cas permet de montrer que notre méthode permet la construction d'arbres de gènes de coût de réconciliation optimaux

CHAPITRE 5. ÉTUDE DE CAS

--.._ ~.,.,. _--..---

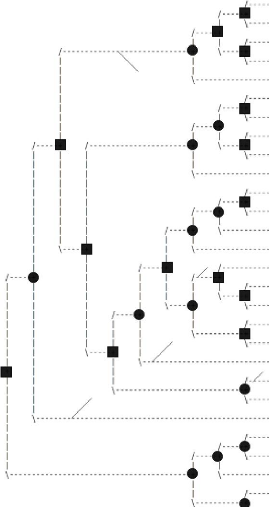
- i

1-

-------

-

^L

I I I

I I k

I

J^r- --

I

¹1^.

f

k-

EN5F 9668$321977 ENSFVG4UCW rZU r3 ENSP6E069323329 EN5PMEMA13961 FNSMJSFIE3E0I37i87 ENSPUd5I1d55I7 ENSPO6659A161Z6 ENSMJSPOINEBUDA720 ENSMJSPOME4130O32 ENSETAF60005.196'51 EN5F 96690345243 EN5P! !EW1Z3a1 ENSMUSNO0E0505592 ENSETPF900E6304195 ENSIIR8Ad354A, kriSPOEUUDA15ZEU ENSP46$50A7323.S EN5B7APOIMEi 6424 ENSEARMIE+3E4a.54Z3 ENSBTANO.5 0522603 EN51115P500 6113245 FN5RTPPAEt7F.0013174F1 ENSLAAF'9d9E412aà12 EN5P26699073245 EN5MJ5PR M1399$1 ENSR1AP!Eb64I238a EN56ARP600E01196615 EN5MLP999E6823556

44

FIGURE 5.1 -- Arbre de gènes de la famille MAG obtenu avec notre méthode

45

CHAPITRE 5. ÉTUDE DE CAS

4 -ENSDARP00000126612

· ENSTRUPO0000006444

- ENSBTAP00000011656

·

--
·E N S BTA P00000049B61

GEN SP00000401502

.' ENSP00000262262

~
·E N S BTAP00000055070

· ENSMUSP00000113245 -ENSMUSP00000058875 .#
·ENSMUSP00000004728

· EN SBTAP00000031748

/
·ENSMUSP00000032667
_.--ENSPOO000413861

· ENSP00000323328

· ENSP00000291707 \
·EN5P00000321077

· ENSBTAP00000022603

· ENSP00000354090

EN SP00000470259 ¹ENSP00000455510

o
·E N S B TAP0000002 6431

· -ENSBTAPODO00055422

· ENSBTAP00000026429

JENSP00000345243 _s ENSP00000412361

· ENSMUSP00000005592 ENSBTAPOO000004195

· ENSDARP00000136924 ^o
·ENSTR UP00000023555

⁴ SP00000376048

.
·E N SBTAP00000052 366

· ENSMUSP00000139564

FIGURE 5.2 -- Arbre de gène de la famille MAG obtenu de Ensembl

CHAPITRE 5. ÉTUDE DE CAS

5.2 Étude de cas de la famille FAM86

Le second cas d'étude concerne la famille FAM86. Les gènes de cette famille subissent également l'épissage alternatif. Il s'agit ainsi d'un bon candidat pour notre étude. Le tableau 5.2 récapitule les informations sur cette famille FAM86.

	Nom de la famille	Source de données	Nombre de gènes	Nombre de protéines
3	FAM86	Ensembl	8	16

TABLE 5.2 - Données utilisées pour l'étude de cas de la famille FAM86

La figure 5.3 présente l'arbre de référence (arbre de gènes) sur lequel viendront se greffer les arbres provenant des groupes restant. L'arbre de gène obtenu comporte 0 pertes de gènes et 3 duplications contre 3 pertes et 4 duplications Notre arbre de gène partage 6 protéines sur 8 avec celui de Ensembl et a un plus petit coût de réconciliation.

46

FIGURE 5.3 - Arbre de gène de la famille FAM86 obtenu de notre modèle

47

CHAPITRE 5. ÉTUDE DE CAS

FIGURE 5.4 - Arbre de gène de la famille FAM86 obtenu de Ensembl

48

CHAPITRE SEPT

CONCLUSION GÉNÉRALE

Parvenu au terme de ce mémoire, dont le but était de proposer un modèle d'évo-lution de l'architecture des gènes en tenant compte de toutes les séquences codantes, nous avons dans un premier temps posé le problème et montré les limites des solutions actuelles. Puis nous avons proposé un modèle d'évolution de protéines et introduit des problèmes d'optimisations dont le but est de reconstruire des arbres de protéines et de gènes, étant donné les arbres d'espèces. Nous avons également proposé une méthode heuristique gloutonne résumée dans un processus à sept étapes pour résoudre le problème posé. Nous avons terminé avec des applications sur des familles de gènes de la base de données Ensembl.

Bien qu'ayant eu des résultats ayant des coûts de réconciliation mouilleurs que ceux d'Ensembl avec cette approche heuristique, il demeure qu'une solution algorithmique exact qui considère simultanément tous les arbres de chaque groupe de l'étape 4 du processus permettra de reconstruire une solution plus précise.

Le problème étant formellement posé, il sera question pour les prochains travaux sur la même problématique d'affiner.

49

Références

[1] Pea Carninci, T Kasukawa, S Katayama, J Gough, MC Frith, N Maeda, R Oyama, T Ravasi, B Lenhard, C Wells, et al. The transcriptional landscape of the mammalian genome. Science, 309(5740) :1559-1563, 2005.

[2] Yann Christinat and Bernard ME Moret. Inferring transcript phylogenies. BMC bioinformatics, 13(9) :1, 2012.

[3] Yann Christinat and Bernard ME Moret. Inferring transcript phylogenies. BMC bioinformatics, 13(9) :1, 2012.

[4] Yann Christinat and Bernard ME Moret. A transcript perspective on evolution. IEEE/ACM Transactions on Computational Biology and Bioinformatics (TCBB), 10(6) :1403-1411, 2013.

[5] Charles Darwin. R.(1859) : On the origin of species by means of natural selection. Murray. London, 1871.

[6] William HE Day, David S Johnson, and David Sankoff. The computational complexity of inferring rooted phylogenies by parsimony. Mathematical bios-ciences, 81(1) :33-42, 1986.

[7] I Dondoshansky and Y Wolf. Blastclust (ncbi software development toolkit). NCBI, Bethesda, Md, 2002.

[8] Robert C Edgar. Muscle : a multiple sequence alignment method with reduced time and space complexity. BMC bioinformatics, 5(1) :1, 2004.

[9] Robert C Edgar. Muscle : multiple sequence alignment with high accuracy and high throughput. Nucleic acids research, 32(5) :1792-1797, 2004.

[10] Heng Li et Al. Incorporating species phylogeny in the reconstruction of gene trees.

[11] R. Durbin et Al. Biological Sequence Analysis. Cambridge university press, 1998.

50

RÉFÉRENCES

[12] Oliver Eulenstein, Snehalata Huzurbazar, and David A Liberles. Reconciling phylogenetic trees. Evolution after gene duplication, pages 185-206, 2010.

[13] Walter M Fitch. Toward finding the tree of maximum parsimony. In Proceedings of the 8th International Conference on Numerical Taxonomy, pages 189-230. Freeman, 1975.

[14] Mark B Gerstein, Can Bruce, Joel S Rozowsky, Deyou Zheng, Jiang Du, Jan O Korbel, Olof Emanuelsson, Zhengdong D Zhang, Sherman Weissman, and Michael Snyder. What is a gene, post-encode? history and updated definition. Genome research, 17(6) :669-681, 2007.

[15] Brenton R Graveley. Alternative splicing : increasing diversity in the proteomic world. TRENDS in Genetics, 17(2) :100-107, 2001.

[16] P. H. The origin of the genetic code. 38 :367-379, 1968.

[17] John P. Huelsenbeck, Fredrik Ronquist, et al. Mrbayes : Bayesian inference of phylogenetic trees. Bioinformatics, 17(8) :754-755, 2001.

[18] Daniel H Huson and David Bryant. Application of phylogenetic networks in evolutionary studies. Molecular biology and evolution, 23(2) :254-267, 2006.

[19] Daniel H Huson, Regula Rupp, and Celine Scornavacca. Phylogenetic networks: concepts, algorithms and applications. Cambridge University Press, 2010.

[20] Safa Jammali, Esaie Kuitche, Ayoub Rachati, Bélanger François, and Aïda Ouangraoua. Aligning coding sequences with frameshift extension penalties. 2016.

[21] Abdellali Kelil. Contribution à l'analyse des séquences de protéines Similarité, Clustering et Alignement. Université de Sherbrooke, 2011.

[22] Christina Kyriakopoulou. From fundamental genomics to systems biology : understanding the book of life, volume 23132. European Communities, 2008.

[23] Weizhong Li and Adam Godzik. Cd-hit : a fast program for clustering and comparing large sets of protein or nucleotide sequences. Bioinformatics, 22(13) :1658-1659, 2006.

[24] David A Morrison. Networks in phylogenetic analysis : new tools for population biology. International journal for parasitology, 35(5) :567-582, 2005.

[25] Luay Nakhleh. Computational approaches to species phylogeny inference and gene tree reconciliation. Trends in ecology & evolution, 28(12) :719-728, 2013.

[26] SB Primrose and RM Twyman. Basic biology of plasmid and phage vectors. Principles of Gene Manipulation and Genomics, 2006.

[27] Richard H Quarles. Myelin-associated glycoprotein (mag) : past, present and beyond. Journal of neurochemistry, 100(6) :1431-1448, 2007.

51

RÉFÉRENCES

[28] Vincent Ranwez, Sébastien Harispe, Frédéric Delsuc, and Emmanuel JP Dou-zery. Macse : Multiple alignment of coding sequences accounting for frameshifts and stop codons. PLoS One, 6(9) :22594, 2011.

[29] Vincent Ranwez, Sébastien Harispe, Frédéric Delsuc, and Emmanuel JP Dou-zery. Macse : Multiple alignment of coding sequences accounting for frameshifts and stop codons. PLoS One, 6(9) :e22594, 2011.

[30] Stijn Van Dongen. A cluster algorithm for graphs. Report-Information systems, (10) :1-40, 2000.

[31] Albert J Vilella, Jessica Severin, Abel Ureta-Vidal, Li Heng, Richard Durbin, and Ewan Birney. Ensemblcompara genetrees : Complete, duplication-aware phylogenetic trees in vertebrates. Genome research, 19(2) :327-335, 2009.