|
Université Hassan II
Mohammédia
Faculté des Sciences Juridiques Economiques et
Sociales
Master : Techniques de Modélisation
Economiques et Econométrie
Mémoire de Master d'université sous le
thème
Trafic aérien de passagers et les entrées des
touristes internationaux au Maroc : Quelle relation ?
Préparé par :
Elmostafa ERRAITAB
Sous la supervision de : Ahmed
HEFNAOUI
M. Ahmed Hefanoui, professeur d'enseignement
supérieur à la faculté des sciences juridiques,
économiques et sociales de Mohammédia
Membres de jury :
Président : Ahmed HEFNAOUI
Suffragants :
M. Aziz OUIA : Professeur à la fsjes
Mohammédia
M. Mohammed MOUTMIHI :
Professeur à la fsjes Mohammédia
Année universitaire : 2012/2013
Remerciements
Je tiens, tout d'abord, à exprimer mes remerciements
à M. Hefnaoui Ahmed pour la confiance qu'il a placé en moi
dès le début de ce travail. Il m'a toujours incité
à donner de mon mieux. Je le remercie aussi pour la bienveillante
attention qu'il n'a cessé de me témoigner au cours de mes
recherches.
Mes remerciements vont également aux membres du jury
pour avoir voulu juger ce travail, messieurs Ouia et Moutmihi, je les remercie
pour ses aides et pour ses précieux conseils.
Au terme de ce travail, il m'est agréable d'exprimer ma
reconnaissance à toute personne, qui a contribué, de près
ou de loin, à l'accomplissement de ce travail.
Avant propos :
Ce présent travail est élaboré comme
mémoire de fin d'étude dans le cadre des études
supérieures de troisième cycle, en master intitulé
`'Techniques de modélisation économiques et
économétrie'' au sein de la faculté des sciences
juridiques, économiques et sociales de Mohammédia.
Ce mémoire a pris comme thème `' Trafic
aérien de passagers et les entrées des touristes internationaux
au Maroc : quelle relation ? L'utilisation de la modélisation VAR, la
conception et la mise en oeuvre d'un modèle à correction d'erreur
nous permettra de déterminer l'existence et le sens de causalité
entre ces deux variables.
Les opinions émises dans ce travail sont propres
à l'auteur, le laboratoire, la faculté et l'université
n'entendent donner aucune approbation, ni improbation auxdites opinions.
Sommaire
Remerciements
Avant propos
Introduction générale
CHAPITRE I : Description du trafic aérien
international et national
Section I : Evolution du trafic aérien mondial de
passagers
Section II : Développement du transport aérien au
Maroc.
CHAPITRE II : Modélisation univariée du
trafic aérien
Section I : Introduction aux processus aléatoires non
stationnaires
Section II : Schéma d'analyse des séries
chronologiques et correction des variations saisonnières
Section III : Application aux données du trafic mensuel
régulier de passagers au Maroc
CHAPITRE III : Modélisation multivariée du
trafic aérien : Les processus VAR
Section I : La modélisation VAR
Conclusion générale
Annexes
Liste des figures
Figure 1 : Variation annuelle du trafic
aérien mondial de passagers
2
Figure 2 : Evolution comparée du trafic
mondial de passagers et du PIB mondial
10
Figure 3 : Evolution du volume de trafic
passagers de 2002 à 2012.
12
Figure 4 : Répartition de la
capacité par type d'établissement
13
Figure 5 : Evolution du volume des
entrées des touristes étrangers de 2000 à 2012
14
Figure 6 : Traduction du plan
stratégique en matière des développements des
infrastructures
15
Figure 7 : Augmentation de l'offre des
compagnies aériennes desservant le Maroc
16
Figure 8 : Evolution du trafic aérien
par segment entre 2002 et 2912
18
Figure 9 : Liaisons régulières
internationales de la RAM depuis Casablanca
19
Figure 10 : Distribution de l'offre du trafic
aérien au départ du Maroc
19
Figure 11 : Evolution du Yield sur le
marché Maroc-Union européenne
20
Figure 12 : Evolution du part de marché
des compagnies a bas prix (LCC)
21
Figure 13 : développement de l'offre de
siège par aéroport
22
Figure 14 : Evolution du trafic charter
23
Figure 15 : Evolution du nombre de passagers
en mode charter transportés par type de compagnie
24
Figure 16 : Evolution du trafic charter par
aéroport
24
Figure 17 : Répartition des passagers
transportés par des vols charter par provenance
25
Figure 18 : Evolution de la part (%) du trafic
domestique
25
Figure 19 : Répartition du trafic
domestique par aéroport
26
Figure 20 : Exemple d'un processus non
stationnaire (changement de tendance)
29
Figure 21 : Simulation d'un processus avec
tendance déterministe
29
Figure 22 : Simulation d'un processus de
marche aléatoire (Random Walk)
31
Figure 23 : Histogramme des estimations de
l'estimateur rho
37
Figure 24 : Stratégie de test de Dickey
Fuller
39
Figure 25 : Evolution mensuelle du trafic
régulier de passagers
47
Figure 26 : Moyenne de la série du
trafic par saison (mois)
48
Figure 27 : la méthode de la bande
appliquée sur la série du trafic régulier
50
Figure 28 : Série corrigée des
variations saisonnières
53
Figure 29 : Autocorrélogramme d'ordre
12 de la série des résidus.
56
Figure 30 : Corrélogramme de la
série en différence première.
63
Figure 31 : Evolution comparée de la
chronique empirique (actuel) et la chronique calculée (fitted)
65
Figure 32 : Histogramme de la série des
réalisations des résidus
67
Figure 33 : Le corrélogramme de la
série des résidus
68
Figure 34 : Lien entre le volume de trafic
passagers et le volume des touristes
73
Figure 35 : Evolution des la série
mensuelle des entrées des touristes par voie aérienne, poste
frontière Med V
74
Figure 36 : Moyenne des entrées des
touristes par saison (mois), poste frontière Med V.
74
Figure 37 : Evolution comparée da
série brute et la série ajustée des variations
saisonnières
75
Figure 38 : Fonctions d'autocorrélation
simple et partielle de la série des entrées des touristes pour un
retard de 12.
76
Figure 39 : Fonctions de réponses
impulsionnelles
83
Liste des tableaux
Tableau 1 : Evolution du nombre de
fréquences mensuelles entre 2003 et 2009 par type de compagnie
2
Tableau 2 : Evolution du trafic aérien
au Maroc sur la période 2002-2012.
17
Tableau 3 : Développement du nombre de
sièges (milliers) par aéroport entre 2005 et 2010
22
Tableau 4 : Répartition de l'offre de
trafic entre les compagnies traditionnelles et LCC
23
Tableau 5 : Tableau de Buys et Ballot
51
Tableau 6 : Résumé des des
calculs des deux critères pour les retards de 1 à 3.
79
Tableau 7 : Résumé des
prévisions pour le premier trimestre 2013 pour les deux variables.
80
Tableau 8 : Prévisions avec prise en
compte des variations saisonnières
80
Tableau 9 : Analyse des chocs sur les varables
pax_adj et tour_adj
82
Tableau 10 : Décomposition de la
variance
83
Tableau 11 : Résultats des testes de
Dickey et Fuller appliqués sur les deux variables
89
Introduction générale
Le transport par la voie aérienne est devenue
incontournable, tant par sa vitesse que par sa flexibilité. L'avion a
révolutionné le transport transatlantique, permettant de relier
touts les continents en une même journée. Il a permis de relier
des régions extrêmement reculées, qui auraient
nécessité d'énormes investissements en infrastructure pour
des moyens de transport terrestre.
Sur les 20 dernières années, le volume mondial
de passagers transportés par voie aérienne a augmenté de
127%, soit un taux de croissance annuel moyen de 4,96%, sensiblement proche du
TCAM du PIB mondial sur la même période, qui était de
l'ordre de 5,78%.
En 2001, le ministère du tourisme au Maroc a
adopté la vision de 2010, qui avait pour ambition de faire du Maroc
l'une des principales destinations touristiques au niveau de la
méditerranée, cette vision avait comme objectif principal
l'attraction de 10 millions de touristes à l'horizon 2010, pour ce
faire, le Maroc s'est engagé sur une politique de libéralisation
du trafic aérien par la signature d'un accord d'open sky en 2006 avec
l'union européenne. Comme conséquence, le volume du trafic
passager transité par les différents aéroports du Maroc a
augmenté de 64,26% entre 2005 et 2012, soit un TCAM de 7,35%.
Profitant de l'accord de libéralisation du trafic
aérien entre le Maroc et l'UE, les compagnies aériennes ont
augmenté sensiblement leur offre, ainsi, entre 2003 et 2009, les
compagnies aériennes desservant le marché marocain ont
augmenté leur offre de 1685 fréquences mensuelles
supplémentaires, les compagnies low cost européennes ont
contribué activement à cette augmentation d'offre, sur les 1685
fréquences mensuelle supplémentaires, les compagnies LC ont
crée 960 fréquences supplémentaires, soit 57% de l'offre
de trafic au Maroc.
Face aux changements de l'offre en matière de trafic
aérien au Maroc, la demande a changé en conséquence. Au
moment où le trafic international régulier a
réalisé une bonne performance sur la période 2002-2012,
avec un TCAM de 9,68%, le trafic en mode charter, transit et le domestique ont
connu des baisses sur la même période, ceci est expliqué,
en partie, par la stratégie des compagnies LC qui optent pour des lignes
courtes et pointes à pointe.
L'introduction des compagnies LC a reconfiguré le
marché du trafic aérien au Maroc, elles ont contribué
à la diversification des choix des consommateurs par la création
de nouvelles lignes et de nouvelles fréquences. Aussi, les compagnies LC
ont réduit les tarifs des billets, rendant ainsi le service de transport
aérien accessible à un large public.
La reconfiguration du marché de transport aérien
suite à l'accord d'open sky nécessite une étude
académique sérieuse, servant comme base théorique et
pratique pour les intervenants du secteur. En effet, la croissance
significative du volume de trafic aérien nécessite des
installations aéronautiques et aéroportuaires adaptées. En
absence d'une modélisation du trafic adaptée, difficile de
comprendre et de prévoir son évolution future, ceci étant
dit, les planificateurs du secteur n'auront pas assez de moyens pour bien
adapter les installations aéroportuaires à la demande actuelle et
future. Faire des prévisions erronées de la demande du trafic
peut s'avérer très couteuses, en effet, des prévisions de
la demande de trafic sous-estimé peuvent causer des congestions, des
retards et un turnover élevé des installations. Aussi, des
prévisions de la demande de trafic surestimées causent de
sérieux problèmes budgétaires pour les autorités
gestionnaires. Ainsi, il s'avère cruciale de mettre à la
disposition des planificateurs des aéroports des modèles de
demande de trafic aérien. L'intérêt de ce travail est
double, premièrement, il constitue un travail théorique pionnier
de modélisation du trafic au Maroc, à notre connaissance, et
jusqu'à la rédaction de ce travail, il n'y a pas un document de
recherche en matière de modélisation de la demande de trafic au
Maroc. Deuxièmement, ce travail a un intérêt pratique, il
servira comme document de base pour les décideurs, et surtout les
planificateurs des installations aéroportuaires au Maroc.
Au niveau de ce travail, pour modéliser la demande de
trafic aérien, on a utilisé dans un premier temps les
modèles de type ARIMA, ce choix est justifié par la
difficulté d'accès aux variables explicatives de la demande de
trafic aérien au Maroc, à titre d'exemple, le prix est une
variable essentielle pour l'explication de la demande de trafic1(*), au Maroc, malheureusement, on a
pas encore un indicateur spécifique du transport aérien2(*), permettant le suivi du prix
des services aériens. Les données sur cette variable `'Tarifs par
route'' est disponible au niveau de la base des données OAG,
néanmoins, l'abonnement à cette base de données est
très cher. Dans un deuxième temps, on a utilisé la
modélisation VAR, en fait, en absence des théories
économiques explicatives du sens de la relation entre la demande de
trafic aérien et le volume des touristes transités par la voie
aérienne, la modélisation de type VAR semble l'approche la plus
adaptée.
L'objectif de ce travail consiste à répondre
à la question problématique suivante : Dans quelle mesure
les modélisations de type ARMA et VAR permettent de comprendre et
prévoir la demande de trafic aérien au Maroc ?
Afin de répondre à cette question, on va essayer
d'analyser les caractéristiques du trafic aérien au Maroc dans le
premier chapitre. Notre analyse du marché de transport aérien au
Maroc nous a permis de détecter les stratégies des compagnies
desservant le marché marocain, ainsi, on a trouvé que les
compagnies traditionnelles, comme la RAM et Air France, se concentrent sur des
destinations lointaines et utilisent l'aéroport Mohammed V comme hub de
ses opérations, par contre, les compagnies low cost (LC),
préfèrent des lignes courtes de pointe à pointe entre les
aéroports marocains à vocation touristique, comme Marrakech et
Agadir et les aéroports secondaires d'Europe.
Au niveau du deuxième chapitre de ce travail, on a
essayé d'appliquer l'approche de Box&Jenkins sur la chronique du
trafic aérien de passagers au Maroc, l'approche de Box&Jenkins
s'applique sur des séries stationnaires et corrigées des
variations saisonnières, or, la stationnarité peut être de
deux types, TS ou bien DS3(*), la nuance entre ces deux types de non
stationnarité à de fortes implications économiques et
statistiques. Notre analyse préliminaire de la série du trafic de
passagers a montré que celle-ci est affectée d'une tendance
saisonnière, de plus, les deux approches de décomposition de la
série se convergent et donnent le même résultat, le
schéma de décomposition de notre série est de type
multiplicatif, afin de lisser la série des variations
saisonnières, on a utilisé la méthode des moyennes
mobiles.
L'application de la stratégie de Dickey&Fuller sur
la série du trafic passagers a montré que celle-ci est une
réalisation d'un processus stationnaire en tendance, cette conclusion
contraires aux intuitions, nous a poussé à approfondir l'analyse,
afin de statuer sur la nature du processus générateur de la
série, si il est stationnaire en tendance, une condition s'avère
nécessaire, il faut que l'aléa soit un bruit blanc, or, l'analyse
des réalisations des aléas a montré que celles-ci sont
autocorrélés, ceci remet en cause la validité des
distributions asymptotiques des tests de D&F. les tests de D&F
augmentés surmontent cette contrainte, ils prennent en compte
l'éventuelle autocorrélation des résidus par l'inclusion
d'un ou plusieurs termes autorégressifs différenciés. Le
nombre de termes autorégressifs retardés a été
déterminé par les deux critères d'Akaike et Shwartz, selon
ces deux critères, pour blanchir les résidus, il faut inclure
trois termes autorégressifs différenciés. L'application du
test d'ADF a montré cette fois que la série est non stationnaire
de type stochastique, elle est une réalisation d'un processus de type
marche au hasard. L'identification selon l'approche de Box&Jenkins par les
deux fonctions d'autocorrélation simple et partielle a montré que
le processus est une réalisation d'un SARIMA(1,1,1), avec s=12. Par
différents tests sur les paramètres estimés et la
série des résidus, on a validé le modèle
estimé.
La modélisation univariée consiste à
détecter la logique d'évolution passée par l'analyse des
l'historique des réalisations de la série, et puis, on suppose
que cette logique d'évolution se reproduira plus au moins de la
même manière, or, à moyen et long terme, le
phénomène étudié peut subir de profonds
changements, ainsi, cette approche de modélisation devient
inefficace.
Dans l'objectif de surmonter les limites de la
modélisation univariée, on a essayé d'utiliser au niveau
du troisième chapitre la modélisation multivariée (VAR).
En absence d'une théorie économique d'identification du sens de
causalité entre les variables, la modélisation VAR s'avère
la plus adaptée dans ce contexte, pour le cas de notre variable, qui est
le volume de trafic passagers, elle est à la fois une variable
expliquée et explicative des entrées des touristes
internationaux. L'identification de notre modèle VAR nous a permis de
retenir un modèle à deux retards (p=2), ce modèle a
été utilisé pour calculer des prévisions d'un
horizon de trois mois pour les deux variables.
La décomposition de la variance et l'analyse de la
causalité au sens de Granger nous a permis de tirer la conclusion que la
variable des entrées des touristes cause au sens de Granger le volume de
trafic passagers, selon la même terminologie de Granger, on a
trouvé que la variable du trafic passagers ne cause pas les
entrées des touristes.
Lorsque les variables ont une tendance d'évolution
commune, le risque de tomber dans le problème de régression
fallacieuse est élevée quand on veut chercher l'existence d'une
relation linéaire entres les dites variables, au niveau du dernier
chapitre, on a utilisé le test d'Engle et Granger pour tester
l'éventuelle existence d'une relation de cointégration entre la
variable du trafic aérien et les entrées des touristes au Maroc,
les résultats de ce test confirment la cointégration de ces deux
variables, à cet effet, on a spécifié et estimé un
modèle à correction d'erreur, dans le même sens, le test de
Johansen nous a permis de confirmer les résultats du test d'Engel et
Granger.
CHAPITRE I :
Description du trafic aérien international et national
1) Evolution du trafic
aérien mondial de passagers
1.1)Historique du trafic
aérien mondial de passagers : Evolution contrastée
Entre 1970 et 2011, le taux de croissance annuel moyen du
trafic aérien mondial de passagers est de 6,32%, néanmoins, ce
taux moyen, certes positif, cache des disparités entre des
périodes de fortes augmentation et des périodes de
récession de l'activité du transport aérien. De 1970
à 1979, le TCAM était de l'ordre de 12%, profitant ainsi des
années glorieuses d'augmentation continue et soutenue du PIB mondial. En
1980, et suite au choc pétrolier, qui a conduit à une
modification brutale de l'offre de pétrole, combiné à une
hausse du prix et une baisse de la production, le trafic mondial a
baissé de 0,74%.
De 1981 à 1992, le trafic mondial de passagers a repris
sa tendance haussière, profitant de l'augmentation soutenue des
activités mondiales.
En 1993, le trafic mondial a connu une baisse importante de
presque -0,5%, rampant ainsi avec dix années consécutives
d'augmentation du volume de trafic aérien, cette baisse est survenue
suite à la contraction des activités économiques à
cause de la guerre du golf en 1991.
En corrélation avec la contraction des activités
mondiales et la baisse du PIB en Europe et en Amérique du nord en 2008
suite à la crise économique et financière, le trafic
aérien n'a augmenté en 2008 que de 0,21% par rapport à son
volume en 2007, on doit noter au passage que le trafic mondial en 2008 n'a
été sauvé que par la bonne performance des régions
d'Asie et du Moyen orient, en contre partie, le volume de trafic a
été contracté en 2008 au niveau de l'Europe et
l'Amérique du nord.
Figure 1 : Variation
annuelle du trafic aérien mondial de passagers

Source : Base de données de la banque mondiale,
indicateur transport aérien de voyageurs
1.2) Evolution comparée
du trafic aérien mondial et du PIB mondial
Comme le montre la figure 1.2, l'évolution du trafic
aérien mondial laisse présager que ce secteur est très
corrélé à l'évolution des activités
économiques, mesurées par l'évolution du PIB, en effet,
l'augmentation des activités économiques permet la
création des groupes internationaux et pousse vers la mondialisation
économique, favorisant ainsi le déplacement des cadres
supérieurs entre leurs filiales, ceci induit le développement du
trafic aérien pour motif affaires. De plus, l'augmentation des
activités économiques conduit à une augmentation du
PIB/tête, ce qui induit les déplacements pour motif tourisme et
voyages d'agrément.
Figure 2 : Evolution
comparée du trafic mondial de passagers et du PIB mondial

Source : Base de données de la banque mondiale
2)Développement du
transport aérien au Maroc.
2.1)Chronologie de la politique
de libéralisation du transport aérien au Maroc
En 2001, le Maroc s'est engagé sur une vision qui
consistait à l'attraction de 10 millions de touristes pour l'horizon
2010, à cet effet, le Maroc s'est engagé fortement sur une
politique de libéralisation du marché de trafic aérien
afin de favoriser la création de nouvelle compagnies et surtout
augmenter l'offre de transport aérien afin de rendre la destination
Maroc plus compétitive en terme de prix. Pour contrecarrer la
concurrence des autres compagnies étrangères, l'opérateur
nationale en matière de transport aérien, la Royal Air Maroc
(RAM) a crée sa propre filiale low cost, Atlas Bleu4(*).
En 2006, le Maroc représenté par le
ministère du transport, a signé un accord historique avec l'union
européen, cet accord consiste à une libéralisation
progressive du secteur de transport aérien et à un alignement
progressif sur la législation européenne5(*) en matière de
réglementation aéronautique.
Entre 2008 et 2012, le Maroc a adopté une
stratégie qui vise à développer et moderniser ses
plates-formes aéroportuaires, ceci étant dit, le ministère
de la tutelle a crée une nouvelle direction, dénommée la
Direction du Transport Aérien6(*) (DTA) au sein de la Direction Générale
de l'Aviation Civile (DGAC).
2.1.1)Impact de la politique de
libéralisation sur le volume de trafic au Maroc
En 2002, le volume de trafic passagers au Maroc était
de l'ordre de 6,7 millions de passagers, en 2004, le volume de passagers a
atteint 7,7 millions de passagers, soit un taux de croissance annuelle
moyen7(*) de 7%. En 2012,
ce le volume de trafic passagers a enregistré 15,2 millions de
passagers, soit un taux de croissance annuelle moyen entre 2004 et 2012 de
9%.
Le graphique 1.1 montre clairement que depuis la
libéralisation du secteur, le volume de passagers n'a cessé
d'augmenter, néanmoins, en 2012, le volume de trafic a baissé de
3,6% relativement à l'année 2011, cette baisse est
expliqué par l'effet de la crise économique et financière
mondiale.
Figure 3 : Evolution du
volume de trafic passagers de 2002 à 2012.

Source : Calculs de l'auteur sur la base des
données ONDA.
2.1.2)Stimulation de la demande
du transport aérien par les actions du ministère du tourisme
A travers une politique concertée entre les
différents acteurs du transport aérien, le ministère du
tourisme a adoptée en 2001 la vision de 2010 afin de faire du Maroc
l'une des principales destinations touristiques africaines, cette vision avait
les objectifs suivants :
· L'attraction de 10 millions de touristes à
l'horizon 2010, dont 70% sont des touristes internationaux
· Augmentation de la capacité litière pour
atteindre 230.000 lits par la création de 160.000 lits
supplémentaires.
· Allocation d'un montant d'investissement de 9 milliards
d'euros, pour l'aménagement de nouvelles stations balnéaires.
· Le montant prévu des recettes en devises est de
48 milliards d'euros, ces rentrées de devises devraient amener le
tourisme à contribuer à hauteur de 20% au PIB national.
Afin d'atteindre les objectifs de la vision 2010, le
ministère du tourisme a mené plusieurs actions, en 2001, il a
lancé le plan Azur qui vise à créer six nouvelles stations
balnéaires touristiques, de plus, en 2002, il a lancé les plans
de développement régionaux (PDR) pour améliorer les
destinations touristiques existantes comme celle d'Agadir, Tanger et
Tétouan. Dans l'objectif de contrôler la poursuite des objectifs
via des indicateurs fiables, le ministère a crée en 2005
l'observatoire du tourisme (OT), cet observatoire constitue une banque de
données sur le secteur8(*). Coté réglementaire, le ministère
a procédé en 2006 à une réforme de la taxe de
promotion touristique.
2.2) Contribution de la vision
2010 au niveau de développement des rentrées des touristes.
La vision de 2010 a contribué à l'augmentation
de la capacité d'hébergement au Maroc, en effet, la
capacité des établissements d'hébergement touristiques a
passé de 45.000 lits en 2000 à 162.000 lits en 2009, cette offre
est très variée, les hôtels classés
représentent 72% de la capacité litière classée,
les maisons d'hôtes, représentent quant à elles, 8% de la
capacité totale.
Figure 4 :
Répartition de la capacité par type
d'établissement

Source : Ministère du tourisme, département
du tourisme
L'augmentation et l'amélioration de l'offre des
établissements d'hébergement a eu un impact positif sur le volume
de fréquentation touristique, et par là, sur le trafic
aérien. Entre 2000 et 2012, le taux de croissance annuel moyen des
entrées des touristes internationaux était de l'ordre de 7%, ce
taux de croissance annuel remarquable, place la destination Maroc au dessus de
la moyenne des pays du bassin méditerranéens9(*).
Figure 5 : Evolution du
volume des entrées des touristes étrangers de 2000 à
2012

Source : observatoire du tourisme, ministère du
tourisme
Les plans de développement touristiques de la vision
2020, tablent sur 20.000 de touristes par an, ce développement
nécessite une amélioration des installations
aéroportuaires et une intensification de l'offre aérienne.
2.2.1)Développement des
infrastructures aéroportuaires
En tant que gestionnaires des plates formes et installation
aéroportuaires, l'Office National Des Aéroports (ONDA) est un
acteur clé de développement du transport aérien au
Maroc.
L'ONDA a été crée en 1990, il pour
mission la gestion des installations et infrastructures aéroportuaires
et assurer les services de navigation aériennes. De par ses missions,
l'ONDA a mis en place un ensemble de stratégies dans l'objectif est de
contribuer au développement du transport aérien au Maroc. A cet
effet, l'ONDA a intensifié l'offre aéroportuaire par la mise en
place des infrastructures de qualité répondant aux normes
internationales en matière de sûreté et de
sécurité.
Figure 6 : Traduction du
plan stratégique en matière des développements des
infrastructures

Source : Plan de développement du transport
aérien au Maroc, étude menée par le cabinet ALG pour le
compte de la DTA, ministère du transport.
Comme le montre la figure 1.4, l'ONDA s'est lancé sur
plusieurs de projets, allant de la rénovation des installations
aéroportuaires jusqu'à la construction de nouvelles
aérogares, ces investissements de taille viennent comme réponse
à une demande accrue du service de transport aérien,
néanmoins, ces investissements doivent être planifiés afin
qu'ils ne soient pas surestimés ou bien sous-estimés, une bonne
planification des investissements suppose des prévisions fiables de la
demande adressé au trafic aérien10(*).
2.2.2)Développement de
l'offre aérienne au Maroc
Les compagnies aériennes ont augmenté
énormément leur offre depuis l'année 2003, tout type de
compagnies confondues, elles ont augmenté l'offre entre 2003 et 2009 de
1.685 fréquences mensuelles supplémentaires.
Tableau 1 : Evolution du
nombre de fréquences mensuelles entre 2003 et 2009 par type de
compagnie
|
Type compagnie
|
Nbre fréquences en 2003
|
Nbre fréquences en 2009
|
Nouvelles fréquences
|
|
RAM
|
1042
|
1804
|
762
|
|
LCC UE
|
600
|
960
|
360
|
|
LCC MAROC
|
285
|
804
|
519
|
|
AUTRES RESAUX
|
600
|
644
|
44
|
|
Total
|
2527
|
4212
|
1685
|
Source : OAG, mai 2003-2009
Figure 7 : Augmentation
de l'offre des compagnies aériennes desservant le Maroc

Source : Adaptation sur la base des données OAG
Profitant de l'accord d'open sky signé entre le Maroc
et l'UE en 2006, plusieurs compagnies low cost ont commencé à
desservir la destination Maroc, ainsi, les seules compagnies LCC UE, ont
augmenté leurs fréquences mensuelles de 360 fréquences
supplémentaires entre 2003 et 2006. Les LCC marocaines11(*) ont à leur tour suivi
la tendance et ont augmenté leurs fréquences mensuelles de 519
fréquences. L'opérateur historique marocain du trafic
aérien a contribué à hauteur de 45% du volume des
fréquences supplémentaires entre 2003 et 2009, soit 762
fréquences supplémentaires. Le bras droit de l'Etat marocain en
matière de transport aérien a contribué activement
à l'atteinte des objectifs de la vision 2010, son volume de passagers
transportés a passé de 1,7 millions de passagers internationaux
en 2003 à 5,3 millions de passagers en 2012. De plus que l'augmentation
du volume de l'offre de transport aérien, la structure de cette offre a
changé, les vols point à point12(*) ont augmenté de 40% à 60%.
2.3)Impact des politiques
concertées des différents intervenants sur le volume du trafic au
Maroc
2.3.1)Evolution
contrastée des différents segments du trafic aérien
Tableau 2 : Evolution du
trafic aérien (en millions) au Maroc sur la période
2002-2012.
|
TYPE TRAFIC
|
2002
|
2003
|
2004
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
2012
|
|
REGULIER INTERNATIONAL
|
5,2
|
5,4
|
5,5
|
5,8
|
6,8
|
8,6
|
9,8
|
10,6
|
12,7
|
13,4
|
13,1
|
|
CHARTER INTERNATIONAL
|
1,9
|
1,9
|
1,9
|
1,9
|
1,8
|
1,8
|
1,7
|
1,7
|
1,6
|
1,5
|
1,3
|
|
TRANSIT
|
0,3
|
0,3
|
0,3
|
0,3
|
0,2
|
0,2
|
0,2
|
0,2
|
0,2
|
0,2
|
0,2
|
|
DOMESTIQUE
|
1,3
|
1,3
|
1,3
|
1,3
|
1,6
|
1,5
|
1,1
|
0,9
|
0,8
|
0,6
|
0,5
|
|
Total
|
8,7
|
8,9
|
9,0
|
9,3
|
10,4
|
12,1
|
12,9
|
13,4
|
15,4
|
15,7
|
15,1
|
Source : calculs sur la base de données ONDA
Le taux de croissance moyen annuel entre 2002 et 2012 du
trafic régulier international est de 9,68%, cette augmentation
remarquable était au détriment des autres composantes du trafic,
le trafic charter international à réalisé un TCAM de
3,72%, la majeur partie du trafic charter s'opère à travers les
tours opérateurs. Avec l'introduction des compagnies LCC, elles ont
commencé à remplacer les vols charters par des vols en mode
régulier. A son tour, le trafic en transit a enregistré un TCAM
de (-3,97), cette tendance baissière du trafic en transit est
expliquée par le recours des compagnies à opérer des vols
directs point à point au lieu de faire des escales au niveau du hub de
Casablanca. La baisse importante en terme du TCAM a été
enregistré par le segment du trafic domestique, il a baissé de
9,11% sur la période 2002-2012 ; le développement des autres
modes de transport concurrents tels que le réseau des autoroutes, a
engendré un déplacement d'une partie du marché du trafic
domestique aérien vers ces modes concurrents.
Figure 8 : Evolution du
trafic aérien par segment entre 2002 et 2912

Source : Calculs sur la base des données ONDA.
Depuis l'année 2006, date de signature de l'open Sky
entre le Maroc et l'UE, on constate une croissance régulière du
segment du trafic régulier international, en contre partie, on constate
soit une constante ou bien une diminution des autres segments du trafic.
2.3.2)Distribution de l'offre
du trafic par région
La destination européenne reste le principal
marché avec une part de 83% de l'offre du trafic, l'Afrique centrale et
de l'ouest vient en deuxième position, avec une part de 6%, cette
destination est desservie principalement par la compagnie RAM, comme le montre
la figure 1.7, la RAM utilise le hub de Casablanca comme aéroport de
base pour ses opérations entre l'Europe et l'Afrique centrale et de
l'Ouest.
Figure 9 : Liaisons
régulières internationales de la RAM depuis
Casablanca

Source : OAG, 2009
Figure 10 : Distribution
de l'offre du trafic aérien au départ du Maroc

Source : Adaptation sur la base des données
OAG.
2.4)Evolution et impact de
l'introduction des LCC sur l'offre de transport aérien au Maroc.
L'introduction des compagnies LC a permis une reconfiguration
du marché de transport au Maroc, en effet, ces compagnies ont
contribué activement à la création de nouvelles
destinations et à l'augmentation des fréquences mensuelles vers
la destination Maroc, ainsi, ils ont contribué à
l'élargissement des choix pour les passagers et surtout ils ont
banalisé le service de transport aérien, en effet, par leur
politique de réduction des tarifs, ils ont élargi la
clientèle du service de transport aérien.
Figure 11 : Evolution du
Yield sur le marché Maroc-Union européenne

Source : OAG 2006-2009 ; IATA PAXIS 2006-2009
Le yield sur le marché Maroc-Union européenne,
exprimé en €/passagers-kilomètre est passé de 8,16 en
2006 à 6,69 en 2009, soit un taux de croissance annuel moyen de -6,41%.
Le prix constitue un élément incontournable du mix de chaque
produit, les compagnies LC, par la nature de leur mode de management, qui
consiste à se débarrasser des charges superflues13(*) diminuant ainsi le coût
de revient et par conséquent le prix du billet, elles proposent des
tarifs très concurrentiels14(*) par rapport aux tarifs des compagnies traditionnels,
le prix du billet d'une compagnie LC peut être des fois le 1/3 de celui
d'une compagnie traditionnelle sur le même trajet. Ainsi, il
s'avère que la variable de la moyenne des tarifs sur un trajet
donné, constitue une variable déterminante pour l'explication de
l'évolution du trafic sur ce trajet.
Cette étude descriptive de l'évolution du trafic
nous donne déjà une idée sur les variables censées
expliquer la demande de trafic aérien sur un marché
donnée.
2.4.1) Les compagnies LC n'ont
cessé de consolider leur part de marché depuis la signature
d'open sky
Figure 12 : Evolution du
part de marché des compagnies a bas prix (LCC)

Source : Calculs sur la base des données ONDA.
En 2005, la part des compagnies LC n'était que 11% sur
le marché du transport aérien au Maroc, en 2008, leur part est
passé au bout de quatre ans à 36% du marché, soit un taux
de croissance moyen annuel de 10%. L'augmentation spectaculaire du part de
marché des compagnies LC sur le marché marocain est
expliqué par la coïncidence du processus de libéralisation
du secteur au Maroc avec une phase d'expansion des compagnies LC et surtout
celles d'Europe, en effet, après la saturation du marché
européen, les compagnies LC ont commencé à chercher des
marchés plus éloignés.
2.4.2)Evolution de l'offre
internationale par aéroport
L'introduction et développement des compagnies LC au
marché marocain ont permis l'amélioration de l'offre des
sièges à l'international par aéroport, en effet, cette
offre a passé de 622.000 sièges en 2005 à 1.522.000
sièges en 2010, à cet effet, la part du hub de Casablanca a
passé de 73% en terme du nombre de siège en 2005 à 48% en
2010 (cf. tableau 1.3). L'aéroport qui est arrivé à
augmenter son offre plus que les autres était l'aéroport de
Marrakech, son offre a passé de 75.000 en 2005 à 434.000 en 2010,
augmentant ainsi sa part de l'offre international de 12% à 29%, cette
performance est due à l'installation de deux compagnies LC
pionnières, à savoir Ryan Air et Easy Jet.
Figure 13 :
développement de l'offre de siège par aéroport

Source : OAG 2005-2010
Tableau 3 :
Développement du nombre de sièges (milliers) par aéroport
entre 2005 et 2010
|
Aéroport
|
2005
|
2010
|
Part en 2005
|
Part en 2010
|
|
Mohammed V
|
455
|
726
|
73%
|
48%
|
|
Marrakech
|
75
|
434
|
12%
|
29%
|
|
Agadir
|
30
|
93
|
5%
|
6%
|
|
Tanger
|
57
|
75
|
9%
|
5%
|
|
Autres
|
5
|
194
|
1%
|
13%
|
|
Total
|
622
|
1522
|
100%
|
100%
|
Source : OAG 2005-2010
2.4.3)Distribution de l'offre
par aéroport et par type d'opérateur
Les compagnies LC ont concentré leurs offres sur les
destinations à vocation touristique, à titre d'exemple, au niveau
de l'aéroport Fes-Sais, la part des compagnies LC est de 80%,
néanmoins, la part de ces compagnies au niveau de l'aéroport de
Casablanca est de 21%, alors que les compagnies traditionnelles en
représentent 79%, ainsi, il parait qu'au Maroc, les compagnies LC
développent et créent des routes envers les destinations
touristiques via des vols point à point, alors que les compagnies de
réseau se concentrent au niveau du hub de Casablanca du fait qu'elles
font du long courrier et elles ont besoin d'un aéroport de
correspondance.
Tableau 4 :
Répartition de l'offre de trafic entre les compagnies traditionnelles et
LCC
|
Aéroport
|
Part des Cies traditionnelles
|
Part des LCC
|
|
Mohammed V
|
79%
|
21%
|
|
Marrakech
|
32%
|
68%
|
|
Agadir
|
22%
|
78%
|
|
Tanger
|
35%
|
65%
|
|
Fes Sais
|
20%
|
80%
|
|
Nador
|
33%
|
67%
|
Source : OAG 2010
2.5)Evolution du trafic type
charter au Maroc
Les vols charters ou d'affrètement consiste à
vendre un vol complet, à une date et sur une destination donnée,
le vol est généralement acheté par des tours
opérateurs qui le revendent à sec ou plus couramment
accompagné d'autres prestations telles que l'hôtellerie, le
circuit,...,etc .
2 .5.1) Analyse du trafic
charter
Au moment où le trafic passagers a augmenté de
9% (cf.1.1) sur la période 2005-2009, le trafic charter a baissé
de 13% sur la même période, cette baisse est
corrélée avec l'introduction massive du compagnies LC lors de la
signature de l'accord open sky entre le Maroc et l'union européenne,
avant la signature dudit accord, les tours opérateurs ont profité
du plan de développement touristique au Maroc qui a
démarré dès 2002, ils vendaient des packs complets
contenant le transport et l'hébergement. Suite à la signature de
l'accord de libéralisation du ciel marocain en 2006, les compagnies LC
ont commencé à desservir de nouvelles routes et surtout les
destinations touristiques, du coup, et avec la croissance du tourisme
indépendant, les vols des tours opérateurs charters ont devenu
des lignes régulières desservies par les compagnies LC, à
cet effet, on peut dire qu'il n'y a qu'un changement de mode sans une induction
réelle du trafic, la baisse du trafic charter est expliquée par
une réorientation vers des lignes régulières.
Figure 14 : Evolution du
trafic charter

Source : Calculs sur la base des données ONDA.
Le changement des habitudes des touristes qui commencent
à acquérir des billets directs au détriment des packs
touristiques a contribué à la baisse du trafic charter au
Maroc.
Figure 15 : Evolution du
nombre de passagers en mode charter transportés par type de
compagnie

Source : Base de données ONDA.
La figure 15 montre clairement ce qu'on a déjà
cité plus haut, en effet, le nombre de passagers transportés par
les compagnies LC n'a cessé de diminuer, tout en sachant que le volume
de passagers transportés par ce genre de compagnies n'a cessé
d'augmenter, à tel point que la part des compagnies LC a atteint 80%
pour le cas de l'aéroport Fes-Sais. De ce qui précède, il
semble que la stratégie des compagnies LC sur le marché marocain
c'est de remplacer les lignes du trafic charter par des lignes
régulières.
2.5.2) Trafic charter par
aéroport.
Figure 16 : Evolution du
trafic charter par aéroport

Source : Base de données ONDA
Les deux aéroports à vocation touristique Agadir
et Marrakech, représentent à eux seuls les deux tiers du trafic
charter au Maroc en 2012, ainsi, le trafic charter est lié directement
au trafic pour motif tourisme au Maroc.
Figure 17 :
Répartition des passagers transportés par des vols charter par
provenance

Source : Base de données ONDA.
La région d'Europe constitue la principale source de
trafic charter, ce résultat est compatible avec les statistiques du
ministère du tourisme qui indiquent que la région d'Europe est la
principale région émettrice des touristes vers la destination
Maroc.
2.6) Evolution du trafic
domestique au Maroc.
Figure 18 : Evolution de
la part (%) du trafic domestique

Source : Base de données ONDA
Alors que le trafic international a réalisé un
taux de croissance annuel moyen de 9,46% entre 2005 et 2012, le trafic
domestique a baissé de presque 5% comme moyenne annuelle sur la
même période, en effet, avec l'occord d'open sky, les nouvelles
compagnies, et surtout celles de type low cost, ont commencé à
faire des vols point à point sans passer par le hub de Casablanca,
ainsi, les étapes domestiques du vols à escales ont
été réduites.
Figure 19 :
Répartition du trafic domestique par aéroport

Source : Base de données ONDA
Le hub de Casablanca, à lui seul, constitue presque la
moitié du trafic domestique. Les vols proprement domestiques sont
effectués exclusivement par la RAM, l'autre partie de trafic est
constitué par les vols de continuation.
A partir de cette analyse, descriptive soit elle, on peut
avoir une idée sur les variables censées expliquer le trafic
aérien ; l'augmentation des activités économiques et
la mondialisation des économies pousse vers la division international du
système productif, favorisant ainsi le développement et la
création des firmes multinationales, le transport aérien semble
le moyen le plus efficace pour répondre aux exigences en termes de
déplacements des haut cadres entre leur filiales, ceci a
contribué à l'augmentation des vols pour motifs affaires.
La concurrence induite par l'introduction des compagnies LC a
permis une réduction des tarifs des billets, comme n'importe quel
produit, le demande du trafic aérien est une fonction inverse du prix,
toute baisse du prix du service, induit une demande supplémentaire.
Au niveau des chapitres suivants, on va essayer de chercher
une modélisation adaptée du trafic aérien.
CHAPITRE II :
Modélisation univariée du trafic aérien
1) Introduction aux
processus aléatoires non stationnaires
Le fait qu'un processus soit stationnaire ou non conditionne
le choix de la modélisation que l'on doit adopter. En règle
générale, si l'on s'en tient notamment à la
méthodologie de Box et Jenkins (cf. figure 24), si la série
étudiée est issue d'un processus stationnaire, on cherche alors
le meilleur modèle parmi la classe des processus stationnaires pour la
représenter, puis on estime ce modèle. En revanche si la
série est issue d'un processus non stationnaire, on doit avant toutes
choses, chercher à la »stationnariser», c'est à dire
trouver une transformation stationnaire de ce processus. Puis, on
modélise et l'on estime les paramètres associés à
la composante stationnaire.
La difficulté réside dans le fait qu'il existe
différentes sources de non stationnarité et qu'à chaque
origine de la non stationnarité est associée une méthode
propre de stationnarisation. Nous allons donc commencer par présenter
deux classes de processus non stationnaires, selon la terminologie de Nelson et
Plosser (1982) : les processus TS (Time Stationary) et les processus DS
(Differency Stationary). Dans la section suivante, nous présenterons les
méthodes de stationnarisation pour chacune de ces classes de processus.
Mais au delà des enjeux de modélisation
économétriques, nous verrons dans cette partie, que l'origine de
la non stationnarité a de très fortes implications au niveau des
interprétations économiques des résultats.
1.1) Définition de la
stationnarité au second ordre :
Définition : Un processus (  ) est dit stationnaire au second ordre, ou stationnaire au sens faible,
ou stationnaire d'ordre deux si les trois conditions suivantes sont satisfaites
: ) est dit stationnaire au second ordre, ou stationnaire au sens faible,
ou stationnaire d'ordre deux si les trois conditions suivantes sont satisfaites
:  8 ; 8 ;
 , indépendant de t, l'espérance est constante (elle est
inchangée dans le temps). , indépendant de t, l'espérance est constante (elle est
inchangée dans le temps).
 , indépendant de t. autrement dit, la covariance entre une
composante d'une date t et une autre composante d'une autre date t+h ne
dépend que de l'écart de temps (le retard `è') entre
les dates, et non de la date t elle-même : par exemple on a , indépendant de t. autrement dit, la covariance entre une
composante d'une date t et une autre composante d'une autre date t+h ne
dépend que de l'écart de temps (le retard `è') entre
les dates, et non de la date t elle-même : par exemple on a  . .
Figure 20 : Exemple d'un
processus non stationnaire (changement de tendance)

Processus non stationnaire de type tendance
déterministe :
Considérons le processus suivant :
 , avec , avec , le processus correspond à la somme d'une fonction
linéaire du temps et d'un bruit blanc. , le processus correspond à la somme d'une fonction
linéaire du temps et d'un bruit blanc.
Figure 21 : Simulation
d'un processus avec tendance déterministe

Le processus n'est pas stationnaire, en effet,
l'espérance mathématique dépend de t, elle croit avec le
temps, à chaque date de la variable aléatoire  a une espérance plus grande que celle de a une espérance plus grande que celle de , l'origine de la non stationnarité provient de l'inclusion de la
tendance. On dit alors que la non stationnarité est de type
déterministe. , l'origine de la non stationnarité provient de l'inclusion de la
tendance. On dit alors que la non stationnarité est de type
déterministe.
De plus que ces deux processus non stationnaires (Processus
changement de tendance et processus incluant une tendance temporelle), il
existe d'autres types de processus non stationnaire. Considérons le
processus suivant, que l'on qualifie de marche aléatoire pure (Random
Walk Process) ou marche aléatoire sans dérive :  (1.1) (1.1)
Avec  . Dans ce type de processus, la non stationnarité n'est pas de
type déterministe, en effet, le processus . Dans ce type de processus, la non stationnarité n'est pas de
type déterministe, en effet, le processus  ne comporte pas de fonction déterministe du temps. ne comporte pas de fonction déterministe du temps.
Le processus  peut se réécrire sous la forme : peut se réécrire sous la forme :
 (1.2) (1.2)
Sous cette forme, on peut facilement calculer les deux moments
d'ordre 1 et 2.
Le moment d'ordre 1 est :
  (1.3) (1.3)
Donc le processus  a une espérance nulle et donc il satisfait la deuxième
condition de stationnarité. Voyant maintenant si le processus a une espérance nulle et donc il satisfait la deuxième
condition de stationnarité. Voyant maintenant si le processus  satisfait la première condition15(*). satisfait la première condition15(*).
 (1.4) (1.4)
La variance du processus  n'est pas convergente, le processus n'est pas convergente, le processus  ne satisfait pas la première condition de stationnarité.
Néanmoins, l'examen d'une réalisation d'un processus de marche
aléatoire ne permet pas à priori de tirer une conclusion sur la
stationnarité ou non du processus, d'où l'intérêt
d'un test d'hypothèses de stationnarité. ne satisfait pas la première condition de stationnarité.
Néanmoins, l'examen d'une réalisation d'un processus de marche
aléatoire ne permet pas à priori de tirer une conclusion sur la
stationnarité ou non du processus, d'où l'intérêt
d'un test d'hypothèses de stationnarité.
Figure 22 :
Simulation d'un processus de marche aléatoire (Random Walk)

La non stationnarité de ce type de processus (Random
Walk) tient au fait que les chocs  s'accumulent au cours du temps, ce qui accroît la variance de s'accumulent au cours du temps, ce qui accroît la variance de  au fur et à mesure que le temps passe. Dans ce cas, on dit que
la non stationnarité est de type stochastique. au fur et à mesure que le temps passe. Dans ce cas, on dit que
la non stationnarité est de type stochastique.
Le type de non stationnarité, déterministe ou
stochastique à de fortes implications que ce soit sur le plan
statistique ou bien sur l'analyse dynamique.
1.2) Stationnarité
déterministe : Trend stationary (TS)
 est un processus TS s'il peut s'écrire sous la forme : est un processus TS s'il peut s'écrire sous la forme :
 où où  est une fonction du temps et est une fonction du temps et  est un processus stochastique stationnaire. est un processus stochastique stationnaire.
Ce type de processus est non stationnaire, on peut citer un
cas très simple d'un processus TS non stationnaire,  , pour ce processus, , pour ce processus,  , dépend de t. en contrepartie, le processus , dépend de t. en contrepartie, le processus  défini par l'écart entre défini par l'écart entre  et la composante déterministe est stationnaire ; et la composante déterministe est stationnaire ;  est un bruit blanc qu'est stationnaire par définition. est un bruit blanc qu'est stationnaire par définition.
1.3)Stationnarité
stochastique : Differency stationnary (DS)
 est un processus DS d'ordre d, si le processus filtré
défini par est un processus DS d'ordre d, si le processus filtré
défini par  est stationnaire est stationnaire
Dans ce type de processus, la non stationnarité a une
source stochastique.
1.3.1) Propriété
des processus DS :
Un processus non stationnaire  est un processus DS intégré d'ordre d, noté I(d),
si le polynôme est un processus DS intégré d'ordre d, noté I(d),
si le polynôme  défini en l'opérateur retard L, associé à
sa composante autorégressive admet d racines unitaires : défini en l'opérateur retard L, associé à
sa composante autorégressive admet d racines unitaires :
 avec avec  (1.5) (1.5)
Ou  est un processus stationnaire, et si les racines du polynôme est un processus stationnaire, et si les racines du polynôme  sont toutes supérieures à l'unité en module. Pour
mieux illustrer ceci, donnons l'exemple suivant : sont toutes supérieures à l'unité en module. Pour
mieux illustrer ceci, donnons l'exemple suivant :
Exemple : considérons le processus ARMA(2,2)
suivant :  , avec , avec  et et  , et , et  , on admet que xt est non stationnaire et l'on cherche
à déterminer si xt est un processus I(d) et quel est
alors son degré d'intégration. Pour cela il suffit de
déterminer le nombre de racines unitaires de , on admet que xt est non stationnaire et l'on cherche
à déterminer si xt est un processus I(d) et quel est
alors son degré d'intégration. Pour cela il suffit de
déterminer le nombre de racines unitaires de  . .
Soient  les racines de les racines de  , on a , on a  et et  .dès lors, le processus xt est I(1), en effet : .dès lors, le processus xt est I(1), en effet :

Ou  admet une racine admet une racine  inférieure à 1 en module. inférieure à 1 en module.
Définition : une marche aléatoire (Random Walk)
est un processus AR(1) intégré d'ordre 1, noté I(1) :
 (1.6) (1.6)
Où  est un bruit blanc i.i.d (0, est un bruit blanc i.i.d (0, ). Si c=0, on a dans ce cas une marche aléatoire pure : ). Si c=0, on a dans ce cas une marche aléatoire pure :
 . (1.7) . (1.7)
Les processus DS ont une propriété de
persistance des chocs, ceci signifie que contrairement aux processus TS, les
chocs  conservent une influence sur la variable I(d). conservent une influence sur la variable I(d).
1.4)Les conséquences
associées à la distinction entre TS et DS :
Les conséquences statistiques de la non
stationnarité :
Les propriétés de stationnarité ou non
des séries déterminent le type de
modélisation et les propriétés
asymptotiques des estimateurs.
Le fait que le processus soit non stationnaire conditionne
à la fois le choix de la modélisation et les
propriétés asymptotiques des estimateurs des
paramètres ; ceci dit, la non stationnarité affecte les
propriétés asymptotiques des statistiques des tests usuels sur
les paramètres. Pour bien comprendre cet enjeu statistique, on va
essayer de simuler une régression entre deux processus de marche
aléatoire qui n'ont théoriquement aucun lien :
 et et  , on va essayer de faire une simulation de réalisation de T=1000
observations de xt et yt, par la méthode MCO16(*), on va essayer d'estimer le
modèle suivant : , on va essayer de faire une simulation de réalisation de T=1000
observations de xt et yt, par la méthode MCO16(*), on va essayer d'estimer le
modèle suivant :
 (1.8) (1.8)
Théoriquement parlant, on s'attend à ce que  , à priori, il n'existe aucune relation entre les deux variables. , à priori, il n'existe aucune relation entre les deux variables.
Le programme sous Eviews de simulation de 1000 observations de
xt et yt nous donne les résultats suivants :
Le programme sous Eviews est le suivant :

Une fois le programme est compilé, le résultat
est reporté ci-dessous :
Le résultat du programme est le suivant :

Cet exemple est une illustration de ce que l'on appelle la
régression fallacieuse (Spurious Regression). En effet, on
s'attendait à ce que  , mais le t-statistique relatif à , mais le t-statistique relatif à  est largement supérieure au seuil de significativité. est largement supérieure au seuil de significativité.
1.5) Les conséquences
économiques de la non stationnarité :
La prise en compte de la non stationnarité a eu des
implications très fortes sur l'analyse économiques des
séries macroéconomiques et microéconomiques, en effet, la
prise en compte de la non stationnarité d'origine stochastiques (DS) a
eu de fortes implications sur les schémas de décomposition
cycle/tendance, ces schémas de décomposition ont
été utilisé pour analyser surtout des séries
macroéconomiques telles le PIB, taux d'inflation, l'évolution des
agrégats monétaires ...etc. dans ce type d'analyse, on suppose
que la série est composée d'un cycle permanent
modélisé par une composante tendancielle17(*), et une composante
stochastiques (innovations), pour modéliser les séries
macroéconomiques, les macroéconomistes utilisaient jusqu'à
la fin des années 80 les schémas de décomposition, cette
décomposition est effectuée à l'aide de l'extraction d'une
tendance déterministe et étudier par la suite la série des
innovations, l'esprit de cet analyse est que les séries suivent une
tendance déterministe qui vient d'être affectée par les
perturbations aléatoires, ces perturbations sont les évolutions
conjoncturels.
Néanmoins, la crise des années 70 a remis en
cause ce type d'analyse, après la crise on s'attendait à ce que
les séries gagnent leur tendance déterministe (niveau
potentiels), mais rien n'a été fait, ceci a conduit à
s'interroger sur le déterministe de la composante tendancielle.
Comme on va le voir par la suite, l'élimination d'une
tendance déterministe de la série est propre aux séries de
type TS, on rappelle que les séries de type TS s'écrivent comme
suit :
 , l'élimination de la tendance déterministe de la
série ne laisse que les perturbations qui sont supposées non
stationnaires. Or, les séries ne sont pas tous de type TS, selon Chan,
Hayya et Ord (1977), p. 741, l'élimination d'une tendance
linéaire d'une marche aléatoire crée artificiellement une
forte corrélation positive des résidus dans les premiers
retards. , l'élimination de la tendance déterministe de la
série ne laisse que les perturbations qui sont supposées non
stationnaires. Or, les séries ne sont pas tous de type TS, selon Chan,
Hayya et Ord (1977), p. 741, l'élimination d'une tendance
linéaire d'une marche aléatoire crée artificiellement une
forte corrélation positive des résidus dans les premiers
retards.
De ce qui précède, il s'avère que la
stationnarisation des séries constitue une étape fondamentale de
la modélisation des séries temporelles.
Ceci étant dit, l'analyse préliminaire qu'on
doit effectuer sur n'importe quelle série, c'est de savoir est ce
qu'elle est de type DS ou bien TS.
1.6)Test de racine
unitaire : Test de Dickey Fuller
Le test de racine unitaire de Dickey et Fuller (1979) est un
test de non stationnarité, considérons le processus AR(1)
suivant :
 (1.9) (1.9)
Où  est la matrice des régresseurs exogènes qui peut
consister à une constante ou bien une constante et un trend, ñ et
ä sont des paramètres à estimer. åt est
supposé un bruit blanc. est la matrice des régresseurs exogènes qui peut
consister à une constante ou bien une constante et un trend, ñ et
ä sont des paramètres à estimer. åt est
supposé un bruit blanc.
Le test de racine unitaire consiste à tester
l'hypothèse nulle de présence d'une racine unitaire contre une
hypothèse alternative unilatérale18(*) ;

Sous l'hypothèse H0, le processus (1.9)
s'écrit comme une marche aléatoire19(*) (Random Walk).
A première vue, ce test peut être vu comme
n'importe quel test unilatéral, il consiste à utiliser une
statistique qui suit la loi de Student sous l'hypothèse H0,
néanmoins, le test de DF diffère des tests classiques du fait que
la distribution asymptotique de la statistiques de Student liée à
l'hypothèse nulle ñ=1 n'est pas standard, autrement dit, au
niveau de la statistique de Student liée à l'hypothèse
nulle, on ne peut pas utiliser cette fois les seuils standards de la lois
Sdudent, qui est approximé par la loi normale, raison pour laquelle, au
niveau du test DF on utilise des seuils différents qui sont
calculés par Dickey et Fuller.
De plus que le changement des seuils de significativité
du test de DF, on doit aussi noter que ces seuils ne sont pas les mêmes,
suivant que le processus (1.9) contient la constante, la tendance ou non. A ce
stade, une question se pose, doit on inclure la constante et le
trend d'une manière systématique ? Afin de répondre
à cette question, Dickey et Fuller ont proposé une
stratégie de test, dénommée stratégie de test de
DF.
Par un exercice de simulations par la méthode de
Monté Carlo, on va montrer que la distribution asymptotique de
l'estimateur  du processus (1.9) sans constante et sans trend est non
symétrique. du processus (1.9) sans constante et sans trend est non
symétrique.
Pour ce faire, on va tirer N échantillons du processus
marche aléatoire
 (1.10), chaque échantillon sera de taille T suffisamment
élevée, pour faire cet exercice on va tirer N=100
échantillons, avec T=5000 observations pour chaque
échantillon. (1.10), chaque échantillon sera de taille T suffisamment
élevée, pour faire cet exercice on va tirer N=100
échantillons, avec T=5000 observations pour chaque
échantillon.
Le programme sous Eviews est le suivant :

Ce mini programme nous donne vers sa fin un vecteur contenant
100 estimations de l'estimateur  , on construisant l'histogramme de ces 100 estimations, le resultat est
reporté ci-dessous : , on construisant l'histogramme de ces 100 estimations, le resultat est
reporté ci-dessous :
Figure 23 : Histogramme
des estimations de l'estimateur rho

Les résultats de ces simulations montrent bel et bien
que l'estimateur  est convergeant, sa moyenne est de 0,9996, de plus, les estimations
semblent être concentrées autour de la vrai valeur 1. Le
résultat le plus intéressant de cet histogramme est que
l'estimateur est asymétrique, ce résultat est bien claire
visuellement comme il est confirmé par la statistique du Skewness. est convergeant, sa moyenne est de 0,9996, de plus, les estimations
semblent être concentrées autour de la vrai valeur 1. Le
résultat le plus intéressant de cet histogramme est que
l'estimateur est asymétrique, ce résultat est bien claire
visuellement comme il est confirmé par la statistique du Skewness.
1.7)Stratégie du test de
Dickey Fuller :
Comme nous l'avons déjà mentionné, les
seuils de significativité du test dépendent de l'inclusion au
niveau du processus (1.10) d'une constante, d'une constante et d'un trend ou
non, pour discriminer entre ces trois situations de ce processus, Dickey et
Fuller ont proposé une stratégie de test de détection de
la non stationnarité conditionnellement au modèle choisi. On
considère les trois modèles suivants :
Modèle 1 :  (1.11) (1.11)
Modèle 2 :  (1.12) (1.12)
Modèle 3 :  (1.13) (1.13)
Pour ces trois modèles, on teste l'hypothèse
nulle  contre l'hypothèse alternative contre l'hypothèse alternative . .
C.Hurlin20(*), dans sons cours de processus stochastique,
résume la stratégie de test de Dickey Fuller comme suit :
Le principe général de la stratégie de tests est le
suivant. Il s'agit de partir du modèle le plus général,
d'appliquer le test de racine unitaire en utilisant les seuils correspondant
à ce modèle, puis de vérifier par un test approprié
que le modèle retenu était le »bon». En effet, si le
modèle n'était pas le »bon», les seuils utilisés
pour le test de racine unitaire ne sont pas valable. On risque alors de
commettre une erreur de diagnostic quant à la stationnarité de la
série. Il convient dans ce cas, de recommencer le test de racine
unitaire dans un autre modèle, plus contraint. Et ainsi de suite,
jusqu'à trouver le »bon» modèle, les »bons»
seuils et bien entendu les »bons» résultats.
Figure 24 :
Stratégie de test de Dickey Fuller

Au niveau de cette stratégie, on commence par tester la
présence de racine unitaire au niveau du modèle le plus
général (1.13), si l'hypothèse de présence de la
racine unitaire est acceptée, dans ce cas on fait un autre test de
nullité du coefficient â de la tendance conditionnellement
à la présence de la racine unité, l'hypothèse
unitaire est la suivante :

Pour tester l'hypothèse  , on utilise une statistique qui suit la loi de Fisher mais
avec les seuils calculés par Dickey et Fuller, si l'hypothèse , on utilise une statistique qui suit la loi de Fisher mais
avec les seuils calculés par Dickey et Fuller, si l'hypothèse
 est acceptée, dans ce cas le modèle (1.13) n'est pas le
modèle adapté pour représenter le processus, on doit donc
effectuer le test de racine unitaire sur le deuxième modèle
(1.12). Si au contraire l'hypothèse est acceptée, dans ce cas le modèle (1.13) n'est pas le
modèle adapté pour représenter le processus, on doit donc
effectuer le test de racine unitaire sur le deuxième modèle
(1.12). Si au contraire l'hypothèse  est rejetée, dans ce cas le troisième modèle est
le bon modèle et il est intégré d'ordre 1, on dit qu'il
I(1). est rejetée, dans ce cas le troisième modèle est
le bon modèle et il est intégré d'ordre 1, on dit qu'il
I(1).
Si on revanche on avait au préalable rejeté
l'hypothèse H0 de présence de la racine unité,
on teste la nullité de â par un test de Student usuel, Si
l'hypothèse â=0 est retenu, on doit revenir au deuxième
modèle (1.12) et tester la présence de la racine unitaire, si
â est différent de 0, le modèle est un TS. Ont refait les
mêmes étapes jusqu'à trouver le bon modèle.
Le test de Dickey Fuller simple décrit ci-dessus
présuppose que les aléas åt des
différents modèles sont une réalisation d'un bruit blanc,
or, rien ne nous garantit que les aléas soient des bruits blancs, de
plus, la plupart des séries économiques sont
caractérisées par l'autocorrélation des aléas, le
test de Dickey Fuller augmenté prend en considération cette
possibilité d'autocorrélation des aléas.
1.8) Test de Dickey Fuller
augmenté
L'approche de Dickey Fuller consiste à inclure dans le
modèle un ou des termes autorégressifs
différenciés, cette approche permet de blanchir les
résidus.
1.8.1) Prise en compte de
l'autocorrélation des résidus par la méthode de Dickey
Fuller
Considérons le processus suivant d'ordre AR(1), avec
les innovations åt sont autocorrélées d'ordre
p-1.
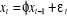 (1.14) (1.14)
Et åt s'écrit ainsi :  (1.15) (1.15)
avec  est un bruit blanc. est un bruit blanc.
On substitue åt par son expression , l'équation (1.15) s'écrit ainsi : , l'équation (1.15) s'écrit ainsi :

De cette transformation, un processus de type AR(1) avec
autocorrélation des résidus d'ordre p-1, peut être
transformé en une représentation de type AR(p), avec les
innovations sont cette fois ci un bruit blanc.
En résumé, pour blanchir les résidus, la
méthode de Dickey et Fuller consiste à introduire des termes de
retards différenciés d'ordre p, jusqu'à ce stade, une
question se pose, comment détermine-t-on l'ordre de retard p ?
1.8.2) Détermination du
nombre de retards p
Si l'autocorrélation des résidus est d'ordre p,
on doit inclure p termes différenciés retardés afin de
tenir compte de l'autocorrélation des aléas, ceci est dit dans le
cas où l'ordre d'autocorrélation est connu, or, cet ordre n'est
pas toujours connu.
Partant de l'idée qu'un bon modèle est celui qui
mainmise les deux critères d'information Akaike21(*) et Schwartz, on commence
à tester plusieurs modèles incluant plusieurs termes p et on
compare les deux critères d'informations, le modèle final qui
sera retenu est celui qui va minimiser ces deux critères.
Une fois que le nombre de retard optimal p est défini,
on obtient une réalisation du processus des innovations  , comme on a déjà noté plus haut, il faut que ces
innovations , comme on a déjà noté plus haut, il faut que ces
innovations  soient un bruit blanc. soient un bruit blanc.
1.8.3) Tests
d'autocorrélation des résidus
Pour montrer que les innovations  sont une réalisation d'un bruit blanc, on utilise le test de Box
et Pierce. Soit rn l'autocorrélation empirique d'ordre n des
résidus sont une réalisation d'un bruit blanc, on utilise le test de Box
et Pierce. Soit rn l'autocorrélation empirique d'ordre n des
résidus  , le test a pour hypothèse nulle , le test a pour hypothèse nulle  contre contre  tel que tel que  , la statistique de test est la suivante : , la statistique de test est la suivante :
 , cette statistique suit approximativement une , cette statistique suit approximativement une , loi khi-deux à (N-k) ddl . nous rejetons don l'hypothèse
nulle de bruit blanc, au seuil á, si la statistique calculée est
supérieure à la valeur , loi khi-deux à (N-k) ddl . nous rejetons don l'hypothèse
nulle de bruit blanc, au seuil á, si la statistique calculée est
supérieure à la valeur  lus dans la table au seuil (1-á) et N degré de
liberté. lus dans la table au seuil (1-á) et N degré de
liberté.
Nous pouvons utiliser aussi une autre statistique, dont les
propriétés asymptotiques sont meilleures, dérivée
de la première qu'est le  de Ljung Box, pour un ordre N, ce test correspond à
l'hypothèse nulle ; de Ljung Box, pour un ordre N, ce test correspond à
l'hypothèse nulle ;  , la statistique est construite ainsi : , la statistique est construite ainsi :
 (1.16) (1.16)
Cette statistique est elle aussi distribuée selon un
 à N degré de liberté et dont les règles de
décision sont identiques à la statistique
précédente. à N degré de liberté et dont les règles de
décision sont identiques à la statistique
précédente.
1.9) Etude de la
saisonnalité :
1.9.1) Analyse de variance
à un facteur
a) signification théorique du test
Pour bien illustrer la notion d'analyse de variance a un
facteur, on va utiliser la notation suivante :
Répétitions
Notations :
j
I
I
r
I
I
1
I
I
Moyenne
I
I
yi
I
I
1
I
I

I
I
i
I
I
I
I
I
On suppose qu'on a I facteurs, chaque facteur est
répété r fois, ou bien on peut dire qu'on a I
échantillons, chaque échantillon contient r individus. L'analyse
de la variance consiste à tester l'hypothèse que les
échantillons ont la même moyenne , cela revient à dire qu'il n'y a pas de différence
significative entre les facteurs. , cela revient à dire qu'il n'y a pas de différence
significative entre les facteurs.
b) Décomposition de la variabilité :
équation d'analyse de la variance
 (1.17) (1.17)
La variabilité totale est expliquée d'une part
par la variabilité due aux facteurs ou bien variabilité inter
classe et la variabilité résiduelle ou intra classe. En faisant
la somme et en élevant au carré les termes de l'équation
de décomposition de la variance, ceci donne :
 (1.18) (1.18)
1.9.2) Test global de l'effet
d'un facteur
L'intuition du test est la suivante, on observe des moyennes
par facteur assez différentes, la différence entre ces moyennes
on va la jauger à l'aune de la variance résiduelle, pour ce
faire, on va calculer un rapport entre le carré moyen22(*) des facteurs et le
carré moyen résiduel. Si on a i facteurs avec r
répétitions, dans ce cas on :  et et  . (1.19) . (1.19)
On note que  un estimateur sans biais, sous l'hypothèse H0
d'absence d'effet facteur, l'espérance du carré moyen factorielle
tend vers un estimateur sans biais, sous l'hypothèse H0
d'absence d'effet facteur, l'espérance du carré moyen factorielle
tend vers  , en effet, , en effet,  sous H0, les sous H0, les  sont nuls, dans ce cas, le rapport entre sont nuls, dans ce cas, le rapport entre  et et  serait au alentour de la valeur 1, les rapport entre ces deux termes
sous H0 suit la loi de Fisher. serait au alentour de la valeur 1, les rapport entre ces deux termes
sous H0 suit la loi de Fisher.
 . (1.20) . (1.20)
Règle de décision : selon l'intuition, dans
le cas d'absence d'effet facteur, le rapport entre  et et  tend vers la valeur 1, autrement dit, l'espérance de ce rapport
est 1. On fixe une valeur limite qui nous permet de tracer la zone
d'acceptation et la zone de rejet, si la valeur observée ou
calculée de F est inférieure à la valeur limite de F, on
accepte H0 c'est-à-dire qu'il y a absence d'effet facteur, si
non accepte H1. tend vers la valeur 1, autrement dit, l'espérance de ce rapport
est 1. On fixe une valeur limite qui nous permet de tracer la zone
d'acceptation et la zone de rejet, si la valeur observée ou
calculée de F est inférieure à la valeur limite de F, on
accepte H0 c'est-à-dire qu'il y a absence d'effet facteur, si
non accepte H1.
1.9.3) Analyse de la variance
et étude de la saisonnalité :
Appliquons le test d'ANOVA pour détecter la
saisonnalité, revient à teste l'hypothèse nulle d'absence
de saisonnalité, c'est-à-dire l'absence d'effet facteur, qui est
le facteur mois dans ce cas, en cas de rejet de l'hypothèse nulle, on
peut dire que l'effet du facteur mois (saisonnalité) est
significatif.
En cas de détection da la saisonnalité de la
série chronologique étudiée, la correction de la
saisonnalité s'impose, la section suivante traite les schémas de
dessaisonalisation et quelques méthodes de correction de la
saisonnalité.
2)Schéma d'analyse
des séries chronologiques et correction des variations
saisonnières.
Les séries temporelles observées à des
fréquences trimestrielles ou bien mensuelles présentent souvent
des mouvements cycliques qui reviennent touts les trimestres ou touts les mois.
A titre d'exemple, les ventes de glaces augmentent pendant la saison
été de chaque année, de même, les ventes de jouets
atteignent le pic pendant chaque mois d'Achoura de l'année. La
correction des variations saisonnières se rapportent au processus
d'élimination de ces mouvements cycliques saisonniers d'une série
et l'extraction de la composante tendance sous-jacente de la série.
2.1) les composantes d'une
série chronologique
On peut généralement distinguer, dans
l'évolution d'une série chronologique, quatre composantes.
2.1.1) Tendance à long
terme ou trend
Le trend représente l'évolution à
très long terme du phénomène, liée à la
croissance générale de l'économie
2.1.2) Mouvement
cyclique
Autour de la tendance à long terme ont lieu de
fluctuations, liées aux variations conjoncturelles et, notamment,
à la succession de phase du cycle économique :
prospérité, crise, dépression, reprise. Par la suite, nous
ne cherchons pas à dissocier trend et mouvement cyclique, on va les
désigner conjointement sous le terme de `'mouvement
extra-saisonnier `' ou, par mouvement conjoncturel.
2.1.3) Variations saisonnières.
Les variations saisonnières sont des fluctuations plus
au moins régulières qui se superposent au mouvement
extra-saisonnier. Leur période peut être journalière
(trafic horaire), hebdomadaire ou annuel. Elles ont de multiples causes, cycle
des saisons, mode de vie, coutumes, etc., dont les effets se produisent
sensiblement à date fixe.
2.1.4) Les variations accidentelles ou
résiduelles
Autour des mouvements précédents se produisent
des fluctuations aléatoires. Elles sont dues soit à un grand
nombre de petites causes -les fluctuations sont alors, en
général, de faible amplitude- soit à l'intervention des
événements occasionnels : grève, krach financier,
modification de la législation fiscale, sociale ou économique,
etc. Elles représentent dans l'évolution de la série la
part dont les composantes précédentes ne peuvent rendre compte.
On leur donne parfois, pour cette raison, le nom de fluctuations
résiduelles.
2.2) les modèles de
décomposition
La série est décomposée en trois
composantes :
-la composante extra-saisonnière ou conjoncturelle
-la composante saisonnière
-les variations aléatoires
Ces trois constituants supposent un certain nombre
d'hypothèses concernant le mode de composition et la nature de ceux-ci.
Désignons le mois par j et l'année par i :
Yij la valeur observée de la série
chronologique ;
Cij la valeur de la composante
conjoncturelle ;
Sij la composante saisonnière et
åij les variations résiduelles
Les modèles de composition les plus simples des
éléments constituants une série chronologique sont les
schémas additif ou multiplicatif.
2.2.1) Schéma additif
Le schéma additif s'écrit sous la forme
suivante :
 (2.20) (2.20)
Ce schéma suppose que la composante saisonnière
de la série, comme la variation résiduelle, est
indépendante du mouvement extra-saisonnier.
2.2.2) Schéma multiplicatif
Le schéma multiplicatif prend la forme suivante :
 (2.21) (2.21)
Cette forme de décomposition admet que la composante
saisonnière, représentée par  , est proportionnel au mouvement conjoncturel. , est proportionnel au mouvement conjoncturel.
2.3) les méthodes de
décomposition
Décomposer une série chronologique consiste donc
à estimer, pour chaque date d'observation, les valeurs de la composante
conjoncturelle ct et de la composante saisonnière
st.
Deux grandes catégories de méthodes sont
utilisées à cette fin : les méthodes analytiques et
les méthodes empiriques.
2.3.1) Les méthodes
analytiques :
Dans les méthodes de ce type, on fait une
hypothèse sur la forme analytique des composantes conjoncturelle et
saisonnière.
On met à titre d'exemple, les hypothèses
suivantes :
-le mouvement conjoncturel est une fonction linéaire du
temps :
 . (2.22) . (2.22)
-le mouvement saisonnier est une fonction rigoureusement
périodique de période p=12 prenant les valeurs  pour une série mensuelle, on a ainsi ; pour une série mensuelle, on a ainsi ;
 et et  etc. etc.
Dans le cas d'un schéma de composition additif :
 , en remplaçant ct et st par leur forme
analytique, ce qui donne : , en remplaçant ct et st par leur forme
analytique, ce qui donne :
 (2.23) (2.23)
Soit en posant :
 , ce qui donne : , ce qui donne :
 (2.24) (2.24)
L'estimation par une méthode appropriée telle
que MCO nous fournit les valeurs de  et et  . .
La méthode analytique présente un certain nombre
d'avantage. Elle jouit, en particulier, de fondements théoriques solides
et permet d'évaluer la variances des paramètres estimés,
néanmoins, elle possède un inconvénient majeur, celui de
n'être applicable qu'à des séries dont la tendance
extra-saisonnière peut être correctement représentée
par une fonction analytique de forme linéaire, exponentielle,
polynôme,....etc. or, pour la plupart des séries chronologiques
relatives à des phénomènes économiques, l'allure de
la composante extra-saisonnière ne permet pas de retenir des
schémas d'évolution simples.
2.3.2) Méthode empirique.
Contrairement aux méthodes analytiques, les
méthodes empiriques ne supposent aucune hypothèse sur l'allure du
mouvement extra-saisonnier, cependant, en l'absence de référence
à un modèle précis, il n'est pas possible de bâtir
une méthode d'analyse rigoureuse. On en est réduit à des
recettes de calcul empirique, toutefois, ces méthodes sont très
utilisées pour l'analyse des phénomènes
économiques. La détermination de la forme du mouvement
extra-saisonnier et la recherche des coefficients saisonniers se font notamment
par le procédé des moyennes mobiles, cette méthode est
facile à mettre en oeuvre et d'application générale, et
elle est implémentée au niveau de la plupart des logiciels de
traitement des séries chronologiques.
La méthode de filtrage par moyennes mobiles est parmi
les techniques de désaisonnalisation les plus utilisées tout
simplement, parce qu'elle est facile à calculer, facile à mettre
à jour, et permet d'éliminer les fluctuations saisonnières
sans modifier les autres composantes de la chronique.
Cette méthode n'est autre qu'une transformation
mathématique de la série : elle s'agit d'une succession de
moyennes arithmétiques de longueur choisie égale à L
(appelée ordre de la moyenne mobile). La formule générale
de filtrage par moyennes mobiles d'ordre p est la suivante:
Soit une série chronologique Y tel que :

On appelle moyenne mobile d'ordre p la série Y,
l'opération transformant celle-ci en une nouvelle série Z par le
calcul de la suite de moyennes successives :


2.3.3) Propriétés de la moyenne mobile :
Si la composante saisonnière est rigoureusement
périodique, par exemple d'ordre p, l'opérateur moyenne mobile de
même longueur p, élimine la composante saisonnière. Cette
propriété est la base des procédés empiriques de
corrections des variations saisonnières, de plus, la méthode des
moyennes mobiles permet à la composante extra-saisonnière de
traverser le filtre sans être déformée et de lisser les
fluctuations résiduelles.
3) Application aux données du
trafic mensuel régulier de passagers au Maroc
3.1) Analyse
préliminaire de la série
La série objet de notre application empirique retrace
l'évolution du trafic régulier enregistré aux
différents aéroports du Maroc de janvier 2005 à
décembre 2012, soit 96 observations, les vols réguliers sont des
vols programmés sur une saison23(*) donnée, suivant des horaires et des
itinéraires fixes, identifié par un numéro de vol.
Pour étudier les séries chronologiques, on
commence on général par une représentation graphique afin
d'avoir une idée sur les différents composantes comme la
saisonnalité et la tendance.
Figure 25 : Evolution
mensuelle du trafic régulier de passagers

Source : Service Statistiques et Prévisions,
ONDA.
Un examen graphique de la série montre clairement le
caractère saisonnier de la série ainsi que la présence
d'une tendance haussière du trafic.
Figure 26 : Moyenne de
la série du trafic par saison (mois)

Source : Service Statistiques et Prévisions,
ONDA.
La figure ci-dessus montre que la moyenne saisonnière
varie d'un mois à l'autre, en effet, la moyenne connait son point de pic
pendant le mois d'août où il y a déplacement massif des
voyageurs pendant la période des vacances, alors qu'elle connait son
point de creux pendant le mois de février.
3.1.1)
Détection de la saisonnalité par le test de
Fisher :
Le test sera effectué sous Excel, par l'utilisation de
l'utilitaire d'analyse de la variance, le test consiste à tester
l'hypothèse nulle d'absence de saisonnalité contre
l'hypothèse alternative.
Résultats du test
|
Analyse de variance: un facteur
|
|
|
|
|
|
|
|
|
|
|
|
|
RAPPORT DÉTAILLÉ
|
|
|
|
|
|
|
Groupes
|
Nombre d'échantillons
|
Somme
|
Moyenne
|
Variance
|
|
|
|
janvier
|
8
|
3664455
|
458056,875
|
7036825869
|
|
|
|
février
|
8
|
3214141
|
401767,625
|
6819098395
|
|
|
|
mars
|
8
|
3727747
|
465968,375
|
8172010040
|
|
|
|
avril
|
8
|
4097696
|
512212
|
6949824894
|
|
|
|
mai
|
8
|
3796177
|
474522,125
|
6095280603
|
|
|
|
juin
|
8
|
3994929
|
499366,125
|
9290312803
|
|
|
|
juillet
|
8
|
5148270
|
643533,75
|
1,6572E+10
|
|
|
|
août
|
8
|
5062838
|
632854,75
|
6078539798
|
|
|
|
septembre
|
8
|
4159654
|
519956,75
|
1,0451E+10
|
|
|
|
octobre
|
8
|
4038308
|
504788,5
|
1,3736E+10
|
|
|
|
novembre
|
8
|
3817104
|
477138
|
8249671591
|
|
|
|
décembre
|
8
|
4113541
|
514192,625
|
8325934375
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ANALYSE DE VARIANCE
|
|
|
|
|
|
|
Source des variations
|
Somme des carrés
|
Degré de liberté
|
Moyenne des carrés
|
F
|
Probabilité
|
Valeur critique pour F
|
|
Entre Groupes
|
4,1485E+11
|
11
|
3,7713E+10
|
4,199
|
5,9973E-05
|
1,9045
|
|
A l'intérieur des groupes
|
7,5443E+11
|
84
|
8981364593
|
|
|
|
|
|
|
|
|
|
|
|
Total
|
1,1693E+12
|
95
|
|
|
|
|
Source : Calcul de l'auteur sur la base des
données du trafic aérien
Le test de Fisher montre clairement que la valeur
calculé 4,19 est largement supérieur à la valeur critique
de F à 5% qui est égale à 1,90. Ainsi, on rejette
l'hypothèse H0 d'absence de saisonnalité et on accepte
l'hypothèse alternative d'existence de la saisonnalité.
3.1.2)
Décomposition de la série du trafic régulier de
passagers.
Pour décomposer la série chronologique de trafic
on va utiliser deux méthodes, l'une graphique et l'autre analytique.
a) La méthode graphique
La méthode graphique appelé la méthode de
la bande, qui consiste à tracer la droite qui passe par les minima et la
droite qui passe par les maxima. Deux cas peuvent se présenter :
Si les droites sont à peu près
parallèles, dans cas le modèle de décomposition est
additif ;
Si les droites ne sont pas parallèles entre
elles ; le modèle est multiplicatif.
Figure 27 : la
méthode de la bande appliquée sur la série du trafic
régulier

Source : Calcul de l'auteur sur la base des
données de l'ONDA.
On remarque que les droites passants par les minima et les
maxima ne sont pas parallèles, en effet, les droites se divergent avec
le temps, ceci implique que la variance est une fonction croissante du temps.
Sur la base de cette méthode graphique, on peut dire que le
modèle de décomposition est multiplicatif. Pour s'assurer du bien
fondé de la méthode de décomposition de la bande, on va
utiliser une méthode analytique plus objective.
b) La méthode analytique du tableau de Buys et
Ballot
Cette méthode consiste à calculer pour chacune
des années la moyenne et l'écart type, puis à
vérifier la liaison entre l'écart type et la moyenne par la
méthode des moindres carrés, autrement dit, on doit chercher
estimer le modèle suivant :  . (3.25) . (3.25)
Deux cas se présentent :
-l'écart type n'est pas une fonction de la moyenne, le
modèle est additif ; la pente de la droite est non
significativement différente de 0 et peut être
considérée comme nulle, l'écart type est à peu
près constant dans le temps.
-l'écart type est fonction de la moyenne, le
modèle est multiplicatif. La pente de la droite est significativement
différente de 0.
Tableau 5 : Tableau de
Buys et Ballot
|
Étiquettes de lignes
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
2012
|
Moyenne
|
Variance
|
|
MED V
|
4329514
|
4846010
|
5762246
|
6131425
|
6321049
|
7158696
|
7204948
|
7080972
|
6104357,5
|
1010874,68
|
|
janvier
|
323825
|
382439
|
402513
|
486760
|
450674
|
513035
|
570728
|
534481
|
458056,875
|
78467,972
|
|
février
|
285062
|
298425
|
345854
|
437523
|
406867
|
461111
|
493828
|
485471
|
401767,625
|
77244,4891
|
|
mars
|
330660
|
348593
|
423898
|
490464
|
478932
|
560311
|
561648
|
533241
|
465968,375
|
84560,6811
|
|
avril
|
369789
|
446172
|
482190
|
489892
|
515398
|
582923
|
613609
|
597723
|
512212
|
77981,3874
|
|
mai
|
353518
|
385994
|
423782
|
486168
|
499897
|
558836
|
550032
|
537950
|
474522,125
|
73029,929
|
|
juin
|
343443
|
385847
|
467354
|
503334
|
514770
|
594343
|
596849
|
588989
|
499366,125
|
90161,0986
|
|
juillet
|
442019
|
502375
|
607997
|
623144
|
665861
|
778969
|
818502
|
709403
|
643533,75
|
120419,293
|
|
août
|
479904
|
549434
|
659713
|
676177
|
671494
|
710251
|
637224
|
678641
|
632854,75
|
72929,571
|
|
septembre
|
404971
|
435369
|
487071
|
445102
|
470128
|
616093
|
638112
|
662808
|
519956,75
|
95625,4032
|
|
octobre
|
315638
|
345907
|
475446
|
524435
|
559356
|
617578
|
594313
|
605635
|
504788,5
|
109631,169
|
|
novembre
|
324870
|
362868
|
463472
|
473049
|
521387
|
561489
|
547642
|
562327
|
477138
|
84961,5363
|
|
décembre
|
355815
|
402587
|
522956
|
495377
|
566285
|
603757
|
582461
|
584303
|
514192,625
|
85353,3396
|
|
Total général
|
4329514
|
4846010
|
5762246
|
6131425
|
6321049
|
7158696
|
7204948
|
7080972
|
6104357,5
|
1010874,68
|
Nous constatons que l'écart type de la série
augmente avec le temps, de plus, la moyenne de la série augmente
à son tour avec le temps, ce qui traduit l'existence d'une tendance
comme composante de la série qui augmente avec le temps.
La régression de l'écart type annuelle sur la
moyenne annuelle nous permet d'estimer le modèle suivant :
 (3.26) (3.26)
La valeur t de Student calculée de la pente est de
15,19, supérieure à la valeur théorique de Student
à 5% qui est de 2,62, dans ce cas on accepte l'hypothèse
alternative H1 que la valeur de la pente est significativement
différente de 0. Ainsi, il s'avère bel et bien que l'écart
type annuelle de la série est une fonction croissante avec la moyenne
annuelle de la dite série et par conséquent le modèle de
décomposition est de type multiplicatif.
Les deux méthodes de décomposition graphique et
analytique concourent à la même conclusion que le modèle de
décomposition de la série est multiplicatif.
c) Correction de la série des variations
saisonnières.
Maintenant que nous savons que la série est
affectée d'une tendance saisonnière et que le modèle de
décomposition de la série chronologique est de type
multiplicatif, nous procédons à l'estimation de la composante
saisonnière et de la retirer de la tendance, pour ce faire, on va
utiliser la méthode de la moyenne mobile qu'on a abordée ses
contours théoriques au troisième paragraphe de la sous section
2.3.
Pour désaisonnaliser la série du trafic, on va
exécuter la commande suivante sous Eviews : seas(options)
series_name name_adjust [name_fac],
-tel que (option) désigne le modèle de
décomposition, m pour un modèle multiplicative et a pour un
modèle additif
-Series_name indique l'intitulé de la série
à corriger ;
-name_adjust est le nom qu'on va attribuer à la
série corrigée des variations saisonnières et ;
-[name_fac] est le nom qu'on va donner aux facteurs
saisonniers.
L'exécution de la commande nous donne les
résultats suivants :
Coefficients saisonniers
|
Date: 02/04/13 Time: 14:43
|
|
Sample: 2005M01 2012M12
|
|
Included observations: 96
|
|
Ratio to Moving Average
|
|
Original Series: PAXREG
|
|
Adjusted Series: PAX_ADJ
|
|
|
|
|
|
|
|
Scaling Factors:
|
|
|
|
|
|
|
|
1
|
0.939103
|
|
2
|
0.813950
|
|
3
|
0.940598
|
|
4
|
1.032110
|
|
5
|
0.944515
|
|
6
|
0.993388
|
|
7
|
1.276256
|
|
8
|
1.272791
|
|
9
|
1.004974
|
|
10
|
0.966333
|
|
11
|
0.918118
|
|
12
|
0.991644
|
|
|
|
|
|
|
La visualisation des la série brute et la série
CVS ou bien ajustée sur un même graphique nous permet d'avoir une
idée sur l'impact de la correction sur la série initiale,
Figure 28 :
Série corrigée des variations saisonnières

Source : Calculs de l'auteur sur la base des données de
l'ONDA
Comme on a déjà mentionnée plus haut, la
correction de la série par la méthode des moyennes mobiles a
permis d'éliminer les variations saisonnières sans toucher
à la tendance.
Maintenant que nous avons détecté et
corrigé la série de ses variations saisonnières, on doit
tester l'existence de la stationnarité, savoir de quel type si elle
existe et puis rendre la série stationnaire par la méthode
adaptée au type de stationnarité.
3.2) Application de la
stratégie des tests de racine unitaire de Dickey et Fuller sur la
série du trafic
La figure 2 montre bien que le processus
générateur de la série ne semble pas satisfaire la
condition d'invariance de l'espérance et de la variance, à cet
effet, on va essayer dans ce qui va suivre d'appliquer la stratégie des
tests de D&F sur la série pour s'assurer si elle est
déjà non stationnaire ou pas, en cas de détection de la
non stationnarité, on doit déterminer son type, si elle
déterministe (TS), ou bien elle est de type stochastique (DS).
Estimation du premier modèle 3
Selon la stratégie du test de D&F, on commence par
estimer le modèle 3, c'est le modèle général qui
contient à la fois la tendance et la constante :
 (3.27) : modèle 3 (3.27) : modèle 3
Pour estimer le modèle 3 on doit tout d'abord commencer
par créer sou Eviews la série du trafic en différence
première ( ) et créer ensuite la série du trend. ) et créer ensuite la série du trend.
L'estimation du modèle 3 par la méthode MCO est
la suivante :
|
Dependent Variable: D(PAX_ADJ)
|
|
|
Method: Least Squares
|
|
|
|
Date: 02/06/13 Time: 09:53
|
|
|
|
Sample (adjusted): 2005M02 2012M12
|
|
|
Included observations: 95 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
PAX_ADJ(-1)
|
-0.598404
|
0.096759
|
-6.184470
|
0.0000
|
|
@TREND(1)
|
1733.036
|
315.0931
|
5.500077
|
0.0000
|
|
C
|
137741.2
|
24581.89
|
5.603360
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.294521
|
Mean dependent var
|
2572.661
|
|
Adjusted R-squared
|
0.279184
|
S.D. dependent var
|
39935.04
|
|
S.E. of regression
|
33905.20
|
Akaike info criterion
|
23.73159
|
|
Sum squared resid
|
1.06E+11
|
Schwarz criterion
|
23.81224
|
|
Log likelihood
|
-1124.251
|
F-statistic
|
19.20388
|
|
Durbin-Watson stat
|
2.216245
|
Prob(F-statistic)
|
0.000000
|
|
|
|
|
|
|
Source
|
|
|
|
|
Source :
On commence tout d'abord par tester la présence d'une
racine unitaire au niveau de processus en testant la nullité du
paramètre  , ce qui nous intéresse particulièrement c'est la
statisistique de Student tö associée à la
variable endogène retardée pax_adj(-1), celle-ci est égale
à -6,18,cette valeur est à comparer avec les seuils24(*) tabulés par D&F
pour le troisième modèle, le logiciel Eviews fournit les valeurs
des seuils de D&F pour les trois modèles et pour les seuils à
1%, 5% et 10%. Au seuil de 5%, le seuil critique est , ce qui nous intéresse particulièrement c'est la
statisistique de Student tö associée à la
variable endogène retardée pax_adj(-1), celle-ci est égale
à -6,18,cette valeur est à comparer avec les seuils24(*) tabulés par D&F
pour le troisième modèle, le logiciel Eviews fournit les valeurs
des seuils de D&F pour les trois modèles et pour les seuils à
1%, 5% et 10%. Au seuil de 5%, le seuil critique est  . Ainsi, dans ce cas pour un niveau de risque de 5%, . Ainsi, dans ce cas pour un niveau de risque de 5%,  , dans ce cas on rejette l'hypothèse nulle de racine unitaire
(ö=0). , dans ce cas on rejette l'hypothèse nulle de racine unitaire
(ö=0).
Tests d'hypothèses jointes :
Les tests d'hypothèse jointes concernent les
modèles 2 et 3, ils permettent de détecter la présence de
la racine unitaire conjointement à la nullité des coefficient
á,â, ou bien les deux à la fois.
Après le test de racine unitaire, on effectue pour le
modèle 3 le test de la première hypothèse jointe :
 contre l'hypothèse alternative l'un des paramètres est
différent. Pour discriminer entre ces deux hypothèses, on va
calculer une statistique qui est analogue à la loi de Fisher, les seuils
critiques de cette statistique sont tabulés par D&F. contre l'hypothèse alternative l'un des paramètres est
différent. Pour discriminer entre ces deux hypothèses, on va
calculer une statistique qui est analogue à la loi de Fisher, les seuils
critiques de cette statistique sont tabulés par D&F.

Ou :  est la somme des carrés des résidus du modèle 3
contraint sous l'hypothèse est la somme des carrés des résidus du modèle 3
contraint sous l'hypothèse . .
T : le nombre d'observations utilisées pour
estimer les paramètres du modèle.
Pour effectuer ce test, on va exécuter le programme
batch en annexe (n° annexe) sous Eviews, le test  qui est supérieure à la valeur lue dans la table de
D&F à 1% ( qui est supérieure à la valeur lue dans la table de
D&F à 1% ( ), dans ce cas on rejette ), dans ce cas on rejette  . .
Selon la stratégie du test de racine unitaire de
D&F, en cas de rejet de l'hypothèse de racine unitaire conjointement
à l'hypothèse , on teste la nullité du coefficient â lié au trend
par un test t de Student standard. Le , on teste la nullité du coefficient â lié au trend
par un test t de Student standard. Le  est supérieur au seuil de t tabulé à 5% , dans ce
cas on rejette l'hypothèse nulle de nullité de â.
D'après ces deux tests, le modèle 3 est un modèle TS
(trend stationary) stationnaire en tendance. est supérieur au seuil de t tabulé à 5% , dans ce
cas on rejette l'hypothèse nulle de nullité de â.
D'après ces deux tests, le modèle 3 est un modèle TS
(trend stationary) stationnaire en tendance.
3.2.1) Analyse de
l'autocorrélation empririque de la série des résidus
L'estimation du modèle 3 suppose que l'aléa  est un processus stationnaire de type bruit blanc, il convient alors de
s'assurer qu'il possède bien les propriétés d'un bruit
blanc. Surtout il convient de s'assurer que celle-ci n'est pas
autocorrélé, puisque par définition on est un processus stationnaire de type bruit blanc, il convient alors de
s'assurer qu'il possède bien les propriétés d'un bruit
blanc. Surtout il convient de s'assurer que celle-ci n'est pas
autocorrélé, puisque par définition on  , si , si  . A cet effet, on va étudier le corrélogramme de la
série des résidus obtenue lors de l'estimation du modèle
3. . A cet effet, on va étudier le corrélogramme de la
série des résidus obtenue lors de l'estimation du modèle
3.
Figure 29 :
Autocorrélogramme d'ordre 12 de la série des
résidus.

Source ;
Pour un ordre k allant de 1 à 12, le
corrélogramme montre la réalisation de l'autocorrélation
empirique d'ordre k définie pour une série zt
par :
 (3.28) (3.28)
La première colonne nous visualise
l'autocorrélation simple (AC) alors que la deuxième colonne
indique l'autocorrélation partielle (PAC), les rhos estimés sont
visualisés par des traits pointillés, le trait qui sort de
l'intervalle de confiance indique qu'il est significativement différent
de la valeur nulle.
On remarque que les autocorrélations simples d'ordre
4,5,7 et 12 sortent de l'intervalle de la région de confiance de
l'hypothèse de nullité, ceci signifie que la série des
résidus du modèle estimé est autocorrélée,
dans ce cas le processus  générateur de la série des résidus n'est
pas un bruit blanc. Or si le processus générateur de la série des résidus n'est
pas un bruit blanc. Or si le processus  n'est pas un bruit blanc i.i.d., cela remet en cause la validité
de l'ensemble des distributions asymptotiques de tests de Dickey et Fuller et
donc les conclusions que nous avons dressé quant à la non
stationnarité de la série. Ceci étant dit, Il est donc
nécessaire de tester la non stationnarité de la série en
prenant tout en compte l'autocorrélation des perturbations n'est pas un bruit blanc i.i.d., cela remet en cause la validité
de l'ensemble des distributions asymptotiques de tests de Dickey et Fuller et
donc les conclusions que nous avons dressé quant à la non
stationnarité de la série. Ceci étant dit, Il est donc
nécessaire de tester la non stationnarité de la série en
prenant tout en compte l'autocorrélation des perturbations  : les tests de Dickey Fuller augmentés viennent pour
remédier à cette lacune, leurs objet et de modéliser les
processus stochastique tout en prenant en compte l'autocorrélation des
perturbations : les tests de Dickey Fuller augmentés viennent pour
remédier à cette lacune, leurs objet et de modéliser les
processus stochastique tout en prenant en compte l'autocorrélation des
perturbations . .
3.3) Tests de Dickey Fuller
augmentés
Ne pas prendre en considération l'hypothèse de
l'autocorrélation des aléas  lors de l'estimation du modèle de Dickey Fuller, viole une
hypothèse essentielle du modèle, en effet, la violation de cette
hypothèse rends les statistiques des tests de Dickey Fuller non
asymptotiques, par conséquent les seuils de significativité des
tests de racine unitaires seront différents. lors de l'estimation du modèle de Dickey Fuller, viole une
hypothèse essentielle du modèle, en effet, la violation de cette
hypothèse rends les statistiques des tests de Dickey Fuller non
asymptotiques, par conséquent les seuils de significativité des
tests de racine unitaires seront différents.
Il y a deux approches permettant de tenir compte de
l'éventuelle autocorrélation des aléas  : :
a) Approche de Philips et Perron (1988) : cette approche
consiste à proposer une correction des estimateurs des MCO et des
statistiques de Student associées à ces estimateurs prenant en
compte la possible autocorrelation des résidus.
b) L'approche de Dickey Fuller (1979) : contrairement
à l'approche de Philips et Perron, cette approche consiste à
contrôler directement l'autocorrélation dans le modèle et
non au niveau des estimateurs, cette approche consiste à inclure une ou
plusieurs termes autorégressifs différenciés.
Dans la suite, on va utiliser la deuxième approche, car
elle mène à une représentation similaire à celle du
test de Dickey Fuller simple, ainsi, nous retrouvons les mêmes
distributions asymptotiques et nous utilisons par conséquent les
mêmes tables de Dickey Fuller qu'on a utilisé
précédemment (cf. ss 1.8.1).
Si on prend en compte l'autocorrélation d'ordre p+1 des
innovations  pour un processus d'ordre AR(1), les trois modèles
utilisés pour développer le test ADF sont les suivants : pour un processus d'ordre AR(1), les trois modèles
utilisés pour développer le test ADF sont les suivants :
Modèle 4 :  (3.29) (3.29)
Modèle 5 :  (3.30) (3.30)
Modèle 6 :  (3.31) (3.31)
3.3.1)Stratégie du test
ADF :
La stratégie du test ADF consiste en une
première étape à déterminer le nombre de retards p
permettant de rendre les résidus une réalisation d'un processus
de bruit blanc, dans la seconde étape, il suffit d'appliquer la
stratégie séquentielle du test de Dickey Fuller simple (cf.
figure 2) aux modèles (3.29), (3.30) et (3.31).
Le principal avantage de la démarche d'ADF, c'est que
les seuils de significativité pour les tests DF et ADF de racine
unitaire sont identiques.
3.3.2) Application
des tests de Dickey Fuller augmentés (ADF) sur la série du
trafic :
La présence de l'autocorrélation des
résidus constitue une violation d'une hypothèse fondamentale
d'application des tests de DF simples, en effet, comme on a déjà
noté plus haut (cf section 3.3), les distributions ne sont plus
asymptotiques et les seuils de significativité des tests seront
différents, les tests ADF viennent pour prendre en considération
l'autocorrélation des résidus.
Suivant la stratégie de D&F, on commence par
estimer le modèle 6, qui contient à la fois la tendance et la
constante. Pour fixer le nombre de retards optimal, on va utiliser le
critère d'information de Schwarz, selon ce critère, pour blanchir
la série des résidus, on doit utiliser trois termes
différenciés retardés.
Les résultats du test ADF sont consignés au
tableau ci-dessous
|
Null Hypothesis: PAX_ADJ has a unit root
|
|
|
Exogenous: Constant, Linear Trend
|
|
|
Lag Length: 3 (Automatic based on SIC, MAXLAG=6)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic
|
Prob.*
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic
|
-1.728309
|
0.7308
|
|
Test critical values:
|
1% level
|
|
-4.060874
|
|
|
5% level
|
|
-3.459397
|
|
|
10% level
|
|
-3.155786
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation
|
|
|
Dependent Variable: D(PAX_ADJ)
|
|
|
Method: Least Squares
|
|
|
|
Date: 02/25/13 Time: 16:06
|
|
|
|
Sample (adjusted): 2005M05 2012M12
|
|
|
Included observations: 92 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
PAX_ADJ(-1)
|
-0.203340
|
0.117653
|
-1.728309
|
0.0875
|
|
D(PAX_ADJ(-1))
|
-0.697894
|
0.135016
|
-5.168968
|
0.0000
|
|
D(PAX_ADJ(-2))
|
-0.554213
|
0.131170
|
-4.225141
|
0.0001
|
|
D(PAX_ADJ(-3))
|
-0.311303
|
0.105147
|
-2.960641
|
0.0040
|
|
C
|
85526.74
|
42547.35
|
2.010154
|
0.0475
|
|
@TREND(2005M01)
|
508.8135
|
370.5493
|
1.373133
|
0.1733
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.467018
|
Mean dependent var
|
2510.240
|
|
Adjusted R-squared
|
0.436031
|
S.D. dependent var
|
40584.28
|
|
S.E. of regression
|
30477.93
|
Akaike info criterion
|
23.55039
|
|
Sum squared resid
|
7.99E+10
|
Schwarz criterion
|
23.71485
|
|
Log likelihood
|
-1077.318
|
F-statistic
|
15.07127
|
|
Durbin-Watson stat
|
2.077710
|
Prob(F-statistic)
|
0.000000
|
|
|
|
|
|
|
|
|
|
|
3.3.3) Interprétation des résultats et tests
d'hypothèses jointes
La statistique du t empirique lié au coefficient
ö=-1,78 est supérieure à la valeur lue dans la table
à 1% (=-4,06), dans ce cas, on retient l'hypothèse nulle
d'existence d'une racine unitaire, la série n'est pas stationnaire.
Selon la stratégie des test de D&F, après le test de
recherche du racine unitaire on doit effectuer les tests d'hypothèses
jointes.
L'hypothèse jointe consiste à tester la
nullité du coefficient de la tendance conjointement à la
nullité de ö,  , pour tester l'hypothèse , pour tester l'hypothèse  on doit calculer la statistiques suivante : on doit calculer la statistiques suivante :
 où : où :
 est la somme des carrés des résidus du modèle 6
contraint par est la somme des carrés des résidus du modèle 6
contraint par  . .
La statistique  est analogue à la loi de Fisher, les seuils critiques de cette
statistique sont tabulés par D&F. est analogue à la loi de Fisher, les seuils critiques de cette
statistique sont tabulés par D&F.
Pour une taille d'échantillon de 100 observations
(T=100) pour le modèle 3 contenant la constante et la tendance, la
valeur critique de F tabulée par D&F est 6,49, on a alors,  , dans ce cas on retient , dans ce cas on retient  . .
En poursuivant toujours le schéma de la
stratégie de D&F, on doit tester une autre hypothèse jointe
en cas d'acceptation de l'hypothèse jointe  , cette hypothèse consiste à tester la nullité
simultanée des coefficients , cette hypothèse consiste à tester la nullité
simultanée des coefficients  . .
 . .
Pour discriminer entre l'hypothèse 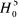 et l'hypothèse alternative, on va utiliser une statistiques F,
elle aussi analogue à loi de Fisher, dont les valeurs sont
tabulées par D&F. et l'hypothèse alternative, on va utiliser une statistiques F,
elle aussi analogue à loi de Fisher, dont les valeurs sont
tabulées par D&F.

La valeur critique de Fuller à 5% pour un
échantillon de taille 100 du test F pour le modèle 6 contenant la
tendance et la constante est 6,49, dans ce cas on a  , dans ce cas on accepte , dans ce cas on accepte  de la nullité des coefficient c, b et ö. de la nullité des coefficient c, b et ö.
La stratégie des tests de D&F nous emmène
à l'estimation des paramètres du modèle 5 en cas
d'acceptation de l'hypothèse  , le modèle 5 de par sa construction ne contient pas la tendance
mais par contre il contient la constante, il s'écrit comme suit : , le modèle 5 de par sa construction ne contient pas la tendance
mais par contre il contient la constante, il s'écrit comme suit :
 . .
Estimation du modèle 5 et test de racine unitaire
:
|
Null Hypothesis: PAX_ADJ has a unit root
|
|
|
Exogenous: Constant
|
|
|
|
Lag Length: 3 (Automatic based on SIC, MAXLAG=6)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic
|
Prob.*
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic
|
-1.320082
|
0.6175
|
|
Test critical values:
|
1% level
|
|
-3.503049
|
|
|
5% level
|
|
-2.893230
|
|
|
10% level
|
|
-2.583740
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation
|
|
|
Dependent Variable: D(PAX_ADJ)
|
|
|
Method: Least Squares
|
|
|
|
Date: 02/28/13 Time: 15:15
|
|
|
|
Sample (adjusted): 2005M05 2012M12
|
|
|
Included observations: 92 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
PAX_ADJ(-1)
|
-0.050461
|
0.038226
|
-1.320082
|
0.1903
|
|
D(PAX_ADJ(-1))
|
-0.816838
|
0.104092
|
-7.847245
|
0.0000
|
|
D(PAX_ADJ(-2))
|
-0.632572
|
0.118706
|
-5.328918
|
0.0000
|
|
D(PAX_ADJ(-3))
|
-0.347751
|
0.102258
|
-3.400722
|
0.0010
|
|
C
|
33600.81
|
19599.07
|
1.714409
|
0.0900
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.455333
|
Mean dependent var
|
2510.240
|
|
Adjusted R-squared
|
0.430291
|
S.D. dependent var
|
40584.28
|
|
S.E. of regression
|
30632.64
|
Akaike info criterion
|
23.55034
|
|
Sum squared resid
|
8.16E+10
|
Schwarz criterion
|
23.68739
|
|
Log likelihood
|
-1078.315
|
F-statistic
|
18.18264
|
|
Durbin-Watson stat
|
2.111856
|
Prob(F-statistic)
|
0.000000
|
|
|
|
|
|
|
|
|
|
|
L'application du test D&F augmenté sur le
modèle 5 contenant la constante montre la présence d'une racine
unitaire de la série Pax-adj, en effet, la statistique
tö de la variable endogène retardée Pax-adj(-1)
=-1,32, cette valeur est à comparer avec la valeur des seuils de D&F
pour le deuxième modèle. Au seuil de 5%, on a  , selon l'estimation du modèle 5, la , selon l'estimation du modèle 5, la  , on alors , on alors  dans ce cas on accepte l'hypothèse nulle de la présence
d'une racine unitaire (ö=0). dans ce cas on accepte l'hypothèse nulle de la présence
d'une racine unitaire (ö=0).
L'acceptation de la présence d'une racine unitaire au
niveau du modèle 5 nous emmène à tester l'hypothèse
jointe  , cette hypothèse suppose la nullité de ö
conjointement à la nullité de la constante ; , cette hypothèse suppose la nullité de ö
conjointement à la nullité de la constante ;  contre l'hypothèse alternative contre l'hypothèse alternative  au moins un des éléments est différent. au moins un des éléments est différent.

La valeur de la statistique  , cette valeur est à comparer avec les valeurs de la distribution
théorique de ö pour le modèle 5 au niveau de la table IV de
D&F, pour une taille d'échantillon de 100 observations et pour un
risque d'erreur de 5%, la valeur limite est 4,71, ainsi on a , cette valeur est à comparer avec les valeurs de la distribution
théorique de ö pour le modèle 5 au niveau de la table IV de
D&F, pour une taille d'échantillon de 100 observations et pour un
risque d'erreur de 5%, la valeur limite est 4,71, ainsi on a  dans ce cas on accepte l'hypothèse nulle dans ce cas on accepte l'hypothèse nulle 
Après le test de l'hypothèse , il faut tester la nullité de la moyenne , il faut tester la nullité de la moyenne  de la série. de la série.
|
Hypothesis Testing for PAX_ADJ
|
|
|
Date: 03/04/13 Time: 15:39
|
|
|
Sample: 2005M01 2012M12
|
|
|
Included observations: 96
|
|
|
Test of Hypothesis: Mean = 0.000000
|
|
|
|
|
|
|
|
|
|
|
Sample Mean = 504795.9
|
|
|
Sample Std. Dev. = 89724.46
|
|
|
|
|
|
|
Method
|
Value
|
Probability
|
|
t-statistic
|
55.12398
|
0.0000
|
|
|
|
|
|
|
|
|
La moyenne de la série est largement et
significativement différent de 0. Le processus générateur
de la série est une marche au hasard sans dérive.
3.3) L'identification du
processus générateur ARMA
La série étant stationnarisée, il faut
par la suite chercher quel est le processus générateur de la
chronique dans la classe des processus ARMA linéaire et stationnaire.
La recherche du processus générateur dans la
classe des processus ARMA stationnaire constitue l'étape
d'identification dans l'approche de Box&Jenkins, elle consiste à
trouver parmi les processus ARMA celui qui est susceptible de
représenter au mieux les données empiriques.
L'identification du processus ARMA selon l'approche de
Box&Jenkins se fait par la comparaison entre des caractéristiques
empiriques de la chronique et théoriques des processus ARMA.
xt
Identification
ARAM
1
1
3
Comparaison
Caractéristiques théoriques
Caractéristiques empiriques
2
Selon l'approche de Box&Jinkins, pour identifier le
processus ARMA générateur, on doit recourir à la fonction
d'autocorrélation simple FAC et à la fonction
d'autocorrélation partielle FAP de la chronique en question.
Les deux fonctions d'autocorrélation simple et
partielle sont alors calculées sur la série en différence
première.
Figure 30 :
Corrélogramme de la série en différence
première.

3.3.1) Analyse des
fonctions FAC et PAC.
Les traits pointillés du corrélogramme
désigne les rk, un terme qui sort de l'intervalle de
confiance est significativement différent de 0.
Test d'un coefficient d'autocorrélation
Le test d'hypothèses pour un terme ñk
est le suivant :

Sous l'hypothèse H0, l'intervalle de
confiance du coefficient ñk est donné par :

Si le coefficient calculé se trouve en dehors de
l'intervalle de confiance calculé, il est significativement
différent de 0 au seuil á.
l'analyse du corrélogramme des deux fonctions
d'autocorrélation simple et partielle de la série en
différence première nous révèle que le premier
terme ainsi que le terme d'ordre 12 de la fonction d'autocorrélation
simple sont différents de 0, de plus, les termes de
l'autocorrélation partielle connaissent une décroissance amortie,
ainsi, on peut anticiper que le processus est un SARIMA(1,1,1), avec s=12, dans
ce cas le processus s'écrit ainsi : ARIMAs(P,D,Q),
ARIMA12(1,1,1), en développant le processus il s'écrit
ainsi : 
3.3.2) Estimation et test de
validation du modèle ARMA
Maintenant que le processus générateur de la
série est identifié, on peut estimer dans un premiers temps les
paramètres du modèle retenu et dans un deuxième temps
vérifier par des tests statistiques la validité du modèle
retenu.
3.3.2.1)Estimation du modèle identifié
L'estimation du modèle identifié consiste
à estimer les paramètres des parties AR et MA du processus,
l'échantillon qu'on va utiliser est le résultat d'une
transformation en différence première25(*).
Les résultats d'estimation du modèle sont
consignés au tableau ci-dessous
|
Dependent Variable: DPAX
|
|
|
|
Method: Least Squares
|
|
|
|
Date: 03/21/13 Time: 19:15
|
|
|
|
Sample (adjusted): 2006M02 2012M12
|
|
|
Included observations: 83 after adjustments
|
|
|
Convergence achieved after 13 iterations
|
|
|
Backcast: 2006M01
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
AR(1)
|
-0.357064
|
0.112406
|
-3.176563
|
0.0021
|
|
AR(12)
|
0.576252
|
0.091244
|
6.315502
|
0.0000
|
|
MA(1)
|
-0.401964
|
0.133873
|
-3.002567
|
0.0036
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.573728
|
Mean dependent var
|
2192.625
|
|
Adjusted R-squared
|
0.563072
|
S.D. dependent var
|
41089.16
|
|
S.E. of regression
|
27160.16
|
Akaike info criterion
|
23.29237
|
|
Sum squared resid
|
5.90E+10
|
Schwarz criterion
|
23.37979
|
|
Log likelihood
|
-963.6332
|
Durbin-Watson stat
|
1.931330
|
|
|
|
|
|
|
|
|
|
|
|
Inverted AR Roots
|
.93
|
.80+.48i
|
.80-.48i
|
.45-.82i
|
|
.45+.82i
|
-.03-.95i
|
-.03+.95i
|
-.51-.82i
|
|
-.51+.82i
|
-.86+.47i
|
-.86-.47i
|
-.99
|
|
Inverted MA Roots
|
.40
|
|
|
|
|
|
|
|
|
|
|
|
|
3.3.2.2) Les tests de validation du modèle
estimé
la partie AR du modèle ARMA estimé est
stationnaire, en effet, les racines du polynôme  sont à l'extérieur du plan complexe, on a sont à l'extérieur du plan complexe, on a  et et  . .
De plus, la racine de la partie MA est a son tour
extérieure du cercle unité du plan complexe, ceci assure la
condition d'inversibilité du processus MA.
Les coefficients de AR(1) AR(12) et MA(1) sont tous
significativement différents de 0, les trois coefficients ont tous des t
de Student largement supérieurs à 1,96 en valeur absolue.
3.3.2.3) Analyse des résidus.
La qualité de l'estimation du processus est
mesurée par la différence entre la chronique calculée et
la chronique empirique, la série des résidus calculée sur
la base de la différence entre les valeurs observées et les
valeurs calculées doit être une réalisation d'un bruit
blanc.
Figure 31 : Evolution
comparée de la chronique empirique (actuel) et la chronique
calculée (fitted)

La confrontation entre la chronique empirique et la chronique
calculée nous montre que les deux séries se comportent à
peu près de la manière, ceci est un signe d'une bonne
qualité d'ajustement.
Comme on a déjà noté plus haut, la
série de résidus doit être une réalisation d'un
processus de bruit blanc normal.
3.3.2.4)Test de nullité de la moyenne des
résidus.
La série est dite une réalisation d'un bruit
blanc normal si l'espérance de sa moyenne est nulle.
|
Hypothesis Testing for RESIDARMA
|
|
|
Date: 03/24/13 Time: 13:46
|
|
|
Sample (adjusted): 2006M02 2012M12
|
|
|
Included observations: 83 after adjustments
|
|
Test of Hypothesis: Mean = 0.000000
|
|
|
|
|
|
|
|
|
|
|
Sample Mean = 2926.754
|
|
|
Sample Std. Dev. = 26664.81
|
|
|
|
|
|
|
Method
|
Value
|
Probability
|
|
t-statistic
|
0.999969
|
0.3203
|
|
|
|
|
|
|
|
|
la valeur de la statistique du tá/2 est
inférieure à 1,96, dans ce cas on ne peut pas rejeter
l'hypothèse H0 de nullité de la moyenne de la
série des résidus.
3.3.2.5)Test de normalité de la série des
résidus
La normalité de la série des résidus une
condition nécessaire pour effectuer les tests de Student sur les
paramètres estimés et aussi pour calculer des intervalles de
confiance prévisionnels.
· Tests du Skewness (asymétrie) et de Kurtosis
(applatissement)
Le coefficient de Skewness est calculé par la formule
suivante :  tel que uk est le moment centré d'ordre k. tel que uk est le moment centré d'ordre k.
Le coefficient de Kurtosis  . Si la distribution est normale et le nombre d'observation est
suffisamment grand, on a alors : . Si la distribution est normale et le nombre d'observation est
suffisamment grand, on a alors :
 et et

Sur la base de  et et  on construit les statistiques suivantes : on construit les statistiques suivantes :
 et et  , ces deux statistiques on va les comparer à 1,96. Si , ces deux statistiques on va les comparer à 1,96. Si  et et  dans ce cas on ne peut pas rejeter les deux hypothèses nulles de
symétrie et d'aplatissement. dans ce cas on ne peut pas rejeter les deux hypothèses nulles de
symétrie et d'aplatissement.
Figure 32 :
Histogramme de la série des réalisations des
résidus

la réalisation de la série des résidus
nous fournit les valeurs de Skewness  et de Kurtosis et de Kurtosis . .
Dans ce cas on a  on a alors on a alors  dans ce cas on ne peut pas rejeter l'hypothèse nulle, la
série des résidus est symétrique. dans ce cas on ne peut pas rejeter l'hypothèse nulle, la
série des résidus est symétrique.
De plus, on  on accepte l'hypothèse nulle H0 d'applatissement
normal. on accepte l'hypothèse nulle H0 d'applatissement
normal.
La série des résidus a une espérance de
moyenne nulle,elle est symétrique et a un applatissement normal, dans ce
cas il semble que la série des résidus est une réalisation
d'un bruit blanc normal.
· Test de Jarque et Bera
Le test de Jarque et Bera consiste à calculer la
statistique s qui est dérivée de  et et  , en effet, la statistique s est
calculée comme suit : , en effet, la statistique s est
calculée comme suit :  , cette statistique suit la loi khi-deux à 2 degrés de
liberté. Si , cette statistique suit la loi khi-deux à 2 degrés de
liberté. Si  on rejette la normalité des résidus au seuil á. on rejette la normalité des résidus au seuil á.
Pour la série des résidus dont on dispose, on
 , dans ce cas on accepte l'hypothèse nulle de normalité
des résidus au seuil 5%. , dans ce cas on accepte l'hypothèse nulle de normalité
des résidus au seuil 5%.
Une série est dite réalisation d'un bruit blanc
si elle n'est pas autocorrélée, le corrélogramme de la
série des résidus nous visualise les termes rk qui
sont significativement différents de 0.
Figure 33 : Le
corrélogramme de la série des résidus

Les termes du corrélogramme de la série des
résidus sont tous à l'intérieure l'intervalle de
confiance.
3.3.2.6)Tests de recherche d'autocorrélation
Comme on a déjà noté plus haut, une
série est une réalisation d'un bruit blanc si elle n'est pas
autocorrélée, pour tester l'autocorrélation
résiduelle, on va utiliser les deux tests de Box-Pierce et de
Ljung-Box.
· Test de Ljung-Box
Ce test permet de tester l'hypothèse nulle
H0 suivante :
 contre l'hypothèse alternative H1 qu'il existe au
moins un ñi significativement différent de 0. La
statistique Q est calculé comme suit : contre l'hypothèse alternative H1 qu'il existe au
moins un ñi significativement différent de 0. La
statistique Q est calculé comme suit :  . .
Sous l'hypothèse nulle, cette statistique est
distribuée asymptotiquement comme un ÷2, avec le
degré de liberté est égal au nombre de retards. Si la
série représente les résidus d'une estimation ARMA, le
degré de liberté doit être ajustée, il est
égal au nombre de retards retenus moins les termes AR et MA
estimés.
Cette statistique en l'absence d'autocrrélation suit un
÷2á, avec í=K-(p+q), tel que k le nombre de
retards, p est l'ordre de la partie AR et q est l'ordre de la partie MA. Pour
un retard k=15, on a Q=12,947 et
÷2(5% ; (15-(1+1))=22,36, on a alors Q<
÷2(5% ;13), le test de Box-Pierce ne nous permet pas de
rejeter H0, dans cas touts termes ñi tel que
i=1,2....15 sont tous non significativement différents de 0.
· Tests d'homoscédasticité des
résidus.
Contrairement au test de Durbin-Watson qui ne permet de
détecter que la corrélation sérielle d'ordre 1, le test LM
peut être utilisé pour tester une autocorrélation d'ordre
p, de plus, ce test peut être utilisé même lors de
l'inclusion des variables endogènes retardées en tant que
variables explicatives.
L'hypothèse nulle du test LM c'est qu'il n'y a pas
d'autocorrélation d'ordre p. ce test consiste a construire une
régression entre les résidus, la matrice des régresseurs X
et les résidus de retard p, à partir de cette regression on
calcule LM=n*R2 , cette statistique LM est distribuée sous
H0 comme un ÷2 à p degrés de
liberté.
|
Breusch-Godfrey Serial Correlation LM Test:
|
|
|
|
|
|
|
|
|
|
|
|
|
F-statistic
|
0.955433
|
Probability
|
0.389101
|
|
Obs*R-squared
|
0.996804
|
Probability
|
0.607501
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Test Equation:
|
|
|
|
Dependent Variable: RESID
|
|
|
|
Method: Least Squares
|
|
|
|
Date: 03/24/13 Time: 23:58
|
|
|
|
Presample missing value lagged residuals set to zero.
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
AR(1)
|
-0.082577
|
0.140996
|
-0.585672
|
0.5598
|
|
AR(12)
|
-0.043805
|
0.098213
|
-0.446017
|
0.6568
|
|
MA(1)
|
0.482640
|
0.623271
|
0.774366
|
0.4411
|
|
RESID(-1)
|
-0.356139
|
0.644836
|
-0.552293
|
0.5823
|
|
RESID(-2)
|
-0.327184
|
0.280628
|
-1.165898
|
0.2472
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.012010
|
Mean dependent var
|
2926.754
|
|
Adjusted R-squared
|
-0.038656
|
S.D. dependent var
|
26664.81
|
|
S.E. of regression
|
27175.31
|
Akaike info criterion
|
23.31636
|
|
Sum squared resid
|
5.76E+10
|
Schwarz criterion
|
23.46207
|
|
Log likelihood
|
-962.6287
|
Durbin-Watson stat
|
2.017588
|
|
|
|
|
|
|
|
|
|
|
le test LM nous donne la valeur de n*R2=0,996,
cette valeur est à comparer au ÷2 à 2 dll, en
effet, on a  , on a , on a  , dans ce cas on ne peut pas rejeter l'hypothèse nulle que la
chronique des résidus est bel et bien homoscédastique. , dans ce cas on ne peut pas rejeter l'hypothèse nulle que la
chronique des résidus est bel et bien homoscédastique.
CHAPITRE III :
Modélisation multivariée du trafic aérien : Les
processus VAR
1) La modélisation
VAR
1.1) Définition d'un modèle VAR
Pour bien définir un modèle VAR, on va commencer
par le cas simple où on a que deux variables,  et et  , ces deux variables sont définies par la relation
suivante : , ces deux variables sont définies par la relation
suivante :
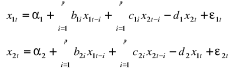  (1.1) (1.1)
Les variables  et et  sont considérées stationnaires, les innovations
å1t et å2t sont des bruits blancs, de
variances sont considérées stationnaires, les innovations
å1t et å2t sont des bruits blancs, de
variances  et et  constantes et sont non corrélées, constantes et sont non corrélées,  . Le processus vectoriel . Le processus vectoriel  peut s'écrire sous la forme d'un processus AR(p). En
effet ; peut s'écrire sous la forme d'un processus AR(p). En
effet ;
 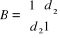   (1.2) (1.2)
On a alors immédiatement :
 (1.3) (1.3)
On qualifie cette représentation de VAR (Vectorial
Autoregressive) d'ordre p, noté VAR(p).
L'expression matricielle (1.3) est qualifiée de
représentation structurelle. On constate que dans cette
représentation le niveau de  a un effet immédiat sur a un effet immédiat sur  et vice versa. L'estimation de ce modèle suppose donc d'estimer
(4*p)+4 paramètres. Cette forme structurelle suppose l'estimation de
plusieurs paramètres, raison pour laquelle on est amené à
travailler sur la forme réduite du modèle VAR. ce modèle
est obtenu en multipliant les deux termes de l'expression (1.3) par
B-1, il s'écrit alors sous la forme suivante : et vice versa. L'estimation de ce modèle suppose donc d'estimer
(4*p)+4 paramètres. Cette forme structurelle suppose l'estimation de
plusieurs paramètres, raison pour laquelle on est amené à
travailler sur la forme réduite du modèle VAR. ce modèle
est obtenu en multipliant les deux termes de l'expression (1.3) par
B-1, il s'écrit alors sous la forme suivante :
 (1.4) (1.4)
Avec :

Selon l'expression (1.4), le niveau de  ne dépend plus directement du niveau de ne dépend plus directement du niveau de  mais il ne dépend que des valeurs passées de mais il ne dépend que des valeurs passées de  et et  et de l'innovation et de l'innovation  . .
Dans la spécification (1.4), les erreurs  et et  sont fonction des innovations sont fonction des innovations  et et  . .
L'expression (1.4) peut s'écrire à l'aide de
l'opérateur de retard :
 (1.5) (1.5)
La représentation VAR (1.5) est dite stationnaire si
elle satisfait les conditions suivantes :
  ; ;
 ; ;
  . .
Un processus VAR(p) est stationnaire si le polynôme
défini à partir du déterminant  a ses racines à l'extérieur du cercle unité du
plan complexe. a ses racines à l'extérieur du cercle unité du
plan complexe.
1.2) Estimation des paramètres du modèle
VAR
L'estimation des paramètres du modèle VAR
suppose que les séries sont stationnaires26(*).
1.2.1) Approche d'estimation
Pour estimer les coefficients d'un modèle VAR, on peut
estimer les paramètres de chaque équation du VAR par MCO ou bien
par le maximum de vraisemblance.
Soit le modèle VAR(p) estimé : 
On doit signaler que le vecteur 
1.2.2) Détermination du nombre de retard d'un
modèle VAR
Pour déterminer le nombre de retards optimal pour un
VAR(p), on estime tous les modèles VAR pour des ordres p allant de 0
à un certain ordre h fixé soit par le nombre de retards maximum
pour la taille de l'échantillon considéré ou bien par une
théorie ou une intuition économique. Pour chacun des ces
modèles, on calcule la fonction AIC(p) et SC(p) de la façon
suivante :
 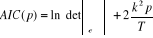
 où T est le nombre d'observations, k est le nombre de variables
du système et où T est le nombre d'observations, k est le nombre de variables
du système et  est la matrice des variances covariances des résidus du
modèle. est la matrice des variances covariances des résidus du
modèle.
1.3)Application sur la série du trafic
aérien
La série du trafic aérien a été
analysée au chapitre II consacré à l'analyse
univariée, en effet, cette série est affectée d'une
tendance saisonnière et elle n'est pas stationnaire. La procédure
de Box&Jenkins a montré que la série du trafic est
stationnaire par la différence première.
Un lien très étroit existe entre
l'évolution des activités économiques et
l'évolution de la demande de trafic aérien, l'accroissement des
activités économiques induit une augmentation du PIB. Le tourisme
est considéré comme une partie des loisirs, l'augmentation de la
richesse induit plus de dépenses consacrées aux loisirs et in
fine plus de dépenses pour le tourisme.
Figure 34 : Lien
entre le volume de trafic passagers et le volume des touristes

Source : C. Bontemps. Demand for air transportation.
Cours de MBA Aviation. Luis Business School.
Le graphique (1.1) montre que le volume des touristes est
à la fois une variable explicative et expliquée par le volume de
trafic aérien, par conséquent, la modélisation des deux
chroniques par un modèle de type VAR s'avère acceptable.
1.3.1)Source des données des entrées de
touristes.
Les données sur les entrées des touristes par
voie aérienne ont été collectées sur la base des
fiches de police de la Directions Générale de la Sureté
Nationale (DGSN) au niveau de chaque poste de frontière aérien,
ces fiches contiennent plusieurs informations pertinentes, on cite à
titre d'exemple, poste de frontière d'entrée, la provenance, la
destination, la nationalité, motif de voyage....etc.
1.3.2)Analyse préliminaire de la chronique des
entrées des touristes
Figure 35 : Evolution
des la série mensuelle des entrées des touristes par voie
aérienne, poste frontière Med V

Source : Calculs de l'auteur sur la base des
données du ministère du tourisme.
La série mensuelle des entrées des touristes au
niveau du poste frontière MedV semble affectée d'une composante
saisonnière, la chronique enregistre des pics pendant la saison
d'été et des creux pendant la saison hivernale.
Figure 36 : Moyenne
des entrées des touristes par saison (mois), poste frontière Med
V.

Source : Calculs de l'auteur sur la base des
données du ministère du tourisme.
La moyenne de la chronique des entrées des touristes
par saison montre bel et bien que la chronique est affectée d'une
tendance saisonnière, à cet effet, il convient d'éliminer
cette composante saisonnière. L'analyse de la série
révèle que le modèle de décomposition est de type
multiplicatif.
Figure 37 : Evolution
comparée da série brute et la série ajustée des
variations saisonnières

Source : Calculs de l'auteur sur la base des
données du ministère du tourisme
La désaisonnalisation de la série a permis
lisser la série, les pics et les creux ont été
atténués, de plus, la tendance a été
conservée.
1.3.3) Etude de la stationnarité de la chronique des
entrées des touristes.
a)Etude des fonctions
d'autocorrélation simple et partielle.
Les corrélogrammes des fonctions
d'autocorrélation simple (AC) et partielle (PAC) montre que la
série n'est pas une réalisation d'un bruit blanc, en effet, le
corrélogramme de l'AC a tous ses termes à l'extérieur de
l'intervalle de confiance à 5%, de plus, le premier terme du
corrélogramme de la PAC est significativement différent de 0. La
chronique est autocorrélée et par conséquent le processus
générateur de la chronique n'est pas une réalisation d'un
bruit blanc. La statique Q de Ljung-Box pour un retard de 12 est  , selon ce test, on refuse l'hypothèse de nullité des
coefficients , selon ce test, on refuse l'hypothèse de nullité des
coefficients  pour pour  . .
Figure 38 : Fonctions
d'autocorrélation simple et partielle de la série des
entrées des touristes pour un retard de 12.

Source : Calculs de l'auteur sur la base des
données du ministère du tourisme
b)Test de Dickey et Fuller
augmenté.
Les fonctions d'autocorrélation nous ont permis de
conclure que le processus générateur de la chronique des
entrées des touristes n'est pas une réalisation d'un bruit blanc,
à partir des tests de Dickey et Fuller on va essayer d'examiner si le
processus est non stationnaire.
Tableau : Résultats du test ADF
|
Null Hypothesis: TOUR_ADJ has a unit root
|
|
|
Exogenous: Constant
|
|
|
|
Lag Length: 3 (Automatic based on SIC, MAXLAG=11)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic
|
Prob.*
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic
|
-1.493422
|
0.5326
|
|
Test critical values:
|
1% level
|
|
-3.503049
|
|
|
5% level
|
|
-2.893230
|
|
|
10% level
|
|
-2.583740
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation
|
|
|
Dependent Variable: D(TOUR_ADJ)
|
|
|
Method: Least Squares
|
|
|
|
Date: 04/14/13 Time: 17:04
|
|
|
|
Sample (adjusted): 2005M05 2012M12
|
|
|
Included observations: 92 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
TOUR_ADJ(-1)
|
-0.052935
|
0.035445
|
-1.493422
|
0.1389
|
|
D(TOUR_ADJ(-1))
|
-0.702376
|
0.098581
|
-7.124833
|
0.0000
|
|
D(TOUR_ADJ(-2))
|
-0.595958
|
0.111316
|
-5.353774
|
0.0000
|
|
D(TOUR_ADJ(-3))
|
-0.477265
|
0.097849
|
-4.877557
|
0.0000
|
|
C
|
10196.29
|
5139.257
|
1.984001
|
0.0504
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.438565
|
Mean dependent var
|
789.0132
|
|
Adjusted R-squared
|
0.412752
|
S.D. dependent var
|
15100.29
|
|
S.E. of regression
|
11571.67
|
Akaike info criterion
|
21.60332
|
|
Sum squared resid
|
1.16E+10
|
Schwarz criterion
|
21.74038
|
|
Log likelihood
|
-988.7528
|
F-statistic
|
16.99001
|
|
Durbin-Watson stat
|
2.095171
|
Prob(F-statistic)
|
0.000000
|
|
|
|
|
|
|
|
|
|
|
la statistique du t-Student liée à la
variable TOUR_ADJ(-1)=-1,49, cette statistique est à comparer avec les
valeurs critiques tabulées par Dickey et Fuller, pour un risque d'erreur
de 5%, la valeur critique tabulée est de  , on a , on a  , dans ce cas on ne peut pas rejeter l'hypothèse nulle du test
(Null Hypothesis: TOUR_ADJ has a unit root), le processus
générateur n'est pas stationnaire. Le test d'ADF nous montre de
plus que le processus générateur n'est pas stationnaire, il est
aussi de type DS, dans ce cas, pour stationnariser la série, il faut
passer en différence. , dans ce cas on ne peut pas rejeter l'hypothèse nulle du test
(Null Hypothesis: TOUR_ADJ has a unit root), le processus
générateur n'est pas stationnaire. Le test d'ADF nous montre de
plus que le processus générateur n'est pas stationnaire, il est
aussi de type DS, dans ce cas, pour stationnariser la série, il faut
passer en différence.
Tableau : Résultats du test ADF sur la
série TOUR_ADJ en différence première.
|
Null Hypothesis: D(TOUR_ADJ) has a unit root
|
|
|
Exogenous: Constant
|
|
|
|
Lag Length: 2 (Automatic based on SIC, MAXLAG=11)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic
|
Prob.*
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic
|
-11.45268
|
0.0001
|
|
Test critical values:
|
1% level
|
|
-3.503049
|
|
|
5% level
|
|
-2.893230
|
|
|
10% level
|
|
-2.583740
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation
|
|
|
Dependent Variable: D(TOUR_ADJ,2)
|
|
|
Method: Least Squares
|
|
|
|
Date: 04/14/13 Time: 17:25
|
|
|
|
Sample (adjusted): 2005M05 2012M12
|
|
|
Included observations: 92 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
D(TOUR_ADJ(-1))
|
-2.837527
|
0.247761
|
-11.45268
|
0.0000
|
|
D(TOUR_ADJ(-1),2)
|
1.102552
|
0.184721
|
5.968743
|
0.0000
|
|
D(TOUR_ADJ(-2),2)
|
0.487106
|
0.098307
|
4.954945
|
0.0000
|
|
C
|
2746.655
|
1245.069
|
2.206025
|
0.0300
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.798767
|
Mean dependent var
|
-87.28984
|
|
Adjusted R-squared
|
0.791907
|
S.D. dependent var
|
25543.59
|
|
S.E. of regression
|
11652.28
|
Akaike info criterion
|
21.60690
|
|
Sum squared resid
|
1.19E+10
|
Schwarz criterion
|
21.71654
|
|
Log likelihood
|
-989.9172
|
F-statistic
|
116.4346
|
|
Durbin-Watson stat
|
2.084168
|
Prob(F-statistic)
|
0.000000
|
|
|
|
|
|
|
|
|
|
|
le passage en différence première de la
série TOUR_ADJ a permis de la stationnariser, en effet,  dans ce cas on rejette l'hypothèse nulle H0
d'existence d'une racine unitaire. La différence première a
permis de stationnariser la chronique. dans ce cas on rejette l'hypothèse nulle H0
d'existence d'une racine unitaire. La différence première a
permis de stationnariser la chronique.
1.4) Spécification du modèle VAR
Le volume des touristes est à la fois une variable
explicative et expliquée par le volume de trafic aérien (cf.S
4.3), a cet effet, on va essayer de modéliser, sous la forme VAR, le
volume de trafic (pax_adj) et le volume des entres des touristes (Tour_adj),
pour ce faire, on dispose des données mensuelles corrigées des
variations saisonnières sur les deux séries de janvier 2005
à décembre 2012, soit 96 observations, ceci est dit, notre
modèle VAR qu'on doit estimer ses paramètres sera comme
suit :
 , où le vecteur , où le vecteur
1.4.1)Détermination de l'ordre du modèle
VAR
Pour déterminer l'ordre du modèle VAR, on va
utiliser les deux critères d'Akaike et Shwarz, le bon modèle est
celui qui minimise ces deux critères. On va estimer le modèle VAR
pour des décalages allant de 0 à 3 retards.
Pour un ordre h=2, le modèle sera écrit
ainsi :

Estimation du modèle VAR pour un ordre h=1

pour un VAR(p), les formules de calcul des critères
d'AIC et SC sont les suivantes :
 et et

Pour calculer ces deux critères, on doit
générer la matrice des résidus et calculer le
déterminant de la matrice des variances covariances.
On a  , soit le déterminant de , soit le déterminant de 
Pour p=1
Ona  et et
 . .
Tableau 6 :
Résumé des des calculs des deux critères pour les retards
de 1 à 3.
|
p
|
n
|
SC
|
AIC
|
|
1
|
95
|
39,4219
|
39,3143
|
|
2
|
94
|
39,1537
|
38,9373
|
|
3
|
94
|
39,2064
|
38,8818
|
Source : Calculs de l'auteur sur la base des
données ONDA et MT.
D'après le tableau ci-dessus, il s'avère que le
modèle de deux retards est celui qui minimise le critère de
Shwarz (39,15)27(*)
1.4.2)Estimation des paramètres du modèle
VAR(2)
Le modèle VAR(2) estimé s'écrit
ainsi :
 (-0,25) (4,16)
(4,91) (-1,47) (-0,25) (4,16)
(4,91) (-1,47)
R2=0,88, (.) =t de Student
 (-1,44) (1,09)
(4,68) (2,04) (-1,44) (1,09)
(4,68) (2,04)
R2=0,86, (.) =t de Student.
1.4.3)Prévision du trafic aérien via le
modèle VAR
La modélisation VAR en tant que telle, a pour objectif
de déceler les liens contemporains et dynamiques entre les variables,
sans tenir compte de restrictions issues des théories
économiques. Les liens dynamiques de court terme représentent les
principaux déterminants de l'évolution future de chaque variable.
Si une telle hypothèse peut être acceptée pour une
évolution à court terme, il est évident que pour un
horizon de moyen ou long terme les prévisions par la modélisation
VAR s'avère d'une utilité limitée. Le modèle VAR
qu'on spécifié et estimé ses paramètres on va
l'utiliser pour faire une prévision du premier trimestre de
l'année 2013.
Les prévisions sont calculées comme suit :
 

Tableau 7 :
Résumé des prévisions pour le premier trimestre 2013 pour
les deux variables.
|
Période
|
PAX_ADJ
|
TOUR_ADJ
|
|
2012m11
|
612477,6
|
166852
|
|
2012m12
|
589226,6
|
154480,7
|
|
2013m1
|
572745,165
|
158961,7718
|
|
2013m2
|
574723,791
|
157934,3101
|
|
2013m3
|
561529,242
|
157521,6735
|
Source : Calculs sur la base des données ONDA et
ministère tourisme
Le tableau ci-dessous donne les résultats des
prévisions tout en tenant compte des coefficients saisonniers de chaque
variable
Tableau 8 :
Prévisions avec prise en compte des variations
saisonnières
|
Période
|
PAX_ADJ
|
TOUR_ADJ
|
CS PAX_ADJ
|
CS TOUR_ADJ
|
PAX
|
TOUR
|
|
2012m11
|
612477,6
|
166852
|
0,918118
|
0,860283
|
562327
|
143540
|
|
2012m12
|
589226,6
|
154480,7
|
0,991644
|
1,037483
|
584303
|
160271
|
|
2013m1
|
572745,165
|
158961,7718
|
0,939103
|
0,78607
|
537867
|
124955
|
|
2013m2
|
574723,791
|
157934,3101
|
0,81395
|
0,777723
|
467796
|
122829
|
|
2013m3
|
561529,242
|
157521,6735
|
0,940598
|
0,906472
|
528173
|
142789
|
Source :
Pour juger la qualité des prévisions fournies par
notre modèle VAR, on doit calculer la variance de l'erreur de
prévision, sa formule est la suivante : 
 est calculée comme suit : est calculée comme suit :  avec avec  et et 
La variance de l'erreur de prévision pour chacune des
prévisions de k variables  se lit sur la première diagonale de la matrice se lit sur la première diagonale de la matrice  .l'intervalle de prévision pour un seuil de (1-á) est
calculé comme suit : .l'intervalle de prévision pour un seuil de (1-á) est
calculé comme suit :  . .
Selon la formule de la variance de l'erreur de
prévision ; on a pour h=1

La variance de l'erreur de prévision pour  est égale à 906 000 000, alors que la variance de l'erreur
de prévision de la variable est égale à 906 000 000, alors que la variance de l'erreur
de prévision de la variable  . .
L'intervalle de confiance pour  est donné par : est donné par : 
Les deux bornes de l'intervalle de confiance de la variable des
entrées des touristes pour le premier mois de l'année 2013 est
donnée par : 
Pour l'horizon h=2, on a  ,or on a : ,or on a : 
Ce qui donne : 
Selon les résultants de l'estimation de notre
modèle VAR(2) retenu on a : 
On a : 

L'intervalle de confiance pour  est donné par : est donné par : 
On peut aussi calculer l'intervalle de confiance (h=2) pour la
deuxième variable :

On constate que les intervalles de confiance
s'élargissent au fur et à mesure que l'horizon h augmente, ceci
est dû à l'accroissement de la variance de l'erreur de
prévision.
1.4.4)Réponses impulsionnels et structure dynamique du
modèle VAR
Un choc sur la  variable n'affecte pas directement que cette variable n'affecte pas directement que cette  variable mais le choc est transmis aux autres variables endogènes
à travers la structure dynamique du modèle VAR. la fonction de
réponse impulsionnelle retrace l'effet d'un choc des innovations
à un moment donnée sur les valeurs actuelles et futures des
variables endogènes. Pour illustrer l'effet d'un choc des innovations
sur les autres variables, on va essayer de simuler l'effet d'un choc d'une
unité positive sur la première variable, pour se faire, on va
créer une matrice de choc d'ordre (2,1) qui va contenir les valeurs 1 et
0. variable mais le choc est transmis aux autres variables endogènes
à travers la structure dynamique du modèle VAR. la fonction de
réponse impulsionnelle retrace l'effet d'un choc des innovations
à un moment donnée sur les valeurs actuelles et futures des
variables endogènes. Pour illustrer l'effet d'un choc des innovations
sur les autres variables, on va essayer de simuler l'effet d'un choc d'une
unité positive sur la première variable, pour se faire, on va
créer une matrice de choc d'ordre (2,1) qui va contenir les valeurs 1 et
0.
On a le choc suivant : 
En période t on a :  ; ;
En période t+1 on a : 
Tableau 9 : Analyse des
chocs sur les varables pax_adj et tour_adj

Figure 39 : Fonctions
de réponses impulsionnelles

Source : Calculs de l'auteur
On constate que l'effet du choc s'estompe avec le temps, d'une
période à une autre, l'effet du choc sur les deux variables
diminue progressivement, ceci est une caractéristique des modèles
VAR stationnaires.
1.4.5)Décomposition de la variance
Alors que la fonction d'impulsion retrace les effets d'un
choc survenu sur une variable endogène et ses répercussions sur
les autres variables du VAR, la décomposition de la variance
sépare la variation d'une variable endogène sur les composantes
du choc du modèle VAR. ainsi, la décomposition de la variance
nous informe sur l'importance relative de chaque innovation en termes d'impact
sur les variables du VAR.
Tableau 10 :
Décomposition de la variance
|
|
|
|
|
|
|
|
|
Variance Decomposition of PAX_ADJ:
|
|
|
|
|
Period
|
S.E.
|
PAX_ADJ
|
TOUR_ADJ
|
|
|
|
|
|
|
|
|
|
1
|
30932.54
|
45.34642
|
54.65358
|
|
|
(6.74186)
|
(6.74186)
|
|
2
|
37290.05
|
31.24334
|
68.75666
|
|
|
(5.63641)
|
(5.63641)
|
|
3
|
41310.35
|
29.63427
|
70.36573
|
|
|
(6.11597)
|
(6.11597)
|
|
4
|
46283.70
|
23.61931
|
76.38069
|
|
|
(5.53493)
|
(5.53493)
|
|
5
|
48985.59
|
21.33160
|
78.66840
|
|
|
(5.69667)
|
(5.69667)
|
|
6
|
52232.64
|
18.76608
|
81.23392
|
|
|
(5.60431)
|
(5.60431)
|
|
7
|
54572.30
|
17.19234
|
82.80766
|
|
|
(5.68499)
|
(5.68499)
|
|
8
|
56862.63
|
15.83713
|
84.16287
|
|
|
(5.77399)
|
(5.77399)
|
|
9
|
58792.14
|
14.82564
|
85.17436
|
|
|
(5.90729)
|
(5.90729)
|
|
10
|
60530.44
|
13.99886
|
86.00114
|
|
|
(6.06035)
|
(6.06035)
|
|
|
|
|
|
|
|
|
|
Variance Decomposition of TOUR_ADJ:
|
|
|
|
|
Period
|
S.E.
|
PAX_ADJ
|
TOUR_ADJ
|
|
|
|
|
|
|
|
|
|
1
|
13281.72
|
0.000000
|
100.0000
|
|
|
(0.00000)
|
(0.00000)
|
|
2
|
15060.58
|
1.449920
|
98.55008
|
|
|
(2.07392)
|
(2.07392)
|
|
3
|
17288.37
|
1.106487
|
98.89351
|
|
|
(1.92657)
|
(1.92657)
|
|
4
|
19012.91
|
1.368384
|
98.63162
|
|
|
(2.76744)
|
(2.76744)
|
|
5
|
20301.58
|
1.227298
|
98.77270
|
|
|
(3.23367)
|
(3.23367)
|
|
6
|
21549.50
|
1.234151
|
98.76585
|
|
|
(3.85394)
|
(3.85394)
|
|
7
|
22513.43
|
1.187400
|
98.81260
|
|
|
(4.40273)
|
(4.40273)
|
|
8
|
23414.18
|
1.167276
|
98.83272
|
|
|
(4.91653)
|
(4.91653)
|
|
9
|
24167.35
|
1.148313
|
98.85169
|
|
|
(5.37767)
|
(5.37767)
|
|
10
|
24844.78
|
1.132374
|
98.86763
|
|
|
(5.78552)
|
(5.78552)
|
|
|
|
|
|
|
|
|
|
Cholesky Ordering: TOUR_ADJ PAX_ADJ
|
|
|
|
|
Standard Errors: Monte Carlo (100 repetitions)
|
|
|
|
|
|
|
|
|
|
|
|
Source :
le tableau ci-dessus relatif à la
décomposition de la variance nous indique que la variance de l'erreur de
prévision de pax_adj est due à 14% à ses propres
innovations et à 86% aux innovations de tour_adj. La variance de
l'erreur de prévision de la deuxième variable (tour_adj) est en
revanche due à 98% à ses propres innovations et à 2% aux
innovations de pax_adj.
1.5)Analyse de la causalité entre les deux
variables
On dit que la variable x1t cause la variables
y2t au sens de Granger si la prédictibilité de
y1t est améliorée lorsque l'information relative
à x2t est incorporée dans l'analyse.
La décomposition de la variance nous a donné une
idée préliminaire en termes d'influence réciproque entre
les deux variables en cas d'un choc d'innovation sur l'une des variables,
néanmoins, pour avoir une idée plus précise sur le sens de
causalité dans le sens de Granger, on doit mener soit un test de Fisher
classique ou bien calculer un ratio de vraisemblance.
Soit un VAR(2) : 
Dans le sens de Granger, on dit que la variable y2t
ne cause pas la variable y1t si les coefficients de y2t
au niveau de la première équation sont significativement nuls,
autrement dit, dire que y2t ne cause pas y2t consiste
à tester l'hypothèse suivante H01 :

Pour tester l'hypothèse H0, on va mener
un test de Fisher classique qui consiste à discriminer entre
l'hypothèse H0 et l'hypothèse alternative, pour se
faire, on va estimer le modèle contraint et le modèle libre et
puis comparer leurs sommes des carrées des résidus.
1.5.1)Test de causalité entre le volume de trafic
passagers (pax_adj) et les entrées des touristes (tour_adj)
a)Test de la
première hypothèse H01 : tour_adj ne cause pas pax_adj
Estimation du modèle contraint : 
R2=0,84 SCRR=1,08E+11
n=94
Estimation du modèle libre :
 R2=0,88 SCRR= 85200000000 n=94 R2=0,88 SCRR= 85200000000 n=94
Calcul de la statistique F de Fisher : 
On a  , on rejette l'hypothèse H0, la variable tour_adj
explique significativement la variable pax_adj. Selon la terminologie de
Granger, on dit que la variable les entrées des touristes (tour_adj)
explique le volume du trafic de passagers (pax_adj). , on rejette l'hypothèse H0, la variable tour_adj
explique significativement la variable pax_adj. Selon la terminologie de
Granger, on dit que la variable les entrées des touristes (tour_adj)
explique le volume du trafic de passagers (pax_adj).
b)Test de la
deuxième l'hypothèse H02 : le volume de passagers (pax_adj)
ne cause pas la variables des entrées des touristes (tour_adj).
Cette hypothèse consiste à tester la
nullité du bloc des paramètres de la variable pax_adj au niveau
de la deuxième équation du modèle VAR, ceci revient
à tester l'hypothèse H02 : 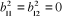
Pour tester la nullité de l'hypothèse
H02 on va passer par un test de Fisher classique qui va discriminer
entre le modèle libre et le modèle contraint sous
H02.
Estimation du modèle contraint sous H02 :

R2=0,85 SCRR= 1,62E+10
n=94
Estimation du modèle libre :
 R2=0,85 SCRR= 1,57E+10
n=94 R2=0,85 SCRR= 1,57E+10
n=94
On a  dans ce cas on accepte H02, le volume du trafic passagers ne
cause pas les entrées des touristes. dans ce cas on accepte H02, le volume du trafic passagers ne
cause pas les entrées des touristes.
Il est important de noter que l'énnoncé
`'tour_adj cause traf_adj dans le sens de Granger n'implique pas que le volume
de trafic est l'effet ou bien le résultat des entrées des
touristes, la causalité au sens de Granger indique l'amélioration
de la prédictibilité de la variable pax_adj lorsque l'information
antérieure sur la variable tour_adj est incorporée dans
l'analyse, la causalité n'est pas interprétée ici avec son
sens commun.
1.6)Problèmes d'estimation des variables
intégrées.
Plusieurs problèmes se posent lorsqu'on veut
vérifier l'existence d'une relation linéaire entre plusieurs
variables dont certaines ont une tendance stochastique (donc une racine
unitaire), et lorsqu'on veut estimer les paramètres de cette
relation.
Même si, dans la réalité, aucune relation
linéaire ne lie ces variables, une estimation par MCO peut donner des
résultats qui font croire faussement qu'une telle relation existe et
qu'elle est importante (R2 élevé,
t-stats des paramètres estimés significatifs...). C'est
le phénomène bien connu de régression fallacieuse
ou régression factice (spurious regression en
anglais) [GRA 1974] et [PHI 1986]. En fait, l'existence d'une réelle
relation a long terme entre des variables intégrées est soumise a
certaines conditions, appelées cointégration entre les
variables intégrées. En d'autres termes, si les
variables sont intégrées (ce que l'on vérifie avec les
tests de racine unitaire), il faut vérifier leur éventuelle
cointégration pour savoir si elles entretiennent réellement une
relation à long terme. Ces conditions de cointégration sont
détaillées dans ce chapitre, ainsi que des méthodes
permettant de vérifier empiriquement une éventuelle
cointégration entre des variables intégrées
observées.
En cas de cointégration entre les variables
explicatives et la variable dépendante, les tests d'hypothèse
usuels ne suivent pas les lois Student ou asymptotiquement normales, toutefois,
d'autres techniques d'estimation permettent de générer des tests
d'hypothèse sur les coefficients cointégrants, qui utilisent des
distributions connues.
1.6.1)Définition de la cointégration :
Des processus stochastiques  intégrés du même ordre d sont
cointégrés s'il existe une combinaison linéaire de ces
processus qui est intégrée d'un ordre inférieur à
d. il faut qu'il existe une b > 0 et des valeurs intégrés du même ordre d sont
cointégrés s'il existe une combinaison linéaire de ces
processus qui est intégrée d'un ordre inférieur à
d. il faut qu'il existe une b > 0 et des valeurs  vérifiant : vérifiant :
 est est  et ; et ;
Chaque variable est 
Le vecteur  est le vecteur de cointégration est le vecteur de cointégration
1.6.2)Test de cointégration d'Engle et Granger
Le test d'Engle et Granger est une méthode de
vérification de l'existence d'une relation de cointégration entre
des variables intégrées et d'estimation de cette relation. Cette
méthode est valable sous l'hypothèse arbitraire qu'il existe un
seul vecteur de cointégration entre les variables utilisées, et
que b=d.
Le raisonnement est le suivant : en cas de
cointégration entre les variables  , il existe des valeurs , il existe des valeurs  telles que ; telles que ;
 est est 
Est donc tel que :  est aussi est aussi 
Et donc telles que :  est aussi est aussi 
Où les coefficients sont normalisés :  . .
Tout processus  est forcément égal à une constante plus un
processus est forcément égal à une constante plus un
processus  d'espérance nulle. La stationnarité de d'espérance nulle. La stationnarité de  implique que : implique que :

Où u est une constante et í est un processus
stochastique stationnaire  d'espérance nulle, la cointégration implique que : d'espérance nulle, la cointégration implique que :
 , les coefficients cointégrants normalisés , les coefficients cointégrants normalisés  sont les seuls pour lesquels í possède les
propriétés suivantes : sont les seuls pour lesquels í possède les
propriétés suivantes :
Il est stationnaire  ; ;
· Il n'a pas de tendance stochastique ;
· Il n'a pas de racine unitaire et ;
· Il a une variance constante
Les coefficients cointégrants de l'équation
précédente sont susceptibles d'être estimés par
MCO.
Tester la cointégration entre les variables revient
donc à estimer par MCO une équation linéaire où
l'une de ces variables est régressée sur les autres et à
tester si le résidu a une racine unitaire. Si l'on ne rejette pas
l'hypothèse de racine unitaire pour le résidu estimé, les
variables de l'équation ne sont pas cointégrées ; si
on la rejette, elles le sont.
1.6.3)Cointégration et mécanise à
correction d'erreur
Selon le théorème de représentation de
Granger, en cas de cointégration entre des variables
intégrées d'ordre 1, l'évolution de chacune d'elles est
régie nécessairement par un modèle à correction
d'erreur. Pour chaque variable cointégrée, un modèle
linaire existe, où la variation de la variable est une fonction de ses
variations passées et variations passées des autres variables,
ainsi que de la valeur passée de l'expression
cointégrée.

Où  est un processus stochastique de type bruit blanc. Un tel modèle
est dit à correction d'erreur ou bien mécanisme à
correction d'erreur. est un processus stochastique de type bruit blanc. Un tel modèle
est dit à correction d'erreur ou bien mécanisme à
correction d'erreur.
L'expression cointégrée retardée,
notée  , représente l'écart par rapport à la relation
d'équilibre à la période , représente l'écart par rapport à la relation
d'équilibre à la période  . Le paramètre ëi correspond donc au taux de
réaction de la variable Yi à l'écart
précédent par rapport à l'équilibre.
ëi mesure ainsi l'intensité avec laquelle la variable
Yi varient pour corriger l'erreur de la période . Le paramètre ëi correspond donc au taux de
réaction de la variable Yi à l'écart
précédent par rapport à l'équilibre.
ëi mesure ainsi l'intensité avec laquelle la variable
Yi varient pour corriger l'erreur de la période  par rapport à l'équilibre. C'est pourquoi on parle de
modèle à correction d'erreur, le paramètre
ëi doit forcément avoir un signe négatif. par rapport à l'équilibre. C'est pourquoi on parle de
modèle à correction d'erreur, le paramètre
ëi doit forcément avoir un signe négatif.
a)Test de
cointégration entre deux variables
La démarche de Granger et Engel est
réalisée en deux étapes, la première étape
consiste à tester l'ordre d'intégration des variables, les deux
variables doivent être intégrée de même ordre, si
non, elles ne peuvent pas être cointégrée. La
deuxième étape de la démarche consiste à estimer la
relation de long terme, on estime par MCO l'équation suivante :

La relation de cointégration est accéptée
si le résidu et issu de la régression
précédente est stationnaire28(*). Si le résidu est bel et bien stationnaire, on
peut estimer le modèle à correction d'erreur
b)Estimation du
modèle à correction d'erreur
Une fois que le test de cointégration conclut que les
deux variables sont non stationnaires et cointégrées, on doit
estimer leurs relations à travers d'un modèle à correction
d'erreur (ECM).
· Estimation du modèle à correction
d'erreur en deux étapes
La première étape consiste à estimer par
MCO la relation de long terme  , la deuxième étape consiste à estimer par les MCO
de la relation dynamique (court terme) : , la deuxième étape consiste à estimer par les MCO
de la relation dynamique (court terme) :

· Test de cointégration entre le volume de
passagers et les entrées de touristes
Pour tester la cointégration entre la variable pax_adj
et tour_adj on va adopter la démarche de Granger et Engel. Comme on a
déjà noté plus haut, le test se déroule en deux
étapes, la première étape consiste à tester si les
deux variables sont intégrées du même ordre alors que la
deuxième étape vise à estimer la relation de long
terme.
· Etape 1 : identification de l'ordre
d'intégration des variables.
Avant d'identifier l'ordre d'intégration des variables,
on doit s'assurer si elles sont non stationnaires en niveau. Le tableau
ci-dessous visualise les résultats des tests.
Tableau 11 :
Résultats des testes de Dickey et Fuller appliqués sur les deux
variables
|
Modèle
|
t Stat de pax_adj
|
seuil du test à 5%
|
t Stat de tour_adj
|
seuil du test à 5%2
|
|
1
|
2,17
|
-1,94
|
1,76
|
-1,94
|
|
2
|
-1,32
|
-2,89
|
-1,49
|
-2,89
|
|
3
|
-1,72
|
-3,45
|
-0,92
|
-3,45
|
Source : Calculs de l'auteur
Les résultats des trois tests ADF appliqués sur
les deux variables montrent que les deux séries sont non stationnaires
en niveau. Les trois tests d'ADF concluent que
tö1>cá pour les trois modèles.
· Stationnarisation des deux chroniques.
Les tests de Dickey Fuller indiquent que les deux
séries sont stationnaires par différence première, elles
sont toutes les deux I(1), à cette étape, on peut dire
que les deux séries risquent d'être cointégrées.
La condition nécessaire de la cointégration est
vérifiée, les deux séries sont intégrées du
même ordre, à cet effet, on peut estimer par MCO la relation de
long terme :  . .

N=96 R2=0,92
L'estimation par MCO de la relation de long terme nous permet
de générer la série des résidus, parmi les
conditions d'acceptation de l'existence d'une relation de long terme entre les
deux séries, la série des résidus issue de l'estimation de
la relation de long terme doit être stationnaire.
· Test de stationnarité de la série des
résidus.
Le test de DF appliqué sur la série des
résidus nous indique qu'elle est stationnaire en niveau.
|
Null Hypothesis: RESID_EC has a unit root
|
|
|
Exogenous: Constant
|
|
|
|
Lag Length: 1 (Automatic based on SIC, MAXLAG=11)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic
|
Prob.*
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic
|
-3.723227
|
0.0052
|
|
Test critical values:
|
1% level
|
|
-3.501445
|
|
|
5% level
|
|
-2.892536
|
|
|
10% level
|
|
-2.583371
|
|
|
|
|
|
|
|
|
|
|
|
Source : Calculs de l'auteur
Les conditions de cointégration sont tous
vérifiées, les deux séries sont toutes les deux I(1) et de
plus, les résidus issus de l'estimation de la relation de long terme
sont bel et bien stationnaire, dans ce cas, on peut estimer le modèle
à correction d'erreur. Estimer le modèle à correction
d'erreur consiste à estimer le modèle suivant : 

N=95 R2=0,66
Le coefficient de rappel (-0,86) de et-1 est
significativement négatif, dans ce cas on peut accepter la
représentation à correction d'erreur.
Si la relation à court terme est déviée
du niveau d'équilibre, le terme de cointégration ou bien le terme
de correction d'erreur intervient pour corriger progressivement cette relation
à travers une série d'ajustements à court terme
partielles, le coefficient mesure la vitesse d'ajustement de la ième
variable endogène vers la relation d'équilibre.
1.6.4)Test de Johansen et
estimation du modèle VECM.
Comme on l'a déjà montré (cf , ss
4.6.3.b), les deux séries du trafic passagers et les entrées des
touristes sont cointégrées, aussi, lors de l'estimation du
modèle VAR, on a trouvé que l'ordre du VAR est de 2, ainsi, on
peut estimer la matrice ð et construire le test de Johansen, ce test nous
permet de détecter le nombre de relations de cointégration.
a)Test de Johansen
On va supposer que la relation de cointégration ainsi
que la relation VAR contiennent toutes les deux une constante.
Le test mené sous Eviews nous permet d'avoir les deux
valeurs propres, on a :

A partir de ces valeurs propres on peut calculer une
statistiques dénommée la trace :

Où n représente le nombre d'observation, k le
nombre de variables, ëi est la ième valeur
propre et r est le rang de la matrice.
Cette statistique suit une loi de probabilité similaire
à la loi de ÷2 tabulée par Johansen et Joseluis
(1990).
Premièrement, on commence par tester H0 que
le rang de la matrice r=0 contre H1 r>0

La valeur critique à 5% du test est 15,50 ; le
résultat du test nous emmène à rejeter l'hypothèse
nulle, le rang de la matrice est différent de 0 et par conséquent
les deux séries sont non stationnaires. Ce résultat confirme ceux
obtenus par les tests de Dickey et Fuller.
Deuxièmement, on teste l'hypothèse
H0 que le rang de la matrice r=1 contre H1 r>1, dans
ce cas la trace est : 
La valeur critique à 5% du test est 3,84 ; dans ce
cas on est amené à accepter l'hypothèse nulle, le rang de
la matrice r=1, à cet effet, l'hypothèse d'existence d'une
relation de cointégration est acceptée.
b)Estimation du modèle vectoriel à
correction d'erreur (VECM)
Dans un premier temps, on a estimé le VECM avec
l'hypothèse d'existence de la constante au niveau de la relation de
cointégration et au niveau du VAR, néanmoins, on a trouvé
que la constante n'est pas significative au niveau du VAR, à cet effet,
on a retenu la spécification de l'existence de la constante au niveau de
la relation de cointégration et son absence au niveau du VAR.
L'estimation du modèle VECM est la suivante :

c)Validation du modèle VECM
Les coefficients de rappel des deux équations du VECM
ont bien le signe attendu, ils sont touts les deux négatifs,
néanmoins, le coefficient de rappel de la deuxième
équation, bien qu'il a le signe attendu il est non significatif.
Conclusion du troisième chapitre
La modélisation VAR et VECM permet à la fois de
distinguer les effets de court et long terme d'un choc sur l'une des deux
séries et aussi de mieux appréhender la dynamique de leurs
interactions, en effet, cette étude montre que l'impact des
entrées des touristes au Maroc est permanent sur le volume de trafic.
Bien que les résultats de cette étude soient
intéressants, une spécification théorique intégrant
l'impact des autres variables sur le volume de trafic telles que le niveau
moyen des tarifs par ligne, fréquence hebdomadaire par ligne, ....etc
s'avère nécessaire pour confirmer ces résultats.


Conclusion
générale
L'objectif premier de ce travail c'était de trouver une
modélisation adéquate de la demande du trafic aérien au
Maroc, servant comme base de simulation et projection de trafic.
Dans un premier temps, nous avons utilisé la
modélisation univariée, par l'utilisation de l'approche de
Box&Jenkins, cette approche a nécessité un traitement
préliminaire de la chronique du trafic aérien au Maroc, à
cet effet, on a corrigé la chronique des variations saisonnières
et puis on a étudié la stationnarité de la chronique. Les
différents tests de Dickey et Fuller augmentés appliqués
sur la chronique ont montré que celle-ci est non stationnaire de type
DS.
Dans un deuxième temps, on a utilisé la
modélisation de type VAR pour trouver une éventuelle relation
entre le volume de passagers et les entrées de touristes au Maroc,
étant donné que les deux chroniques ont une tendance commune, le
risque de commettre une régression fallacieuse est élevé,
à cet effet, on a utilisé un modèle à correction
d'erreur afin de dégager la relation de long terme entre les deux
variables.
Le deuxième objectif de ce travail était de
faire des prévisions via les modèles spécifiés et
estimés. Les modèles spécifiés appliqué
d'une manière ex ante sur la série ont permis de la retracer,
néanmoins, la variance des erreurs de prévisions, et du coup les
intervalles de confiance étaient larges.
Les apports de travail
L'apport principal de ce travail réside au niveau de la
modélisation, en effet, l'apport de la modélisation se situe
à un niveau à la fois économique et
économétrique. A partir des estimations du modèle VAR
à correction d'erreur, on a mis en évidence la relation entre le
trafic passagers et les entrées des touristes au Maroc, de plus, on a
trouvé que la relation de causalité entre ces deux variables
existent uniquement dans un sens, en se basant sur les tests de
causalité de Granger, on a trouvé qu'il n'existe pas une relation
de feedback entre le volume de passagers et les entrées des
touristes.
Au niveau économétrique, à nos
connaissances et jusqu'à la date de rédaction de ce travail, pour
la première fois au Maroc, le demande de trafic aérien est
modélisé par un modèle à correction d'erreur, ce
travail a permis de mettre en évidence, via un outil de
modélisation robuste, la relation entre la demande de trafic et les
entrées des touristes au Maroc. De plus, on doit noter que notre
procédure d'estimation ne concerne pas uniquement la demande de trafic
aérien, elle est transposable à tout autre secteur comprenant des
séries non stationnaires.
Extensions possibles
Il serait intéressant d'approfondir les travaux que
nous avons mené dans le cadre d'une thèse de recherche, à
défaut d'avoir l'accès aux données, ce travail reste
incomplet, en effet, n'expliquer le trafic aérien rien que par les
entrées des touristes est une vision réduite de la
réalité. La demande de trafic aérien est expliqué
par plusieurs variables, entre autre le prix des services aériens.
Aussi, faire une segmentation du trafic selon les motifs de déplacement
(affaire, tourisme, ...) serait d'une importance extrême, en effet,
à titre d'exemple, même si le prix des services aériens est
une variable clé de l'explication de la demande du trafic aérien,
il n'a pas la même élasticité pour tous les segments du
trafic, si le trafic pour motif tourisme est très élastique au
prix, la demande de trafic pour motif affaire est inélastique ou bien
moins élastique au prix. La mobilité est en effet davantage
liée à un motif qu'à un mode de transport, celui-ci
n'étant qu'un moyen de le satisfaire.
Le marché de transport aérien au Maroc a subi
une mutation après 2006, le volume de passagers ainsi que la
capacité aéroportuaire a fortement augmenté, ainsi, faire
une modélisation du trafic sur une période avant et après
cet événement phare suppose la constante des paramètres
estimés, à cet effet, il serait judicieux d'intégrer la
possibilité d'une rupture dans la relation de cointégration afin
de prendre en compte l'éventuelle instabilité des
paramètres.
Bibliographie
Ouvrages
BOURBONNAIS, Régis, Econométrie, Dunond,
coll. « Eco sup », 2004, 329 pages
BOURBONNAIS, Régis. et Michel, TERRAZA, Analyse des
séries temporelles. Application à l'économie et à
la gestion, Dunod, deuxième édition, 2008, 329 pages
DOR, Eric, Econométrie. Cours et exercices adaptés
aux besoins des économistes et gestionnaire, sciences de gestion, coll.
« synthex », 2004, 290 pages
GRAIS, Bernard, Méthodes statistiques, Dunod, 3ème
édition, coll. « Eco sup », 2003, 400 pages
HAMILTION, James D, Time Series Analysis, Princetion university
press, 1994, 407 pages
MONINO, Jean-louis. et al, Statististiques descriptives, Dunod,
2007, 269
MURRAY, R. Spiegel, probabilités et statistiques,
McGraw-Hill, 1992, 385 pages
PAVAUX, Jaques, l'économie du transport aérien la
concurrence impraticable, Economica, 1994, 418 pages
Articles en format imprimé
ABED, Seraj. Y et al, "An econometric analysis of international
air travel demand in Saudi Arabia", Journal of air transport
management, N 7, 2001, 143-148
BASAR, Gosen et Chandra, BHAT, "A parameterized consideration set
model for airport choice: an application to the San Francisco Bay Area",
Transportation Research Part B, N 38, 2004, 889-904
DIEBOLD, Francis x et al, "Unit root tests are useful for
selecting forecasting models", NBER Working paper series,
6928,February 1999
ISHII, Jun et al, "Air travel choices in multi-airport markets",
Journal of Urban Economics, N 65, 2009, 216-227
MADAS, Michael, A et Konstantinos, G. ZOGRAFOS,"Airport slot
allocation : a time for change?", Transport Policy, N 17, 2010,
274-285
SELLNER, Richard et Philip, NAGL, "Air accessibility and growth e
The economic effects of a capacity expansion at Vienna International Airport",
Journal of Air Transport Management, N XXX, 2010, 1-5
SURYANI, Erma et al, "Air passenger demand forecasting and
passenger terminal capacity expansion: A system dynamics framework",
Experts sytems with applications, N 37, 2010, 2324-2339
Article en format électronique
HANSMAN, R. John. The Impact of Information Technologies on Air
Transportation. [document électronique].
http://dspace.mit.edu/handle/1721.1/37324
HSIAO, Chieh-Yu et Mark, HANSEN."A passenger demand model for air
transportation in a hub-and-spoke network", Transportation Research Part E:
Logistics and Transportation Review. [en ligne]. Volume 47, N 6, (Novembre
2011). http://sciencedirect.com/science/article/pii/S1366554511000718
HURLIN, Christophe. `' Econométrie appliquée
et séries temporelles. Chapitre 2 Tests de non stationnarité et
processus aléatoires non stationnaires''. [document
électronique].
http://univ-orleans.fr/deg/masters/ESA/CH/CoursSeriesTemp_Chap2.pdf
KING, Robert G et al. Stochastic Trends and Economic
Fluctuations. [document électronique]. NBER Working paper, N
2229, 1992, http://www.nber.org/papers/w2229
KING, Robert G et Charles I. Plosser. `'Real Business Cycles and
the Test of the Adelmans''. [document électronique]. NBER Working
paper, N 3160, 1989,http://www.nber.org/papers/w3160.pdf?new_window=1
Annexes :
Annexe 1 :
Résumé des propriétés des fonctions
d'autocorrélation simple et partielle
|
Processus
|
Fonction autocorrélation simple
|
Fonction d'autocorrélation
partielle
|
|
AR(1)
|
Décroissance exponentielle   ou sinusoïdale ( ou sinusoïdale (  ) )
|
Premiers retard non nul, les autres coefficients nuls pour
des retards >1
|
|
AR(2)
|
Décroissance exponentielle ou sinusoïdale selon
les signes de   et et  
|
Premiers et second retards non nuls, les autres coefficients
nuls pour des retards >2
|
|
AR(p)
|
Décroissance exponentielle et/ou sinusoïdale
|
Les p premiers retards non nuls, les autres coefficients nuls
pour des retards >p
|
|
MA(1)
|
Premiers retard non nul, les autres coefficients nuls pour
des retards >1
|
Décroissance exponentielle (  ) ou sinusoïdale amortie ( ) ou sinusoïdale amortie (  ) )
|
|
MA(2)
|
Premiers et second retards non nuls, les autres coefficients
nuls pour des retards >2
|
Décroissance exponentielle ou sinusoïdale selon
les signes de   et et  
|
|
MA(q)
|
Les q premiers retards non nuls, les autres coefficients nuls
pour des retards >q
|
Décroissance exponentielle et/ou sinusoïdale
|
|
ARMA(1,1)
|
Décroissance géométrique à partir
du premier retard, le signe est déterminé par  
|
Décroissance exponentielle (  ) ou sinusoïdale amortie ( ) ou sinusoïdale amortie (  ) )
|
|
ARMA (p, q)
|
Décroissance exponentielle ou sinusoïdal amortie
tronquée après (q-p) retards
|
Décroissance exponentielle ou sinusoïdal amortie
tronquée après p-q retards
|
Annexe 2
Programme de Dickey&Fuller simple sous Eviews
'TESTS DE DF:'
equation eq3.ls pax_adj c pax_adj(-1) @trend
scalar scr3=@ssr
scalar ddl3=@regobs-@ncoef
genr dpax=pax_adj-pax_adj(-1)
equation eq2c.ls dpax c
scalar scr3c=@ssr
scalar f3=((scr3c-scr3)/2)/(scr3/ddl3)
Annexe 3 :
Programme de Dickey&Fuller augmenté
'TESTS DE DFA'
genr dpax=pax_adj-pax_adj(-1)
equation eq6.ls dpax pax_adj(-1) D(pax_adj(-1)) D(pax_adj(-2))
D(pax_adj(-3)) c @trend
scalar scr6=@ssr
scalar ddl6=@regobs-@ncoef
equation eq6c.ls dpax c D(pax_adj(-1)) D(pax_adj(-2))
D(pax_adj(-3))
scalar scrd=@ssr
scalar f6=((scrd-scr6)/2)/(scr6/ddl6)
'TEST DE DFA hypothèses jointes H5'
equation eq7.ls dpax D(pax_adj(-1)) D(pax_adj(-2))
D(pax_adj(-3))
scalar scr5c=@ssr
scalar ddl5c=@regobs-@ncoef
scalar f5=((scr5c-scr6)/3)/(scr6/ddl6)
'TEST DE DFA du modèle 5'
equation eq8.ls dpax pax_adj(-1) D(pax_adj(-1)) D(pax_adj(-2))
D(pax_adj(-3)) c
scalar scr5=@ssr
scalar ddl5=@regobs-@ncoef
equation eq9.ls dpax D(pax_adj(-1)) D(pax_adj(-2))
D(pax_adj(-3))
scalar scrmc5=@ssr
scalar F4=((scrmc5-scr5)/2)/(scr5/ddl5)
'stationnarisation'
'equation eqst.ls totpharsa c @trend
'genr res=resid
Table des matières
Introduction générale
2
CHAPITRE I : Description du trafic
aérien international et national
9
1) Evolution du trafic aérien
mondial de passagers
9
1.1)Historique du trafic aérien mondial de
passagers : Evolution contrastée
9
1.2) Evolution comparée du trafic
aérien mondial et du PIB mondial
10
2)Développement du transport
aérien au Maroc.
10
2.1)Chronologie de la politique de
libéralisation du transport aérien au Maroc
10
2.1.1)Impact de la politique de
libéralisation sur le volume de trafic au Maroc
11
2.1.2)Stimulation de la demande du transport
aérien par les actions du ministère du tourisme
12
2.2) Contribution de la vision 2010 au niveau de
développement des rentrées des touristes.
13
2.2.1)Développement des infrastructures
aéroportuaires
14
2.2.2)Développement de l'offre
aérienne au Maroc
15
2.3)Impact des politiques concertées des
différents intervenants sur le volume du trafic au Maroc
17
2.3.1)Evolution contrastée des
différents segments du trafic aérien
17
2.3.2)Distribution de l'offre du trafic par
région
18
2.4)Evolution et impact de l'introduction des LCC
sur l'offre de transport aérien au Maroc.
20
2.4.1) Les compagnies LC n'ont cessé de
consolider leur part de marché depuis la signature d'open sky
21
2.4.2)Evolution de l'offre internationale par
aéroport
21
2.4.3)Distribution de l'offre par aéroport
et par type d'opérateur
22
2.5)Evolution du trafic type charter au Maroc
23
2 .5.1) Analyse du trafic charter
23
2.5.2) Trafic charter par aéroport.
24
2.6) Evolution du trafic domestique au Maroc.
25
CHAPITRE II : Modélisation
univariée du trafic aérien
28
1) Introduction aux processus
aléatoires non stationnaires
28
1.1) Définition de la stationnarité
au second ordre :
28
1.2) Stationnarité
déterministe : Trend stationary (TS)
31
1.3)Stationnarité stochastique :
Differency stationnary (DS)
31
1.3.1) Propriété des processus
DS :
31
1.4)Les conséquences associées
à la distinction entre TS et DS :
32
1.5) Les conséquences économiques de
la non stationnarité :
34
1.6)Test de racine unitaire : Test de Dickey
Fuller
35
1.7)Stratégie du test de Dickey
Fuller :
37
1.8) Test de Dickey Fuller augmenté
40
1.8.1) Prise en compte de l'autocorrélation
des résidus par la méthode de Dickey Fuller
40
1.8.2) Détermination du nombre de retards
p
40
1.8.3) Tests d'autocorrélation des
résidus
41
1.9) Etude de la saisonnalité :
41
1.9.1) Analyse de variance à un facteur
41
1.9.2) Test global de l'effet d'un facteur
42
1.9.3) Analyse de la variance et étude de la
saisonnalité :
43
2)Schéma d'analyse des séries
chronologiques et correction des variations saisonnières.
43
2.1) les composantes d'une série
chronologique
43
2.1.1) Tendance à long terme ou trend
43
2.1.2) Mouvement cyclique
43
2.1.3) Variations saisonnières.
44
2.1.4) Les variations accidentelles ou
résiduelles
44
2.2) les modèles de décomposition
44
2.2.1) Schéma additif
44
2.2.2) Schéma multiplicatif
45
2.3) les méthodes de
décomposition
45
2.3.1) Les méthodes
analytiques :
45
2.3.2) Méthode empirique.
46
2.3.3) Propriétés de la
moyenne mobile :
46
3) Application aux
données du trafic mensuel régulier de passagers au Maroc
47
3.1) Analyse préliminaire de la
série
47
3.1.1) Détection de la
saisonnalité par le test de Fisher :
48
3.1.2) Décomposition de la
série du trafic régulier de passagers.
49
3.2) Application de la stratégie des tests
de racine unitaire de Dickey et Fuller sur la série du trafic
53
3.2.1) Analyse de l'autocorrélation
empririque de la série des résidus
55
3.3) Tests de Dickey Fuller augmentés
57
3.3.1)Stratégie du test ADF :
57
3.3.2) Application des tests de Dickey
Fuller augmentés (ADF) sur la série du trafic :
58
3.3.3) Interprétation des
résultats et tests d'hypothèses jointes
59
3.3) L'identification du processus
générateur ARMA
61
3.3.1) Analyse des fonctions FAC et PAC.
63
3.3.2) Estimation et test de validation du
modèle ARMA
64
CHAPITRE III : Modélisation
multivariée du trafic aérien : Les processus VAR
71
1) La modélisation VAR
71
1.1) Définition d'un modèle VAR
71
1.2) Estimation des paramètres du
modèle VAR
72
1.2.1) Approche d'estimation
72
1.2.2) Détermination du nombre de retard
d'un modèle VAR
72
1.3)Application sur la série du trafic
aérien
73
1.3.1)Source des données des entrées
de touristes.
73
1.3.2)Analyse préliminaire de la chronique
des entrées des touristes
73
1.3.3) Etude de la stationnarité de la
chronique des entrées des touristes.
75
1.4) Spécification du modèle VAR
78
1.4.1)Détermination de l'ordre du
modèle VAR
78
1.4.2)Estimation des paramètres du
modèle VAR(2)
79
1.4.3)Prévision du trafic aérien via
le modèle VAR
79
1.4.4)Réponses impulsionnels et structure
dynamique du modèle VAR
81
1.4.5)Décomposition de la variance
83
1.5)Analyse de la causalité entre les deux
variables
84
1.5.1)Test de causalité entre le volume de
trafic passagers (pax_adj) et les entrées des touristes (tour_adj)
85
1.6)Problèmes d'estimation des variables
intégrées.
86
1.6.1)Définition de la
cointégration :
87
1.6.2)Test de cointégration d'Engle et
Granger
87
1.6.3)Cointégration et mécanise
à correction d'erreur
88
1.6.4)Test de Johansen et estimation du
modèle VECM.
90
Conclusion générale
93
Annexes :
97
* 1 Le prix constitue la
variable clé pour l'explication de la demande du trafic, surtout pour le
segment de la demande du trafic type touriste, où la demande est
très élastique au prix.
* 2 L'indice des prix à
la consommation IPC, calculé mensuellement par le HCP utilise une
division consacrée au secteur de transport avec toutes ses variantes
(maritime, routier, ferroviaire et aérien).
* 3 La stationnarité de
type TS désigne la non stationnarité de type déterministe
(Time stationnary), la non stationnarité de type DS
désigne la non stationnarité de type aléatoire
(Differency stationnary).
* 4 Cette compagnie a disparu
suite aux nombreuses problèmes, la dite compagnie a utilisé une
partie de la flotte de la compagnie mère RAM ainsi qu'une partie du
personnel, la flotte et le personnel ne sont pas adaptés au mode de
gestion des compagnies LCC qui consiste à brader les prix par touts les
moyens afin de gagne une part de marché supplémentaire.
* 5 Cet alignement consiste
à une convergence avec l'UE en matière réglementaire.
* 6 Cette direction a pour
objectif de mener des études en vue de développement et
création de nouvelles routes et fréquences et marketer la
destination Maroc via la négociation et la signature des accords au
niveau du secteur du transport aérien, elle vise en outre à
mettre en place un observatoire de transport aérien.
* 7 Le taux de croissance moyen
sur plusieurs périodes est calculé comme suit : 
* 8La modélisation de la
demande du transport aérien qui sera l'objectif primordial de notre
étude, on va utiliser les données issues de l'OT.
* 9 Au niveau des pays du bassin
méditerranéen, la Turquie vient en tête avec une moyenne
annuelle de 12%, suivi de l'Egypte de 11% et puis le Maroc et la
Slovénie avec 7%
* 10 La modélisation a
des fins de prévision de la demande du trafic fera partie des deux
prochains chapitres.
* 11 Les LCC marocaines sont
représentées par les compagnies ariennes suivantes : Atlas
Bleu (disparue), Jet4You (absorbée par JetAirFly) et Air Arabia
Maroc.
* 12 Ils sont des vols directs
sans faire des escales à Casablanca
* 13 Les compagnies LC utilise
par exemple l'internet comme moyen de distribution de billets (billet
électronique), ainsi, elles, elles éliminent les frais d'agence,
système d'information, frais de dossier...etc. de plus, ces compagnies
utilisent des aéroports secondaires où il y a moins de frais
d'aéroport. La plupart des compagnies LC facturent également
l'enregistrement de bagage ainsi que d'autres services à bord, qui
deviennent source de profit.
* 14 En économie
industrielle, on peut considérer que les compagnies LC constituent un
marché à part entière, dans ce sens, difficile de dire que
les compagnies LC concurrencent les traditionnelles, chaque type à sa
propres clientèle, c'est un peu comme la clientèle des petits
taxis et celle des grands taxis.
* 15 Un processus  est considéré comme stationnaire au second degré
s'il vérifie au moins deux conditions. La première condition est
que la variance doit être convergente alors que la deuxième
condition est que l'espérance mathématique du processus est considéré comme stationnaire au second degré
s'il vérifie au moins deux conditions. La première condition est
que la variance doit être convergente alors que la deuxième
condition est que l'espérance mathématique du processus  ne doit pas dépendre du temps. ne doit pas dépendre du temps.
* 16 Moindres carrées
ordinaires
* 17 Cette composante
tendancielle est modélisée en général par une
fonction linéaire du temps.
* 18 En revanche, le test de
KPSS multiplicateur de Lagrange, évalue l'hypothèse nulle de  contre l'hypothèse alternative contre l'hypothèse alternative 
* 19 Ce processus on a
déjà étudié ses propriétés, il est
non stationnaire
* 20 C. Hurlin : cours
d'économétrie appliquée et séries temporelles,
U.F.R économie appliquée, maîtrise d'économie
appliquée, cours de tronc commun. Chapitre 2.
* 21 La formule du
critère d'Akaike est la suivante : , tel que k est le nombre de paramètres alors que T est le nombre
d'observation, alors que le critère de Schwartz est défini comme
suit : , tel que k est le nombre de paramètres alors que T est le nombre
d'observation, alors que le critère de Schwartz est défini comme
suit : 
* 22
Généralement, on désigne par carré moyen la somme
des carrés des écarts divisée par son degré de
liberté, ainsi : 
* 23 On distingue deux saisons,
la saison hiver (winter) qui commence du dimanche de la dernière semaine
d'octobre de l'année n et se termine le samedi de la dernière
semaine du mois de mars de l'année n+1.
* 24 Comme on a
déjà noté plus haut, la statistique tö ne
suit pas la distribution standard de Student, pour ce faire, on doit utiliser
les valeurs limites tabulées par D&F pour les trois
modèles.
* 25 Transformer
l`échantillon en différence première consiste à
faire la transformation suivante : 
* 26 Les techniques de
stationnarisation des séries ont été
détaillées aux chap II
* 27 Le modèle VAR(2) ne
minimise que le critères de SC et pas de AIC, le principe de parcimonie
nous emmène à retenir le modèle qui minimise l'un des deux
critères, en effet, l'ajout d'une retard supplémentaire conduit
à l'estimation de quatre paramètres supplémentaire pour un
VAR(2),ceci induit une perte de degré de liberté.
* 28 La stationnarité du
résidu est testée à l'aide des tests de D&F et ADF
| 


