III.2.4 Forme discrétisée :
éléments finis
La solution analytique du système d'équations
(III.12, III.13) est en général inaccessible. On est donc conduit
à chercher une solution approchée par une méthode
numérique : la méthode des éléments finis. Cette
méthode est un cas particulier de la méthode de Galerkin
: le champ de températures et les fonctions test appartiennent
au même espace de dimension finie.
III.2.4.1 Représentation
élémentaire (ou locale) du champ de températures
Le champ de températures dans l'élément
(e) a pour expression [21]:
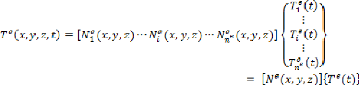
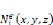
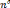
36
Chapitre III Modélisation Thermomécanique du
Problème
: Le nombre de noeuds de l'élément
: Les fonctions d'interpolation élémentaires
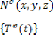
: La matrice d'interpolation élémentaire
: Le vecteur de température des noeuds de
l'élément (e). III.2.4.2 Représentation globale du
champ de températures
Le champ de températures sur l'ensemble du domaine V
a pour
expression:
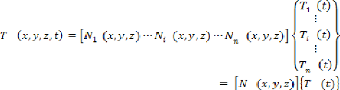
n : Le nombre de noeuds du maillage
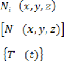
: Les fonctions d'interpolation (ou fonctions de forme) : La
matrice d'interpolation
: Le vecteur des températures nodales
Les fonctions d'interpolation vérifient les relations
:
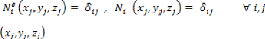
: Coordonnées du noeud j.
III.2.4.3 Partition des degrés de
liberté
Effectuons une partition des degrés de liberté
en températures inconnues
et connues [23] :
où le vecteur regroupe les températures (connues)
des noeuds situées sur la surface .
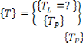
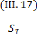
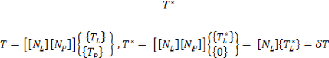
D'où l'expression de T et
37
Cette partition induit une partition de la matrice
d'interpolation :
Chapitre III Modélisation Thermomécanique du
Problème
III.2.4.4 Discrétisation de la forme
intégrale faible De l'expression du champ de températures T :
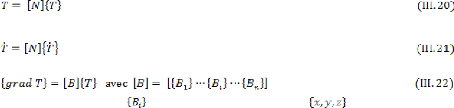
on déduit
Et
Pour un problème spatial, s'écrit dans le
repère orthonormé :
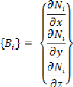
De même :
En remplaçant ces relations dans l'équation
(III.12 ), il vient [21]:
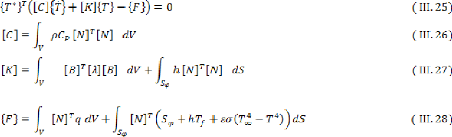
38
[C] : La matrice de capacité thermique (J/K)
[K] : La matrice de conductivité thermique (W/K)
: Le vecteur des flux nodaux (W)
: Le vecteur des températures nodales (K)
La discrétisation en espace du problème par la
méthode des éléments finis conduit à la
résolution d'un système d'équations en temps, en
général du premier ordre. La figure III.2 représente
l'organigramme principal par la M.E.F en utilisant la méthode des
substitutions successives.
Chapitre III Modélisation Thermomécanique du
Problème
Début
Lire les données de contrôle
Evaluation pour chaque élément : La
matrice de capacité thermique La matrice de conductivité Vecteur
de flux
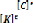
Assemblage des matrices
élémentaires
Pour la construction des matrices
globales
C T+K U = q

K T = q
Application de la méthode de
substitution
successive
39
Test de convergence

Fin
Fig.III.2 : Organigramme
principal de résolution de système d'équations par la
M.E.F.
| 


