III.1.3.1.3 Filtre de Canny : [02]
L'approche de Canny est présentée en
monodimensionnel, cette approche cible trois critères qui doivent
valider un détecteur de contour :
1- Garantir une bonne détection, c'est-à-dire une
réponse forte même à de faibles contours.
2- Garantir une bonne localisation.
3- Une faible multiplicité des maximums dus au bruit.
a. Étapes d'une détection de contours par
filtre de Canny
L'objectif est bien de calculer le module du gradient de
l'image analysée. Souvent avant d'appliquer le filtre de Canny, un
filtrage au préalable est opéré sur l'image au moyen d'un
filtre gaussien. Les différentes étapes sont
énumérées ci-après :
Ø Convolution de l'image initiale avec
un filtre passe-bas gaussien bidimensionnel (ou convolution 1D dans chacune des
deux directions)
(III.11)
Ø Convolution de l'image lissée
avec le filtre de Canny ou la dérivée de gaussienne dans les
directions horizontales et verticales. (filtre Sobel ).
Ø Calcul du module du gradient à partir des deux
images représentant les gradients de l'image filtrée passe-bas
dans les directions horizontales et verticales.
Défauts de l'approche contour
classique:
Les méthodes classiques de segmentation
échouent dans certains cas:
§ Si les images sont bruitées.
§ Si les images contiennent de faux contours.
Une solution a été proposée est celle des
modèles deformables, ce terme apparu dans les années 80 dans les
travaux de Terzopoulos a ouvert un domaine de recherche très actif et
fructueux dans les travaux de segmentation en particulier. Ces modèles
peuvent avoir plusieurs notations dans la littérature tels que: Contours
actifs , surfaces actives, balloons, contours deformables ou surfaces
deformables.
III.2 Contours déformables : [15]
[35]
Le principe des contours actifs est de faire
évoluer un contour (fermé ou non) initial vers une position
d'équilibre, c'est-à-dire en direction des bords de l'objet
à détecter. Entre deux itérations, la vitesse des points
est régie par une équation mettant en jeu des forces à
appliquer au contour, généralement selon la normale.
Ces forces dépendent des données
présentes dans l'image (intensité, gradient...) et des
propriétés de régularité du contour. La position
d'équilibre peut être définie comme le minimum d'une
fonctionnelle d'énergie dont la dérivée correspond aux
forces à appliquer.
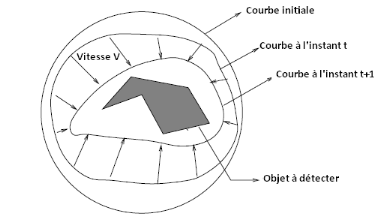
Dans la figure suivante figure- II.02 - , on a contours
initiale ( courbe initiale) qui est représentée par le cercle
extérieur, sous l'influence des forces internes et externes , le contour
se déforme jusqu'à atteindre l'objet, qui es t en gris.
III.2.1. Les différents types de contours :
[15]
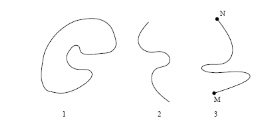
Nous pouvons définir trois types de
contours actifs différents utilisés (voir figure III.3) :
1. les contours déformable
fermés où Vt0 =
Vtn-1 (le point de départ est celui
d'arrivée)
2. les contours déformable à
extrémités libres (tous les points sont susceptibles de
bouger)
3. les contours déformable à
extrémités fixes où les positions
V0 et Vn-1 sont fixes dans le temps
ainsi que les dérivées premières en ces points (les points
de départ et d'arrivée restent fixes)
| 


