Dédicaces
Je dédie ce mémoire de projet de fin
d'étude
A ceux qui nous ont toujours bercé avec l'amour
et l'affectation, ma mère et toute ma famille sans
exception.
A tous mes amis et à toute la promotion de
2 009
Et à toutes les personnes que j'aime
Naima
Dédicaces
Je dédie ce mémoire de projet de fin
d'étude
A ceux qui nous toujours bercé avec l'amour et
l'affectation, mes chers parents et toute ma famille sans
exception.
A tous mes amis et à toute la promotion de
2 009
Et à toutes les personnes que j'aime
Farida
Remerciements
nous remercions en premier lieu le dieu tout
puissant de npus avoir accordé la puissance et la volonté pour
terminer ce travail.
nous tenons à remercier très vivement notre
encadreur Melle Meddeber.L qui nous a motivé et
ramené à notre objectif
ces emerciement s'adressent plus particuliérement à
Meddeber Sihem, B.Malika et Chenek
Redouane . et tous ce qui ont contribuée de prés ou de
loin à l'élaboration de cette étude et qui ont bien voulu
sacrifier un peu de leur temps pour nous aider
nous remercions Mr Berrached.N et
Mme Hendel, qui nous honorés en juger notre
travail.
Table des matières
Introduction générale
Chapitre I : Télédétection et
prétraitement
I. La
télédétection........................................................................................5
I.1.Définition............................................................................................5
I.2 Principe et différents étapes de
la
télédétection...............................................5
I.3. La les appareils d'acquésition (les
capteur de satellite).....................................6
I.4 Satellites d'observation de la
terre..............................................................7
I.4.1 Les
satellites...................................................................................7
I.4.2. Les différents types de
satellites...........................................................8
I.4.2.1. Satellite de
défilement...................................................................8
I.4.2.2. Satellite
géostationnaire.................................................................8
I.5. Structure des images de
télédétection (Images
satellitaires)................................9
I.5.1 Mode
d'acquisition...........................................................................9
I.5.2 Structure numérique d'une image
satellitaire.............................................10
II.
Prétraitement.........................................................................................11
II.1 Correction au niveau du
distributeur........................................................11
II.2 Correction au niveau de
l'utilisateur.........................................................11
II.2.1 Affichage en niveau de
gris..............................................................12
II.2.2 Filtrage
Numérique........................................................................13
II.2.2.1 Les filtres
passe-bas..................................................................13
II.2.2.1.1 Les
filtres linéaire................................................................14
II.2.2.1.2 Les filtres non
linéaire.........................................................15
II.2.2.2 Les filtres
passe-haut.............................................................17
II.2.3 Négative
d'image...............................................................................18
II.2.4
Seuillage.................................................................................19
II.2.5
Histogramme...........................................................................20
II.2.5.1 Histogramme
cumulé............................................................21
II.2.5.2 Egalisation de
l'histogramme...................................................22
II.2.5.3 Etirement
d'histogramme........................................................23
III.
Conclusion..........................................................................................24
Chapitre II : Etat de l'art
I.
Introduction.............................................................................................26
II. État de
l'art.........................................................................................
26
II.1 Localisation des
bâtiments.....................................................................27
II.1.1 Détection de bâtiments par
imagerie aérienne ou satellitaire............27
II.1.2 Plan de
cadastre......................................................................27
II.2 Calcul du relief d'un
terrain...............................................................27
II.2.1 Détection de bâtiments par
analyse du MNE et MNT..........................27
II.2.2 Génération d'un MNE par
stéréovision............................................28
II.2.3 Génération d'un MNE avec capteur
actif (laser)..................................28
II.2.4 Génération d'un MNE à partir
d'une image de profondeur......................28
II.2.5 Dérivation d'un MNT à partir
d'un MNE..........................................29
II.2.6 filtrage d'un
MNE.....................................................................29
II.3 Détermination des hauteurs de bâtiments par
ombrages.................................30
II.3.1 Détermination des hauteurs de batiments
de façon semi-automatique à l'aide d'outils
interactifs...........................................................................................30
II.4 Forme des
bâtiments...........................................................................30
II.4.1 Formes complexes d'un groupe de
bâtiments........................................32
II.4.2 Correction manuelle des
hauteurs.....................................................33
II.4.3 Correction manuelle des
hauteurs.....................................................34
II.5 Approche choisie: une méthode automatique
raffinée par une méthode semi
automatique.......................................................................................35
Chapitre III :Localisation des structures urbaines par
segmantation et generation des modéles numériques de
terrain
Partie(I) : Localisation des structures urbaines
par segmentation ...........................37
I.
Introduction ..................................................................................37
II.
Définition.....................................................................................37
III. Détection de contour
« L'approche contour »
...........................................................38
III.1 Contours
classiques.........................................................................38
III.1.1
Définition..............................................................................38
III.1.2 Principe de
base.....................................................................38
III.1.3 Les principaux algorithmes classiques
connus..............................38
III.1.3.1 Les opérateurs
dérivatifs du premier ordre (gradient) et du deuxième
ordre
(Laplacien) ..................................................................38
III.1.3.1.1 Les détecteurs de
gradient...............................................39
III.1.3.1.2 Les opérateurs
dérivatifs du deuxième ordre (le Laplacien).......40
III.1.3.1.3 Filtre de
Canny ...................................................41
III.2 Contours
déformables......................................................................42
III.2.1. Les différents types de
contours ...................................................43
III.2.2. Les différents modèles des
contours défomable..................................43
III.2.2.1 La méthode de détection
par Snake ...........................................44
III.2.2.1.1 Principe de base de la
méthode ...........................................44
III.2.2.1.2 Application pratique au cas du
contour actif ...........................46
III.2.2.2 Les contours actifs
géométriques : ensemble de niveau ''Level Set''.46
III.2.2.2.1
Introduction .................................................................46
III.2.2.2.2
Principe d'évolution de la courbe
C......................................48
IV
Conclusion.............................................................................................53
Partie(II) : Génération des
modèles numériques de
terrain.................................54
I Introduction
............................................................................................54
II Un Modèle
Numérique de
Terrain........................................................................54
II.1. Types de
MNT......................................................................54
II.2 Autre modèle
numérique
utilisé......................................................55
III. Génération d'un modèle
numérique de
terrien :.............................................55
III.1. Génération d'un
modèle numérique de terrien a partir d'une image d
télédétection en utilisant
l'OpenGL..................................................................
55
III.1.1 La bibliothèque graphique
OpenGL.......................................56
III.1.2 Pipe-line de
Rendu ...............................................................56
III.1.3 Les Bibliothèques
coexistant avec OpenGL.................................57
III.1.4 Les principales
instructions :.....................................................57
III.1.4.1 Les fonctions de
gestion d'une fenêtre....................................57
III.1.4.2 La fonction
d'affichage .....................................................58
III.1.4.3 Les primitives
géométriques................................................58
III.1.5 principe de
génération d'un MNT par
OpenGL ..............................60
III.1.5.1 lecture d'une image
Bitmap ..............................................60
III.1.5.2 Réalisation du mode
filaire du terrain....................................61
IV.
Conclusion ...........................................................................................64
Chapitre IV Résultats et
implémentations
1
Introduction ....................................................................................60
II. Les différentes méthodes
implémentées
...................................................67
II.1 Localisation des structures urbaines
.......................................................67
II.1.1 Segmentation
....................................................................67
II.1.1.1 Approche 1 : Contour
non-déformable....................................68
II.1.1.1.1. Les operateurs dérivateur''
gradient et Laplacien''.....................68
II.1.1.1.2. Le filtre de Canny
.............................................................71
II.1.1.1.3 Seuillage par
hystérésis de l'image gradient
..............................73
II.1.1.2 Approche 2 : Contour
déformable.......................................74
II.1.1.2.1 Les
Snakes ...................................................................74
II.1.1.2.2 Méthode d'ensemble de niveau zéro
Level Set ...................76
II.2 Génération des modèles
numériques .......................................81
II.2.1. Affichage par SDL
........................................................81
II.2.2. Affichage par OpenGL
...................................................84
II.2.3 Génération
d'un modèle 3 démentions par logiciel 3DEM .............87
II.3 Construction des structures urbaines
d'une ville ............................91
II.3.1 Données cadastrales
.......................................................92
II.3.1.1 Aménagement du secteur
A de la ville d'Arzew ..................92
II.3.1.2 Aménagement du secteur
B de la ville d'Arzew..................92
Conclusion.......................................................................................95
Conclusion générale
Introduction générale
La visualisation du paysage urbain en 3 dimensions constitue
un problème auquel la recherche informatique s'efforce d'apporter,
depuis une quinzaine d'années, des solutions, certes de plus en plus
performantes mais relativement parcellaires. Les technologies contribuant
à l'émergence de nouveaux modes de représentation 3D
progressent en effet rapidement, mais ces avancées sont issues de
secteurs de recherche - SIG, télédétection,
synthèse d'image - dont les objectifs diffèrent sensiblement des
problèmes spécifiques de visualisation et de simulation des
grands paysages. Par conséquent, si les questions algorithmiques
fondamentales - structuration des données, fonctions de visualisation 3D
... - semblent aujourd'hui résolus pour les objectifs d'analyse et de
représentation spatiales des données géographiques, il
reste extrêmement difficile et laborieux d'appliquer ces acquis
informatiques à la réalisation de simulations paysagères
à des échelles d'espace et de temps où la visualisation du
paysage en 3D permettrait d'étudier utilement les interactions spatiales
entre phénomènes urbains et géomorphologiques.
Le présent travail, se propose d'explorer des
méthodologies de simulation et de visualisation en 3D du paysage urbain.
L'intégration d'images satellites dans ce modèle de
représentation vectorielle du paysage est un aboutissement
nécessaire du présent projet, ce travail ne constitue pas
à proprement parler une utilisation directe des technologies de
télédétection mais plutôt une méthodologie de
constitution d'une scène urbaine 3D capable d'accueillir les
résultats d'un travail de télédétection, de
traitement d'images et des outils de DAO.
Dans notre projet, nous essayons de réaliser un
modèle 3D d'une scène urbaine qui se base sur les étapes
suivantes :
· Localisation des bâtiments sur une image
satellitaire, aérienne ou sur une carte;
· Calcul du relief du terrain;
· Détermination de la hauteur des bâtiments;
· Détermination de la forme des bâtiments
(principalement les toitures);
· Augmentation du réalisme de la scène
(ex.: utilisation de textures).
Pour l'exploitation correcte et efficace de la quantité
d'information des images de télédétection dans la
construction 3D des scènes urbaines, nous devons obligatoirement passer
par une étape de localisation qui intègre plusieurs modules de
traitement d'images en commençant par l'application des
opérateurs de prétraitement jusqu'au dernier module qui est la
segmentation soit par contour, soit par région. Notre
problématique concernant la segmentation était comment à
partir d'une image aérienne, satellitaire à haute
résolution ou une carte extraire les différentes constructions et
structures afin de les intégrer dans un modèle numérique
de terrain (MNT). De ce fait, nous avons intégré la
deuxième étape qui consiste à calculer le modèle de
relief du terrain qui se base sur la génération du modèle
numérique de terrain (MNT) et le modèle numérique
d'élévation (MNE), mais le problème qui se pose dans une
telle situation est comment faire la reconnaissance des différentes
zones avec leurs textures pour que le modèle devient plus utile dans
plusieurs domaines (Aménagement, environnement, hydrologie,
télécommunications et défense, etc...) .
Concernant la 3ème étape, nous avons
fait recours aux méthodes de DAO plus précisément, nous
avons utilisé le logiciel AutoCad et un plan cadastral afin de
construire les blocs des bâtiments tout en réservant leurs
hauteurs et leurs superficies obtenus à partir de la base de
données urbaine d'Arzew.
Finalement, pour rendre le modèle de la reconstruction
3D de la scène plus réel, nous devons intégrer tout ce qui
texture dans notre modèle de terrain.
Plan du mémoire
Afin de décrire le travail effectué, ce
mémoire comporte quatre chapitres principaux qui décrivent les
travaux cités ci-dessus et qui ont pour finalité la
reconstruction 3D des scènes urbaines y compris une phase de
segmentation avec les levels set, une phase de génération d'un
modèle numérique de terrain (MNT) des images satellitaires et
enfin une phase de structuration des blocs de bâtiments par AutoCad .
Après cette introduction générale, nous
passons au premier chapitre qui englobe deux parties dont la première
résume les principales notions et définitions sur la
télédétection et l'imagerie satellitaire, et la
deuxième traite les prétraitements implémentés des
images satellitaires et les différents filtres utilisés dans le
but d'améliorer la qualité de l'image.
Le deuxième présente un état de l'art sur
les différentes méthodes de reconstruction 3D d'une scène
urbaine avec la présentation de notre problème.
Le troisième chapitre comporte deux parties dont nous
présentons dans la première les principales méthodes de
segmentations (Approche Contour et Région) utilisées dans notre
projet, et nous traitons dans la deuxième les différentes
techniques utilisées pour la génération du terrain.
Nous abordons dans le quatrième chapitre l'étude
expérimentale des différentes approches vues en chapitre deux et
trois plus les différents résultats obtenus ainsi que les
interprétations adéquates.
Nous terminons par une conclusion qui contient
une évaluation des travaux effectués et les perspectives pour
leurs continuations.
I. La télédétection :
L'observation d'une planète « la terre
par exemple », a évoluée grâce aux satellites qui
peuvent visualiser à distance ses caractéristiques
topographiques.
I.1. Définition :
La
télédétection est la technique qui,
par l'acquisition d'images, permet d'obtenir de l'information sur la surface de
la Terre sans contact direct avec celle-ci. Elle englobe tout le processus qui
consiste à capter et à enregistrer l'énergie d'un
rayonnement électromagnétique émis ou
réfléchi.
I.2. Principe et différente étapes de la
télédétection : [29]
Dans la plupart des cas, la
télédétection implique une interaction entre
l'énergie incidente et les cibles. Le processus de la
télédétection au moyen des systèmes imageurs
comporte les sept étapes que nous élaborons ci-après.
Notons cependant que la télédétection peut
également impliquer l'énergie émise et utiliser des
capteurs non-imageurs.
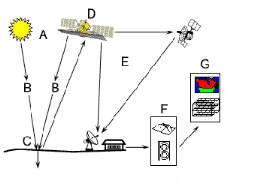
1. Source d'énergie ou d'illumination (A)
- À l'origine de tout processus de télédétection se
trouve nécessairement une source d'énergie pour illuminer la
cible.
2. Rayonnement et atmosphère (B) - Durant
son parcours entre la source d'énergie et la cible, le rayonnement
interagit avec l'atmosphère. Une seconde interaction se produit lors du
trajet entre la cible et le capteur.
3. Interaction avec la cible (C) - Une fois
parvenue à la cible, l'énergie interagit avec la surface de
celle-ci. La nature de cette interaction dépend des
caractéristiques du rayonnement et des propriétés de la
surface.
4. Enregistrement de l'énergie par le capteur
(D) - Une fois l'énergie diffusée ou émise par la
cible, elle doit être captée à distance (par un capteur qui
n'est pas en contact avec la cible) pour être enfin
enregistrée.
5. Transmission, réception et traitement
(E) - L'énergie enregistrée par le capteur est
transmise, souvent par des moyens électroniques, à une station de
réception où l'information est transformée en images
(numériques ou photographiques).
6. Interprétation et analyse (F) - Une
interprétation visuelle et/ou numérique de l'image traitée
est ensuite nécessaire pour extraire l'information que l'on
désire obtenir sur la cible.
7. Application (G) - La dernière
étape du processus consiste à utiliser l'information extraite de
l'image pour mieux comprendre la cible.
Ces sept étapes couvrent le processus de la
télédétection, du début à la fin.
I.3. Les appareils d'acquisition (les capteurs de
satellites) : [29]
En télédétection, les capteurs sont
les instruments qui permettent de transformer le rayonnement
électromagnétique en informations perceptibles et analysables par
l'oeil humain. Plus spécifiquement, un capteur désigne "un
instrument qui recueille de l'énergie radiative provenant de la
scène visée et délivre un signal électrique
correspondant mesurable".
Au niveau des capteurs, il existe deux types :
Les capteurs passifs: Ce sont
les capteurs qui reçoivent le rayonnement de la terre, qu'il soit
émis par celle-ci ou reflété. En général,
les capteurs qui utilisent une source d'énergie externe pour observer
les objets (par exemple qui utilisent la lumière solaire pour observer
la Terre) sont appelés «capteurs passifs ».
Les capteurs actifs: Le
principal inconvénient des capteurs passifs est que, si le ciel est
nuageux ou s'il fait sombre, on ne peut plus les utiliser. Par
conséquent, un autre type de capteurs doit être utilisé. Il
s'agit des capteurs dit "actifs". On les appelle capteurs actifs car ils
émettent eux-mêmes les rayonnements pour « illuminer »
les objets de manière à ce que l'énergie
réfléchie puisse être mesurée.
I.4. Satellites d'observation de la terre :
[31]
1.4.1. Les satellites : Le satellite
représente une plate forme idéale pour l'observation de la terre
et ça à l'aide d'un ou plusieurs capteurs.
Un satellite se compose de deux sous-ensembles :
§ une plate forme : qui sert à
supporter une ou plusieurs charges utiles pour leurs fournir les ressources
nécessaire à leurs fonctionnement.
§ La charge utile : qui correspond
à l'ensemble d'élément que peut transporter un
véhicule spatiale et qui est destiné à remplir une mission
déterminée.

I.4.2. Les différents types de satellites
Selon leurs caractéristiques astronomiques, on peut
distinguer deux types de satellites :
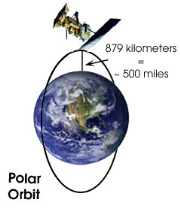
I.4.2.1. Satellite à défilement :
Ils permettent une observation cyclique de la terre. Ils ont une
altitude comprise entre 800 km et 1000 km, et ils décrivent une
orbite polaire, ils leurs faut environ 105 mn pour faire le tour de la terre.
Ce type de satellite est très utile dans le domaine de la
cartographie.
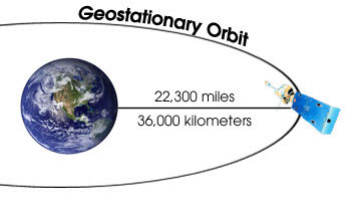
I.4.2.2. Satellite
géostationnaire : Ils ont une position fixe par rapport
à la terre ainsi ils peuvent assurer une surveillance continue d'une
partie globale, ils sont caractérisés par une inclinaison nulle.
De plus, ils sont animés d'un mouvement circulaire. Ce type de satellite
est très répondu dans le domaine de la
météorologie.
I.5. Structure des images de
télédétection (Images satellitaires) : [30]
I.5.1 Mode d'acquisition
Les données envoyées par les capteurs, ne
sont pas des images toutes faites. Elles doivent être composées
à partir d'informations fournies par les capteurs du satellite. Avec un
satellite récent, différents modes d'acquisition
existent :
a. Mode panchromatique
L'image est acquise par un capteur numérique qui mesure
la réflectance dans une seule bande spectrale. Les données
panchromatiques sont représentées sous forme d'images en niveaux
de gris. Elle sert principalement à obtenir des informations de type
« géométriques » (formes, dimensions,
surface).

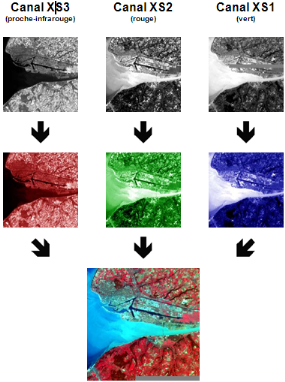
b .Mode multispectrale
L'acquisition de l'image multispectrale s'effectue par un
capteur numérique qui mesure la réflectance dans de nombreuses
bandes spectrales. Ces multiples valeurs de réflectance se combinent
pour créer des images couleur. Elle sert principalement à obtenir
des informations à caractère « qualitatives »
(ex. classification des types de végétation).
L'illustration ci-dessous montre le codage des trois canaux
d'une multispectrale SPOT:
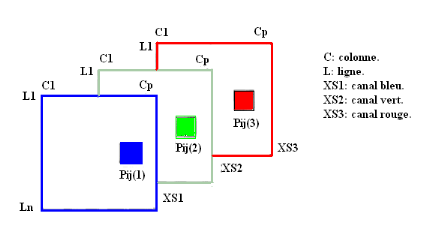
I.5.2 Structure numérique d'une image
satellitaire :
Une image numérique est donc un tableau
à deux dimensions (figure I.7). Ainsi, une image SPOT de dimensions 60 X
60 km avec une taille de pixel de 20 X 20 m correspond à un tableau de
3000 lignes X 3000 colonnes.
Ces images brutes ne sont pas prêtes à exploiter.
Elles nécessitent un certain nombre de corrections,
réalisées soit par les distributeurs, soit par les utilisateurs.
II. Prétraitements : [12]
Le traitement, souvent appelé
prétraitement, regroupe toutes les techniques visant à
améliorer la qualité d'une image. De ce fait, la donnée de
départ est l'image initiale et le résultat est également
une image. La restauration d'images a pour objet la réduction, voir
l'élimination des distorsions introduites (bruits) par le système
ayant servi à acquérir l'image. Son but est d'obtenir une image
qui soit la plus proche possible de l'image idéale qui aurait
été obtenue si le système d'acquisition était
parfait.
II.1 Correction au niveau du
distributeur : il y a deux types de corrections :
radiométriques et géométriques.
1. Radiométriques
Elimination des bruits radiométriques qui sont en
raison : de déficience des capteurs; de problèmes de
transmission des données; d'interprétation
(codage/décodage).
2. Géométriques
Les effets de rotondité de la terre, les
mouvements du satellite, les déformations dans les
périphéries de l'image (surtout si le capteur est incliné)
sont autant de facteurs rendant nécessaires des corrections
géométriques qui peuvent être
réalisées par le distributeur, et aussi par l'utilisateur
directement sous logiciel de traitement d'image pour but d'améliorer sa
visibilité, ce qui est introduit dans la partie suivante de ce
chapitre.
II.2 Correction au niveau de l'utilisateur :
Il existe 2 grandes familles de méthodes :
1. Les méthodes globales : Dites aussi
ponctuelles, elles modifient chaque point de l'image indépendamment de
ses voisins à partir d'une information globale sur l'image. On distingue
3 grandes classes d'opérations:
§ La modification de l'histogramme.
§ Le rehaussement de contraste.
§ L'utilisation de la couleur.
2. Les méthodes locales : Elles
travaillent sur des voisinages de pixels et donc localement dans l'image. On
distingue 2 grandes classes de filtrage :
§ Le filtrage linéaire.
§ Le filtrage non-linéaire.
Dans notre cas, nous avons essayé d'implémenter
quelques méthodes de prétraitement toujours dans le but soit
d'améliorer la qualité de l'image soit d'en extraire des
informations pertinentes afin de faciliter une analyse antérieur. Parmi
ces techniques nous pouvons citer les opérations plus importantes.
§ La réduction du bruit par filtrage.
§ La modification d'histogramme.
§ La banairisation des images par seuillage.
§ Le rehaussement de contraste.
§ Renforcement de contour.
II.2.1 Affichage en niveau de gris :
Une image est représentée par une
matrice de dimension « nombre de lignes »
X « nombre de colonnes » .Chaque élément
de la matrice, nommé pixel, représente l'intensité
lumineuse comprise entre 0 et 255, soit 256 niveau de gris. Le niveau de gris
0 correspond au noir tandis que 255 est représenté en blanc. Il
est nécessaire de passer vers un affichage en niveau de gris pour
certaines applications, telle que le seuillage, ou bien pour avoir toutes les
informations de base pour une analyse antérieure.
Algorithme
Début
Charger l'image (Image [i][j]) ;
Pour i=0 jusqu'à hauteur
Pour j=0 jusqu'à largeur
R= valeur du canal rouge ;
G= valeur du canal vert ;
B= valeur du canal bleue ;
Moy= (R+G+B)/3;
ING[i][j] =Moy;
fin
fin
Affichage d'ING ;
Fin
Résultats :
|
|
|
Image originale
|
Niveaux de gris
|
II.2.2 Filtrage Numérique : [34]
Pour améliorer la qualité visuelle de
l'image, on doit éliminer les effets des bruits (parasites) en lui
faisant subir un traitement appelé filtrage. Généralement,
son principe consiste à remplacer la valeur de pixel central par une
combinaison prédéfinie de valeurs des pixels adjacents, soit par
la convolution de l'image brute par un filtre prédéfini, ou par
l'application des méthodes qui cherchent la valeur la plus
homogène par rapport aux éléments de la fenêtre.
On distingue généralement quatre types de filtres :
§ Les filtres passe-bas
§ Les filtres passe-haut
§ Les filtres passe-bande
§ Les filtres directionnels
II.2.2.1 Les filtres passe-bas :
Consistant à atténuer les composantes de l'image ayant une haute
fréquence. Ce type de filtrage est généralement
utilisé pour atténuer le bruit de l'image, c'est la raison pour
laquelle on parle habituellement de lissage.
II.2.2.1.1 Les filtres linéaire:
Nous avons utilisé trois types de filtre passe
bas linéaire. Ces derniers sont des filtres qui se basent sur le
produit de convolution et dont le principe est de remplacer la valeur du pixel
central par la moyenne des valeurs des pixels avoisinantes. La
différence entre les trois types de filtre réside dans la
distribution des coefficients de la matrice du filtre (masque).
|
Filtre moyenneur
|
Filtre conique
|
Filtre pyramidal
|
|
|
|
Algorithme
Début
Charger l'image (IM [i][j])
Lire la taille du masque T
Définir le masque M(T,T)
Pour i= (T/2) jusqu'à
(hauteur-T/2)
Pour j= (T/2) jusqu'à
(largeur-T/2)
K1=0 ; // Ligne du masque
Somme =0
Pour n= i-(T/2) jusqu'à
(i+(T/2)+1)
K2=0 ; //colonne du
masque
Pour m= j-(T/2) jusqu'à
(j+(T/2)+1)
Data[K1][K2]=IM[n][m] ;
K2++
fin
K1++
fin
Pour K=0
jusqu'à T
Pour L=0 jusqu'à T
Somme=Somme + (data [K][L] * masque[K][L])
R=Somme / (Somme des coefficients de masque)
IMF[i][j]=R
fin
fin
fin
fin
Affichage d'IMF ;
Fin
Résultats :
|
-
|
|
|
|
Image originale
|
Filtre moyenneur
|
Filtre pyramidal
|
Filtre conique
|
· Défauts : d'après ce
qu'on a obtenu comme résultats, nous avons pu en déduire quelques
défaut des filtres linéaires tels que :
o Certaines fréquences détruites.
o Images dégradée.
o Contours altérés.
o Plus la taille du filtre augmente, plus l'image devient plus
floue.
II.2.2.1.2 Les filtres non-linéaires :
Le médian :
L'idée est simple : prenons un ensemble de pixels au voisinage
d'un pixel donné. Rangeons les niveaux de gris de cet ensemble de pixels
en ordre croissant et choisissons le niveau de gris qui arrive en position
médiane. Ce niveau de gris sera celui du pixel donné :
|
|
|
|
|
|
|
|
19
|
23
|
42
|
|
|
|
11
|
25
|
31
|
|
|
|
60
|
25
|
12
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19
|
23
|
42
|
|
|
|
11
|
150
|
31
|
|
|
|
60
|
25
|
12
|
|
|
|
|
|
|
|
Médiane
|
11
|
12
|
19
|
23
|
25
|
31
|
42
|
60
|
150
|
Bruit
Algorithme :
Début
Chargement de l'image (IM[i][j]) ;
Lire la taille du masque (T) ;
Pour i=T/2 jusqu'à
hauteur-(T/2)
Pour j=T/2 jusqu'à
largeur-(T/2)
K=0 ;
Pour l= i-(T/2) jusqu'à
i+(T/2)+1
Pour m= i-(T/2) jusqu'à
i+(T/2)+1
V[K]=IM[l][m] ;
K++ ;
fin
fin
Triage croissant de (V[K]) ;
IMF[i][j]=V[T/2] ;
fin
fin
Fin
Résultats :
|
|
|
Image originale
|
Filtrage par la méthode de
médiane
|
II.2.2.2 Les filtres passe-haut :
À l'inverse des passe-bas, les filtres passe-haut atténuent les
composantes de basse fréquence de l'image et permettent notamment
d'accentuer les détails et le
contraste, et de renforcer les contours.
Ces filtres ont le même principe que les filtres passe-
bas, la seule différence est dans les coefficients des masques qui
peuvent prendre des valeurs négatives.
|
Filtre 1
|
Filtre 2
|
Filtre3
|
|
|
|
Résultats :
|
|
|
|
|
Image originale
|
Filtre (1)
|
Filtre (2)
|
Filtre (3)
|
· Défauts :
Cette classe des filtres est
applicable que sur les images non bruitées.
II.2.3 Négative d'image : Il
s'agit là tout simplement de mettre le complément à 255 de
chaque composante de tous les pixels de l'image. Le résultat obtenu est
appelé négatif.
Algorithme:
Début
Chargement de l'image (image [i][j])
Pour i=0 jusqu'à
hauteur
Pour j=0 jusqu'à largeur
IMinv[i][j]=255-image[i][j];
fin
fin
Fin
Résultat :
|
|
|
Image originale
|
Image négative
|
II.2.4 Seuillage :
L'opération dite de "seuillage simple" consiste
à mettre à zéro tous les pixels ayant un niveau de gris
inférieur à une certaine valeur (appelée seuil,
en anglais treshold) et à la valeur maximale les pixels ayant
une valeur supérieure. Ainsi le résultat du seuillage est une
image binaire contenant des pixels noirs et blancs, c'est la raison pour
laquelle le terme de binarisation est parfois employé. Le
seuillage permet de mettre en évidence des formes ou des objets dans une
image. Toutefois la difficulté réside dans le choix du seuil
à adapter.
Algorithme
Début
Chargement de l'image (image[j][i]) ;
Lire la valeur du seuil(S) ;//pour un seul seuil
Lire la valeur des seuils (S1, S2) ; //pour deux seuils
Pour i=0 jusqu'à hauteur
Pour j=0 jusqu'à
largeur
Si (image [i][j] >= S)
//pour un seul seuil
Si (S1<=image [i][j]<= S2) //pour deux
seuils
Image[j][i]=255;
Sinon
Image [i][j]=0;
finSi
fin
fin
Fin
Résultat :
|
|
|
|
Image originale
|
Seuillage par un seul seuil
S=94
|
Seuillage par deux seuils
S1=61 et S2=37
|
II.2.5 Histogramme : [7]
L'histogramme est un vecteur de dimension 1×256.
Chaque élément du vecteur h(i) représente le nombre des
pixels de l'image possédant le niveau de gris i, on peut donc assimiler
l'histogramme à la densité de probabilité des
intensités lumineuses.
§ Une image est dite faiblement
contrastée si elle n'utilise pas toute la dynamique des
256 niveaux disponibles.
§ Un histogramme concentré dans un intervalle de
plus bas niveau de gris indique une image très sombre.
§ Un histogramme concentré dans un intervalle de
plus haut niveau de gris indique une image trop claire.
Algorithme :
Début
Chargement de l'image (image[i][j])
Initialisation du contenu de V[256] à 0
Pour i=0 jusqu'à hauteur
Pour j=0 jusqu'à
largeur
V[image[j][i]]+=1 ;
fin
fin
Afficher l'histogramme ;
Fin
Résultats :
II.2.5.1 Histogramme cumulé :
L'histogramme cumulé représente la
distribution cumulée des intensités des pixels d'une image,
c'est-à-dire le nombre de pixels ayant au moins une intensité
lumineuse donnée : C'est également un tableau de
256 valeurs. Chaque élément hc(i)
est calculé par une sommation discrète et
représente le nombre de pixels de l'image possédant un niveau de
gris inferieur ou égale à i.
hc(i) peut être calculé par
l'équation suivante :
(I.1)
La figure ci-dessous représente une image et son
histogramme cumulé associé :
II.2.5.2 Egalisation de l'histogramme :
Pour améliorer l'information contenue dans
l'image, on utilise une technique appelée linéarisation
de l'histogramme ou encore égalisation
d'histogramme. La transformation est construite de telle façon
que le nouvel histogramme soit plat (distribution uniforme des niveaux de
gris).
Pour une image qui présente un pic dans les niveaux
sombres, cela revient à étendre la dynamique de la zone sombre au
détriment de celle de la zone claire. De telle manière à
tendre vers un même nombre de pixels pour chacun des niveaux de
l'histogramme .cette opération vise à augmenter les nuances dans
l'image. (voir figure)
Soit G le niveau de gris d'un pixel, le niveau de gris de
l'image après l'opération d'égalisation sera :
(I.2).
Algorithme :
Début
Charger l'image IM
Calcul du nombre de pixels
Pour i=0 jusqu'à hauteur
Pour j=0 jusqu'à
largeur
IM[i][j]=(V[IM[i][j]]*255/Nb_pixel
fin
fin
Afficher l'histogramme ;
Afficher l'image ;
Fin
Résultat :
|
|
|
Histogramme égalisé
|
Image améliorée
|
II.2.5.3 Etirement d'histogramme :
Il s'agit d'améliorer le contraste de l'image. La
distribution des valeurs des niveaux de gris est regroupée entre deux
valeurs Min et Max, on peut étaler la
dynamique de cette dernière en portant le niveau Min à 0 et le
niveau Max à N-1.
L'algorithme de travail est basé sur la relation
suivante
()
Résultats
|
|
|
Image originale
|
Histogramme avant l'étirement
|
|
|
|
Image améliorée
|
Histogramme après l'étirement
|
III. Conclusion :
La télédétection nous fournit des
images que nous exploitons. Ces derniers seront par la suite
améliorées et traitées par un ensemble de techniques de
traitement d'image afin de les préparées pour les étapes
d'analyse et d'interprétation.
Dans ce chapitre, nous avons mis en valeur les principaux
processus dans une chaine de traitement. Cependant, quelques méthodes
ont des caractéristiques et des conditions qu'il faut les connaitre pour
les exploitées correctement afin d'avoir de bons résultats.
En générale, tous les résultats obtenus
sont bons par rapport aux images originales. Si on parle du lissage, le filtre
médian donne un bon résultat sans dégradation de la
qualité de l'image (quelques bruits restent toujours), par contre les
autres filtres rendent l'image très lisse mais avec beaucoup de floue ce
qui nous a poussé d'appliquer d'autres types de filtres (les filtres
passe-haut) pour rehausser les contours des images lissées. D'autres
techniques d'améliorations ont été utilisés telles
que les histogrammes (Etirement, égalisation) qui offrent un grand
avantage vis-à-vis l'étape de prétraitement.
Pour le seuillage, le choix des seuils est important pour
avoir une bonne segmentation. Et pour les autres méthodes (le
négatif ou qui sont basée sur les histogrammes) se faites d'une
manière automatique.
Enfin, dans le cas ou les images sont en trichromes, il suffit
d'appliquer les méthodes décrites, sur chaque canal (le rouge, le
vert, le bleu) tout seul, en suite on fait le fusionnement des trois canaux.
I. Introduction:
La reconstruction virtuelle de scènes urbaines en
3D à partir d'images aériennes ou satellitaires est
utilisée dans plusieurs applications. Il y a quelques années,
lorsqu'on voulait montrer un grand projet de construction (complexe commercial,
centre hospitalier, etc.), les architectes et promoteurs nous
présentaient une belle maquette. De nos jours, pour nous impressionner
davantage, on nous présente parfois des images ou même des
animations virtuelles de la future construction, accompagnées de
l'environnement actuel autour du site. Les architectes peuvent aussi se servir
de reconstructions urbaines pour valider leurs projets durant la phase de
création. Toutefois, reconstruire une ville virtuelle à partir de
photographies aériennes ou images satellitaires est un problème
complexe. Dans le présent travail, plusieurs approches sont
résumées. Parmi celles-ci, certaines idées ont
été retenues afin de réaliser notre projet sur la
reconstruction 3D des scènes urbaines en se basant sur les
méthodes de segmentation et de génération de terrain
3D .
II. État de l'art :
Au cours des quinze dernières années,
différentes approches ont été proposées pour la
reconstruction 3D de sites urbains. Ces approches sont très
variées, tant sur le plan des données nécessaires en
entrée que sur celui des types de zone supportés (ex.: relief
plat ou accidenté) et du degré d'automatisation de la
méthode. Les méthodes dépendent aussi du degré de
précision désirée. Parfois, on peut se contenter d'une
reconstruction grossière alors que dans d'autres cas, on veut
reproduire plus fidélement un petit secteur.
Dans la majorité des approches
développées, le principe de base consiste
généralement à diviser le problème de
reconstruction en plusieurs sous-problèmes.
1. Localiser les bâtiments sur une image satellitaire,
aérienne ou sur une carte;
2. Calculer le relief du terrain;
3. Trouver la hauteur des bâtiments;
4. Trouver la forme des bâtiments (principalement les
toitures);
5. Augmenter le réalisme de la scène (ex.:
utilisation de textures).
Selon les données disponibles, les méthodes
existantes tentent de résoudre un sous-ensemble de ces
sous-problèmes.
Selon les données disponibles, les méthodes
existantes tentent de résoudre un sous-ensemble de ces
sous-problèmes.
II.1 Localisation des bâtiments :
II.1.1 Détection de
bâtiments par imagerie aérienne ou satellitaire :
Une autre façon de trouver la localisation des
bâtiments dans une ville est l'utilisation d'images multispectrales
(aériennes ou satellitaires) à haute résolution. Avec des
algorithmes de segmentation prenant en compte des caractéristiques
spectrales et géométriques, on peut détecter la
localisation des principaux bâtiments, c'est cette approche qu'on a
adopté.
II.1.2 Plan de cadastre :
Une façon simple et populaire de connaître la
localisation de bâtiments est l'utilisation des plans de cadastre des
municipalités. Chaque fois qu'un permis de construction est émis,
le plan de cadastre de la municipalité est mis à jour. Cette
source d'information est donc d'une bonne précision. L'information
inscrite dans ces plans se limite généralement à la
localisation planaire (2D) de la base du bâtiment et de ses principales
caractéristiques comme le type de bâtiment, le nombre
d'étages, etc. Par contre, des données comme la hauteur et la
forme architecturale ne sont souvent pas disponibles. De plus, le plan de
cadastre sous forme électronique, dans un SIG (système
d'information géographique), n'existe pas toujours.
II.2 Calcul du relief d'un terrain :
II.2.1 Détection de
bâtiments par analyse du MNE et MNT :
Il est également possible de détecter à la
fois la position et la hauteur des bâtiments par l'usage
d'un modèle numérique d'élévation (MNE) et d'un
modèle numérique de terrain (MNT). Le MNE est une
représentation du relief brut d'une scène. Il inclut les arbres,
les bâtiments, etc. Par contre, le MNT est une représentation du
niveau du sol sans tenir compte des bâtiments.
Pour détecter
les bâtiments, il ne suffit que de faire la différence entre le
MNE et le MNT. La soustraction du MNE par le MNT donne en quelque sorte tout ce
qui dépasse du niveau du sol. Pour discriminer les arbres des
bâtiments, on peut analyser la forme des segments ou avoir recours
à des images multispectrales de la zone d'études.
II.2.2 Génération d'un MNE par
stéréovision :
Une façon classique d'obtenir un modèle
numérique d'élévation (MNE) est le recours à
l'application d'algorithmes de stéréovision sur des paires de
photos aériennes. La génération des MNE et des MNT est un
problème bien documenté.
II.2.3 Génération d'un MNE avec capteur
actif (laser) :
Le MNE peut aussi être généré
à l'aide d'équipements spécialisés comme un
dispositif laser déterminant l'élévation de points au sol.
Le recours au laser permet d'obtenir des MNE avec une très bonne
précision de l'ordre du décimètre près.
II.2.4 Génération d'un MNE à partir
d'une image de profondeur :
On peut générer un MNE encore une fois a partir
des variations de dégradation des niveaux de gris présentent
dans une image satellitaire, l'image résultante est appelée une
carte de profondeur. Une fois cette dernière est
générée on peut tracer notre MNE sous une vue 3D.



II.2.5 Dérivation d'un MNT à partir d'un
MNE :
Le modèle numérique de terrain (MNT) peut
être déduit à partir d'un MNE. En filtrant les "bosses" du
MNE, on peut obtenir un MNT.
II.2.6 filtrage d'un MNE :
Nous remarquons dans la figure que le MNE est fortement
bruité (des pics ressortent à plusieurs endroits) ce qui
nécessite un filtrage (lissage) a fin d'obtenir de meilleurs
résultats. Une première passe peut être faite avec un
filtre médian avec un filtrage de 7*7 dans le but d'éliminer les
valeurs extrêmes. Par la suite , afin d'adoucir les courbes de niveau ,
en fait appel au filtre gaussien.

II.3 Détermination des hauteurs de
bâtiments par ombrages :
Par l'analyse des ombres des bâtiments, on peut
déduire la hauteur de ceux-ci. Plusieurs méthodes de
détection d'ombres existent
II.3.1 Détermination des hauteurs de
bâtiments de façon semi-automatique à l'aide d'outils
interactifs :
Dans certains cas, l'usage d'une méthode simple et
semi-automatique peut suffire pour effectuer une reconstruction en 3D. En
supposant qu'on a le MNT et le plan de cadastre d'une scène, on peut
déjà générer un premier modèle 3D dans
lequel les bâtiments ont une hauteur par défaut. Ce modèle
peut être affiché à l'écran sous n'importe quel
angle et l'utilisateur peut éditer manuellement la hauteur des
bâtiments à l'aide de l'information qu'il dispose.
On peut
aussi prendre des photos au sol ou sur le toit des édifices offrant une
bonne vue. Ces photos peuvent être superposées au modèle 3D
initialement créé. En trouvant des points de correspondance entre
le modèle virtuel et une photo, on peut déduire la position de la
caméra qui a capté l'image. Avec un nombre suffisant de points
(3), on peut aussi trouver l'orientation de la caméra. En affichant le
modèle 3D par dessus la photo en arrière plan, l'utilisateur peut
récupérer l'information des hauteurs avec une bonne
précision.
II.4 Forme des bâtiments :
L'information qui est sans doute la plus difficile à
récupérer est la forme des bâtiments. Puisqu'on
s'intéresse généralement qu'à obtenir la
reconstruction grossière d'une ville, on peut souvent se contenter de
représenter les bâtiments avec des primitives
géométriques simples. Par exemple, avec les quatre primitives
présentées ci-dessous, on peut approximer une grande proportion
des bâtiments. Ces primitives peuvent être
paramétrées à l'aide de variables décrivant la
hauteur du bâtiment, les angles de toiture, etc.
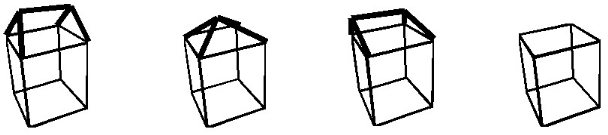
Pour trouver quelle est la primitive qui correspond le mieux
à un bâtiment, plusieurs approches sont possibles. Puisque les
toitures sont généralement constituées de surfaces
diffuses et planaires, l'illumination de ces dernières renferme des
indices. On peut alors faire la segmentation d'une image aérienne
dans les zones où se trouvent des bâtiments.

Pour paramétrer les primitives de bâtiment, on peut
recourir au MNE. Avec les moindres carrés, on minimise l'erreur entre le
modèle virtuel et le MNE. Par contre, pour que ce soit applicable, il
faut disposer d'un MNE à une très bonne précision.
Tout
comme pour les hauteurs de bâtiments, on peut aussi utiliser des outils
interactifs. L'utilisateur sélectionne un bâtiment et choisit la
primitive qui correspond le mieux en fonction de ce qu'on peut voir dans les
images photo.
II.4.1 Formes complexes d'un groupe de
bâtiments :
Une situation difficile à traiter est les groupes de
bâtiments. Ces derniers, ne pouvant plus être
représentés par de simple primitives, doivent être
modélisés par des solides plus complexes. Ce problème peut
être résolu en décomposant la base du bâtiment
(tiré d'un plan de cadastre ou détecté automatiquement) en
un nombre minimal de rectangles afin de couvrir l'ensemble du bâtiment.
Ces rectangles peuvent se chevaucher. Un exemple de décomposition est
montré ci-dessous :

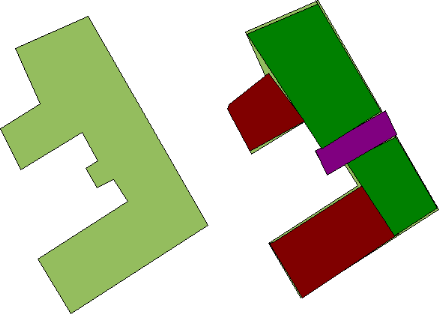
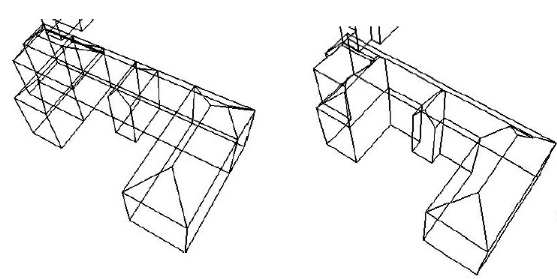
Les rectangles obtenus sont ensuite traités
indépendamment. Les toitures sont alors détectées pour
chaque rectangle de la même façon que s'il s'agissait d'un
bâtiment à part entière. Enfin, une dernière
étape consiste à faire la fusion des primitives obtenues. Cette
fusion s'effectue comme une union de solides, qui est souvent utilisée
en infographie pour modéliser des objets complexes.
II.4.2 Correction manuelle des hauteurs :
Comme dernière étape, des photos peuvent
être superposé au modèle virtuel afin de corriger la
hauteur de certains bâtiments.
 
Sur l'analyse (figure (II .5)), les lignes rouges
représentent les frontières du pavillon central sur la photo et
les lignes bleues sont les frontières du modèle 3D. On voit
clairement que la hauteur du pavillon central est trop grande sur le
modèle 3D par rapport à la photo correspondante. De plus, le
centre culturel ne devrait pas être visible sous cet angle.


II.4.3 Superposition des blocs
construits avec le MNE :
Le MNT obtenu, qui est en réalité encore un MNE,
n'est pas encore bien filtré. Certains obstacles, principalement des
arbres, dépassent du sol et cachent certains angles. Il y a aussi des
zones entre les bâtiments rapprochés qui causent problème.
Le niveau du terrain fait une pente à côté des
bâtiments. Sur certaines photos prises entre deux bâtiments.

Ce résultat obtenu des bâtiments n'est pas si
mal. On peut y reconnaître la forme des principaux bâtiments. En
traitant mieux le MNT utilisé, on pourrait réduire les pentes
entourant les édifices. En résumé, la détermination
des hauteurs de bâtiment par le MNE ou par la DAO constitue
déjà un bon début.
II.5 Approche choisie: une méthode
automatique raffinée par une méthode semi-automatique :
Le choix de l'approche a été basé sur des
critères de faisabilité (temps et données disponibles).
Initialement, nous nous somme orienté au début vers une
méthode automatique pour détecter à la fois la position et
la hauteur des bâtiments par l'analyse d'un MNE et d'un MNT
générés par le calcul de la profondeur de
l'image.
En cours de route, puisque les résultats du MNE
n'étaient pas satisfaisants, nous avons passé à une
méthode semi-automatique. Cette méthode, consiste à
évaluer les hauteurs à partir de photos prises au sol et du plan
cadastral que l'on superpose au modèle virtuel.
De ce fait, notre approche de reconstruction 3D englobe les
différents modules suivants :
1. Une localisation des différentes structures urbaines
par plusieurs méthodes de segmentation qui se basent soit sur l'approche
contour ou région à partir d'une image satellitaire ou un plan
architectural.
2. Génération des modèle
numériques (MNE : Élévation, MNT : Terrain)
à partir de la profondeur des images satellitaires.
3. Filtrage du modèle numérique
d'élévation (MNE) dans le but de lisser les pentes.
4. Construction des différentes structures urbaines par
AutoCAd à partir du plan cadastral, images aériennes, et
d'autres informations sur le site à traiter.
5. La dernière étape est celle de la
construction finale c.à.d. dépôt des structures construites
sur le MNE.
Dans le but d'obtenir un MNE le plus précis
possible et une construction exacte des objets urbains, il est
nécessaire d'avoir :
- Plan de cadastre.
- Images aériennes.
- Des images avec une bonne résolution spatiale.
- Photos prises au sol : Afin de réaliser la partie
semi-automatique (pour déterminer la hauteur des bâtiments), on
doit disposer de plusieurs photos prises à des endroits
stratégiques à l'aide d'un appareil photo numérique.
- Points de référence au sol : Afin d'estimer la
taille des pixels au sol, on aura besoin de quelques points de
référence au sol. On a obtenu des points à l'aide d'une
image satellitaire.
Partie(I) : Localisation des structures urbaines
par segmentation
I. Introduction :
La segmentation est une étape importante dans
l'imagerie satellitaire pour l'extraction des informations qualitatives de
l'image.
Fondamentalement, la segmentation est un processus qui
consiste à découper une image en régions connexes
présentant une homogénéité selon un certain
critère, comme par exemple la couleur. L'union de ces régions
doit redonner l'image initiale. Dans notre travail l'étape de
segmentation est très importante pour la localisation des
bâtiments sur les images aériennes ou satellitaires à haute
résolution en se basant sur une segmentation soit par région ou
par contour.
II. Définition : [11]
La segmentation est définie comme le processus
de partitionnement de l'image en régions homogènes et
indépendantes. Selon cette définition, les
« régions » sont composées de plusieurs
pixels montantes une homogénéité dans au moins une de
leurs caractéristiques (niveau de gris, textures, etc.,). Il existe
plusieurs méthodes de segmentation dont on a choisi quelques une afin de
les adaptées à notre cas de localisation. Nous allons
présenter dans ce chapitre une description générale du
principe théorique de fonctionnement de quelques méthodes qui se
base soit sur l'approche région soit sur l'approche contour.
On peut distinguer deux grands types d'approches :
· L'approche «
Contour » : qui s'intéresse aux zones de
changements de l'image.
· L'approche
« Régions » : qui s'intéresse
aux zones homogènes.
Il est à signalé que la robustesse et les
performances des méthodes de segmentation peuvent varier en fonction du
type d'application, c'est pour cela qu'il est très important de faire un
choix adéquat au type de cette dernière.
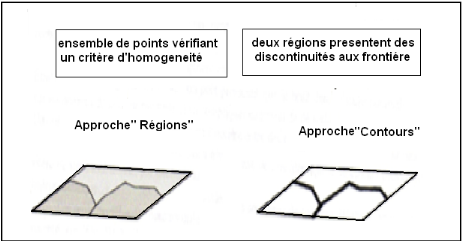
III. Détection de contour
« L'approche contour » :
III.1 Contours classiques
L'obtention des contours est une étape importante
dans le processus d'interprétation automatique d'une image cela permet
de matérialiser les contours des objets recherchés.
III.1.1 Définition :
Un contour peut être considérer comme une
frontière entre deux régions différentes (suivant un
critère de similarité donné; par exemple un niveau de gris
identique à un epsilon prés ou une couleur identique...).
III.1.2 Principe de base :
La détection d'un contour est
généralement basée sur la détection du changement
à la frontière de deux régions. De ce fait, on peut
pressentir que le bruit dans l'image (anomalies sur les niveaux de gris, par
exemple...) va compliquer ce travail de détection.
Les méthodes de détection des contours comportent
en générale deux phases :
· D'abord trouver les pixels censés appartenir
à un contour (éventuellement avec mesure de certitude) en
s'appuyant sur une propriété particulière. On appellera
ces points: des ponts-candidats ou des ponts
contour.
· Puis relier ces ponts contours de façon à
obtenir de véritables contours (lignes; courbes,...).
III.1.3 Les principaux algorithmes classiques
connus :
Les algorithmes de détection de contours
consistent à identifier les contours d'une image en repérant les
forts changements d'intensités lumineuse de l'image.
Les principaux algorithmes connus (Sobel, Prewitt,
Canny, Deriche, Laplacien,...).
III.1.3.1 Les opérateurs dérivatifs
du premier ordre (gradient) et du deuxième ordre
(Laplacien) :
Les méthodes classiques de détection
de contours actuelles sont des méthodes dérivatives qui
détectent les variations locales d'intensité des pixels d'une
image. Les contours sont alors détectés :
· Soit par extraction des maxima locaux de la
dérivée première «
gradient »
· Soit par extraction des passages par zéro de la
dérivée seconde directionnelle. On verra que
moyennant quelques approximations, cette deuxième approche revient
à extraire les passages par zéro du
Laplacien.
III.1.3.1.1 Les détecteurs de gradient :
Dans la pratique, il est possible d'utiliser des
détecteurs de gradient pour repérer les contours d'une image. Ces
méthodes sont réalisées par un filtrage linéaire,
dont les filtres sont obtenus à l'aide de masques appliqués sur
des fenêtres de 3x3 pixels. Parmi les filtres classiques les plus
utilisés, on peut citer ceux de Sobel,
Prewitt, Robert. Dans notre projet on a
travaillé avec les operateurs de «Sobel et Prewitt». Ces
méthodes, combinées à un post-traitement adéquat
(seuillage, fermeture des contours, etc...) sont nécessaires afin
d'avoir un contour bien défini et complet pour nos traitements
ultérieurs.
a. Formulation mathématique :
Dans le cas discret, les dérivées dans
les directions horizontales et verticales au point de coordonnées (x, y)
approchées par de simple différences finies :
(III.1)
Pour l'axe horizontal x, le gradient noté, est
donné par :
(III.2)
Pour l'axe vertical y, le gradient noté, est donné
par :
(III.3)
On calcule la norme du gradient donnée par :
(III.4)
b. Opérateurs de Sobel, Prewitt et
Robert :
Ø Prewitt qui estime un maximum du gradient en
utilisant les masques de convolution suivants :
Et
Ø Sobel qui estime aussi un maximum du gradient en
utilisant les masques de convolution suivants :
Et
Ø Les filtres de Roberts sont une approche
discrète de la dérivée partielle d'ordre 1 il est
exprimé par les masques suivants :
Et
Le calcul du gradient sur une image peut être obtenu par
deux convolutions : l'une mettant en évidence les contours
horizontaux, l'autre les contours verticaux :
(III.5)
(III.6)
III.1.3.1.2 Les opérateurs dérivatifs du
deuxième ordre (le Laplacien) :
Dans la pratique, lorsqu'on utilise une
méthode dérivative de seconde ordre, c'est le `'Laplacien'' qui
est utilisé car il permet de simplifier les calculs et donc il est moins
couteux en temps de calcul.
a. Principe:
Extraire les maxima locaux du gradient revient
également à chercher les zéros de la dérivée
seconde directionnelle. C'est-à-dire :
= 0
(III.7)
Où :
I(x, y) : est l'intensité
lumineuse du point de coordonnées (x,y)
g : la direction du gradient G.
Le Laplacien d'un signal bidimensionnel continu est
défini par :
(III.8)
Après une approximation de la dérivée
seconde :
On aura :
(III.10)
Donc, pour calculer le Laplacien en chaque pixel de l'image, nous
pouvons filtrer l'image par le filtre linéaire suivant :
III.1.3.1.3 Filtre de Canny : [02]
L'approche de Canny est présentée en
monodimensionnel, cette approche cible trois critères qui doivent
valider un détecteur de contour :
1- Garantir une bonne détection, c'est-à-dire une
réponse forte même à de faibles contours.
2- Garantir une bonne localisation.
3- Une faible multiplicité des maximums dus au bruit.
a. Étapes d'une détection de contours par
filtre de Canny
L'objectif est bien de calculer le module du gradient de
l'image analysée. Souvent avant d'appliquer le filtre de Canny, un
filtrage au préalable est opéré sur l'image au moyen d'un
filtre gaussien. Les différentes étapes sont
énumérées ci-après :
Ø Convolution de l'image initiale avec
un filtre passe-bas gaussien bidimensionnel (ou convolution 1D dans chacune des
deux directions)
(III.11)
Ø Convolution de l'image lissée
avec le filtre de Canny ou la dérivée de gaussienne dans les
directions horizontales et verticales. (filtre Sobel ).
Ø Calcul du module du gradient à partir des deux
images représentant les gradients de l'image filtrée passe-bas
dans les directions horizontales et verticales.
Défauts de l'approche contour
classique:
Les méthodes classiques de segmentation
échouent dans certains cas:
§ Si les images sont bruitées.
§ Si les images contiennent de faux contours.
Une solution a été proposée est celle des
modèles deformables, ce terme apparu dans les années 80 dans les
travaux de Terzopoulos a ouvert un domaine de recherche très actif et
fructueux dans les travaux de segmentation en particulier. Ces modèles
peuvent avoir plusieurs notations dans la littérature tels que: Contours
actifs , surfaces actives, balloons, contours deformables ou surfaces
deformables.
III.2 Contours déformables : [15]
[35]
Le principe des contours actifs est de faire
évoluer un contour (fermé ou non) initial vers une position
d'équilibre, c'est-à-dire en direction des bords de l'objet
à détecter. Entre deux itérations, la vitesse des points
est régie par une équation mettant en jeu des forces à
appliquer au contour, généralement selon la normale.
Ces forces dépendent des données
présentes dans l'image (intensité, gradient...) et des
propriétés de régularité du contour. La position
d'équilibre peut être définie comme le minimum d'une
fonctionnelle d'énergie dont la dérivée correspond aux
forces à appliquer.
Dans la figure suivante figure- II.02 - , on a contours
initiale ( courbe initiale) qui est représentée par le cercle
extérieur, sous l'influence des forces internes et externes , le contour
se déforme jusqu'à atteindre l'objet, qui es t en gris.
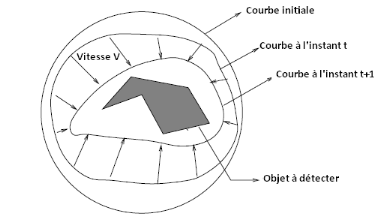
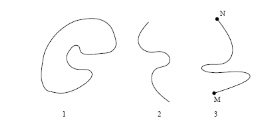
III.2.1. Les différents types de contours :
[15]
Nous pouvons définir trois types de
contours actifs différents utilisés (voir figure III.3) :
1. les contours déformable
fermés où Vt0 =
Vtn-1 (le point de départ est celui
d'arrivée)
2. les contours déformable à
extrémités libres (tous les points sont susceptibles de
bouger)
3. les contours déformable à
extrémités fixes où les positions
V0 et Vn-1 sont fixes dans le temps
ainsi que les dérivées premières en ces points (les points
de départ et d'arrivée restent fixes)
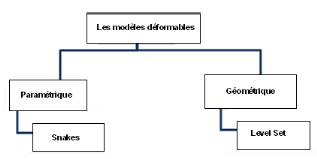
III.2.2. Les différents modèles des
contours déformables: [15]
La figure III.4 représente la classification des
contours déformable, qui se composent de deux familles
· Les contours déformable paramétriques
(Snake).
· L es contours déformable
géométriques (Level Set, contours actifs
géodésique).
Les contours déformable paramétriques ,
ont pour principe de se déformer itérativement pour atteindre les
frontières d'objet à détecter.
Depuis 1988 , d'autres théories ont
été proposées pour compléter le modèle des
contours actifs ainsi , Caselles , Kimmel et Shapiro proposent en 1997 le
modèle de contours actifs géodésiques qui se rapprochent
de la détection de contours par Snake , mais a pour avantage de pouvoir
se séparer pour détecter plusieurs objets en même temps.
comme pour les Snake, on initialise le contour prés de objets à
détecter dans l'image, et on fait évoluer cette courbe de
façon à minimiser son énergie.
III.2.2.1 La méthode de détection par
Snake : [02]
III.2.2.1.1 Principe de base de la
méthode :
La méthode de détection par Snake, ou
contour actif, consiste à placer aux alentours de la forme à
détecter une ligne initiale de contour. Cette ligne va
se déformer progressivement selon l'action de plusieurs forces qui vont
la tirer ou la pousser vers la forme.
Les forces impliquées vont dériver de (3)
énergies associées au Snake:
· Une énergie propre, due uniquement à la
forme du contour, dite énergie interne: E
int.
· Une énergie potentielle imposée par
l'image: E image. C'est elle qui va attirer la
ligne du snake vers les contours réels présents sur l'image.
· Une énergie E cont
qui exprime certaines contraintes supplémentaires qui peuvent être
imposées par l'utilisateur vu le Snake qu'il veut obtenir
a. L'énergie interne
Elle va dépendre uniquement de la forme du Snake. C'est
une contrainte de régularité sur la courbe. Elle s'écrit:
E int = (a(s)).||(Vs(s)||2 +
b(s)).||(Vss(s)||2)
(III.12)
a et b sont les poids respectifs accordés à la
dérivée première Vs et à la dérivée
seconde Vss. On ajustera a et b pour trouver un intermédiaire entre un
contour souple mais pas forcement très régulier (et qui pourra
alors se caler sur des coins et des angles aigus) et un contour très
régulier qui suivra bien le contour sans s'accrocher sur des petites
aspérités.
b. L'énergie potentielle liée à
l'image :
Elle caractérise les éléments vers
lesquels on veut attirer le Snake sur l'image. Pour notre problème,
puisqu'il s'agit de détecter des contours, on va s'intéresser aux
lignes de fort gradient:
E
image= -gradient(i)
(III.13)
Pour certains problèmes, on peut choisir d'attirer le
Snake vers des zones présentant d'autres caractéristiques: vers
les zones les plus sombres par exemple.
c. L'énergie de "contrainte".
Elle est définie par l'utilisateur selon les
spécificités du problème. On peut par exemple imposer une
distance minimale ou maximale entre deux points consécutifs du contour
actif. Elle va s'exprimer en fonction de V(s) uniquement:
E cont=E cont(s)
(III.14)
d. Energie totale du contour actif :
[16]
L'énergie totale en un point du Snake V(s) va donc
s'écrire:
E totale(V(s), Vs(s), Vss(s)) = E int(V,
Vs, Vss) + E image(V) + E cont(V).
Nous avons affaire à un nombre de points Vi fini. On
exprime directement Ei: énergie au point Vi en fonction de tous les
points V du Snake en utilisant notamment:
Vis(s)= Vi - Vi-1 et
Viss(s)= Vi+1 - 2Vi + Vi-1
Ce qui nous permet de discrétiser la formule de Ei:
énergie au point Vi sous la forme:
Ei totale(Vi-1, Vi, Vi+1) = E int(Vi-1, Vi, Vi+1) + E
image(Vi) + E cont(Vi).
Et donc l'énergie totale du snake vaut:
E totale(Vi-1, Vi, Vi+1) = somme (Ei) = somme (Ei
int(Vi-1, Vi, Vi+1) + Ei image(Vi) +
Eicont(Vi))
(III.15)
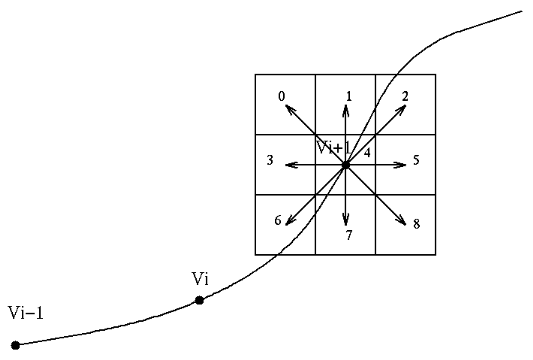
III.2.2.1.2 Application pratique au cas du contour
actif : [02]
Appliquons cette méthode à notre Snake.
Nous partons d'un premier contour initialisé par l'utilisateur
lui-même. Nous allons le parcourir progressivement et en chaque point
éventuellement déplacer le point pour que sa nouvelle position
optimise l'énergie du Snake.
Chaque point a 9 déplacements possibles a chaque
étape comme le montre la figure suivante:
III.2.2.2 Les contours actifs
géométriques : ensemble de niveau ''Level
Set'' :
III.2.2.2.1 Introduction : [39]
La méthode des Ensembles de Niveau Zéro
est une méthode de simulation numérique utilisée pour
l'évolution des courbes et des surfaces dans les domaines discrets .
Cette méthode permet de faire évoluer une courbe
paramétrique fermée C(p) suivant une équation du type
=FN
(III.16)
Où t est le temps, F
est la vitesse d'évolution et N est la normale unitaire
à la courbe.
Chaque point de la courbe C évalue
suivant la direction normale à la courbe avec
Une vitesse F.
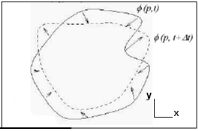
L'avantage principal de cette méthode est la
possibilité de gérer automatiquement le changement de topologie
de la courbe en évolution. La courbe C peut être divisée en
deux ou trois courbes, Inversement plusieurs courbes peuvent fusionner et
devenir une seule courbe. La méthode des Ensembles de Niveau Zéro
est capable de réaliser ce changement en utilisant une fonction d'ordre
supérieure.
Pour une courbe plane C(p), un tableau bidimensionnel de
nombres réels ö(x,y) est utilisé pour sa
représentation. L'évolution de la courbe signifie la mise
à jour de tout le tableau ö(x,y).
D'abord nous initialisons (en ö(x,y)) à
zéro les pixels correspondants au passage de la courbe C, après
il faut calculer pour le reste des éléments du tableau, la
distance euclidienne à la courbe C, qui sera négative à
l'intérieur et positive à l'extérieur. Autrement dit, le
tableau bidimensionnel ö sera rempli de la manière suivante :
zéro tout le long de la courbe C, et la valeur de la distance
euclidienne au point le plus proche de la courbe pour tout le reste. S'il
s'agit d'un élément à l'intérieur de la courbe C
(c'est une courbe fermée) le signe de son contenu sera
négatif.
III.2.2.2.2 Principe d'évolution de la courbe
C: [39]
Etant donné Ù une sous ensemble
borné de R2, avec ??Ù en tant que sa frontière.
Puis une image de deux dimensions U0 on peut la définie comme
U0 : Ù -->R. dans ce cas Ù n'est qu'un
rectangle grillé fixe. Maintenant on considérer
l'évolution de la courbe C dans Ù, comme le frontière d'un
sous ensemble ouvert w de Ù. En d'autres ; w c Ù, et C est
le frontière c de w(C=??w).
L'idée principale est d'enfoncer la propagation de la
courbe comme une fonction de dimension supérieure d'ensemble du niveau
zero. on définir la fonction comme suit :
Où d est la forme de distance (x,y) à ??w dans
t=0, et le signe plus ou moins est choisir si le point (x,y) es t à
l'extérieure ou à l'intérieur de la sous ensemble w .
Maintenant l'objectif est d'introduire une équation
pour l'évolution de la courbe .
La courbe évoluer dans la direction de sa normale
suivant l'équation dérivée partial suivant
,
Ou l'ensemble {(x,y)} définir le contour initial, et F
la vitesse de propagation. Pour certin forme de la vitesse F, ceci est
réduit à l'équation standard de Hamilton-Jacobi. Il y a
plusieur avantages principaux à cette formulation. Le premier est que
Ø(x,y,t) raste toujours une fonction tant que F est lisse. Quand la
surface Q est évoluée, la courbe C peut se divisée en
plusieurs courbes, se fusionnée en un seul et changer la topologie.
Un autre avantage est que des propriétés
géométriques de la courbe sont facilement
déterminées à partir d'un ensemble de niveau particulier
de la surface Q. Par exemple, le vecteur de la normal pour chaque point de la
courbe est donné par :
N=
(III.17)
Et la courbure K est obtenue à partir de la divergence
du gradient du vecteur normal d'unité au front :
K=div=
(III.18)
En fin, un autre avantage est que nous pouvons
évoluée des courbes dans les dimensions supérieures
à deux la formulation précédente peut être
facilement généralisé pour des dimensions
élevées. C'est utile en propageant une courbe pour segmenter des
données de volume.
a. Contour active avec un
« arrêt-au-bord » : [39]
Le but maintenant est de définir une fonction
de vitesse F à partir des données de l'image. Malladi et al.
Accomplissent ceci en divisons d'abord F dans deux composants :
F=FA+FG.
FA représente un terme constant d'advection
qui forcera la courbe pour s'étendre ou se contracter
uniformément basé sur son signe. Ceci agit comme la force
d'inflation utilisée dans les modèles traditionnels de
« serpents ». Le deuxième terme FG
dépend de la géométrie de la courbe et agit pour
lisser les régions de grande courbure.
Cependant , nous avant besoin également d'une
méthode pour arrêter l'évolution de la courbe à la
frontière de l'objet. Si on suppose que les frontières sont
définies par le gradient de notre image U0, nous pouvons
créer une fonction « d'arret-au-bord » g :
g(u0)=,p1
(III.19)
Ou G0(x ; y)*U0(x, y) est
simplement la convolution de U0 .
La fonction g(U0) a des valeurs proches de ZERO
(0) dans les régions ou le gradient de l'image est élevé,
et desvaleurs proches de UN(1) dans des régions homogènes.
Une autre fonction « d'arret-au-bord » qui
tend plus rapidement vers zéro sur les frontières peut etre
définie comme siut :
g(u0)=
multiplier notre fonction de vitesse F par cette fonction
« d'arret-au-bord » g. On applique les changements
ci-dessus, alors l'équation 2 peut etre récrit comme suite :
=g(u0)(FA+
FG).(x,y ,0)=(x,y )
Maintenant pour discrétiser , on utilise l'approche des
différences finies. Soit l'étape de temps et (xi,
yj) les poits de grille pour1.j .Et on prend=(,nune approximation de
avec n0, . Les différences finies sont décrites par la notation
suivante :
=-. -
=-. - -
(III.20)
Malladi et Al utilise un terme constante d'advection
FA=1 et utilise des approches introduite par sethian et al pour
estimes
FA :=1/2
(III.21).
La force restante fG est basée
sur la courbure K(Equation3).Malladi et al. Multiplier cette force par une
restante négatif très petite å et prend une approximation
de | Ø|,on utilisant des défférences centrales.Donc une
estimation de FG | Ø| est :
FG=-- cK
(III.22)
Alors pour faire évoluer, on résolue la
discrétisation suivant de équation (6) :
(III.23)
b. Contour active sans arrêt aux
bords : [17]
Rappelant que la courbe C peut etre considérer comme
étant la frontière d'une sous ensemble ouvert de Ù
(c'est-à-direC=w). Notons la région par intérieur (C) et
la région Ù\par extérieur(C). Au lieu de fonder le
modèle sur une fonction « d'arret-au-bord » nous
allons interrompu l'évolution de la courbe par l'intermédiaire de
l'approche de minimisation d'énergie.
Considérons le cas simple d'une image u0
formé par deux régions d'intensité constante par morceau.
Notons les valeurs de l'intensité par et. En plus supposans que l'objet
à détecté a une région de bord C0 et
d'intensité. Par suit intérieur (C0),
l'intensité de u0est approximativement, alors que pour
extérieur (c0), l'intensité de u0 est
approximativement . Puis on considèrent un terme d'ajustement .
F1(C)+F2(C)=
Nous pouvons dire que l'on est sur les bords de l'objet
quand
En effet, si la courbe est à l'intérieur de
l'objet :
Si elle est à
l'extérieur :
Si elle est sur le bord
: :
On obtient donc une énergie F en fonction de C, c1 et
c2 telle que :
F(C, c1, c2)=longueur(C)+v.superficie(C) +
+
Avec , , ,sont des paramètres positifs.
Longueur (c) est un paramètre de lissage de la
courbe.
la méthode du LevelSet est utilisé pour faire
évoluer la courbe C. Cette méthode permet de propager une courbe
qui est représentée par lorsque est égal à 0.
Pour cela, on crée une nouvelle image de même
taille que l'image I que l'on veut traiter. Dans cette image, on a la courbe C
pour =0, on est à l'intérieur de la courbe pour >0, et
à l'extérieur pour <0. On initialise alors
indépendamment de I. On calcule alors la distance signée
.c'est-à-dire en partant d'une image dont la valeur est -1 à
l'extérieur et + 1 à l'intérieur et on cherche à
avoir une valeur qui tend vers 0 au bord, qui croît vers
l'intérieur et qui décroît vers l'extérieur. La
distance signée est donnée par l'équation suivante .Pour
le cas continu.

(III.24)
Pour le cas en discret :
(III.25)
Avec :
En revenant à l'image I, on a alors une nouvelle
fonction
(C, c1, c2)=longueur ()+v.superficie() +
+
On définit alors la fonction Heaviside H :
(III.26)
La fonction Dirac est définie par
(III.27)
On exprime les termes de l'énergie F de la
manière suivante :
L'expression de l'énergie peut alors s'écrire de
la forme suivante :
En gardant Ø fixé, et en minimisant
l'énergie F selon c1 et c2, on peut facilement exprimer ces constantes
c1 et c2 en fonction de Ø :
(III.28)
En gardant alors c1 et c2 fixés, on minimise
l'énergie selon Ø pour obtenir l'équation de
Euler-Lagrange pour Ø:
où div est la courbure [3] qui permet de garder une
courbe lisse.
En discret, l'équation d'évolution est de la
forme :
Avec :
K=div=
ET.
est la vitesse d'évolution.
Pour les images multi spectrales, le principe reste le
même, il suffit juste de considérer ces images comme plusieurs
images mono spectrales. On obtient alors pour les moyennes:
et on obtient pour l'évolution de
(III.29).
IV. Conclusion :
Dans cette partie nous avons traité les
différentes méthodes de segmentation qui se basent sur deux
approches « Contour et Région » en commençant
par les modèles classique jusqu'au modèle évolués.
Pour les méthodes basées contour, deux approches ont
été définies la première consiste a intègre
les différents modèles dérivables non déformables
par contre la deuxième approche consiste a appliquer des modèles
déformables tel que les Level Set vue la complexité des images
satellitaires.
Ces modèles se basent sur l'évolution d'une
courbe initiale sous l'influences d'une force interne ( qui définit les
propriétés de la courbe elle-même) et une force externe (
définit les propriétés de l'image à segmenter) , on
a traiter deux types de contours déformables , les contours
paramétriques ( Snake) et les contours géodésiques (Level
Set).
Partie(II) : Génération des
modèles numériques de terrain
I. Introduction :
Les modèles numériques tridimensionnelles urbains
représentent souvent le modèle de base d'un systèmes
d'information topographique (SIT) ; ainsi la précision des SIT est
directement a mettre en relation avec celle des modèles qui lui sert de
support. L'intérêt dans la 3D c'est rapidement focaliser sur des
possibilités lier a la visualisation des maquettes virtuelles en 3D.
Pour réaliser cette dernière nous devons obligatoirement passer
par une étape de génération des modèles
numériques soit de terrain, soit d'élévation ce qui fait
l'objet de ce chapitre.
II. Un Modèle Numérique de
Terrain : [36]
Un modèle numérique de terrain (MNT) est une
représentation de la topographie (altimétrie et/ou
bathymétrie) d'une zone terrestre (ou d'une planète tellurique)
sous une forme adaptée à son utilisation par un calculateur
numérique (ordinateur).
En cartographie, les altitudes sont habituellement
représentées par des courbes de niveaux et des points
cotés. Suivant la taille de la zone couverte, la plupart des MNT
utilisent pour les petites zones, un maillage régulier carré ou
pour les grandes zones, un maillage pseudo carré dont les
côtés sont des méridiens et des parallèles.
Il permet ainsi :
- de reconstituer une vue en
images de
synthèse du terrain,
- de déterminer une trajectoire de survol du terrain.
- de calculer des surfaces ou des volumes.
- de tracer des profils topographiques.
D'une manière générale, de manipuler de
façon quantitative le terrain étudié.
II.1. Types de MNT :
On peut distinguer les MNT selon le type de maillage
utilisé :
- maillage carré/rectangulaire
- maillage hexagonal
- maillage triangulaire régulier
- maillage triangulaire quelconque
En fonction du type de maillage, la représentation
informatique du MNT varie. Dans le cas de maillages rectangulaires, on peut
utiliser des tableaux, mais dans les autres cas, les structures de
données sont plus complexes.
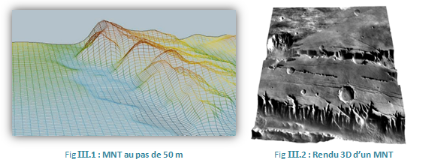
II.2 Autre modèle numérique
utilisé
Modèle numérique
d'élévation : MNE [36]
C'est l'ensemble discret de valeurs numériques qui
modélisent la surface du terrain naturel et le sursol d'une zone
géographique. Le semis de points "MNE" comprend tous les
éléments du terrain : TN {sol, ruptures de pente,...}, le
bâti, le sommet de la végétation, les routes, les ouvrages
divers... hors les artefacts créés par la présence
d'objets isolés (voitures, piétons, panneaux,...) et les surfaces
en eau.
III. Génération d'un modèle
numérique de terrien :
III.1. Génération d'un
modèle numérique de terrien a partir d'une image d
télédétection en utilisant l'OpenGL
De nombreuses techniques existent pour la
génération de terrains en 3D. Certaines sont basées sur
les fractales, d'autres sur des fonctions de bruit.
La technique des champs de hauteur heightfields qui consiste
à calculer le relief du terrain à partir d'une image en niveaux
de gris est utilisée pour faciliter l'exploitation des images
grâce aux bibliothèques JPEG, TIFF et BMP.
III.1.1 La bibliothèque graphique OpenGL :
[26]
OpenGL est un système graphique crée par
« Silicon Graphics » qui permet de
visualiser une scène 2D ou 3D. Les objets de cette scène peuvent
être composés de points, de lignes, de polygones, de quadriques.
Ils possèdent des attributs graphiques : paramètres de
réflexion, couleur, texture. L'éclairage de la scène est
réalisé par des lumières de différents types (spot,
lumière à l'infini).
III.1.2 Pipe-line de Rendu :
Voici le pipeline complet :
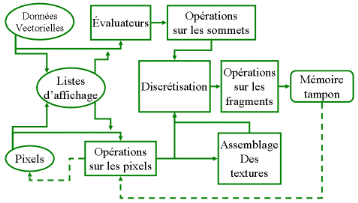
Intéressons-nous à l'évolution des
données vectorielles
:
[Données]->[Evaluateurs]->[Opérations sur les
sommets et assemblage de
primitives]->[Discrétisation]->[Opérations sur les
fragments]->[Image]
· Les Evaluateurs produisent
une description des objets à l'aide de sommets et de facettes.
· Les Opérations sur
les sommets sont les transformations spatiales (rotations et translations)
qui sont appliquées aux sommets, les calculs d'éclairage et de
coordonnées de texture.
· L'assemblage de
primitive regroupe les opérations de clipping :
élimination des primitives qui sont en dehors d'un certain espace et de
transformation perspective.
· La discrétisation
(Rasterization) est la transformation des primitives
géométriques en fragments correspondant aux pixels de
l'image.
· Les Opérations sur les
fragments vont calculer chaque pixel de l'image en combinant les
fragments qui se trouvent à l'emplacement du pixel. On trouve entre
autres la gestion de la transparence, et le Z-buffer (pour l'élimination
des surfaces cachées).
III.1.3 Les Bibliothèques coexistant avec
OpenGL : [37]
GLU : OpenGL Utility Library contient les
routines de bas niveau pour gérer les matrices de transformation et de
projection, la facettisation des polygones et le rendu de surface.
Les bibliothèques d'extension du système de
fenêtres permettent l'utilisation du rendu OpenGL. Il s'agit de
GLX pour X Windows (fonctions ayant pour préfixe glX)
et de WGL pour Microsoft Windows (fonctions ayant pour préfixe wgl).
GLUT : OpenGL Utility Toolkit est une boite
à outils indépendante du système de fenêtrage,
écrite par Mark Kilgard pour simplifier la tâche d'utiliser des
systèmes différents (fonctions ayant pour préfixe
glut).
III.1.4 Les principales instructions :
III.1.4.1 Les fonctions de gestion
d'une fenêtre : [26]
|
Fonction
|
rôle
|
|
glutInit(int * argc, char **argv)
|
initialise GLUT et traite les arguments de la ligne de
commande.
|
|
glutInitDisplayMode(unsigned int mode
|
permet de choisir entre couleurs RVB et couleurs indexées,
et de
déclarer les buffers utilisés.
|
|
glutInitWindowPosition(int x, int y)
|
spécifie la localisation dans l'écran du coin haut
gauche de la fenêtre.
|
|
glutInitWindowSize(ind width, int size)
|
spécifie la taille en pixels de la fenêtre.
|
|
int glutCreateWindow(char * string)
|
crée une fenêtre contenant un contexte OpenGL et
renvoie
l'identificateur de la fenêtre. La fenêtre ne sera
affichée que lors du premier glutMainLoop()
|
III.1.4.2 La fonction d'affichage : [26]
|
glutDisplayFunc(void (*func)(void))
|
spécifie la fonction à appeler pour l'affichage
|
|
glutPostRedisplay(void)
|
permet de forcer le réaffichage de la fenêtre.
|
Les couleurs : Les couleurs sont
définies en OpenGL de deux manières :
Couleurs indexées :
256 couleurs sont choisies, et on se
réfère au numéro de la couleur (son index). C'est un mode
qui était intéressant lorsque les écrans d'ordinateurs
ne savaient afficher que 256 couleurs simultanées.
Couleurs RVBA :
Une couleur est définie par son intensité sur 3
composantes Rouge, Vert, Bleu. La quatrième composante est
appelée canal Alpha, et code l'opacité.
La couleur d'un objet est spécifiée par l'appel
de glColor (...).
III.1.4.3 Les primitives
géométriques :
Déclaration :
glBegin(GLenum mode) : ouvre la
déclaration des sommets de la primitive
glEnd(void) : termine cette
déclaration
Il y a dix types de primitives différents, qui
correspondent à des points, des lignes, des triangles, des
quadrilatères, et des polygones convexes.
|
GL_POINTS
|
GL_LINES
|
GL_LINE_STRIP
|
GL_LINE_LOOP
|
GL_TRIANGLE
|
|
|
|
|
|
|
GL_TRIANGLE_STRIP
|
GL_TRIANGLE_FAN
|
GL_QUADS
|
GL_QUAD_STRIP
|
GL_POLYGON
|
|
|
|
|
|
a. Le vecteur normal en un point :
C'est grâce au vecteur normal que l'on peut
spécifier l'orientation de la surface dans l'espace, et en particulier
l'orientation par rapport aux sources de lumière. L'appel à
glNormal*() donne une valeur à la normale courante.
Elle sera associée aux points spécifiés par les appels
suivants à glVertex*().
b. Le modèle d'ombrage :
Chaque facette d'un objet peut être affichée d'une
unique couleur (ombrage plat) ou à l'aide de plusieurs couleurs (ombrage
lissé). OpenGL implémente une technique de lissage appelée
Ombrage de Gouraud. ce choix s'effectue avec glShadeModel(GLenum
mode).
c. Elimination des surfaces
cachées :
OpenGL utilise la technique du Z buffer (ou buffer de
profondeur) pour éviter l'affichage des surfaces cachées.
On ne voit d'un objet que les parties qui sont devant et pas
celles qui se trouvent derrière. Pour chaque élément de la
scène la contribution qu'il aurait à l'image s'il était
visible est calculée, et est stockée dans le Z buffer avec la
distance de cet élément à la caméra (c'est cette
distance qui est la profondeur). Chaque pixel de l'image garde donc la couleur
de l'élément qui est le plus proche de la caméra. Dans le
cas plus complexe d'un objet transparent, il y a une combinaison des couleurs
de plusieurs éléments.
d. Fonctions utilisées
glutInitDisplayMode(GLUT_DEPTH | ... )
glEnable(GL_DEPTH_TEST)
glClear (GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT) Avant
l'affichage d'une scène.
III.1.5 principe de génération d'un MNT
par OpenGL :
On peut résumer la méthodologie suivie par les
différentes étapes suivantes :
1. On charge une image de format BMP , TIFF, JPEG,..
2. Supposant que le pixel qui a une grande
intensité ,est le point le plus haut dans la scène, donc on
peut calculer les changements d'hauteur de chaque pixel en fonction de son
intensité,
3. et enfin, on définit le type de préemptives,
`TRIANGLES `'
III.1.5.1 lecture d'une image
Bitmap :
Pour lire une image BMP, il faut l'ouvrir en lecture binaire,
puis tout simplement récupérer les structures de données.
Puis ; on stocke nos valeurs dans un tableau de pixel de dimensions
précisées plus haut dans les configurations. Ce tableau sera un
tableau d'entiers appelé "map" d'une taille de 80x80
(ce qui fait déjà 6400 points à placer, sachant qu'un
point est lui même composé d'un rectangle composé de 2
triangles ...) et les images qui contiennent l'information de la hauteur ont
des tailles différentes donc il faut tout remettre en
échelle.
Algorithme :
pour j=1 jusqu'àl `hauteur de l'image
pour j=1 jusqu'àl `hauteur de l'image
id=80/h ;
jd=80/w ;
tab[id][jd]=extraction d'hateur d'image;
fin
fin
Avec di et dj, deux variables flottantes pour avoir une mise
à l'échelle.
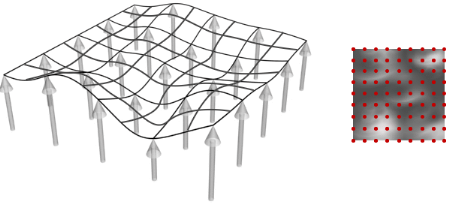
III.1.5.2 Réalisation du mode filaire du
terrain
Dans un premier temps, il y aura une génération
d'un maillage carré dans le plan XY qui est qu'un ensemble de polygones
carrés composés de deux triangles collés les uns aux
autres pour éviter d'avoir des soucis au niveau de l'affichage de
certaines formes (En cas d'utilisation d'un rectangle simple). De plus ils
permettent une meilleure précision mais évidemment cela à
un coût : 2 sommets supplémentaires ...
Voici la différence de rendu filaire :

On remarque une différence assez flagrante au niveau de la
précision.
L'opération se réalise très facilement
avec deux boucles imbriquées. Une fois le maillage est
créé, il n'y a plus qu'affecter aux sommets de chaque polygone
une coordonnée en Z. En fonction de la position du sommet
considéré dans le maillage, on établit une correspondance
avec un pixel de l'image en niveaux de gris. Si le pixel correspondant est
noir, l'élévation du sommet sera minimale, alors que s'il est
blanc, la hauteur sera maximale.
§ Déclaration des
variables :
int i,j;
double ajout = CONFIG_taille_carre /
CONFIG_max_points,posi,posj;
§ La construction des triangles :
glColor3f(1.0f,0.0f,0.0f); // rouge
for(i=0,posi=0;i<CONFIG_max_points-1;i++, posi += ajout) {
glBegin(GL_TRIANGLES);
for(j=0,
posj=0;j<CONFIG_max_points-1;j++, posj += ajout){
glVertex3d(posi,posj,map[i][j]);
glVertex3d(posi,posj+ajout,map[i][j+1]);
glVertex3d(posi+ajout,posj+ajout,map[i+1][j+1]);
glVertex3d(posi,posj,map[i][j]);
glVertex3d(posi+ajout,posj+ajout,map[i+1][j+1]);
glVertex3d(posi+ajout,posj,map[i+1][j]);
}
glEnd();
}
a. Coloration des traits
On définit la couleur des traits, avec la fonction
glColor3f (R, G, B). On entre alors dans une double boucle dans
laquelle i et j sont incrémentés par un pour parcourir le tableau
des hauteurs. Voir figure (III.12)
b. Ajout des textures
Une texture est une image qui est appliquée à
des vertex puis peinte.
On peut appliquer plusieurs formats d'images (tga, bmp) mais
pour plus de facilité, nous allons utiliser des images de type bitmap
étant pour sa simplicité.
Une fois on a la matrice des pixels, la largeur et la hauteur
de l'image, on doit lui fournir un pointeur vers un entier pour lui assigner
une texture afin de l'appliquer.
On prend donc un tableau de textures qu'on le déclare
comme suit :
GLuint
texture [2];
Notre première texture sera donc texture [0] puis texture
[1] ...
§ Application des textures
Chargement de l'image de texture
if (CONFIG_filaire) {
glPolygonMode(GL_FRONT_AND_BACK, GL_LINE);
glDisable(GL_TEXTURE_2D);
}
else {
glPolygonMode(GL_FRONT_AND_BACK, GL_FILL);
glEnable(GL_TEXTURE_2D);
}
Par exemple si on prend deux types de textures (terrain et
eau), on donne donc le numéro "0" au terrain, et le numéro "1"
à l'eau. Ensuite, on teste si nous sommes en mode texturé ou pas,
si c'est le cas on active la texture, et on précise le mode d'affichage
des polygones (filaire ou linéaire).
Maintenant attaquons nous au placement de la texture. Une
texture se place selon 2 points (U et V) que l'on associe à un vertex.
Ce chiffre définit en fait la position à laquelle nous nous
plaçons sur la texture, si ce chiffre est supérieur à
1.00, la texture est alors répétée ou plus affichée
(ce qui dépend du mode texturé appliqué, par défaut
elle est répétée). De plus, les axes sont inversés,
c'est à dire que le U correspond au Y et le V au X. Pour notre terrain,
on ne veut évidemment pas la répéter,
on va donc choisir une valeur comprise entre 0 et 1.
glBegin(GL_TRIANGLES);
for(i=0,posi=-20 ;i<MAX_POINTS-1;i++, posi += ajout)
{
for(j=0, posj=-20;j<MAX_POINTS-1;j++, posj += ajout)
{
glVertex3d(posi,posj,(int)map[i][j]*20/256);
glVertex3d(posi,posj+ajout,(int)map[i][j+1]*20/256);
glVertex3d(posi+ajout,posj+ajout,(int)map[i+1][j+1]*20/256);
glVertex3d(posi,posj,(int)map[i][j]*20/256);
glVertex3d(posi+ajout,posj+ajout,(int)map[i+1][j+1]*20/256);
glVertex3d(posi+ajout,posj,(int)map[i+1][j]*20/256);
}
}

glEnd();
IV. Conclusion :
On a définit dans ce chapitre les différentes
méthodes de construction d'un MNT en utilisant la bibliothèque
graphique OpenGL ce qui nous à aider de l'intégrer et le
visualiser sur notre logiciel soit en mode filaire ou texturé qu'on le
trouve dans le chapitre suivant en se basant sur les étapes de
génération du terrain à partir d'une image.
Implémentation et résultats :
I. Introduction :
On propose dans ce chapitre l'implémentation des
différentes méthodes étudiées afin de reconstruire
une scène urbaine 3D. Nous commençons tout d'abord par
étudier les méthodes de localisation des structures urbaines
d'où la nécessité d'utilisé les différentes
approches de segmentation basées contour, dans notre cas nous nous
sommes orientés vers deux types, celui des contours déformable ou
non déformable. Cette opération de segmentation est faite soit
sur une image aérienne, satellitaire à haute résolution ou
une carte. Une autre opération peut être lancé en
parallèle est celle de la génération automatique d'un
modèle numérique de terrain ou d'élévation. Et
comme dernière étape de notre travail, nous avons fait recours
aux logiciels de DAO plus précisément
« Autocad » afin de construire les différentes
structures urbaines tout en gardant leurs aspects réel (Superficie,
hauteur, formes, ...).
Le diagramme ci-dessous illustre les différentes
étapes utilisées ainsi que les méthodes
intégrées pour chaque problème :
Nous avons présenté dans le premier
chapitre les différentes méthodes de prétraitement des
images de télédétection, qui ont comme finalité la
restauration et l'amélioration de nos images acquises.
Concernant le module de segmentation, nous avons opté
pour l'approche contour dont on a présenté en chapitre 3
«les différentes techniques de détection de contours ,
passant par les méthodes classiques (les operateurs dérivateur du
premier ordre (Sobel, Prewitt, Canny,...) et du deuxième ordre
(Laplacien))et les méthodes basé sur l'évolution d'une
courbe initialisé par l'utilisateur qui sont les contours actifs
paramétrique (Snake) et géodésique (Level Set) . Dans ce
présent chapitre, on compare les résultats obtenus par ces
techniques, leurs avantages et leurs inconvénients.
On illustre également dans ce chapitre comment
générer le modèle numérique de terrain et
d'élévation (MNT, MNE) sous une vue 3D à partir d'une
image 2D, tout en citon les différents outils utilisés lors de la
création du modèle numérique y compris les deux
bibliothèques graphiques, OpenGL et SDL.
Finalement, pour la construction des structures urbaines, on a
fait appel à Autocad pour garder l'aspect sémantique des
données (Superficie, Hauteur, Forme,...).
II. Les différentes méthodes
implémentées :
II.1 Localisation des structures
urbaines :
II.1.1 Segmentation :
II.1.1.1 Approche 1 : Contour
non-déformable
II.1.1.1.1. Les operateurs dérivateur'' gradient
et Laplacien'' :
a. Les opérateurs dérivateurs du premier
ordre : Sobel, Prewitt :
Les étapes de détection des contours par la
méthode de gradient sont résumés dans l'organigramme
suivant :
Algorithme :
Début
Chargement de l'image IM[i][j]
Lire SobelH
Lire SobelV
Pour i=0 jusqu'à hauteur
Pour j=0 jusqu'à largeur
s1=0 ; s2=0 ; s=0 ;
Pour l=0 jusqu'à 3
Pour m=0 jusqu'à 3
s1=s1+ IM [i-m-1][j-l-1]*SobelH[x][y];
s2=s2+ IM [i-m-1][j-l-1]*SobelV[x][y];
s=;
data[i][j]=s ;
Fin
Fin
if (seuil< data [i][j])
data [i][j]=255;
sinon
data [i][j]=0;
fin
fin
Fin
Détection par le gradient :
En entrer : valeur de Seuil.
1. Première étape : calculer
le gradient suivant l'axe vertical de l'image.
(IV.1)
2. Deuxième étape : calculer
le gradient de l'image suivant l'axe horizontal.
(IV.2)
3. Troisième étape : calculer
la norme de gradient de l'image.
(IV.3)
4. Quatrième étape : Suppression des
non-maxima
Si la norme du gradient en un pixel (x,y) est inferieure a la
norme du gradient d'un de ses 2 voisins le long de la direction du gradient,
alors mettre la norme pour le pixel (x,y) a zero
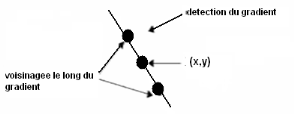
Figure-IV.3 : Etape de suppression des
non-maxima
5 - Seuillage des contours
(hystérésis)
Utilise deux seuils : un seuil haut (Sh) et un seuil bas
(Sb)
Pour chaque pixel de la norme du gradient :
ï Si norme(x,y) < Sb, alors le pixel est mis a
zéro (non-contour)
ï Si norme(x,y) > Sh, alors le pixel est un
contour
ï Si Sb = norme(x,y) = Sh, alors le pixel est un contour
s'il est connecté a un autre pixel déjà
acceptéé comme contour
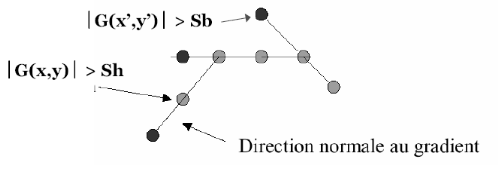
Figure-IV.4 : Etape de seuillage
Résultats obtenu :
|
|
|
|
Image originale
|
Détection de contours par l'operateur
SOBEL(seuil=136)
|
Détection de contours par l'operateur
PREWITT(seuil=136)
|
Ces filtres sont moins sensibles au bruit que ceux de Robert
car le fait d'introduire un moyenneur local sur le domaine couvert par le
masque diminue leur sensibilité au bruit, concernant la qualité
du contour, les deux opérateurs fournissent un contour moyen.
b. Les opérateurs dérivateurs de
deuxième ordre `' Laplacien'' :
La détection de contours par Laplacien consiste à
convoluer l'image par le filtre suivant :
Résultats :
|
|
|
Image originale
|
Laplacien (seuil = 26)
|
Figure-IV.4 : Détection de
contours par le Laplacien
Remarque : on remarque que
L'opérateur de Prewitt se révèle très peu
différent de celui de Sobel. On peut toutefois noter qu'il est
légèrement plus sensible au bruit, et que : La détection
de contours par Laplacien est très sensible aux bruits.
Comparaison des méthodes de détection de
contours :
|
Opérateurs
|
Sensibilité
au bruit
|
Epaisseur des contours
|
Localisation
|
Matrices
|
|
Opérateur de
Prewitt
|
peu sensible
|
épais
|
centré
|
3x3
|
|
Opérateur de
Sobel
|
Assez sensible
|
moyen
|
centré
|
3x3
|
|
Opérateur de Laplacien
|
Sensible
|
très fins
|
centré
|
3x3
|
Tab.IV. 1. Tableau comparatif des méthodes de
détection de contours.
II.1.1.1.2. Le filtre de Canny:
a. Critères de l'approche de
Canny :
- Détection : Bonne détection
des points de contours (notamment pour les contours faibles).
- Localisation : Localisation faible des
points de contours.
- Unicité de la détection :
Pour un contour, on a un seul point de contour.
b. Algorithme de Canny :
Premier étape : appliquer un filtre
gaussien c'est-à-dire filtré d'abord l'image avec un filtre
gaussien G.
(IV.4)
I' (i, j) =G(x, y)*I (i, j)
(IV.5)
Filtre Passe-bas pour enlever le bruit.
Deuxième étape : calculer le
gradient en chaque pixel de l'image.
La norme du gradient :
(IV.6)
L'angle du gradient :
(IV.7)
Troisième étape :
Approximation de l'angle du gradient à un multiple de 45°
pré.
Quatrième étape :
(IV.8)
Alors
(IV.9)
Cinquième étape : Seuillage
par hystérésis
Soit (Sh , Sb) deux seuils tel que
Sh> Sb
> Alors (x, y) point contour ainsi tous les points
reliés à (x, y) le long du gradient
>
(IV.10)
>
(IV.11)
Resultats :
|
|
|
Image originale
|
L'operateur `'Canny''
|
Figure II. 5 : Détection de contours par
Canny
II.1.1.1.3 Seuillage par hystérésis de
l'image gradient :
Algorithme :
Début
Chargement de l'image IM[i][j]
Lire la valeur des seuils (Sh, Sb) ;
Calcul l'image moyenne : moy[i][j] =(R+G+B) /3 ;
Pour (x=0, jusqu'a x<3)
Pour (y=0, jusqu'a y<3)
S1=S1+(moy[i-x-1][j-y-1]*Sobel[x][y]) ;
S2=S2+(moy[i-x-1][j-y-1]*Sobel[x][y]) ;
S= ;
IMA[i][j]=S;
Si (IMA [j][i]< Sb)
IMA[j][i]=0;
Si (IMA [j][i]>Sh)
IMA[i][j]=IM[i][j] ;
Si (IMA [j][i]<Sh & IMA
[j][i]>Sb)
IMA[i][j]=IM[i][j] ;
fin
fin
Fin
Résultats obtenus :
|
|
|
Image originale
|
Exemple1 : Sb=114, sh=145
|
Figure-II.6 - Seuillage
hystérésis
L'opération de seuillage est une étape
clé dans le domaine de traitement d'image, elle permet le passage d'une
image couleur à une image binaire construite par deux intensités
(que du blanc sur les contours, et du noir), mais le problème majeur du
seuillage est le choix du seuil qui peut donner meilleur résultat comme
il peut donner de mauvais résultat.
II.1.1.2 Approche 2 : Contour
déformable
II.1.1.2.1 Les Snakes :
Les contours actifs, ou `'Snake'', permettent de segmenter des
images par détection de contours.
Leur utilité est
particulièrement bien illustrée en imagerie médicale, les
surfaces intéressantes étant en général des formes
bien régulières.
L'approche classique consiste à déformer un
contour vers le bord de l'objet à détecter, en minimisant une
fonctionnelle définie en fonction de l'image et ayant pour effet de
régulariser la courbe. Depuis, de nombreuses améliorations ont
été apportées au modèle initial. En effet, celui-ci
présentait de nombreux inconvénients : sensibilité
à l'initialisation, au bruit, réglage difficile des
différents paramètres, fausses détections dues à la
présence de minima locaux de la fonctionnelle.
Organigramme :
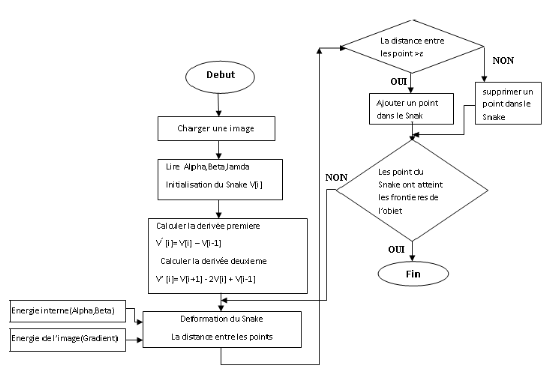
Organigramme IV.3 : Principe du
Snake
Nous avons testé la méthode des contours actifs
sur des images de zone urbaine avec une haute résolution, sans aucun
prétraitement ou amélioration.
Résultats obtenu :

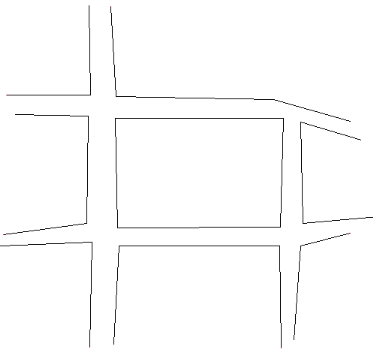
Dans la figure IV.8, nous remarquons que le snake
initial a convergé vers la route dans certains cas, dans d'autre,
à cause d'une part de l'ombre portée des bâtiments sur la
route et d'autre part de l'existence des objets qui occultent la route
(voiture, arbre, marquage au sol) il n'a pas convergé vers la route; car
ces objets changent la radiométrie de la route dont le snake s'appuie
pour optimiser son déplacement.
II.1.1.2.2 Méthode d'ensemble de niveau
zéro Level Set :
a. Avec « Arrêt aux
bords »
Cette méthode est basée sur la définition
d'une fonction (g) appelée `'fonction d'arrêt aux bords'' garantit
l'arrêt de l'évolution de la courbe sur les bord de l'objet
à détecté.
Début
Charger une image ;
Initialiser par ;
Pour chaque itération faire
Pour (x,y) faire
Calculer g () ;
Calcular FA ;
Calcular FG ;
Fin
Calculer ;
Fin
Fin
Cette méthode est simple à
implémenter, mais le problème qui s'impose est que la courbe
arrête son évolution sur les premiers bords trouver, donc on a un
problème de changement de topologie.
b. Sans « arrêt aux
bords » :
Algorithme :
Début
Initialisation de par, n=0
Pour un nombre fixe d'itération faire
Calcule de C1() et
C2(Ø0)
Calcule le terme de la courbure K
Calcule
Fin
Résultats obtenu :
1. Avec arrêt aux bords :

Initialisation de la courbe
 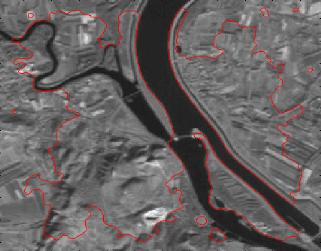
Résultats après 200
itérations Résultats après 1000
itérations
Figure IV.7 Méthode de Level set avec
« arrêt aux bords »
2-sans arrêt aux bords :

Initialisation de la courbe
 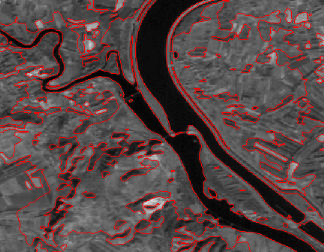
Résultats après 10
itérations Résultats après 200
itérations
Figure IV .8 Méthode de Level set sans
« arrêt aux bords »
On remarque que si la courbe initial était au milieu de
l'image ?t=0.1, le cycle de réinitialisation est une itération et
=0.001x(255)2. Après 4 itérations la courbe se
stabilise sur les frontières des objets de l'image.
Si on laisse les mêmes conditions, et on change
seulement le ?t vers une valeur maximal (5500), après une seule
itération on a le même résultat que la première
On remarque aussi, que la méthode avec arrêt au
bords donne de bon résultats seulement dans les régions qui ont
un gradient élevé. Il faut que la courbe initiale soit proche et
complètement contenue à l'intérieur de l'objet. Cette
méthode est très lente ; pour faire un changement de
topologie il faut initialiser à l'aide de plusieurs courbes.
La deuxième méthode peut détecter les
objets dont les bords ne sont pas nécessairement définis par un
gradient ; elle permet de faire un changement de topologie à partir
d'une seule courbe initiale ; elle est rapide et donne de bon
résultats.
D'après les essais précédents, il est
claire que la méthode de minimisation d'énergie semble plus
éfficace, plus rapide et plus précise que la méthode
d'arrêt au bord.
Les objets avec des contours lissés ne peuvent pas
être segmenté avec l'approche `'d'arrêt aux bords'', la
courbe va éventuellement se rétracter sur elle-même.
Cependant l'initialisation de l'approche de minimisation
d'énergie nous permet d'aboutir à la segmentation
désirée.
§ Les avantages des LEVEL SETS :
- Prise en compte des changements de topologie automatique.
- Grandeurs géométriques intrinsèques
(normales entrante/sortante, courbure) faciles à calculer.
- Extension à la 3D simple : il suffit d'ajouter une
coordonnée à l'équation d'évolution de la fonction
ö : on a alors un volume ö(x, y, z, t).
- Discrétisation de ö avec une grille définit
dans le domaine de l'image.
- Utilisation des méthodes numériques connues pour
calculer les dérivées.
§ Les inconvénients des LEVEL
SETS :
L'implémentation implique plusieurs
problèmes :
- On doit construire une fonction initiale ö(x, y, z,
t=0) de manière à ce que son niveau zéro corresponde
à la position initiale du contour.
- L'équation d'évolution n'est
dérivée qu'au « Level set
zéro » ; la fonction vitesse v n'est donc pas
définie(en générale) pour les autres Level sets.
- La déformation constante peut causer la formation de
coins saillants sur le modèle initiale lisse. Ce coin peut perturber les
déformations successives, Puisque la définition de la normale
devient ambiguë. Parfois nécessaire de recalculer la fonction
distance par rapport au niveau zéro.
§ comparaison entre les'' Snake'' et'' Level
Set'':
Les modèles paramétriques'' Les
Snake''
- Représentation explicite des modèles sous leur
forme paramétrique pendant la déformation
- Implémentation rapides (temps réel).
- Adaptation à la topologie des objets difficiles.
- Nécessité de réinitialiser les
paramètres de la courbe.
Les modèles géométriques'': Les
Level-Sets (courbes de niveaux) `'
- Représentation implicite des modèles comme un
ensemble de niveaux d'une fonction scalaire de dimension supérieure
- Adaptation à la topologie de ces modèles est
automatique
- Modèles utilisant la théorie de
l'évolution de courbes ou les Level-Sets (courbes/ensembles de
niveaux).
- Les courbes/surfaces évoluent en fonction de mesures
géométriques résultant d'une évolution, et donc
indépendantes de paramètres.
- Les courbes sont représentées comme un ensemble
de niveaux d'une fonction de dimension supérieure.
- Les changements de topologies (fusion, séparation,
etc..) sont gérés automatiquement.
- L'évolution de la courbe s'arrête sur les contours
de l'objet.
- On étudie l'évolution de la courbe en utilisant
uniquement des mesures géométriques (normal, courbure, ...) et
non pas des quantités dépendant de paramètres
(dérivées d'une courbe spécifique).
II.2 Génération des modèles
numériques :
Image choisie
- On a travaillé sur une image (.bmp) à partir d'un
MNT de la Wilaya de Sidi Belabess en utilisant le logiciel ENVI 4.0.

Figure-IV -09-MNT de Belabess
II.2.1. Affichage par SDL :
Pour afficher notre terrien, on utilisée une autre
bibliothèque graphique `'SDL Component Suite/LE'', exactement le
composant `'Plot3D''.en basant toujours sur l'intensité des pixels.
a. Le composant `'Plot3d'' :
Plot3d supporte l'exposition de trois surfaces
dimensionnelles. Les surfaces sont définies par une grille rectangulaire
de valeurs de la hauteur, et peut être envisagé de tout angle et
dans toute direction.
b. L'usage de Plot3D :
L'usage de Plot3D est simple:
- mettez le composant sur une forme.
- mettez ses paramètres et chargez les
données. Par la suite le correspondre 3D surface est affiché et
peut être manipulé par les méthodes disponibles et
propriétés.
- Le donnée de la surface est entreposé dans la
matrice rectangulaire GridMat.
- La surface 3D est affichée en utilisant les angles
autour deux axes: l'axe x est horizontal dépend de la
propriété (ViewAngleX). L'axe z est
perpendiculaire au surface basse, sa direction dépend de la
propriété ViewAngleX.
- La surface 3D peut être tournez autour d'axe z en
mettant la propriété ViewAngleZ.
Les angles de envisagement peuvent aussi être mis
interactivement en maintenir le bouton de la souris gauche et
déplaçant la souris si la propriété
MouseAction est mis à maRotate,
maRotXOnly, maRotZOnly ou
maRotAndZoom. Déplacer la souris dans direction
horizontale change l'angle autour du z axe, en le déplaçant
verticalement affecte l'angle autour du x axe. Les propriétés
CentX et CentY déterminent la place de
la surface sur l'écran.
Organigramme :
Résultats obtenus :
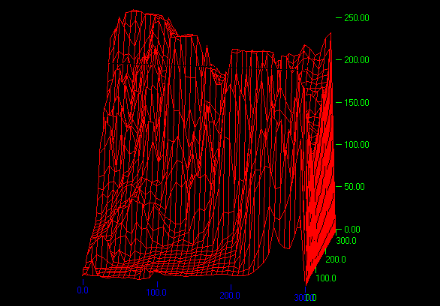
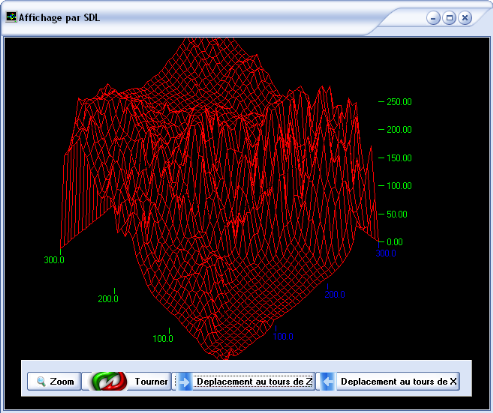
Figure IV.10 : Visualisation d'un MNT par
SDL
II.2.2. Affichage par OpenGL :
Pour afficher le terrien par l'OpenGL, on a basé sur le
même principe de SDL (intensité des pixels), mais avec un effet
d'ombrage, et on peut aussi ajouter la texture.
On a utilisé deux modes d'affichage, filaire et
texture.
Organigramme : présente les principales étapes de
l'algorithme
On a de types de modèles :
a. Modèle filaire :
Dans ce modèle, on voit que le degré
d'intensité `'éclairage'' varie selon la hauteur obtenue à
partir de l'image. On peut dire que c'est une dégradation de niveau de
l'intensité.
b. Modèle texture : Pour ce
modèle, on a suivie les mêmes étapes que le modèle
filaire précédent mais on utilise les dégradations de
niveau suivant des couleurs (R, G, B) avec l'effet d'ombre.
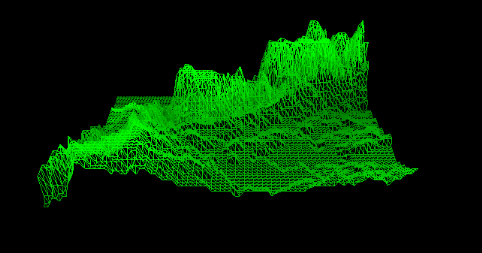
Figure IV.11 : Mode filaire

Figure IV.12 : Mode texture
c. Les modèles colorés :
On suivit les même étapes que les modèles
précédents mais on utilise la dégradation de niveau
suivant le couleur, Voir la figure ci-dessous :


figure- IV-13- visualisation d'un MNT par OpenGL en
mode filaire et texture coloré
II.2.3 Génération d'un modèle 3
démentions par logiciel 3DEM :
La disponibilité d'images
géoréférencée est un élément
déterminant pour la facilité de visualisation 3D des terriens
virtuels avec ou sans superposition de traces GPS. Le choix du "format" de
géoréférencement nous permet d'échanger les
informations par l'intermédiaire d'un fichier .txt. Pour obtenir une
image géoréférencée dans un format plus standard
(du type GeoTiff) que l'on peut ensuite utiliser avec n'importe quel programme
de visualisation et avec n'importe quel MNT (modèle numérique de
terrain), on doit apporter quelques manipulations sur ce fichier.
Pour visualiser ce modèle, il faut avoir un
modèle numérique de terrain, une image satellite et le fichier de
géoréférencement associé
a. Présentation de logiciel :
3DEM utilise le SGI/Microsoft bibliothèques OpenGL
pour générer le terrien en 3D.
Les scènes 3DEM peuvent être sauvées dans les
formats suivants :
b. Ouverture avec 3DEM :
On lance le programme 3DEM et on charge le modèle
numérique de terrain (.tif) puis l'image satellite, 3DEM trouve
automatiquement le fichier (.txt) du même nom.
Figure IV.14 : Sélection de l'image
et du fichier de géoréférencement à napper sur le
MNT
Puis 3DEM nous montre une prévisualisation de l'image.
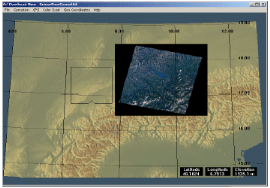
Figure IV.15 : Image satellite
géoréférencée sur le MNT
Avec une visualisation 3D, on constate les limites de
résolution de ce MNT. Ensuite la création d'une image
géoréférencée au format GeoTiff que l'on pourra
utiliser avec un MNT plus détaillée, ou un autre programme de
visualisation.

Figure IV.16 : Résolution du MNT 1
km
c. Création d'une Nappe GeoTiff :
On commence par enlever la grille, puis il faut choisir
soigneusement la zone à enregistrer ainsi que la résolution de
l'image Geotiff en sélectionnant cette zone et en traçant par la
souris un rectangle autour de la zone qui nous intéresse.
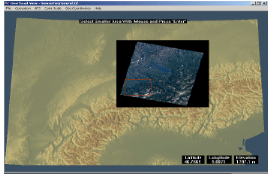
Fig -IV-17- Sélection de la zone
d'intérêt
3DEM enregistre une image Geotiff avec la résolution telle
qu'elle apparait à l'écran alors Il faut la régler
soigneusement.
Fig -IV-18- Réglage de la résolution
à l'écran
En dernier lieu, il faut enlever l'ombrage.
Figure IV.19 : Désactivation de
l'ombrage
Génération d'un
modèle 3 démentions par logiciel Landscape Modeler :
1. Présentation de logéciel
Ce logéciel est un modeleur de terrain en 3D. Il permet
d'éditer dans un monde en 2D un terrain est modifiant les altitudes des
points d'une grille. L'édition peut se faire manuellement, mais il
également possible de faire du Height Mapping, c'est à dire
générer une grille d'altitude en fonction d'un bitmap. Les
grilles peuvent être sauvegardées/chargées.
2. Utilisation de logeciel
L'utilisateur agit sur
l'altitude des points d'une grille pour former des reliefs. Soulever ou
abbaisser un point entraîne les autres et forme un montagne ou un
cratère sous-marin.
Pour pouvoir modeler le terrain plus rapidement,
il est possible d'étendre la selection de sommets grace à un
curseur rectangulaire, et ainsi de créer rapidement un plateau ou un
fond sous-marin .
Des couleurs sont générées automatiquement
de manière à produire un rendu agréable. En dessous du
niveau initial, les somets sont bleus avec deux nuances pour imiter les fonds
marins, et au dessus existe une échelle de couleurs allant du vert
foncé au blanc (neige).
Un polygone transparent recouvrant toute la
map fait affice de surface de l'eau et rend les fonds marin plus
crédibles.
La table des couleurs actuelle est du plus profond au plus
élevé :
1. bleu foncé (fond marin profond)
2. bleu clair (fond marin peu profond)
3. jaune (sable)
4. vert foncé (forêt)
5. vert clair (paturages)
6. gris (rocaille)
7. blanc (neige)
Résultats obtenus :



a) Mode texture
b) Mode filaire
Figure IV.20 : Génération d'un MNT
par Landscape Modeler
II.3 Construction des structures urbaines d'une
ville :
Dans cette partie, nous avons essayé
d'implémenter des méthodes automatique qui génèrent
rapidement les formes des structures urbaines, mais cette tâche devient
très difficile si on prend en considération les informations
réelles de ces objets telles que leurs superficies, tailles et formes
complexe. Ce qui nous a poussées à utiliser un logiciel
très performant dans le domaine de l'architecture qui est l'AutoCad.
Pour se faire, nous devons avoir obligatoirement un plan de
cadastre obtenu à l'aide d'une image aérienne et d'autre mesures
sur le sol, une enquête bien complète de la structure des
bâtiments (R+1, R+2,...).
Dans notre cas nous avons travaillé sur la ville
d'Arzew dont on dispose de toutes les données possibles :
II.3.1 Données cadastrales:
II.3.1.1 Aménagement du secteur A de la ville
d'Arzew:
a. secteur A : SECTEUR DE L'HABITAT
INDIVIDUEL :
Reparti en plusieurs lotissements en suivant la même
typologie du bâti, ces espaces seront affectés pour de l'habitat
individuel, d'une part pour donner un caractère spécifique
à cette partie de l'agglomération chef lieu de la commune
d'Arzew ; et d'une autre part satisfaire les besoins de la population en
matière d'habitat.
|
Désignation
|
Surface m2
|
|
Habitats individuels
Espaces verts
voiries
|
31927.00
636.50
28821.04
|
|
Total
|
61384.54
|
Les conditions d'occupation du programme projeté:
|
ILOT
|
Affectation
|
Surface m2 Assiette
|
C.E.S
|
C.O.S
|
Hauteur max.
|
|
P1
|
Habitat individuel
|
3790.00
|
0.71
|
1.42
|
R+1
|
|
P2
|
Habitat individuel
|
1125.50
|
0.72
|
1.44
|
R+1
|
|
P3
|
Habitat individuel
|
2655.00
|
0.67
|
1.34
|
R+1
|
|
P4
|
Habitat individuel
|
5779.00
|
0.72
|
1.44
|
R+1
|
|
P5
|
Habitat individuel
|
4081.00
|
0.73
|
1.46
|
R+1
|
|
P6
|
Habitat individuel
Espace vert
|
1263.00
54.00
|
1317.00
|
0.68
-
|
1.37
-
|
R+1
-
|
|
P7
|
Habitat individuel
|
976.00
|
0.73
|
1.47
|
R+1
|
|
P8
|
Espace vert
|
367.50
|
-
|
-
|
-
|
|
P9
|
Habitat individuel
Espace vert
|
825.00
80.00
|
905.00
|
0.60
-
|
1.20
-
|
R+1
-
|
|
P10
|
Habitat individuel
|
1154.00
|
0.67
|
1.33
|
R+1
|
|
P11
|
Habitat individuel
|
1368.00
|
0.69
|
1.37
|
R+1
|
|
P15
|
Habitat individuel
Espace vert
|
3073.50
135.00
|
3208.50
|
0.58
-
|
1.10
-
|
R+1
-
|
|
P16
|
Habitat individuel
|
3590.00
|
0.80
|
1.50
|
R+1
|
|
P17
|
Habitat individuel
|
1510.00
|
0.80
|
1.50
|
R+1
|
|
P18
|
Habitat individuel
|
3737.00
|
0.70
|
1.35
|
R+1
|
II.3.1.2 Aménagement du secteur B de la ville
d'Arzew:
b. SECTEUR B : SECTEUR DES ÉQUIPEMENTS.
Le secteur B représentant les
équipements ; offre des service en matière
d'éducation et d'approvisionnement et de culte.
|
Désignation
|
Surface m2
|
|
Equipements et services
Espaces verts
Voiries
|
17872.50
2991.50
7167.60
|
|
Total
|
28031.60
|
Les conditions d'occupation du programme projeté:
|
ILOT
|
Affectation
|
Surface m2 Assiette
|
C.E.S
|
C.O.S
|
Hauteur max.
|
|
P12
|
Espace vert
|
674.00
|
-
|
-
|
R+1
|
|
P13
|
Mosquée
|
1813.00
|
0.82
|
1.15
|
-
|
|
P14
|
Parking
Espace vert
|
596.50
10.50
|
607.00
|
-
|
-
|
R+1
-
|
|
P19
|
Espace vert
|
2307.00
|
-
|
-
|
-
|
|
P20
|
A.E.F
|
11354.00
|
0.26
|
0.50
|
R+1
|
|
P21
|
Marché couvert
|
3689.00
|
0.29
|
0.33
|
R+1
|
|
P22
|
Parking
|
420.00
|
-
|
-
|
-
|
TABLEAU RECAPITULATIF GENERAL
|
Surface de la zone d'étude
|
89416.14 m² - 8.94 Ha
|
|
Surface des espaces verts
|
3628.00 m² - 0.36 Ha
|
|
Surface de la voirie
|
35988.64 m² - 3.60 Ha
|
|
Surface des équipements
|
17972.50 m² - 1.79 Ha
|
|
Surface de l'habitat
|
31927.00 m² - 3.19 Ha
|

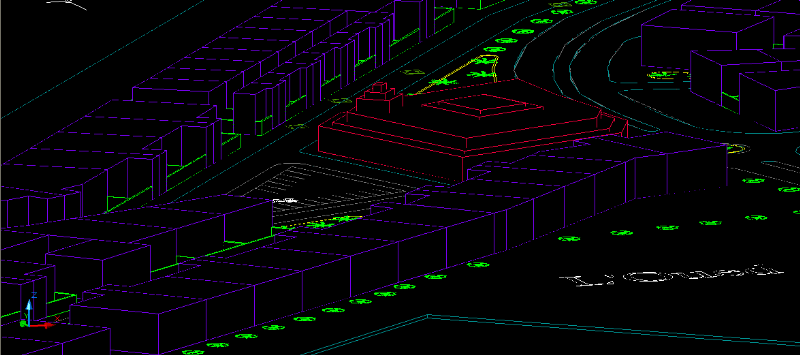



On n'a pas pu entamer la dernière étape de
superposition des différents résultats issus des étapes
vues précédemment, car la tâche de composition est
très compliquée et on n'avait pas le temps pour la terminer.
Conclusion :
Après plusieurs essais au niveau de la
segmentation soit par les méthodes classiques basées sur la
dérivée de premier ordre et de deuxième ordre, ou la
méthode de modèles déformables(Snake et LEVEL SET) , les
résultats des deux méthodes sont largement différents ,
si on prend en compte la sensibilité aux bruits, les Level set nous
donne de bons résultats
Et pour la modélisation en 3D, on trouve que la
méthode par OpenGL fournit un modèle plus élargie et
dynamique pour la navigation sur le terrain et plus précis que la
méthode par SDL qui ne permet pas d'intégrer les textures sur le
modèle filaire.
Conclusion générale
Au cours de cette période de projet de fin
d'étude nous avons essayé de faire le premier pas vers la
reconstruction 3D des villes, ce projet est très difficile à
réaliser vue la nécessité d'avoir tout les outils et les
données nécessaires pour arriver à l'objectif voulu. Lors
de la réalisation de ce projet, nous étions obligées de
mener une étude à propos du traitement des données de
télédétection en particulier la segmentation des images
satellitaires et la génération des modèles
numériques de terrain. Nous avons développé un processus
de segmentation ayant pour objectif d'intégrer différents types
de données satellitaires (dans notre cas, XS1, XS2, XS3, multi spectrale
de SPOT de la ville d'Oran) dans un modèle numérique de terrain
(MNT).
Donc notre problématique était comment
réaliser une reconstruction 3D des scènes urbaines en se
basant sur les méthodes de segmentation et de génération
de terrain 3D.
En effet, pour aboutir à cette fin nous avons
développé une méthode qui se base sur un processus
comprenant différentes phases dont la première concerne les
prétraitements de toutes les données mises en jeu. La
deuxième étape consiste à effectuer une segmentation des
images utilisant les modèles déformables Level Set, cette
méthode est basée sur l'évolution d'une courbe initialiser
par l'utilisateur, et se déforme jusqu'à ce qu'elle atteint les
frontières des objets dans le but de localiser les différentes
structures urbaines. Et comme dernière phase nous avons
implémenté les techniques d'OpenGL pour générer
notre modèle de terrain (MNT) à partir des résultats
obtenus dans l'étape de segmentation Autocad qui est un logiciel
très performant dans le domaine architecturel afin de tracer les
différentes structures urbaines en prenant en considération leurs
contenus sémantiques pour les déposer finalement sur le
modèle numérique de terrain.
Ce travail que nous avons réalisé était
entièrement bénéfique pour nous .Il nous a permis
d'apprendre et d'acquérir des connaissances tout à fait nouvelles
pour nous que se soit en télédétection (principe, types de
satellites, modes d'acquisition des satellites, comment interpréter les
comportements spectraux des occupations du sol...etc.), en traitement d'image
(différents types d'images, études des histogrammes...etc.) ou
en informatique (la programmation proprement dite, la maîtrise efficace
de la partie de traitement d'image en builder C++ version 6, les
bibliothèques graphiques OpenGL, SDL...), Autocad.
Bibliographie
[1] Michel-Claude Girard et Colette M.Girard.
.
« Traitement des données de
télédétection » Dunod, Paris
1999
[02] Ouvrage collectif par J.-P.COCQUEREZ et
S.PHILIPP
Analyse d'image : filtrage et
segmentation Paris 2-225-84923 2000
[03] ALAIN DIETERLEN
Groupe LAB.EL, Laboratoire MIPS
Université de Haute Alsace, Mulhouse, France
Traitements bas niveau d'images, Transformations
locales
[04] Medina Rubén, Garreau Mireille, Jugo
Diego, Castillo Carlos, Toro Javier GIBULA, Universidad de
los Andes, Merida 5101, Venezuela LTSI, Université de Rennes I, 35042
Rennes, France
Segmentation of Ventricular Angiographic
Images Using Fuzzy Clustering 1999
[05] LOONEY, C. G
Interactive clustering and merging with a new fuzzy
expected value, Pattern Recognition Lett
35, 187-197
2002
[06] FORGY. E
Cluster analysis of multivariate data: efficiency
versus interpretability of
classifications, Biometrics 21, 768-776
1965
[07] P. BONNET
« Cours de Traitement d'Image »
USTL
[08] François Cariou & Rudolf Le Gall
« ANALYSE D'UNE IMAGE
SATELLITAIRE »
[09] Alain Boucher
« Détection de contours »
IFI
[10] Jean-Christophe Baillie
« SEGMENTATION module D9 : Traitement d'Image et Vision
Artificielle »ENSTA
2003
[11] Stéphane Lhomme
« Identification des bati à prtir d'images
satellitaires à très haute résolutions
spatiales »
Université Luis pasteur I, Strasbourg France Décembre
2003.
[12] Henri Maitre
« Le
traitement des images » Tome 2 TSI télécom Pris
2004
[13] JeanJacques
« Les contours actifs, une
méthode de segmentation application à l'imagrie
médicale» université
Fronçois Reblais
2003
[14] Vincent Barra - Christophe Tilmant
«Segmentation d'images par
contours actifs implicites (level set) » 2006
[15] M. Beladgham, F. Derraz, M.
Khélif
« Segmentation d'images médicales IRM par
la méthode d'ensembles de
niveaux (Level_Sets) » Université Abou-
Bekr Belkaid -Tlemcen
[16] Flore Faille et Caroline Labrot et Magali
Motlik
«Détection de contours par Snake sur
des images en couleur » Copyright 1999
[17] Nicolas Brossier &Cyril Cassisa
«TRAITEMENT D'IMAGE Active Contours without
Edges for Vector-Valued
Images» ESINSA
2004
[18] J.A. Sethain
«Level Set methods and fast marching
methods» Combridge University Press 1999
[19] L.D. Cohen
«Active contour medels and balloons»
Mars 1991
[20] T.Chan & J.Shah
«Active contour without edges»
Fevrier 2001
[21] Olfa Besbes -- Ziad Belhadj -- Nozha Boujemaa
« Adaptive Satellite Images Segmentation
by Level Set Multiregion Competition » .pdf
INRIA
2006
[22] Jonas Larsen & Thomas Greve Kristensen
«An overview of the implementation of Level
Set methods, including the use of the
Narrow Band method» 9 Décembre
2005
[23] J.-P. COCQUEREZ et S. PHILIPP
« Analyse d'images : filtres et
segmentation » Paris 2-225-84923 2000
[24] Stanley Osher & Ronald P. Fedkiw
« Level Set Methods:An Overview and Some Recent
Results »
[25] Hugues Talbot
« Image Analysis and Processing
Segmentation» ESIEE - ECP 2006
[26] Eric BITTAR
« Cours OpenGL» Université de
Reims
[27] Mark J. Kilgard NVIDIA Corporation
« Avoiding 19 Common OpenGL
Pitfalls» 10 Juillet
2000.
[28] Éric Beaudry
« Reconstruction d'une ville en 3D
à partir d'images photo : essais sur Sherbrooke
[29]
http://www.ccrs.nrcan.gc.ca/ccrs/learn/tutorials/tutorials_f.html
« Notions fondamentales de
télédétection »
[30]
http://ressources.ciheam.org/om/pdf/a04/CI911175.pdf
Michael DESHAYES, Pierre MAUREL « L'image
spatiale et son contenue » 1990
[31]
http://rwww.rncan.gc.ca/
Centre Canadien de télédétection
Glossaire des termes de télédétection 2005
[34]
www.ensta.fr/_manzaner/Cours/Poly/Filtrage.pdf
Généralités sur les filtres
[35]
http://www.teina.org/Enseignement/2006-2007/TIF
Les modèles déformables et Level Sets
(courbes de niveaux)
[36]
http://fr.wikipedia.org/
Modèle numérique de terrain
[37] http://www.sit de zero.com/
Modélisation
[38]
http://www.kookyoo.net/dossier/Jeux-Video/bmp-terrain-3D-generation-terrain-opengl/
[C++/OpenGL]/
Génération d'un terrain 3D à
partir d'un bitmap
[39] Boukebir.Z & Chenak
Redouane « Intégration d'une Clasification Floue d'Images
Satellitaires pour Génération d'un Modèle de Terrain en
3D ».
PFE Electronique USTO
2008.
[40] Mahjoub Youcef & Moha,,ed Mahmoud
« segmentation d'image satellitaire par la methode d'ensemble de
niveaux (LEVEL SET) ».
PFE Informatique USTO
2007
Annex
1-Matériels et Environnement:
1-1-support de travail :
· Pentium 4 3.4GHz.
· 512 Mb de mémoire vive.
· 80 Go la taille du disque dure.
· Carte graphique (nVidia GeForce FX 5500).
1-2-Langage de programmation :
pour la réalisation de notre logiciel on a utilisés
le langage de programmation `'Borland C++Builder.6''.
Borland C++Builder est un environnement de programmation visuelle
orienté objet permettant le développement d'applications 32 bits
en vue de leur déploiement sous Windows et sous Linux. En utilisant
C++Builder, on peut créer de puissantes applications avec un minimum de
programmation, grace à La diversité de ses outils,et de ses
composants de son menu principale.
Et en plus nous avons utilisé la bibliothèque SDL
et OpenGL pour l'affichage du terrain.
figure-01- la page principale de 'Borland C++Builder.6
2. Présentation du logiciel:
2-1- Interface principale:
la fenêtre principale est composée de 5 menus
principaux qui regroupent les différents prétraitements, ainsi
que les différents méthodes de segmentation et de
modélisation présentées dans les chapitres
précédents.

2-1-1- menu (1) :chargement des
images :
- il permet de charger des images multi spectrales (RGB).
- il permet aussi de fusionner les carnaux (canal R, canal G,
canal B) pour avoir des images multi spectrales en différents modes.
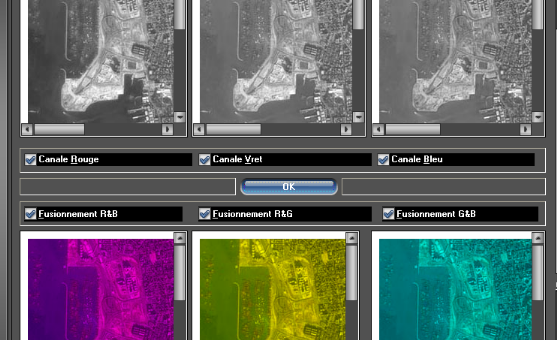 
figure-02-chargement d'image à traité et
fusionnement des canaux
2-1-2- menu (2) : prétraitement.
- il permet de afficher les image en niveau de gris.
- trouver l'image négative.
- seuillage par un seul seuil ou deux seuils.
- filtrage des images par différents filtre passe-bas et
passe-haut.
- trouver les différents histogrammes (normale,
cumulé, égalisé, étiré).
- il permet d'enregistrer l'image traitée, et de quitter
l'application.
figure-03- prétraitement des images
satellitaires
2-1-3- menu (3) : Modélisation en
3D :
- permet de charger une image et la
modéliser en 3D par SDL et OpenGL.
- permet de déplacer le terrien vers différents
direction.
- permet de zoomer le terrien et le tourner.
- afficher le terrien en deux modes différents
(filaire et texture).
 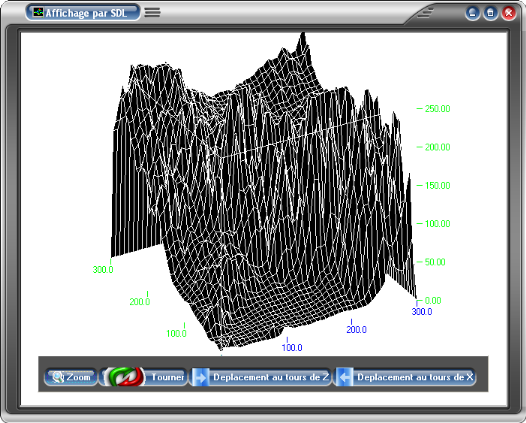
figure-04- affichage par SDL.
 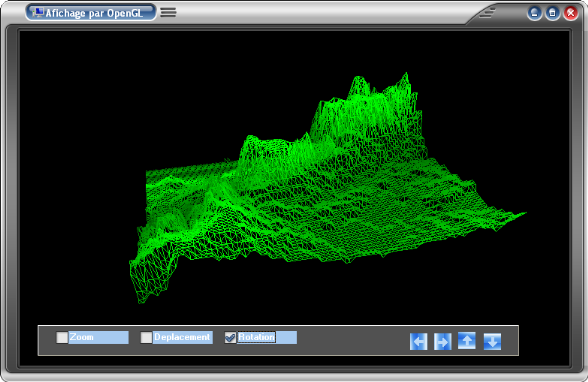
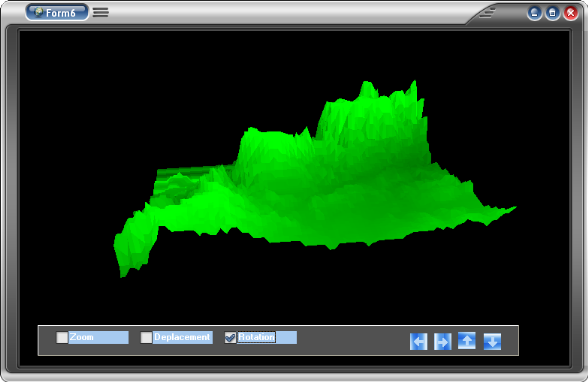
figure-05- affichage par OpenGL en mode filaire et
texture
2-1-4- menu (4) :détection de
contours :
- détection de contour par les operateurs
dérivateurs de premier et de deuxième ordre.
- détection de contours par la méthode de Canny et
Deriche.
- détection de contours par la méthode de seuillage
(Hystérésis).
figure-06- différents méthodes de
détection de contour
2-1-5- les modèles
déformable :
- la détection de contours par les modèles
déformables paramétrique `'Snake''.
- la détection de contours par les modèles
déformables géométriques.
figure-07-détection de contours par la
méthode des modèles déformables.
| 


