III.1 LA DEVIATION DE LA LUMIERE
III.1.1 Théorie de la relativité
générale
Quand on étudie un mouvement qui n'est pas lent en
particulier la lumière, il faut renoncer à un
développement en de la métrique .Toutes les composantes de la
métrique doivent être
connues au même ordre, en fait en puissance de
G . On a la providence que l'approximation
linéaire en G, la métrique post --
newtonienne donne la métrique désirée :
avec , (III.1)
Où ã=1 dans la
théorie de la relativité générale. La
déviation (voir fig. 1 page suivante) des rayons lumineux par un corps
massif statique et à symétrie sphérique relève de
l'étude des géodésiques46 du genre
lumière de cette métrique linéarisée.
46 Lexique.
dans l'approximation linéaire du champ
Soit la géodésique du genre lumière de
vecteur -- dérivée pour un paramètre affine
ë. L'équation de la
géodésique s'écrit sous la forme simplifiée :
(III.2)
Nous considérons une perturbation de la trajectoire de
l'espace -- temps
minkowskien dont le vecteur de propagation a pour composantes (1,
1, 0, 0). Le vecteur de
propagation est une perturbation sous la forme . La perturbation
satisfait
donc l'équation :
(III.3)

Déplacement apparent
A
Observateur
Figure 1 (prise dans la référence [1])
Cette relation (III.3) s'intègre comme ceci :
(III.4)
Avec la condition que ; la déviation
Ä pour une trajectoire d'impact
x2=b
est égale à äk2
à ë=8. Donc :
dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp
(III.5)
On peut tracer avec valeur adimensionnée de ( =
) comme sur
la courbe suivante pour le cas du Soleil ( = 2x
1 Omkg , c = 3x 1 08m
· sH
)
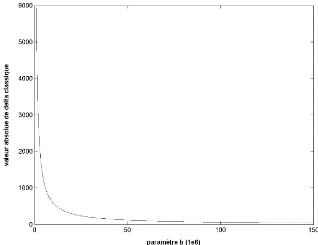
Courbe 1 (tracée dans MATLAB)
On remarque la déviation de la lumière au
alentour d'une masse statique, et à symétrie sphérique
(exemple cas du Soleil), est inversement proportionnelle au paramètre
d'impact de cette masse. On assiste donc à une décroissance de la
déviation au fur et mesure qu'on s'éloigne de la masse. On note
donc que la valeur maximale de la déviation est obtenue
lorsque la lumière frôle pratiquement la masse, comme on le voit
sur la figure suivante :

Figure 2 (Voir bibliographie [16])
dans l'approximation linéaire du champ
? ? ? ? ?
Les rayons lumineux sont fortement déviés au
voisinage de la masse.
On constate donc que pour b rayon du
Soleil, on trouve [2] (résultat vérifié
par
EDDINGTON dès 1919 lors d'une
éclipse totale du Soleil). Dans le cas newtonien on a .
III.1.2 Théorie de la gravité quantique de
BOHM dans l'approximation linéaire du champ
Comme dans le cadre de la théorie
précédente, on suppose qu'un rayon lumineux approche un corps
massif à symétrie sphérique et statique à partir de
l'infini le long de la direction du paramètre affine ë
(dans le même plan que le précédent
(x1,x2)) avec pour
paramètre d'impact b. L'équation de la
géodésique (III.2) est également valable ici et toujours
est le vecteur de
propagation. Donc on a : ; on est ici dans les mêmes
conditions que dans le
1
paragraphe précédent :
(III.6)
or . Pour simplifier, nous considérons
seulement47 le terme
a00 comme contribution de
Öq : or on a vu que quand
ici quand , et l=0 :
(III.7)
Si on remplace (III.7) dans (III.6) :
47 Si on veut une métrique qui ne dépend
pas des angles sphériques à l'infini, seuls les coefficients de
sont non
nuls. Les comportements de et sont similaires, ainsi nous
considérons le premier (en considérant le second
ne change pas l'interprétation physique.
dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp
(III.8)
Bien sûr le premier terme est le terme classique de la
déviation classique, le second représente celui des corrections
quantiques. Nous représentons également sur la
courbe 2 suivante :

Courbe 2 (Tracée dans MATLAB)
On a tracé ici sur un même graphique, le cas
classique précédent et la déviation selon la
théorie de la gravité quantique de BOHM. On
constate que la prédiction quantique de BOHM, indique que la
déviation de la lumière oscille autour du résultat
classique (à cause de sa dépendance à b à l'aide de
fonctions sinus et cosinus). Lorsque le paramètre d'impact est
pratiquement égal (en rapport 1) au rayon de la masse, la
déviation est maximale et diffère très peu du
résultat classique (effet quantique pratiquement négligeable).
Mais plus, on s'éloigne de la masse (b de plus en plus grand), plus les
effets quantiques deviennent significatifs face à la déviation
classique jusqu'à ce qu'ils soient presque observables aussi important
que la déviation classique. On observe alors des oscillations de la
déviation de BOHM autour de celle
d'EINSTEIN. On peut donc dire ici que la déviation de
BOHM généralise celle
d'EINSTEIN en rendant compatible la prédiction de la
relativité générale à celle de la mécanique
quantique.
dans l'approximation linéaire du champ
| 


