III.5 Adéquation du modèle
1. Modèle ARMA( 1, 0)
(a) Condition de stationnarité
Pour un processus autorégressif d'ordre 1, la condition
de stationnarité entraîne que le coefficient autorégressif
soit compris dans l'intervalle ]-1 ;1[.
Dans le cas du modèle présent, ce coefficient
qui est égal à 0,43 appartient à cet intervalle. Donc, ce
processus est stationnaire.
(b) Analyse des résidus
Les résidus ont une valeur presque nulle :
-0,0002. Le test individuel et collectif de bruit blanc indique que les
résidus de la série donne lieu à un bruit blanc, comme le
traduit la série des statistiques Q de BOX et PIERCE. En effet, les
coefficients des corrélations simples et partielles calculées
pour la série des résidus de la régression de ce
modèle sont inférieures aux statistiques Q théoriques au
seuil = 5 %.
(c) Corrélogramme des résidus
2.
Modèle ARMA(1, 1)
(a) Condition de stationnarité
Le coefficient du polynôme autorégressif du
modèle est égal à -0,4912. La condition de
stationnarité est vérifiée pour ce processus, car -1 <
-0,4912 < 1.
(b) Condition d'inversibilité
Le polynôme moyenne mobile du modèle a comme
coefficient : 0,9751. Comme la valeur de cette racine se situe dans
l'intervalle [-1 ; 1], nous concluons que la condition
d'inversibilité est vérifiée pour ce processus.
(c) Analyse des résidus
La moyenne des résidus est de 5,91. Le test individuel
et collectif de bruit blanc indique que les résidus de la série
donne lieu à un bruit blanc, comme le traduit la série des
statistiques Q de BOX et PIERCE. Les coefficients des corrélations
simples et partielles calculées pour la série des résidus
de la régression de ce modèle sont inférieures aux
statistiques Q théoriques au seuil = 5 %.
(d) Corrélogramme des résidus
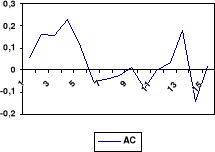
3. Modèle ARMA(2, 1)
(a) Condition de stationnarité
Le polynôme autorégressif du modèle donne
comme racines : 0,23 et -0,66. Le module de cette racine ayant une valeur de
 0,698
qui est inférieur à l'unité, nous concluons que la
condition de stationnarité n'est pas vérifiée pour ce
processus.
(b) Condition d'inversibilité
Le polynôme moyenne mobile du modèle a comme
coefficient : 0,95. Comme la valeur de cette racine se situe dans l'intervalle
[-1 ; 1], nous concluons que la condition d'inversibilité est
vérifiée pour ce processus.
(c) Analyse des résidus
La moyenne des résidus est de 9,96. Le test individuel
et collectif de bruit blanc indique que les résidus de la série
donne lieu à un bruit blanc, comme le traduit la série des
statistiques Q de BOX et PIERCE. Les coefficients des corrélations
simples et partielles calculées pour la série des résidus
de la régression de ce modèle sont inférieures aux
statistiques Q théoriques au seuil = 5 %.
(d) Corrélogramme des résidus
Ce modèle doit être rejeté par qu'il n'est
pas stationnaire.
4. Modèle ARMA(1, 2)
(a) Condition de stationnarité
Le coefficient du polynôme autorégressif du
modèle est égal à 0,8689. La condition de
stationnarité est vérifiée pour ce processus parce que -1
< -0,4912 < 1.
(b) Condition d'inversibilité
Le polynôme moyenne mobile du modèle a pour
coefficient : -0,2879 et
-0,3889. Comme les valeurs de ces coefficients se situent dans
l'intervalle [-1 ; 1], nous concluons que la condition
d'inversibilité est vérifiée pour ce processus.
(c) Analyse des résidus
La moyenne des résidus est de 15,07. Le test
individuel et collectif de bruit blanc indique que les résidus de la
série donne lieu à un bruit blanc, comme le traduit la
série des statistiques Q de BOX et PIERCE. Les coefficients des
corrélations simples et partielles calculées pour la série
des résidus de la régression de ce modèle sont
inférieures aux statistiques Q théoriques au seuil = 5 %.
(d) Corrélogramme des résidus
Après adéquation des modèles ci-dessus,
nous retenons le modèle ARMA(1, 1), pour les raisons suivantes :
- il présente le plus faible écart-type des
résidus ;
- il donne la plus faible valeur du critère de
SCHWARTZ (SBIC)
| 
