1.1.1.10. Histogramme cumulé
L'histogramme cumulé représente la distribution
cumulée des intensités des pixels d'une image. En plus de
l'histogramme classique, il peut être intéressant dans certains
cas
8
de travailler sur l'histogramme cumulé. Ce dernier
s'obtient en associant à chaque niveau de gris i le nombre
hi de pixels de l'image qui ont une valeur
inférieure ou égale à i.
En quelque sorte, cela revient à calculer l'histogramme de
l'image et d'associer à chaque niveau i la somme des
hi (nombre de pixel de l'image qui ont une valeur
égale à j) pour ] = ~.
En formule :
hti~ = Eo<1<tihti= ho + h1 +
·
·
· ..............hti (1)
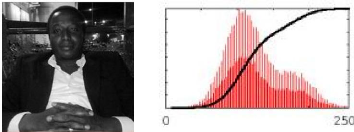
Figure 2: Image en niveau de gris et son histogramme
cumulé
La figure 2 est en niveau de gris, c'est une
représentation sur un seul canal ; c'est la quantification la plus
courante. L'histogramme est la représentation graphique de cette image
en niveau de gris.
a) Modification de l'histogramme
L'histogramme est un outil très utile pour
étudier la répartition de composantes d'une image mais il permet
également de corriger le contraste et l'échelle des couleurs pour
des images surexposées ou sous-exposées : On parle dans ce cas
d'exemples des images qu'on n'arrive pas à identifier ou qu'on n'arrive
pas à lire compte tenu des pixels non lumineux.
En outre sa modification n'altère pas les informations
contenues dans l'image mais les rend plus ou moins visibles. La modification
d'un histogramme est généralement représentée sur
une courbe (appelée courbe tonale) indiquant la modification globale des
composantes de l'image avec en abscisse les valeurs initiales et en
ordonnée les valeurs après modification.
9
|
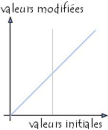
Figure 3: Modification d'histogramme
La figure ci-contre montre l'histogramme lorsqu'aucun mouvement
n'a eu lieu.
|
Comme illustre la figure suivante, la diagonale indique la
courbe telle que les valeurs initiales sont égales aux valeurs finales,
c'est-à-dire lorsque aucune modification n'a eu lieu. Les valeurs
à gauche de la valeur moyenne sur l'axe des abscisses
représentent les pixels "clairs" tandis que ceux à droite
représentent les pixels foncés.
b) Étirement de l'histogramme
L'étirement d'histogramme (aussi appelé
"linéarisation d'histogramme" ou "expansion de la dynamique") consiste
à répartir les fréquences d'apparition des pixels sur la
largeur de l'histogramme.
Ainsi il s'agit d'une opération consistant à
modifier l'histogramme de telle manière à répartir au
mieux les intensités sur l'échelle des valeurs disponibles. Ceci
revient à étendre l'histogramme afin que la valeur
d'intensité la plus faible soit à zéro et que la plus
haute soit à la valeur maximale.
De cette façon, si les valeurs de l'histogramme sont
très proches les unes des autres, l'étirement va permettre de
fournir une meilleure répartition afin de rendre les pixels clairs
encore plus clairs et les pixels foncés proches du noir. Il est ainsi
possible d'augmenter le contraste d'une image. Par exemple une image trop
foncée pourra devenir plus "visible".

a) Image Originale b) Image Étirée c)
Histogramme
Figure 4: Étirement et Histogramme de l'image
Étirée
10
L'image 4.a) est l'origine ou la source, en 4.b), nous avons une
image étirée de l'image originale en niveau de gris. En 4.c)
c'est une représentation de l'histogramme de l'image
étirée.
c) Égalisation d'histogramme
Il peut arriver que les pixels d'une image, bien qu'occupant tout
l'espace de valeurs disponible entre 0 et 255, soient « agglutinés
», c'est-à-dire que l'histogramme n'est pas uniforme. C'est le cas,
par exemple, sur les images suivantes :
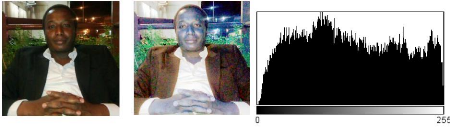
a) Image Originale b) Image Égalisée c)
Histogramme
Figure 5 : Égalisation et Histogramme de l'image
égalisée
L'image 5.a) est l'originale ou la source, l'image 5.b) nous
donne la forme égalisée de l'image originale. On remarque que la
couleur est devenue vive. Enfin en 5.c) une présentation de
l'histogramme. Ce qui nous saute très vite aux yeux, c'est que cette
image contient beaucoup de pixels très sombres ou très clairs, et
relativement peu de pixels d'une luminosité « moyenne ».
| 


