4.6.3 Le modèle MF modifié
En observant les horizons h = 1, 2, 3, 4, 5, 6, 7, 8 et 12 de
la figure 4.17, cela permet de constater que les trois approches
appliquées au modèle MF modifié battent la marche
aléatoire. Toutes les trois séries de R E affichent
des valeurs positives pour ces horizons.
69

Figure 4.17 Séries
RIE du modèle MF modifié par approche
et horizon
À l'opposé, sur les horizons h= 9, 10, 11, de la
période 1986-1988, le modèle MF modifié fait pire que la
marche aléaoire. Ainsi pour h = 9, les trois séries ont des
valeurs négatives en 1986, environ -0.74. Pour h=10, de 1986 à
1988, les trois séries prennent les valeurs négatives qui varient
entre -0.70 et -0.026. Enfin pour h=11 de l'année 1987, l'approche
récursive et l'approche roulante 10 ans affichent les valeurs
négatives qui sont respectivement -0.07 et -0.05.
En considérant les trois approches du modèle MF
modifié, on peut constater que leurs performances relatives varient
suivant des périodes de l'échantillon de prévision. De
janvier 1986 à décembre 1991, C'est l'approche roulante 5 ans qui
est plus performante que les deux autres approches, au niveau de tous les douze
horizons. Pour la période 1992-2009, les approches récursives et
roulantes 10 ans ont des performances proches. On peut toutefois remarquer que
l'approche récursive a un léger avantage aux horizons h= 3, 5, 6,
8, 11, 12. De 2010 à 2014, l'approche
70
récursive se montre la plus performante dans la plupart
des horizons sauf les horizons h=9, 10, 11 et 12.
4.6.4 Le modèle PE modifié
Les trois approches appliquées au modèle PE
modifié battent la marche aléatoire pour les horizons h = 1, 2,
3, 4, 5, 6, 7, 8 et 12 (voir figure 4.18). À ces horizons, toutes les
trois séries de sont positives. Par contre, sur les
horizons h= 9, 10, 11, de la
période 1986-1988, le modèle PE
modifié ne fait pas mieux que la marche aléaoire. Ainsi pour h =
9, les trois séries ont des valeurs négatives en 1986, environ
-0.83. Pour h=10, de 1986 à 1988, les trois séries prennent les
valeurs négatives qui varient entre -0.84 et -0.005. Enfin pour h=11 de
l'année 1987, les trois approches affichent les valeurs négatives
qui oscillent entre -0.096 et -0.009.
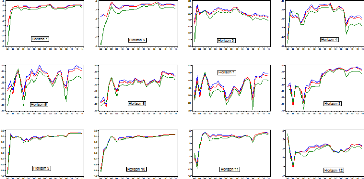
Sur la période janvier 1986-décembre 1991,
aucune approche ne domine nettement. Concernant la période 1992-2008,
l'approche récursive fait mieux que les autres
Figure 4.18 Séries du modèle PE
modifié par approche et horizon
La figure 4.19 affiche les séries de la statistique
obtenues avec le VAR et avec
l'approche roulante 5 ans appliquée aux modèles MF,
POTI, PPA, PE modifiés.
71
approches aux horizons h = 1, 2, 3, 4, 5, 6, 7, 8, 11, 12.
Pour la période 2009-2014, sur les huit premiers horizons, l'approche
récursive est encore meilleure.
Au terme des sous sections précédentes
consacrées à l'étude par horizon des modèles
POTI, PPA, MF, PE modifiés, sur la base du
critère , nous avons constaté ceci :
- pour les horizons de 1 à 8 et l'horizon 12 les
modèles POTI et MF modifiés font mieux que la marche
aléatoire. Cependant pour les horizons 9, 10, 11, ces modèles
font pire que la marche aléatoire.
- Les modèles PPA et PE modifiés font pire que
la marche aléatoire pour les horizons 1, 9, 10 et 11.
- Sur la période 1986-1991, l'approche roulante 5 ans
appliquée aux modèles POTI, PPA, MFmodifiés, fait mieux
que toutes les autres approches pour les douze horizons.
- Sur la période 1992-2014, c'est l'approche
récursive qui performe plus que les approches roulante 5 ans et roulante
10 ans dans l'ensemble.
Dans la sous-section suivante, nous déterminerons, sur
la période 1986-1991, le meilleur modèle pour l'approche roulante
5 ans. Ensuite pour la période 1992-2014, nous rechercherons aussi le
meilleur modèle mais pour l'approche récursive.
| 


