|
MAI 2016
UNIVERSITÉ DU QUÉBEC À MONTRÉAL
PERFORMANCE PRÉVISIONNELLE DE MODÈLES DE TAUX DE
CHANGE FONDÉS SUR LA VALEUR ACTUALISÉE
MÉMOIRE
PRÉSENTÉ
COMME EXIGENCE
PARTIELLE
DE LA MAÎTRISE EN ÉCONOMIQUE
PAR
OLOKPO YVES OSCAR KADJO
REMERCIEMENTS
Je suis reconnaissant au Seigneur qui m'a permis de
réaliser cette étude. J'adresse ma gratitude à toute ma
famille qui m'a soutenu.
Mes remerciements vont à l'endroit de mon directeur de
mémoire, le professeur Alain Paquet qui s'est immensément investi
dans cette recherche pour la rendre possible.
Mes remerciements vont également au professeur Yvon Fauvel
pour son précieux appui technique.
Je remercie toute l'administration du département des
cycles supérieurs en économique de l'UQAM pour la qualité
de leurs services.
Merci à mes amis de classe pour leur encouragement et leur
aide.
Merci à M. et Mme Guindo , Mme Dabiré Rose pour les
lectures et soutien. Merci à tous ceux qui ont contribué à
cette étude.
TABLE DES MATIÈRES
LISTE DES FIGURES vii
LISTE DES TABLEAUX ix
LISTE DES ABRÉVIATIONS, SIGLES ET ACRONYMES x
RÉSUMÉ xii
INTRODUCTION 1
CHAPITRE I
MODÈLES DE TAUX DE CHANGE 3
1.1 Modèles basés sur la balance commerciale 3
1.1.1 Le taux de change et la balance des transactions courantes
3
1.1.2 Le taux de change et la parité absolue du pouvoir
d'achat (PAPA) 4
1.1.3 Le taux de change réel et le taux de change nominal
6
1.2 Les modèles financiers du taux de change 8
1.2.1 Les modèles d'équilibre à prix
flexibles et choix de portefeuilles 8
1.2.2 Le taux de change et l'arbitrage financier 11
CHAPITRE II
LES TRAVAUX EMPIRIQUES SUR LE TAUX DE CHANGE 13
2.1 La performance des modèles structurels 13
2.1.1 Prédictions des modèles monétaires de
taux de change 13
2.1.2 Critiques de Meese et Rogoff (1983) 14
iv
2.2 La performance des modèles de valeurs
actualisées 17
2.2.1 Modélisations et performance du taux de change
fondé sur la valeur
actualisée 17
CHAPITRE III
LE MODÈLE ÉCONOMÉTRIQUE 21
3.1 Les données 21
3.1.1 Présentation des données 21
3.1.2 Transformation et caractérisation des données
23
3.2 Spécification des modèles 24
3.2.1 Modélisation de la variation du taux de change
fondée sur la valeur
actualisée 24
3.2.2 Modélisation VAR du taux de change 26
3.3.1 Tests de racines unitaires et de stationnarité 27
3.3.2 Estimations MCO, estimation du VAR. 27
3.3.3 Prévision 29
CHAPITRE IV
PRÉSENTATION ET ANALYSE DES RÉSULTATS EMPIRIQUES
À LA
FRÉQUENCE MENSUELLE 35
4.1 Analyse graphique et statistiques descriptives en
fréquence mensuelle 35
4.1.1 Variable expliquée LISt + 1 : la variation du
taux de change USD/CAD 35
4.1.2 Variables explicatives : 37
4.2 Tests de stationnarité et analyse des
régressions à la fréquence mensuelle 39
4.2.1 Tests de stationnarité 39
4.2.2 Modifications des modèles initiaux 40
4.2.3 Analyse des estimations MCO des modèles 41
v
4.3 Analyse préliminaire de la précision des
modèles 43
4.4 Performance prévisionnelle des modèles; analyse
du critère U de Theil 45
4.4.1 Modèle POTI modifié 45
4.4.2 Modèle PPA modifié 46
4.4.3 Modèle MF modifié 48
4.4.4 Modèle PE modifié 50
4.4.5 Les meilleurs modèles selon le critète U de
Theil 52
4.5 Performance prévisionnelle des modèles: analyse
du critère ÄREQM 55
4.5.1 Le modèle POTI modifié 55
4.5.2 Le modèle PPA modifié 57
4.5.3 Le modèle MF modifié 58
4.5.4 Le modèle PE modifié 60
4.5.5 Les meilleurs modèles selon le critère
ÄREQM 62
4.6 Performance prévisionnelle des modèles :analyse
du critère RHE2 65
4.6.1 Le modèle POTI modifié 66
4.6.2 Le modèle PPA modifié 67
4.6.3 Le modèle MF modifié 68
4.6.4 Le modèle PE modifié 70
4.6.5 Les meilleurs modèles selon le critère RHE2
71
4.7 Performance prévisionnelle des modèles :
analyse des critères IPA et IPM 74
4.7.1 Performance en fonction des approches
prévisionnelles (critère IPA) 75
4.7.2 Comparaison des performances des modèles POTI,
PPA, MF et PE
(critère IPM) 76
vi
4.8 Sommaire des principaux résultats de
l'étude empirique à la fréquence
mensuelle 77
CHAPITRE V
PRÉSENTATION ET ANALYSE DES RÉSULTATS EMPIRIQUES
À LA
FRÉQUENCE TRIMESTRIELLE 79
5.1 Analyse graphique et statistiques descriptives à la
fréquence trimestrielle 79
5.2 Tests de stationnarité et analyse des
régressions à la fréquence trimestrielle 80
5.3 Analyse préliminaire de la précision des
modèles 80
5.4 Performance prévisionnelle des modèles :
analyse du critère U de Theil 80
5.5 Performance prévisionnelle des modèles :
analyse des critères IPA et IPM 81
CONCLUSION 82
APPENDICE A
RÉSULTATS DE L'ÉTUDE À LA
FRÉQUENCE MENSUELLE. 84
APPENDICE B
RÉSULTATS DE L'ÉTUDE À LA
FRÉQUENCE TRIMESTRIELLE 87
BIBLIOGRAPHIE 97
LISTE DES FIGURES
Figure Page
4.1 Graphiques des variables de l'étude 35
4.2 Séries REQM des modèles et approches 44
4.3 Séries U de Theil du modèle POTI modifié
par approche et horizon 45
4.4 Séries U de Theil du modèle PPA modifié
par approche et horizon 47
4.5 Séries U de Theil du modèle MF modifié
par approche et horizon 49
4.6 Séries U de Theil du modèle PE modifié
par approche et horizon 51
4.7 Séries U de Theil de l'approche roulante 5 ans et
récursive par modèle (1986-
1991) 52
4.8 Séries U de Theil de l'approche récursive par
modèle (1992-2014) 54
4.9 Séries ÄREQM du modèle POTI modifié
par approche et horizon 56
4.10 Séries ÄREQM du modèle PPA modifié
par approche et horizon 57
4.11 Séries ÄREQM du modèle MF modifié
par approche et horizon 59
4.12 Séries ÄREQM du modèle PE modifié
par approche et horizon 60
4.13 Séries ÄREQM : l'approche roulante 5 ans par
modèle (1986-1991) 63
4.14 Séries ÄREQM de l'approche récursive par
modèle (1992-2014) 64
4.15 Séries RHE2 du modèle POTI modifié par
approche et horizon 66
4.16 Séries RHE2 du modèle PPA modifié par
approche et horizon 67
viii
4.17 Séries RHE2 du modèle MF modifié par
approche et horizon 69
4.18 Séries RHE2 du modèle PE modifié par
approche et horizon 70
4.19 Séries RHE2 de l'approche roulante 5 ans par
modèle (1986-1991) 72
4.20 Séries RHE2 de l'approche récursive par
modèle (1992-2014) 73
B.1 Graphiques des variables de l'étude (
fréquence trimestrielle) 87
B.2 Séries REQM des modèles et
approches(trimestrielles) 92
B.3 Séries U de Theil des modèles POTI, PPA, MF,
PE modifiés par approche
(1986-2014,trimestrielles) 93
B.4 Séries U de Theil de l'approche 5 ans par
modèle (1986-1991, trimestrielles)
94
B.5 Séries U de Theil de l'approche récursive
par modèle (1992-2014,
trimestrielles) 95
LISTE DES TABLEAUX
|
Tableau
|
Page
|
|
2.1
|
Estimation des modèles de James, Marsh et Sarno (2012)
|
20
|
|
4.1
|
Statistiques descriptives(fréquence mensuelle)
|
36
|
|
4.2
|
Tableau des Tests ADF et KPSS à niveau (fréquence
mensuelle)
|
39
|
|
4.3
|
Estimations MCO des modèles (fréquence mensuelle)
|
42
|
|
A.1
|
Coefficients de corrélation (fréquence mensuelle)
|
84
|
|
A.2
|
Tests de racine unitaire et stationnarité en
différence première (fréquence
|
|
|
mensuelle)
|
85
|
|
A.3
|
Indicateurs IPA et IPM (fréquence mensuelle)
|
86
|
|
B.1
|
Statistiques descriptives(fréquence trimestrielle)
|
88
|
|
B.2
|
Tableau des Tests ADF et KPSS à niveau (fréquence
trimestrielle)
|
89
|
|
B.3
|
Tests de racine unitaire et stationnarité en
différence première (fréquence
|
|
|
trimestrielle)
|
90
|
|
B.4
|
Estimations MCO des modèles (fréquence
trimestrielle)
|
91
|
|
B.5
|
Indicateurs IPA et IPM(fréquence trimestrielle)
|
96
|
LISTE DES ABRÉVIATIONS, SIGLES ET ACRONYMES
ADF Augmented Dickey Fuller
CAD Dollar canadien
IPA Indicateur de Performance par Approche
IPM Indicateur de Performance par Modèle
KPSS Kwiatkowski-Phillips-Schmidt-Shin
Kurt kurtosis
MCO Moindre carré ordinaire
MF Modèle financier
PE Prix de l'énergie; soit le modèle PE
PIB Produit intérieur brut
POTI Parité ouverte des taux d'intérêt
PPA Parité des pouvoirs d'achat
R Statistique R2 hors
échantillon
E
Skew Skewness
Stati Stationnaire
xi
USD Dollar américain
VAR Vecteur auto régressif
ÄREQM Variation de la racine de l'erreur quadratique
moyenne
RÉSUMÉ
Ce travail étudie la performance prévisionnelle,
hors échantillon, de plusieurs modèles1 de taux de
change fondés sur la valeur actualisée. La période
d'étude est de 1976 à 2014. Étant donné
l'évidence de racine unitaire, les modèles initiaux ont
été modifiés en différenciant les variables
explicatives. L'étude a été faite sur la base des
fréquences mensuelle et trimestrielle. Les horizons de prévision
sont de 1 à 12 mois et 1 à 4 trimestres selon les
fréquences. Les approches de prévision appliquées sont
l'approche récursive, les approches roulantes 5 ans et 10 ans. Les
résultats empiriques montrent qu'avec la fréquence mensuelle,
tous les modèles font mieux que la marche aléatoire sur les
horizons 2 à 8 et 12. Il ressort aussi de l'étude que l'approche
récursive appliquée au modèle financier obtient la
meilleure performance prévisionnelle avec la fréquence mensuelle.
Pour la fréquence trimestrielle, c'est l'approche récursive
appliquée au modèle POTI qui détient la meilleure
performance. En plus, pour chaque modèle, l'étude
révèle que la justesse de prévision s'est
détériorée pendant 2008, l'année de la crise
financière.
Mots clés: Canada, prévision, approches,
horizons.
1 POTI modifié : Parité Ouverte des
Taux d'Intérêt/ PPA modifié : Parité des Pouvoirs
d'Achat / MF modifié : Modèle financier/ PE modifié :
modèle avec le Prix de l'Énergie/ modèle VAR.
INTRODUCTION
La fin du système de Breton-Wood, depuis les
années 70, a donné naissance au système de change
flexible. Dans un tel régime, le taux de change entre deux devises est
endogène et s'ajuste â différentes influences
réelles et monétaires, financières et non
financières, qui reflètent l'état de l'économie.
Pour chercher â comprendre ces relations, plusieurs modèles de
détermination et de prévision de l'évolution du taux de
change ont été conçus.
Des analyses réelles et financières servent,
généralement, de fondement à la détermination des
taux de change. L'approche réelle établit une relation entre le
taux de change et la balance commerciale et réfère aussi à
l'approche d'équilibre. Quant à l'approche financière,
elle tient compte des déterminants financiers du taux de change.
En plus des approches macroéconomiques, figure
l'approche économétrique basée sur les modèles
à valeur actualisée. Cette démarche consiste à
considérer des variables fondamentales pour expliquer les fluctuations
du taux de change. La performance en terme de capacité
prévisionnelle d'une telle modélisation dépend, entre
autres, de la nature (stationnaire ou non) des séries, de la
formalisation de la vraie relation qui lie les variables, et
particulièrement des évènements majeurs, dont par exemple
la crise financière de 2008. Cette dernière constitue une
perturbation majeure qui a profondément affecté les
marchés financiers mondiaux. L'économie américaine a ainsi
été affectée et cela, beaucoup plus comparativement
à l'économie canadienne. Environ un quinquennat après une
aussi importante crise, il est judicieux d'étudier son incidence sur la
performance des modèles économiques en général et
en
2
particulier sur la modélisation du taux de change
USD/CAD. Plus spécifiquement, il est d'un grand intérêt de
vérifier comment se comporte le modèle macroéconomique de
taux de change USD/CAD fondé sur les valeurs actualisées. Ce
modèle de taux de change présente-t-il une meilleure
capacité prévisionnelle que la marche aléatoire? Quelles
sont alors les variables fondamentales pertinentes dans la dynamique à
court terme et à long terme de ce modèle de taux change? Le
vecteur de cointégration (s'il existe) est-il unique? Les coefficients
de ce vecteur sont-ils invariants?
En d'autres termes, l'objectif de ce travail est
d'étudier la performance prévisionnelle des modèles de
taux de change fondés sur les valeurs actualisées,
spécifiquement pour le taux de change USD/CAD.
Dans un premier chapitre, nous présentons une revue de
la littérature théorique et empirique du taux de change. Ensuite,
les composantes des modèles théoriques considérés
sont analysées. Enfin, nous procédons à l'analyse
empirique et à la comparaison de la performance prévisionnelle
des modèles avec celle de la marche aléatoire.
Mundell (1960) alors explique la dynamique du taux de
change par l'état du solde des échanges extérieurs.
Celui-ci est lui-même relié au niveau de la demande interne.
Ce
CHAPITRE I
MODÈLES DE TAUX DE CHANGE
La littérature sur les taux de change est abondante et
diversifiée. Elle comporte des travaux théoriques et empiriques
relatifs aux variables qui peuvent sous-tendre l'évolution du taux de
change. Ces travaux qui visent à dégager les déterminants
du taux de change et à en prévoir l'évolution peuvent
être répartis en deux centres d'intérêt. Le premier
concerne les modèles basés sur la balance commerciale. Le second
met en exergue le rôle des facteurs financiers et monétaires.
1.1 Modèles basés sur la balance
commerciale
1.1.1 Le taux de change et la balance des transactions
courantes
Les travaux d'Alfred Marshall (1879) et Abba Lerner (1946)
établissent une proposition importante qui lie le taux de change
réel et la balance commerciale nominale. Cela est appelé
condition de Marshall-Lerner (ML). Cette condition stipule que la
dépréciation du taux de change améliore la balance
commerciale nominale si la somme des valeurs absolues des
élasticités-prix des demandes d'exportation et d'importation est
supérieure à 1. Dans le cas contraire, elle
détériore ou n'a aucun effet sur la balance commerciale nominale.
De même, durant la période des taux de change fixes, l'état
des balances courantes était retenu comme ce qui influençait le
taux de change.
4
point de vue est aussi soutenu par Fleming (1962).
D'après cette théorie, les devises sont demandées
essentiellement pour acheter des biens et services étrangers. L'offre de
devises correspond alors aux revenus d'exportation. Cette théorie est
donc basée sur les paiements courants avec l'étranger. Ainsi les
pays à monnaie faible sont ceux qui ont une balance commerciale
déficitaire. A l'opposé, les pays dont la devise est forte sont
caractérisés par un solde extérieur positif. Ceci serait
compatible avec ce qui a été observé au Japon. Ce pays a
connu des excédents structurels à l'égard des
États-Unis au cours des années 80 et 90. Il en a
résulté une appréciation substantielle du yen
comparativement au dollar.
1.1.2 Le taux de change et la parité absolue du
pouvoir d'achat (PAPA)
La théorie de la parité des pouvoirs d'achat
(PPA) explique les taux de change par les niveaux relatifs des prix entre pays.
Soutenue par David Ricardo (1817), la théorie de la PAPA défend
l'idée que « la valeur de la monnaie est partout la même
». Cela signifie que, à l'équilibre, le taux de change doit
refléter l'égalité du pouvoir d'achat des deux devises
considérées. En régime de taux de change fixe, si le prix
réel des biens diffère d'un pays à l'autre, la demande
supplémentaire de biens dans le pays où ils sont « le moins
cher » va engendrer un accroissement des prix ; il y a ajustement du taux
de change par les prix. Dans le cadre du flottement des cours de change, il y a
ajustement au différentiel de prix par la variation des cours de change.
Les variations du taux de change reflètent donc le différentiel
d'inflation. Gustave Cassel (1922) définit le niveau du taux de change
nominal d'équilibre comme celui qui assure la parité du pouvoir
d'achat entre deux monnaies. Cela comporte deux versions qui sont la
parité absolue du pouvoir d'achat (PAPA) et la parité relative du
pouvoir d'achat (PRPA).
5
La version de la PAPA se formule comme suit :
' (1.1)
avec
et : respectivement les niveaux des prix domestique et
étranger à la période t.
: le taux de change à la période t qui exprime
le nombre d'unités de la monnaie domestique requis pour une unité
de devise étrangère.
e e P *
e
P S
t ? 1 t ? 1
t ? 1
. P *
L'équation (1.1) exprime une condition de non arbitrage
ou d'équilibre. La PAPA prévaut si on considère des biens
échangeables et parfaitement identiques. Cette version se réalise
en l'absence de toute forme d'entrave au commerce international (taxes
douanières, barrières non tarifaires...) et en négligeant
les coûts de transport ainsi que les coûts d'information.
?
La PAPA implique la parité relative du pouvoir d'achat
(PRPA). Ainsi à partir de l'équation 1.1 relative á la
période t, on exprime sa forme anticipée pour la période
t+1. Ensuite on fait le rapport des deux équations et on aboutit
à ceci :
? P e ?
t ? 1
log ? ?
? S P *
? ? e
t ? 1 t ? 1
? log ? ? ? log ?
*
(1.2)
? S t ? ? P t
t.
Pt St
En appliquant la transformation logarithmique aux membres de
l'équation (1.2), on obtient : ? P t ?
e . . (1.3)
On peut définir les changements anticipés en %
entre t et t+1 dans le niveau des prix domestiques, dans le niveau des prix
étrangers (avec astérisques) et dans la valeur du taux de change
comme suit:
6
alors l'équation (1.3) peut être reformulée
comme suit :
. (1.7)
Pour des valeurs numériques suffisamment faibles,
l'équation (1.7) peut être approximée comme suit:
. (1.8)
L'équation (1.8) constitue la condition de
parité relative des pouvoirs d'achat (PRPA). Ainsi si le taux
d'inflation domestique anticipé est supérieur au taux d'inflation
étranger anticipé, alors le marché va anticiper une
dépréciation de la monnaie domestique entre t et t+1.
1.1.3 Le taux de change réel et le taux de change
nominal
La PAPA implique la PRPA certes, mais il est bien possible que
la PRPA soit valide sans que la PAPA le soit. Nous retenons deux cas de
figure.
Dans un premier cas, supposons que deux pays produisent des
biens identiques. Cependant, il existe des coûts de transport, des tarifs
douaniers ou des différences dans les taxes à la consommation
entre ces deux économies nationales. L'équation de
7
la PAPA (équation 1.1) ne tient plus. Il y a alors un
écart au niveau des prix représenté par un facteur . Ce
contexte est formalisé par l'équation suivante :
' (1.9)
par suite
. (1.10)
Toutefois si le facteur est fixe, c'est-à-dire , alors ,
l'équation
(1.10) redevient identique à l'équation (1.8) et
la parité relative des pouvoirs d'achat (PRPA) reste valide. :
Qt P t
S . P
t t
? ? ? ? ? ? ? ? ? ? ?
e e * e
, 1 %
% S t , t 1 t ,
t 1 t t Q t , t
1
Dans le second cas de figure, nous considérons qu'entre
deux pays donnés, les biens échangés ne sont pas tous
identiques. Ainsi, le prix relatif des biens domestiques par
rapport aux biens étrangers serait défini par le
taux de change réel :
% ? , ? 1 ? 0
Qt t
? * . (1.11)
Si les biens domestiques et étrangers sont identiques et
échangeables entre les pays
sans aucune restriction, alors =1 et la PAPA tient. Dans le cas
contraire, et
la PAPA ne tient plus.
En supposant un taux de change réel variable cela implique
que
e
. (1.12)
e
La PRPA ne tient que si Ainsi, toute dépréciation
anticipée du taux de
change est égale à l'écart entre les
variations relatives des prix domestiques et
8
étrangers. En d'autres termes, la
dépréciation anticipée du taux de change se déduit
de l'écart d'inflation entre pays. (domestique et étranger).
M t ? P t L Y t j t CI
t
Vu ainsi, on parle alors de l'approche d'équilibre de
la détermination du taux de change.
1.2 Les modèles financiers du taux de change
Les théories relatives aux déterminants
financiers du taux de change peuvent être scindées en deux grands
axes. Le premier montre l'influence des variables monétaires et
financières. Il est constitué du modèle monétaire
à prix flexible, des modèles de choix de portefeuilles et de la
théorie de l'efficience des marchés. Le second axe est relatif
à l'instabilité des taux de change.
* * . * ( * , *, * )
1.2.1 Les modèles d'équilibre à prix
flexibles et choix de portefeuilles 1.2.1.1 Le modèle d'équilibre
à prix flexible
La théorie d'équilibre du taux de change fut
développée par Frenkel (1976). La fonction de demande de monnaie
de chaque pays jumelée avec la définition de taux de change
réel en sont la base.. A l'équilibre sur les marchés
domestique et étranger de la monnaie, on a les équations
suivantes :
(1.13)
(1.14)
Mt
M*
t
où et sont les stocks de monnaie domestique et
étrangère, et sont les
niveaux des prix domestique et étranger, et sont les
niveaux des revenus réels
domestique et étranger, et sont les taux
d'intérêt nominaux domestique et
9
étranger, et sont les coûts de
l'intermédiation financière domestique et
étranger.
? ? ?
M a ( i ,
i * , , * ) W ,
On suppose dans ce modèle que la quantité
réelle de monnaie demandée est théoriquement une fonction
négative du taux d'intérêt nominal et une fonction positive
des revenus réels bruts des ménages et du coût de
l'intermédiation financière.
? ? ?
B b ( i ,
i * , , * ) W ,
A partir de l'équation (1.11) qui définit le taux
de change réel et des équations (1.13) et (1.14), on obtient la
formule suivante du taux de change nominal en fonction du taux de change
réel :
? ? ?
SF c ( i ,
i * , , * ) W ,
Le taux de change augmente si la masse monétaire
domestique augmente, ou si la demande réelle de monnaie domestique
diminue par rapport à leurs contreparties
étrangères. De même le taux de change
augmente si le prix des biens étrangers
augmente relativement au prix
des biens locaux. Ce prix relatif est tributaire de l'offre et de la demande
des deux types de biens.
W ? M ? B ?
SF ,
1.2.1.2 Les modèles de choix de
portefeuilles
McKinnon (1969), Branson (1975) ainsi que Kouri (1976) ont
conçu les premiers modèles relatifs à l'équilibre
de portefeuille. Soit
|
(1.16) (1.17) (1.18) (1.19)
|
10
. (1.21)
avec
· M : le stock de monnaie nationale;
· B : les obligations;
· F : les détentions nettes d'actifs en devises
étrangères;
· W : la richesse totale;
· S : le cours des devises étrangères
exprimé en monnaie nationale; SF=
(1--a--b)W= f ( i
, i * , , * ) cr cr W
· i et i* : les taux d'intérêt sur les titres
domestiques et étrangers respectivement;
· et : les risques sur les titres domestiques et
étrangers respectivement;
· a, b, c : des paramètres dont les valeurs
expriment des fractions de la richesse totale W.
La relation comptable (1.19) est la contrainte budgétaire
des investisseurs, mesurée par leur richesse globale. Il faut en effet
satisfaire la relation suivante :
. (1.20)
Ainsi les équations de comportement (1.18) et (1.20) ne
sont pas indépendantes. En fonction de la position créditrice ou
débitrice du pays par rapport à l'étranger, F peut
être positif ou négatif. La forme réduite suivante du
modèle :
11
L'équation (1.21) est équivalente à :
. (1.22)
Selon l'équation (1.22), le taux de change est
déterminé par le processus des choix de portefeuille. Ce qui
permet une répartition de la richesse entre monnaie nationale, titres
nationaux et étrangers, conformément aux désirs des
investisseurs. On peut dire que le taux de change est le prix qui assure
l'équilibre sur les différents marchés d'actifs nationaux
et étrangers.
A(1 * )
? t , t ?
1
1.2.2 Le taux de change et l'arbitrage financier
Les hypothèses de base retenues sont le
non-contrôle des capitaux entre pays, l'absence de barrière
fiscale, l'absence des coûts de transaction, et les anticipations
rationnelles des investisseurs pendant les arbitrages. En plus l'arbitrage
financier peut être posé comme le choix entre un placement
obligataire domestique et un placement obligataire étranger. Ainsi un
investisseur doté d'un capital financier dont le montant en monnaie
domestique est A, peut le placer sur son territoire de résidence.
À la fin
de la période, cela lui rapporte . En optant pour
l'étranger, son
(1 ) . (1 ). 1
* e
A + i + = + i
S
t , t 1 t ,
t + 1 t +
investissement initial converti en devise
étrangère est et son rendement en fin
A
i
S
de période est
t
|
. En égalisant ces deux rendements sur la base du taux
de
|
|
change anticipé par l'investisseur, on obtient :
12
La transformation logarithmique appliquée de part et
d'autre de l'équation (1.23) permet d'obtenir ceci :
f
t ? t ? s t ? i
t t ? ? i t t ? 1 / ,
1 , 1
f t ? 1 / t
? log F t ? 1 / t s t ?
log S t
' (1.24)
ou approximativement,
|
.
(1 + , + 1 ) = . (1 + , + 1 ). +
i F
t t t t t 1 /t
|
(1.25)
|
|
Cette dernière équation est la condition de
parité ouverte des taux d'intérêt nominaux
(POTI). Ainsi un écart positif entre les taux
d'intérêt nominaux domestique et
étranger est égal à une
dépréciation anticipée de la monnaie domestique.
A
A i
S t
L'investisseur peut par contre préférer transiger
sur le marché des changes à terme. Il
opte ainsi pour un taux de change à terme ( ) pour la
conversion de ses futurs
revenus liés à ses investissements
à l'étranger. Dans ce cas, on obtient :
*
' (1.26)
d'où on a approximativement,
'
(1.27)
avec et . L'équation (1.27) représente la
condition de
parité couverte des taux d'intérêt nominaux
(PCTI).
. (2.1)
CHAPITRE II
LES TRAVAUX EMPIRIQUES SUR LE TAUX DE CHANGE
Le taux de change est une variable macroéconomique
importante. Cependant, sa modélisation et sa prévision comportent
bien des difficultés. Plusieurs modèles empiriques ont donc
été considérés. Ces modèles pourraient
être répartis en modèles structurels et en modèles
non structurels dont la modélisation fondée sur la valeur
actualisée. De nombreux auteurs se sont alors penchés sur la
performance empirique de ces modèles. Ainsi, dans ce chapitre, nous
étudierons d'abord la performance des modèles structurels de taux
de change. Ensuite, nous nous intéresserons à la performance des
modèles de taux de change fondés sur les valeurs
actualisées.
* *
( ) ( ) ( i i * )
s m m
= -- -- ço y --
y + 2 --
2.1 La performance des modèles structurels
La classe des modèles structurels est
diversifiée. Cette section analysera certaines approches
macroéconomiques de détermination du taux de change qui sont
souvent employées.
2.1.1 Prédictions des modèles
monétaires de taux de change
Les modèles monétaires de taux de change
comportent deux grandes variantes, dont celle à prix flexible qui fut
étudiée par Frenkel (1976) et Bilson (1981). Ces modèles
peuvent être représentés d'une manière
générale comme suit :
14
Cette formalisation empirique découle de la
log-linéarisation du modèle théorique de l'équation
(1.15):
(2.2)
En posant , , , , on obtient
approximativement l'équation (2.1).
Les auteurs ont donc contraint à l'unité le
coefficient du terme . Dans leur
spécification, ils ont aussi contraint le taux de change
réel en imposant la
parité absolue des pouvoirs d'achat. En plus, les
auteurs ont fait abstraction des coûts de transport ou des
différentiels de taxation entre les pays.
L'équation (2.1) prédit premièrement
qu'un revenu relatif plus élevé induit une monnaie plus forte. Le
mécanisme explicatif est qu'un revenu relatif plus élevé
induit une demande de monnaie relative plus importante citeris paribus. La
seconde prédiction est qu'un taux d'intérêt
élevé induit une monnaie plus faible. Cela s'explique par le fait
qu'un taux d'intérêt plus élevé implique une demande
de monnaie relativement plus faible. Dans le modèle de Mundell-Fleming,
des revenus plus élevés impliquent des importations plus
élevées, toutes choses égales par ailleurs, et par
conséquent une monnaie plus faible.
2.1.2 Critiques de Meese et Rogoff (1983)
L'étude de Meese et Rogoff (1983) portant sur la
performance des modèles structuraux de taux de change demeure une
référence. Dans cette étude, les auteurs ont
comparé les prévisions hors échantillon de plusieurs
modèles structuraux de taux de change à celui de la marche
aléatoire. Les modèles structuraux étudiés sont un
modèle monétaire à prix flexibles (Frenkel-Bilson), un
modèle monétaire à prix
15
rigides (Dornbusch-Frankel) et un modèle à prix
rigides des actifs et qui tient compte de la balance des paiements
(Hooper-Morton). Tous ces trois modèles structuraux
considérés sont basés sur une fonction de demande de
monnaie commune. La forme générale de l'équation du taux
de change utilisée est :
, (2.3)
où
Qt ? 1
· : logarithme du taux de change;
· ) : différentiel dans la quantité
détenue de monnaie domestique et étrangère;
· : différentiel entre les PIB domestique et
étranger respectivement;
· : différentiel des taux d'intérêt
domestique et étranger respectivement;
· : différentiel entre les taux d'inflation
domestique et étranger respectivement;
· : soldes (excédentaires ou déficitaires)
des balances commerciales domestique et étrangère
respectivement;
· u : terme d'erreur.
L'équation (2.3) est obtenue à partir de la
log-linéarisation du modèle théorique
représenté par l'équation (1.15). Les auteurs ont
contraint le taux de change réel
en imposant la parité absolue des pouvoirs d'achat. Ils
ont aussi posé .
En plus ils ont retenu plus de variables explicatives pour le
taux de change nominal mais ont omis les coûts de l'intermédiation
financière.
16
En fonction des contraintes imposées aux coefficients
de l'équation (2.3), on détermine chacun des trois modèles
étudiés par les auteurs. Trois cas de figure se présentent
:
- Cas 1 : , soit le modèle de Frenkel-Bilson.
- Cas 2 : , soit le modèle de Dornbusch-Frenkel avec
rigidité nominale.
- Cas 3 : , , , , , , , soit le modèle de
Hooper-Morton avec rigidité nominale possible.
Dans leur étude, Meese et Rogoff (1983) ont conclu que
la marche aléatoire faisait mieux que les modèles structuraux sur
un horizon de un à douze mois pour les taux de change dollar/mark,
dollar/pound, dollar/yen courant 1970. Leur méthodologie d'estimation a
consisté à considérer d'une part des équations avec
des coefficients contraints et d'autre part une approche VAR. Les
critères pour mesurer la performance des différents
modèles sont l'erreur quadratique moyenne et l'erreur absolue moyenne.
Pour ces auteurs, la faible performance des modèles structuraux de taux
de change a plusieurs causes. Ce sont, entre autres, une prime de risque
variable et volatile dans le temps, un taux de change réel volatil
à long terme, des manquements dans la formulation de l'inflation
anticipée et de la demande de monnaie.
Suite aux conclusions de Meese et Rogoff (1983), plusieurs
travaux ont été réalisés pour améliorer la
spécification et la performance prédictive des modèles de
taux de change. Parmi ceux-ci il y a les modèles de taux de change
fondés sur la valeur actualisée.
17
La formalisation empirique de l'équation (1.13) suivant
l'approche monétaire du taux de change de la décennie 1970, est
:
2.2 La performance des modèles de valeurs
actualisées
Les modèles standards de valeurs actualisées
considèrent que le taux de change est déterminé par la
combinaison de variables macroéconomiques futures anticipées. Ces
variables sont appelées variables fondamentales. Selon ces
modèles le taux de change est déterminé par
l'équilibre sur les marchés des actifs. Pour Obstfeld et Rogoff
(1996), le taux de change est alors assimilable au prix d'un actif. Dans cette
optique, cette section abordera dans un premier temps la modélisation du
taux de change spot fondée sur la valeur actualisée. En second
moment, l'implication de cette modélisation sur la formulation de la
variation du taux de change sera étudiée.
2.2.1 Modélisations et performance du taux de change
fondé sur la valeur actualisée
Notre travail adopte la modélisation de Engel et West
(2005). Cette modélisation du taux de change fondée sur la valeur
actualisée a des fondements théoriques. Ces fondements sont
représentés par les équations (1.11), (1.13) et (1.25).
|
Ainsi la log-linéarisation de l'équation (1.11) est
:
On en déduit :
|
.
'
|
(2.4)
(2.5)
|
où est le logarithme du taux de change nominal, sont les
logarithmes des
prix domestiques et étrangers respectivement, est le
logarithme du taux de change réel.
18
, (2.6)
où est le logarithme de l'offre de monnaie domestique, est
le logarithme du
niveau des prix domestiques, est le logarithme du revenu national
domestique,
est le logarithme du taux d'intérêt nominal
domestique, est un choc à la
demande de monnaie domestique. Pour
l'économie du pays étranger, les variables
équivalentes sont : . Les paramètres , sont
identiques
pour les deux économies.
i t ? m t p t y t
= - + + T + Vmt ?
Enfin, l'équation (1.25) est modifiée dans le cas
d'une déviation de la condition de la parité non couverte des
taux d'intérêt. Sa reformulation est :
, (2.7)
où capte la déviation.
Dans une approche monétaire et sur la base de
l'équation (2.6), on déduit le taux d'intérêt
domestique:
. (2.8)
1 , a
En remplaçant les taux d'intérêt et de
l'équation (2.7) par leurs formulations
déduites de
l'équation (2.8), on obtient une expression actualisée du taux de
change nominal:
19
. (2.9)
Cette équation (2.9) peut être reformulée en
substituant par l'expression
équivalente de l'équation (2.5). En
réaménageant, on aboutit à :
.(2.10)
Cette expression est une formulation du taux de change nominal
fondée sur la valeur actualisée avec une approche
monétaire (pour la détermination des taux
d'intérêt). Le
facteur d'actualisation est . Les variables fondamentales
observables
(mesurables) sont : . Les variables fondamentales non
mesurables sont et .
Engel et West (2005) montrent analytiquement que dans un
modèle de valeur actualisée avec des anticipations rationnelles,
le taux de change suit une marche aléatoire. Cela est le cas lorsque le
facteur d'actualisation est proche de la valeur unitaire et les variables
fondamentales sont intégrées d'ordre un soit I(1).
Pour l'étude de la variation du taux de change, James,
Marsh et Sarno (2012) considèrent que la variation du taux de change est
déterminée par la combinaison linéaire de variables
macroéconomiques (dites fondamentales). Ainsi ces auteurs ont
étudié le taux de change entre le dollar américain et le
dollar canadien. Ils ont adopté plusieurs modèles de variation de
taux de change. Ces modèles ont été alors estimés
par la méthode des moindres carrés ordinaires. Les
résultats partiels de leur étude sont compilés dans le
tableau suivant2 :
2 Voir page 18 pour la définition des variables
des modèles du tableau.
20
Tableau 2.1 Estimation des modèles de
James, Marsh et Sarno (2012)
|
Modèles
|
Paramatres
|
OE
|
â
|
R2 (%)
|
|
|
-0.070
|
-0.974a
|
0.512
|
|
|
(0.116)
|
(0.586)
|
|
|
|
-0.288
|
0.015a
|
0.828
|
|
|
(0.185)
|
(0.008)
|
|
|
|
0.640
|
-0.003
|
0.328
|
|
|
(0.929)
|
(0.004)
|
|
Notes : Les écarts-types sont entre les
parenthèses. L'échantillon est de janvier 1976 à juin 2010
et comporte des observations mensuelles. Les équations des
modèles sont estimées par la méthode des moindres
carrés ordinaires./ a : significativité statistique à
10%.
Pour ces différents modèles estimés, les
auteurs obtiennent des valeurs faibles pour la statistique R2. En
plus, selon Cuthbertson et Nitzsche (2004), le 2 est faible
(de l'ordre de 0.035) dans les régressions avec les variables
mensuelles.
La variable de taux de change USD/CAD utilisée
est le taux de change comptant en fin de période (). Cette cotation
définit le prix d'une unité de dollar américain
en
CHAPITRE III
LE MODÈLE ÉCONOMÉTRIQUE
Le travail économétrique de ce chapitre porte
d'abord sur quatre modèles de variation du taux de change (POTI, PPA, MF
et PE) et un modèle VAR. Les modèles POTI, PPA, MF modèles
sont ceux étudiés par James, Marsh et Sarno (2012). Pour
méthode d'estimation, nous adoptons, comme ces auteurs, la
méthode des moindres carrés ordinaires. Ensuite, nous
étudions la performance prévisionnelle de tous ces modèles
suivant les approches récursive, roulante 5 ans et roulante 10 ans. Le
modèle de référence est la marche aléatoire.
3.1 Les données
3.1.1 Présentation des données
Cette section présente la banque de données de
base pour les variables de l'économie canadienne et américaine.
Notre étude considère séparément les modèles
à la fréquence mensuelle, puis à la fréquence
trimestrielle. Ceci a pour objectif d'évaluer la robustesse des
résultats obtenus. Nous utilisons des variables
désaisonnalisées. Les données mensuelles vont de janvier
1976 à décembre 2014, ce qui correspond à 468
observations. Quant aux données trimestrielles, c'est un total de 156
observations de mars 1976 à décembre 2014.
L'énergie est mésurée par l'indice des
prix de l'énergie avec 1972=100. La source des données est le
tableau 176-0076 de statistique Canada (CANSIM).
22
dollar canadien. Cette variable provient des statistiques
financières internationales diffusées par le Fonds
Monétaire Intenational (FMI).
Les taux d'intérêt utilisés sont les taux
d'intérêt des marchés monétaires canadiens et
américains. Ces taux d'intérêt sont à
échéance de trois mois. Ils proviennent du « Main Economic
Indicators » de l'OCDE.
L'agrégat monétaire utilisé est M2 pour
le Canada et les États-Unis. Celui ci provient des statistiques
financières internationales diffusées par le Fonds
Monétaire Intenational (FMI).
Les niveaux des prix du Canada et des États-Unis sont
mésurés avec l'indice des prix à la consommation de tous
les biens avec 2010=100. Les statistiques financières internationales
diffusées par le Fonds Monétaire Intenational (FMI) en sont la
source.
Les niveaux de production nationale sont approximés par
l'indice de la production industrielle (2010=100). Ils sont publiés dans
les statistiques financières internationales diffusées par le
Fonds Monétaire International (FMI) . Cette approximation des niveaux de
production nationales par l'indice de la production industrielle a
été également retenue par James, Marsh et Sarno (2012).
Ces auteurs justifient cela par le fait que les données statistiques des
niveaux de production nationales ont généralement une
fréquence trimestrielle alors que l'étude vise une analyse
suivant les fréquences mensuelle et trimestrielle à la fois. Il
semble alors intéressant de retenir l'indice de la production
industrielle dont des données statistiques mensuelles et trimestrielles
sont disponibles.
23
: différentiel des indices de la production
industrielle du Canada et des États-Unis respectivement.
La variable mesure l'indice total des prix sans les prix de
l'énergie. Avec
1972=100. La source des données est aussi le tableau
176-0076 de statistique Canada (CANSIM).
p t ? p t *
3.1.2 Transformation et caractérisation des
données
Les transformations et caractérisations des variables
sont faites suivant l'approche de James, Marsh et Sarno (2012).
3.1.2.1 Les logarithmes des variables
A l'exception des taux d'intérêt, toutes les
autres variables macroéconomiques du Canada et des ÉtatsUnis sont
transformées en leur appliquant le logarithme naturel. Ensuite les
logarithmes de ces variables sont multipliés par cent. Nous utilisons
l'astérisque pour désigner les logarithmes des variables
macroéconomiques des États-
Unis ( .
y t ? y t *
3.1.2.2 Les écarts de variables
Plusieurs écarts macroéconomiques entre le
Canada et les États-Unis sont construits. Ce sont :
: différentiel des taux d'intérêt du Canada
et des États-Unis respectivement.
: différentiel des agrégats monétaires du
Canada et des États-Unis respectivement.
: différentiel entre les niveaux de prix du Canada et
les États-Unis respectivement.
La représentation spécifique de chacun des trois
modèles empiriques depend de l'expression des variables
macroéconomiques fondamentales représentées par
Xt.
24
Ces écarts permettent de construire les variables
explicatives (dites fondamentales) des modèles du paragraphe suivant.
3.2 Spécification des modèles
Les modèles de variation du taux de change
fondés sur la valeur actualisée qui sont étudiés
sont ceux formalisés par James, Marsh et Sarno (2012). Nous incluerons
dans notre recherche un modèle de variation de taux de change qui inclue
le prix de l'énergie. Cela vise à vérifier la contribution
du prix de l'énergie dans la variation du taux de change.
3.2.1 Modélisation de la variation du taux de change
fondée sur la valeur actualisée
Pour l'analyse empirique, la marche aléatoire sert de
référence. Trois modèles de variation du taux de change
fondés sur la valeur actualisée sont retenus. Ceux-ci sont
formalisés selon les travaux de James, Marsh et Sarno (2012) . De
façon générale, la variation du taux de change
fondée sur la valeur actualisée est alors
représentée par une combinaison linéaire de variables
macroéconomiques dites fondamentales. Cette représentation
générale est la suivante:
' (3.1)
où LSt =St -
St. La composante Xt représente les
variables macroéconomiques (dites fondamentales), w et â sont des
constantes à estimer, ?t+1 est un terme d'erreur
stochastique.
25
Précisons que pour certains modèles, la composante
Xt peut contenir dans son expression le taux de
change St.
3.2.1.1Modèle de la marche aléatoire
Dans ce cas â = 0 et la variation du taux de change est
ceci :
. (3.2)
Le modèle formulé équivaut à la non
prise en compte des variables fondamentales dans la dynamique de la variation
du taux de change.
3.2.1.2 Modèle basé sur la parité ouverte
des taux d'intérêt (POTI) L'équation de la variable
macroéconomique fondamentale est :
xt ?p t ?p t ?
s t
|
On en déduit la modélisation suivante :
|
.
|
|
(3.3)
|
|
.
|
(3.4)
|
La POTI tient lorsque et =1. Selon Cuthbertson et Nitzsche
(2004), en
général le signe de est négatif ( ).
Ainsi si alors et la
monnaie domestique s'apprécie.
3.2.1.3 Modèle basé sur la parité
du pouvoir d'achat (PPA)
Sur la base de la parité du pouvoir d'achat,
l'équation de la variable fondamentale est :
* . (3.5)
On en déduit la modélisation suivante :
26
|
.
La PPA tient lorsque et . Par ailleurs lorsque et
alors . Par conséquent, la monnaie domestique tend
à se déprécier.
3.2.1.4 Modèle basé sur les fondamentaux financiers (MF) Dans
ce cas, l'équation de la variable fondamentale est :
.
|
(3.6)
(3.7)
|
On en déduit la modélisation suivante :
. (3.8)
Pour , et alors . Par conséquent, la
monnaie domestique tend à se déprécier.
3.2.1.5 Modèle basé sur le prix de
l'énergie (PE)
Ce modèle prend en compte l'influence du prix de
l'énergie dans les variations du taux de change.
(3.9)
où la variable mesure l'indice des prix de
l'énergie. La variable mesure l'indice
total des prix sans les prix de l'énergie.
3.2.2 Modélisation VAR du taux de change
Pour cette étude, le modèle VAR de variation du
taux de change est défini ainsi :
27
3 Les variables fondamentales sont définies par
les équations (3.5) et (3.7), page 25. Les variables
d'écart sont : , ), , .
, (3.10)
où le vecteur X (t) est le suivant :
(3.10)
La sélection du nombre approprié de retards dans
le VAR se fait à partir du critère d'information Akaike. On
retient l'ordre qui minimise ce critère.
3.3 Méthodologie
Nous faisons d'abord une investigation des variables des
modèles au moyen de l'analyse des graphiques, des statistiques
descriptives et des tests statistiques de non-stationnarité et de
stationnarité. Ensuite nous estimons les modèles par la
méthode des moindres carrés ordinaires. Enfin nous
procédons à l'étude de la prévision.
3.3.1 Tests de racines unitaires et de
stationnarité
( * )
i i ? i i ( p a ? p a * ( *
)
m e ? m e ( * )
y t ? y t
Le test de racine unitaire (ADF) et le test de
stationnarité KPSS sont appliqués sur la variation du taux de
change, les variables fondamentales et les variables d'écart3
des différents modèles. Le critère d'information d'Akaike
modifié détermine le nombre optimal de retards pour les
différences premières dans les équations de
spécification du test ADF.
3.3.2 Estimations MCO, estimation du VAR.
Dans l'objectif de comparer notre travail à celui de
James, Marsh et Sarno (2012), notre étude adopte d'abord la même
méthode d'estimation que ces auteurs. Ainsi les quatre modèles de
variation de taux de change sont estimés par la méthode des
28
moindres carrés ordinaires. Les coefficients
estimés sont ceux de la matrice de Newey et West. Cette matrice de
variance-covariance des coefficients est asymptotiquement convergente en cas
d'hétéroscédasticité et d'auto-corrélation
des résidus.
|
Les modèles estimés sont respectivement:
|
,
|
|
(3.4)
|
|
|
,
|
(3.6)
|
, (3.8)
, (3.9)
, (3.10)
où le vecteur X (t) est le suivant :
. (3.11)
La sélection du nombre approprié de retards dans
le VAR se fait au moyen du critère d'information Akaike. On retient
l'ordre du VAR qui minimise ce critère.
Notons que ces modèles sont d'abord estimés sur
la base d'une fréquence mensuelle des variables et l'échantillon
initial d'estimation est alors de janvier 1976 à décembre 1985.
Ensuite l'étude est faite en estimant à nouveau les
modèles mais sur la base d'une fréquence trimestrielle. Pour
cette fréquence, l'échantillon initial d'estimation est du
premier trimestre 1976 au dernier trimestre 1985. Finalement, la période
de 1986 à 2014 sert à comparer la performance
prévisionnelle des modèles.
29
3.3.3 Prévision
Cette section traite des approches prévisionnelles des
modèles de la section précédente et de l'évaluation
de la performance prévisionnelle de ceux-ci. Ces modèles sont le
modèle de variation du taux de change avec parité ouverte des
taux d'intérêt ( POTI), le modèle de variation du taux de
change avec parité du pouvoir d'achat (PPA), le modèle de
variation du taux de change avec les fondamentaux financiers (MF). Enfin, nous
avons un modèle qui prend en compte le prix de l'énergie (PE).
3.3.3.1 Approches prévisionnelles
Les approches prévisionnelles appliquées aux
modèles de variation de taux de change (POTI, PPA, MF, PE) sont
l'approche récursive, l'approche roulante 5 ans et l'approche roulante
10 ans .
? Approche récursive
Pour la fréquence mensuelle, on estime initialement les
modèles sur la période 1976m01 à 1985m12. Puis à
partir de 1985m12, on fait les prévisions 1 à 12 périodes
à l'avance. Ensuite on réestime les modèles sur la
période 1976m01 à 1986m01. Puis à partir de 1986m01, on
fait les prévisions 1 à 12 périodes à l'avance. La
même procédure est répétée jusqu'à ce
qu'on parcourt tout l'échantillon de prévision (1986m01-2014m12).
Pour la fréquence trimestrielle, on estime initialement les
modèles sur la période 1976q1 à 1985q4. Puis à
partir de 1985q4, on fait les prévisions 1 à 4 périodes
à l'avance. Ensuite on réestime les modèles sur la
période 1976q1 à 1986q1. Puis à partir de 1986q1, on fait
les prévisions 1 à 4 périodes à l'avance. La
même procédure est répétée jusqu'à ce
qu'on parcourt tout l'échantillon de prévision
(1986q1-2014q4).
30
? Approche roulante 10 ans :
Pour les fréquences mensuelles, on estime, d'abord les
modèles sur la période de 10 ans, c'est-à-dire 1976m01
à 1985m12. Puis à partir de 1985m12, on fait les
prévisions 1 à 12 périodes à l'avance. Ensuite on
réestime les modèles sur une autre période de 10 ans
c'est-à-dire 1976m2 à 1986m1. Puis à partir de 1986m1, on
fait les prévisions 1 à 12 périodes à l'avance. La
même procédure est répétée jusqu'à ce
qu'on parcourt tout l'échantillon de prévision (
1986m01-2014m12). Pour la fréquence trimestrielle, on estime
initialement les modèles sur la période 1976q1 à 1985q4.
Puis à partir de 1985q4, on fait les prévisions 1 à 4
périodes à l'avance. Ensuite on réestime les
modèles sur la période 1976q2 à 1986q1. Puis à
partir de 1986q1, on fait les prévisions 1 à 4 périodes
à l'avance. La même procédure est
répétée jusqu'à ce qu'on parcourt tout
l'échantillon de prévision ( 1986q1-2014q4). Notons que pour
l'approche roulante 5ans, les modèles sont estimés initialement
sur la période 1981m1-1985m12 pour la fréquence mensuelle.
Concernant la fréquence trimestrielle, on fait l'estimation initiale sur
la période 1981q1-1985q4.
3.3.3.2 Évaluation de la performance
prévisionnelle
La particularité de cette étude est qu'elle
évalue les modèles sur chacune des 29 années de
l'échantillon de prévision, de l'horizon 1 à 12 pour la
fréquence mensuelle (horizon 1 à 4 pour la fréquence
trimestrielle). L'échantillon de prévision est de 1986 à
2014. L'évaluation de la performance de prévision se fait hors
échantillon d'estimation.
Nous évaluons la performance prévisionnelle des
modèles empiriques de variation de taux de change (POTI, PPA, MF, PE)
par rapport au modèle de référence qui est la marche
aléatoire. Trois critères statistiques d'évaluation sont
utilisés pour comparer la performance prévisionnelle des
modèles à la celle de la marche aléatoire. Le premier
31
critère est le U de Theil. Le second est la variation
de la racine de l'erreur quadratique moyenne (ÄREQM) suivant l'approche de
Welch et Goyal (2008). Le troisième est la
statistique de Campbell et Thompson (2008). Ensuite les
modèles sont comparés
entre eux pour en déterminer le
plus performant. Les statistiques utilisées pour cela sont deux scores
que nous nommons « Indicateur de Performance par Approche» (IPA) et
« Indicateur de Performance par Modèle» (IPM).
Pour évaluer la précision des modèles
pendant la crise financière, la principale statistique que nous
analysons est la racine de l'erreur quadratique moyenne (REQM)
Les statistiques utilisées sont définies comme
suit: U de Theil =
: variation du taux de change réalisée, :
prévision de la variation du
taux de change par les modèles empiriques (POTI, PPA, MF,
PE), : prévision
de la variation du taux de change par le modèle de
marche aléatoire, h : horizons de prévision, 1,2,....,12. M est
le nombre d'obervations utilisées pour l'estimation des modèles.
N est le nombre d'observations pour les prévisions hors
échantillon.
Une valeur de U de Theil inférieure à 1 signifie
que le modèle empirique de prévision performe mieux que la marche
aléatoire.
.
Plus un modèle est performant, plus les valeurs de la
statistique calculées
lors des prévisions sont faibles. Ainsi après un
choc, les performances prévisionnelles
d'un modèle baissent lorsque les valeurs de la statistique
augmentent.
32
Une valeur positive de la variation de la racine de l'erreur
quadratique moyenne (ÄREQM) signifie que le modèle empirique
étudié performe mieux que la marche aléatoire. Cela est
dû au fait que la racine de l'erreur quadratique moyenne du modèle
empirique étudié est plus faible que celle de la marche
aléatoire.
Une valeur positive de la statistique R E
de Campbell et Thompson (2008) signifie que le modèle empirique
étudié, qui a une plus faible erreur quadratique moyenne,
performe mieux que la marche aléatoire. Plus le modèle empirique
est performant plus la statistique tend vers 1.
IPA : c'est l'Indicateur de Performance par Approche, pour un
modèle donné. Il permet de déterminer la meilleure
approche de prévision pour chaque modèle. Précisons que
pour chaque modèle, il y a trois approches de prévision
(récursive, roulante 5 ans, roulante 10 ans). Cet indicateur est obtenu
à partir des valeurs de U de Theil, dans notre étude. Pour
déterminer cet indicateur, on considère uniquement chaque
modèle (soit POTI, soit PPA, soit MF, soit PE), ses trois approches de
prévision et tous les douze horizons à la fois. Ainsi prenons
comme exemple uniquement le modèle POTI. On applique au modèle
POTI les trois approches de prévision (récursive, roulante 5 ans
et roulante 10 ans). On a alors trois binômes (modèle-approche)
à comparer. Ce sont les binômes (modèle-approche)
POTI-recursive, POTI-roulante 5ans, POTI-roulante 10ans. Par la suite, pour
chaque année,
4 Ces 29 moyennes annuelles de U de Theil serviront
aussi pour le calcul du score IPM du paragraphe suivant.
33
on évalue avec chaque binôme
(modèle-approche), les prévisions de 12 horizons (4 horizons pour
les fréquences trimestrielles). On obtient 12 valeurs de U de Theil par
année, pour chaque binôme (modèle-approche). On calcule
alors la moyenne annuelle de ces 12 valeurs de U de Theil (moyenne de 4 valeurs
pour les fréquences trimestrielles). Puisque l'échantillon de
prévision total comporte 29 années, on doit alors calculer 29
moyennes annuelles de U de Theil4, pour chacun des trois
binômes c'est-à-dire pour chacune des trois approches de
prévision du modèle POTI. Par la suite, on compare, année
par année, les moyennes annuelles de U de theil des trois approches du
modèle POTI. On dénombre enfin sur les 29 années, le
nombre d'années durant lesquelles chaque approche du modèle POTI
obtient la moyenne annuelle de U de Theil la plus petite. Chaque approche du
modèle POTI obtient ainsi son score pour l'Indicateur de Performance par
Approche (IPA). Puisqu'il y a trois approches de prévision pour le
modèle POTI, alors on obtient trois scores IPA. On compare alors ces
trois scores IPA. La meilleure approche de prévision pour le
modèle POTI est celle qui obtient la plus grande valeur de IPA. Cette
plus grande valeur de IPA est donc de fait le meilleur score IPA du modele
POTI.
On reprend la même démarche pour les trois autres
modèles (PPA, MF et PE). Pour chaque modèle on déterminera
la meilleure approche de prévision. On déterminera donc trois
autres meilleurs score IPA.
IPM : c'est l'Indicateur de Performance de Modèle. Il
permet de déterminer le meilleur modèle. Il est aussi obtenu
à partir des valeurs de U de Theil, dans notre étude. Cet
indicateur est plus général car il compare à la fois tous
les quatre modèles empiriques (POTI, PPA, MF et PE) auxquels sont
appliqués les trois approches de prévision (récursive,
roulante 5 ans, roulante 10ans). On a donc douze éléments ou
binômes à comparer à la fois. Chaque binôme est
constitué d'un modèle auquel est
34
appliqué une approche de prévision. On calcule
les moyennes annuelles de U de Theil5 des douze binômes
(modèles-approche de prévision). Ensuite on les compare entre
elles. On dénombre ainsi pour chaque modèle et l'approche qui lui
est appliquée, le nombre d'années durant lesquelles ce
modèle et cette approche ont la plus petite moyenne annuelle de U de
Theil. C'est leur score IPM. On aura au total douze scores IPM à
déterminer. Le modèle-approche le plus performant de
manière générale est celui qui détient la plus
grande valeur IPM. C'est aussi de fait le meilleur modèle.
5 Pour le calcul des moyennes, on procède
comme avec l'indicateur IPA de la section précédente. Ces
moyennes annuelles de U de Theil sont en fait identiques à celles
calculées dans le cas du score IPA.
Figure 4.1 Graphiques des variables de l'étude
CHAPITRE IV
PRÉSENTATION ET ANALYSE DES RÉSULTATS
EMPIRIQUES À LA
FRÉQUENCE MENSUELLE
Ce chapitre présente les principaux résultats
empiriques obtenus avec les variables à la fréquence
mensuelle.
4.1 Analyse graphique et statistiques descriptives en
fréquence mensuelle
4.1.1 Variable expliquée LS 1 : la variation du taux
de change USD/CAD
La figure 4.1 montre les graphiques des variables de
l'étude. Le tableau 4.1 renferme les statistiques descriptives
associées à ces variables.

36
Sur les périodes 1976m01-1986m02, 1991m10-2002m01 et
2007m10-2009m03, les variations moyennes du taux de change sont respectivement
0.27, 0.29, 1.27. Ces
Tableau 4.1 Statistiques
descriptives(fréquences mensuelles)
|
Variables
|
Moy
|
Ecar-T
|
skew
|
Kurt
|
P1
|
P4
|
|
0.051
|
1.970
|
0.797
|
9.69
|
-0.05
|
0.114
|
|
1.039
|
1.565
|
0.406
|
3.121
|
0.848
|
0.393
|
|
5.065
|
4.392
|
0.298
|
1.886
|
0.982
|
0.918
|
|
-230.07
|
14.405
|
-0.83
|
3.061
|
0.980
|
0.910
|
|
-11.548
|
6.172
|
0.286
|
2.611
|
0.868
|
0.612
|
|
-15.584
|
11.992
|
-0.474
|
2.456
|
0.954
|
0.835
|
|
-239.17
|
16.804
|
-0.071
|
1.756
|
0.931
|
0.793
|
|
6.506
|
0.571
|
0.488
|
2.006
|
0.987
|
0.932
|
|
5.486
|
0.268
|
0.575
|
2.493
|
0.974
|
0.879
|
Notes : le nombre d'observations est 468. P
représente les coefficients d'autocorrélation.
La variable . Oscille autour de zéro, mais avec une
volatilité variable. Les
variations du taux de change se font avec une fréquence
importante mais ont une amplitude relativement réduite sur la
période de janvier 1976 à janvier 2000. La moyenne de la
série entière est 0.05 avec un écart-type de 1.97 qui
traduit une dispersion peu importante. Cette série n'a pas une
distribution normale.
37
moyennes positives traduisent une hausse du taux de change
USD/CAD. Par conséquent, il s'est produit une dépréciation
du dollar canadien par rapport à la devise américaine. Sur les
périodes 1986m02-1991m10, 2002m3-2007m10, 2009m3-2011m04, les variations
moyennes du taux de change sont respectivement -0.32, - 0.68, -0.98. Ces
moyennes négatives traduisent une baisse du taux de change USD/CAD, soit
une appréciation relative du dollar canadien.
4.1.2 Variables explicatives :
Toutes les variables explicatives sont
caractérisées par des mouvements importants à la hausse
comme à la baisse.
La variable i - i' mesure le différentiel des taux
d'intérêt entre le Canada et les États-Unis. Sur la figure
4.1, ce différentiel affiche des valeurs positives mais qui
décroissent de janvier 1976 à octobre 1978. Cela s'explique par
le fait que les taux d'intérêts canadiens sont supérieurs
aux taux américains au début. Mais par la suite les taux
d'intérêt américains augmentent plus vite, réduisant
ainsi le différentiel. Après cette période, c'est une
brusque tendance à la baisse. En septembre et octobre 2008, une hausse
brusque des taux d'intérêts américains explique les valeurs
négatives du différentiel. La moyenne de la variable est 1.04 et
son écart-type est 1.56. Le différentiel des taux
d'intérêt est donc moins volatil que la variation de taux de
change ( Ls +1).
La variable p - p' de la figure 4.1 représente la
différence logarithmique de niveau de prix entre le Canada et les
États-Unis (2010=100). Ce différentiel des niveaux de prix
affiche, en grande partie, des valeurs positives de 1976 à octobre 2007.
Cela est dû au fait que le niveau des prix est en général
plus élevé au Canada. Dans la période de l'année
2008, il y a une importante hausse des prix aux États-Unis. Cela
explique les valeurs négatives du différentiel à cette
période. La moyenne est 5.065 et l'écart-
38
type est 4.392. Le différentiel des prix est donc plus
volatil que la variation de taux de change.
La variable est la différence logarithmique
d'agrégats monétaires (M2) entre
le Canada et les États-Unis. Sur la figure 4.1, toutes
les valeurs de cette variable sont négatives. Cela s'explique par le
fait que la masse monétaire des États-Unis est plus importante
que celle du Canada. Mais l'accroissement de la masse monétaire au
Canada réduit le différentiel. Avec un écart-type de
14.405, le différentiel d'agrégats monétaires est plus
volatil que la variation du taux de change.
La variable représente la différence
logarithmique des indices de la production
industrielle entre le Canada et les États-Unis
(2010=100). Les valeurs de cette variable sont en grande partie
négatives. Cela est dû à l'indice de la production
industrielle des États-Unis qui est plus élevé que celui
du Canada. Cette variable est plus volatile que la variation du taux de change
avec un écart-type de 6.172.
La variable représente la variable fondamentale pour le
modèle de la
parité des pouvoirs d'achat (PPA). Elle est en grande
partie négative. Cette variable est plus volatile que la variation du
taux de change avec un écart-type de 11.992.
La variable représente la variable fondamentale pour
le
modèle financier (MF). Elle est négative. Cette
variable est plus volatile que la variation du taux de change avec un
écart-type de 16.804.
Les variables et représentent respectivement l'indice
des prix (1972=100) de
l'énergie et l'indice des prix des produits de base
sauf l'énergie. Ces deux variables ont des allures proches. Elles ont
une tendance à la hausse.
39
La valeur critique du test ADF à 5% est -2.867/ La
valeur asymptotique critique du test KPSS est 0.463/ La deuxième colonne
indique le nombre de retards dans l'équation empirique pour le test
ADF.
4.2 Tests de stationnarité et analyse des
régressions à la fréquence mensuelle
4.2.1 Tests de stationnarité
Les tests de Dickey Fuller Augmenté ont été
appliqués aux variables pour vérifier la la présence de
racines unitaires. Le test de KPSS a été appliqué pour
tester la
|
stationnarité.
Tableau 4.2 Tableau des Tests ADF et KPSS
à niveau (fréquence mensuelle)
|
|
Variables
|
Nombre de retards
|
Adf-t
|
Kpss-
|
résultat
|
|
11
|
-5.148
|
0.165
|
stationnaire
|
|
6
|
-2.607
|
0.76
|
Non stationnaire
|
|
16
|
-1.233
|
0.682
|
Non stationnaire
|
|
14
|
-2.514
|
1.446
|
Non stationnaire
|
|
12
|
-1.900
|
0.622
|
Non stationnaire
|
|
1
|
-1.886
|
0.365
|
Non stationnaire
|
|
3
|
-1.695
|
0.925
|
Non stationnaire
|
|
16
|
-1.631
|
1.679
|
Non stationnaire
|
|
10
|
-1.520
|
2.064
|
Non stationnaire
|
40
. (4.4)
Le test ADF et le test KPSS permettent de conclure que la
variable expliquée
est stationnaire alors que les variables explicatives ne sont pas
stationnaires. Cependant, les différences premières des variables
explicatives sont stationnaires (voir Appendice A, Tableau A.2, ).
4.2.2 Modifications des modèles initiaux
Rappelons que la représentation générale
initiale des trois modèles (POTI, PPA, MF)
La variable dépendante ( ) est stationnaire I(0). La
variable explicative ( est
I(1) alors que sa différence première est I(0). est
donc stationnaire. Le
modèle général initial sera alors
modifié en utilisant la différence première (
des
variables explicatives. De même on utilisera la différence
première des variables qui
mesurent l'énergie ( .
4.2.2.1 Modèle construit autour de la
parité ouverte des taux d'intérêt (POTI modifié)
. (4.1)
4.2.2.2 Modèle construit autour de la
parité du pouvoir d'achat (PPA modifié)
. (4.2)
4.2.2.3 Modèle construit autour des fondamentaux
financiers (MF modifié)
. (4.3)
4.2.2.4 Modèle construit autour du prix de
l'énergie (PE modifié)
41
4.2.3 Analyse des estimations MCO des modèles
Rappelons que Engel et West (2005) montrent analytiquement que
dans un modèle de valeur actualisée avec des anticipations
rationnelles, le taux de change suit une marche aléatoire. Ainsi,
étant donné que le taux de change a un comportment bien
approximé par une marche aléatoire, il n'est pas étonnant
en soi qu'il reste relativement peu de variations à expliquer. Par
conséquent dans cette section, nous vérifions s'il existe un
contenu informationnel révélé par des variations dans les
variables explicatives des modèles de l'étude.
Les résultats des estimations des quatre
modèles6 de taux de change sont compilés dans le
tableau 4.3 à la section suivante. Il ressort de ce tableau que chaque
modèle (POTI, PPA et MF modifiés) a sa constante estimée (
co) qui est différente de zéro et positive. En plus, le signe de
la pente (f.?) estimée n'est pas identique pour tous les modèles.
Enfin, les modèles étudiés ont tous des pouvoirs
explicatifs faibles comme ce fut le cas de l'étude des auteurs James,
Marsh et Sarno (2012)7.
4.2.3.1 Analyse des estimations MCO du modèle
POTI modifié
Le modèle POTI modifié a un coefficient co
positif et égale à 0.29. Ce coefficient est statistiquement
significatif à 1%. Conformément aux prédictions du
modèle POTI, le second coefficient ( f.?) est négatif et
égale à -0.35. Il en découle qu'une variation positive du
différentiel de taux d'intérêt tend à induire une
appréciation de la monnaie canadienne par rapport au dollar
américain ( soit une baisse du taux de change défini comme le
nombre de dollar canadien pour un dollar américain).
6 POTI: Parité ouverte des taux
d'intérêt. PPA : Parité des pouvoirs d'achats. MF :
modèle financier. PE : modèle avec prix de l'énergie.
7 Précisons que ces auteurs n'ont pas fait
les tests de stationnarité. La présence de racine unitaire dans
les variables nous a amené à exprimer les régresseurs en
première différence.
42
8 Les chiffres entre parenthèses sont les
écarts-types estimés. Un, deux et trois astérisques
correspondent respectivement à des seuils de significativité de
1%, 5% et 10%.
Tableau 4.3 Estimations MCO des modèles
(fréquence mensuelle)
|
Modèles Coef8.
|
POTI
|
PPA
|
MF
|
PE
|
|
0.29*
|
0.32*
|
0.29*
|
0.31*
|
|
( 0.096)
|
(0.117)
|
(0.10)
|
(0.134)
|
|
-0.35**
|
0.15***
|
0.016
|
|
|
|
|
|
(4.821)
|
|
(0.158)
|
(0.082)
|
(0.06)
|
|
|
|
|
|
(6.273)
|
|
0.037
|
0.024
|
0.0007
|
0.0002
|
*significatif à 1%, ** : significatif à 5%; ***
: significatif à 10%;
Période d'estimation : janvier 1976- décembre
1985; Nombre d'observations : 120
4.2.3.1 Analyse des estimations MCO du modèle
PPA modifié
Pour le modèle PPA, le coefficient égale 0.32.
Celui-ci est positif et significatif à 1%. Le second coefficient est de
0.15.et significatif. à 10%. Une variation positive
de la variable explicative du modèle ( tend à une
dépréciation de la
monnaie canadienne par rapport au dollar
américain. Ce résultat est aussi conforme aux prédictions
du modèle PPA.
43
4.2.3.2 Analyse des estimations MCO du modèle MF
modifié
Pour le modèle MF, le coefficient est de 0.29. Il est
positif et significatif à 1%. Le second coefficient est de 0.016. Une
variation positive de la variable explicative du
modèle , tend à une dépréciation
de la monnaie
canadienne par rapport au dollar américain. Cela est
conforme aux prédictions du
modèle MF. Notons toutefois que le coefficient n'est
pas statistiquement
significatif.
4.2.3.3 Analyse des estimations MCO du modèle PE
modifié
Pour le modèle PE modifié, le coefficient est de
0.31. Ce coefficient est positif et
significatif à 1%. Le coefficient est égale
à -0.23 et .est égale à -0.959. Une
variation positive
de ces deux variables explicatives du modèle tend à une
appréciation de la monnaie canadienne par rapport au dollar
américain. Cependant les
coefficients et ne sont pas statistiquement significatifs.
4.3 Analyse préliminaire de la précision
des modèles
Ce paragraphe préliminaire étudie la
précision des modèles POTI, PPA, MF et PE auxquels sont
appliquées chacune des trois approches de prévision
(récursive, roulante 5 ans, roulante 10 ans). Nous analysons alors les
erreurs de prévision de ces modèles et approches. Une attention
est portée sur l'ampleur des erreurs de prévision autour de
l'année de la crise financière (2008). Pour cela, nous utilisons
comme critère la racine carrée de l'erreur quadratique moyenne
(REQM). L'échantillon de prévision de l'étude est
1986-2014., soit 29 années. Pour chaque année (sur la figure
4.2), les prévisions sont évaluées sur douze horizons
(h=1,2,...,12). Or, pour chaque horizon, nous calculons une valeur de REQM. Par
conséquent, chaque année comporte douze valeurs de REQM. Pour
tout l'échantillon de prévision (29 années), nous obtenons
une serie de REQM avec 348 observations (12*29). Ainsi en effectuant des
prévisions à l'aide d'un modèle et une approche
donnés, nous
44
construisons une série de REQM comportant 348
observations sur la période 19862014. Puisqu'à chaque
modèle sont appliquées trois approches de prévision, nous
construisons alors trois séries de REQM à partir d'un
modèle et des trois approches. (voir figure 4.2).

Notes: Chaque année comporte 12 horizons. Pour
chaque horizon est calculée une valeur de REQM. Ainsi chaque
année comporte 12 valeurs de REQM. Pour tout l'échantillon de
prévision (1986-2014), chaque série de REQM comporte 348
observations.
Figure 4.2 Séries REQM des modèles
et approches
Pour tous les quatre modèles (POTI, PPA, MF, PE
modifiés) et pour toutes les trois approches (récursive, roulante
5 ans, roulante 10 ans), les graphiques sont presqu'identiques. Les trois
premières années (1986-1988) enregistrent des valeurs
élevées de REQM. Ensuite ces valeurs baissent de façon
importante. Cependant, en 2008, les valeurs sont élevées. Cette
hausse débute déjà quelques années avant 2008 et
continue encore pendant les années après.
Figure 4.3 Séries U de Theil du
modèle POTI modifié par approche et horizon
45
Nous pouvons alors affirmer que pendant la crise
financière, les performances prévisionnelles des modèles
et approches ont baissé avec une augmentation des erreurs de
prévision.
4.4 Performance prévisionnelle des
modèles; analyse du critère U de Theil
Cette section analyse les performances des modèles et
approches de prévision en considérant chacun des douze horizons
de prévision. Le modèle de référence est la marche
aléatoire. Le critère de comparaison est le U de Theil. Ainsi les
modèles et approches sont plus performants que la marche
aléatoire lorsque les valeurs de U de Theil sont inférieures
à l'unité. L'échantillon de prévision est de
janvier 1986 à décembre 2014. Il sera subdivisé en deux ou
trois parties selon les modèles. Sur chaque partie, on
déterminera, pour un modèle donné, l'approche qui performe
le mieux. Précisons que l'approche la plus performante est celle dont la
série de U de Theil a les valeurs les plus faibles.
4.4.1 Modèle POTI modifié

46
Les trois séries (récursive, roulante 5 ans,
roulante 10 ans) du modèle POTI modifié font mieux que la marche
aléatoire sur les horizons h = 1, 2, 3, 4, 5, 6, 7, 8 et 12. À
ces horizons, on observe des valeurs de U de Theil inférieures à
l'unité sur tout l'échantillon de pévision (1986-2014).
Ces valeurs de U de Theil sont comprises entre 0.67 et 0.94. Cela signifie que
de 1986 à 2014, le modèle POTI modifié bat la marche
aléatoire avec un score compris entre 33% et 6%. Par contre sur les
horizons h= 9, 10, 11, le modèle POTI modifié ne bat pas toujours
la marche aléaoire. En effet pendant la période de 1986 à
1988, les trois séries affichent des valeurs de U de Theil
supérieures à l'unité. Ainsi pour h = 9 et en 1986, les
trois séries ont des valeurs avoisinant 1.33, soit le modèle POTI
modifié fait 33% pire que la marche aléatoire. Pour h=10 et
pendant les années 1986, 1987 et 1988, les trois séries ont les
valeurs oscillant entre 1.02 et 1.34. Cela équivaut à une pire
performance du modèle POTI modifié de l'ordre de 2% à 34%.
Enfin pour h=11 de l'année 1987, les trois séries prennent des
valeurs comprises entre 1.03 et 1.056 soit une pire performance comprise entre
3% et 5.6 par rapport à la marche aléatoire
La comparaison des trois approches du modèle POTI
modifié permet de constater que leurs performances relatives sont
proches mais varient suivant des périodes de l'échantillon de
prévision. De janvier 1986 à décembre 1991, l'approche
roulante 5 ans est plus performante que les deux autres approches, au niveau
des horizons 5 à 12. Pour la période 1992-2008, c'est l'approche
récursive qui performe mieux sur tous les douze horizons. De 2009
à 2014, l'approche récursive se montre la plus performante, dans
la plupart des horizons c'est-à-dire dans les horizons 1 à 8.
4.4.2 Modèle PPA modifié
Les trois séries (récursive, roulante 5 ans,
roulante 10 ans) du modèle PPA modifié font mieux que la marche
aléatoire sur les horizons h = 2, 3, 4, 5, 6, 7, 8 et 12 (Figure 4.4).
À ces horizons, on observe des valeurs de U de Theil inférieures
à l'unité sur
Figure 4.4 Séries U de Theil du
modèle PPA modifié par approche et horizon
47
tout l'échantillon de pévision (1986-2014). Ces
valeurs de U de Theil sont comprises entre 0.67 et 0.93. Cela signifie que de
1986 à 2014 et pour les horizons 2 à 8 et 12, le modèle
PPA modifié bat la marche aléatoire avec un score compris entre
33% et 7%. Toutefois sur les horizons h= 1, 9, 10 et 11, il y a des
années où le modèle PPA modifié ne bat pas la
marche aléaoire . Ainsi pour h= 1 et en 1986, les trois séries de
PPA modifié ont des valeurs autour de 1.02, soit un pire score d'environ
2% par rapport à la marche aléatoire. Pour h=9 et en 1986, les
trois séries ont des valeurs avoisinant 1.35. Cela équivaut
à une mauvaise performance avoisinant 35%, par rapport à la
marche aléatoire. Pour h=10, les trois séries ont des valeurs
oscillant entre 1.007 et 1.36 pendant la période 1986-1989 soit un
mauvais score de 0.7% à 36%. Enfin pour h = 11, les trois séries
ont des valeurs comprises entre 1.03 et 1.06, en 1987. Cela signifie que le
modèle PPA modifié fait pire à hauteur de 3% et 6% par
rapport à la marche aléatoire
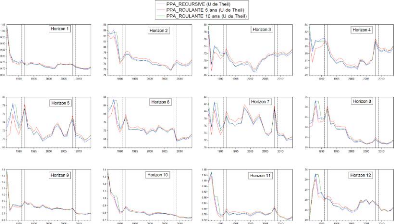
48
Les performances relatives des trois approches du
modèle PPA modifié sont proches et varient suivant des
périodes de l'échantillon de prévision. Ainsi de janvier
1986 à décembre 1991, l'approche roulante 5 ans est plus
performante que les deux autres approches, au niveau de tous les douze
horizons. Pour la période 1992-2008, les approches récursive et
roulante 10 ont des performances proches. Toutefois, de l'horizon 5 à
12, l'approche récursive est légèrement la meilleure.
Concernant la période 2009-2014, c'est l'approche récursive qui
se montre la plus performante, pour la plupart des horizons.
4.4.3 Modèle MF modifié
Les trois séries (récursive, roulante 5 ans,
roulante 10 ans) du modèle MF modifié font mieux que la marche
aléatoire sur les horizons h = 1, 2, 3, 4, 5, 6, 7, 8 et 12. À
ces horizons, on observe des valeurs de U de Theil inférieures à
l'unité sur tout l'échantillon de pévision (1986-2014).
Ces valeurs de U de Theil sont comprises entre 0.63 et 0.99. Cela signifie que
de 1986 à 2014 et pour les horizons 1, 2 à 8 et 12, le
modèle MF modifié bat la marche aléatoire avec un score
compris entre 37% et 1%.
49
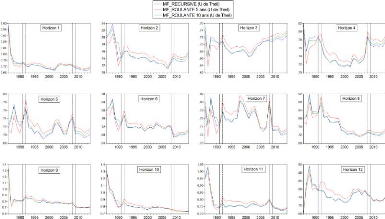
Figure 4.5 Séries U de Theil du
modèle MF modifié par approche et horizon
À l'opposé, sur les horizons h= 9, 10, 11, il y
a des années durant lesquelles le modèle MF modifié
performe moins bien que la marche aléaoire. C'est ainsi que pour h = 9,
les trois séries ont des valeurs avoisinant 1.30 en 1986. Pour h=10, les
trois séries ont des valeurs oscillant entre 1.012 et 1.30 durant les
années 1986, 19987 et 1988. Enfin pour h=11, les deux séries
relatives aux approches récursive et roulante 10 ans affichent
respectivement 1.027 et 1.03. Ainsi, pour les horizons h= 9, 10, 11 et sur la
période 1986-1988, le modèle MF modifié fait pire que la
marche aléatoire à hauteur de 3% à 30%.
Au niveau de la comparaison, on note que les performances
relatives des trois approches sont proches. Cependant, on remarque que pour la
période 1986-1991, l'approche roulante 5 ans a la meilleure performance
sur les douze horizons. Pour les périodes 1992-2008 et 2009-2014, on
note que l'approche récursive du modèle MF modifié fait
mieux que les deux autres approches dans la majorité des horizons.
50
4.4.4 Modèle PE modifié
Sur la figure 4.6, les trois séries (récursive,
roulante 5 ans, roulante 10 ans) du modèle PE modifié font mieux
que la marche aléatoire sur les horizons h = 2, 3, 4, 5, 6, 7, 8 et 12.
À ces horizons, on observe des valeurs de U de Theil comprises entre
0.65 et 0.99 sur tout l'échantillon de pévision (1986-2014). Le
modèle PE modifié bat alors la marche aléatoire entre 1%
et35%. Par contre sur les horizons h= 1, 9, 10 et 11, le modèle PE
modifié ne bat pas toujours la marche aléaoire. Ainsi pour h = 1,
la série concernant l'approche roulante 5 ans a une valeur de U de Theil
égale à 1.13 en 1986. Pour h = 9, les trois séries ont des
valeurs avoisinant 1.35 en 1986. Pour h=10, les trois séries ont des
valeurs qui oscillent entre 1.002 et 1.36, dans la période 19861988.
Enfin pour h=11, les trois séries ont des valeurs comprises entre 1.004
et 1.047. Ainsi le modèle PE modifié fait pire que la marche
aléatoire à 0.2%-35%.
- Les modèles PPA et PE modifiés font pire que
la marche aléatoire pour les horizons 1, 9, 10 et 11.
51
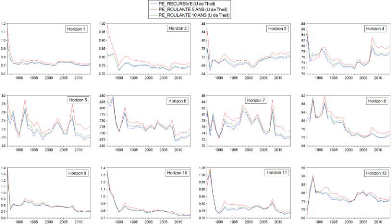
Figure 4.6 Séries U de Theil du
modèle PE modifié par approche et horizon
La comparaison des trois approches sur les périodes de
l'échantillon de prévision nous révèle que leurs
performances relatives sont proches. Toutefois, l'approche récursive
s'avère la plus performante sur les douze horizons durant toute la
durée de l'échantillon de prévision (1986-2014).
Au terme de ces sous-sections, l'étude par horizon des
modèles POTI, PPA, MF et PE modifiés, selon le critère U
de Theil, permet de remarquer que les performances relatives des modèles
étudiés sont proches. Cependant, on note les différences
suivantes :
- pour les horizons de 1 à 8 et l'horizon 12 les
modèles POTI et MF modifiés font mieux que la marche
aléatoire. Cependant pour les horizons 9, 10, 11, ces modèles
font pire que la marche aléatoire.
52
-Pour les modèles POTI, PPA et MF modifiés,
l'approche de prévision roulante 5 ans est la plus performante durant la
période 1989-1991. Quant au modèle PE modifié, sur cette
période (1986-1991), c'est l'approche récursive qui est la plus
performante.
Pour tous les modèles, l'approche récursive est
plus performante que les approches roulante 5 ans et roulante 10 ans pendant la
majeur partie de la période 1992-2014.
Dans la sous-section qui suit, nous recherchons le meilleur
modèle pour la période 1986-1991. Ensuite nous déterminons
le meilleur modèle pour la période 1992-2014.
4.4.5 Les meilleurs modèles selon le
critète U de Theil
4.4.5.1 Le meilleur modèle pour la
période 1986-1991
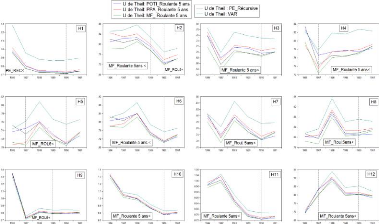
Figure 4.7 Séries U de Theil de
l'approche roulante 5 ans et récursive par modèle
(1986-1991)
53
La figure 4.7 affiche les séries de la statistique U de
Theil obtenues avec l'approche roulante 5 ans appliquée aux trois
modèles que sont MF, POTI, PPA modifiés. Pour le modèle PE
modifié, c'est l'approche récursive qui lui est appliquée.
Le VAR a fait l'objet d'une prévision statique. La période de
comparaison est de janvier 1986 à décembre 1991, pour les douze
horizons de prévision. Le modèle MF modifié se distingue
par ses meilleures performances prévisionnelles. En effet sur les
horizons h = 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 et 12 le modèle MF
modifié (avec l'approche roulante 5 ans) est le plus performant. Le
modèle MF modifié auquel est appliquée l'approche roulante
5 ans permet d'avoir les séries U de Theil les plus basses. Les valeurs
de ces séries sont les plus proches de la valeur nulle. Cela signifie
que le modèle MF modifié auquel on applique l'approche roulante 5
ans permet d'avoir les plus faibles erreurs lors des prévisions.
Au total, selon la statistique U de Theil, pour la
période initiale (1986-1991) de l'échantillon de
prévision, le meilleur modèle est le modèle
MFmodifié auquel est appliquée l'approche roulante 5 ans.
4.4.5.2 Le meilleur modèle pour la
période 1992-2014
La figure 4.8 présente les séries de la
statistique U de Theil obtenues avec le VAR et avec l'approche récursive
appliquée aux quatre modèles que sont MF, POTI, PPA, PE
modifiés. La période de comparaison est de janvier 1992 à
décembre 2014, pour les douze horizons de prévision.

54
- pour la période 1986-1991, le meilleur modèle
est le modèle MF modifié auquel est appliquée l'approche
roualnte 5 ans.
Figure 4.8 Séries U de Theil de
l'approche récursive par modèle (1992-2014)
La figure 4.8 montre que les différences de
performances prévisionnelles ne sont pas très grandes. Cependant,
l'analyse graphique des douze horizons nous permet de constater que pour la
période 1992-2010 et sur l'ensemble des douze horizons, c'est l'approche
récursive appliquée au modèle MF modifié qui est
meilleure. Enfin pour la période 2010-2014, l'approche récursive
appliquée au modèle POTI performe particulièrement sur 5
horizons.
À la fin de la section 4.4 consacrée à
l'analyse de la performance prévisionnelle des modèles POTI, PPA,
MF et PE modifiés, sur la base du critère U de Theil, nous
remarquons que les modèles étudiés ont des performances
relatives proches. Cependant, nous notons que:
55
-pour la période 1992-2014, le meilleur modèle
est le modèle MF modifié auquel est appliquée l'approche
récursive.
-pour les horizons h=1, 2, 3, 4, 5, 6, 7, 8 et 12, les
performances prévisionnelles des modèles MF et POTI
modifiés sont meilleures à celle de la marche aléatoire.
Ces modèles font pire sur les horizons 9, 10 et 11.
- Les modèles PPA et PE modifiés battent la
marche aléatoire sur les horizons h= 2, 3, 4, 5, 6, 7, 8 et 12 mais ils
font pire sur horizons 1, 9, 10 et 11.
4.5 Performance prévisionnelle des
modèles: analyse du critère ÄREQM
La variation de la racine carrée de l'erreur
quadratique moyenne (ÄREQM) est le critère utilisé pour
l'étude des performances des modèles et leurs trois approches de
prévision. La marche aléatoire demeure la
référence. Ainsi une valeur positive de la statistique ÄREQM
indique que le modèle (auquel est appliquée une approche de
prévision) fait mieux que la marche aléatoire. Nous disposons de
douze horizons pour l'analyse. L'échantillon de prévision est de
janvier 1986 à décembre 2014. Il sera subdivisé en deux ou
trois parties selon les modèles. Sur chaque partie, on
déterminera, pour un modèle donné, l'approche qui performe
le mieux. Notons que l'approche la plus performante est celle dont les valeurs
de ÄREQM sont les plus élevées.
4.5.1 Le modèle POTI modifié
Au niveau des horizons h = 1, 2, 3, 4, 5, 6, 7, 8 et 12 de la
figure 4.9, les trois approches (récursive, roulante 5 ans, roulante 10
ans) appliquées au modèle POTI modifié font mieux que la
marche aléatoire. En effet, pour ces horizons, toutes les trois
séries de ÄREQM sont positives.

56
Figure 4.9 Séries ÄREQM du
modèle POTI modifié par approche et horizon
Cependant, sur les horizons h= 9, 10, 11, le modèle
POTI modifié ne fait pas toujours mieux que la marche aléaoire.
Cela s'observe pendant la période 1986-1988. Ainsi pour h = 9, les trois
séries ont des valeurs négatives en 1986. Pour h=10, les trois
séries ont des valeurs négatives en 1986,1987 et 1988. Enfin pour
h=11, les trois séries ont des valeurs négatives en 1987.
En comparant les trois approches du modèle POTI
modifié entre elles, on constate que leurs performances relatives sont
aussi proches. Cependant, quelques différences existent suivant des
périodes de l'échantillon de prévision. Ainsi de janvier
1986 à décembre 1990, l'approche roulante 5 ans est plus
performante que les deux autres approches, au niveau de tous les douze
horizons. Ensuite c'est l'approche récursive qui se révèle
la plus performante de 1992 à 2014, dans la plupart des horizons.
Figure 4.10 Séries ÄREQM du
modèle PPA modifié par approche et horizon
57
Durant tout l'échantillon de prévision, les
courbes présentent une tendance générale à la
hausse, quelque soit l'horizon. Cela décrit le fait que les
modèles sont moins performants à court terme. Cependant à
moyen et long terme , les performances des modèles
s'améliorent.
4.5.2 Le modèle PPA modifié
Les horizons h = 2, 3, 4, 5, 6, 7, 8 et 12 de la figure 4.10
montrent que les trois approches appliquées au modèle PPA
modifié font mieux que la marche aléatoire. Toutes les trois
séries de ÄREQM sont en effet positives pour ces horizons. Par
contre, sur les horizons h= 1, 9, 10 et 11, de la période 1986-1988, le
modèle PPA modifié ne fait pas toujours mieux que la marche
aléaoire. Ainsi en 1986, sur h = 1 et 9, les trois séries ont des
valeurs négatives, comprises entre -0.49 et -0.02. Pour h=10, de 1986
à 1988, les trois séries ont les valeurs négatives
oscillant entre -0.12 et -0.01. Enfin pour h=11 de l'année 1987, les
trois séries prennent des valeurs négatives comprises entre -0.09
et -0.045.

58
En comparant les trois approches du modèle PPA
modifié, on constate que leurs performances relatives sont proches.
Cependant, quelques nuances existent en fonction des périodes de
l'échantillon de prévision. Ainsi, de janvier 1986 à
décembre 1991, l'approche roulante 5 ans est plus performante que les
deux autres approches, au niveau de tous les douze horizons. Pour la
période 1992-2008 aucun modèle ne domine clairement. Cependant
à partir de 2009, l'approche récursive se montre la plus
performante, dans la plupart des horizons.
Durant tout l'échantillon de prévision, les
modèles sont moins performants à court terme. Cependant à
moyen et à long terme, les performances des modèles
s'améliorent avec des courbes qui ont une tendance à la
hausse.
4.5.3 Le modèle MF modifié
L'oservation des horizons h = 1, 2, 3, 4, 5, 6, 7, 8 et 12 de
la figure 4.11 permet de constater que les trois approches appliquées au
modèle MF modifié battent la marche aléatoire. Toutes les
trois séries de ÄREQM affichent des valeurs positives pour ces
horizons. À l'opposé, sur les horizons h= 9, 10, 11, de la
période 1986-1988, le modèle MF modifié fait pire que la
marche aléaoire. Ainsi pour h = 9, les trois séries ont des
valeurs négatives en 1986, environ -0.40. Pour h=10, de 1986 à
1988, les trois séries prennent les valeurs négatives qui varient
entre -0.47 et -0.019. Enfin pour h=11 de l'année 1987, l'approche
récursive et l'approche roulante 10 ans affichent les valeurs
négatives qui sont respectivement -0.039 et -0.05.
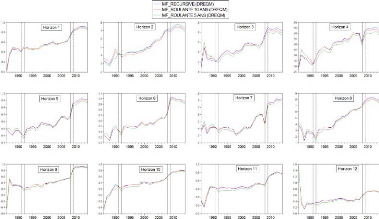
59
Figure 4.11 Séries ÄREQM du
modèle MF modifié par approche et horizon
En considérant les trois approches du modèle MF
modifié, on peut constater que leurs performances relatives sont
similaires, en général. Néanmoins, suivant des
périodes de l'échantillon de prévision, certaines
différences peuvent être notées. Ainsi de janvier 1986
à décembre 1991, l'approche roulante 5 ans est plus performante
que les deux autres approches, au niveau de tous les douze horizons. Pour la
période 19922008 aucun modèle ne domine clairement. Cependant
à partir de 2009, l'approche récursive se montre la plus
performante dans la plupart des horizons sauf les horizons h=10, 11, 12.
Les modèles sont moins performants à court
terme. Cependant à moyen et à long terme, les performances des
modèles s'améliorent avec des courbes qui ont une tendance
générale à la hausse.
60
4.5.4 Le modèle PE modifié
Les trois approches appliquées au modèle PE
modifié battent la marche aléatoire pour les horizons h = 2, 3,
4, 5, 6, 7, 8 et 12 (voir figure 4.12). À ces horizons, toutes les trois
séries de ÄREQM sont positives.
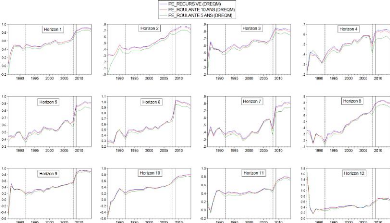
Figure 4.12 Séries ÄREQM du
modèle PE modifié par approche et horizon
Par contre, sur les horizons h= 1, 9, 10, 11, de la
période 1986-1988, le modèle PE modifié ne fait pas mieux
que la marche aléaoire. Ainsi pour h=1, l'approche roulante 5 ans a une
valeur négative de -0.17. Pour h = 9, les trois séries ont des
valeurs négatives en 1986, environ -0.5. Pour h=10, de 1986 à
1988, les trois séries prennent les valeurs négatives qui varient
entre -0.55 et -0.0036. Enfin pour h=11 de l'année 1987, les trois
approches affichent les valeurs négatives qui oscillent entre -0.068 et
- 0.0064.
61
Les trois approches du modèle PE ont leurs performances
relatives qui sont proches mais avec quelques nuances, suivant des
périodes de l'échantillon de prévision. Ainsi, aucune
approche ne s'impose clairement sur la totalité des douze horizons.
Cependant de 1992 à 2008, on note que l'approche récursive fait
légèrement mieux que les deux autres approche. De 2009 à
2014, l'approche récursive performe nettement mieux sur les horizons 1
à 8, mais légèrement mieux sur les horizons 9 à
12.
Les modèles sont moins performants à court
terme. Cependant à moyen et à long terme, les performances des
modèles s'améliorent avec des courbes qui ont une tendance
générale à la hausse. On note toutefois une exception au
niveau de l'horizon h=12 où la période 1986-1988 est
marquée par une forte décroissance des valeurs des
séries.
Au terme des sous- sections précédentes
consacrées à l'étude par horizon des modèles POTI,
PPA, MF, PE modifiés, sur la base du critère ÄREQM, nous
remarquons que les allures des séries issues des modèles sont
similaires, en général. Cependant, on note quelques
différences qui sont les suivantes :
- pour les horizons de 1 à 8 et l'horizon 12, les
modèles POTI et MF modifiés font mieux que la marche
aléatoire. Cependant pour les horizons 9, 10, 11, ces modèles
font pire que la marche aléatoire.
- les modèles PPA et PE modifiés font pire que
la marche aléatoire pour les horizons 1, 9, 10 et 11.
- sur la période 1986-1991, la meilleure approche est
l'approche roulante 5 ans appliquée aux modèles POTI, PPA, MF
modifiés. Cette approche fait mieux que les approches roulante 5 ans et
roulante 10 ans, pour les douze horizons.
62
- sur la période 1992-2014, c'est l'approche
récursive qui performe plus que les approches roulante 5 ans et roulante
10 ans.
Dans la sous-section qui suit, nous rechercherons selon le
critère ÄREQM, sur la période 1986-1991, le meilleur
modèle pour l'approche roulante 5 ans. Ensuite pour la période
1992-2014, nous rechercherons cette fois-là, le meilleur modèle
pour l'approche récursive.
4.5.5 Les meilleurs modèles selon le
critère ÄREQM
4.5.5.1 Le meilleur modèle pour la
période 1986-1991
La figure 4.13 affiche les séries de la statistique
ÄREQM obtenues avec le VAR et l'approche roulante 5 ans appliquée
aux modèles que sont MF, POTI, PPA, PE modifiés. La
période de comparaison est de janvier 1986 à décembre
1991, pour les douze horizons de prévision. Il y a premièrement
le modèle MF modifié qui se distingue par ses meilleures
performances prévisionnelles. Il est suivi par le modèle POTI
modifié.
63
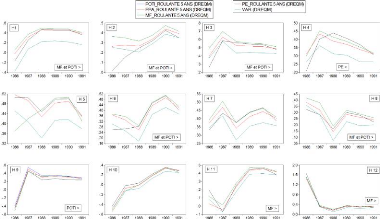
Figure 4.13 Séries ÄREQM :
l'approche roulante 5 ans par modèle (1986-1991)
En effet sur les horizons h = 1, 2, 3, 6 et 8, les
modèles MF et POTI modifiés ont les mêmes performances et y
sont simultanément les plus performants. En plus le modèle MF
domine seul sur les horizons 11 et 12 tandis que le modèle POTI
modifié domine seul l'horizon 9.
Au total, pour la période initiale (1986-1991) de
l'échantillon de prévision, le meilleur modèle est le
modèle MF modifié auquel est aplliquée l'approche roulante
5 ans. Il est plus performant que tous les autres modèles car il les
domine sur 7 horizons, h= 1, 2, 3, 6, 8, 11, et 12. Sur ces horizons, le
modèle MF modifié obtient les plus grandes valeurs de
ÄREQM.
64
Au total, sur l'ensemble de la période 1992-2014, le
meilleur modèle est le modèle MF modifié auquel est
appliquéel'approche récursive.
4.5.5.2 Le meilleur modèle pour la
période 1992-2014
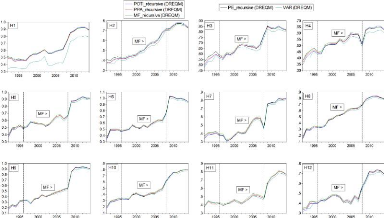
Figure 4.14 Séries ÄREQM de
l'approche récursive par modèle (1992-2014)
La figure 4.14 présente les séries de la
statistique ÄREQM obtenues avec le VAR et l'approche récursive
appliquée aux modèles que sont MF, POTI, PPA, PE modifiés.
La période de comparaison est de janvier 1992 à décembre
2014, pour les douze horizons de prévision. On remarque que dans
l'ensemble, les courbes se ressemblent. Cependant, le modèle MF
modifié affiche des performances prévisionnelles un peu
meilleures.
En effet sur onze horizons de la période 1996-2008, le
modèle MF modifié domine seul tous les autres modèles en
obtenant les plus grandes valeurs de la statistique ÄREQM. Sa courbe est
donc la plus haute.
65
Au terme de la section 4.5 consacrée à l'analyse
de la performance prévisionnelle des modèles POTI, PPA, MF, PE
modifiés, sur la base du critère ÄREQM, nous faisons le
constat que les séries ont des courbes qui se ressemblent, en
général. Néanmoins, certaines différences peuvent
être notées. Ce sont:
- pour la période 1986-1991, le meilleur modèle
est le modèle MF modifié avec l'approche roualnte 5 ans.
-pour la période 1992-2014, le meilleur modèle
est le modèle MF modifié avec l'approche récursive.
-pour les horizons h=1, 2, 3, 4, 5, 6, 7, 8 et 12, les
performances prévisionnelles des modèles MF et POTI
modifiés sont meilleures à celle de la marche aléatoire.
Ces modèles font pire sur les horizons 9, 10 et 11.
- Les modèles PPA et PE modifié battent la
marche aléatoire sur les horizons h= 2, 3, 4, 5, 6, 7, 8 et 12 mais il
fait pire sur horizons 1, 9, 10 et 11.
4.6 Performance prévisionnelle des
modèles :analyse du critère
La statistique est le critère utilisé pour
l'étude des performances des modèles et
leurs trois approches de prévision. Le modèle de
référence demeure la marche
aléatoire. Une valeur de la statistique qui est
positive et proche de un est
l'indication que le modèle (auquel est
appliquée une approche) est plus performant que la marche
aléatoire. L'analyse se fait suivant douze horizons, d'une part. D'autre
part, l'échantillon de prévision est subdivisé en deux ou
trois parties selon les modèles. Sur chacune des parties, on
déterminera, pour un modèle donné, l'approche
66
qui est la plus performante. Soulignons que l'approche la plus
performante est celle
dont la série affiche des valeurs de plus proches de
l'unité.
4.6.1 Le modèle POTI modifié
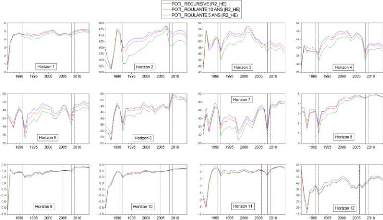
Figure 4.15 Séries du modèle POTI
modifié par approche et horizon
Les horizons h = 1, 2, 3, 4, 5, 6, 7, 8 et 12 de la figure
4.15 montrent que les trois approches appliquées au modèle POTI
modifié battent la marche aléatoire. Toutes les
trois séries de sont en effet positives pour ces
horizons et leurs valeurs tendent
vers 0.5, en général. Par
contre, sur les horizons h= 9, 10, 11, de la période 19861988, la marche
aléatoire fait mieux. Ainsi pour h = 9, les trois séries ont des
valeurs négatives en 1986, environ -0.85. Pour h=10, de 1986 à
1988, les trois séries ont les valeurs négatives oscillant entre
-0.80 et -0.04. Enfin pour h=11 de l'année 1987, les trois séries
prennent des valeurs négatives comprises entre -0.11 et -0.06.
67
La comparaison des trois approches du modèle POTI
modifié permet de constater que de janvier 1986 à décembre
1991, l'approche roulante 5 ans performe plus que les deux autres approches
pour les horizons 3 à 12. Pour la période de janvier 1992
à décembre 2008, l'approche récursive performe plus que
les deux autres
approches. au niveau de tous les douze
horizons. Pour la période 2009-2014, c'est encore l'approche
récursive qui domine sur tous les horizons sauf sur les horizons 9 et
10.
4.6.2 Le modèle PPA modifié
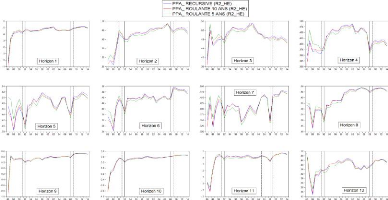
Figure 4.16 Séries du modèle PPA
modifié par approche et horizon
Les horizons h = 2, 3, 4, 5, 6, 7, 8 et 12 de la figure 4.16
permettent de constater que les trois approches appliquées au
modèle PPA modifié font mieux que la marche
aléatoire. Pour ces horizons, toutes les trois
séries de ont des valeurs positives.
Celles-ci avoisinent 0.4 en
moyenne, pendant le dernier quinquenat de l'échantillon de
prévision. Par contre, sur les horizons h= 1, 9, 10, 11, de la
période 1986-1988, le modèle PPA modifié ne fait pas
toujours mieux que la marche aléaoire. En effet, durant 1986, pour h =
1, 9, les trois séries ont des valeurs négatives comprises entre
- 0.9 et -0.37. Pour h=10, de 1986 à 1988, les trois séries ont
les valeurs négatives
68
oscillant entre -0.84 et -0.014. Enfin pour h=11 de
l'année 1987, les trois séries prennent des valeurs
négatives comprises entre -0.13 et -0.06.
Sur la période janvier 1986-décembre 1991, la
comparaison des trois approches du modèle PPA modifié permet de
constater que l'approche roulante 5 ans performe mieux que les deux autres
approches, au niveau de tous les douze horizons. Concernant la période
1992-2008, l'approche récursive et l'appoche roulante 10 ans ont des
performances proches. On remarque toutefois une légère
prééminence de l'approche récursive sur les horizons h =
2, 3, 4, 5, 6,, 11, 12. Pour la période 20092014, sur les huit premiers
horizons, l'approche récursive a une légere
supériorité de prévision.
4.6.3 Le modèle MF modifié
En observant les horizons h = 1, 2, 3, 4, 5, 6, 7, 8 et 12 de
la figure 4.17, cela permet de constater que les trois approches
appliquées au modèle MF modifié battent la marche
aléatoire. Toutes les trois séries de R E affichent
des valeurs positives pour ces horizons.
69

Figure 4.17 Séries
RIE du modèle MF modifié par approche
et horizon
À l'opposé, sur les horizons h= 9, 10, 11, de la
période 1986-1988, le modèle MF modifié fait pire que la
marche aléaoire. Ainsi pour h = 9, les trois séries ont des
valeurs négatives en 1986, environ -0.74. Pour h=10, de 1986 à
1988, les trois séries prennent les valeurs négatives qui varient
entre -0.70 et -0.026. Enfin pour h=11 de l'année 1987, l'approche
récursive et l'approche roulante 10 ans affichent les valeurs
négatives qui sont respectivement -0.07 et -0.05.
En considérant les trois approches du modèle MF
modifié, on peut constater que leurs performances relatives varient
suivant des périodes de l'échantillon de prévision. De
janvier 1986 à décembre 1991, C'est l'approche roulante 5 ans qui
est plus performante que les deux autres approches, au niveau de tous les douze
horizons. Pour la période 1992-2009, les approches récursives et
roulantes 10 ans ont des performances proches. On peut toutefois remarquer que
l'approche récursive a un léger avantage aux horizons h= 3, 5, 6,
8, 11, 12. De 2010 à 2014, l'approche
70
récursive se montre la plus performante dans la plupart
des horizons sauf les horizons h=9, 10, 11 et 12.
4.6.4 Le modèle PE modifié
Les trois approches appliquées au modèle PE
modifié battent la marche aléatoire pour les horizons h = 1, 2,
3, 4, 5, 6, 7, 8 et 12 (voir figure 4.18). À ces horizons, toutes les
trois séries de sont positives. Par contre, sur les
horizons h= 9, 10, 11, de la
période 1986-1988, le modèle PE
modifié ne fait pas mieux que la marche aléaoire. Ainsi pour h =
9, les trois séries ont des valeurs négatives en 1986, environ
-0.83. Pour h=10, de 1986 à 1988, les trois séries prennent les
valeurs négatives qui varient entre -0.84 et -0.005. Enfin pour h=11 de
l'année 1987, les trois approches affichent les valeurs négatives
qui oscillent entre -0.096 et -0.009.
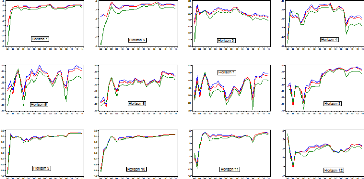
Sur la période janvier 1986-décembre 1991,
aucune approche ne domine nettement. Concernant la période 1992-2008,
l'approche récursive fait mieux que les autres
Figure 4.18 Séries du modèle PE
modifié par approche et horizon
La figure 4.19 affiche les séries de la statistique
obtenues avec le VAR et avec
l'approche roulante 5 ans appliquée aux modèles MF,
POTI, PPA, PE modifiés.
71
approches aux horizons h = 1, 2, 3, 4, 5, 6, 7, 8, 11, 12.
Pour la période 2009-2014, sur les huit premiers horizons, l'approche
récursive est encore meilleure.
Au terme des sous sections précédentes
consacrées à l'étude par horizon des modèles
POTI, PPA, MF, PE modifiés, sur la base du
critère , nous avons constaté ceci :
- pour les horizons de 1 à 8 et l'horizon 12 les
modèles POTI et MF modifiés font mieux que la marche
aléatoire. Cependant pour les horizons 9, 10, 11, ces modèles
font pire que la marche aléatoire.
- Les modèles PPA et PE modifiés font pire que
la marche aléatoire pour les horizons 1, 9, 10 et 11.
- Sur la période 1986-1991, l'approche roulante 5 ans
appliquée aux modèles POTI, PPA, MFmodifiés, fait mieux
que toutes les autres approches pour les douze horizons.
- Sur la période 1992-2014, c'est l'approche
récursive qui performe plus que les approches roulante 5 ans et roulante
10 ans dans l'ensemble.
Dans la sous-section suivante, nous déterminerons, sur
la période 1986-1991, le meilleur modèle pour l'approche roulante
5 ans. Ensuite pour la période 1992-2014, nous rechercherons aussi le
meilleur modèle mais pour l'approche récursive.
4.6.5 Les meilleurs modèles selon le
critère
4.6.5.1 Le meilleur modèle pour la
période 1986-1991
72
La période de comparaison est de janvier 1986 à
décembre 1991, pour les douze horizons de prévision.

Figure 4.19 Séries de l'approche roulante
5 ans par modèle (1986-1991)
Le modèle MF se distingue par ses meilleures performances
prévisionnelles. En effet sur les horizons h = 1, 2, 3, 6, 8, 9, 10, 11
et 12 le modèle MF est le plus performant. Le modèle MF auquel
est appliquée l'approche roulante 5 ans permet d'avoir les
séries les plus élevées. Les valeurs de ces
séries sont les plus proches de l'unité.
Cela signifie que le
modèle MF auquel on applique l'approche roulante 5 ans permet
d'avoir les plus faibles erreures lors des prévisions. Au
total, selon la statistique ,
pour la période initiale (1986-1991) de
l'échantillon de prévision, le meilleur modèle est le
modèle MF auquel est aplliquée l'approche roulante 5 ans.
73
Au total, sur l'ensemble de la période 1992-2014, le
meilleur modèle est le modèle MF auquel est appliquée
l'approche récursive.
4.6.5.2 Le meilleur modèle pour la
période 1992-2014
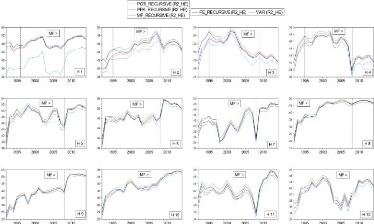
Figure 4.20 Séries de l'approche
récursive par modèle (1992-2014)
La figure 4.20 présente les séries de la
statistique obtenues avec le VAR et avec
l'approche récursive appliquée aux
modèles que sont MF, POTI, PPA, PE. La période de comparaison est
de janvier 1992 à décembre 2014, pour les douze horizons de
prévision. Le modèle MF se distingue par ses meilleures
performances prévisionnelles. En effet sur les douzes horizons de la
période 1992-2014, le modèle MF domine seul tous les autres
modèles en obtenant les plus grandes valeurs de la
statistique . Sa courbe est donc la plus haute.
74
Au terme de la section 4.6 consacrée à l'analyse
de la performance prévisionnelle des modèles POTI, PPA, MF, PE
modifiés, sur la base du critère R E
, nous observons que :
- pour la période 1986-1991, le meilleur modèle
est le modèle MF modifié avec l'approche roualnte 5 ans.
-pour la période 1992-2014, le meilleur modèle
est le modèle MF modifié avec l'approche récursive.
-pour les horizons h=1, 2, 3, 4, 5, 6, 7, 8 et 12, les
performances prévisionnelles des modèles MF et POTI
modifiés sont meilleures à celle de la marche aléatoire.
Ces modèles font pire sur les horizons 9, 10 et 11.
- Les modèles PPA et PE modifiés battent la
marche aléatoire sur les horizons h= 2, 3, 4, 5, 6, 7, 8 et 12 mais ils
font pire sur horizons 1, 9, 10 et 11.
4.7 Performance prévisionnelle des
modèles : analyse des critères IPA et IPM
La description de ces deux critères est faite à
la section 3.3.3.2 du chapitre III. Nous rappelons que le critère IPA
permet de déterminer la meilleure approche de prévision pour un
modèle donné. Le critère IPM, permet de déterminer
le meilleur modèle de prévision.
75
4.7.1 Performance en fonction des approches
prévisionnelles (critère IPA)
4.7.1.1 Le modèle POTI modifié
À ce stade, on considère uniquement le
modèle POTI modifié auquel sont appliqués les trois
approches de prévision (récursive, roulante 5 ans, roulante 10
ans). À partir du Tableau A 3 (Appendice A), on constate que sur un
total de 29 années, il y en a 22 au cours desquelles c'est l'approche
récursive qui détient la moyenne annuelle de U de Theil la plus
petite (IPA: 22/29). L'approche roulante Sans détient le minimum au
cours de 6 années (score IPA : 6/29) et l'approche roulante 10ans
obtient le minimum au cours d'une année (IPA: 1/29). Pour le
modèle POTI modifié, l'approche récursive fait donc mieux
que les deux autres approches, sur la base du critère IPA.
4.7.1.2 Le modèle PPA modifié
On considère uniquement le modèle PPA
modifié auquel on applique les trois approches de prévision
(récursive, roulante 5 ans, roulante 10 ans). À partir du tableau
A3 (Appendice A), on note que sur un total de 29 années, il y en a 19 au
cours desquelles c'est l'approche récursive qui détient la
moyenne annuelle de U de Theil la plus petite (IPA:19/29). L'approche roulante
5 ans détient le minimum au cours de 7 années (IPA: 7/29) et
l'approche roulante 10 ans obtient le minimum au cours de 3 années (IPA:
3/29). Pour le modèle PPA modifié, l'approche récursive
fait donc mieux que les deux autres approches, sur la base du critère
IPA.
4.7.1.3 Le modèle MF modifié
À ce stade, on considère uniquement le
modèle MF modifié auquel sont appliquées les trois
approches de prévision (récursive, roulante 5 ans, roulante 10
ans). À partir du tableau A3 (Appendice A), on note que sur un total de
29 années, l'approche récursive détient la moyenne
annuelle de U de Theil la plus petite au cours de 21 années (IPA:
21/29). Il y a 6 années au cours desquelles c'est l'approche roulante S
ans qui détient la moyenne annuelle de U de Theil la plus petite
(IPA:6/29 ).
Au terme de cette section, nous notons, selon le
critère IPA, que l'approche de prévision récursive est la
meilleure pour chaque modèle. En plus, selon le critère
76
L'approche roulante 10 ans obtient le minimum au cours de 3
années (IPA: 5/29). Pour le modèle MF modifié, c'est donc
l'approche récursive qui fait mieux que les deux autres approches, sur
la base du critère IPA.
4.7.1.4 Le modèle PE modifié
À ce stade, on considère uniquement le
modèle PE modifié auquel sont appliquées les trois
approches de prévision (récursive, roulante 5 ans, roulante 10
ans). À partir du tableau A3 (Appendice A), on note que sur un total de
29 années, l'approche récursive détient la moyenne
annuelle de U de Theil la plus petite au cours de 25 années (IPA:
25/29). Il y a 3 années au cours desquelles c'est l'approche roulante 10
ans qui détient la moyenne annuelle de U de Theil la plus petite
(IPA:3/29 ). L'approche roulante 5 ans obtient le minimum au cours d'une
année (IPA: 1/29). Pour le modèle PE modifié, c'est donc
l'approche récursive qui fait mieux que les deux autres approches, sur
la base du critère IPA.
4.7.2 Comparaison des performances des modèles POTI,
PPA, MF et PE (critère IPM)
À ce stade, on compare à la fois tous les quatre
modèles (POTI, PPA, MFet PE modifiés) auxquels sont
appliquées toutes les trois approches de prévision. On utilise
l'Indicateur de Performance de Modèle (IPM). Le tableau A 3 (Appendice
A) donne les différentes valeurs IPM. Il ressort de ce tableau que le
modèle MF modifié auquel est appliquée l'approche de
prévision récursive a la meilleure performance
prévisionnelle annuelle générale avec IPM égale
14/29
77
IPM, le modèle MF auquel est appliquée
l'approche récursive est le meilleur sur l'ensemble de
l'échantillon de prévision.
4.8 Sommaire des principaux résultats de
l'étude empirique à la fréquence
mensuelle
Le chapitre IV de cette recherche a été
consacré à l'étude de la performance prévisionnelle
des modèles POTI, PPA, MF, PE modifiés. La fréquence des
observations était mensuelle.
La non-stationnarité des régresseurs
détectée par les tests ADF et KPSS, nous a amenés à
modifier les modèles initiaux. Les régresseurs des modèles
de l'étude ont donc été exprimés en
différence première. Par la suite, l'étude
préliminaire de la précision des modèles a
révélé une hausse des erreurs de prévision autour
de 2008, année de la crise financière.
Les approches de prévision récursive, roulante 5
ans et roulante 10 ans ont été appliquées aux
modèles pour étudier leurs performances prévisionnelles.
L'échantillon de prévision est janvier 1986 - décembre
2014. Les horizons de prévision vont de 1 à 12. Le modèle
de référence est la marche aléatoire. Les
critères
d'analyse sont les statistiques U de Theil, ÄREQM, , IPA et
IPM.
Concernant l'analyse des performances prévisionnelles des
modèles POTI, PPA, MF et PE modifiés par rapport à la
marche aléatoire, les critères U de Theil, ÄREQM et ,
conduisent aux résultats suivants :
-pour les horizons h=1, 2, 3, 4, 5, 6, 7, 8 et 12, les
modèles MF et POTI modifiés font mieux que la marche
aléatoire. Ces modèles font pire sur les horizons 9, 10 et 11.
Quant aux modèles PPA et PE modifiés, ils battent la marche
aléatoire sur les horizons h= 2, 3, 4, 5, 6, 7, 8 et 12 mais ils font
pire sur les horizons 1, 9, 10 et 11.
78
-Le modèle MF modifié auquel est
appliquée l'approche roulante 5 ans a les meilleures performances sur la
période 1986-1991. le modèle MF mais avec l'approche
récursive présente les meilleures performances sur la
période 1992-2014.
Par ailleurs, le critère IPA montre que sur tout
l'échantillon de prévision, l'approche de prévision
récursive est la meilleure pour chaque modèle. En plus, selon le
critère IPM, le modèle MF auquel est appliquée l'approche
récursive est le meilleur sur l'ensemble de l'échantillon de
prévision
Dans le prochain chapitre, nous présentons le sommaire
des résultats de l'étude des modèles mais avec des
données à fréquence trimestrielle. Cela permet ainsi de
comparer le contenu informationnel des alternatives des variables fondamentales
considérées à une plus faible fréquence.
CHAPITRE V
PRÉSENTATION ET ANALYSE DES RÉSULTATS
EMPIRIQUES À LA
FRÉQUENCE TRIMESTRIELLE
Ce chapitre reprend l'analyse économétrique
faite au chapitre précédent mais à la fréquence
trimestrielle. L'objectif est de verifier si les conclusions du chapitre
précédent demeurent robustes avec des observations
trimestrielles. Nous rappelons que les modèles étudiés
sont POTI, PPA, MF et PE modifiés. Les approches de prévision
sont les approches récursive, roulante 5 ans et roulante 10 ans.
L'échantillon de prévision s'étend du premier trimestre
1986 au dernier trimestre 2014. Les critères d'étude retenus sont
les statistiques U de Theil, IPA et IPM.
Nous présentons sommairement les principaux
résultats de cette étude alors que tous les graphiques et
tableaux sont disposés dans l'Appendice B.
5.1 Analyse graphique et statistiques descriptives
à la fréquence trimestrielle
Les variables étudiées sont identiques à
celles du chapitre précédent mais avec des observations
trimestrielles L'analyse graphique et les statistiques descriptives
révèlent que ces variables présentent des allures
générales similaires aux observations mensuelles. (voir Appendice
B, figure B.1 et tableau B.1).
80
Sur la période 1986-1991, le meilleur modèle est
le modèle POTI modifié auquel est appliquée l'approche
roulante 5 ans. (figure B.4, Appendice B). Le meilleur modèle
5.2 Tests de stationnarité et analyse des
régressions à la fréquence trimestrielle
Les tests ADF et KPSS permettent de conclure que la variable
expliquée est
stationnaire alors que les variables explicatives ne le sont
pas. Cependant, les différences premières des variables
explicatives sont stationnaires (voir Appendice B tableau B.2 et Tableau B.3).
Ces résultats sont identiques à ceux obtenus avec la
fréquence mensuelle. Nous procédons alors aux modifications des
modèles initiaux comme au chapitre IV (voir le paragraphe 4.2.2
Modifications des modèles initiaux, chapitre IV).
L'analyse des estimations (MCO) montre que les modèles
POTI, PPA, MF et PE modifiés ont des constantes estimées (
différentes de zéro et positives. De plus, le signe des pentes
estimées ( ) n'est pas identique pour tous les modèles. Enfin Les
modèles étudiés ont tous des pouvoirs explicatifs faibles.
(Appendice B, tableau B.4).
5.3 Analyse préliminaire de la précision
des modèles
La figure B.2 de l'Appendice B permet de constater autour de
2008, une hausse des valeurs de REQM de tous les modèles avec leurs
approches de prévision. Comme au chapitre IV, les précisions des
modèles se déteriorent pendant la période de la crise
financière.
5.4 Performance prévisionnelle des
modèles : analyse du critère U de Theil
De 1986 à 1997, et sur les quatre horizons de
prévision, tous les modèles ont au moins une valeur de U de Theil
supérieure à l'unité. De 1998 à 2014, tous les
modèles battent la marche aléatoire, sur les quatre horizons
(figure B.3, Appendice B).
81
pour la période 1992-2014 est le modèle POTI
modifié auquel est appliquée l'approche récursive (figure
B.5, Appendice B).
5.5 Performance prévisionnelle des
modèles : analyse des critères IPA et IPM
Pour les modèles POTI, PPA, MF et PE modifiés,
l'approche récursive fait donc mieux que les deux autres approches. le
modèle POTI modifié auquel est appliquée l'approche de
prévision récursive a la meilleure performance
prévisionnelle (Tableau B.5, Appendice B)
Au terme du chapitre V, nous retenons qu'avec la
fréquence trimestrielle, tous les modèles et approches ont
à court terme au moins une observation où ils font pire que la
marche aléatoire. Ce constat est observé pour tous les quatre
horizons.
Selon le critère U de Theil, le meilleur modèle,
sur la période 1986-1991, est le modèle POTI modifié
auquel est appliquée l'approche roulante 5 ans. Pour la période
1992-2014, le meilleur modèle est le modèle POTI modifié
auquel est appliquée l'approche récursive.
Sur la base du critère IPA, l'approche récursive
est la meilleure pour chaque modèle tandis que le critère IPM
montre que le modèle POTI est le meilleur.
9 POTI modifié :
Parité Ouvert des Taux d'Intérêt/ PPA modifié :
Parité du Pouvoir d'Achat / MF modifié : Modèle financier/
PE modifié : modèle avec le Prix de l'Énergie/
modèle VAR.
CONCLUSION
L'objectif de ce travail était d'étudier la
performance prévisionnelle, hors échantillon, de plusieurs
modèles de taux de change fondés sur la valeur actualisée,
spécifiquement pour le taux de change USD/CAD. Les modèles
initiaux sont le modèle de Parité Ouvert des Taux
d'Intérêt (POTI), le modèle de Parité du Pouvoir
d'Achat (PPA), le Modèle financier (MF), le modèle avec Prix de
l'Énergie (PE) et un VAR. L'étude a été faite avec
des observations mensuelles, puis reprise avec des observations
trimestrielles.
Les modèles initiaux ont été
modifiés9 en différenciant les régresseurs pour
obtenir des variables stationnaires. La période d'étude est de
1976 à 2014. L'échantillon de de prévision est de 1986
à 2014. Les horizons de prévision sont de 1 à 12 mois
(fréquence mensuelle) et 1 à 4 trimestres (fréquence
trimestrielle). Les approches de prévision appliquées sont
l'approche récursive, les approches roulantes 5 ans et 10 ans.
Concernant la performance prévisionnelle des
modèles POTI, PPA, MF et PE modifiés par rapport à la
marche aléatoire, l'analyse des critères U de Theil, ÄREQM
et R E , conduit aux résultats communs suivants :
-avec la fréquence mensuelle et pour les horizons h=1,
2, 3, 4, 5, 6, 7, 8 et 12, les modèles MF et POTI modifiés font
mieux que la marche aléatoire. Ces modèles font pire sur les
horizons 9, 10 et 11. Quant aux modèles PPA et PE modifiés, il
battent la marche aléatoire sur les horizons h= 2, 3, 4, 5, 6, 7, 8 et
12, mais ils font pire sur
83
horizons 1, 9, 10 et 11. Cependant avec la fréquence
trimestrielle, les modèles font pire que la marche aléatoire
durant quelques années au début de tous les quatre horizons.
-Au début de l'échantillon de prévision
(1986-1991), l'approche roulante 5 ans est la meilleure pour les fré
quences mensuelle et trimestrielle. Pendant la seconde période
(1992-2014), c'est l'approche récursive qui est la meilleure pour les
deux fréquences. Quelque soit la période de l'échantillon,
le meilleur modèle pour la fréquence mensuelle est le
modèle MF. Pour la fréquence trimestrielle, le meilleur
modèle est le modèle POTI.
Quant à l'analyse des critères IPA et IPM, elle
indique que, pour tout l'échantillon de prévision (1986-2014),
l'approche récursive est la meilleure pour les deux fréquences
à la fois. De même durant cette période, le meilleur
modèle pour la fréquence mensuelle reste le modèle MF.
Tandis que c'est le modèle POTI qui s'impose toujours en
fréquence trimestrielle.
Dans l'ensemble de l'étude, la fréquence
mensuelle est celle qui permet d'obtenir les meilleures performances
prévisionnelles par rapport à la marche aléatoire. Avec
cette fréquence, les modèles POTI et MF battent la marche
aléatoire sur les horizons 1 à 8 et 12. En ce qui concerne les
modèles PPA et PE , ils performent le mieux sur les horizons 2 à
8 et 12.
APPENDICE A
RÉSULTATS DE L'ÉTUDE À LA FRÉQUENCE
MENSUELLE.
Variables
Tableau A.1
|
Coefficients de corrélation (fréquence
mensuelle)
|
|
P1
|
P4
|
P6
|
P12
|
|
-0.051
|
0.114
|
-0.075
|
0.052
|
|
0.848
|
0.393
|
0.310
|
0.041
|
|
0.982
|
0.918
|
0.875
|
0.724
|
|
0.980
|
0.910
|
0.848
|
0.612
|
|
0.868
|
0.612
|
0.466
|
-0.045
|
|
0.954
|
0.835
|
0.750
|
0.489
|
|
0.931
|
0.793
|
0.713
|
0.423
|
|
0.987
|
0.932
|
0.891
|
0.753
|
|
0.974
|
0.879
|
0.822
|
0.599
|
Tableau.A.2 Tests de racine unitaire et
stationnarité en différence première
(fréquence
mensuelle)
|
Variables
|
Nombre Adf-t
de retards
|
Kpss- résultat
|
|
0
|
-18.421
|
0.072
|
Stationnaire
|
|
11
|
-4.123
|
0.441
|
Stationnaire
|
|
16
|
-2.567
|
0.436
|
Stationnaire
|
|
9
|
-4.861
|
0.18
|
Stationnaire
|
|
11
|
-5.392
|
0.128
|
Stationnaire
|
|
11
|
-5.042
|
0.078
|
Stationnaire
|
|
0
|
-21.063
|
0.064
|
Stationnaire
|
|
0
|
-18.853
|
0.040
|
Stationnaire
|
La valeur critique du test ADF à 5% est -2.867/ La
valeur assymptotique critique du test KPSS est 0.463/ La deuxième
colonne indique le nombre de retards dans l'équation empirique pour le
test ADF

Tableau A.3 Indicateurs IPA et IPM
(fréquence mensuelle)
*POTI : Parité ouverte de taux de chage/ PPA :
Parité du pouvoir d'achat,/ MF : modèle financier; PE :
modèle avec prix de l'énergie/IPA : Indicateur de Performance par
Approche /IPM : Indicateur de Performance de Modèle
APPENDICE B
RÉSULTATS DE L'ÉTUDE À LA FRÉQUENCE
TRIMESTRIELLE
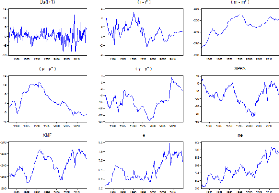
Figure B.1Graphiques des variables de
l'étude ( fréquence trimestrielle)
88
Tableau B.1 Statistiques
descriptives(fréquence trimestrielle)
|
Variables
|
Moy
|
Ecar-T
|
skew
|
Kurt
|
ñ1
|
ñ4
|
|
0.16
|
3.25
|
0.18
|
5.19
|
0.148
|
0.047
|
|
1.04
|
1.53
|
0.41
|
3.1
|
0.869
|
0.598
|
|
5.06
|
4.4
|
0.3
|
1.88
|
0.971
|
0.870
|
|
-222.94
|
14.32
|
-0.83
|
3.05
|
0.986
|
0.914
|
|
-11.55
|
6.15
|
0.29
|
2.62
|
0.973
|
0.832
|
|
-15.59
|
11.95
|
-0.49
|
2.51
|
0.957
|
0.809
|
|
-239.05
|
16.7
|
-0.09
|
1.78
|
0.969
|
0.834
|
|
6.51
|
0.57
|
0.49
|
2.03
|
0.953
|
0.817
|
|
5.49
|
0.27
|
0.57
|
2.47
|
0.966
|
0.851
|
Note : le nombre d'observations est : 156.
89
Tableau B.2 Tableau des Tests ADF et KPSS
à niveau (fréquence trimestrielle)
|
Variables
|
Lag
|
Adf-t
|
V.Addf
|
résul
|
Kpss-
|
V.
|
résultat
|
|
0
|
-10.35
|
0.00
|
Sta
|
0.18
|
0.46
|
St
|
|
4
|
-2.79
|
0.06
|
N.stb
|
0.51
|
0.46
|
N st
|
|
1
|
-0.96
|
0.77
|
N.st
|
0.697
|
0.46
|
N.st
|
|
3
|
-2.497
|
0.12
|
N.st
|
0.84
|
0.46
|
N.st
|
|
4
|
-1.65
|
0.45
|
N.st
|
0.37
|
0.34c
|
N.st
|
|
2
|
-1.93
|
0.31
|
N.st
|
0.21
|
0.46
|
st
|
|
1
|
-1.95
|
0.31
|
N.st
|
0.56
|
0.46
|
N.st
|
|
2
|
-1.77
|
-2.88
|
N. st
|
0.98
|
0.46
|
N.st
|
|
13
|
-0.58
|
-2.88
|
N.st
|
1.22
|
0.46
|
N.st
|
Note : le niveau de significativité est à 5%.
90
Tableau B.3 Tests de racine unitaire et
stationnarité en différence première (fréquence
trimestrielle)
|
Variables
|
Lag
|
Adf-t
|
V.adf
|
résul
|
Kpss-
|
V crit
|
résultat
|
|
4
|
-5.313
|
-2.88
|
stati
|
0.05
|
0.46
|
stati
|
|
5
|
-3.764
|
-2.88
|
Stati
|
0.333
|
0.46
|
stati
|
|
4
|
-2.987a
|
-3.439
|
stat
|
0.278
|
0.46
|
stati
|
|
2
|
-5.01
|
-2.88
|
stati
|
0.142
|
0.46
|
Stati
|
|
13
|
-2.71b
|
-1.94
|
stati
|
0.12
|
0.46
|
Stati
|
|
10
|
-3.127
|
-2.88
|
stati
|
0.06
|
0.46
|
stati
|
|
0
|
-11.74
|
-2.88
|
stati
|
0.09
|
0.46
|
stati
|
|
3
|
-5.20
|
-2.88
|
stati
|
0.04
|
0.46
|
stati
|
Note : les variables sont stationnaires à 5%.
91
10 Les chiffres entre parenthèses sont les
écarts-types estimés. Un, deux et trois astérisques
correspondent respectivement à des seuils de significativité de
1%, 5%, 10%.
Tableau B.4 Estimations MCO des modèles
(fréquence trimestrielle)
|
Modèles Coef10.
|
POTI
|
PPA
|
MF
|
PE
|
|
0.87*
|
0.94*
|
0.88*
|
0.93*
|
|
(0.281)
|
(0.303)
|
(0.292)
|
(0.281)
|
|
-0.142
|
0.11
|
0.03
|
(4.675)
|
|
(0.365)
|
(0.158)
|
(0.073)
|
|
|
|
|
|
(9.091)
|
|
0.0058
|
0.0128
|
0.0028
|
0.0083
|
Légende : significativité à 1% (*); 5%
(**); et 10% (* ** ).
Note : période d'estimation : mars 1976-
décembre 1985. Nombre d'observations : 40
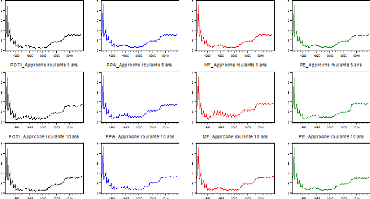
92
Figure B.2 Séries REQM des modèles
et approches(trimestrielles)

93
Figure B.3 Séries U de Theil des
modèles POTI, PPA, MF, PE modifiés par
approche (1986-2014,trimestrielles)
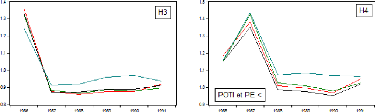
Figure B.4 Séries U de Theil de
l'approche 5 ans par modèle (1986-1991,
trimestrielles)
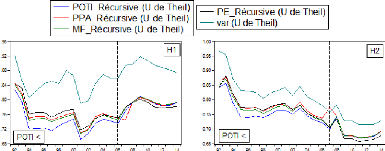
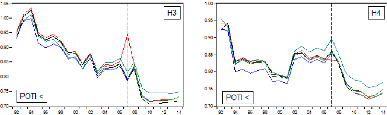
95
Figure B.5 Séries U de Theil de
l'approche récursive par modèle (1992-2014,
trimestrielles)
96
Tableau B.5 Indicateurs IPA et
IPM(fréquence trimestrielle)

*POTI : Parité ouverte de taux de chage/ PPA :
Parité du pouvoir d'achat,/ MF : modèle financier; PE :
modèle avec prix de l'énergie/IPA : Indicateur de Performance par
Approche /IPM : Indicateur de Performance de Modèle
Chinn, M. (2011). Macro Approaches to Foreign Exchange
Determination. La Follette School Working Paper 2011-013.
BIBLIOGRAPHIE
Abba, P.L. (1946). The economics of control: principles of
welfare economics. New-York: The Macmillan company.
Abhyankar, A., L. Sarno and G. Valente (2005). Exchange Rates
and Fundamentals: Evidence on the Economic Value of Predictability. Journal
of International Economics 66(2)325-348.
Amano, R.A. and S. van Norden (1993). A Forecasting Equation
for the Canada-US Dollar Exchange Rate, in The Exchange Rate and the Economy.
Proceedings of a conference held at the Bank of Canada.
Amano, R.A. and S. van Norden (1998b). Exchange Rates and Oil
Prices. Review of International Economics 6(4), 683-94.
Bailliu, J. and M.R. King (2005). What Drives Movements in
Exchange Rates?. Bank of Canada Review, Autumn.
Berkowitz, J. and L. Giorgianni (2001). Long-Horizon Exchange
Rate Predictability?. Review of Economics and Statistics 83(1),
81-91.
Bilson, F. O. (1978). The monetary approach to exchange rate:
some empirical evidence. International Monetary Fund Staff Paper.
Palgrave Macmillan, vol. 25(1), 48-75, March.
Branson W. (1975). Stocks and flows in international monetary
analysis, dans Ando et al. (dir). International Aspects of Stabilization
Policies, Federal Bank of Boston.
Cassel, G. (1922). Money and foreign exchange after 1914.
New York: Constable and Co.
Cheung, Y.W, M.D. Chinn and A.G. Pascual (2005). Empirical
Exchange Rate Modelsof the Nineties: Are Any Fit to Survive?. Journal of
International Money and Finance 24,1150-1175.
Fleming, J. M. (1962). Domestic financial policies under fixed
and floating exchange rates. International Monetary Fund Staff Papers
9, 369-379.
98
Chinn, M.D. and G. Meredith (2004). Monetary Policy and
Long-Horizon Uncovered Interest Parity. IMF Sta Papers 51(3).
Cuthbertson, K. et Nitzsche, D. (2008). Quantitative
financial economics. Stocks, bonds and foreign exchange (2e
éd.). England : John Wiley & Sons, Ltd.
Diebold, F.X. and R.S. Mariano (1995). Comparing Predictive
Accuracy. Journal of Business and Economic Statistics 13, 253-263.
Diez, A. (2009). Can affine term structure models helps us
predict exchange rates ?. Journal of Money, Credit and Banking
Dornbusch R. (1976). Expectations and exchange rate dynamics.
Journal of Political Economy 84.
Edge, R.M., M.T. Kiley and J.P. Laforte (2010). A Comparison of
Forecast Performance between Federal Reserve StaForecasts, Simple Reduced Form
Models and a DSGE Model. Journal of Applied Econometrics 25(4),
720.754.
Ehrmann, M. and M. Fratzscher (2005). Exchange Rates and
Fundamentals: New Evidence from Real-time Data. Journal of International
Money and Finance 24, 317-341.
Elliott, G. and A. Timmermann (2008). Economic Forecasting.
Journal of EconomicLiterature 46(1): 3.56.
Engel, C. and K.D. West (2004). Accounting for Exchange-Rate
Variability in Present-Value Models When the Discount Factor is Near 1.
American Economic Review 94(2), 119-125.
Engel, C. and K.D.West (2005). Exchange Rate and Fundamentals.
Journal of Political Economy 113, 485-517.
Evans, M.D.D. et Lyons, R. K.(Janvier 2005). Meese-Rogoff redux :
micro-based exchange rate forcasting. National Bureau of Economic Research.
http:/
www.nber.org/papers/w11042.
Ferraro, D., K.S. Rogoand B. Rossi (2011). Can Oil Prices
Forecast Exchange Rates?. ERID Working Paper No. 95, Duke
University
99
Fratzscher, M. (2009). What Explains Global Exchange Rate
Movements During the Financial Crisis. Journal of International Money and
Finance 28, 1390-1407.
Frenkel, J. A. (1976). A Monetary Approach to the Exchange
Rate: Doctrinal Aspects and Empirical Evidence. Scandinavian Journal of
Economics 78, 200-224.
Fonds monétaire international. [s.d]. IMF elibrary
Data. Récupéré de
http://elibraryata.imf.org.proxy.bibliotheques.uqam.ca:2048/DataExplorer.aspx
Granger and A. Timmermann (eds.). Handbook of Economic
Forecasting Vol. 1. Elsevier-North Holland, 100-134.
Groen, J.J. (1999). Long Horizon Predictability of Exchange
Rates: is it for Real?, Empirical Economics 24, 451.469.
Hooper, P. and Morton, J. (1982). Fluctuations in the dollar:
A model of nominal and real exchange rate determination. Journal of
international Money and Finance 1(1), 39-56.
James, J., Marsh, I. W. et Sarno, L. (2012). Handbook of
exchange rates. Hoboken, New Jersey: John Wiley & Sons, Inc.
Kilian, L. (1999). Exchange Rates and Monetary Fundamentals:
What Do We Learn From Long-Horizon Regressions?. Journal of Applied
Econometrics 14(5).
Kilian, L. and M.P. Taylor (2003). Why Is It so Difficult to
Beat the Random Walk Forecast of Exchange Rates?. Journal of International
Economics 60(1), 85-107.
Kilian, L. (1999). Exchange Rates and Monetary Fundamentals:
What Do We Learn From Long-Horizon Regressions?. Journal of Applied
Econometrics 14(5).
Kouri P. (1976). Balance of payments and the foreign exchange
market: a dynamic equilibrium model. Cowles Foundation Discussion Paper
510.
Marshall, A. (1879). The economics of industry.
London: Acmillan and Co.
Messe, R. A. et Rogoff, K. (1983). Empirical exchange rate
models of the seventies. Do they fit out of sample?. Journal of
International Economics 14, 3-24.
McKinnon R. (1969). Portfolio balance and international
payments adjustments, in Mudell R. et Swoboda A. (dir), Monetary Problems of
the International Economy, University of Chicago Press, Chicago.
100
Mundell, R. A. (1960). The monetary dynamics of international
adjustement under fixed and flexible exchange rates. Quarterly Journal of
Economics 74.
Ricardo, D. (1817). On the principles of political economy and
taxation. London.
Rossi, B. (2013). Exchange Rate Predictability. Journal of
Economics Literature 51(4).
Schinasi, G.J. and P.A.V.B. Swamy (1987). The Out-of-Sample
Forecasting Performance of Exchange RateModels when Coefficients are Allowed to
Change. Journal of International Money and Finance 8(3), 375-390.
Statistique Canada. [s.d]. CANSIM-176-0064- taux de change
étranger en dollars canadiens. Récupéré de
http://www5.statcan.gc.ca/cansim
| 










