2.5.1.2 Critère de sélection par la
distance minimale
On calcule la distance de chaque compromis se trouvant sur le
front de Pareto par rapport au point d'origine du repère (f1,
f2) et on sélectionne comme choix final le compromis ayant une
distance minimale (l'équation2.6).
\/dmin = f2 1 + f2 2
(2.6)
2.5.1.3 Critère de sélection par la
distance maximale
L'idée de ce critère est de partir des deux points
A(min(f1), max(f2)) et
B(max(f1),
min(f2)),
les extrêmes du front de Pareto et de calculer la distance
de chaque compromis (solution)
se trouvant sur le front de Pareto par rapport à la droite
D(A, B) passant par les points
A et B. Le compromis (solution) retenu est
celui présentant la distance maximale à la
droite D (voir la Figure2.7).
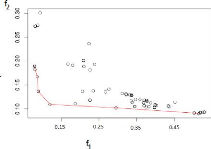
FIGURE 2.6 Les compromis construisant le front de Pareto se
trouvent sur la courbe rouge, comment choisir le meilleur?.
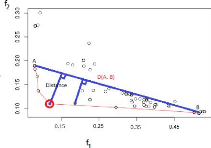
28
FIGURE 2.7 Critère de sélection par la distance
maximale
29
f1
|
a1
a2
a3
..
ai
.. an
|
f2
b1
b2
b3
..
bi
.. bn
|
TABLE 2.1 Les compromis à traiter par le critère
de seuil.
Algorithm 6 Sélection par seuil
1: Initialiser :
Lmax = {Ø}
: // La liste ayant contenu les maximums des couples
(ai, bi)
2: for(i=1; i<=|f1|
; i++)
{
Lmax =
{max(ai, bi)}
}
3: Lk =
min(Lmax)
4: Sélectionner (ak,
bk)
2.5.1.4 Critère de sélection par
seuil
Les critères de sélection par la distance
minimale/maximale peuvent amener à choisir une solution (compromis)
très bonne pour une des fonctions objectif mais beaucoup moins bonne
pour la seconde fonction objectif. Ce critère a été
développé de façon à trouver la solution
étant le meilleur compromis sur les 2 fonctions simultanément.
Sur les deux colonnes associées aux f1 et
f2 dans le fichier des sorties (voir la
Table2.1), on sélectionne le maximum de chaque couple
(ai, bi), on le met dans
une liste Lmax, puis on choisit le compromis
associé à la valeur minimale de cette liste (voir
l'algorithme6).
30
| 


