2.2 Treillis ordinale et treillis algébrique
2.2.1 Définitions algébrique et ordinale d'un treillis
On appelle treillis ou lattis ou encore
ensemble réticulé, un ensemble partiellement
ordonné dans lequel, pour toute paire d'éléments, existent
une borne inférieure et une borne
supérieure[4]. On trouve, également, dans la
littérature deux autres définitions d'un treillis : Une
définition algébrique et une définition ordinale. Ces
définitions introduisent toutes deux la notion de borne
supérieure (ou supremum) et de borne inferieure
(ou infimum) alors qu'il s'agit d'opérateurs binaires dans
la définition algébrique, ce sont des éléments
particuliers dans la définition ordinale.[1]
Définition 1 (Définition
algébrique)
Un treillis ou encore une algèbre de
treillis est un triplet L = (S, V, ?) ou V et ?
sont deux opérateurs binaires sur l'ensemble S qui
vérifient les propriétés suivantes :
- Associativité : Pour tout x, y, z
E S, (x V y) V z = x V (y V
z) et (x ? y) ? z = x ? (y ?
z).
- Commutativité : Pour tout x, y E
S, x V y = y V x et x ? y = y
? x
- Idempotence : Pour tout x E S,
x V x = x = x ? x
8
- Loi d'absorption : Pour tout x, y E
S, x V (x ? y) = x = x ?
(x V y)[1] Définition 2 (Définition
ordinale)
Un treillis est une paire L =
(S,<) où < est une relation d'ordre sur
l'ensemble S, c'est à dire une relation binaire qui
vérifie les proprietés suivantes :
- Réflexivité : Pour tout x E
S, on a xRx.
- Antisymetrie : Pour tout x, y E S,
xRy et yRx impliquent x = y.
- Transitivité : Pour tout x, y, z E
S, xRy et yRz impliquent xRz.[1][3]
Un ensemble sur lequel est défini une relation d'ordre
(partiel ou total) est dit (partiellement ou totalement) ordonné.
Considérons un ensemble S partiellement
ordonné par la relation < (être inférieur ou égal
à) et une partie X de cet ensemble[4] ;
Définition 3 Minorant (Majorant) :
Un élément m(M) de S
qui est inférieur (supérieur) ou égal à tout
élément x de X est un minorant (majorant)
de X.
Définition 4 Elément maximal (minimal)
:
Un élément noté T(1) de X, tel
qu'il n'existe pas d'éléments de X supérieur
(inférieur) à T(1) est un élément maximal
(minimal) de X.
Définition 5 Plus grand (petit)
élément :
Le plus grand (petit) élément
E(e) ou encore le maximum (minimum) de X est
l'élément de X tel que pour tout x E
X, E > x(e < x).
Définition 6 Borne supérieure
(inférieure) :
La borne supérieure (inférieure) de X
Ç S notée VX (?X) ou le supremum
(infimum) de X noté sup(X) (inf(X) ) est le
plus petit (grand) élément de l'ensemble des majorants
(minorants) de X. Les bornes inférieure et supérieure
entre x et y notée respectivement par x ?
y et x V y se définissent de la même
manière que pour une partie X Ç S
Définition 7 Elément universel (nul)
:
L'élément universel (nul) de S est le
plus grand (petit) élément de S. Exemple
1
Soit S = {1, 2, 3, 5,
10, 20, 30} un ensemble partiellement ordonné
par la relation x||y (x divise y).
N.B : x||y peut s'interpréter comme x
< y et x|y comme x < y.
1. Prenons X = {2, 3,5,
10}
Il existe un majorant de X qui vaut 30 et un
minorant qui vaut 1, un élément maximal : 10,
trois élément minimaux : 2, 3, 5 ni
plus grand élément, ni plus petit élément de X. La
borne supérieure de X est 30 et la borne inférieure vaut
1. S
9
n'admet pas d'élément universel, mais un
élément nul : 1.
2. Prenons maintenant X = {2,
5,10}
X compte 3 majorants : 10, 20,
30, un minorant : 1, un élément maximal :
10, deux éléments minimaux : 2 et 5,
un plus grand élément : 10, pas de plus petit
élément. La borne supérieure de X est 10 et la
borne inférieure est 1.
Pour une partie réduite à deux
éléments {x, y}, d'un ensemble ordonné, il peut
exister une borne inférieure, une borne supérieure. Lorsque seule
l'existence de la borne inférieure est vérifiée, on parle
d'inf-demi-treillis. Un sup-demi-treillis est défini
dans le cas dual où seule l'existence d'une borne supérieure est
vérifiée. Un treilis est donc à la fois un
inf-demi-treillis et un sup-demi-treillis[1].
Définition 8 (Relation d'ordre strict)
:
Une relation d'ordre strict notée <
est une relation vérifiant les propriétés suivantes
:
- Irréflexive : Pour tout x E
S, (x, x) E6 R.
- Asymétrique : Pour tout x, y E
S, (x, y) E R implique (y, x) E6
R.
- Transitive : Pour tout x, y, z E S,
(x, y) E R et (y, z) E R = (x, z)
E R.[5]
Définition 9 (Relation de couverture)
:
On dit qu'un couple (x, y) E X x X
avec X C_ S est une couverture ou que y
couvre x (y est successeur immédiat de
x) ou encore x est couvert par y (x est
prédécesseur immédiat de y), s'il
n'existe pas z tel que x < z < y lorsque x <
y. Elle est notée par "-<" et elle se déduit de la
relation d'ordre en supprimant les relations de
réflexivité et de transitivité[6].
Définition 10 (Diagramme de Hasse) :
La représentation graphique d'un treillis s'exprime
à l'aide d'un diagramme, appelé diagramme de Hasse, dans
lequel les noeuds correspondent aux éléments de l'ensemble et les
arcs aux relations de couverture (successeurs et prédécesseurs
immédiats) entre ces noeuds.
Le plus souvent, Relation binaire et Graphe
orienté simple (C'est-à-dire un graphe sans arcs multiples)
s'identifient où chaque élément est
représenté par un sommet du graphe, et où la relation
entre deux éléments x et y est
représentée par un arc du graphe entre le sommet x et le
sommet y. Le diagramme de Hasse, tel que décrit
ci-haut, est une représentation proche de la représentation
habituelle d'un graphe ; les orientations des arcs ne sont pas toujours
représentées parce qu'elles peuvent se déduire du
positionement des noeuds. Ainsi il permet de ne pas surcharger le dessin pour
faciliter une meilleure lisibilité[1].
Exemple 2
Considérons, à titre d'exemple, les diviseurs
de 30 : {1, 2, 3, 5,
6,10,15, 30} ordonnés par la relation
x divise y[4]. Ces éléments forment un treillis dont le
diagramme de Hasse est donné par la figure Figure
2.1.
On peut vérifier que toute paire
d'éléments admet une borne inférieure(p.g.c.d) et
une borne supérieure(p.p.c.m). Ainsi :
- 5 V 6 = 5 x 6 = 30; 5 ? 6 = 1; 6 V 15 = 5 x 3 x 2 = 30; 6 ?
5 = 3; etc. L'élément
10

FIGURE 2.1 - Exemple de treillis universel de ce treillis est 30
et l'élément nul est 1.
Définition 11 (Treillis distributif)
:
Un treillis est distributif si V et ? verifient la
proprieté de distributivité : Pout tout x, y, z E
S, x V (y ? z) = (x V y) ? (x
V z).[5]
Définition 12 (Treillis
complémenté) :
Un treillis est complémenté si tout
élément x E S admet au moins un
complément, c'est-à-dire un élément x' E
S tel que x V x' = T (élément
maximal) et x ? x' = 1 (élément
minimal)[1].
Définition 13 (Treillis
V-Complémenté) :
Un treillis est V-Complémenté si pour tout
élément x E S, il existe un V-complément
(c'est-à-dire un élément x' E S tel que
x V x' = T). Un treillis
?-complémenté est défini dans le cas
dual[1].
Définition 14 (Treillis booléen)
:
Un treillis est booléen s'il est à la fois
distributif et compléménté[1].
Exemple 3
Un exemple classique d'un treillis distributif est
fourni à la figure 2.2(a). La relation d'ordre est la relation
« ... divise... ». L'ensemble P(S) des parties d'un ensemble
S muni de la relation d'inclusion est quant à lui un exemple
classique de treillis booleen (figure 2.2(b))[1]
2.2.2 Irréductibles et générateurs
minimaux d'un treillis
Soient x ? y et x V y les
bornes inférieur et supérieur respectivement. Un
élément d'un treillis est dit réductible s'il est
résultat de x ? y ou x V y. Dans le
cas contraire, il sera dit irréductible.
11
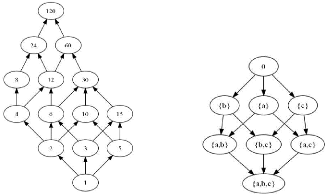
FIGURE 2.2 - Exemple de treillis distributif et treillis
booléen.
Définition 15 (Elements irréductibles)
Soit L = (S, ) un treillis.
- Un élément j E S est appelé
sup-réductible s'il existe dans S des éléments
x1 et x2 tel que j = x1 V
x2 avec x1 < x et x2 <
x. Un élément x de S ne possédant pas de
décomposition de cette forme est dit
sup-irréductible.
- Dualement, un élément in E S est appelé
inf-réductible s'il existe dans S des éléments
x1 et x2 tel que j = x1 ?
x2 avec x1 > x et x2 >
x. Un élément x de S ne possédant pas de
décomposition de cette forme est dit inf-irréductible.
L'ensemble des sup-irréductible et celui des
inf-irréductible du treillis L est noté respectivement
par JL et ML[3].
Proposition 1
Soit L = (S, ) un treillis.
- Un élément j E S est un
sup-irréductible, si et seulement si j couvre un seul
élément dans le diagramme de Hasse.
- Un élément in E S est un
inf-irréductible, si et seulement si in est couvert par un seul
élément dans le diagramme de Hasse.
Définition 16 (Treillis atomistique) :
Un treillis est dit atomistique lorsque tous les
sup-irréductibles sont des atomes (un atome est un
élément qui couvre l'élément minimal I).[3]
Définition 17 (Treillis co-atomistique) :
Un treillis est dit co-atomistique lorsque tous les
inf-irréductibles sont des co-atomes (un co-atome est un
élément qui est couvert par l'élément maximal T).
Tout élément x E S d'un treillis L = (S, ) est la borne
supérieure de l'ensemble de ses prédécesseurs, ainsi que
la borne inférieure de l'ensemble de ses successeurs. La
12

FIGURE 2.3 - Autre exemple de treillis
définition latticielle permet d'établir qu'il
est possible de réduire ces ensembles aux seuls
prédécesseurs sup-irréductibles, et un successeurs
inf-irréductibles[3] :
x = ?Jx = ?{y
sup-irréductible tel que y = x} (2.1)
x = ?Mx = ?{y
inf-irréductible tel que y = x} (2.2)
Par conséquent, les ensembles d'éléments
irréductibles peuvent nous permettre de reconstruire le treillis dans sa
globalité par reconstruction successives de bornes supérieures ou
de bornes inférieures en utilisant respectivement les
sup-irréductibles et les
inf-irréductibles.[1]
Exemple 3
Considérons la figure 2.3. Nous constatons
que seul six éléments possèdent un seul arc
entrant, et forment ainsi l'ensemble des sup-irréductibles
alors que les inf-irrédutibles,
caractérisés, quant à eux, par un seul arc sortant sont au
nombre de huit:
J = {b, f, e, a, c, d} (2.3)
M = {b,l,m,n,d,k,i,c} (2.4)
Quatre sup-irréductibles {b, f, e,
a} sont des atomes et que trois inf-irréductibles
{l, i, c} sont des co-atomes. Ces éléments
irréductibles sont utilisés dans le treillis de la figure 2.4
où dans le noeud de chaque élément x sont
precisés l'ensemble Jx des
sup-irréductibles inférieurs ou égaux à
x ainsi que l'ensemble Mx des
inf-irréductibles supérieurs ou égaux à
x. Les générateurs minimaux de chaque
élément sont, quant à eux, donnés par la table
2.1. On peut ainsi observer que chaque sup-irréductible est son
propre générateur minimal, mais aussi que tous les
éléments, excepté l'élément maximal T, ont
pour unique générateur minimal l'ensemble de leurs
prédécesseurs sup-irréductibles.[1]
TABLE 2.1 - Générateurs minimaux des
éléments du treillis de la figure 2.3
13

FIGURE 2.4 - Treillis de la figure 2.3 où sont
precisés, pour chaque noeud de x, les ensembles
Jx et Mx

14
Définition 18 (Générateur
minimal)
Soit L = (S,=) un treillis et x ?
S un élément du treillis. Un
générateur minimal de x est un sous ensemble B
de Jx tel que x = ?B et qui soit
minimal au sens de l'inclusion, c'est-à-dire pour tout A ?
B, on a x < ?A. La famille
âx des générateurs minimaux de x
se définit par :[6]
âx = {B ? Jx :
x = ?B et x < ?A pour tout A ?
B} (2.5)
Définition 19 (Table et graphe de
dépendance d'un treillis)
La notion d'éléments irréductibles d'un
treillis permet de concevoir des représentations compactes du treillis
entre autre la représentation par une table composée en colonne
par des sup-irréductibles et en ligne par des
inf-irréductibles. Il existe, cependant, une différence
entre une table binaire d'un treillis et une table
complète.[1]
La table (complète) d'un treillis se
définit à partir des relations flèches qui
parti-tionnent les différents liens possibles entre un
sup-irréductible et un inf-irréductible à
l'aide de relations binaires définies sur JL ×ML.
Nous avons entre autre, la relation de comparabilité = qui
permet d'établir une première partition de JL ×
ML en deux parties notées P= et
P6= définit par :
P= = {(j,m) ? JL ×
ML : j = m} (2.6)
P6= = {(j,m) ? JL ×
ML : j =6 m} (2.7)
Définition 20 (Relations
flèches)
Soit L = (S,=) un treillis, j ?
JL et m ? ML. Une relation flèche
est définit comme suit[1] :
- j ? m si j =6 m et
j < m+(unique successeur, dans le diagramme de Hasse,
pour tout m ? ML).
- j ? m si j =6 m et
j- < m avec j- unique
prédécesseur pour tout j ? LL. Notons que les
relations flèches (j ? m et j ?
m ) affinent les cas où j et m ne sont pas
comparables. C'est-à-dire, de cette relation
d'incomparabilité, il en résulte quatre autres
combinaisons possibles qui permet de partitionner l'ensemble de paires (j,
m) ? P6= en quatre parties notées P?,
P?, Pl, P? définit par :
P? = {(j,m) ? JL ×
ML : j ? m et j ?6m} (2.8)
P? = {(j,m) ? JL ×
ML : j ?6m et j ? m} (2.9)
Pl = {(j, m) ? JL ×
ML : j ? m et j ? m} (2.10)
P? = {(j,m) ? JL
× ML : j ?6m et j ?6m} (2.11)
La table d'un treillis se définit comme étant
une représentation tabulaire de ce partionnement.
meture se sont avérées fondamentales
pour plusieurs domaines de l'informatique : Base de données, Analyses
formelles de concepts.
15

TABLE 2.2 - Table du treillis de la figure 2.3
Définition 21 (Table d'un treillis) :
La table T d'un treillis L = (S, <)
est composée des sup-irréductibles qui apparaissent
en colonne et des inf-irréductibles qui apparaissent en ligne.
Ainsi pour m E ML et j E JL, la table
T[m, j] contient x, t, 1,, $ ou o selon que (m, j)
appartienne à P<, Pt, P~, P$
ou Po(cf table 2.2).
Il vient que la table binaire se définit
juste à partir d'une seule partition composée de deux parties
P< et Pg où T[m, j] contient x si (m,
j) E P< et rien dans le cas contraire, c'est-à-dire le
cas où (m, j) E Pg
Notons que lorsque la table (complète)
possède exactement une double flèche sur chacune de ses lignes et
colonnes, alors on parle d'un treillis distributif. Un treillis
atomistique se caractérise quant lui par l'absence de flèche
t dans sa table, alors qu'un treillis co-atomistique se
caractérise par l'absence de flèche 1,. Il en découle que
la table d'un treillis booléen, qui en revanche est à la
fois distributif, atomistique et co-atomistique se
carastérise par une unique double flèche $ sur chacune de ses
lignes et colonnes, ainsi que par l'absence de flèches simples t et
1,.[1]
Définition 22 (Graphe de dépendance)
:
Le graphe de dépendance se définit
pour les sup-irréductibles sur la base de la relation de
dépendance. Soit L = (S, <) un treillis, le
graphe de dépendance du treillis L est un graphe
valué G = (JL, 8, w) tel que :
- 8 relation de dépendance définie sur
JL par j8j'. Alors 8 est une relation de
dépendance s'il existe un élément de l'ensemble S
qui ne majore pas j et j' éléménts
de JL, c'est-à-dire s'il existe x E S tel que
j <6 x, j' <6 x et j < j'
V x ;
- w une valuation des arcs définie pour
chaque relation j8j' de tel sorte que l'arc (j, j') peut
être valué par les générateur minimaux de
x, c'est-à-dire les parties de l'ensemble
Jx défini pour x :[5]
Jx = {j < x
tel que j E JL}
| 


