CHAP II : MODELES DE GESTION DES STOCKS
Pour rédiger ce chapitre, nous avons
consulté les documents ci-après :[2], [3], [4], [6]
Comme nous l'avons dit précédemment tout
logisticien à une mission principale celui de savoir gérer son
stock avec efficacité. Les enjeux de cette gestion sont de servir au
mieux les clients pour une satisfaction optimale tout en maintenant les couts
de stockage les plus bas possibles. Pour réussir cet exercice
d'équilibriste, le gestionnaire s'appuie sur des techniques
éprouvées ; dans ce chapitre nous allons voir certaines de ces
techniques qu'on appelle modèle de gestion des stocks.
Il existe des méthodes qui permettent d'évaluer
les quantités optimales à stocker en fonction des plusieurs
paramètre comme le nombre de commandes, le délai
d'approvisionnement etc. c'est la gestion économique des stocks.
Par ailleurs, les méthodes de gestion sont des
premières méthodes de gestions scientifiques des
approvisionnements des produits.
Remontant de la première guerre mondiale, elles ont
pour origine les travaux de l'ingénieur de la société
Westinghouse F. HARRIS (1915) qui ont conduit au modèle connu
universellement sous le nom de modèle de WILSON ou encore de
modèle « EOQ » de l'anglais qui veut dire « Economic
Order Quantity-modele.»
Mais bien avant, la méthode aurait pu être
négligé et oublié si la crise qui éclata aux USA en
1929 n'était pas venu rappeler l'importance de gérer les stocks
disponibles en moindre coût.
Par la méthode de gestion des stocks on entend une
méthode consistant à reconstituer systématiquement un
stock après consommation, soit dès que celui-ci passe en dessus
d'un certain seuil, soit fréquence déterminée.
Ce sont des méthodes qui ressortent d'une logique de
gestion sur la consommation c'est-à-dire que l'évènement
déclencheur d'un réapprovisionnement est une consommation. Cette
logique conduit à une reconstitution systématique du stock.
Il existe plusieurs modèles de gestion scientifique des
stocks ; les plus connus peuvent être regroupés en deux
catégories que nous allons détailler dans les lignes qui suivent
:
? Les méthodes à avenir certains et
? Les méthodes à avenir aléatoire ou
incertain.
Etant donné que la gestion sur le stock est une
méthode particulière de gestion économique des
approvisionnements, nous
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l
supposons qu'il n'y a pas une méthode archétype
mais chaque méthode présente ses propres avantages et
inconvénients à ses domaines d'application
privilégiés.
Il importe en premier temps au gestionnaire d'effectuer une
analyse des consommations et une classification des articles afin d'identifier
la méthode de gestion la plus appropriée.
Toutes fois, il est important de signaler que les seules
données de consommations sont insuffisante pour classer de
manière pertinente les produits disponibles. Sachant que chaque produits
à son cycle de vie propre, la demande des certains produits est parfois
saisonnier, d'autres ont un caractère continu ou discret ; tous ces
caractères sont également des données
prépondérantes à prendre en compte avant de choisir une
méthode de gestion de données.
Ainsi, comme détailler dans le chapitre
précèdent l'existence de stocks au sein d'une entreprise
amène le gestionnaire à se poser la question du niveau optimal de
stock tout en évitant le sur-stockage et le sous-stockage.
C`est dans ce même optique que vont les
différentes modèles de gestion des stocks. Elles ont pour
objectif de minimiser le cout de gestion dans ce système des contraintes
déterminants la fréquence de réapprovisionnement et la
quantité associée.
Définir une politique d'approvisionnement consiste
essentiellement à répondre donc à ces deux questions :
? Quand approvisionner ?
? Combien commander ?
La réponse à ces deux questions dépend
alors de la politique de la gestion adoptée.
En effet, il est possible de commander soit à date
fixe, soit à date variable. De même que la quantité a
commandée peut être fixe ou variable.
S'appuyant sur ces deux contraintes, quatre combinaisons sont
envisageables. Elles correspondent à autant des méthodes de
gestions de stocks possibles :
1) La méthode de réapprovisionnement :
elle est également appeler « méthode calendaire »
et consiste à commander à date fixe une quantité fixe ;
voisine de la quantité économique de commande ; c'est la formule
de WILSON.
2) La méthode de gestion a point de commande :
elle adopte un
système de commande à date variable mais a
quantité fixe dans la mesure où c'est atteindre d'un niveau
donné de stock appelé « point de commande » qui
déclenche la commande de réapprovisionnement.
3) La méthode de re complètement : il
s'agit ici de commander à date fixe, une quantité variable
puisque le niveau de stock a
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

16
complètements varié en fonction du volume de vente
alors que la date reste la même.
4) La méthode de réapprovisionnement
à la commande : elle consiste à passer la commande d'une
quantité variable, a date variable en fonction de la demande.
SECTION I : METHODE DE GESTION A AVENIR CERTAIN
Les modèles des gestions des stocks peuvent se
différer par rapport aux aspects suivants : le nombre de locations et
échelons, le nombre de produits, les processus de la demande, les
structure des couts, les exigences et mesures des services, les possibles
moments des commande, les traitements des ruptures, les délais de
livraison des marchandises, etc.
Il existe plusieurs modèles d'optimisation de gestion
des stocks notamment :
1. La méthode de WILSON
2. La méthode statistique ;
3. La méthode 20/ 80 . Etc.
Parmi tous ces modèles, nous allons nous atteler sur la
méthode dit de WILSON qui est le plus connu et le plus utilisée
mais pas forcément le plus réaliste.
II.1 MODELE DE WILSON
Le modèle de Wilson ou le modèle de la
quantité économique de commande (EOQ) est le premier
modèle de gestion de stock permettant de déterminer la
fréquence et la quantité optimale de réapprovisionnement.
Elle a été introduite en 1913 par F. HARRIS comme nous l'avons
souligné précédemment.
C'est un modèle déterministe c'est à dire
ces données sont connus avec exactitude car la date et quantité
à réapprovisionner sont fixe. Il a pour but de la
stratégie qu'il faut adopter pour que le total périodique des
commandes ou des fabrications des pièces minimise le cout total de cout
d'acquisition et de possession de stocks pour l'entreprise.
Etant donné que le gestionnaire doit veiller ou niveau
optimal de son stock pour éviter le sous stockage et le sur stockage ;
les différents modèles de gestion a pour objectif de minimiser le
cout de gestion.
En admettant, en effet que la consommation soit constante et
le réapprovisionnement instantané on peut définir pour une
période données de gestion, la fréquence optimal de
réapprovisionnement.
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

17
a) Hypothèses et notations
Supposons les hypothèses suivantes :
( la demande est connue et constante ;
( le réapprovisionnement est instantané
c.-à-d. le délai
de réapprovisionnement est nul
( la rupture de stock est interdite.
Et les notations utilisées sont:
· Consommation par unité de temps : C
· Cout d'entretien du stock : C??
· Cout de réapprovisionnement ou cout de
Lancement : C1
· Quantité commandé : Q
· Période optimale de gestion : 0
· La période de durée a: n
· Quantité a géré pendant n
période : q
Dans ce modèle, l'objectif est de déterminer les
moments de commande et les quantités à commander de
manière de manière à minimiser le cout total lancement et
du stockage.
b) Analyse du problème
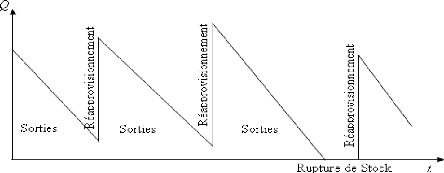
Le processus est la suivante : le stock atteint une
quantité donnée Q au moment du réapprovisionnement puis
diminue progressivement et de façon constante suivant la demande C.
Quand, il atteint le niveau nul, on lance une nouvelle
(réapprovisionnement) commande qui entre en stock aussitôt afin
d'éviter des ruptures de stocks.

Fig. II.1
En simplifiant la représentation nous obtenons un
graphique dit « en dent de scie »
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

18
Fig. II.2
En effet, dans ce modèle, les variables
contrôlables sont Q et la quantité d'un réapprovisionnement
mais la demande C et les couts éventuels c.-à-d. ???? et ????
sont non contrôlables.
c) Modèle et solution
Fig. II. 3

?? ?? ??
Dans le graphique ci-haut nous avons n périodes
de durée ??,
donc n.?? = n nous avons une quantité
q qui
devra être géré.
Pendant chaque période ?? le stock moyen est ?? 2.
Le coût d'entretien du stock pendant chaque ??
période est : ???? * ?? 2 * ?? étant donné qu'il y a n
période, le cout total d'entretien
s'élèvera à :
??
?? * 2 * ???? * ??
Et le coût total de réapprovisionnement sera : ??.
???? puis qu'il y
a n
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

19
Donc le Coût global a géré pendant la
période È sera :
???? ??+ ?? ???? (1)
???? = ?? ??
2
Sachant que ?? * È ? ?? = È ?? étant
donné qu'il y a n période ??
pendant È.
Normalement, la somme de la quantité de stock
utilisée pendant la durée de réapprovisionnement ?? doit
être égale à la quantité de stock disponible pendant
toute la période È de gestion.
Ce qui implique : ?? = È*??
??
En replaçant ?? * ?? par È et n par
È*?? dans (1), on aura :
??
????(??) = È * ?? 2 * ???? + È*??
?? * ???? (2)
L'équation (2) ci-haut est la quantité que l'on
veut minimiser, en la dérivant par rapport à q, les
éléments de cette relation sont représentés sur la
figure ci-après.
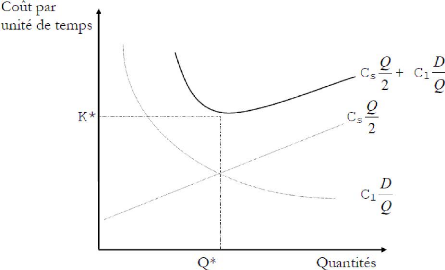
Fig.II.4
On remarque dans la fonction ci-haut que nous n'avons plus qu'une
variable : q.
Lorsque la quantité commandée augmente, le
coût d'approvisionnement (Lancement) diminue alors qu'au même
moment le coût de stockage (la détention du stock) augmente.
D'où, il faut trouver la quantité qui optimise la
fonction de coût.
Ainsi, on peut alors dérivé aisément et on a
:
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

20
?????? È
=
???? 2
Èc
????+??2 ???? ; (3)
|
????
Si
????
|
= 0
|
|
Alors È
2
|
????+ ÈC
q2 ????= 0
|
È???? 2
|
Èc È.?? È.????
+ ??2 ???? ??2 ???? =
2
|
|
??2 * È * ????= 2 * È * ??* ????
Èc 2 * ??* ????
??2 = -2 * * ???? =
È. ????
????
Donc ??2 = 2 * ?? * ????
????
Et on peut tirer la quantité économique à
commander
(4)
??* = v2 * ??* ????
È ????
Il faudra s'assurer qu'on a bien à faire un minimum :
la dérivée seconde doit nécessairement être
positive
??2????
????2
= 2 ?? ???? (5)
??3
L'équation (5) est toujours positive
c'est-à-dire ????et C sont positive et q l'est
toujours.
L'équation (4) est appelé « série
économique » et la valeur optimale de È est appelé
« période économique » correspondant à la valeur
de q est :
|
È=??* ??
|
Avec la
|
??=v2*?? È *??????? ?
|
(6)
|
On a : ??* = v2 * ????
??*?? ??
En remplaçant ??* dans (1) On a:
|
v2*?? È* ????
????
????* = ??*
2
|
????* ??+ ??* ???? (7)
|
Après une série de manipulation on trouve que :
????* = È v2 * ??* ????* ????= v2 * ??* È * ????*
???? (8)
On a donc interpréter ces résultat de cette
manière : en revenant l'expression (2) en fonction de
q, on constate que CT est la somme d'une fonction linaire de
q donc le graphe représentatif passe
par l'origine et d'une fonction de la forme ??/?? ,
représentée par un arc
d'hyperbole (voir figure à haut). La courbe
représentative de CT est donc asymptote à l'hyperbole
pour les petites valeurs de q et asymptotes à la droite pour
toutes grandes valeurs de q.
On constate que le minimum est atteint lorsque
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

21
È
|
*
2
??* =
??C'est-à-dire
|
????*
|
??=
|
È ??
|
|
????
|
|
v2??
|
* ????????
|
Et on a aussi ??* = È.??
??*
Connaissant ??* on peut alors avoir ??* = È.??
= È.v?? .????
2????
v2 ??*????????
Et on remarque que ??* > 1 si ???????? < È2.??
2 c.-à-d. que si???? < ???? * È2.??
2
On a donc intérêt à appliquer la formule
dès que le cout total de stockage de la quantité È * ??
pendant È dépasse le cout de lancement, ce qui est
vérifié dans la pratique.
Dans un contexte déterministe, Harris a donné
une réponse à la question « combien approvisionner ? ».
Il s'agit du concept de quantité économique ou EOQ. Harris a
démontré (formule dite de Wilson) que la quantité optimale
d'approvisionnement était égale à
??* = v2 * ??È * ????
????
Avec :
> Q : la quantité commandé ;
> È : la période de gestion ; > ???? : cout
d'entretien ; > ???? : cout de lancement.
| 


