I.2.1. Trace
Théorique
Le trace théorique consiste à décrire un
arc de cercle partant du point considéré comme origine a la
courbe voisine cela dans le but d'obtenir une succession d'alignements droits
polygonaux. Il consiste également à déterminer
sommairement le sens de cheminement de l'axe de la future route suivant une
pente donnée .
Pour parvenir à déterminer notre tracé
théorique, nous nous sommes référés aux
instructions du cahier de charge qui nous renseignent sur la
déclivité maximale à prendre en compte et
l'échelle du plan à courbe de niveau.
Ayant ces deux éléments, nous déterminons
la distance du cheminement par la formule suivante :  Echelle.
Avec : dch   distance réelle du cheminement
Dh  denivelée ou équidistance
i  déclivité
Pour notre projet nous avons une déclivité
maximale de 10% l'équidistance est de 1m et l'échelle de la
planche est de   d'où :
- d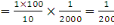 
- d  .
Cette distance réelle du cheminement correspond au
rayon à donner à l'ouverture du compas.
Trois cas peuvent se présenter dans l'étude du
tracé théorique selon que la distance entre deux courbes voisines
et inférieures, égales ou supérieures à la distance
réelle du cheminement d.
1ecas : L'arc du cercle coupe
la courbe en deux points distincts.
E
F
C
0Ici nous avons deux possibilités à exploiter
pour le cheminement.
B
K
Fig 5.a: tracé théorique quand l'arc de cercle
coupe la courbe en deux point.
Nous exploiterons le cheminement qui conduit au plus proche du
point à atteindre. Il est à retenir que ce cas se produit lorsque
la pente réelle du terrain est supérieure à la
déclivité maximale considérée.
2e cas : L'arc du cercle
coupe de la courbe en un seul point.
Il y a qu'une seule possibilité à exploiter
pour évoluer vers la courbe de niveau suivante.
575
0
576
Fig 5.b: tracé théorique quand l'arc de cercle
coupe la courbe en un seul point
L'arc de cercle coupe la courbe voisine en un point unique ce
qui revient à dire que cas indique que la pente du terrain est
égale a la déclivité imposée.
3e cas : L'arc du cercle ne
coupe pas la courbe suivante.
545
0
544
Fig.5.c: tracé théorique quand l'arc de cercle ne
coupe la courbe suivante
Dans ce cas, on a opté le cheminement du choix tendant
vers le point obligéautrement dit le vol d'oiseau. Ce cas indique que
la pente du terrain est inférieure à la déclivité
imposée.
I.2.2. Trace
Réel
Le tracé réel est une amélioration du
tracé théorique par une élimination des différente
lignes brisées rapprochés afin d'obtenir un alignement droits
raccordés deux à deux par des arcs de cercle appelés
courbes de raccordement.
Il est recommandé de ne pas trop s'écarter du
tracé théorique afin d'éviter de grand terrassements,
comme on devra aussi éviter de raccourcir systématiquement le
tracé au risque d'augmenter les déclivités.
Les précautions ci-dessus sont à prendre en
compte pour obtenir un bon tracé réel, car le tracé d'une
route est une opération très importante qui peut influencer les
facteurs techniques et économiques du projet.
Ne dépasse pas 20 à 25 cm
Tracé théorique
Tracé réel
Fig.6: tracé réel
0
| 
