La méthode du calcul du facteur á [i(t)J
pour les courbes de décharge s'articule principalement sur les
caractéristiques de décharge à 20°C. Ce facteur se
déduit de façon relatif ; par rapport à la courbe de
référence. La figure suivante illustre la méthodologie
permettant la détermination de ce facteur pour un courant de
décharge de 8.8A.
Projet fin d'étude Page Zied Jelassi

0,4)F,
a b
ba
Figure 2.15: Détermination du facteur á [i(t)]
pour un courent de décharge de 8.8A par rapport à un
courent
de référence de 0.9A
La détermination du rate factor utilise la forme
polynomiale de la courbe de référence et la courbe de
décharge. La différence à l'origine de l'axe des abscisses
entre ces deux représentations est égale à
(ir-i) Rint, où,
ir, i et Rint
représentent respectivement le courant de référence
(0.9A), le courant de décharge pour lequel on calcule le rate factor et
la résistance interne. Le terme b
représente la capacité maximale pour la
décharge de référence. Le terme a
représente l'intersection entre la forme polynomiale de la
courbe de référence atténuée par la quantité
(ir-i) Rint et la droite de la tension de
coupure y=2.5V. La valeur du rate factor est définit par
l'expression suivante :
a
á( i ) = (2.10)
b
Projet fin d'étude Page Zied Jelassi
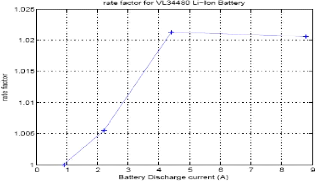
Figure 2.016: Rate factor á pour la batterie Li-Ion
VL34480 calculé pour un courant de référence de
0.9A
La figure précédente représente la courbe
á(i) calculé pour un courant de référence
de 0.9A, ce qui correspond à 0.2C rate et à 20°C.
2.4.3.2.2. Détermination du facteur â [T(t)] et
de ÄE(T)
La technique de détermination du facteur de
température et du potentiel de correction de la dépendance en
température s'appuie sur les courbes de décharge à courent
constant (0.9A) et à différents températures. La figure
illustre cette méthode appliquée à la détermination
du â(-30) et ÄE(-30).

azo
d c
Figure 2.17: Détermination du facteur de
température et du potentiel de correction de la dépendance
en
température
Projet fin d'étude Page Zied Jelassi
De la même façon, cette technique utilise encore
les formes polynomiales des caractéristiques de décharge.
Le terme ÄE(T) représente la
différence entre la forme polynomiale de la courbe de
référence et celle de la courbe de décharge mesurée
à une température T. Après la
détermination de cette valeur, on l'utilise dans le but de
déterminer le facteur de température. Le terme
d est la valeur de capacité pour laquelle le
polynôme de la courbe de décharge vaut 2.5V. Le terme
c représente la valeur de la capacité
pour laquelle le polynôme de la courbe de référence
affaibli par ÄE(T) vaut 2.5V.
La valeur du facteur de température est définit
par l'expression suivante :
c
â( T ) = (2.11)
d
Les figures suivantes présentent les résultats
d'extraction du facteur de température et du potentiel de correction de
la dépendance en température.

(a) (b)
Figure 2.18: Facteur de température (a) et potentiel de
correction de la dépendance de la température
(b) pour la
batterie VL34480 pour une température de référence de
20°C
Après la détermination de ces
paramètres, on arrive à exploiter les équations 15-17 pour
représenter les caractéristiques de décharge à
n'importe quelle température et pour n'importe quel taux de
décharge (ou encore pour n'importe quel courant de décharge).
Projet fin d'étude Page Zied Jelassi
2.4.3.3. Validation du
modèle
Pour la validation de ce modèle, on a utilisé
la superposition des résultats expérimentaux et de simulation. La
figure 2.19 représente la superposition de la caractéristique de
décharge pour 1C-rate et à 20°C fournie par Saft et celle du
modèle.

Figure 2.19: Comparaison directe entre la
caractéristique de décharge (4.4A, 1C) à 20°C et
la
caractéristique générée par le
modèle.
2.4.4. Discussion
Les trois modèles présentés se basent
à la fois sur une équation décrivant le comportement
électrochimique de la batterie et un circuit électrique simulant
son comportement électrique. En plus, ils sont tous dynamiques dans le
sens où on peut prévoir la caractéristique de
décharge de la batterie Li-Ion à différent C-rate. De
plus, ils s'appuient sur les données des fabricants, à savoir les
caractéristiques de décharge à courant constant et/ou
à température constante.
Les trois modèles sont présentés dans
l'ordre de complexité ; du plus simple au plus compliqué. Comme
il a déjà été précisé, les deux
premiers modèles sont inspirés des travaux de C. M. Shepherd. On
remarque bien la ressemblance entre leurs équations
électrochimiques et celle de ce dernier. La différence entre eux
a eu lieu pour détourner les problèmes de boucle
algébrique.
Projet fin d'étude Page Zied Jelassi
Le premier modèle est un modèle assez simple.
Il met en évidence une seule équation pour décrire le
chargement et le déchargement de différents types de batteries et
en particulier les batteries Lithium-Ion. Suivant le signe du courant, on
choisie entre la charge et la décharge.
Le deuxième modèle utilise une série de
paire d'équations suivant le type de batterie, une pour la charge et
l'autre pour la décharge. Par contre, ce modèle ne peut traiter
qu'un nombre limité de type de batteries, qui sont les batteries Li-Ion,
plomb-acide, NiCd et NiMH. La précision de ces deux modèles est
directement liée à la précision avec laquelle on estime la
position des trois points : le point de chargement total, le point qui marque
la fin de la zone exponentielle et celui qui désigne la fin de la zone
nominale et le commencement de la décharge rapide. Pour la
détermination de ces points, on a utilisé les courbes de
décharge publiées par Saft sur la datasheet de la batterie
VL34480. Pour les convertir sous forme de tableur, on a eut recours à un
logiciel de reconnaissance de courbes « CurveUnscan ». Comme les
données du composant Saft sont grossières et que le logiciel de
reconnaissance de courbe est entaché d'une certaine
non-précision, on considère que notre source de données
est moyennement précise.
Le troisième modèle utilise une
régression polynomiale de la caractéristique de
référence pour l'extraction des paramètres. Il emploie la
SOD comme variable de ce polynôme. Pour la détermination de cette
variable, on fait appel à deux facteurs, le facteur de
température et celui du taux de charge. L'idée de ce
modèle est de simuler le comportement de la batterie
considérée à une température et un courant de
décharge bien précis, au contraire des deux autres
modèles. La précision de ce modèle dépend de la
précision de détermination des facteurs á(i),
â(T) et ÄE(T) qui dépend à leur tour
de la précision des données du fabricant.
Les modèles déjà présentés
ont été validés pour des batteries autres que la batterie
Li-Ion et à faible densité énergique. Ces batteries
possèdent des caractéristiques de décharge «
classique » qui semble à la caractéristique de
décharge à 0.9A-C/5 rate et à 20°C. Comme les
caractéristiques de la batterie VL34480 sont compliquées, on a
éprouvé des difficultés à adapter ces
modèles à ce type de batterie à haute densité
énergétique.
Projet fin d'étude Page Zied Jelassi
Pour la validation de ces modèles, on a
préféré comparer directement les résultats de
simulations aux données disponibles sur la datasheet de la batterie VL.
On a superposé ces résultats pour mieux voir leurs ressemblances
et leurs différences. Les figures 2.6, 2.12 et 2.19 représentent
ces résultats.
Pour la validation du modèle d'O. Tremblay et L.A.
Dessaint, on remarque que la sortie de simulation suit celle fournie par le
fabricant. En ce qui concerne le modèle de MathWorks, la sortie est
presque identique à la figure prise de la datasheet. Le modèle de
L. Gao est le modèle le plus compliqué. Sa sortie ressemble en
forme à la caractéristique expérimentale. Mais, elle est
un peu au dessus d'elle.
Pour simuler le comportement de ses batteries, Saft dispose de
plusieurs modèle Simulink. La différence entre les modèles
présentés et les modèles de Saft réside dans la
précision.



