Reconnaissance des objets polyédriques

République Algérienne Démocratique et Populaire
Ministere de l'Enseignement Supérieur et de la Recherche Scientifique

Université Ferhat Abbas S'etif

Faculté des Sciences exactes Département Informatique

Mémoire de fin de cycle

En vue de l'obtention du diplôme d'ingénieur d'état en
Informatique

Theme

La reconnaissance des objets polyedrique

Encadr'e par: R'ealis'e par:

Mme Ait Kaci Azzou Samira M^r Saidani Abderrezak

Mr Felouah Mourad

Jury

Pr'esident :

_Mr

Examinateurs :

_Mr

_Mr

Table des matières

Table des Matières i

Table des Figures v

Introduction Générale 1

1 Les méthodes de reconstrution 3D 3

1.1 Introduction 3

1.2 La vision par ordinateur 3

1.3 description d'un systeme de vision par ordinateur 4

1.3.1 Definition 4

1.3.2 Classification des systemes de vision par ordinateur 5

1.3.2.1 Les systèmes de vision bidimensionnelle 5

1.3.2.2 les systèmes de vision tridimensionnelle 5

1.4 La reconstruction 3D 5

1.4.1 Les deffirentes approches de la reconstruction tridemensionnelle . 5

1.5 Techniques de reconstruction 3D 7

1.5.1 La vision stéréoscopique 7

1.5.1.1 Principe 7

1.5.1.2 L'appariement 8

1.5.1.3 La triangulation 8

1.5.2 Reconstruction a` partir de géométrie epipolaire 10

		1.5.3 Technique basésur les ombrages ou Shape from shading 1.5.4 Représentation par détection de déformation de formes 1.5.5 Méthodes basées sur l'extraction de squelette 1.5.6 La reconstruction par des jonctions caractéristiques 1.5.7 Shape From Motion: Reconstruction a` partir du mouvement . . . 13	12 12 13 14
		1.5.7.1 L'approche basée sur la mise en correspondance	15
		1.5.7.2 L'approche du flot optique	15
		1.5.8 Méthode par space carving (creusage d'un volume 3D)	16
	1.6	Conclusion	16
2	La reconnaissance des objets 3D		17
	2.1	Introduction	17
	2.2	Classification des systém de reconnaissance des objets polyedrique	18
		2.2.1 Acquisition et Représentation Informatique du modèle 3D	18
		2.2.2 Principales approches d'appariement	19
	2.3	La reconnaissance par apparence	25
		2.3.1 définition et caractérisation	25
		2.3.2 Modelisation globale	26
		2.3.3 Modélisation locale	27
	2.4	Conclusion	28
3	La conception et resultat d'experementation		29
	3.1	Introduction	29
	3.2	La reconnaissance des objets polyédrique	29
		3.2.1 Choix des primitives	29
		3.2.2 L'algorithme développépour la reconnaissance des objets polyédrique 30
		3.2.3 algorithme pour la localisation	30
		3.2.3.1 Estimation des primitives	31
	3.3	Calcul de la carte de profondeur	33
		3.3.1 Modèle géométrique de système de vision [Ait06]	33
		3.3.1.1 Description du système	33

3.3.2 Coordonnée projectifs avant et après rotation 35

3.3.3 Relations entre les cordonnes 2D et 3D 36

3.3.4 Conclusion 37

3.4 Suivi d'un segment dans une séquence d'images [ISR07] 38

3.4.1 'Equation de mouvement d'un segment I : 38

3.4.1.1 Application de la méthode 38

3.4.1.2 Algorithme De Suivi : 40

3.5 Résultat d'experementation 41

3.5.1 Application a` des images de synthése 41

3.5.2 Application a` des images réelles 44

3.6 Conclusion 47

4 Environnement de réalisation et d'expérimentation 48

4.1 Introduction 48

4.2 L'envirennement de l'experementation 48

4.3 Langage de programmation 48

4.4 Présentation de l'application 49

4.5 Conclusion 56

Conclusion Générale 57

Bibliographie 59

Annexe A 61

Annexe B 63

Table des figures

1.1 Sch'ema fonctionnel d'un système informatique pour la vision artificielle. . 4

1.2 Une reconstruction projective a` droite 6

1.3 Une reconstruction affine a` droite 6

1.4 Une reconstruction euclidienne a` droite 6

1.5 Synoptique g'en'eral de la vision st'er'eoscopique . 8

1.6 Une configuration possible d'un cube triangul'e. 9

1.7 La configuration miroir d'un cube triangul'e. 9

1.8 M'ethode de reconstruction. 11

1.9 application de la SFS sur une image 2D. 12

1.10 polygones triangulaires d'un lapin et d'une poire. 13

1.11 Squelettes topologiques de quelques objets 13

1.12 Type de jonction 14

1.13 Processus de reconstruction 3D a` partir d'un mouvement 16

1.14 M'ethode par space de l'objet 16

2.1 Sch'ema de l'algorithme d'indexation g'eom'etrique 21

2.2 Exemple de cas o`u un modèle est pr'esent dans la scène. Les coordonn'ees

d'un sous-ensemble des points du modèle sont les mêmes que celles d'un

sous ensemble des points de la scène. 22

2.3 sch'ema processus du d'indexation 24

3.1 Organigramme de la m'ethode de reconnaissance automatique des objets. . 30
3.2 Mod'elisation g'eom'etrique de la tête de vision st'er'eoscopique 34

3.3 Une sequence de trois images. 41

3.4 Extraction des segment de droite des trois images. 42

3.5 Calcul des angles de rotation. 42

3.6 La carte de profondeur. 43

3.7 La reconstruction projective de la scene. 43

3.8 Localisation de l'objet dans la scene. 44

3.9 Sequence d'image reelle 44

3.10 Extraction des segments de contours 45

3.11 Calcul des angle de rotation 45

3.12 La carte de profondeur 46

3.13 La scene reconstruite 46

3.14 Localisation de l'objet dans la scene 47

Remerciements

Nous remercions vivement notre promotrice M^me Ait Kassi Azzou Samira pour avoir acceptéde nous encadrer, et nous suivi durant toute l'année en assurant le suivi scientifique et technique du présent mémoire. Nous la remercions pour sa grande contribution a` l'aboutissement de ce travail, et pour s'être montrée disponible.

Nos remerciements vont aussi aux membre du jury pour l'honneur qu'ils nous fait en acceptant de juger notre travail.

Nous remercions tous qui ont participéde prés ou de loin a` l'élaboration de ce travail.

Auxquels Je dois Ce Que Je Suis
Que Dieu Vous Prot`ege

et Vous Prête Une Bonne Santéet Une Longue Vie

A MES FRERES ET SOEURS

Pour Les Encouragements Continus et L'aide Constant

A MON GRAND PERE et MA GRANDE MERE

A MES AMIS (ES)

A TOUS CEUX QUI M'ONT AIME'

Et Qui Ne Méritent Pas D'être Oubliés

J e dédie ce travail.

Abderrezak.

Auxquels Je dois Ce Que Je Suis
Que Dieu Vous Prot`ege

et Vous Prête Une Bonne Santéet Une Longue Vie

A MES FRERES

Pour Les Encouragements Continus et L'aide Constant

A MA GRANDE MERE

A MES AMIS (ES)

A TOUS CEUX QUI M'ONT AIME'

Et Qui Ne Méritent Pas D'être Oubliés

J e dédie ce travail.

Mourad.

Introduction Générale

La vision est le sens qui nous fournit le plus d'informations sur le monde extérieur, elle nous permet de voir, de décrire, et de reconnaàýtre les objets qui sont présent dans la scéne.

L'être humain est capable de reconnaàýtre les objets rapidement, avec une très grande précision, Cela est réaliségràace au système visuel humain qui est capable d'interpréter les informations sensorielles, c'est-à-dire les informations fournies par l'environnement au système visuel a` un instant donnée. L'interprétation est réalisée gràace au cerveau, qui peut reconnaàýtre et situer les objets, détecter le mouvement ...

Avec la naissance des machines de calcul, des recherches scientifiques sont effectuées, en essayant de concevoir une machine qui peut remplacer le système de vision humain, pour arriver a` des résultats similaires a` la vision humaine.

La vision par ordinateur consiste a` reproduire les résultats obtenus par la vision humaine sur un ordinateur en utilisant des moyens informatiques en remplacant l'oeil par une caméra et le cerveau par un ordinateur.

Un système informatique de vision par ordinateur utilise en entrée une ou plusieurs images numériques acquises a` l'aide de caméra ou d'appareil photo. Ces images subissent un ensemble de traitements dans le but d'extraire le maximum d'informations relatives a` la scène a` reconnaàýtre. Un système informatique de vision par ordinateur utilise en entrée une ou plusieurs images numériques acquises a` l'aide de caméra ou d'appareil photo. Ces images subissent un ensemble de traitements dans le but d'extraire le maximum d'informations relatives a` la scène a` reconnaàýtre.

Le but de notre projet est de contribuer a` la résolution du problème de la reconnaissance d'objets. L'idée de base est d'utiliser les caractéristiques discriminantes de la forme d'un objet pour le reconnaitre. Cette caractéristique correspond a` une partie de la forme du contour et la disribution des points d'interets de l'objet qui sera la seule donnée utilisée pour l'identifier. Pour ce faire, une base de données modèle est utilisée pour effectuer

Intoduction G'en'erale

la reconnaissance d'un objet pr'esent sur l'image. Cette base de donn'ees comporte une description de la partie caract'eristique des objets de la base.

Pour cela notre memoire est organis'e comme suit :

· Chapitre I : Les méthodes de reconstruction 3D Dans ce chapitre on a abord'e la notion de vision par ordinateur, les syst'eme de vision par ordinateur et leurs classification. on a aussi introduit une 'etude sur la reconstruction 3D et quelques m'ethode de reconstruction 3D

· Chapitre II : La reconnaissance des objets polyédrique Dans ce chapitre on a pr'esent'e une classification des syst'eme de reconnaissance des objets et quelque m'ethode de reconnaissance des objets 3D bas'e les histogrammes de couleurs et d'autres m'ethodes bas'ees sur l'apparence

· Chapitre III : on a pr'esent'e la m'ethode utilis'e pour la d'etermination de la carte de profondeur,afin de l'utiliser pour la reconstruction 3D.Ainsi une description de l'algorithme utilis'e pour la reconnaissance des objets poly'edrique.

· Chapitre IV : une description de l'envirennement dans lequel l'application a 'et'e d'evelopp'e, et une description de l'application.

Chapitre1

Les méthodes de reconstrution 3D

1.1 Introduction

La vision est un processus de traitement de l'information. Elle utilise des stratégies bien définies afin d'atteindre ses buts. L'entrée d'un système de vision est constituée par une séquence d'images. Le système lui même apporte un certain nombre de connaissances qui interviennent a` tous les niveaux. La sortie est une description de l'entrée en termes d'objets et de relations entre ces objets .

La vision par Ordinateur est a` la base de tout système de vision artificielle. Un système de vision traite les informations de bas niveau d'abstraction du flux vidéo et image pour en extraire des informations de plus haut niveau d'abstraction : présence d'entités, classe d'entités (document, chaise, mur) et plus précisément l'identitéde l'entité. Dans ce chapitre, on va donner quelque définition concernant la vision par ordinateur et les systèmes de vision et la classification de ces systèmes puis on parle de la reconstruction 3D en citant quelque méthodes utilisépour reconstruire des objets 3D.

1.2 La vision par ordinateur

La vision par ordinateur (aussi appelée vision artificielle ou plus récemment vision cognitive) constitue une des branches de l'intelligence artificielle, c'est un domaine d'investigation et d'applications nées a` la fin des années 50 dont les premières bases théoriques ont étédéfinies dans les années 60. Depuis, étant donnéle spectre très large d'applications, très peu de problèmes ont trouvédes solutions entièrement satisfaisantes. La recherche en vision est divisée en plusieurs approches différentes, chacune étudie des problèmes différents utilisant des techniques différentes.

La vision par ordinateur 2D met l'accent sur les techniques actuelles d'analyse d'image, d'apprentissage et de reconnaissance des formes. La vision par ordinateur 3D approfondit quand a` elle les approches permettant d'extraire d'une ou plusieurs images des informations tridimensionnelles relatives a` la scene photographi'ee. Par exemples l'industrielle, militaires, a'erospatiales, la t'el'ed'etection, la s'ecurit'e et m'edical [HOR 93].

La vision par ordinateur est la discipline qui cherche a` reproduire la perception visuelle humaine sur un ordinateur. Le processus d'acquisition d'images est effectu'e a` l'aide de cam'eras. Ces images seront trait'ees afin de produire une description des 'el'ements qui composent la scene 3D.

La figure 1.1 explique ce processus qui utilise un ensemble d'images et des connaissances afin d'aboutir a` une description d'une scene.

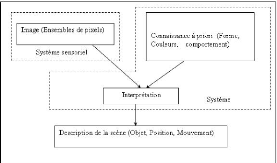
FIG. 1.1 - Sch'ema fonctionnel d'un systeme informatique pour la vision artificielle.

1.3 description d'un systeme de vision par ordinateur

1.3.1 Definition

Un systeme informatique de vision est un ensemble de processus fortement li'es et compos'es de mat'eriels et de logiciels. A l'aide de ces processus et des images prises de la scene, il fournit en sortie une description symbolique puis s'emantique de la scene observ'ee. La description est r'ealis'ee a` l'aide de l'identification des attributs de la scene et des objets qui la composent.

Le systeme informatique recoit en entr'ee une s'equence d'images qu'il traite en utilisant la connaissance sp'ecifique aux diff'erents niveaux de traitements, en sortie il fournira une description en termes d'objets et de relations entre ces derniers.

1.3.2 Classification des systemes de vision par ordinateur

Selon la nature de la scène observ'ee on d'etermin'e le type de système, on distingue deux type de système qui sont :

1.3.2.1 Les systèmes de vision bidimensionnelle

Ces systèmes permettent une acquisition de l'image de la scène 2D, ils n'exploitent pas la notion de profondeur et donc reconnaissent uniquement les objets plans et isol'es. Ces systèmes sont utilis'es dans des domaines spatiaux tels que la t'el'ed'etection et la reconnaissance de caractères, la robotique industrielle...

1.3.2.2 les systèmes de vision tridimensionnelle

Ces systèmes sont capables d'identifier les objets a` partir d'une image d'un monde tridimensionnel, c'est pour cela qu'ils sont utilis'es en robotique car ils permettent a` un robot de se d'eplacer dans un environnement inconnu a` obstacles

1.4 La reconstruction 3D

La reconstruction tridimensionnelle d'un ensemble de points informe sur la structure g'eom'etrique de ce même ensemble.

1.4.1 Les deffirentes approches de la reconstruction tridemensionnelle

· Reconstruction projective

Quand les points sont d'efinis dans un repère projectif. Une telle reconstruction ne contient donc pas d'information critique (absence de la notion d'angle, de longueur, parall'elisme ... ).

FIG. 1.2 - Une reconstruction projective a` droite

· Reconstruction affine

Quand les points sont définis dans un repère affine. Une telle reconstruction contient des informations affines (rapport de longueurs, parallélisme).

FIG. 1.3 - Une reconstruction affine a` droite

· Reconstruction euclidienne

Quand les points sont définis dans un repère euclidien. Cette dernière reconstruction est la plus riche; elle contient les informations que l'homme a l'habitude de manipuler. Nous parlerons dans ce cas de reconstruction euclidienne, car le facteur d'échelle absent ici ne pose pas de problème particulier.

FIG. 1.4 - Une reconstruction euclidienne a` droite

1.5 Techniques de reconstruction 3D

Il existe de nombreuses techniques de reconstruction 3D, On peut répertorier une grande partie des méthodes de reconstruction dans ces quatre catégories :

· Reconstruction a` partir de la texture (Space carving [KUT00]) : Cette méthode basée sur le calcul d'un critère de photoconsistence nécessite d'avoir une lumière constante et homogène tout autour de l'objet.

· Reconstruction a` partir de la géométrie épipolaire[HAR00] : C'est la méthode la plus classique étant donnéqu'on utilise déjàla géométrie épipolaire pour initialiser l'asservissement visuel et que l'on peut estimer les positions des caméras.

· Reconstruction a` partir des contours [BOY97], [LAU95] : Baser la reconstruction 3D sur les contours de l'objet semble être difficilement envisageable sur un objet naturel de forme quelconque avec des contours très irréguliers.

· Reconstruction a` partir du mouvement de la caméra (Factorisation de Tomasi et Kanade) [TRI96].

1.5.1 La vision stéréoscopique

1.5.1.1 Principe

La Vision Stéréoscopique vise a` reconstruire la structure 3D d'une scène. Afin de réaliser cette reconstruction il est nécessaire de connaitre les coordonnées 3D de tous les points d'une scène. La scène est représentée par un couple d'images stéréoscopique. Ces images sont deux représentations de la scène prises sous des angles différents. Chaque point de la scène est projetédans les images de la paire stéréoscopique a` des positions différentes. En vision stéréoscopique pour disposer des coordonnées 3D d'un point il faut disposer des coordonnées de ses deux projections, respectivement dans les images gauches et droites. L'obtention des coordonnées de ces deux projections d'un même point 3D est réalisée gràace a` une phase d'appariement qui vise a` trouver, pour un point donnédans une image,son point correspondant dans l'autre image. Ces deux points sont les projections respectives du même point 3D dans les images droite et gauche.

Le principe de la vision stéréoscopique est résumédans le schéma synoptique de la figure 1.5. Il est a` noter qu'en amont des étapes de la figure 1.5 il est nécessaire de réaliser la calibration du système stéréoscopique de facon a` disposer des paramètres intrinsèques et extrinsèques du système. Ces paramètres seront essentiels dans les phases de rectification et de calcul des positions 3D des points.

La stéréoscopie procède par appariement puis une triangulation

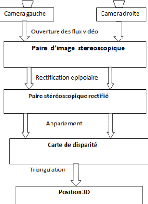
FIG. 1.5 - Synoptique g'en'eral de la vision st'er'eoscopique .

1.5.1.2 L'appariement

Il consiste a` d'eterminer les projections qui se correspondent dans deux images,c'est a` dire quels sont les points 2D repr'esentant les projections d'un même point 3d. Un appariement est donc un n-uplet de points 2D en correspondance

1.5.1.3 La triangulation

C'est une technique d'interpolation de surface, et l'interpolation de surface est le passage du modèle volumique au modèle surfacique. On peut classer la triangulation en deux cat'egories qui sont

· Celle qui s'appuie sur une surface d'efinie implicitement.

· Celle qui s'appuie sur un nuage de points repr'esentant la surface de l'objet

1. La triangulation des surfaces implicites

1. L'algorithme des marching cube

Afin de repr'esenter un volume de donn'ees, on divise ce volume en petits cubes, on fixe un seuil de densit'e par lequel va passer la surface et, a` l'aide des points d'intersection entre les cubes et la surface on polygonise cette dernière et on affiche le r'esultat a` l''ecran. La première difficult'e sous-jacente a` cet algorithme est que, si l'on traite tous les cas de façon s'epar'ee, on a 256 possibilit'es a` traiter (il existe 256 façons qu'une surface courbe peut intersect'e les arêtes d'un cube). Heureusement,

en mettant a` contribution la sym'etrie de rotation on peut r'eduire ce nombre a 23 cas qu'il nous faut traiter s'epar'ement. Dans l'article de Cline et Lorensen [LC87], on parle ici de 14 cas au lieu de 23 car les sym'etries de r'eflexions sont aussi mises a` parti. Cependant, après une 'etude approfondie de la question, il s'est av'er'e que si les symetries de r'eflexion sont utilis'ees des trous ou des inconsistances seront g'en'er'ees dans la surface. Ceci vient du fait que, dans certains cas, la surface se trianguler de façon diff'erente si les sommets du cube qui 'etaient a` l'int'erieur de l'objet passent a` l'ext'erieur et vice-versa. Par exemple si l'on regarde les figures 1.6 et 1.7 qui sont la sym'etrie l'une de l'autre, on peut voir que la surface peut se trianguler de deux façons diff'erentes (les points noirs repr'esentent les sommets du cube a` l'int'erieur de l'objet).

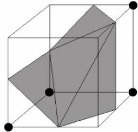
FIG. 1.6 - Une configuration possible d'un cube triangul'e.

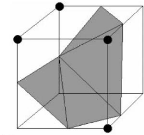
FIG. 1.7 La configuration miroir d'un cube triangul'e.

2. Triangulation a` partir d'un nuage de points

Construction d'un nuage de points pour chaque voxel¹ surfacique en estimant le point par lequel passe la surface,la densit'e du voxel et la normal sont utilis'e pour estimer la position de ce point.

1.5.2 Reconstruction a` partir de géométrie epipolaire

Les principales 'etapes sont repr'esent'ees sur la Figure1.8 .L'extraction de points et l'appariement se font exactement comme pour l'asservissement visuel, a` la diff'erence que l'on travaille sur une s'equence d'images. L''etape de calibration de la paire st'er'eo doit se faire sur des images prises sur le site sans changer les paramètres intrinsèques et extrinsèques des cam'eras. Les paramètres intrinsèques varient en fonction du changement de focale. On utilisera une mire car l'autocalibrage est plus contraignant, n'ecessitant des mouvements sp'ecifiques de la cam'era. On supposera que les paramètres intrinsèques ne varient pas durant toute la phase d'acquisition des images. Une première reconstruction projective est alors r'ealis'ee pour initialiser la suite de la reconstruction, par une m'ethode d'ajustement de faisceaux (Bundle Adjustment).

Ensuite un appariement dense des points appartenant a` la structure est calcul'e a` partir de, paires d'images rectifi'ees (La rectification des images est 'egalement utilis'ee pour l'appariement des points servant a` l'asservissement des cam'eras. Enfin une carte de profondeur dense est calcul'ee pour chaque point appari'e, puis les points 3D sont reli'es entre eux par triangulation (Delaunay). Le plaquage de textures sur les surfaces finit de donner un aspect photo-r'ealiste a` l'objet reconstruit.

Cette m'ethode de reconstruction doit être appliqu'ee sur chaque sous-ensemble de s'equence d'images correspondant a` chaque position du robot autour de l'objet, puis les diff'erentes parties reconstruites sont alors assembl'ees. Il est courant de reconstruire a` partir de sous-ensembles d'images puis de fusionner les modèles partiels ainsi obtenus par une phase d'alignement 3D. Les algorithmes de reconstruction et d'alignement s'appuient sur des correspondances de points ou de droites entre les images. La localisation de ces points ou droites dans les images est affect'ee par un bruit de mesure, influencant la qualit'e des modèles 3D reconstruits.

'Des images 3D sont des images qui représentent une sc`ene en trois dimensions. Le » pixel » est alors appeléun voxel, et représente un volume élémentaire.

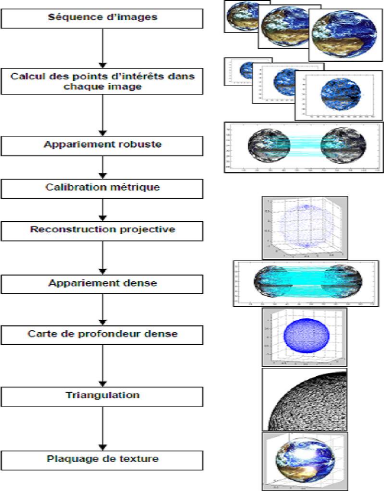
FIG. 1.8 Méthode de reconstruction.

1.5.3 Technique bas'e sur les ombrages ou Shape from shading

Comme son nom l'indique, il s'agit d'extraire une forme a` partir des variations de lumières observées sur la surface d'un objet [ZHA 99], [KOZ 98] au début elle était très peu utilisée dans les systèmes de vision, une des raisons de cet état de fait est l'absence d'algorithmes robustes capables de retrouver les détails fins et discriminants des surfaces des objets (voir figure 1.9). Récemment des études de possibilitéd'utiliser le shape from shading SFS dans la reconnaissance d'objets 3D sont faites [KOZ 98].

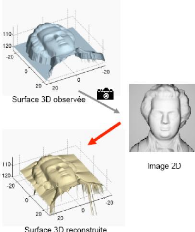
FIG. 1.9 - application de la SFS sur une image 2D.

1.5.4 Repr'esentation par d'etection de d'eformation de formes

Cette approche décrit une nouvelle représentation des formes déformables basées sur des polygones triangulaires (voir figure 1.8), [BAR 98][Cou 2000][Blu 67]elle cherche une structure de correspondance de calibre déformable, o`u on veut trouver une transformation non rigide qui dresse la carte d'un modèle a` une image. Le problème poséest la correspondance de la forme a` l'image, ce dernier est défini en termes d'une fonction d'énergie. Cette fonction d'énergie associe un coàut a` chaque transformation potentielle du modèle. Typiquement la fonction d'énergie est une somme de deux termes, le premier rapproche le modèle déformé, des caractéristiques d'image, tandis que le deuxième pénalise les grandes déformations du modèle. La recherche sur des transformations est faite efficacement en

exploitant les propriétés de cette représentation pour les formes déformables. Cette approche donne une solution optimale globale au problème de correspondance qui permet de détecter des objets déformables sans aucune sorte d'occlusion et le désordre de fond.

FIG. 1.10 - polygones triangulaires d'un lapin et d'une poire.

1.5.5 Méthodes basées sur l'extraction de squelette

La représentation des formes en squelette est introduite par Blum [Bub 98]. Elle a la possibilitéde conserver sous forme compacte un grand nombre d'informations topologiques et géométriques de la forme initiale. Un autre avantage qu'il faut signaler est le fait que les squelettes ont une structure de graphe (voire figure 1.9) qui permet d'utiliser les puissants outils issus de la théorie des graphes. Le squelette d'un objet est une représentation de la forme dans une dimension inférieure. Pour un objet surfacique (2D), le squelette est un ensemble de lignes centrées dans la forme, par contre pour les objets 3D il existe deux types de squelettes. Les squelettes surfaciques qui sont un ensemble de surfaces centrées dans la forme et les squelettes curvilignes 3D qui sont un ensemble de lignes centrées dans la forme.

FIG. 1.11 - Squelettes topologiques de quelques objets.

1.5.6 La reconstruction par des jonctions caractéristiques

Cette méthode est proposée par R.BERGEVIN et A.BUBEL [Het 95]. Elle est basée sur l'extraction des branches de jonction d'objets tridimensionnels aux points d'intérêt dans une image 2D en utilisant un processus de regroupement topologique (Figure1.12).

Pour la reconstruction des objets 2D, avec cette méthode il faut construire un graphe, o`u les noeuds sont les points de jonctions, les arcs sont les contours participant a` la jonction, en suite ce graphe est exploitépour extraire la structure des contours composant l'objet .Le principe de cette méthode est de subdiviser l'image en petites fenêtres pour faciliter l'extraction des jonctions possible. Chaque fenêtre est analysée en la binarisant, puis on extrait les branches en appliquant des opérateurs qui mettent en évidence les lignes de

direction prédominantes [ZHO 96]. A la fin, l'ensemble des branches extraites est organiséen graphe et les positions de jonction extraite sont structurellement validées puis raffinés.

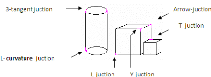
FIG. 1.12 - Type de jonction

1.5.7 Shape From Motion : Reconstruction a` partir du mouvement

L'analyse du mouvement et l'interprétation visuelle d'une sc`ene sont extrêmement liés. En particulier, le mouvement du capteur autour d'un objet peut permettre a` l'observateur de mieux comprendre la forme et la structure de l'objet. En réalitél'origine du mouvement revient a` trois fqcteurs facteurs :

· Le mouvement de l'observateur en respectant la sc`ene (Déplacement de la caméra dans le cas de la stéréoscopie)

· Ou le mouvement des objets dans la sc`ene

· La camera et l'objet de la sc`ene se deplacent Le domaine de suivi de mouvement se divise en deux taches principales :

· Détection de mouvement : consiste a` trouver les objets en mouvement dans la sc`ene par l'utilisation des séquences d'images captées a` des moments différents.

· Estimation de mouvement : consiste a` estimer le déplacement de certaines primitives de l'image.

Différentes approches (approche de flot optique, approches de mise en correspon-
dance; sont utilisées pour la détermination de mouvement et la structure tridimen-

sionnelle de l'objet. Cette dernière, consiste a` trouver les coordonnées 3D d'un points P a` partir d'une séquence d'images. En déplacant une caméra autour d'un objet, on peut construire sa structure tridimensionnelle.

1.5.7.1 L'approche basée sur la mise en correspondance

Cette approche utilise les techniques de l'appariement des indices pour l'estimation du mouvement et le suivi d'objets, ces primitives sont généralement des coins, des segments [Mar 01]. La suite des positions de ces indices visuels dans plusieurs images permet, si l'on utilise suffisamment d'indices appartenant au même objet d'obtenir le mouvement 3D de celui ci. Le principe consiste en un système a` huit équation de la forme

E = T × R

tel que T est une translation et R est une rotation, connaissant huit points de l'objet, la décomposition de E en valeurs singulières permet de retrouver les paramètres du mouvement et la structure 3D. L'estimation du mouvement a` partir des droites donne de meilleurs résultats que ceux donnés par des points caractéristiques.

1.5.7.2 L'approche du flot optique

L'utilisation de cette méthode consiste a` extraire l'information de la vitesse a` partir d'une séquence d'images avec l'hypothèse que l'intensitédes pixels des objets est conservée au cours du déplacement. Le calcule du flux optique consiste a` extraire un champ de vitesses a` partir d'une séquence des images en supposant que l'intensité(ou la couleur) est conservéau cours du déplacement. Sous cette hypothèse, on peut établir une relation entre la vitesse apparente v (déplacement dans l'image d'indices visuels tels que des régions délimitées par des contours supposéreprésenter la projection du mouvement 3D des objets de la scène et /ou du mouvement de la caméra) et les variations spatio-temporelles de l'intensité.

Le principe de cette technique est résumédans les quatre étapes suivantes :

1. La caméra prend plusieurs images de la scène.

2. Détection de mouvement (approche de flot optique, mise en correspondance).

3. Estimation de mouvement (angles de rotation, matrice fondamentale, vecteurs de translation. . .etc.)

4. Estimation de la carte de profondeur .

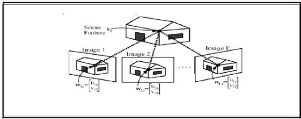
FIG. 1.13 - Processus de reconstruction 3D a` partir d'un mouvement

5. Reconstruire le modèle 3D d'après la carte de profondeur calculée.

1.5.8 Méthode par space carving (creusage d'un volume 3D)

FIG. 1.14 - Méthode par space de l'objet

· Algorithme Algorithme de space carving [PMJ2009])

1. Initialiser un volume englobant fait de N x M x P voxels

2. Choisir un voxel sur la surface courante

3. Projeter ce voxel sur les caméras sur lesquelles il est visible

4. 'Eliminer (ou << creuser >>) si non photo-cohérent

5. Répéter 2-3-4 jusqu'`a convergence

1.6 Conclusion

Dans le présent chapitre on a abordéla notion de la vision par ordinateur et la définition correspondante au système de vision par ordinateur et la classification de ces systèmes selon un critère de profondeur.

On a aussi introduit un aperçu sur quelque méthode de reconstruction 3D en montrant leurs définitions et leurs principes.

Chapitre2

La reconnaissance des objets 3D

2.1 Introduction

La reconnaissance d'objets tridimensionnels est un problème qui ne cesse pas de d'efier la communaut'e de vision par ordinateur. La preuve de l'existence de la solution (le système de vision humain), motive les chercheurs dans ce domaine. Ce problème peut être d'efini par la reconnaissance des objets pr'emod'elis'es dans une base de donn'ees a` partir des donn'ees acquises de la scène. La reconnaissance signifie l'identification et la localisation des objets pr'esents dans la scène. Un système de vision »intelligent» doit être capable de reconnaàýtre les objets existants dans son environnement (identification) et les situer (localisation). La majorit'e des systèmes de reconnaissance d'objets actuels tente de r'esoudre ce problème, en se basant sur un modèle (les objets sont connus a` priori). La plupart de ces systèmes travaillent sur des objets dits rigides (non d'eformables) ou articul'es. Un Système de Reconnaissance d'Objets (SRO) complet comprend diff'erents modules : calibration de capteurs, mod'elisation 3D, traitement d'images de la scène et la reconnaissance proprement dite. Selon le type de capteurs utilis'e, la reconnaissance d'objets 3D peut être trait'ee en 3D/3D (capteurs t'el'em'etriques, st'er'eoscopiques ou s'equences d'images) ou en 2D/3D bas'ee sur une seule image de luminance. L'approche t'el'em'etrique pose des problèmes de mise en oeuvre, de limite de port'ee et de lenteur. L'approche a` plusieurs images (st'er'eo ou s'equences) possède des difficult'es d'appariement entre les diff'erentes images d'entr'ee. Une seule image d'entr'ee ne fournit pas d'informations 3D (profondeur), elle donne lieu a` un grand nombre d'hypothèses sur la reconnaissance. Peu de Systèmes de Reconnaissance d'Objets utilise la dernière approche.

2.2 Classification des syst'em de reconnaissance des objets polyedrique

De nombreuses approches au problème de la reconnaissance d'objets 3D ont 'et'e d'evelopp'ees dans la litt'erature. Elles peuvent être classifi'ees selon les m'ethodes et techniques mises en oeuvre :

· Acquisition et repr'esentation informatique du modèle 3D.

· Approche utilis'ee pour l'appariement.

2.2.1 Acquisition et Repr'esentation Informatique du modèle 3D

Les m'ethodes les plus connues pour l'acquisition du modèle 3D sont la CAO, les capteurs actifs (t'el'emètres laser) et les capteurs passifs (cam'era unique, st'er'eo ou plus). Elles impliquent des m'ethodes de repr'esentation de donn'ees adapt'ees.

1. Méthodes basées sur La CAO

L'approche Conception Assist'ee par Ordinateur (CAO) est la plus dominante car elle d'ecrit un modèle 3D sans erreur de capture; elle est applicable aux environnements industriels. En revanche, elle possède des inconv'enients majeurs :

· L'implication d'un op'erateur humain lors de la mod'elisation de la scène.

· La difficult'e d'application pour des objets naturels.

Plusieurs types de repr'esentation du modèle 3D adapt'es a` la CAO existent

· volumique, la g'eom'etrie constructive des solides consiste en la repr'esentation de l'objet a` mod'eliser en diff'erents 'el'ements simples qui s'appellent primitives et a` les lier par des op'erateurs ensemblistes (union, intersection, etc.)

· Surfacique, la repr'esentation par les bords (BREP : Boundary REPresentation) permet de construire un modèle face/arête/sommet.[SHA99]

2. Méthodes basées sur des mesures capteurs

La m'ethode des capteurs t'el'em'etriques est plus facile a` employer mais elle introduit des mesures impr'ecises et incertaines dans la phase de reconnaissance. Il faudra toujours r'epondre a` certaines questions lors de l'acquisition telles que : »combien de vues fautil pour couvrir toutes les informations n'ecessaires ?» ou»comment faut-il segmenter les images pour obtenir les descriptions surfaciques ou volumiques de l'objet ?». Ce sont des questions auxquelles il est difficile de r'epondre et qui constituent des problèmes ouverts en recherche. Les m'ethodes d'acquisition des modèles 3D en utilisant des capteurs photom'etriques (une seule cam'era statique ou en mouvement, avec ou sans mod'elisation des sources lumineuses, deux cam'eras ou plus), sont les plus difficiles a` mettre en oeuvre. En

effet, elles posent les mêmes problèmes que les m'ethodes appliqu'ees aux capteurs actifs en sus du problème de la projection perspective et de la perspective inverse. Plusieurs techniques ont 'et'e utilis'ees pour calculer la position 3D (techniques st'er'eos, s'equences d'images, etc.) Ces m'ethodes sont rarement employ'ees pour l'acquisition des modèles 3D dans les SRO. Mais, elles sont prometteuses car moins on'ereuses, plus g'en'erales et adapt'ees a` de nombreux environnements. La repr'esentation des scènes r'ef'erenc'ee capteurs peut se d'ecomposer en deux types selon ceux-ci (actifs ou passifs). Le problème d'ecisif de la repr'esentation est la segmentation des donn'ees en primitives fiables pour la reconnaissance. Or, le processus de segmentation est d'etermin'e par le type de repr'esentation utilis'e. En g'en'erales repr'esentations 3D sont surfaciques ou volumiques.

La capture passive des scènes est la plus proche du système de vision humaine. L'utilisation des images de niveaux de gris introduit elle aussi le problème de segmentation. Les deux principales m'ethodes utilis'ees a` ce niveau sont l'approche contour et l'approche r'egion. Il existe d'ailleurs des systèmes qui m'elangent les deux approches.

2.2.2 Principales approches d'appariement

L'appariement ou la mise en correspondance entre la scène et son modèle 3D est le point crucial d'un SRO. L'approche de l'appariement utilis'ee dans un SRO marque souvent ses performances. Nous pr'esentons ci-dessous un aperçu de la complexit'e algorithmique de ce problème, puis les principales approches de r'esolution.[SHA99]

Complexitéde l'appariement

soit :

O : l'ensemble des caract'eristiques d'un objet (sommets et/ou arêtes et/ou faces ...) D : l'ensemble des caract'eristiques des donn'ees de son image

n : le nombre des caract'eristiques de l'objet

m : le nombre des caract'eristiques des donn'ees de son image

l min (n, m); m >= n car il y a souvent plusieurs objets dans la scène, dont le modèle 3D n'est pas connu. Une solution optimale peut être trouv'ee en cherchant tous les appariements possibles. Du fait d'occlusions et de caract'eristiques du capteur utilis'e, il faut comparer un sous-ensemble (de taille i) de D et de O [HORAUD 1993]. Le nombre de possibilit'es d'appariement entre O et D est :

N=	X j i=k	cn i .cm i .i! =	X j i=k	n! (n - 1)!.i! ×	m!	= m!.n!.	X j i=k		1

k repr'esente le nombre d'appariement minimal pour trouver une transformation objet/capteur. N s'accroàýt rapidement en fonction du nombre d'objets dans la base.

Exemple Soit un objet contenant 18 sommets, l'extraction de ces sommets dans une image 2D fournit 11 points. Le nombre de possibilit'es d'appariement

_c11

i .c18

i .i! = 4.34 × 10³⁴

1 1

N= _X

i=3

Pour trouver une solution optimale, il faut v'erifier toutes ces possibilit'es.

solution

Deux techniques d'appariement pr'edominent :

· l'approche graphe.

· l'approche hachage g'eom'etrique (indexation g'eom'etrique).

L'approche bas'ee sur les règles d''evidences peut compl'eter les deux approches pr'ec'edentes

1. Travaux basés sur l'approche graphe

Dans l'approche graphe, les noeuds repr'esentent les primitives de l'objet et les arêtes repr'esentent les relations entre elles. Le problème se ramène donc a` un problème d'isomorphisme, puisque la scène est en g'en'eral un sous graphe du graphe de l'objet. Malheureusement ce problème NP-complet<sup>1</sup> est très difficile a` r'esoudre et devient insoluble quand le nombre de modèles dans la base est important. Les essais pou r'eduire la taille du graphe utilis'e pour l'appariement ont conduit a` des diff'erentes techniques.

Ayache et Faugeras [AYA 86] ont propos'e l'utilisation d'un triplet de segments ayant un sommet commun. Cette technique permet de r'eduire consid'erablement le nombre d'appariements possibles. Lowe [LOW 87] a propos'e l'am'elioration du traitement d'images. Il a 'etabli des critères de regroupement des indices 2D afin d'obtenir des primitives consistantes qui facilitent l'appariement. Par ailleurs, un degr'e de probabilit'e est attribu'e a` une hypothèse d'appariement afin de r'eduire l'espace des solutions et enfin, une reconstruction 3D est effectu'ee pour v'erifier les hypothèses d'appariement.

Pampagnin et Devy [PAMP91] ont introduit le Graphe de Compatibilit'e qui regroupe dans ses noeuds toutes les hypothèses d'appariement entre une chaàýne de segments 2D et une face d'un aspect du modèle 3D dont les arcs repr'esentent les compatibilit'es entre hypothèses d'appariement. L'utilisation du Graphe d'Aspects permet de limiter la taille du graphe de compatibilit'e.

2. Travaux basés sur l'approche du hachage géométrique

Lamdan et Wolfson [LAM 1988] ont introduit le Hachage G'eom'etrique (HG). Il
consiste en la cr'eation hors ligne d'une table de hachage (TabH) et une reconnais-
sance en ligne. La table de hachage contient les diff'erents aspects des objets du

'Ensemble des problèmes pouvant être résolus par des algorithmes Non déterministes en temps Polynomial. Complet : veut dire qu'il n'existe pas un algorithme P efficace pour le résoudre [SED 90].

modèle 3D, exprim'es dans des bases diff'erentes (une base peut être repr'esent'ee par 2, 3 points ou arêtes) [WOLFSON 1992]. Cette expression est bas'ee sur des invariants ou des quasi invariants g'eom'etriques [BIN 1993] et [GROS 1995]. Pour chaque entr'ee dans cette table, il y a une liste des modèles susceptibles de satisfaire l'appariement. La reconnaissance en ligne est obtenue par mise en correspondance de points 2D, exprim'es a` leur tour dans diff'erentes bases, avec le contenu de la table de hachage. Cette approche a l'avantage de r'eduire l'espace de recherche des modèles possibles, sp'ecialement dans les grandes bases de donn'ees (problème d'indexage). Son d'efaut est l'augmentation rapide de la taille de la table de hachage en fonction du nombre de modèles.

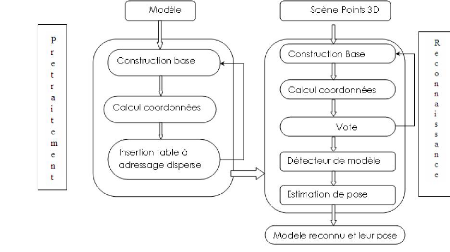
2.1.l'algorithme d'indexation géométrique

L'algorithme d'indexation g'eom'etrique est sch'ematis'e a` la figure 2.1 . Il se divise en deux phases, une phase de pr'etraitement (hors-ligne) et une phase de reconnaissance (en-ligne). Cette subdivision permet de r'eduire le temps de r'eponse a` l'usager, en effectuant une seule fois le pr'etraitement sur la banque de modèles, avant d'appliquer la reconnaissance sur plusieurs scènes diff'erentes. [BUS2001]

1.

FIG. 2.1 - Sch'ema de l'algorithme d'indexation g'eom'etrique

Prétraitement La phase de prétraitement consiste en trois étapes, qui sont répétées pour chacun des modèles reçus en entrée. Tout d'abord, une base est construite avec trois points du modèle. Ensuite, les coordonnées de chaque autre point du modèle sont calculées dans cette base. Finalement, ces coordonnées sont insérées dans une table a` adressage dispersé(hash table), avec quelques autres informations pertinentes (le modèle, la base et le point). Ces étapes sont répétées pour toutes les bases possibles dans le modèle. Il y a donc de la redondance dans le traitement, mais ceci est fait pour permettre la reconnaissance même si un des points d'une base n'est pas présent (ou est trop bruité) dans la scène. C'est ce qui fait que l'indexation géométrique est robuste aux occultations, c'est a` dire les cas o`u certains objets ne sont que partiellement visibles dans la scène.

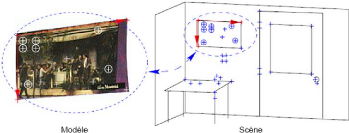
FIG. 2.2 - Exemple de cas o`u un modèle est présent dans la scène. Les coordonnées d'un sous-ensemble des points du modèle sont les mêmes que celles d'un sous ensemble des points de la scène.

C'est le fait de calculer les coordonnées des points du modèle dans une base formée elle aussi de points du modèle, qui fait en sorte que l'indexation géométrique permet de reconnaàýtre un modèle peu importe sa pose dans une scène 3D. En effet, lorsqu'un modèle est présent dans une scène, il y a une transformation qui amène un sous-ensemble de points du modèle vers un sous-ensemble de points de la scène. Comme les coordonnées de ces points du modèle coincideront avec celles des points correspondants de la scène, l'algorithme détectera ce modèle. La figure 2.2 en montre un exemple. Le modèle est un poster et, dans la scène, ce poster est accrochésur le mur, au dessus de la table. Les coordonnées qui coincident sont encerclées. [BUS2001] En bref, le but du prétraitement est d'extraire des informations utiles concernant les modèles et de les emmagasiner de façon rapidement accessible. La reconnaissance consiste a` extraire des informations similaires dans la scène et a` chercher si elles sont présentes dans les modèles. Essentiellement, les informations utilisées sont des

descriptions g'eom'etriques des modèles, invariantes a` leur position et orientation dans l'espace. Ceci gràace a` la formation de r'ef'erentiels de coordonn'ees (ou bases) a` partir de points de chaque modèle, dans lesquels le reste du modèle est repr'esent'e. L'indexation g'eom'etrique est une approche de reconnaissance d'objets robuste aux occultations, c'est-à-dire les cas o`u certains modèles pr'esents dans la scène ne sont que partiellement visibles. Elle permet d'effectuer la reconnaissance simultan'ee de plusieurs objets dans une banque de modèles efficacement, sans besoin de traiter chacun ind'ependamment. Aussi, il est possible de choisir le type de transformation qui nous int'eresse entre un modèle et son instance dans la scène, que ce soit par exemple des transformations rigides, similaires ou affines.

Reconnaissance La phase de reconnaissance d'ebute de la même façon que la phase de pr'etraitement. Une base est construite avec trois points de la scène, puis les coordonn'ees de chaque autre point de la scène sont calcul'ees dans cette base. Pour chacune de ces coordonn'ees, un vote est effectu'e. Le vote se fait de la façon suivante. Premièrement, on cherche dans la table a` adressage dispers'e les bases de modèle qui, au pr'etraitement, ont donn'e des coordonn'ees approximativement 'egales a` celles du point de la scène. Deuxièmement, l'ensemble des points ayant servir a` construire la base du modèle est compar'e a` l'ensemble des points ayant servi a` construire la base dans la scène pour valider la correspondance des bases. Si c'est le cas, un vote est ajout'e pour cette paire de bases. Dans l'algorithme original, le vote est toujours unitaire, mais on peut aussi utiliser un vote pond'er'e ayant un poids variable entre 0 et 1, selon la distance entre les coordonn'ees. Une fois le vote compl'et'e, une nouvelle base est choisie dans la scène et les 'etapes pr'ec'edentes de la phase de reconnaissance sont r'ep'et'ees jusqu'àce que toutes les combinaisons de trois points de la scène aient 'et'e parcourues (en r'ealit'e, il n'est pas n'ecessaire de traiter chacune des bases. Si une certaine paire de bases a obtenu un grand nombre de votes, un modèle est d'etect'e dans la scène. Les points de ce modèle sont retir'es de la scène, ainsi d'autres modèles pourront être reconnus en r'ep'etant la phase de reconnaissance (nous verrons que ceci peut être fait d'une façon plus efficace). Finalement, la position des modèles reconnus dans la scène est d'etermin'ee par une estimation de pose. [BUS2001]

Le processus d'indexation Le processus d'indexation analyse une image et essaye de trouver quels objets y sont pr'esents dans la scène. L'impl'ementation actuelle permet l'analyse des images contenants un ou plusieurs objets a` la fois.

. Prend une image, elle peut contenir plus d'un objet

· Essaye de réduire au mieux le bruit contenu dans l'image

· Divise le graphe-image en composantes connexes de facon que chaque composante provienne au mieux possible d'un objet identique. Pour chacun de ces graphes le même processus d'indexation. :

(a) Extrait respectivement les figures fondamentaux et les intersections.

(b) Calcul le code de hachage pour chaque graphe et chaque intersection. Celui-ci est obtenu de la même facon que pour le processus de la base de données.

(c) Fournit la liste de modèle respectif en indexant dans la base de modèle.

Les modèles qui ont recus le plus de votes sont sélectionnés comme les candidats les plus proches de l'objet en question La même procédure est répétée pour le reste des composants connexes (objets) dans l'image [SOS92]

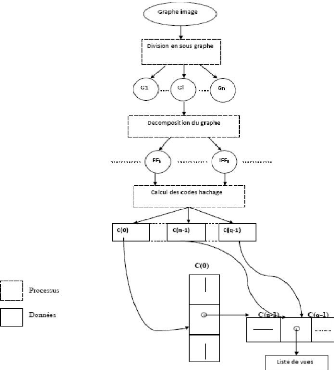
FIG. 2.3 - schéma processus du d'indexation

2.3 La reconnaissance par apparence

Dans la suite on va définir ce que nous entendons par reconnaissance par apparence, on va fournir une classification de principales méthodes existantes en exposant leurs avantages et leurs inconvénients

2.3.1 définition et caractérisation

La reconnaissance par apparence, toute méthode de reconnaissance qui cherche a` modéliser des objets (2D ou 3D) directement par leur image percue et non pas par un modèle construit a` partir d'une conception abstraite particulière. Le facteur commun a` toutes les méthodes qui entrent dans la catégorie » par l'apparence » est qu'elles modélisent des objets 3D par un ensemble d'image prises dans des conditions particulières. Ces conditions sont liées aux contraintes de reconnaissance qui sont imposées au problème que le système censéa` résoudre. Les conditions qui sont généralement considérées sont la plupart du temps liées aux changements d'éclairage ou au déplacement de l'objet dans l'image. Dans la majoritédes applications qui implémentent cette approche, elle est couplée a` une indexation, bien que ceci ne soit pas une condition obligatoire. Dans ce cas, la structure globale des algorithmes se présente comme montrée dans l'algorithme suivant : [LAM 98]

alogorithme1 : squelette d'une reconnaissance par l'apparence s'aidant d'une indexation.

Lors de la phase de reconnaissance, il n'est pas toujours necessaire que l'image pr'esent'ee soit une copie conforme d'un des modèles index'es. De facon g'en'eral, on distingue deux grands classes dans les m'ethodes de reconnaissance par l'apparence. L'une regroupe les approches qui considèrent une image comme une entit'e indivisible, donnant g'en'eralement lieu a` un index unique pour image. L'autre qui mod'elisent les objets par un ensemble de caract'eristique h'et'erogènes d'esignant des parties plus ou moins grandes dans l'image, on parlera de m'ethodes globales pour les unes, locales pour les autres.

2.3.2 Modelisation globale

Les mod'elisations globales sont principalement centr'ees autour d'une même approche, la m'ethode ne considère plus les images comme des matrices n x m de valeurs de niveau de

gris, mais comme des vecteurs de taille nm contenant ces mêmes valeurs. Ainsi, couvrant l'espace des apparences possibles d'un objet par Ó images modèles, il est possible de calculer une matrice de covariance de dimension nm x nm qui capte la variation entre les diff'erents modèles. La matrice est obtenue en calculant la moyenne M des vecteurs modèles Mi=l..k et en posant :

Ó= _Xk (Mi - M)(Mi - M)^k

i=1

Les vecteurs propres de cette matrice forment alors une base dans laquelle il est possible d'exprimer l'espace d'efini par les modèles. La base optimale en d dimensions, au sens des moindres carr'es, est obtenue en prenant les vecteurs propres ayant les d plus grandes valeurs propres, ce qui permet de faire une r'eduction consid'erable de la dimension de l'espace sans perte de qualit'e visuelle (d est nettement inf'erieur a` k), car cette d'ecomposition est en fait une analyse en composantes principales. Une image est donc repr'esent'ee comme un point dans l'espace de ces vecteurs propres, et la reconnaissance revient a` faire une recherche du plus proche voisin dans l'espace a` d dimensions consid'er'ees. [LAM 98]

L'avantage principal de cette approche est sa r'eduction consid'erable des dimensions pour la repr'esentation d'une image. Dans le cas d'une image 512 x 512 (vecteur de dimension 512² = 2293620, on prend typiquement les 10 plus grandes valeurs propres, ce qui revient a` une r'eduction de dimension d'un facteur d'ordre 10⁴. Ceci permet de r'ealiser des indexations efficaces et des recherches rapides, Malheureusement ses inconv'enients sont de taille :

· Le fait que l'approche soit globale la rend particulièrement sensible a` des occultations.

· Les changements d''eclairage, ou des transformations g'eom'etriques lors de la prise de vue influent directement sur la repr'esentation finale de l'image.

2.3.3 Modélisation locale

La classe des approches par mod'elisation locale est très h'et'eroclite. On admet g'en'eralement que son origine se trouve dans la m'ethode de reconnaissance Geometrie hashing. Dans cette approche, le modèle n'est plus l'image toute entière, comme dans la section pr'ec'edente. Par contre, un modèle est repr'esent'e par un ensemble fini de configurations locales dans l'image. Ces configurations sont g'en'eralement s'electionn'ees suivant un critère de pertinence, et imposent donc une segmentation sur les images. Dans le cas de points, il pourrait s'agir de minima d'autocorr'elation, par exemple, et dans le cas de contours ce pourraient être des maxima locaux de la norme du gradient. Le but principal des m'ethodes

locales est de mettre en correspondance des configurations d'une image inconnue avec des configurations de modèles déjàobservés. Le taux de mise en correspondance et la cohérence géométrique entre celles-ci sont alors des mesures permettant de classer les modèles et de sélectionner celui qui est le plus ressemblant a` l'image requête. Les méthodes diffèrent principalement dans leur façon de caractériser les configurations et dans leur manière de trier les modèles plausibles. Elles ont ceci en commun avec les approches géométriques qu'il s'agit intrinsèquement de trouver un sous-ensemble optimal d'appariement. Elles en diffèrent par le fait qu'il n'existe a priori pas de structuration entre les configurations. La comparaison s'arrête là, par contre. Afin d'accélérer cette mise en correspondance, les méthodes caractérisent les configurations par des descripteurs. Ces descripteurs sont choisis afin d'absorber une partie des déformations qui peuvent apparaàýtre lorsque l'objet est observédans des conditions différentes.

2.4 Conclusion

Beaucoup de problèmes dans la reconnaissance d'objets n'ont pas étérésolus et les systèmes actuels montrent leurs limites. Chaque SRO se concentre sur quelques aspects du problème en supposant que les autres aspects sont résolus ou le seront dans le futur. Apres la définition de la reconnaissance d'objets, on a vu des critères de classification des systèmes de reconnaissance des objets (SRO). Ils sons basés sur les méthodes employés pour acquisition, la représentation modèle 3d et l'appariement entre celui-ci avec les données capteur. On a aussi présentéquelque méthode de reconnaissance des objets, en montrant leurs principes, leurs avantages et leurs inconvénients. On a décrit ce qu'on appelle l'indexation géométrique ainsi l'algorithme d'indexation géométrique, on a présentéune méthode de reconnaissance base sur les histogrammes de couleurs et une autre basée sur l'appariement en montrant leurs acquis et leurs échecs

Chapitre3

La conception et resultat d'expérimentation

3.1 Introduction

L'extraction de l'information concernant la structure des formes presentées dans une image est un problème très délicat dans le domaine de la vision par ordinateur. Bien qu'il ait étéétudiédepuis longtemps, il n'y a pas de méthode qui soit en même temps robuste, rapide et générale.

3.2 La reconnaissance des objets polyédrique

3.2.1 Choix des primitives

· Les segments 3d fournissent une représentation simplifiée pour la scène.

· Un objet polyédrique est un ensemble de segments 3D.

· Les segments facilitent la détection des jonctions.

La méthode de la reconnaissance qu'on a développésuit les étapes représentées par l'organigramme suivant :

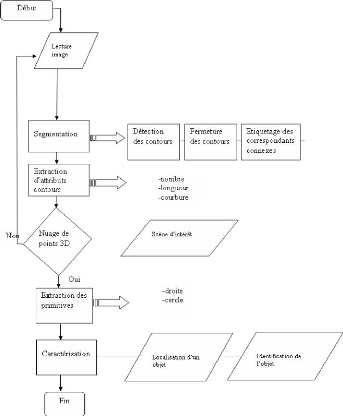
FIG. 3.1 - Organigramme de la méthode de reconnaissance automatique des objets.

3.2.2 L'algorithme développépour la reconnaissance des objets polyédrique

3.2.3 algorithme pour la localisation

1. Prendre une séquence d'images

2. 'Etablire un appariement (Suivi de segment de droite).

3. Déterminer le mouvement

4. D'eterminer les coordonn'ees X, Y, Z.

5. Reconstruction carte de profondeur(Reconstruction projective).

6. D'eterminer :

(a) Les segments 3D.

(b) D'eterminer les jonctions

(c) Calculer les angles

(d) Reconnaàýtre la forme pr'esente dans la scène

· D'eterminer les jonctions

3.2.3.1 Estimation des primitives

(a) Intersection segment / segment Soient 2 segments 3D [A1A2] et [B1B2].
Trouver l'intersection I de ces 2 segments en fonction de A1,A2,B1,B2.

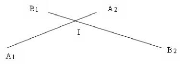
Solution :

Toujours sous forme param'etrique :

I est sur [B1B2] il s'exprime donc en param'etrique par

I = B + tB (B2 - B1)

I est aussi sur [A1A2] donc : I = A + tA (A2 - A1) Notez que le paramètre t est diff'erent sur chaque segment. Dans le cas g'en'eral, tA tB . On pose les vecteurs

VA = A2 - A1 et VB = B2 - B1

En remplaçant ceci dans les 2 'equations pr'ec'edentes, on obtient : I = A + tA VB = B +tA VB

On a donc une 'equation a` 2 inconnues tA et tB . En projetant cette 'equation sur l'axe X et sur l'axe Y,et sur Z on obtient un système lin'eaires de 3 'equations a` 2 inconnues :

A1.x + tAVA.x = B1.x + tBVB.x A1.y + tAVA.y = B₁.y + tBVB.y A1.z + tAVA.z = B1.z + tBVB.z

Soit :

tAVA.x - tBVB.x = B1.x - A.x tAVA.y - t_BVB.y = B₁.y - A.y tAVA.z - tBVB.z = B1.z - A.z

Ou sous forme matricielle, en posant le vecteur T = tA,tB,0

le vecteur R = B -A Et la matrice 3x3

M= ~~~~~~~~

~~~~~~~~

VA.x VB.x 0
VA.y VB.y 0
VA.z VB.z 1

On obtient le système lineaire matriciel suivant :

MT = R

Si le determinant 3x3 de M est non nul, l'equation a une unique solution qui se trouve en inversant la matrice M, l'inverse de M etant noteM^-1 On a :

T = M^-1R

Remarque : seule la connaissance d'une des 2 valeurs TA ou TB nous suffit pour trouver l'intersection I.

En notant ' det ' le determinant de 2 vecteurs 3D. Nous obtenons donc pour tA par exemple :

tA = det((B - A),vB)/det(vA,vB)

(b) Calculer les angles on peut utiliser le produit scalaire. En utilisant les definitions suivantes :

AB : vecteur de A a` B

- AC : vecteur de A a` C

|| : norme des vecteur (longueur (positif))

BAC : angle entre le sommet A et les points B et C

- Le produit scalaire . S'écrit de la manière suivante :

AB . AC = |AB|×|AC|×cos (BAC)

Et donc on peux récupérer l'angle

Angle = arccos ( prodscalaire(AB,AC) /norme( AB) . norme(AC))

- Reconnaàýtre la forme présente dans la scène

On regroupe les segments en quatre, pour chaque jonction on calcule
l'angle Si les angles sont équivaux est prés de 90°on détecte un polyèdre

Conclusion

IL faudra d'abord calculer la carte de profondeur, pour cela on va utiliser l'algorithme de développement de la section suivante [NAB 09]

3.3 Calcul de la carte de profondeur

3.3.1 Modèle géométrique de système de vision [Ait06]

3.3.1.1 Description du système

La figure 2.1 nous illustre un modèle géométrique d'un système de vision stéréoscopique non anthropomorphe (est un système dont les axes des caméras ne sont pas coplanaires), équipéde deux caméras en mouvement de rotation. Dont on a :

- IM1 (resp. IM2) est le plan de projection de la camra1 (resp. camra2), - L1, L2 : les lentilles des deux caméras (centres optiques),

- P1, P2 : points d'impact des axes optiques sur les plans IM1, IM2,

- (P1, U1, V1) : repère cartésien orthonormé-dit théorique- liéau plan IM1, construit ainsi :

- P1U1 est parallèle aux lignes de l'image IM1,

- P1U1 est parallèle aux colonnes de l'image IM1 (sur une caméra CCD¹ les lignes sont perpendiculaires aux colonnes [ABI89]),

- l'unité, que ce soit sur _O1U1 ou _O1V1 est soit le pixel ou le millimètre (mm). Le passage d'une unitéa` l'autre (pixel-mm par exemple) obéit a` la transformation suivante :

U1 = (ex).u1

'Charged Coupled Device

V1 = (ez).v1

Sachant que (ex, ez) représentent les facteurs de changements d'échelle et (U1, V1) (resp. (u1, v1)) Les coordonnées d'un point image dans le système o`u l'unitéest le pixel (resp. le mm)

- (P2 U2 V2) : repère cartésien orthonormé-dit théorique- lier au plan IM2, construit de manière analogue a` (P1 U1 V1),

- (O1 x1 y1 z1) [resp. (O2 x2 y2 z2)] : Repère cartésien orthonormé-dit théorique- liéa` la camra1 (resp la camra2) construit de la manière suivante :

- O1 (resp. O2) est situésur l'axe optique de la camra1 (resp. camra2) a` une distance d1 (resp. d2) de P1 (resp. P2). La valeur de d1) (resp. d2)) peut varier d'un mouvement a` un autre ; le centre de rotation de la caméra n'est pas connue et peut changer a` chaque rotation (voir figure)

- O1O1 ^(resp. _O2O2) est parallèle a` P1V1 (resp. P2V2),

- L'unitéutilisée sur ce repère est le mm,

- O1x1 et O2x2 sont colinéaires.

- è1 ( resp. è2 ) : angle de rotation de la camra1 (resp. camra2) autour de l'axe O1z1 (resp. O2z2),

- p : distance entre O1 _et O2,

- è2 : angle d'inclinaison de la camra2 par rapport a` la camra1 ;

- f : distance focale.

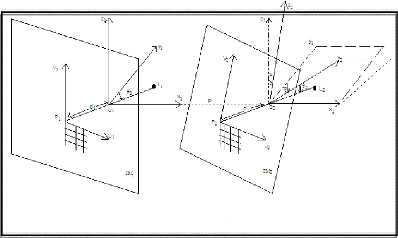
FIG. 3.2 - Modélisation géométrique de la tête de vision stéréoscopique.

3.3.2 Coordonnée projectifs avant et après rotation

Un point P(x,y,z) se projette sur le plan image en un point P1(U1); V1)) sur l'image1, et en un point P2(U2); V2)) sur image2, comme sera ^montrédans les fonctions suivantes :

· Avant rotation

(a) Sur IM1

U = (ex).f.		- cos(è1).x + sin(è1).y
		sin(è1).x + cos(è1).y + d1 - f
V = (ez).f.	-Z
	sin(è1).x + cos(è1).y + d1 - f

(b) Sur IM2

U2 = (ex).f.

- cos(è2).(x - p) + sin(è2).(y. cos(?) + z. sin(?)) sin(è2).(x - p) + cos(è2).(y. cos(?) + z. sin(?)) + d2 - f

sin(?).y - cos(?).z

V2 = (ez).f. sin(è2).(x - p) + cos(è2).(y. cos(?) + z. sin(?)) + d2 - f

Apres un certain nombre de rotation des caméras d'un angle (a1 ,a2 ) autour de _O1z1 (resp.O1z2 ) a` partir de sa position de départ a1 (resp. a2 ); Les cordonnées de projection du point objet P(x,y,z) sur les deux images IM1 et IM2 changent.

(a) i. Sur IM1

U = (ex).f.		- cos(è1 + a1).x + sin(è1 + a1).y
		sin(è1 + a1).x + cos(è1 + a1).y + d1 - f
V = (ez).f.	-Z
	sin(è1 + a1).x + cos(è1 + a1).y + d1 - f

ii. Sur IM2

cos(è2 + a2).(x - p) + sin(è2 + a2).(y. cos(?) + z. sin(?))

Uk 2 = (ex).f. sin(è2 + a2).(x - p) + cos(è2 + a2).(y. cos(?) + z. sin(?)) + d2 - f

3.3.3 Relations entre les cordonnes 2D et 3D

u1 = ex.f	- cos(è1).x + sin(è1).y
	sin(è1).x + cos(è1).y + d1 - f

-z

sin(è1).x + cos(è1).y + d1 - f

On note que x=X.(d1-f) ,y=Y.(d1-f) donc on aura

_v1 = ex. f

- cos(è1).X + sin(è1).Y

u1 = ex.f sin(è1).X + cos(è1).Y + 1 (1)

v1 = ex.f

-Z sin(è1).X + cos(è1).Y + 1 (2)

On divise (1) sur (2), on aura

.Y (3)

X

?

R

?

R?_..Z = cos(è1).X - sin(è1).Y cos(è1) sin(è1) Z = .

R

uk = ex . f 1

- cos(è1 + á).x + sin(è1 + á).y sin(è1 + á).x + cos(è1 + á).y + d1 - f

On a aussi

vi = ex._f

-z

sin(è + á1).x + cos(è1 + á).y + d1 - f On note que x=X.(d-f) ,y=Y.(d-f) donc on aura

uk = ex.f 1	- cos(è1 + á).X + sin(è1 + á).Y (4) sin(è1 + á).X + cos(è1 + á).Y + 1
v^k1= ex.f		-Z (5) sin(è1 + á1).X + cos(è1 + á).Y + 1

On remplace (3) dans (5)

vi = ez. f.	cos(è1) 1 .X + sin(è1) 1 .Y R0 R0
	sin(è1 + á1).X + cos(è1 + á).Y + d1 - f

Donc on a

X.(sin(è1 + á).v^k₁ + ez.f ^cos(è1) )+ Y.(v^k ₁. cos(è1 + á) - ez.f.^sin(è1) ) + v1 = 0

_R0 _R0

1 1

On remplace :

A = sin(è1 + á).v^k₁ + ez.f cos(è1)

R0 1

B = v^k₁. cos(è1 + á) - ez.f. sin(0è1)

1

C = v1

Donc on a A.X + B.Y + C = 0 X = On remplace x dans (4) on aura			-B.Y - C
			A
u^k1 = ex.f		- cos(è1 + á). A (-B.Y-9 + sin(è1).Y
		sin(è1).(^-B.X^-C) + cos(è1).Y + 1
sin(è1).(	-B.Y - C A ).u^k 1+u^k 1. cos(è1).Y +uk 1 = ex.f(- cos(è1+á).(					-B.Y - C A )+sin(è1).Y

1 +uk1 . sin(è1+á).C+ex.f. cos(è1+á).C

(-u^k )

Y = A

-ex. f.sin(è1+ á) + u^k₁. cos(è1 + á) . sin(è1+á).B-_Aex.f. cos(è1+á).B

3.3.4 Conclusion

Dans cette section on a présentécomment calculer la 3^eme coordonnée a` partir des coordonnées 2D par les différentes équations et leur démonstration . Après qu'on a trouvéla relation entre les coordonnées 2D et les coordonnées 3D, on remarque que, pour déterminer X, Y, Z il nous faut d'abord déterminer les angles de rotation á et è ; et pour cela nous allons exploiter le suivi d'un groupe de segments dans une séquence d'image.

3.4 Suivi d'un segment dans une s'equence d'images [ISR07]

Soit v0 = ai,0.u0 + bi, 0 l'equation d'un segment i dans une image o`u ai,0 est la pente du segment i dans l^'image0 et (u0, v0)les coordonnees 2D d'un point de segment de droite.

-a⁰ cos (á

ex^b f

D'apr`es certaines transformations on aura : ak. sm " = 0 =

(a) .

ä

Remarque :

Nous pouvons constater que l'expression des coordonnees images d'un point est de même forme dans les deux images (gauche et droite). C'est pourquoi, la relation entre les pentes des segments de droite dans les images successives droites va être de la même forme que celle obtenue par les segments des images gauches, donc il suffit de developper la relation sur les donnees de l'image IM1.

3.4.1 'Equation de mouvement d'un segment I :

,

Apr`es rotation d'un angle á : ai 1-ai,0 cos(á)sin(á) = bi,0

ex.f (6)

Apr`es rotation d'un angle â : ai,1-ai,0 cos(â)

sin(â) = bi,0

ex.f (7)

3.4.1.1 Application de la m'ethode

A partir du rapport entre les deux equation (6) et (7) on peut deduire que :

ai,1-ai,0 cos(á) ai,2-ai,0 cos(â) =

sin á sin â

Si on applique le même principe pour le segment j on obtient : aj,1-aj,0 cos(á) aj,2-aj,0 cos(â) =

sin á
sin â

ai,1-ai,0 cos(á) cos(á)

A partir de cette derni`ere equation on aura

cos(â) aj,2-aj,0 cos(â)

(aj,1.ai,0-ai,1.aj,0. cos(â))+(ai,2.aj,0-aj,2.ai,0. cos(á)+(aj,1.ai,2-ai,1.aj,2) =

0 si on remplace

c1 = aj,1.ai,0 - ai,1.aj,0

c2 = ai,2.aj,0 - aj,2.ai,0

c3 = aj,1.ai,2 - ai,1.aj,2

On aura :

c1 cos(â) + c2 cos(á) + c3 = 0 (A)

C'est une equation a` 2 inconnus, pour resoudre cette equation il faut une autre equation a` 2 inconnus, pour cela il suffit de prendre 2 autres segments

k et l, on aura : c_p,1 cos(â) + _cp,2 cos(á) = cp,3 (B)

Tel que :

cp,1 = al,1.ak,0 -- ak,1.al,0

cp,2 = ak,2.al,0 -- al,2.ak,0

cp,3 = al,1.ak,2 -- ak,1.al,2

La resolution de ce système d'equations (A) et (B) :

{

c1. cos(â) + c2. cos(á) = c3 cp,1. cos(â) + _cp,2. cos(á) = cp,3 Si det(c1 * cp,2 -- c2 * cp,1) =6 0

Alors :

cos(á) = ((c3*cp,2)-(cp,3*c2))

det

cos(â) = ((c1*cp,3)-(c3*cp,1))

det

La resolution de ce système necessite 4 segments dans 3 sequences d'images. La valeur de la solution est le mouvement effectuepar la camera pour l'obtention de l'image suivante donc une valeur qui reste constante si les segments consideres correspondent aux bons appariements. Nous pouvons enoncer la proposition suivante :

proposition :Soient i, j, k, l quatre segments de IM0, de IM1 i1, j1, k1l1 et i2,j2, k2, l2 de IM2 Les valeurs cos(á)et cos(â)obtenues après resolution du système correspondent aux mouvement reel de la camera si et seulement si chaque triplet de segments (i, i1, _i2),(j, j1, j2), (k, k1, k2),(l, l1, l2) contient le même segment dans les differentes images. La solution ayant engendrele plus grand score en nombre de quadruples de segments obtenus, sera la bonne

solution. Ainsi nous pouvons dire que nous avons résolu deux problèmes : le problème d'appariement et celui du mouvement des caméras.

3.4.1.2 Algorithme De Suivi :

Début

Extraction de contour de chaque image (IM1; IM2; IM3) Segmente les images (IM1; IM2; IM3)

Extraction de primitives (segments de droite) de IM1; Calculer la pente de chaque segment de IM1

Extraction de primitives (segments de droite) de IM2; Calculer la pente de chaque segment de IM2;

Extraction de primitives (segments de droite) de IM3; Calculer la pente de chaque segment de IM3;

Regrouper en groupe de quatre les segments de IM1 dans T1; Regrouper en groupe de quatre les segments de IM2 dans T2; Regrouper en groupe de quatre les segments de IM3 dans T3; - Pour tout groupe de segments de IM1 faire

- Pour tout groupe de segments de IM2 faire

- Pour tout groupe de segments de IM3 faire

- Calculer (cos a, cos â)

- Fin pour

- Fin pour

- Fin pour

Calculer le score pour chaque solution trouvée;

Choisir les groupes de segments qui engendrent le plus grand score;

Etablir la correspondance entre les segments de droite dans les différentes images ayant engendrés le plus grand score.

Fin.

Remarque :

- Les valeurs de cos(a)et cos(â)correspondent au mouvement effectuépar la caméra.

- - La bonne solution de cos(a) et cos(â) correspond a` la valeur ayant engendrée le plus grand score.

Conclusion (Méthode ) :

l'avantage de cette méthode est qu'elle permet de résoudre le problème d'estimation du mouvement.

On remplace cos(á) ou cos(/3)dans les formules précédentes, on aura les coordonnées 3D (X, Y, Z) de chaque point de l'image.

3.5 Résultat d'experimentation

3.5.1 Application a` des images de synthése

Dans la suite on va présentéles résultats obtenus On va appliquer nos algorithmes sur une séquence de trois images,voir la figure suivante :

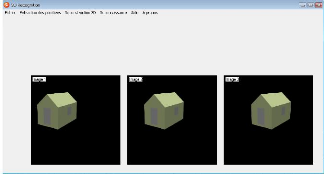
FIG. 3.3 - Une sequence de trois images.

Suivi avec les segments de droite

La premiere chàose a` faire est d'extraire les contours des images de la sequence, puis on effectue une segmentation de contours par une approximation de contours en segment de droite. La figure suivante montre le résultat

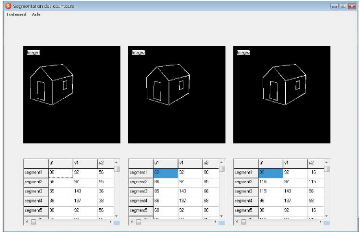
FIG. 3.4 - Extraction des segment de droite des trois images.

Calcul des angles de rotation : Aprés qu'on a extrait les segments de droite de la séquence d'images, on a appliquél'algorithme de suivi 3.4.1.2, on aura le resulatat suivant :

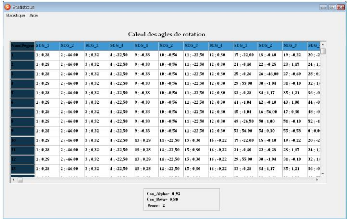
FIG. 3.5 - Calcul des angles de rotation.

La carte de profondeur : Le calcul de la carte de profondeur consiste a` calculer les coordonnées tridemensionnelle (X,Y,Z).

Apres qu'on a trouvéles angles de rotation á et 3 , on remplace ses valeurs dans les formules de X,Y et Z. Le resultat est montrésur la figure

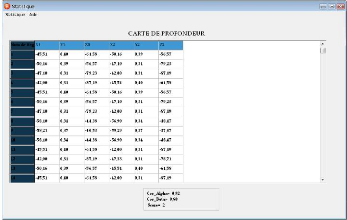
FIG. 3.6 - La carte de profondeur.

La reconstruction projective : La reconstruction 3D est la présentation tridemensionnelle de la sc`ene. Apres qu'on a trouvéla carte de profondeur,on peut donc utiliser les valeurs de X,Y et Z pour une reconstruction projective le résultat est montrésur la figure suivante

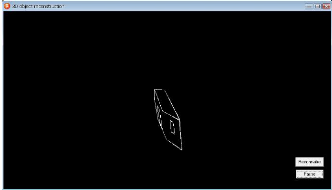
FIG. 3.7 - La reconstruction projective de la scene.

Localisation de l'objet polyédrique : La localisation de l'objet consiste a` determiner sa position dans scene pour une eventuelle identification. Apres qu'on a arrivéa` une reconstruction projective de la sc`ene, nous avons appliqués l'algorithme que nous avons développés pour la localisation de l'objet polyedrique. On a obtenu le resultat suivant :

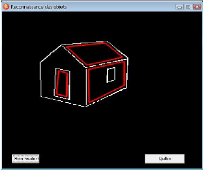
FIG. 3.8 - Localisation de l'objet dans la scene.

3.5.2 Application a` des images réelles

Dans la suite on va appliquer nos algorithme sur une séquence de trois images captées par une camera en mouvement de rotation.

La figure suivante montre la sequence d'images

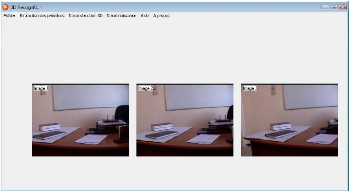
FIG. 3.9 - Sequence d'image reelle

Suivi avec les segments de droite

On extrait les contours des images de la sequence, puis on effectue une segmentation de contours par une approximation de contours en segment de droite. La figure suivante montre le résultat

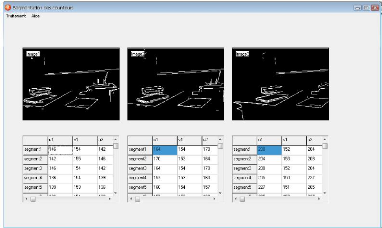
FIG. 3.10 - Extraction des segments de contours

Calcul des angles de rotation :

Apres l'extraction des segments de droite des trois images on a ^appliquél'algorithme de la section 3.4.1.2 ,on aura le résultat suivant :

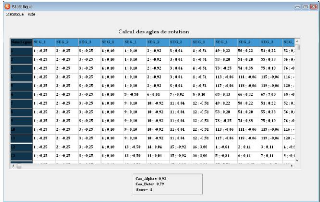
FIG. 3.11 - Calcul des angle de rotation

La carte de profondeur

On remplace la valeur de á et 3 dans les formules de X,Y,Z .Le resultat est montrésur la figure suivante :

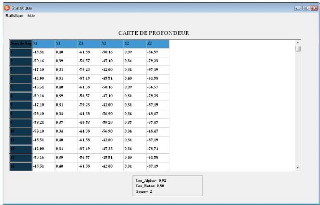
FIG. 3.12 - La carte de profondeur

La reconstruction 3D

La carte de profondeur est calculédonc on peut l'utiliser pour la reconstruction projective, le resultat obtenu est montrésur la figure

FIG. 3.13 - La scene reconstruite

Localisation de l'objet polyédrique

FIG. 3.14 - Localisation de l'objet dans la scene

3.6 Conclusion

Dans ce présent chapitre nous avons montrés l'algorithme dévloppépour la localisation tridemensionnelle,bien sàur a` partir d'une scene reconstruite. On a vu que pour se faire il faut calculer la carte de profondeur, ainsi nous avons présentél'aspect théorique et algorithmique de la méthode qui nous a permet de faire le suivi et la mise en correspondance d'un groupe de segments dans une séquence d'image prise par une caméra en mouvement. Les résultats d'expérementation sur des images de sinthése ont montrés la faisabilitéde l'algorithme,et sur les images réelle ont confirméque l'algorithme pouvais bien localiser certains formes dans la scéne.

Chapitre4

Environnement de realisation et

d'experimentation

4.1 Introduction

Ce chapitre est introduit pour la description du l'envirennement dans lequel on developpénotre application, ainsi que les défirentes composantes de l'application

4.2 L'envirennement de l'experementation

l'application a étédeveloppésur un micro ordinateur portable intel RPentium Core Duo inside 1.6 GHZ,1.6 GHZ ,et une carte graphique Mobile intel R945GM Express Chipset Family (224.0 MB) dans un systéme Windows XP professionnel.

4.3 Langage de programmation

Le langage utilisépour notre application est le Borland C++ Builder, c'est un environnement de développement intégrépour le langage C++ sous Windows. L'environnement de développement s'appuie sur un éditeur d'interface graphique associéa` un éditeur de code source. Il permet de développer des applications graphiques qui peuvent être liées aux bases de données .

Tout d'abord C++ est un outil RAD, c'est a` dire tournévers le développement rapide d'applications (Rapid Application Development) sous Windows. En un mot, C++ Builder permet de réaliser de facon très simple l'interface des applications et de relier aisément le code utilisateur aux événements

Windows, quelle que soit leur origine (souris, clavier, événement système, etc. )[ISI 99]

Cet envirennement possède les caractristiques suivantes :

· Syntaxe claire du langage C++.

· Facilitéde prise en main atteinte gràace a` des outils de conception visuelle.

· Augmentation de la productivitégràace a` la diversitéde ses outils.

· Facilitéde compréhension de la structure de l'application a` l'aide d'une fenêtre qui permet de visualiser la hiérarchie des objets.

· Flexibilitéet puissance atteinte gràace a` l'éditeur de code et l'inspecteur d'objets.

· Présence d'une bibliothèque riche en composants

Le développement de notre application sous l'environnement C++ Builder 6 consiste a` :

· Concevoir une interface graphique qui assure la communication entre l'utilisateur et le logiciel.

· Spécifier les propriétés des différents composants utilisés (Fenêtres, Boutons, Zone d'édition, etc.....).

· Spécifier le code source associéa` l'exécution d'une action par l'utilisateur.

4.4 Pr'esentation de l'application

3D Recognition est le logiciel qu'on développédont le but est de contribuer a` résoudre le problème de la reconstruction 3D et la reconnaissance des objets polyédrique a` partir d'une carte de profondeur et ceci a` partir d'une séquence d'images prises par une caméra en mouvement de rotation Dans la suite on va

décrire notre application en illustrant les déférentes interfaces qui l'a ^composéfenêtre principale

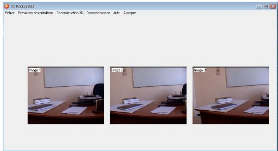
Elle compte une barre d'outils.

La barre d'outils : compte cinq menus

· Fichier

· Extraction de primitives

· Reconstruction 3D

· Reconnaissance

· Aide

· A propos

(a) Le menu fichier compte quatre item

L'item Ouvir compte trois sous items

- image1 : sert a` ouvrir l'image une de la sequence d'image. - imege2 : sert a` ouvrir l'image deux de la sequence d'image. - image3 : sert a` ouvrir l'image trois de la sequence d'image. L'item Enregistrer sert a` enregistrer les trois images.

L'item Enregistrer sous sert a` enregistrer les trois images dans endroit bien defini. L'item Quitter sert a` fermer et quitter l'application.

(b) Le menu Extraction de primitives : sert a` extraire les differentes primitives des trois images. Il compte deux item

L'item points d'interets pour extraire les differentes points d'interet des trois images et determine leurs cordonnees dans le plan image L'item Contours pour extraire les contours de la scene sur les trois images

(c) Le menu Reconstruction 3D pour afficher le modéle 3D reconstruit de la sc`ene.

(d) reconnaissance sert a` reconnaitre l'objet present dans la sc`ene.

(e) Le menu Aide : pour afficher l'aide

(f) Le menu A propos une fenetre d'information

Les déffirentes fenetres secondaires Extraction de primitives

1. Les points d'interets

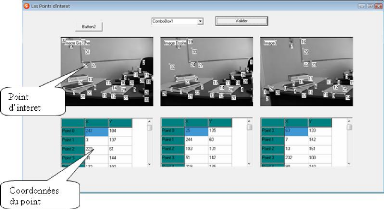
Les contours

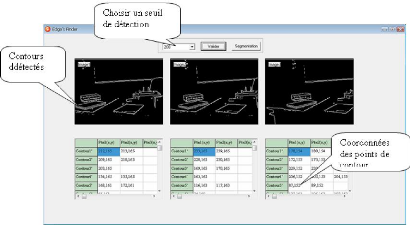
Les segments de contour

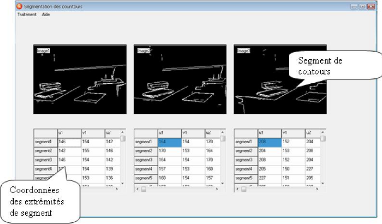
La fenetre »Les segment de contour compte deux menus»

1. Traitement

2. Aide: Pour afficher l'aide Le menu Traitemment compte quatre item

- Segmentation de contour : pour afficher les segments de contours des trois images.(Voir haut de page)

- suivi : comporte deux sous items

- Appariemt : pour faire de l'appariement des segments de droite

- Quitter : pour fermer la fenetre et revenir a` la fenetre principale

L'item Suivi compte deux sous items

(a) Suivi avec les segment de droite.

Cette interface contient un menu Statistique

(b) Calcul des angles de rotation cette interfece sert a` afficher les valeur de cos á et cos 3 calculé

Le menu Statistique compte item

· Groupe des segments : sert a` afficher l'ensemble des segments de l'image et ses pentes (voir haut de page)

· Regroupement des segments

· Carte de profondeur

· Quitter : pour quitter la fenêntre et revenir a` la fenêntre principale

L'item Regroupemnt de segment : Regroupement des segments : sert a` afficher l'ensemble des segment sur l'ensembles des images et ses pentes.

L'item carte de profondeur : sert a` calculer et afficher les coordonnées 3D des extrémités de segments.

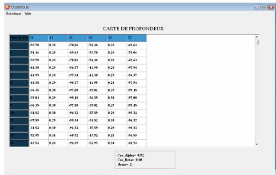
On clique sur le menu reconnaitre de la barre d'outil de la fenêtre principal on aura la fenêtre principale.

la fenêtre sert a` afficher les surfaces des objets detectés sur l'image, elle met des carres en rouge pour chaque surface detecté

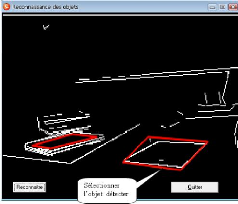
4.5 Conclusion

Dans ce chapitre on a présentél'envirennement dans lequel on a realiséce logiciel, et une description du l'application qu'on developpé,esperant bien qu'on a bien illustréles déffirentes interfaces du logiciel

Conclusion Générale

Les problèmes pos'es par la vision par ordinateur sont multiples et encore loin d'être r'esolus car ils sont souvent très complexes. C'est un sujet de recherche qui passionnent les chercheurs depuis plus de trente ans. Dans le cadre de ce m'emoire nous avons concentr'e notre travail sur une petite partie du vaste domaine de la vision par ordinateur : la reconstruction 3D et la reconnaissance d'objet.

La reconnaissance d'objets est une tâche qui peut paraàýtre très simple pour un op'erateur humain. Effectivement il est capable de s'adapter a` une grande vari'et'e de situations comme par exemple le changement de fond, les variations d'illuminations, les occultations, ou les changements de points de vue.

l'inverse, la reconnaissance d'objet est une tâche très complexe a` r'ealiser par une machine. En effet, durant le processus de perception, l'homme utilise une large quantit'e d'informations : deux collections de points disponibles sur les r'etines, et une quantit'e très importante de connaissances. Ces informations sont trait'ees avec une rapidit'e et une robustesse incroyables et avec une qualit'e telle qu'il peut même la plupart du temps »reconnaàýtre» un objet qu'il n'a jamais vu. L'homme est donc sans nul doute le plus parfait des systèmes de reconnaissance.

Sans aller jusqu'a l'id'ee utopique de le copier, on doit donc essayer d'imiter quelques unes de ses facult'es. une m'ethode de d'etection automatique des objets bas'ee sur l'attribut classiquement utilis'e : les segments de droite .les r'esultats obtenus sont int'eressants.

Partant de ce constat, après une 'etude bibliographique sur les m'ethodes de reconnaissance d'objet et de pr'etraitement des images, pr'eparant de manière robuste la segmentation par d'etection de contour. De plus, cet algorithme est rapide et a 'et'e test'e et valid'e sur un grand nombre d'images très diverses.

Comme perspective, les attributs extraits servent seulement a` confirmer la pr'esence d'un objet. Il est n'ecessaire d'extraire d'autres attributs et d'appliquer un algorithme de classification pour aboutir a` une m'ethode de reconnaissance complète. Quoi qu'il en soit,

la méthode développée est automatique et sans connaissance a priori sur les objets, c'est`a-dire que ne n'avons pas de modèles des objets seulement des considérations simples de formes comme la présence de droites, de cercles et d'ellipses. Elle permet de segmenter l'image prétraitée avec une meilleure qualitéde contours et de sélectionner automatiquement dans les images les contours les plus pertinents (qui serviront ensuite a` reconnaàýtre l'objet). Problème posépar cette méthode est les problèmes d'occultations et de bruits

Pour conclure sur les perspectives de travail. Pour l'approche classique, on peut compléter l'extraction d'attributs de la méthode de reconnaissance par les segments par l'ajout d'attributs tels que la courbure des contours ou différents descripteurs de formes. Pour cela, l'utilisation de l'information de couleur. Enfin cette approche classique pourrait être améliorée en implémentant une méthode de classification pour finaliser le système de reconnaissance.

Bibliographie

[AIT 06] . AIT KACI AZZOU, S LARABI. A new method to track line segment in sequence of image using only its s lope JCS 2(10), 2006.

[AYA 86] AYACHE. Vision stéréoscopique et perception multisensorielle : Application a` la robotique mobile. Cillection science informatique, Intel Edition 1989.

[BAR,GOS 98] . Barsi, L. Gosta, D.Geiger et D.Jacobs. »Determining the similarity of deformable shapes» 1998.

[BEN 09] N.BEN IKHLEF et M.BEN AMRAOUI . Elaboration de carte de profondeur.Application sur les images. Memoire d'ingeniorat UFAS 2009

[BIN 93] .O. BINFORD ET T.S. LEVITT, <<QUASI INVARIANTS : THEORY AND EXPLOITATION>>, IN PROCEEDINGS OF DARPA, IMAGE UNDERSTANDING WORKSHOP 1993.

[BLU 67] . Blum. A Transformation for Extracting New Descriptors of Shape, In Models for the Perception of Speech and Visual Form, (W.Wathen-Dunn, ed.), Cambridge Press, 1967

[BUB 98] . Bubel, R. Bergevin, Classifying junctions by vector quantization, in : Vision Interface'98, 1998

[Bus2001] Martin Bus. Reconnaissance d'objets a` partir de points 3D obtenus par appariement stéréoscopique pour la localisation absolue d'un robot mobile

[COL 96] V. Colin de verdiere. Reconnaissance d'objets par leurs statistique de couleurs

[COU 2000] J.Coughlan, A.Yuille,C.English et D.Snow » Efficient deformable template detection and localization without user initialization» 2000.

[FUN 95] B.V.FUNT and G.D Finlayson. Color constant color indexing

[GRO 95] . GROS, <<Matching and clustring : two steps towards object modeling in com-
puter vision >>,the international journal of robotics research, 14(5), Octobre, 1995

Bibliographie

[HEA 94] G. Healay and D.Slater. using illumination invariant color histogram descriptor for recognition.

[Het 95] F.Hetitger.Feature detection using suppression and enchancement. Technical Report 163. Communication Technology Laboratory. Swiss Federal Institute of Technology ITH 1995

[HOR 93] Radu Horaud et Oulivier Monga , vision par ordinateur 1993(first edition) [ISI 98] ISIMA 1988,1999. Introduction a` C++ builder

[ISR07] .ISRIG K.KEZAR Suivi d'un objet dans une séquence d'images application a` des images réelles, mémoire d'ingéniorat UFAS 2007

[Jai 96] A.Jain,Y.Zhong et S.Lakshmanam » Object matching using deformable templates» IEEE PAMI, 1996

[KOZ 98] R. Kozera » An overview of the shape from shading problem» Machine Graphics and Vision, 1998.

[LAM 98] Bart LAMIROY . Reconnaissance et modelisation des objets 3D a l'aide d'invariant projectifs et affines.

[NAG 95] K. Nagoa . Recognition 3D objects using photometric invariants.

[SCH 97] :ernt SCHIELLE . Reconnaissance des objets utilisant des histogrammes de champs réceptifs.

[SHA 99] Shaheen Mudar . Reconnaissance d'Objets Polyédriques a` partir d'une image vidéo pour la téléopération

[SOS92] Humberto Sossa . Reconnaissance d'objets polyédriques par indexation dans une base de modèles.

[SWA 90] M.J. SWAIN. Color indexing technical report

[PJM 09] Pierre-Marc Jodoin »Vision par ordinateur» Hiver 2009

[ZHA 99] R. Zhang, P.-S. Tsai, J. Cryer and M. Shah. Shape from shading : A survey. IEEE Trans. on Pattern Analysis and Machine Intelligence, August 1999. Webliographie

[1] Programming With Intel Ipp (Integrated Performance Primitives) And Intel Opencv (Open Computer Vision) Under Gnu Linux. A Beginner's Tutorial, Jérôme Landré.

[2] Yahoo! OpenCv Discussion Group : http :// tech.groups.yahoo.com/group/OpenCV/

1. Matrice Fondamentalle La matrice fondamentale est la matrice qui permet de lier les coordonn'ees dans le repère image r'ef'erence d'un point avec l''equation d'une droite appel'ee droite 'epipolaire dans l'image correspondante. S'il existe le point correspondant se trouve sur cette droite.

2. 'Epipolaire (géométrie) la g'eom'etrie 'epipolaire est la g'eom'etrie qui d'ecrit la conformation d'un capteur st'er'eoscopique. On distingue particulièrement dans cette g'eom'etrie les 'epipôles et les lignes 'epipolaires.

3. Distorsion Le ph'enomène de distorsion peut se manifester de diverses facons mais se traduit toujours par une d'eformation des r'esultats. Dans ce cas, la distorsion se traduit par une d'eformation visuelle des images visualis'ees. On aborde 'egalement la notion de distorsion radiom'etrique qui se traduit par une d'eformation du spectre d'intensit'e lumineuse.

4. Paramètres intrinsèques : Ce sont des paramètres inh'erents a` la cam'era qui permettent d''etablir la transformation permettant de passer du repère cam'era au repère image. On parle de matrice cam'era.

5. Paramètres extrinsèques Ce sont des paramètres qui permettent d''etablir les 'equations de passage entre le repère cam'era et le repère de calibration. Ils sont au nombre de 12 et repr'esentent une rotation ainsi qu'une translation. Ces paramètres varient selon la position de la mire de calibration.

6. Rectification :La rectification est une 'etape du processus de vision 3D qui vise a` simplifier la contrainte 'epipolaire en rendant les lignes 'epipolaires parallèles : après

la rectification des images la recherche de correspondant se réduira a` une simple recherche sur la ligne correspondante dans l'autre image au lieu de prendre place sur la ligne épipolaire.

7. Distance focale : La distance focale est la distance qui sépare le point nodal d'émergence (ou centre optique) du capteur. Plus la focale est longue et plus l'angle de vision est faible.

8. Corr'elation : La corrélation est l'action de mettre en correspondance les points similaires. On forme des paires de points. Les outils pour la corrélation sont les mesures de similitude et l'algorithme d'appariement.

Open Cv (Open Computer Vision) est une Librairie Open Source qui comporte un certain nombre d'algorithmes et d'exemples de code pour la vision par ordinateur. Cette librairie vise a` simplifier la conception d'applications d'edi'ees a` la vision en temps r'eel, la reconnaissance de contours, la segmentation etc... Le fait qu'elle soit Open Source signifie qu'elle est très 'evolutive puisque le d'eveloppement de nouvelles fonctions, nouveaux algorithmes, sont r'ealis'es par une vaste communaut'e. Par ailleurs Open Cv est bâti sur IPL (Intel Image processing library), dont elle reprend le format d'images (IPL Image) ainsi qu'un certain nombre de fonctions de filtrage, etc. Elle impl'emente 'egalement un certains nombres d'algorithmes exclusifs. La librairie rajoute 'egalement un certain nombre de notions telles que la gestion des espaces couleurs RGB. Open Cv est compos'ee de quatre grands blocs de fonctions.

- CxCore comporte les Fonctions de base d'Open Cv (fonctions de dessin, de gestion des points etc.)

- Cv comporte les Fonctions principales du traitement de l'image : un certain nombre de fonctions de filtrage (Sobel, Canny...) ainsi que les fonctions de calibration, appariement etc...

- HighGui comporte les fonctions de gestion des interfaces graphiques. Celle-ci sont simplifi'ee et permettent principalement la cr'eation de fenêtres graphiques dans lesquelles seront affich'ees des images ou des flux vid'eo.

- CvCam contient un certain nombre de fonctions de gestions de Webcams, utiles pour ouvrir des flux vid'eo.

Par ailleurs OpenCv dispose d'une communaut'e importante qui se manifeste sur un certain nombre de groupes de discussion. Nous avons pour notre part utilis'e le groupe de discussion Yahoo! qui est un des groupes les plus actifs.

Notons par ailleurs que la librairie fonctionne sous windows Linux, et est adapt'ee pour les langages C++ et Python.