Etude d'un glissement de terrain par différente méthodes

IV.9. Analyse des talus par la méthode des éléments finis :

Dans les références bibliographiques on peut trouver très large type d'éléments et des méthodes de résoudre des problèmes par la méthode des éléments finis. On a concentré dans cette description sur la formulation utilisé dans le logiciel SAS-FEM.

IV.9.1. Type d'élément finis :

L'élément linéaire triangulaire a été le premier type de l'élément 2D développé pour l'analyse des structures planes. La formulation est également plus simple par rapport les éléments finis en 2D. Il a été trouvé que l'élément linéaire triangulaire est moins précis par rapport aux éléments linéaires quadrilatère. Cependant, la réalité est que l'élément triangulaire est encore très utile à cause de sa manière adaptative à la géométrie complexe.

Les éléments triangulaires sont normalement utilisés lorsque l'on veut mailler un model 2D comprenant une géométrie complexes avec des angles aigus. En outre, la simple configuration topologique de triangulaire, permet de développer des programmes générateurs de maillage automatiquement et facilement. Le logiciel SAS-FEM comporte un générateur facile et relativement puissant qui peut générer un maillage pour n'importe quelle structure complexe

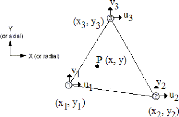
IV.9.2. Développement de la fonction d'interpolation : Considérant un élément triangle plane à 3 noeuds :

] u

[ (

- x y x y y y x x x y

- ) ( ) ( )

- - + -

1 3 3 1 3 1 3 1

+

+

u x y N x y u N x y u N x y u ( , ) ( , ).

= ( , ) .

1 1 + 2 2 + ₃ ( , ) . 3

Page 81

Chapitre IV : Les méthodes de calcul.

On va écrire u(x,y) et v(x,y) a chaque point P dans l'élément en fonction de : u1, u2, u3, v1, v2, v3. La plus simple forme est d'assumé que u(x,y) et v(x,y) sont des polynômes linaire. Noté que ces équations sont des équations approximés. Aussi u(x,y) et v(x,y) sont indépendant.

u ( x , y ) = a₁ +a₂x +a ₃y (1)

v ( x , y ) = b₁ +b₂x +b₃y (2)

Il faut trouver les constants de chaque équation (1) et (2) après appliquer les condition aux limites par exemple la fonction u(x,y) on a :

? ?

? ?

? ?

? ?

?

?

y 1

y

y 2

y x y x y

u₁

a₁

x₂

x₂

x₃

x₃

-

3

1

1

?

?

y

y y

u₂

a₂

y₂

-

2

A

?

?
? ? ?

?

?

?

?

?

?

?

u₃

a₃

x₃

- - y y

2 3 3 1 1

- x x x

- x x

-

2 1 3 2 1

- -

1 3 1 2

1

?

?

?

a₁

u₁

y 1

x 1

u₁

y 1

= +

a a x a

+

1 2 1 3

1

?

a₂

u₂

y 2

x 2

y 2

?

?

u a a x a

= + +

2 2 2 2 3

a₃

u₃

?

1

y 3

?

?

?

?

?

?

?

?

?

? ?

? ?

? ?

? ?

? ?

? ?

? ?

u a a x a

= + +

3 1 2 3 3

x y

3 3

Donc :

[ ( x y x y y y x x x y u

- ) ( ) ( )

- - + - ]

2 3 3 2 3 2 3 2

u x y

( , )

1

2

A

[ (

- x y x y y y x x x y u

- ) ( ) ( )

- - + - 1 ] 3

1 2 2 1 2 1 2

1

2

A

2

A

1

2

1

(6)

(7-a)

(3)

(5)

Avec la même procédure on aura pour le variable v(x,y) :

v x y N x y v N x y v N x y v ( , ) ( , ) . = + + 1 1 2 ( , ) . 2 3 ( , ) . 3

(7-b)

Où : N1, N2, N3 sont les fonctions d'interpolation de l'élément triangle, ses variation est présenté comme suite :

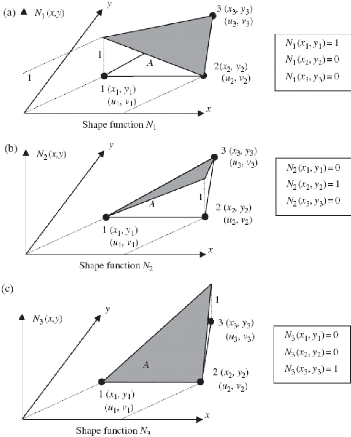
> Donc dans chaque élément on peut écrire:

? ? ? ?

??

u 1 ?

?

v 1 ?

.

?
??

? 0 0 N 0

??? =

??? u x y

( , ) N N

1 2 3

v x y

( , ) ?? 0 N 1 0 N 2 0 N₃

u 2 ? (8)

?
?

??

?

?

v₂
u₃

? u₃

IV.9.3. Développent de déformation et contrainte :

En deux dimensions il y a trois composantes majeur de contrainte ó T = { ó _x ó ó . La

xy }

y

déformation correspondante est å T = { å _x å y åxy}. La déformation peut être exprimé :

?

u

?x

?v

?y

? ? u ? v ?

? + ?

? ? y ? x ?

_å

å

å

x

=

y

=

xy

(2.9)

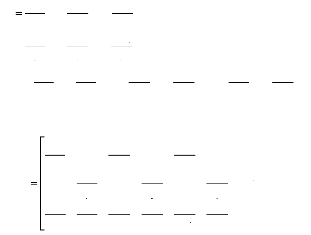
De l'équation (2.6) et (2.7) the déformation sont donné par:

+

?N₃

?N₁

+

u₁

u₂

u 3

?x

?x

? ? N ? N ?

2 2

+ ? u + v ?

2 2

? ? y ? x ?

?? N ? N ?

3 3

+ ? u + v ?

3 3

? ? y ? x ?

x

=

?y

å

? ?

?

?N₁

?N₁

+

?

?

?

u₁

v₁

?y

?x

En écriture matricielle

?N₂

?x

?N₁

v₁ + ^?N2 v2

?y

? N 2

0 0

? N 2

? y

? N 2

?N₃

?y ?x ?y

? N 3

?y

? N 3

?x

? ? ? ? ? ? ? ? ?

u 1

v 1

u 2

v 2

u 3

v 3

??

?
?

??

?

?

? N 3

0 0

?x

??å

xy

å_x

å_y

?N₁

?x

0

?N₁

?y

0

?N₁

?y

?N₁

?x

.

?

?

?

??

?

??

? N 2

? x

+

v 3

å

å

y

=

xy

?N₃

?y

(2.10)

(2.11)

Ou bien:

{å } = [ B .]{ U} (2.12)

où: [ B] est la matrice déformations-déplacements égale à:

Page 83

1

[ B]

?

?

?

??

A

2

y 2 - ?

0 x - x 0 x - x 0 x - x (2.13)

3

x1- -

Y3

0

Y3

Y1

0

Y1 Y2

0

2

1

2 1

3

x 3 - x ₂ y 2 - y 3

- x ₃ y 3 - y 1

x 2 - x 1

. Y

1 - y2

Pour le développement des contraintes en deux dimensions. La relation déformationcontrainte peut être considérée soit contrainte-plane, soit déformation plane dépond de la structure étudiée.

Généralement l'analyse des talus en deux dimensions sont considérés comme problème déformation plane, oil la relation est donné par:

ó x E?- í) ? ( 1 + 0( 1 - 2í) ?óxy ? 0 Ou bien :

?? ? ( 1-^íí ) ^00?^?åe^xy^? (1-2v)^?1 1 0 låx), I 2 ?` '

(2.14)

{ó } = [ D .]{å} (2.15)

Avec: [ D] matrice de comportement (caractéristiques de matériau). A partir de l'équation (2.12) et (2.15) on peut écrire:

{ó } = [ D ][.B.]{ U} (2.16)

IV.9.4. Résolution Eléments Finis :

Après assemblage des matrices élémentaires dans la matrice de rigidité globale, la forme finale est comme suite :

[ K .]{ U} ={ P}

oil :

{ U} : Vecteur de déplacements

[ K] : matrice de rigidité globale égale à:

[ K ] = ? [B] ^T [ D] [ B] dV = [B] ^T [ D] [ B]? dV = Ah. [B] ^T [ D] [ B] (2.17)

V V

{ P} : le vecteur global des forces composé de

Forces de corps { Pb } = ?	[ N ] ^T [ b] dV (2.18)
Forces de tractions { Pt } = ?		[ N ] ^T [ t] dA (2.19)

Et forces nodales{ Pn} .

IV.9.5. Modélisation des matériaux en SAS-FEM :

L'analyse élastique-plastique en deux dimensions de déformation-plane est utilisée, oil le comportement du matériau de sol est modélisé par le critère de Mohr-Coulomb. Ce dernier, est considéré comme le critère le plus utilisée dans la pratique géotechnique. Le critère de Mohr-Coulomb peut être exprimé comme :

F =I 3 1

sin

ö + ? - 1 ? J cos è sin sin è ö c . cos 2 ?? ?? - 3

ö (2.20)

oil

ö : est l'angle de frottement interne,

c : est la cohésion

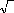
1 ? 3 J ?

- 1

è = sin ? ( ) ?

3 3 (2.21)

3 / 2

3 ? 2 J 2 ?

I₁ = (ó _x + ó_y + ó _z) = 3ó_m (2.22)

1 2

[ ( 2 ² ) ( ó ó ó ó ó ó ô ô ô

2 2

J ó ó ó ) ] 2

+ + + (2.23)

² 3

= + + - + +

x y z x y y z z x xy yz zx

2 2 2

J s s s = 2 . . s

3 x y z + ô ô ô - ô - ô - ô

s s (2.24)

xy yz zx x yz y zx z xy

s_x = óx-óm ;;s_yy= ó -ó_m ; s_{z x}= ó-ó_m (2.25))

y'

Le modèle de matériau décrit ci-dessus se compose de six paramètres

· Angle de frottement(ö))

· Cohésionn (c )

· Dilation(ø/ )

· Module de Young (E)

· Module de Poisson (í )

· Poids volumique de sole (ã )