II-4 Comportement du variogramme
II.4.1 Comportement du variogramme à l'origine
Le comportement du variogramme à l'origine renseigne
sur la continuité et la régularité spatiale du
phénomène observé (DEVEUGHELE et RIZZOLI, 1976). Plusieurs
cas peuvent se présenter. Les comportements
énumérés ci-dessous ne sont pas toujours observables de
façon nette sur un variogramme expérimental. Ce dernier ayant en
générale une allure irrégulière. Une estimation
à partir d'une telle représentation parait difficile ; il faut
donc ajuster à un modèle théorique pour une
caractérisation au mieux du phénomène.
Application de la métliode de krigeage ordinaire
aux épaisseurs de gravier en prospection
minéralogique
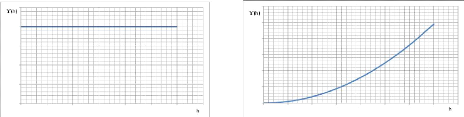
Figure 5a : allure horizontale constante Figure 5b :
allure parabolique
Elle traduit un phénomène
complètement
aléatoire : toutes les valeurs prises par
la
variable régionalisée Z(x) sont indépendantes
Cas (figure b)
les unes des autres. (Equation 15, annexe 2)
Elle traduit un phénomène très
régulier. La
quantité Z(x+h)-Z(x) est proportionnelle à
h au
voisinage de l'origine. (Equation 16, annexe 2)
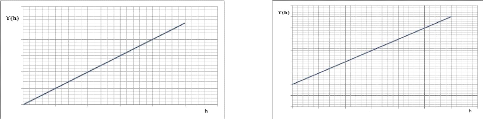
Figure 5c : Allure linéaire Figure 5d : valeur
à l'origine non nulle
tradut un phénomène moins que
Elle traduit un phénomène
très régulier La nulle
linéaire
le précdent mais possède une cotinuité en
quantité Z(x+h)-Z(x) est
proportonnelle à h au voisinag de l'orgine (Equation
1
moyenne. (Equation 17, annexe
2)
Elle traduit un effet de pépite. L'effet de
pépite peut représenter des erreurs d'analyse, de réelles
micro-structures ou/et des structures d'une certaine taille
non-détectées par un échantillonnage insuffisant.
Figure 5 (a, b, c, d) : allures
fréquentes de variogrammes II.4.2 Comportement du
variogramme aux grandes distances
|
Au delà d'une certaine distance, il arrive que le
variogramme tende vers une limite finie C appelée
palier. La distance a correspond au seuil
d'indépendance des valeurs et s'appelle la portée, i.e. absence
de corrélation possible entre les échantillons espacés de
plus de a,
|
|
|
Figure 6 : Variogramme avec palier
|
Application de la metliode de krigeage ordinaire aux
epaisseurs de gravier en prospection mineralogique
II.4.3 Présence d'une dérive
La dérive exprime le comportement très variable des
variogrammes du paramètre suivant les différentes directions
observées souvent aux grandes distances.
II.5 Calage du variogramme à un modèle
théorique
Le calage est l'ajustement du variogramme expérimental
à un modèle théorique. Il existe plusieurs modèles
théoriques dont les plus utilisés sont :
- le modèle linéaire : ce modèle est sans
palier ;
- le modèle puissance : il croit très vite et n'a
pas de palier ;
- le modèle exponentiel : ce modèle croit à
l'origine plus vite mais tend moins vite vers sa limite comparativement au
modèle sphérique ;
- le modèle sphérique : il a une allure
linéaire à l'origine et atteint vite son palier contrairement au
modèle exponentiel.
Le choix d'un modèle n'est pas quelconque, il est
lié d'une part au comportement à l'origine et d'autre part
à l'existence ou non d'un palier. Dans le domaine minier, les
modèles de calage les plus récurrents sont les modèles
linéaire et sphérique.
II.5.1 Caractéristiques du modèle
sphérique Le modèle sphérique ou schéma de
MATHERON se caractérise par :
- l'effet de pépite notée Co :
c'est l'ordonnée à l'origine de la courbe du variogramme. Il
quantifie la variance d'estimation entre deux point proches ; il traduit
l'irrégularité du phénomène spatial à
l'échelle d'étude ;
- le palier noté a2 : c'est
l'ordonnée maximale de la courbe. Il quantifie la variance moyenne entre
un point et la limite de sa zone d'influence ;
- la portée notée a : elle
correspond à l'abscisse à partir de laquelle la courbe à
une variable n'est plus corrélée.
Le modèle sphérique est défini par
l'équation18 (cf. annexe 2). II.5.2 Caractéristiques du
modèle linéaire
Le modèle linéaire se caractérise par une
allure constante horizontale traduisant un
phénomène
complètement aléatoire. Il se définit par
l'équation 19 (cf. annexe 2).
Application de la metliode de krigeage ordinaire aux
epaisseurs de gravier en prospection mineralogique
L'approximation se fait soit par la variance de l'ensemble des
échantillons, soit par la moyenne des variances des couples de points de
la zone de stationnarité locale.
II.6 Etude quantitative du
variogramme
Elle représente la phase réelle de
l'étude de l'estimation des variables régionalisées ; et
ne concerne que les variables qui présentent le modèle
sphérique. Elle se résume dans le calcul des différentes
variances dont le développement figure ci-dessous.
II.6.1 Variance de dispersion
Elle représente la variance de l'ensemble des valeurs
prises par la variable régionalisée Z(x) pour toutes les
implantations possibles dans un bloc de volume v (DEVEUGHELE et RIZZOLI, 1976)
qu'on note a2 (o/v) (Equation 20, annexe 2). La variance de
dispersion est reliée au variogramme par l'équation 21 (voir
annexe 2).
La variance de dispersion permet de préciser dans quelle
mesure la valeur estimée en un point est représentative de tous
les autres points de notre zone.
II.6.2 Variance d'estimation ou d'extension
C'est la variance de l'erreur qu'on commet en estimant la
variable aléatoire régionalisée au point x par la valeur
au point (x+h). Plus généralement, si V est un volume du bloc
à estimer et v celui du bloc qui sert à estimer V (v est donc un
ensemble de prélèvements ponctuels), la variance d'estimation du
volume V par v traduit l'erreur induite par cette opération. (Equations
22 & 23, voir annexe 2)
Dans la pratique, nous avons souvent affaire à des
panneaux carrés ou rectangulaires ou à des blocs ; les variances
peuvent s'exprimer à l'aide de fonctions auxiliaires faisant l'objet
d'abaques dans le cas des principaux schémas types de variogramme.
II.6.3 Isotropie et anisotropie
La continuité spatiale n'est pas nécessairement
la même dans toutes les directions. Il y a isotropie lorsque le
variogramme est identique dans toutes les directions de l'espace ; dans le cas
contraire, on parle d'anisotropie. On distingue deux principaux types
d'anisotropie : l'anisotropie géométrique et l'anisotropie
zonale.
flrojet de Fin d'Etude (flFE)
Application de la methode de krigeage ordinaire aux
epaisseurs de gravier en prospection mineralogique
Bien que dans la nature il existe une très grande
variété d'anisotropies, en géostatistique, on ne peut
modéliser aisément que les anisotropies
géométriques. Il faut donc toujours rechercher si anisotropie il
y a ; le principe est aisé.
III Krigeage
III.1 Définition
Le krigeage est une méthode d'estimation
linéaire. Fondamentalement ; il représente un estimateur
linéaire sans biais optimal (au sens de la moindre variance) obtenue par
combinaison linéaire des informations disponibles. Son
intérêt réside dans le fait qu'un échantillonnage ne
fournit des informations exactes sur le minerai qu'au point d'où
proviennent ces données. Il faut alors une méthode précise
pour estimer la valeur aux points intermédiaires ou bien les moyennes
sur des blocs. Le krigeage donne la meilleure estimation sans biais, la
précision de celle-ci dépend alors de plusieurs facteurs :
ü Nombre d'échantillons et la qualité des
données en chaque point ;
ü Position des échantillons dans la
minéralisation ;
ü Distance entre les échantillons et le point ou le
bloc dont on veut estimer la valeur ;
ü Continuité spatiale de la variable
étudiée.
Il existe plusieurs types de krigeage dont le krigeage universel,
le krigeage simple, le krigeage ordinaire. Le krigeage ordinaire est la
méthode la plus utilisée.
III.2. Krigeage ordinaire
C'est le krigeage dans le cas d'une moyenne inconnue. Les
équations correspondantes d'un bloc v sont les équations 3 et 4
(voir annexe 2) :
Nous disposons par exemple de n valeurs de teneur ( t(xi)) en
n positions (xi, 1=i=n) : t(x1), t(x2),..., t(xn) et nous souhaitons
estimer la variable t(x) par une combinaison linéaire de ces
données (t(x) est la teneur au point x ou la moyenne dans un bloc v)
Posons : t*(x)= ? I ëi t(xi) (Equation 1)
t*(x) la teneur estimée et t(x), la teneur à
estimer.
Les facteurs de pondération yi sont choisis de telle sorte
que l'estimateur soit :
Application de la methode de krigeage ordinaire aux
epaisseurs de gravier en prospection mineralogique
* Sans biais : E(t(x) - t*(x))= 0 (Equation 2)
*De variance minimale : Var ((t(x)- t*(x)) minimale, cette
variance sera appelée variance de krigeage.
En conclusion, le krigeage d'une variable
régionalisée est fonction des paramètres tel que l'effet
de pépite, la portée, le palier, l'isotropie, lesquels
dépendent de l'étude variographique. C'est une
méthode d'interpolation optimale dont l'objectif est de proposer une
cartographie corrigeant la tendance spatiale par la prise en compte des
dépendances locales.
.
III.3. Autres estimateurs
linéaires
Il existe également plusieurs autres types
d'estimateurs linéaires dont la méthode des rectangles, la
méthode des iso-grades qui arrivent à donner des estimations
linéaires en des points sur une parcelle.
Ces méthodes étant certes des méthodes
d'estimation linéaire, le krigeage reste la méthode d'estimation
par excellence qui offre des résultats très satisfaisants.

Application de la metliode de krigeage ordinaire aux
epaisseurs de gravier en prospection mineralogique
| 


