III.1. Caractéristiques physico-chimiques de
l'argile naturelle de Mindif
Les caractéristiques physico-chimiques de l'argile brute
utilisée lors de cette étude sont Consignées dans le
tableau 4.
Tableau 4: Caractéristiques
physico-chimique de l'argile brute de Mindif
|
Paramètre
|
%H
|
%PAF
|
%IG
|
d
|
P
|
????
|
??????????
|
|
Valeur
|
8,33
|
19,09
|
61,43
|
1,33
|
66,58
|
8,20
|
7,65
|
%H : taux d'humidité ; %PAF : perte au feu ; %IG :
indice de gonflement ; d : densité ;
P : porosité ; ???? :
potentiel d'Hydrogène ; ?????????? : point de charge nul.
III.1.1. Taux d'humidité
La valeur du taux d'humidité indique le
caractère hygroscopique de l'argile. Cette eau correspond à l'eau
libre d'hydratation qui s'évapore à partir de 100°C. La
quantité de cette relativement basse serait due au fait que l'argile a
été prélevé en saison sèche. (Hyun et
al.,2001).
III.1.2. Perte au feu
Le résultat 19,09% pour la perte au feu, indique que
l'eau de constitution des minéraux argileux s'est évaporée
(valeur moyenne comprise entre 4,6 à 19% du poids des minéraux
selon sa nature minéralogique). Ce résultat reflète
également la faible valeur de la matière organique par rapport
à la fraction minérale (Baize,2018).
III.1.3. Indice de gonflement
Le mécanisme d'hydratation des argiles est
conditionné par divers paramètres à savoir la structure du
matériau, l'espace interfoliaire, la concentration des constituants
chimiques et même l'histoire du matériau. La valeur de l'indice de
gonflement est importante, ceci peut être due à la finesse et
à une forte ionisation des particules entrant dans la constitution de
l'argile (Tejeogue,2019).
46
III.1.4. Le pH
La mesure du pH d'une suspension
d'un échantillon de sol dans l'eau rend compte de la concentration en
ion H30+à l'état
dissocié dans le liquide surnageant. Le résultat de 8,20
révèle la légère basicité de l'argile qui
serait due aux sels solubles basiques comme les carbonates et les bicarbonates
alcalins ou les silicates qui rentrent généralement dans la
composition des argiles
III.1.5. Le pHpzc
Le pHpzc correspond à la
valeur de pH du milieu pour laquelle la
résultante des charges positives et négatives de la surface est
nulle. Les résultats obtenus sont représentés dans le
tableau A.1 de l'annexe et représentés par la figure 13
ci-dessous :
pHfinal = pHinitial pHfinal =
f(pHfinal)
2 4 6 8 10 12
pHinitial (ppm)
Figure 13: Détermination du point de
charge nul de l'argile brute de Mindif
La courbe de la figure 13 montre que l'intersection se produit
à une valeur du pH= 7,65 correspond au point
de charge nul. La charge extérieure a été provoquée
par les interactions entre les ions dans la solution et les groupes
fonctionnels de l'argile. La charge extérieure d'un solide dépend
du type d'ions actuels dans la solution, des caractéristiques de la
surface, de la nature de l'adsorbant, et du pH de la
solution. A pH inférieur au
pHpzc, la charge de surface du matériau est
globalement positive et à pH supérieur
au pHpzc, elle est négative (Injagbemi et
al.,2009 ;Roberto et al.,2008).
47
III.2 Analyse statistique de la quantité
adsorbée (pourcentage d'élimination) du
Métronidazole
Tableau 5: Analyse statistique de la
quantité adsorbée (pourcentage d'élimination) du
Métronidazole
|
Quantités
|
temps
|
masse
|
pH
|
Qe
|
Qe
|
Qe
|
%R
|
%R
|
%R
|
|
adsorbées/Facteurs
|
|
|
|
ABM en
mg/g
|
ASM en
mg/g
|
APM mg/g
|
ABM
|
ASM
|
APM
|
|
Minimum
|
60
|
0,17
|
11
|
0,45
|
0,65
|
1,34
|
4,75%
|
6,93%
|
14,20
|
|
Maximum
|
31,5
|
0,01
|
3
|
80,92
|
82,86
|
99,93
|
50,57%
|
51,79%
|
62,46%
|
48
Les quantités d'adsorption (pourcentage
d'élimination) vont de l'ordre de 0,45 mg/g à 80,92mg/g (4,75%
à 50,57%) ;0,65mg/g à 82,86mg/g (6,93% à 51,79%) et de
1,34mg/g à 99,93mg/g (14,20% à 62,46%) respectivement pour
l'argile brute, l'argile sodique et l'argile pontée. Nous pouvons
constater que l'utilisation de l'argile pontée (intercalée en
aluminium) (APM) aboutit à des meilleurs rendements d'élimination
que l'argile brute, et l'argile sodique(ABM et ASM ). Ce résultat peut
s'expliquer par le fait que la distance interfoliaire est plus importante dans
l'argile pontée que l'argile brute et sodique à cause de la
substitution des cations de cette zone par ceux d'aluminium. Des
résultats similaires ont été obtenus par Thiebault en
(2016), lors de l'adsorption des produits pharmaceutiques par interactions
organo-minérales.
De notre analyse, il ressort que l'adsorption est favorable
à un pH acide (pH = 3) , un pH inférieur au
pH au point de la charge nulle pour nos adsorbants , avec une valeur
de 7,65 (pHzpc). Les variations du pH attribuées à la
charge (matériaux) à différents niveaux de pH et
aux charges éléctriques du métronidazole . le pKa du
métronidazole est de 2,55. Ainsi, cet antibiotique a une charge positive
à des pH acides et est protonés (MNZ-H+). Il est
également connu qu'à des pH inferieur à pHZpc ,
la charge de surface de l'adsorbant est positif.
Ceci peut s'expliquer par la charge positive des groupements
de surface. En effet, ces charges favorisent l'échange ionique (Fumba et
al.,2014). Des résultats similaires ont été
obtenus par Tiago en (2019) lors de l'adsorption de Triméthoprime par
l'argile modifiée ainsi que Ngakou en (2017) , lors de l'adsorption de
la phénacétine (médicament ) en solution aqueuse. La
diminution de la quantité du métronidazole adsorbée avec
l'augmentation du pH peut s'expliquer par le fait que la
solubilité augmente avec le pH et les charges négatives
au niveau de la surface de nos argiles augmentent les répulsions
électrostatiques entre l'adsorbat et les groupes hydroxyles à la
surface de l'argile. L'ensemble des résultats expérimentaux sont
consignés dans le tableau A.3 de l'annexe.
L'étude des effets de différents
paramètres d'adsorption et leurs interactions a été mise
en évidence et diverses méthodes statistiques ont
été appliquées, il s'agit de diagramme de pareto, les
effets principaux, les interactions entre les facteurs, l'analyse des variances
qui indique l'importance des facteurs étudiés et la surface de
réponse.
III.2.1. Analyse des variances (ANOVA)
Cette analyse statistique permet de déterminer les
facteurs qui régissent l'adsorption du métronidazole par nos
adsorbants à savoir l'argile brute, sodique et l'argile pontée,
et, de même que la signification de chaque effet. L'analyse des variances
(ANOVA) a permis de déterminer
49
les effets principaux, d'interaction quadratique des
différents variables et les résultats sont
présentés dans les tableaux ci-dessous pour chaque
matériau. Les tableaux d'analyse comprennent : le coefficient du
modèle l'erreur standard, la valeur du test t student et le niveau de
confiance des facteurs.
Tableau 6:Analyse de la variance pour Qe de
l'argile brute
|
Source
|
Somme des
carrés
|
DDL
|
Moyenne quadratique
|
Rapport F
|
Proba.
|
|
A:temps
|
1,89467
|
1
|
1,89467
|
0,01
|
0,9074
|
|
B:masse
|
2708,83
|
1
|
2708,83
|
19,93
|
0,0003
|
|
C:Ph
|
2945,33
|
1
|
2945,33
|
21,67
|
0,0002
|
|
AA
|
39,4516
|
1
|
39,4516
|
0,29
|
0,5970
|
|
AB
|
14,5506
|
1
|
14,5506
|
0,11
|
0,7475
|
|
AC
|
90,1888
|
1
|
90,1888
|
0,66
|
0,4266
|
|
BB
|
716,259
|
1
|
716,259
|
5,27
|
0,0347
|
|
BC
|
2841,72
|
1
|
2841,72
|
20,91
|
0,0003
|
|
CC
|
705,867
|
1
|
705,867
|
5,19
|
0,0359
|
|
Erreur totale
|
2310,67
|
17
|
135,922
|
|
|
|
Total (corr.)
|
12374,8
|
26
|
|
|
|
R carré R carré
S R carré (ajust) (prév)
0,572049 90,22% 85,04% 73,75%
D'après ce tableau, on remarque que le coefficient de
détermination R2 est d'ordre (0.9022), on peut dire que
90.22% des observations sont expliquées par le modèle. En outre,
les valeurs de P sont trouvées inferieures à 0.05 pour le facteur
masse et pH ; les interactions BC, BB et CC. De ce fait, ces facteurs et
interactions sont significatifs.
50
Tableau 7:Analyse de la variance pour Qe de
l'argile sodique
|
Source
|
Somme des
carrés
|
DDL
|
Moyenne quadratique
|
Rapport F
|
Proba.
|
|
A:TEMPS
|
7,28221
|
1
|
7,28221
|
0,06
|
0,8033
|
|
B:MASSE
|
3997,31
|
1
|
3997,31
|
35,13
|
0,0000
|
|
C:PH
|
3302,69
|
1
|
3302,69
|
29,02
|
0,0000
|
|
AA
|
17,6334
|
1
|
17,6334
|
0,15
|
0,6987
|
|
AB
|
1,21047
|
1
|
1,21047
|
0,01
|
0,9191
|
|
AC
|
17,2663
|
1
|
17,2663
|
0,15
|
0,7017
|
|
BB
|
1037,24
|
1
|
1037,24
|
9,11
|
0,0077
|
|
BC
|
3217,21
|
1
|
3217,21
|
28,27
|
0,0001
|
|
CC
|
649,343
|
1
|
649,343
|
5,71
|
0,0288
|
|
Erreur totale
|
1934,64
|
17
|
113,802
|
|
|
|
Total (corr.)
|
14181,8
|
26
|
|
|
|
R carré R carré
S R carré (ajust) (prév)
0,381213 95,42% 93,00% 87,89%
51
Tableau 8:Analyse de la variance pour Qe de
l'argile pontée
|
Source
|
Somme des
carrés
|
DDL
|
Moyenne quadratique
|
Rapport F
|
Proba.
|
|
A:TEMPS
|
3,2172
|
1
|
3,2172
|
0,02
|
0,8866
|
|
B:MASSE
|
7143,26
|
1
|
7143,26
|
46,55
|
0,0000
|
|
C:PH
|
4454,6
|
1
|
4454,6
|
29,03
|
0,0000
|
|
AA
|
0,87258
|
1
|
0,87258
|
0,01
|
0,9408
|
|
AB
|
0,0472646
|
1
|
0,0472646
|
0,00
|
0,9862
|
|
AC
|
31,9645
|
1
|
31,9645
|
0,21
|
0,6539
|
|
BB
|
1930,78
|
1
|
1930,78
|
12,58
|
0,0025
|
|
BC
|
4652,62
|
1
|
4652,62
|
30,32
|
0,0000
|
|
CC
|
636,516
|
1
|
636,516
|
4,15
|
0,0576
|
|
Erreur totale
|
2608,6
|
17
|
153,447
|
|
|
|
Total (corr.)
|
21462,5
|
26
|
|
|
|
R carré R carré
S R carré (ajust) (prév)
0,206402 98,42% 97,58% 96,12%
D'après la littérature, on dit que qu'un facteur
est signifiant ou bien important lorsque leur probabilité (valeur de P)
est inférieure à 0,05. (Khelifi, 2018).
Les résultats de nos analyses modèle
proposé sont très signifiants (valeur de P < 0,05). Pour
l'ensemble de nos adsorbants (ABM,ASM et APM), les facteurs masse (B), et
????(C) ont un efffet signifiant (valeur de P< 0,05). On remarque que les
interactions BC, BB et CC sont également signifiants. Cependant, le
facteur temps (A) et les interactions AB,AA ont un effet non signifiant.
Le R2 de nos adsorbants est de l'ordre de 90,22% ;
95,42% et 98,21% respectivement pour l'argile brute(ABM), l'argile sodique(ASM)
et l'argile pontée (APM). Nous pouvons dire que cette étude a
donné des paramètres d'adéquation largement satisfaisants.
Le R2 a montré que les trois facteurs étudiés
étaient suffisants pour modéliser l'adsorption du
métronidazole. Le R2 ajusté montre que le
modèle est bien ajusté avec l'expérimentation.
C'est-à dire qu'il
52
tient compte des différents paramètres qui
régissent cette adsorption. Ensuite, le R2 prévu
dénote que ce modèle s'applique pour la prévision. Il est
fiable pour la conjecture d'un pourcentage d'adsorption dans des conditions pas
expérimentées, à condition que les paramètres
considérés appartiennent au domaine d'étude. Pour Haaland,
la pertinence du modèle est justifiée si l'ensemble des
R2 sont supérieures à 0,75 (Haaland,1989). D'autres
travaux ont trouvé des valeurs de R2 très
élevés mais en étudiant 4 facteurs (Dil,2018). Obtenir des
valeurs similaires avec uniquement 3 facteurs témoigne du choix
judicieux des facteurs.
En combinant les conclusions de l'erreur relative moyenne et
de l'adéquation du modèle, on conclut que ce modèle
décrit très bien l'adsorption du métronidazole, est fiable
et prend en considération l'ensemble des paramètres qui
régissent cette adsorption.
III.2.2. Modélisation et optimisation du plan
factoriel complet
Diagramme de Pareto
L'utilité du diagramme de Pareto des effets
normalisés est remarquable ; il sert entre autres, à comparer la
valeur relative et la signification statistique des effets principaux et des
effets d'interaction. Dans notre cas, le test t de student est également
effectué pour déterminer si les effets sont significativement
différents de zéro ou non. (Aloui,2021)
Sur ce diagramme, les colonnes horizontales représentent
les valeurs de t student de chaque effet pour chaque paramètre. Ce
diagramme permet aussi de classer les facteurs ainsi que leur interaction selon
leurs niveaux d'influences sur les réponses du modèle.
L'histogramme montre la contribution de chaque facteur ou interaction sur la
variation de la réponse, Y, par ordre décroissant
(Assaad,2015)
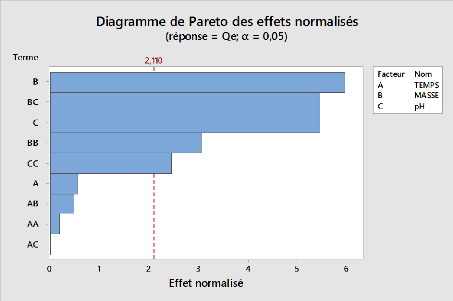
53
Figure 14:Diagramme de pareto des effets
normalisés pour l'adsorption du métronidazole pour l'argile
brute
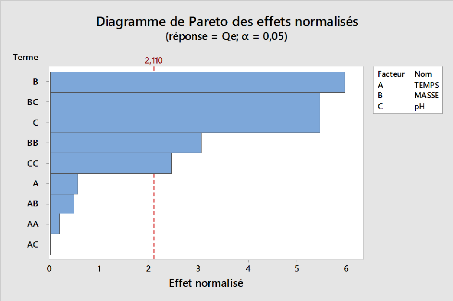
Figure 15:Diagramme de pareto des effets
normalisés pour l'adsorption du métronidazole par l'argile
sodique
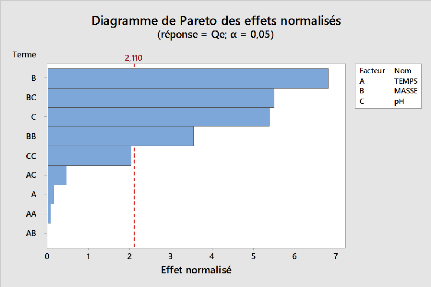
54
Figure 16:Diagramme de pareto des effets
normalisés pour l'adsorption du métronidazole par l'argile
pontée
III.2.3. Analyse des principaux facteurs
examinés et leurs interactions
Les facteurs masse (B), le pH(C) ; les interactions BC et BB,
sont les plus significatifs dans l'adsorption du métronidazole par nos
argiles. Il ressort également que le pH, est le facteur qui
contrôle l'électrostatique d'interaction entre l'adsorbant et
l'adsorbat, sur la base de résultats de l'analyse ANOVA et le diagramme
de Pareto, il semble évident que l'élimination du
métronidazole nécessite un pH bas de la solution. Lorsque nous
introduisons des doses faibles de matériaux dans un milieu acide nous
remarquons une accumulation considérable de quantité
adsorbées du métronidazole. Le pH influence donc notablement la
fixation du métronidazole sur nos argiles préparées. La
capacité maximale d'adsorption du métronidazole a
été observée à pH=3 pour nos trois adsorbants
utilisés et la capacité diminue avec l'augmentation du pH. Au
regard de nos résultats, nous constatons que les rendements
d'élimination du métronidazole augmentent avec la diminution de
la masse.
Le suivi de la teneur résiduelle a été
effectué en fonction du temps d'agitation (3 ; 31,5 ; 60min). Les
résultats présentés sur le diagramme de Pareto et de
l'analyse ANOVA montrent que la cinétique de fixation du
métronidazole est très rapide (Benzaoui,2018). Nous pouvons
cependant constater que l'utilisation de l'argile pontée présente
le meilleur rendement
55
d'élimination du métronidazole que l'argile
sodique et brute. Nous pouvons déduire que la masse et le ????
sont les meilleures variables du procédure globale d'adsorption.
L'adsorption est optimale à un pH et une masse faible (pH=3 et
m=0,01g).
III.2.4. Optimisation des facteurs influents par la
méthodologie de surface de réponse
L'optimisation de surfaces de réponse vise à
déterminer quantitativement les variations de la réponse
vis-à-vis des facteurs d'influence significative. Dans cette partie nous
présentons et discutons l'effet des facteurs en l'occurrence
l'adsorption du métronidazole par l'ABM, l'ASM et l'APM. La
démarche consiste à représenter la variation de la
réponse en fonction de deux facteurs uniquement, le troisième
étant maintenu fixe.
Surface de réponse pour l'argile brute de
Mindif

8
pH
60
40
Qe
20
10
- 10
20
0
MASSE
12
Valeurs de maintien
TEMPS 31,5
MASSE 0,09
pH 7

20
10
0
12
- 10
TEMPS
4
pH
Qe
Qe
0
TEMPS
MASSE
Figure 17:Diagramme de surface de réponse
de Qe pour l'adsorption du MNZ par ABM
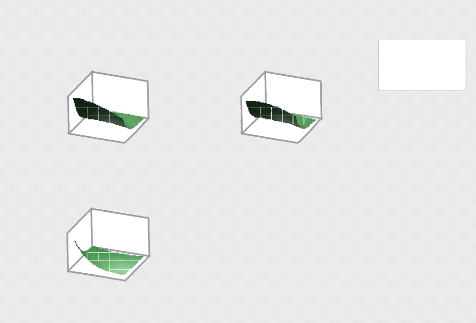
Qe
g
e de
rfa c
ra m mes
Valeurs de maintien
TEMPS 31,5
MASSE 0,09
pH 7
Qe
40
60
20
0
MASSE
8
4
12
pH
Qe
20
10
0
,16
0
Dia
TEMPS
MASSE
15
10
Qe
de su
5
12
0
8
TEMPS
4
pH
56
Figure 18:Diagramme de surface de Qe pour
l'adsorption du MNZ par ASM
Surface de réponse pour l'argile
pontée de Mindif
Valeurs de maintien
TEMPS 31,5
MASSE 0,09
pH 7

Qe
50
75
25
0
MAS
SE
8
0
,
1 6
12
pH

Qe
40
20
0
0
,1 6
TEMPS
MAS
SE
8
pH
20
10
12
TEMPS
4
-
0
1 0
Qe
Figure 19: Diagramme de surface de
réponse pour l'adsorption du MNZ par l'APM
57
Les figures (17,18,19) représentent donc le diagramme
de surface de réponse (3D) pour mieux explorer la relation
éventuelle entre les variables sélectionnées ,
l'augmentation du taux d'adsorption (qe) est observé à partir des
niveaux bas pH(3) acide et masse (0,01g)avec une quantité
adsorbée supérieure à 60mg/g (taux d'élimination
supérieur à 50%). Cependant, avec l'APM, la quantité
adsorbée est supérieure à 75mg/g (le pourcentage
d'élimination est supérieur à 60%) et ce résultat
est obtenu à un pH acide (pH = 3).
En prenant en considération que les mécanismes
interactionnels initiant l'adsorption des produits pharmaceutiques sont
essentiellement basés sur les affinités de charges entre
adsorbant et adsorbat, une modification de leur état de protonation
engendre inévitablement des répercussions sur les
quantités adsorbées (De Oliveira et al.,2015). Le pH est
l'un des principaux paramètres à gouverner les processus
d'adsorption. Celui-ci est d'autant plus important puisqu'il intervient
directement sur l'état de protonation des groupements fonctionnels des
molécules ionisées ou ionisables entraînant une
évolution des espèces en solution mais également sur
l'état de charge en surface des matériaux et leur structure. En
effet, il est bien connu qu'un pH très acide conduit à une
dégradation des feuillets octaédriques de l'argile avec une
libération potentielle des cations Al3+ ou Mg2+
pouvant se substituer aux cations sodium, entraînant ainsi une
déstructuration des couches du minéral argileux modifiant les
charges de surfaces et les propriétés d'adsorption (Metz et
al.,2005). Et la quantité maximale est également obtenu
à une masse faible (m=0,01g), un résultat similaire a
été obtenu par Aloui ,2021 lors de la biosorption des produits
pharmaceutiques par les fibres de Luffa Cylindrica. En effet, la
quantité du métronidazole adsorbée décroit avec
l'augmentation de la masse des matériaux et tend à se stabiliser
pour une valeur de masse élevée. Au demeurant, la diminution de
la concentration des argiles, entraine la dispersion des grains dans la phase
aqueuse. Par conséquent, les surfaces adsorbantes seront plus
exposées. Ceci facilitera l'accessibilité d'un nombre de sites du
support à la molécule du métronidazole. D'autre part
l'augmentation de la masse entrainera une croissance des interactions
électrostatiques entre particule de l'adsorbant qui conduit à la
désorption du métronidazole de sites d'adsorbant entrainant ainsi
une agglomération des particules adsorbantes formants ainsi des
agrégats. Il y a une diminution de la surface de contact par le fait que
des sites actifs de nos adsorbants deviennent masquées.
III.3. Influence du temps de contact
La cinétique exprimée en termes de
quantité de soluté adsorbée en fonction du temps de
contact est l'une de plus importantes caractéristiques
définissant l'efficacité d'une adsorption.
58
La célérité avec laquelle
l'équilibre thermodynamique est atteinte en fonction de la vitesse de
diffusion de l'adsorbat et de l'interaction adsorbat-adsorbant (Sinha,2020).
L'adsorption du métronidazole en solution aqueuse de concentration
initiale de 80ppm et de volume de 20mL est faite en utilisant une masse de
0,01g d'argile brute, d'argile sodique et d'argile pontée. Les
résultats des quantités adsorbées pour les
différents temps de contact croissant sont répertoriés
dans le tableau A6,A7 et A8 de l'annexe et répresenté par la
figure 20 ci-contre
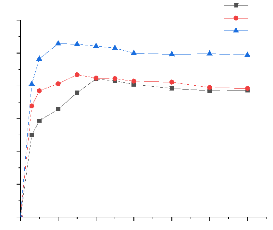
Cinétiques d'adsorption du Métro sur les
argiles
0 10 20 30 40 50 60
100
80
60
40
20
0
120
ABM
ASM
APM
temps (min)
Figure 20:Cinétique d'adsorption du
Métronidazole sur les argiles
L'allure des courbes, nous montre qu'il y a une forte
affinité entre les molécules du métronidazole et les
supports étudiés. Elle nous montre que le processus d'adsorption
se déroule en deux étapes assez distinctes : au cours de la
première étape l'adsorption est très rapide dès les
premières minutes et l'optimum est atteint au bout de 20 min ,15min et
10min respectivement pour l'argile brute, l'argile sodique et l'argile
pontée. Cette adsorption rapide (instantanée) pourrait concerner
les sites d'adsorption de surface où de forte affinité accessible
au métronidazole dès les premiers instants de la mise en
suspension de nos matériaux adsorbants dans la phase liquide contenant
le métronidazole en solution. Ceci pourrait s'expliquer par l'existence
de nombreux sites disponibles à la surface de l'adsorbant permettant la
fixation rapide des molécules d'adsorbat (Ghemit,2020 ;Thiebault et
al.,2015). Les quantités maximales adsorbées sont
84,22mg/g ; 86,74mg/g ; 105,75mg/g respectivement pour l'argile brute, l'argile
sodique et l'argile pontée. Nous remarquons que les quantités
adsorbées du métronidazole
augmentent de l'argile brute à l'argile pontée
via l'argile sodique. Ceci serait due au fait que la distance interfoliaire est
importante de l'argile brute à pontée en passant par l'argile
sodique à cause de la substitution des cations de cette zone par ceux de
sodium (cas de l'argile sodique) ou par ceux d'aluminium (cas de l'argile
pontée). La deuxième étape, montre une augmentation lente
des quantités adsorbées du métronidazole jusqu'au temps
d'équilibre, caractéristique du processus de diffusion à
travers de site moins accessibles (obstrués) avant d'atteindre un
équilibre d'adsorption où tous les sites seront occupés
(Madikizel et Chimika, 2016). Des résultats similaires ont
été observés par des études menées par
Oliviera et al.,2017, lors de l'adsorption du diclofenac par une
montmorillonite organophile.
Dans la suite de ce travail, les temps 20min, 15min et 10min
sont considérés comme temps de contact pour nos adsorbants
respectifs.
III.4. Influence de la concentration
Les expérimentations pour évaluer l'influence de
la concentration sur l'adsorption du métronidazole ont été
faite à dans les conditions optimales des résultats obtenus
précédemment à savoir une masse de 0,01 g ; un temps de
contact de 20min, 15min, 10 min respectivement pour l'argile brute, sodique et
pontée ; avec un pH = 3 , mais avec les solutions de concentrations
différentes en métronidazole, variant de 10 à 80ppm. Les
résultats sont présentés dans le tableau (annexe) et sur
la figure ci-après
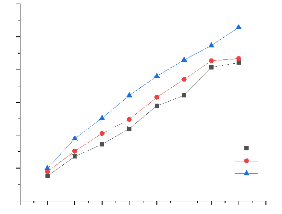
Influence de la concentration sur l'adsorption du
Métro sur les argiles
120
100
80
60
40
20
0
0 10 20 30 40 50 60 70 80 90
ABM
ASM
APM
Concentration (ppm)
59
Figure 21:influence de la concentration sur
l'adsorption du Métronidazole sur les argiles.
60
Les résultats montrent que la capacité
d'adsorption augmente avec la hausse des teneurs initiales de soluté
jusqu'à 80ppm et il n'y a pas de palier dans la gamme de concentrations
étudiées. Ceci peut traduire le fait que le taux de saturation
n'est pas atteint et que nos matériaux pourraient encore adsorbés
des quantités remarquables (importantes) du métronidazole.
L'augmentation a permis de déterminer le seuil de la saturation de nos
adsorbants.
III.5. Etude de la cinétique
d'adsorption
Cette étude permet de fournir des informations
relatives au mécanisme d'adsorption et sur sur le mode de transfert de
soluté de la phase liquide à la phase solide. Pour notre cas,
nous avons appliqué quatre modèles à savoir le
modèle pseudo-premier ordre, pseudo-second ordre, modèle
d'Elovich, modèle de diffusuion intra-particulaire. Les figures 22, 23,
24 présentent les courbes des équations linéarisées
de ces quatres modèles cinétiques.
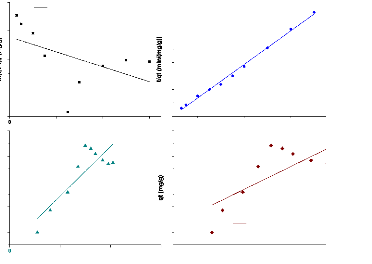
Metro/ABM
20 40 60
0 20
40 60
t (min)
))
y = 9,82364x + 44,60737 R2 =
0,729
t (min)
Modèle cinétique de Diffusion
Intraparticulaire
y = 4,17581x + 53,45942 R2 =
0,547
90
80
70
60
50
90
80
70
60
50
2 4 6
t (
ln(t) (min)
0 2 4 6
t1/2 (min1/2)
3
2
0,6
0,4
1
0,2
0
0,0
Cinétique Pseudo-second ordre
y = 0,01253x +0,01046 R2 =
0,996
Cinetique Pseudo-premier ordre
y = - 0,02615x + 2,78119 R2 =
0,256
0,8
4
Modèle Cinétique d'Elovich
Figure 22:modèle cinétique de
l'adsorption du métronidazole par l'argile brute
61
Metro/ASM
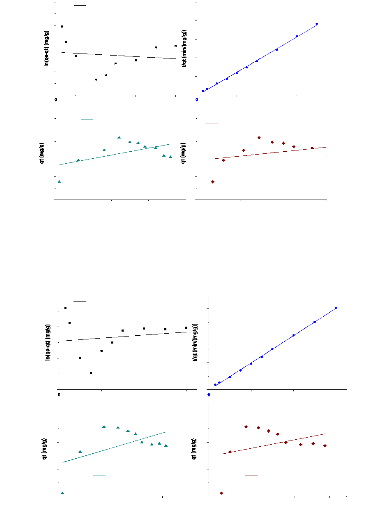
Cinetique Pseudo-premier ordre
y = - 0,00473x + 1,84308 R2 =
0,018
20 40 60
t (min)
Modèle Cinétique d'Elovich
y = 2,97366x + 71,82536 R2 =
0,293
1 2 3 4
ln(t) (min)
Cinétique Pseudo-second ordre
y = 0,01266x - 0,00837 R2 =
0,998
20 40 60
2 4 6
t1/2 (min1/2)
4
3
2
1
0
100
90
80
70
60
1,0
0,8
0,6
0,4
0,2
0,0
100
90
80
70
60
t (min)
Modèle cinétique de Diffusion
Intraparticulaire
y = 0,96488x + 75,91379 R2
=0,128
Figure 23:modèle cinétique de
l'adsorption du métronidazole par l'argile sodique
Metro/APM
20 40
60
0,6
Cinétique Pseudo-second ordre
y = 0,01012x - 0,00361 R2 =
0,999
Cinetique Pseudo-premier ordre
y = 0,00969x + 1,08438 R2 =
0,024
2
0
0,4
2 4
ln(t) (min)
t1/2 (min1/2)
4
0,2
-2
0,0
110
100
90
80
110
100
90
80
t (min)
Modèle Cinétique d'Elovich
y = 3,76514x + 88,40259 R2 =
0,272
20 40 60
t (min)
Modèle cinétique de Diffusion
Intraparticulaire
y = 1,25093x + 93,44152 R2
=0,125
Y1
.
2 4 6 8
(m
tq t (m Figure 24:modèle cinétique de
l'adsorption du métronidazole par l'argile pontée
62
Tableau 9:constante de vitesse et coefficient de
corrélation des modèles cinétiques
|
Modèles
|
Pseudo-premier ordre
|
Pseudo-second ordre Elovich Diffusion
intra-particulaire
|

Param ètres
k1
(min-1)
Qe
(mg/g
)
k2
R2 (g/min
.g)
Qe
(mg/g)
R2 á â R2
C
m2.S-
1
Kint
(mg.L.min1/2
)
R2
|
|
|
0,25
|
|
|
0,99
|
|
|
|
|
|
|
|
ABM
|
0,3
|
84,22
|
|
0,05
|
84,2
|
|
1,35.1033
|
29,34
|
0,729
|
53,5
|
4,17
|
0,547
|
|
|
|
6
|
|
|
6
|
|
|
|
|
|
|
|
|
|
0,01
|
|
|
0,99
|
|
|
0,29
|
|
|
|
|
ASM
|
0,51
|
88,74
|
|
0,01
|
86,74
|
|
6,64.103
|
4,637
|
|
75,9
|
0,96
|
0,128
|
|
|
|
8
|
|
|
8
|
|
|
3
|
|
|
|
|
|
|
0,02
|
|
|
0,99
|
|
|
0,27
|
|
|
|
|
APM
|
1,54
|
105,7
|
|
0,01
|
105,75
|
|
1,09.104
|
4,660
|
|
93,4
|
1,25
|
0,125
|
|
|
|
4
|
|
|
9
|
|
|
2
|
|
|
|
A la suite des résultats de la modélisation,
nous constatons que le processus d'adsorption du métronidazole sur les
différents matériaux adsorbants est bien représenté
par le pseudo-second ordre car les valeurs de coefficients de
corrélations sont proches de 1 (R2=0,996 ;
R2=0,997 ; R2=0,999). En effet, les valeurs de la
capacité d'adsorption à l'équilibre calculée par le
modèle pseudo-second ordre (qe= 84,22 mg/g ; qe=88,74mg/g qe=105,7mg/g)
sont très proches de celles déterminées
expérimentalement (qe=84,2mg/g ; qe=86,74mg/g ; qe=105,75mg/g). Ces
résultats corroborent plusieurs résultats , plusieurs
études ; Rosa et al.,2021 ; Ilaria et al.,2013 ; ainsi
que Julia et al., 2019, qui ont obtenu que le modèle
cinétique d'adsorption de métronidazole par argile est celui du
second ordre. Ce modèle explique
l'hétérogénéité des sites de fixation.
Le mécanisme d'adsorption se fait selon
l'hypothèse du modèle cinétique de pseudo-ordre en deux
étapes :
- La première est la diffusion du métronidazole
vers la surface de l'adsorbant
- La seconde est l'interaction entre molécules
d'adsorbats (métronidazole) et la surface des adsorbants (argiles).
III.6. Etude des isothermes d'adsorption
L'étude des isothermes est réalisée afin
de clarifier le phénomène d'adsorption. Les isothermes
d'adsorption sont très indispensables pour la compréhension du
mécanisme d'adsorption (Khelifi, 2018). De manière
générale, elles fournissent des informations sur
l'amélioration des adsorbants, une description de l'affinité et
de l'énergie de liaison entre
63
l'adsorbat et l'adsorbant (existence des interactions
latérales entre molécules ou non) et de la capacité
d'adsorption (Quilong et al., 2007).
Les isothermes montrent que les quantités du
métronidazole adsorbées augmentent avec les quantités du
métronidazole en solution, puis à se stabiliser. Aussi, une
grande affinité, particulièrement entre l'adsorbant et l'adsorbat
a été observée. Selon la classification de Gil et
al., les isothermes sont de type L, ce type est
caractérisé par une forte attraction entre l'adsorbat et
l'adsorbant à travers des interactions d'échange ionique.
(Gomri,2017)
Afin de mieux élucider le phénomène
d'adsorption à l'équilibre, quatre modèles d'isothermes
sont choisis : les modèles de Langmuir, Freundlich, Dubinig-Radushkevich
et Temkin.
Les figures(25,26,27) ci-après illustrent les courbes
des isothermes pour nos différents matériaux d'argile.
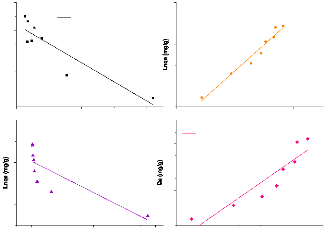
Isothermes Linéaires Metro/ABM
100
80
60
40
20
4
3
Isotherme de Langmuir
y = -0,0137x + 0,0184 R2 =
0,821
0,0 0,2 0,4
Isotherme de Freundlich
y = 0,62985x + 2,10336 R2=
0,965
0 2 4
1/Ce (1/ppm)
Isotherme de DRK
y = -1,86848.10-6x + 4,02515 R2
= 0,665
LnCe (ppm)
Isotherme de Temkin
y = 25,08962x -16,50157 R2= 0,842
0 200000 400000 600000 800000
å2
1 2 3 4
LnCe (ppm)
5
0,020
0,018
0,016
0,014
5
4
3
Lnq
Figure 25:Isothermes linéaires
d'adsorption du métronidazole par l'argile brute
64
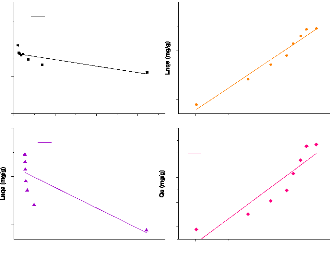
Isothermes Linéaires Metro/ASM
LnCe (ppm)
100
1/Ce (1/ppm)
0,0 0,3 0,6 0,9
Isotherme de Freundlich
y = 0,46703x + 2,77026 R2=
0,967
0 2 4
5
Isotherme de DRK
y = - 4,43427.10-7x + 4,08553 R2
= 0,813
80
Isotherme de Temkin
y = 20,278*x + 6,55599 R2=
0,855
60
40
20
4
3
0 1000000 2000000 3000000
å2
0 2 4
LnCe (ppm)
0,03
0,02
0,01
0,00
5
4
3
Isotherme de Langmuir
y = - 0,00583x + 0,01634 R2 =
0,699
Figure 26:Isothermes linéaires
d'adsorption du métronidazole par l'argile sodique.
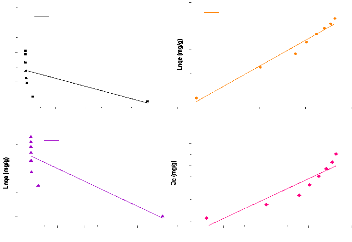
Isothermes Linéaires Metro/APM
0 4 8 12 16 20
-2 0 2 4
5
Isotherme de Langmuir
y = - 2,04534.10-4x + 0,0132 R2
= 0,381
Isotherme de Freundlich
y = 0,26923x + 3,6634 R2=
0,976
4
3
0,018
0,015
0,012
LnCe (ppm)
120 Isotherme de Temkin
y = 13,30332x + 45,87606 R2=
0,858
90
60
30
0 10000000 20000000 30000000 40000000
50000000
150
å2
-2 0 2 4
LnCe (ppm)
5
1/Ce (1/ppm)
)g
Isotherme de DRK
y = -2,63687.10-8x + 4,26187 R2
= 0,674
4
3
(m
/)gg
Figure 27:Isothermes linéaires
d'adsorption du métronidazole par l'argile ponté
.
65
Tableau 10:Récapitulatif des constantes
et des coefficients de corrélation des isothérmes
|
Modèles
|
Langmuir
|
|
|
Freundlich
|
|
|
Temkin
|
|
|
|
D--R
|
|
|
|
Paramètres
|
RL
|
KL
|
Qm (mg/g)
|
R2
|
Kf
|
N
|
R2
|
Qm
(mg/g)
|
KT
|
B
|
R2
|
E
(KJ/mol)
|
Â
10-6
|
Qm (mg/g)
|
R2
|
|
ABM
|
0,034
|
0,744
|
72,99
|
0,82
|
8,2
|
1 ,6
|
0,965
|
84,22
|
25,089
|
4,77
|
0,842
|
323,64
|
4,7
|
51,10
|
0,665
|
|
ASM
|
0,368
|
0,368
|
166,66
|
0,69
|
16,1
|
2,1
|
0,967
|
86,74
|
20,28
|
1,3.10-6
|
0,855
|
640,18
|
1,3
|
56,05
|
0,813
|
|
APM
|
0,0005
|
64,7
|
4901,9
|
0,38
|
43,5
|
3,7
|
0,976
|
105,75
|
13,30
|
14,48
|
0,858
|
253,41
|
1,19
|
66,86
|
0,674
|
66
Les résultats montrent que les valeurs de coefficient
de corrélation R2 pour les modèles de Freundlich et
Temkin donnent une meilleure corrélation pour les différents
supports.
Au demeurant, l'isotherme de Freundlich décrit
convenablement et mieux le phénomène d'adsorption du
métronidazole par nos adsorbants. Des résultats allant dans le
même sillage ont été obtenus par Rosa et al.,2021
lors de l'adsorption de l'ibuprofène par argile. Ainsi que Calabres et
al., 2013 lors de l'adsorption du métronidazole par la
montmorillonite. Les quantités maximales calculées sont
très proches des valeurs expérimentales. La constante n obtenue
par le modèle de Freundlich renseigne sur la nature de l'adsorption.
Nous constatons que les valeurs de n sont supérieures à 1 ; cela
signifie que l'adsorption est favorable et la capacité d'adsorption
augmente et de nouveaux sites d'adsorption apparaissent., l'adsorption se fait
avec une grande intensité et est caractérisée par une
hétérogénéité entre la surface de nos
argiles du métronidazole.
Les paramètres adimensionnels ???? obtenus
pour chacun de nos matériaux sont compris entre 0 et 1, cela signifie
que l'isotherme de Langmuir est favorable.
Les valeurs d'énergie d'adsorptions des
résultats expérimentaux sont égales à 323,64 ;
640,18 et 253,41 respectivement pour l'argile brute, l'argile sodique et
l'argile pontée. Ces valeurs sont supérieures à 80Kj/mol,
ce qui signifie que l'adsorption est de type chimique. (Talami,2017). Au vu des
résultats obtenus, il semble que les trois adsorbants (ABM, ASM et APM)
n'adsorbent pas avec la même capacité. Ainsi, l'APM s'avère
la plus efficace et ceci serait dû à un plus grand
écartement des feuillets de l'argile pontée. Le paramètre
K de Freundlich de l'APM présente des maxima d'adsorption nettement
supérieures à ceux de l'ABM et l'ASM.
67
|
|



