I.3-2 Représentation graphique d'une transformation
La courbe 1-2 représente la variation de P en fonction de
V, au cours d'une transformation.
Travail élémentaire We= -P.
Le produit P. represente, sur le diagramme, l'aire du rectangle
hachuré A-B-C-D.
I.3-3 Travail mécanique
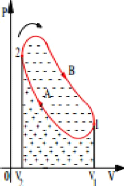
échangé au cours d'un cycle

Mémoire de fin d'études en vue de
l'obtention du diplôme grade Master
22
Le cycle 1-A-2-B peut se décomposer en deux
transformations ouvertes :
- Transformation ouverte 1-A-2 - Transformation ouverte 2-B-1
Le travail mécanique échangé au cours d'un
cycle est donné par la formule : Wcycle= (W1-A-2) + (W2-B-1)
I.3-4 Température constante, transformation
isotherme Etat 1 --* P1 - V1- T1
Etat 2 --* P2 - V2- T2
Equation de la forme y = représentée par une
hyperbole équilatère. Loi de Mariotte : P.V=
constante
I.3-5 Pression constante, transformation isobare
Etat 1 --* P1 - V1- T1
Loi de Gay Lussac = constante
Etat 2 --* P2 - - T2
Si T1 augmente jusqu'à T2, le volume augmente.
On désigne par a le coefficient moyen
d'augmentation de volume par degré.
L'expérience montre que a = =
constante
a= d'où V2 = V1 (1 +
at)
V2 = V1 (1 + )
I.3-6 Volume constante, transformation isochore
Etat 1 --* P1 - V1- T1
Loi de Charles = constante

Mémoire de fin d'études en vue de
l'obtention du diplôme grade Master
23
Etat 2 ? P2 - - T2
Si T1 augmente jusqu'à T2, le volume augmente.
On désigne par ? le coefficient moyen d'augmentation de
pression par degré.
L'expérience montre que ? = = constante
? = d'où P2 = P1 (1 + ?t)
P2 = P1 (1 + )
I.3-7 Transformation polytropique
Elle est caractérisée par une transformation
avec échange de chaleur avec milieu extérieur (dQ?0), avec «
k » l'exposant polytropique :
PVk = constante
T = constante
TVk-1 = constante
I.3-8 Transformation adiabatique
Il s'agit d'une transformation sans échange de chaleur
avec le milieu extérieur (dQ= 0). Avec
????? l'exposant adiabatique, on a : ?où Cp
chaleur spécifique à P constante et Cv
chaleur
spécifique à V constant.
PV? = constante
?
T ? = constante TV?-1 = constante
I.4 Equation d'état des gaz parfaits
Un gaz parfait est caractérisé par les
équations ci-après :
PVM = RT (1 mole) Pv = rT (1 Kg)

Mémoire de fin d'études en vue de
l'obtention du diplôme grade Master
24
Avec
? VM : volume molaire ?m3/mole?
? R : constante universelle des gaz parfaits égale
à 8,319 ?
?
?
? P : pression ?Pa?
? T : température ?K?
? v : volume massique ?m3/Kg?
? r = une constante relative du gaz ?
? M : masse molaire ?Kg?
De manière générale : PV = nRT (n?mole?)
PV = mrT (m?Kg?)
? V : volume effectif ?m3?? m : nM
I.5 Grandeur d'énergies
I.5-1 Travail échangé avec le milieu
extérieur
dW = - PdV
si W ? 0 le système (S) reçoit du travail. Si W ? 0
le système (S) fournit du travail.
| 


