IV.2. Modèle temporel des perturbations EM
La simulation temporelle des perturbations EM permet la
détection et l'analyse des phénomènes transitoires. Ces
phénomènes transitoires réunissent à la fois le
module et la phase de la présentation fréquentielle du champ
rayonné. Alors, ces phénomènes échappent aux normes
CEM en vigueur puisque ces dernières s'intéressent souvent
à l'amplitude des émissions.
En plus, les résultats en régime temporel
contiennent autant d'informations que ceux en régime fréquentiel
et leurs mesures sont plus rapides.
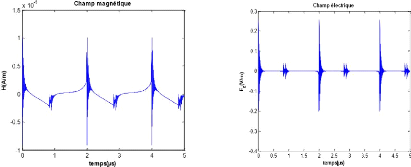
Figure XIX : Composantes (a) Hy du champ magnétique et
(b) Ez du champ électrique
Dans ce qui suit, nous allons déduire, à partir
du spectre de courant IS simulé et de la réponse
fréquentielle de champ EM, les formes d'onde du champ magnétique
et du champ électrique. La reconstruction de ces signaux temporels
à partir de ces spectres du champ EM se fait en utilisant la
transformée de Fourier inverse. Pour le champ magnétique, et de
la même façon pour le champ électrique, la formule
s'écrit :
1-1(t) = E
1-1(??????)e-??27c?????? (37)
??=0
IV.3. Interprétation des résultats
Dans cette simulation, nous nous sommes
intéressés, dans un premier temps, à la
modélisation du rayonnement d'un prototype de câblage
reflétant les phénomènes EM dus au câblage
automobile.
Nous avons pu associer notre câblage à un
convertisseur DC-DC. Cette configuration reflète une application de
systèmes électroniques embarqués dans laquelle la
distribution de l'énergie à différents niveaux se fait
à travers des DCDC à partir d'une batterie.
Le découpage dans le convertisseur de puissance
génère des perturbations HF qui se propagent vers une charge via
le câble. Le rôle du câble dans une telle configuration n'est
pas anodin. En effet, il modifie le spectre de perturbations et participe
énormément au rayonnement du système complet.
Une simulation des formes d'onde du champ magnétique et
champ électrique s'est avérée possible. Ainsi, nous avons
pu présenter en temporel le champ EM même si nous n'avons pas pu
le valider par des mesures essentiellement à cause de la
difficulté de la réalisation de sondes temporelles de mesure.
V. Conclusion
De nos jours, la modélisation des émissions EM
rayonnées des systèmes électroniques embarqués
constitue un grand challenge d'autant plus que ces émissions
représentent un risque énorme pour le bon fonctionnement des
systèmes et aussi pour l'homologation CEM.
La difficulté de rendre compte de ce
phénomène lié à ces systèmes est une
évidence et elle est accentuée par la forte intégration
électronique. En effet, la modélisation EM, elle-même,
nécessite une association de plusieurs méthodes
numériques. Cela dépend des dimensions et surtout de la
géométrie. Alors, le choix d'une méthode de
modélisation EM adéquate pour chaque sous structure ou
l'association de plusieurs méthodes est une solution possible mais
demeure très délicate. De plus, pour intégrer ce
phénomène EM au modèle de l'électronique
embarquée, nous avons besoin d'un modèle électrique du
comportement EM des structures qui rayonnent le plus telles que les bus bars,
les câbles et les plans de masse.
Dans cet article, nous avons porté notre choix
à la méthode PEEC. Par sa formulation intégrale et par sa
possibilité de décrire les phénomènes EM sous forme
de circuit équivalent, la méthode PEEC correspond au besoin de
modéliser le câblage dans son environnement électrique
d'autant plus que la discrétisation est restreinte aux seuls
conducteurs.
Nous avons pu associer notre câblage à un
convertisseur DC-DC. Cette configuration reflète une application de
systèmes électroniques embarqués dans lesquels la
distribution de l'énergie à différents niveaux se fait
à travers des convertisseurs DC-DC à partir d'une batterie.
Le découpage dans le convertisseur de puissance
génère des perturbations HF qui se propagent vers une charge via
le câble. Le rôle du câble dans une telle configuration n'est
pas anodin. En effet, il modifie le spectre de perturbations et participe
énormément dans le rayonnement du système complet.
Une simulation des formes d'onde du champ magnétique
et champ électrique s'est avérée possible. Ainsi, nous
avons pu présenter en temporel le champ EM.
Les simulations en régime temporel dans le domaine de
la CEM est une nécessité. Elles permettent, contrairement
à des simulations fréquentielles, de prédire les
transitoires de champ EM.
VI. BIBLIOGRAPHIQUE
[1] Directive Européenne 2004/108/CE, du parlement
européen et du conseil, 15 Décembre 2004.
[2] Directive Européenne 89/336/CEE, du parlement
européen et du conseil, 03 Mai 1989.
[3] F. DUVAL, "Gestion du câblage des masses
électriques dans un véhicule automobile : Application CEM",
Thèse de Doctorat, Université de Paris Sud XI, 2007.
[4] I. Yahi ,"Modélisation des sources de rayonnement
au sein d'un véhicule automobile avec prise en compte de la
présence du plan de masse" Thèse de Doctorat, Université
de Rouen, 2009
[5] I. Yahi, F. Duval, A. Louis, "A New Capacitive Coupling
Consideration in PEEC Method" 2emc Symposium on embedded EMC, October 2007
[6] M. Besacier, "Adaptation de la méthode PEEC à
la représentation électrique des structures d'électronique
de puissance", Thèse de Doctorat, Institut National Polytechnique de
Grenoble, 2001.
[7] Cyril Buttay, "Contribution à la conception par la
simulation en électronique de puissance : application à
l'onduleur basse tension" thèse Doctorat Institut National des Sciences
Appliquées de Lyon, 30 Novembre 2004.
[8] E. Clavel, "Vers un outil de conception de câblage
: le logiciel INCA", Thèse de Doctorat, Institut National Polytechnique
de Grenoble, 1996.
[10] Jean-Paul Gonnet, "Optimisation des canalisations
électriques et des armoires de distribution", Thèse de doctorat
de l'université Joseph Fourier, 2005.
[9] Sergey V. Kochetov, "Time- and frequency-domain modeling of
passive interconnection structures in field and circuit analysis", rapport de
habilitation, 2008.
[10] Ekman Jonas, Lundgren Urban, "Analysis of printed antenna
structures using the partial element equivalent circuit (PEEC) method",
Conference proceedings: electromagnetic computations - methods and
applications. - Uppsala, Sweden 2001.
[11] A. Ruehli, "Equivalent circuit models for three dimensional
multiconductor systems", IEEE Transactions on Microwave Theory and Techniques,
vol. 22, no. 3, pp. 216-221, mars 1974.
[12] A. E. Ruehli, P. A. Brennan, "Efficient Capacitance
Calculations for Three-Dimensional Multiconductor Systems", IEEE Transactions
on Microwave Theory and Techniques, vol. 21, no. 2, p. 76-82. , February
1973.
[13] A. Ruehli and H. Heeb, "Circuit models for
three-dimensional geometries including dielectrics", IEEE Trans. Microwave
Theory Tech., vol.40, p. 1507-1516, July 1992
[14] K. M Coperich, A. E. Ruehli, and A. Cangellaris, "Enhanced
Skin Effect for Partial Element Equivalent Circuit (PEEC) Models". IEEE
Transactions Microwave Theory and Technique, 48, 1435- 1442, 2000.
[15] J. Garrett, A. E. Ruehli, and C. R. Paul, "Accuracy and
Stability Improvements of Integral Equation Models using the Partial Element
Equivalent Circuit (PEEC) Approach", IEEE Trans. Antennas Propagat., vol. 46,
no. 12, pp. 1824-1831, December 1998.
[16] A. E. Ruehli, G. Antonini, and A. Orlandi, "Extension of
the Partial Element Equivalent Circuit Method to Non Rectangular Geometries",
in: Proceeding. of the Int. Symposium on EMC, pages 728733, Seattle,
Washington, USA, August 1999.
[17] G. Antonini, A. E. Ruehli, J. Esch, J. Ekman, A. Mayo and
A. Orlandi, "Nonorthogonal PEEC Formulation for Time- and Frequency-Domain EM
and Circuit Modeling", IEEE Transactions on Electromagnetic Compatibility, vol.
45, no. 2, pp. 167-176, May 2003.
[18] A. Müsing, J. Ekman and J.W. Kolar, "Efficient
Calculation of Non-Orthogonal Partial Elements for the PEEC Method ", IEEE
Transactions on Magnetics, vol. 45, issue3, p 11401143, March 2009.
[19] Martin Ludwig Zitzmann, "Fast and Efficient Methods for
Circuit-based Automotive EMC Simulation" Thèse de doctorat de
l'université de Nürnberg, Allemagne 2007.
[20] Kenneth L. Kaiser, "Electromagnetic Compatibility Handbook:
Circuits, Signals and Systems" ,Chapter 3, CRC Press, 2004.
[21] E.Vialardi, "Une technique de réduction d'ordre
couplée à des modèles PEEC: application sur des
équipements aéronautiques", Thèse de doctorat de
Politechnico de torino, 2003.
[22] F. Duval "Gestion du câblage des masses
électriques dans un véhicule automobile : Application CEM",
Thèse de Doctorat, Université de Paris Sud XI, 2007.
[23] G. Antonini, J. Ekman, and A. Orlandi, "3D PEEC capacitance
calculations", Proceedings of the IEEE International Symposium on EMC, Boston,
USA, pp. 630-635, August 2003.
[24] J. Ekman, "Electromagnetic Modeling using the Partial
Element Equivalent Circuit Method", PhD Dissertation, EISLAB: Embedded Internet
System Laboratory, Computer Science and Electrical Engineering, Lulea
University of Technology, 2003.
[25] J. Ekman, "Electromagnetic Simulations Using The Partial
Element Equivalent Circuit (PEEC) Approach", in Proceeding of Progress in
Electromagnetics Research Symposium, Honolulu, HI, USA, 13-16 October 2003.
[26] SPICE, from EECS Department of the University of California
at Berkeley,
http://bwrc.eecs.berkeley.edu/Classes/IcBook/SPICE
[27] SPICEWIN, version 3.5f de SPICE de Berkeley, compile pour
les systèmes d'exploitation Microsoft,
http://embedded.eecs.berkeley.edu/pubs/downloads/spice/index.htm
[28] Mathias Enohnyaket "PEEC Modeling and Verification for
Broadband Analysis of AirCore Reactors", dissertation of PhD from University of
Technology lulea, Sweden 2007.
[29] V. Ardon, O. Chadebec, J-M. Guichon, E. Vialardi,
"Extraction des capacités parasites de structures d'électronique
de puissance", Numelec08, 2008.
[30] V. Ardon, J. Aimé, O. Chadebec, E. Clavel, Y. Le
Floch, "Evaluation du modèle capacitif d'une structure
d'électronique de puissance", CEM08 14ème colloque international
et exposition sur la compatibilité électromagntique-JS08
journée scientifique URSI-France, 2008.
[31] Vincent Ardon, Jérémie Aimé, Olivier
Chadebec, Edith Clavel, Enrico Vialardi, "MoM and PEEC Method to Reach a
Complete Equivalent Circuit of a Static Converter" Proceeding EMC Zurich
2009.
[32] J. Ekman and S. Niska, "Combining 2D Transmission Line
Models with 3D PEEC Models", in Proceeding. of EMB04, Gothenburg, Sweden,
2004.
| 


