III.2. Source de perturbations
D'une manière générale, pour les mesures des
perturbations conduites, on utilise un RSIL (réseau stabilisateur
d'impédance de lignes) implémenté dans le logiciel de
simulation Matlab. Dans cet article, pour la mesure de la tension aux bornes de
la diode de roue libre, nous utilisons un oscilloscope
numérique virtuel intégré dans le
simulateur pouvant aller jusqu'à 1GHz. Dans notre cas, nous ne
dépassons pas la fréquence 300MHz parce que le circuit ne
perturbe pas au-delà de cette fréquence. Le type d'oscilloscope
virtuel utilisé admet deux configurations d'impédance propre :
50? et 1M?. Pour s'assurer que le fonctionnement du circuit n'est pas
modifié, nous utilisons le simulateur de mesure en haute
impédance. Nous obtenons ainsi la tension réelle aux bornes de la
diode (Figure VII). En observant de plus près cette forme d'onde, nous
déterminons, à travers la Figure VIII, les temps de montée
et de descente.
Figure IX - Hacheur série

Figure X - Mesure de la tension aux bornes de la diode
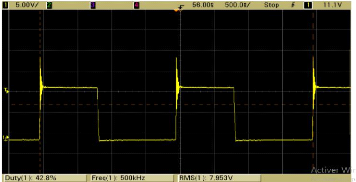
Figure XI :Mesure de la tension aux bornes de la diode
Lors d'une commutation rapide, des oscillations sont
observées au niveau du transistor de découpage (ou de la diode).
Dans notre cas, nous distinguons des oscillations qui sont loin d'être
négligeables. Elles sont générées lors de la
fermeture du MOS. Physiquement, cette ondulation est due aux capacités
intrinsèques du MOS et surtout aux inductances en série. Pour
réduire ces oscillations, la solution est de minimiser ces
inductances.
L'objectif de ce qui suit est de déterminer la fonction
de transfert qui relie un signal de référence (Figure VIII) et la
tension du transistor avec ondulations. Dans ce cas, nous considérons le
signal de référence un signal trapézoïdal qui permet
de prendre en compte a priori le temps de montée et le temps de descente
du signal à obtenir (Figure VIII). Cela facilite l'obtention de la
fonction de transfert souhaitée puisqu'en soustrayant le signal
trapézoïdal du signal global de perturbation nous obtenons un
signal tel que décrit l'équation suivante :
??(??) =
????.??-????.??????(w??).??(??) (34)
Où ???? est une tension caractérisant
la variation exponentielle des points maximum de la tension d'ondulation, w
est la pseudo-pulsation. L'identification des différentes
constantes dans l'équation (35) se fait à partir des mesures. De
cette façon, nous déterminerons la fonction de transfert de la
tension de perturbations qui s'écrit sous la forme de l'équation
suivante :
?????????????????????%o??????
3,967*1017
??(??) = = (35)
??????????è????
??2+9,92*1017??+3,967*1017
Avec ?? = ??w (36)
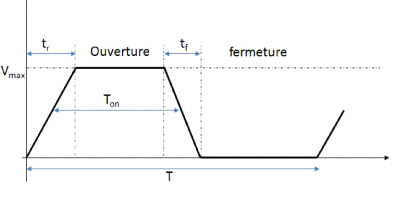
Figure XII : Signal trapézoïdal de
référence
Vtrapèze Est la transformée de Laplace
du signal trapézoïdal (Figure XII) définie à l'aide
du temps de montée, du temps de descente, de la tension maximale, de la
période et des temps d'ouverture et de fermeture.
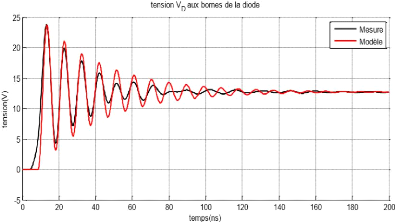
Figure XIII : Comparaison entre perturbations mesurées
et simulées
Le temps de montée est assez petit afin d'assurer la
génération des ondulations mesurées. Le temps de descente
permet de générer le temps descente mesuré avec des
ondulations négligeables. À partir d'un signal
trapézoïdal périodique, il devient facile de
générer les perturbations au niveau de la diode et cela pendant
le temps nécessaire pour dépasser la période transitoire
et nous situer en régime permanent lors de la simulation.
La Figure XIII montre une très bonne concordance entre
notre modèle et la perturbation réelle définie par la
tension aux bornes de la diode.
| 


