II.3.1 Modélisation des émissions
rayonnées
La détermination des émissions rayonnées
d'un système de câblage passe par deux principales étapes :
par le calcul des émissions conduites et par la déduction des
émissions rayonnées. La première consiste à
déterminer pour chaque cellule de discrétisation le courant qui
la traverse. Ensuite, connaissant, à la fois, la géométrie
et la valeur de courant à chaque fréquence, nous utilisons
l'approche de calcul analytique pour définir la contribution de chacune
des cellules de discrétisation. Le champ EM en un quelconque point de
l'espace est la contribution de chacune des cellules et il est obtenu en
sommant les différentes composantes des champs magnétique et
électrique.
II.3.1.1 Équations d'ondes en milieu
homogène
Ces équations d'ondes sont obtenues à partir des
équations de Maxwell décrites dans le premier chapitre. Pour les
champs électrique et magnétique auxquels nous nous
intéressons, les équations d'ondes, en un point ?? et à
l'instant t, sont données respectivement par :
? ?
? × ?
|
? × ??
|
(?? , ??)+ ??0??0????2 ??? (?? , ??) = -??0
??2 ?????? (?? , ??)
?? (23)
|
|
? ?
? × ?
|
? × ??
|
(?? ,??) + ??0??0 ????2 ??? (?? , ??) = ??0??? (?? , ??)
??2 (24)
|
|
Où ??? est le champ
électrique, ??? est le champ magnétique et ??0 et ??0 sont
respectivement la perméabilité magnétique et la
permittivité électrique de l'air (vide).
En utilisant les relations de constitution (1), (2) et (3)
qui sont décrites précédemment, les équations
d'onde (23) et (24) s'écrivent :
?
???
(?? , ??) -??0??0 ????2 ??? (?? , ??) = 1
??2 ??0 ??? (?? , ??) + ??0 ?????? (?? , ??)
?? (25)
|
? ?
? × ?
|
? × ??
|
(?? , ??) + ??0??0 ????2 ??? (?? , ??) = ? × ?? (?? ,
??)
??2 (26)
|
??? (?? , ??) = 1
??0
?? × ?? (?? , ??) (27)
|
On sait que les champs ???
|
(?? , ??) et ???
|
(?? , ??) peuvent être écrits en fonction du
potentiel vecteur ?? et du
|
potentiel scalaire ??. La notion de potentiels a
été utilisée dans le but de simplifier la
résolution des équations de Maxwell.
II.3.1.2. CHAMP MAGNETIQUE ET CHAMP ELECTRIQUE
D'une manière générale, le champ
magnétique (27) est donné en fonction du potentiel vecteur ??
tandis que le champ électrique (28) dépend, en plus, du potentiel
scalaire ??.
??? (?? , ??) = - ???? (?? ,??)
???? - ?? (??(?? , ??)) (28)
II.3.1.3. CHAMPS ELECTROMAGNETIQUES PROCHE ET
LOINTAIN
Dans la littérature, lorsqu'il s'agit de définir
les champs EM proche et lointain, on fait appel aux dipôles
élémentaires : électrique dit de Hertz (Figure II.a) et
magnétique sous forme de boucle (Figure II.b). Pour une fréquence
donnée, suivant la distance d'observation, les champs électrique
et magnétique que ce type de dipôle génère sont
interdépendants ou pas. Ainsi, on définit 3 zones (Figure III)
qui sont : la zone champ proche, zone de transition et champ lointain.
La première région (zone 1) appelée
région de champ proche réactif a pour limite une distance r
inférieure à 0,62v??3/?? où D est la plus
grande dimension de l'antenne et X est la longueur d'onde.
La seconde région (zone 2) appelée région
de champ proche rayonnant est aussi nommée zone de Fresnel en
référence à la terminologie optique car les expressions
des champs dans cette région se réduisent aux
intégrales de Fresnel. Cette région s'étend
entre ?? = 0,62v??3/?? et une distance r inférieure à
D2/X.
La troisième région (zone 3) nommée
région de champ lointain ou zone de Fraunhofer correspond à une
zone où la distribution angulaire du champ est essentiellement
indépendante de la distance r par rapport à l'antenne.
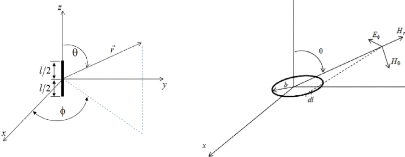
Figure II : Dipôle électrique (a) et dipôle
magnétique (b)

Les notions de champ proche et de champ lointain sont souvent
mises en évidence en considérant l'impédance d'onde ???? .
Elle n'est que le rapport entre le champ électrique transverse
(transverse par
Figure III - Régions : du champ proche au champ lointain
[64]
rapport au vecteur entre le point d'observation et le centre du
dipôle) ??? ?? et le champ magnétique
?
transverse ?? ?? :
???? = |??? ??| (29)
|???? ??|
Cette impédance dépend de la fréquence du
travail, de la distance par rapport à la source et de la
géométrie de la source. Cela est autant vrai qu'on est proche de
la source. Mais, lorsque les conditions d'espace libre et de champ lointain
sont remplies, le champ électrique et le champ magnétique sont
couplés par le rapport invariant ??0 (30). Dans ces conditions, le champ
électromagnétique est une onde plane.
Dans l'équation (30), ??0 est l'impédance
caractéristique du vide qui est donnée par ??0 =120?? = 377??h??
.
|??? ??(???8)| (30)
|???
??0 = ??(???8)|
Lorsque la source est de dimensions comparable ou bien
supérieure à la longueur d'onde, le calcul basé sur le
dipôle d'Hertz devient erroné. Il devient donc nécessaire
de discrétiser la source en des petites
La Figure IV montre la variation de l'impédance d'onde des
dipôles électrique et magnétique en fonction de la distance
par rapport aux dipôles.

Figure IV - Impédance d'onde des dipôles
électrique et magnétique
Dans la Figure IV, ZH est l'impédance d'onde du
dipôle magnétique et ZE est l'impédance d'onde du
dipôle électrique.
Dans la zone très proche du dipôle,
l'impédance d'onde relative au dipôle électrique tend vers
des valeurs supérieures à ??0 contrairement au cas
magnétique où l'impédance y est inférieure. Dans le
cas du dipôle électrique, nous parlons de champ à haute
impédance. Dans le cas du dipôle magnétique, nous parlons
d'un champ à basse impédance. Dans les deux cas,
l'impédance tend vers ??0 quand la distance d'observation est assez
lointaine de la source. Cela n'est vrai que si la source est de faible
dimension vis-à-vis de la longueur d'onde. Une première condition
sur la définition du champ proche s'applique sur les dimensions du
système rayonnant qui doivent être très petites devant la
longueur d'onde. Cette condition ne peut pas être respectée pour
les systèmes de câblage et surtout pour des HF.
En effet, dans les normes CEM, le rayonnement EM est pris en
compte dès la fréquence 30MHz. La longueur d'onde à cette
fréquence est égale à 10 m. Ainsi, pour pouvoir utiliser
la définition des zones champ proche, il ne faut pas que les dimensions
des systèmes étudiés dépassent 1m.
cellules dont chacune représente un dipôle
infiniment petit. Les courants formant ces dipôles sont
déterminés à partir d'une méthode numérique,
dans notre cas de la méthode PEEC.
III. Application au rayonnement de
câblages
La gestion de câblage embarqué au sein d'un
véhicule automobile ne dépend pas que des caractéristiques
des câbles. Les puissances véhiculées par ces câbles
doivent également être prises en compte. L'environnement joue un
rôle prépondérant. À cette problématique, on
doit ajouter que les sources de perturbations embarquées sont souvent
très différentes ainsi que le spectre des puissances
associées. Les solutions préventives à préconiser
dépendent ainsi d'une multitude de facteurs. La prédiction des
perturbations EM est donc une étape primordiale dans l'objectif par
exemple de respect des normes en vigueur.
Nous étudions dans ce paragraphe l'association d'un
système de câblage à une source de perturbations qui est un
convertisseur DC-DC. Nous nous intéressons à la propagation des
perturbations de la source vers le câblage. Une évaluation des
émissions rayonnées est effectuée en régime
fréquentiel et une comparaison avec des mesures en champ proche est
réalisée. Pour terminer, nous effectuons à l'aide du
modèle précédent une prédiction des perturbations
dans le domaine temporel en s'appuyant sur l'analyse fréquentielle.
| 


