CHAPITRE I : GENERALITES SUR LES INCUBATEURS D'OEUFS
I.1 Introduction
Le présent chapitre parle des différents
paramètres d'incubations comme la température et le taux
d'humidité qui conditionnent le bon fonctionnement d'un incubateur
d'oeufs. Nous considérons que ces derniers sont relatifs aux oeufs des
poules et sont physiquement mesurables au moyen des capteurs comme la sonde de
température, le capteur d'humidité, etc. Ces capteurs
interagissent avec un système intelligent qui régule
automatiquement tous les paramètres d'incubations par rapport aux
consignes fixées. Nous donnerons quelques étapes du
développement embryonnaire d'un poussin. Et pour clore ce chapitre, nous
parlerons brièvement des différents matériaux
utilisés pour la fabrication des incubateurs.
I.2 Définition de concepts de base
I.2.1 Incubateur d'oeufs :
L'incubateur est un appareil consistant essentiellement en une
enceinte close, aseptique, maintenue à température et
humidité constantes par des systèmes de régulation, et
où sont placés les oeufs pour la durée de leur incubation.
Il existe deux types d'incubateurs : les incubateurs à ventilation
naturelle ou statique et les incubateurs à ventilation forcée ou
dynamique où l'air est brassé par un ventilateur. Les incubateurs
fonctionnent soit à l'électricité, au gaz ou au
pétrole et ont des capacités variant entre 8 et 200 oeufs pour
les petits producteurs à plus de 100000 oeufs pour les grandes fermes
(KHADIDJA, 2016).
I.2.2 Incubateur d'oeufs intelligent :
D'une manière générale un incubateur
d'oeufs intelligent est tout incubateur doté d'un système de
régulation de la température et de l'humidité ; et d'un
système de retournement automatique des oeufs. Il est capable
d'acquérir les données provenant de ses capteurs, les traiter et
ensuite les communiquer à l'homme à travers une interface
graphique (Microsoft experiences, 2018).
I.2.3 La chaleur
La chaleur est un paramètre important concernant
l'incubation d'oeufs, c'est elle qui permet le développement
embryonnaire. Lorsque l'on met deux corps de températures
différentes en contact, leurs températures ont tendance à
s'égaliser au cours d'un transfert spontané d'énergie.
Nous appelons cette forme d'énergie la chaleur. La chaleur, notée
Q, est
~ 3 ~
une forme d'énergie (mesurée en joules).
À l'échelle macroscopique, c'est la mesure d'un changement
d'énergie interne d'un système thermodynamique, lorsqu'aucun
travail n'est effectué (Cleynen, 2014).
I.2.4 Conception d'un incubateur d'oeufs :
Concevoir un incubateur d'oeuf revient à trouver son
aspect esthétique avec une référence spécifique
à sa forme et sa capacité d'accueil. La conception d'un
incubateur d'oeufs peut être considérée comme signifiant
tous les processus de visualisation, calculs de dimensionnements, raffinement
et spécification des détails tels que la température
d'incubation, le taux d'humidité, l'apport en oxygène, etc.
Concevoir en général commence par un besoin ou une exigence ou,
alternativement, une idée ; et se termine par un ensemble de dessins ou
des représentations informatiques et autres informations permettant de
fabriquer le produit (Childs, 2004).
I.3 Types d'incubation d'oeufs
I.3.1 Incubation naturelle
En fonction de sa race, la poule peut couver en moyenne 8
à 14 oeufs. Elle commence la couvée lorsqu'elle a fini de pondre.
Cette phase de couvaison se caractérise par une maintenance dans le nid,
le retournement des oeufs et une posture agressive lors d'une approche. En
effet, la poule ne quitte le nid que très brièvement pour
s'alimenter et boire. En outre, elle a besoin du calme pour mener à bien
la couvée. Pendant la couvée, elle fournit la température,
l'humidité et la ventilation nécessaires au bon
développement des oeufs. L'éclosion intervient au bout de 21
jours d'incubation. Le taux d'éclosion varie selon plusieurs facteurs.
Ainsi, des études rapportent respectivement des taux d'éclosion
qui varie entre 50% et 60% (KAZED, 2011).
Après l'éclosion, la poule prend soin de ses
poussins en leur apprenant à rechercher la nourriture et les
protège également des agressions extérieures. Les
activités de couvaison et d'élevage des poussins accroissent la
longueur du cycle reproductif chez la poule de 58 jours pour atteindre environ
74 jours (16 jours de ponte et de constitution de la couvée + 21 jours
d'incubation + 37 jours d'élevage des poussins = 74 jours). Cette
situation constitue une limite à la productivité de la poule et
l'incubation artificielle pourrait être une solution à envisager
pour augmenter le rendement de la production (Seydou, 2011). La figure I-1
illustre une couvaison naturelle, on peut clairement y voir la posture que
prend la poule lorsqu'elle couve ses oeufs.
~ 4 ~

Figure I-1:Couvaison naturelle (Combes, 2020)
I.3.2 Incubation d'oeufs artificielle
I.3.2.1 Historique
La couveuse artificielle ou «l'incubateur d'oeufs »
ne date pas d'aujourd'hui. En effet, depuis plusieurs siècles les
Égyptiens construisaient ces machines. En Égypte ancienne ils
s'appelaient «les Mammals», c'étaient de véritables
constructions en maçonnerie comportant des fours chauffés
à la bouse de chameau au-dessus desquels se trouvaient les chambres
d'incubation. Un seul homme s'occupait d'un Mammal pouvant incuber plusieurs
oeufs. Il n'était pas rétribué mais tirait son
bénéfice de sa production en livrant 80 poussins pour 100 oeufs
mis à couver. Actuellement presque tous les incubateurs fonctionnent
à l'électricité, il existe d'autres modèles
à pétrole et à gaz (Seydou, 2011).
I.3.2.2 Définition
L'incubation artificielle est une technique de
reconditionnement thermique favorable au développement embryonnaire qui,
à partir d'une quantité d'oeufs pondus, permet d'obtenir le
maximum de poussins viables au coût le plus bas possible. Cette technique
utilise des incubateurs qui sont conçus pour régulariser la
chaleur, l'humidité, la ventilation et la rotation des oeufs afin
d'accomplir un développement embryonnaire normal (voir la figure
I-2).

Figure I-2: Incubation artificielle (ANDD, s.d.)
~ 5 ~
I.3.3 Principe de l'incubation
artificielle
Le principe d'incubation d'oeufs est toujours le même :
une enceinte étanche, généralement doublée de
matériaux isolants (exothermiques), dans laquelle se trouve
principalement une source de chaleur, une source d'humidité et
accessoirement des orifices permettant le renouvellement progressif d'air. Pour
ces incubateurs, on peut également y trouver des mécanismes
facilitant le retournement des oeufs.
I.3.4 Types d'incubateurs d'oeufs artificiels
Il existe généralement deux modèles
d'incubateurs artificiels :
· Les incubateurs à ventilation naturelle ou
statique et
· Les incubateurs à ventilation forcée ou
dynamique où l'air est rénové par un ventilateur
(Galinette, s.d.).
I.3.4.1 Les incubateurs statiques ou
classiques
Dans les incubateurs d'oeufs statiques le chauffage
s'effectue en haut. Pour des modèles électriques il s'agit d'une
résistance chauffante tapissant la face inférieure du plafond, de
même, il existe d'autres types qui utilisent des lampes à
incandescences comme on peut le voir à la figure I-3. Dans des
modèles à gaz ou à pétrole, le chauffage se fait
par une flamme permanente ou bien par l'intermédiaire d'un
réservoir d'eau chaude (Vendéens, 2017).

Figure I-3:Couveuse Classique (Essaim, s.d.)
Selon ces incubateurs, la température est toujours
élevée en haut qu'en bas à cause de l'emplacement des
sources de chaleur, et en plus l'air chaud se rassemble vers le sommet de
l'enceinte fermée. Par conséquence, la température de la
couveuse est de plus en plus basse en allant de haut vers le bas. C'est pour
cela les oeufs sont disposés sur un seul plateau sur le même
niveau, pour bénéficier de la même température. La
température doit être fixée à 39°C, et elle
" 6 "
est mesurée au sommet des oeufs. De plus, le
retournement des oeufs cinq à sept fois par jour est nécessaire
(Vendéens, 2017).
I.3.4.2 Les incubateurs dynamiques
Dans ces genres d'incubateurs, l'air intérieur est
brassé par un ventilateur. Ce dernier doit être placé loin
des oeufs et des poussins naissants, et il doit être
protégé par une grille pour ne pas les blesser. Il existe
d'autres modèles où l'air est aspiré par un aspirateur de
haut vers le bas puis le réinjecte dans l'incubateur après une
phase de réchauffage et de filtrage. Par conséquent, la
température est parfaitement uniforme dans l'ensemble de l'appareil.
C'est pour cela qu'on peut y mettre les plateaux d'oeufs sur différents
niveaux. Dans ce type de couveuses, la température doit être
réglée à 37,8°C ou 38°C, et elle est
mesurée au sommet des oeufs. Notons que les modèles dynamiques
sont plus techniques que les modèles statiques (Vendéens, 2017).
La figure I-4 illustre le modèle d'un incubateur dynamique.

Figure I-4:Incubateur Dynamique (Alibaba, 2018)
I.3.5 Incubation mixte
Ce dernier type d'incubation utilise les deux classes
citées ci-dessus, à savoir commencer cette incubation sous des
poules et terminer dans la couveuse artificielle, ou bien l'inverse (KHADIDJA,
2016).
I.4 Paramètres agissant sur l'incubation
artificielle
La réussite de l'incubation artificiel est
régit par le contrôle des certains paramètres qui
facilitent le développement cellulaire des embryons. Ces derniers
doivent être fixés par rapport aux consignes bien
définies.
~ 7 ~
I.4.1 La température
Une couveuse doit fournir une température comparable
à celle d'une poule qui chauffe ses oeufs avec son corps. Si la
température ambiante descend en dessous de 35°C, il faut se servir
d'une couveuse équipée d'un chauffage. Le maintien de la bonne
température nécessite une bonne isolation (KHADIDJA, 2016).
Le paramètre température joue un rôle
très important pendant la régulation de l'incubateur artificiel.
En effet, en cours d'incubation, les températures à
considérer sont :
· Un refroidissement de 20°C pouvant aller
jusqu'à 12 heures cumulées durant la période d'incubation
;
· On peut considérer notre couveuse comme
fortement compromise si T = 40°C ;
· Les surchauffes provoquent un développement
anarchique des cellules et donnent des poussins déformés ;
· Il est déconseillé d'atteindre une
température de 44°C, parce qu'à partir de cette
température les oeufs sont à jeter (Hubbard, 2010).
I.4.1.1 Le réglage de la température
pendant l'incubation
Le facteur essentiel de la réussite de l'incubation
est la température, surtout pendant la première semaine. La
température optimale lors des deux premières semaines est de
38,9°C avec un écart maximal de 0,5°C vers le haut ou vers le
bas. Au-delà de 40,5°C, les températures sont mortelles pour
les embryons. Une hausse de température et une baisse d'humidité
peuvent donner ensemble des résultats désastreux. Une
température trop basse retarde l'éclosion des oeufs, mais est
toutefois moins dangereuse qu'une température trop élevée.
A partir du 19ième jour de l'incubation, la température doit
baisser à 36,1°C car les poussins produisent eux-mêmes de la
chaleur. Les poussins nouveau-nés qui gardent le bec ouvert essayent de
perdre de la chaleur en respirant fortement, cela indique une surchauffe de la
couveuse (KHADIDJA, 2016). La figure I-5 illustre quelques facteurs à
réunir pour avoir une température constante.
" 8 "
Chauffer les oeufs
Garder la température
stable
Réguler la température
Conserver la
température
Ampoules
Radiateur
Résistance chauffante
Régulateur
Thermostat
Caisse isolante
Figure I-5: Les astuces à utiliser pour avoir une
température stable (KHADIDJA, 2016)
Le développement embryonnaire est essentiellement
régi par la température. Il s'agit là d'un
paramètre capital dans la détermination des conditions
d'incubation. Pour garder ce dernier stable, nous devons avoir une source de
chaleur pilotée par un régulateur, la caisse de l'incubateur doit
être isolée du milieu extérieur pour éviter une
déperdition énergétique considérable.
I.4.1.2 La production de chaleur par
l'embryon
Il est communément admis qu'au cours du
développement embryonnaire deux grandes périodes se
succèdent : l'une endothermique, en tout début d'incubation et
d'une durée d'environ 8-9 jours, et l'autre, exothermique, en fin
d'incubation et d'une durée approximative de 7-8 jours. Entre les deux,
une étape dite isothermique, souvent très courte, est parfois
mentionnée (Hubbard, 2010).
Romijn et Lokhorst ont été les premiers
à déterminer la chaleur produite par l'embryon en fonction des
jours d'incubations en utilisant la méthode de la calorimétrie
direct et inverse comme l'illustre la figure I-6.
~ 9 ~

Figure I-6: La chaleur produite durant d'incubation
(Hubbard, 2010)
I.4.2 L'humidité
L'humidité relative (HR) varie fortement avec la
température. Si ce niveau n'est pas bon, les embryons se
déshydratent dans l'oeuf ou ne parviennent pas à éliminer
les gaz toxiques qu'ils produisent. Un bon niveau d'humidité s'obtient
en installant dans la couveuse des
~ 10 ~
récipients remplis d'eau. L'humidité relative
se mesure à l'aide d'un thermomètre à cuvette humide ou
avec un hygromètre (KHADIDJA, 2016).
Les effets des paramètres de l'humidité de
l'air ou humidité relative (RH) sur les résultats d'incubation
sont importants, ces paramètres sont :
· L'oeuf perd beaucoup d'humidité à
travers les pores de sa coquille, donc il faut éviter la
déshydratation des oeufs en contrôlant l'humidité dans la
couveuse ;
· L'humidité assure le bon développement
de l'embryon mais également facilite le bêchage en rendant la
coquille plus fragile ;
· Pendant l'éclosion, le bon niveau
d'humidité doit être maintenu. Si l'air est sec, les poussins se
déshydratent rapidement et meurent ;
· Les meilleurs résultats d'incubation sont
obtenus avec une humidité relative variant entre 50 et 60% pendant les
18 premiers jours et de 75% au plus pendant les trois derniers jours
d'incubation (Hubbard, 2010).
Le tableau I-1 donne les différentes
conséquences qui surviennent en ayant une mauvaise hygrométrie
dans l'incubateur :
Tableau I-1:Conséquences d'une mauvaise
hygrométrie sur le développement embryonnaire
Evolution d'incubation
|
Hygrométrie trop élevée
|
Hygrométrie trop basse
|
OEuf
|
Augmentation de la contamination et développement des
bactéries
|
Fuite hydrique entrainant des adhérences
|
Embryon
|
Mort tardive par défaut de perte d'eau
|
|
Eclosion
|
Prématurée
|
Eclosion tardive
|
Poussin
|
Faible, non mobile, poisseux, oedèmes sous-
cutanés
|
Sec, petit, déshydraté, adhérant à
la coquille
|
Cordon ombilical
|
Mal cicatrisé
|
Sec
|
|
I.4.3 L'aération
L'oeuf à couver est un être vivant qui respire,
une bonne ventilation est donc nécessaire pour assurer le bon
développement de l'embryon. La ventilation apporte de l'oxygène
à
" 11 "
l'embryon et élimine le dioxyde de carbone (CO2)
excédentaire. Une ventilation déficiente peut provoquer
l'étouffement des poussins dans l'oeuf. Le renouvellement d'air est
réalisé par le réglage des trappes d'entrée et de
sortie d'air au niveau des couveuses. En outre, la ventilation permet de
régler la température et l'humidité dans la couveuse
(Hubbard, 2010).
I.4.4 Le retournement d'oeufs
Les oeufs doivent être retournés
régulièrement, sinon les résultats d'incubation seront
très bas. Il est recommandé de retourner les oeufs trois fois par
jour pendant les premiers 19 jours et après le retournement n'est plus
nécessaire. Le retournement des oeufs peut être facilité
par un mécanisme automatique (KHADIDJA, 2016).
· L'opération de retournement a pour but
d'éviter le collage de l'embryon sur la coquille, d'éviter au
maximum les positions anormales de l'embryon et de permettre également
une meilleure répartition de la chaleur sur toute la surface des
oeufs.
· Le retournement des oeufs s'effectue entre deux
positions possibles, 45 degré par rapport à la verticale.
· Ce dernier doit s'effectuer au minimum trois fois par
jour. Tout choc exagéré provoque la mort des embryons (Hubbard,
2010).
I.5 Les étapes d'incubation d'oeufs
I.5.1 Tri et désinfection des
oeufs
Le tri a pour objectif d'obtenir un taux élevé
de réussite à l'incubation. Les oeufs à couver doivent
être frais, propres, de poids convenable et sans anomalies de taille et
de forme comme le montre la figure I-7 autant nous avons en largeur ; 1,4 fois
nous aurons en longueur. Ainsi donc, les oeufs présentant des anomalies
de la coquille et des formes anormales sont à écarter.
Placés dans l'incubateur, les meilleurs résultats
d'éclosion s'obtiennent avec des oeufs âgés de 3 à 4
jours et de poids compris entre 30 et 70 g en fonction des races. Les oeufs de
55 à 60 g éclosent mieux que ceux de 60 à 70 g selon les
races. Cependant, ces oeufs doivent êtres fécondés et
provenus de poules saines et bien nourries. En effet, leur insuffisance
alimentaire réduit la fertilité des oeufs et augmente la
mortalité embryonnaire (Hubbard, 2010).
La désinfection a pour but d'éliminer les
impuretés et germes qui se trouveraient sur la coquille des oeufs et qui
pourraient compromettre les résultats d'éclosion. Cette
opération doit être effectuée rapidement après la
collecte des oeufs. Toutefois, il est déconseillé de laver les
oeufs à l'eau sous peine d'éliminer la fine couche protectrice
qui les recouvrent et les protègent
~ 12 ~
des invasions microbiennes. Différentes
méthodes de désinfection sont utilisées. Cette
opération doit être réalisée dans une salle à
une température de 22 à 26°C pendant 20 à 30 minutes
(Galinette, s.d.).

Figure I-7: OEuf idéal pour la couvaison (Hubbard,
2010)
I.5.2 Stockage des oeufs
Après la désinfection, les oeufs doivent
être conservés dans un local aéré mais à
l'abri des courants d'air, du soleil et des poussières. La durée
de conservation des facultés d'éclosion des oeufs dépend
de la température de la pièce dans laquelle les oeufs sont
stockés avant l'incubation. Pour une température de stockage de 7
à 15°C, la conservation des facultés d'éclosion est
bonne pendant 6 jours. Ensuite, elle diminue progressivement à partir du
début de la seconde semaine. La température de la salle de
stockage doit être maintenue entre 17 et 18°C pour une durée
de 3 à 4 jours (Hubbard, 2010).
Afin de limiter les pertes d'eau par évaporation qui
aura pour effet d'abaisser le taux d'éclosion et la vitalité du
poussin, l'humidité relative de la salle de stockage doit être
maintenue entre 70 et 85%. Durant leur stockage, les oeufs à couver sont
placés dans une position pointe en bas pour un stockage de courte
durée. Pour des durées de stockages supérieures à 7
jours, un stockage pointe en haut permet de limiter les pertes
d'éclosion dues au stockage. Aussi, il est recommandé de les
retourner pendant le stockage afin d'éviter que le jaune adhère
à la coquille. Les oeufs ne doivent jamais être stockés
directement sur le sol, mais sur des palettes en bois ou de
préférence en plastique (Galinette, s.d.).
~ 13 ~
I.5.3 Préchauffage et incubation des
oeufs
Pour obtenir un bon taux d'éclosion, il est
nécessaire de préchauffer les oeufs avant leur mise en
incubation. Ce procédé permet d'éviter un choc thermique
aux oeufs et également un démarrage plus rapide et plus
homogène au développement des embryons. Un préchauffage
compris entre 25°C et 28°C est préférable pendant une
heure. L'un des facteurs essentiels de la réussite de l'incubation est
la régulation parfaite de la température, surtout pendant la
première semaine. Pour les couveuses à ventilation naturelle, la
température optimale doit être maintenue à 38,9°C lors
des deux premières semaines d'incubation, et ramenée à
36,1°C à partir du 19èmejour d'incubation. Cela
est dû au faite que les poussins produisent aussi de la chaleur. Pour les
couveuses à ventilation forcée, la température
idéale pour un meilleur développement de l'embryon et une
éclosion optimale, est de 37,7°C ou 37,8°C. Cette
température est déterminante également pour la croissance
correcte du poussin après l'éclosion. Les basses
températures retardent l'éclosion et ses effets sont très
déconseillés par rapport aux températures
élevées (Galinette, s.d.).
I.5.4 Le développement embryonnaire
Le développement d'un oeuf fécondé
commence par la division cellulaire, dès qu'il traverse l'oviducte de la
poule. Quand elle pond l'oeuf, l'embryon se refroidit et le
développement est suspendu. Si on casse l'oeuf à ce
moment-là, le disque germinal mesure déjà 4mm. Le
développement de l'embryon commence quand la température de
l'oeuf dépasse 26,6 °C. Dans le tableau I-2 figurent les
différentes étapes du développement embryonnaire pour
arriver à un poussin le 21ième jour (Cie, 2019).
Tableau J-2: les différentes étapes du
développement embryonnaire d'un oeuf de poule (Cie, 2019)
Avant la ponte
|
Fécondation, division et croissance des
cellules. Certaines cellules se regroupent en tissus (pour
assumer ultérieurement certaines fonctions)
|
Entre la ponte et la couvaison/ incubation
|
Arrêt de la croissance cellulaire. Il y a
déjà entre 50 000 et 80 000 cellules.
|
Jour 1
|
L'embryon est déjà constitué des 3 couches
de cellules:
|
|
~ 14 ~
· l'ectoderme: qui donnera la peau, les
plumes, le bec, le système nerveux, les griffes, les yeux et la bouche
;
· le mésoderme: qui donnera le
squelette, les muscles, le sang et les organes reproducteurs ;
· l'endoderme: qui donnera les organes
respiratoires, les systèmes sécréteurs et digestifs.
|
16 heures
|
Premiers signes de ressemblance avec un embryon de poulet
|
18 heures
|
Apparition du tube digestif
|
20 heures
|
Apparition de la colonne vertébrale
|
21 heures
|
Début de la formation du système nerveux
|
22 heures
|
Début de la formation de la tête
|
Jour 2
|
25 heures
|
Début de la formation du coeur
|
35 heures
|
Début de la formation de l'oreille
|
42 heures
|
Le coeur commence à battre
|
Jour 3
|
60 heures
|
Début de la formation des voies respiratoires
|
62 heures
|
Début de la formation des pattes
|
64 heures
|
Début de la formation des ailes
|
Jour 4
|
Début de la formation de la langue. Le coeur quitte sa
forme simple et devient un coeur complètement formé; il est
toujours en train de battre mais reste encore à l'extérieur du
corps. Des membranes amniotiques se forment et constituent un sac amniotique
dans lequel l'embryon va flotter jusqu'à la fin de son
développement. Le liquide amniotique et les retournements de l'oeuf vont
permettre à l'embryon de se positionner correctement pour
l'éclosion.
|
Jour 5
|
Début de la formation des organes permanents et
différenciation sexuelle. La structure aortique commence à se
former et à s'épaissir.
|
|
~ 15 ~
Jour 6
|
Début de la formation du bec. Les pattes et les ailes
sont presque complètement développées.
|
Jour 7
|
La membrane commence à s'épaissir mais reste
transparente
|
Jour 8
|
Début de la formation des plumes
|
Jour 9
|
La membrane n'est plus transparente. L'embryon commence à
vraiment ressembler à un poussin.
|
Jour 10
|
Début du durcissement du bec. Les os commencent à
se former
|
Jour 13
|
L'ovaire de droite de l'embryon femelle commence à
dégénérer
|
Jour 14
|
L'embryon se met en bonne position pour pouvoir briser la
coquille
|
Jour 16
|
Les écailles, les griffes et le bec deviennent plus
fermes. L'albumen est déjà quasi tout consommé. Il reste
le jaune comme nourriture.
|
Jour 17
|
Le bec se tourne vers la poche d'air.
|
Jour 19
|
Le vitellus (jaune) commence à entrer dans le corps de
l'embryon
|
Jour 20
|
Le sac vitellin est complètement aspiré
à l'intérieur du corps de l'embryon. Le poussin occupe presque
tout l'espace intérieur de l'oeuf, à l'exception de la chambre
à air. Il lui devient difficile d'obtenir de l'oxygène au travers
de la coquille. Du coup, les muscles du cou se contractent et le bec perce la
poche d'air située du côté du gros bout de l'oeuf. Les plus
faibles, notamment ceux qui manquent de vitamines du groupe B, n'y survivront
pas.
|
|
" 16 "
Jour 21
Eclosion du poussin: les coups de bec alternent avec des
mouvements des pattes. De cette manière, le poussin découpe le
gros bout de l'oeuf, jusqu'à pouvoir en sortir.
|
|
|
|
I.5.5 Mirage des oeufs
Le mirage est une opération qui consiste à
éclairer l'intérieur de l'oeuf à l'aide d'un appareil
appelé mireuse ou mire-oeuf doté d'une source lumineuse (voir la
figure I-8). Le mirage est une opération très importante car il
permet de détecter les oeufs clairs (non fécondés), les
embryons morts et de voir si le développement du poussin dans l'oeuf se
déroule normalement. Habituellement deux mirages sont pratiqués.
Le premier est effectué au 7ème ou
9ème jour d'incubation et permet de retirer les oeufs non
fécondés et le second au 18ème jour
d'incubation, ce dernier mirage permet de retirer les oeufs à embryons
morts. Le mirage doit être fait avec précaution car il est
responsable de 1 à 3% de mortalité embryonnaire (Galinette,
s.d.).

Figure I-8: Mirage de l'oeuf (Brahmaland, 2015)
On peut clairement voir sur la figure I-9 à quoi
ressemble un oeuf fécondé qui est soumis au mirage.
" 17 "
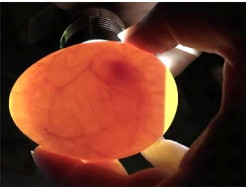
Figure I-9:Mirage d'un oeuf fécondé
(Couveuse fr, 2021)
I.5.6 Eclosion des oeufs
Après le dernier mirage, les oeufs peuvent être
transférés dans un éclosoir si le dispositif existe,
sinon, l'éclosion peut se poursuivre dans l'incubateur. Dans tous les
cas, l'humidité relative qui était de 50 à 60% durant les
18 premiers jours, doit être élevée au plus à 75%
afin que l'éclosion puisse se dérouler normalement. A partir du
18èmejour, aucune autre manipulation n'est faite
jusqu'à l'éclosion. La sortie des poussins intervient au
21ème jour d'incubation. Il faut au poussin une durée
de douze heures pour briser la coquille et se libérer. A la sortie, le
poussin emmène avec lui l'enveloppe contenant le jaune, ce qui constitue
une réserve alimentaire supplémentaire pour sa première
semaine de vie hors de la coquille. C'est la présence de ce jaune qui
permet le transport des poussins sur de grandes distances et pendant plusieurs
jours sans qu'il faille les nourrir ou les abreuver (Galinette, s.d.).
I.6 Matériaux de fabrication des incubateurs
d'oeufs
I.6.1 Ossature des porte-plateaux
L'ossature des porte-plateaux est généralement
fabriquée en acier inoxydable pour éviter la corrosion dû
la rouille qui attaque facilement les aciers ordinaires en présence d'un
air trop humide (entre 50% et 75% pour l'incubateur). Il existe une grande
variété d'aciers inoxydables possédant une
résistance, soudabilité ou ténacité
différente ; comme l'acier inoxydable austénitique, ferritique,
duplex (austéno-ferritique), martensitique et l'acier inoxydable
à durcissement par précipitation (Steel Knowledge, 2017). On
utilise habituellement l'acier inoxydable ferritique parce qu'ils coûtent
moins cher que les nuances austénitiques de même résistance
à la corrosion et sont utilisés dans des applications en
intérieur ou dans des
Figure I-11: Rouleau d'aluminium utilisé pour le
revêtement intérieur de l'incubateur (Arcan, 2019)
" 18 "
atmosphères peu corrosives. Pour améliorer leur
soudabilité, on utilise l'alliage au titane. Nous retrouvons quelques
informations supplémentaires à l'annexe J.
I.6.2 Les plateaux
Les plateaux sont généralement fabriqués en
plastiques avec des mesures standard que l'on retrouve sur le marché,
nous retrouvons généralement de modèles de 30cm/30cm pour
30 oeufs de poule comme le montre la figure I-10 et l'annexe K.

Figure I-10: Plateau en plastique de 30 oeufs (Fermenet,
2020)
I.6.3 Le revêtement intérieur de
l'incubateur
Pour augmenter la conductivité thermique des surfaces
intérieures de l'incubateur, l'intérieur est tapissé d'une
mince tôle d'aluminium que l'on retrouve sur forme de rouleau comme
l'illustre la figure I-11

" 19 "
I.6.4 Les parois de l'incubateur
Les parois de l'incubateur sont généralement
faites en bois grâce à sa bonne inertie thermique. Cependant, il
existe plusieurs types de bois, les plus utilisés sont ceux qui
présentent plusieurs couches appelés communément multi
triplex que l'on peut voir à la figure I-12.

Figure I-12: Planche de bois utilisée pour la
fabrication des parois de l'incubateur (Dema, 2019)
I.7 Conclusion
Dans ce premier chapitre, nous avons abordé d'une
manière générale les incubateurs et les paramètres
d'incubation. Sans doute, l'incubation naturelle reste le plus actif mais
conduit à une production trop faible. En effet l'incubation artificielle
est recommandée pour satisfaire les grandes demandes de consommation. Le
bon fonctionnement de couveuses est basé sur la bonne régulation
de la température, de l'humidité, la ventilation et le
retournement d'oeufs. Les pertes en productions expliquent les erreurs de
réglages de ces quatre paramètres. Pour produire un incubateur
d'oeufs performant et capable de donner un rendement approprié, il faut
faire une bonne étude de conception et effectuer un choix judicieux des
matériaux de construction. Dans le chapitre II nous allons dimensionner
la partie mécanique de l'incubateur en faisant une étude statique
de l'ossature de porte-plateaux.
" 20 "
CHAPITRE II : DIMENSIONNEMENT MECANIQUE DE
L'INCUBATEUR
II.1 Introduction
Dans ce chapitre il est question de faire l'étude
statique de l'ossature des porte-plateaux en utilisant le logiciel de dessin
assisté par ordinateur SolidWorks. Cette étude a pour but de
rendre l'ossature résistante et capable de supporter les
différentes contraintes auxquelles elle sera soumise. Ensuite suivra la
détermination du couple résistant dû aux poids des oeufs et
des porte-plateaux (contraintes du système) dans le but de faire le
choix du moteur de retournement d'oeufs.
II.2 Cahier de charge de la partie mécanique de
l'incubateur d'oeufs
Dans cette partie nous définissons le problème
à résoudre par l'étude statique qui sera effectuée
sur l'ossature des porte-plateaux de l'incubateur d'oeufs, l'objectif ainsi que
le périmètre (limite) de cette étude.
II.2.1 Contexte et définition du problème
de dimensionnement de la partie mécanique
de l'incubateur d'oeufs
La capacité d'accueil de l'incubateur est de 600 oeufs
de poule, un oeuf de poule a une masse moyenne de 63 g pour les petits oeufs et
73 g pour les gros oeufs (François, 2020). L'ossature des porte-plateaux
doit être en mesure de supporter le poids total des oeufs ainsi que celui
du moteur de retournement (dont la masse vaut 5 kg) sans qu'elle ne puisse se
déformer de façon permanente.
II.2.2 Objectif de dimensionnement de la partie
mécanique de l'incubateur d'oeufs
Nous devons concevoir une ossature résistante,
légère et ayant une stabilité dimensionnelle. Le
dimensionnement devra tenir compte de la norme ISO 630-6 : 2014 relative aux
aciers de constructions, tous les matériaux qui seront utilisés
dans la fabrication de l'incubateur existent déjà et ont des
mesures dimensionnelles bien précises. Nous devons déterminer le
couple moteur capable de vaincre le couple résistant dû au poids
de l'ossature afin d'assurer un retournement d'oeufs sécurisé.
II.2.3 Périmètre de l'étude
statique de l'ossature des porte-plateaux de l'incubateur
d'oeufs
Ici, nous nous limiterons qu'à l'étude statique
de l'ossature, il ne nous sera pas nécessaire de mener l'étude
dynamique vu que les vitesses développées par le système
sont trop petites (vitesse du moteur inférieur à 1 tr/min).

Figure II-1: Propriétés physiques des
porte-plateaux
Figure II-2: Propriétés physiques des
plateaux
" 21 "
II.2.4 Description fonctionnelle des besoins pour
l'étude statique des porte-plateaux
Nous aurons à utiliser les matériaux qui
figurent dans le tableau II-1 avec spécification de leurs
propriétés physiques. Vu que la température
intérieure de l'incubateur flotte autour de 38 degré Celsius, il
ne nous sera pas nécessaire de donner les limites de température
de ces matériaux.
Tableau II-1:Propriétés mécaniques des
matériaux utilisés pour la conception de l'ossature de
porte-
plateaux
Référence du modèle
|
Propriétés
|
|
Matériau: Acier allié
inoxydable
Type de modèle: Linéaire
élastique isotropique
Limite d'élasticité: 241, 275
N/mm2
Limite de traction: 448, 082
N/mm2
Module d'élasticité: 190000
N/mm2
Coefficient de Poisson: 0, 26
Masse volumique: 7, 3 g/cm3
Module de cisaillement: Coefficient de dilatation
thermique:
|
78000 N/mm2
1, 5.10-5 /Kelvin
|
|
Matériau : ABS PC
Linéaire élastique
Type de modèle: isotropique
Limite de traction: 40 N/mm2
Module d'élasticité: 2410
N/mm2
Coefficient de Poisson: 0, 3897
Masse volumique: 1, 07
g/cm3
Module de cisaillement: 862, 2 N/mm2
|
|
~ 22 ~
Matériau: Fonte grise
Linéaire élastique
Type de modèle: isotropique
Critère de ruine par défaut :
Contrainte de Mohr-Coulomb
Limite de traction: 151, 658
N/mm2
Limite de 572, 165 N/mm2
compression:
Module d'élasticité: 66178, 1
N/mm2
Coefficient de Poisson: 0, 27
Masse volumique: 7, 2 g/cm3
Module de 50000 N/mm2
cisaillement:
Coefficient de
dilatation thermique: 1,
2.10-5/Kelvin

Figure II-3 : Propriétés physiques du support
des porte-plateaux
Pour le retournement d'oeufs, nous aurons besoin d'un moteur
fournissant un écartement angulaire de 45 degrés des parts et
d'autres du plan horizontal des plateaux d'oeufs et ayant une vitesse
d'entrainement inférieure ou égale à 1tour/minute car
toute vitesse exagérée risquerait d'endommager les oeufs en
incubation (Hubbard, 2010). Pour cela nous auront à utiliser le moteur
pas à pas réputé pour sa bonne précision concernant
les mouvements angulaires.
II.3 Présentation du modèle
théorique de l'incubateur d'oeufs
La partie mécanique de la couveuse est
constituée du système de retournement d'oeufs, l'ensemble des
porte-plateaux ainsi que de toute la structure extérieure qui constitue
en gros l'incubateur comme l'illustre la figure II-4. Nous avons utilisé
le logiciel Solidworks pour dessiner les différentes parties
mécaniques et simuler l'étude statique du système afin
d'obtenir les résultats de déformation transversale et
longitudinale de l'ossature des porte-plateaux. Nous avons utilisé la
méthode déductive pour le dimensionnement de l'ossature des
porte-plateaux ; ce qui nous a permis d'obtenir la forme tubulaire creuse pour
le cadre de l'ossature. Cette forme nous a fournis des résultats
satisfaisants dans le domaine des déformations transversale et
longitudinale.
~ 23 ~

Figure II-4: Modèle de l'incubateur
réalisé avec SolidWorks
II.4 Description du modèle théorique de
l'ossature des porte-plateaux
La figure II-5 illustre le modèle théorique de
l'ossature des porte-plateaux sur lequel sera faite l'étude statique.
L'ossature de porte-plateaux est constituée de cinq porte-plateaux en
Acier inoxydable ferritique de type X3CrTi17 (voir l'annexe H), ayant chacune
une dimension de 600×600mm et une épaisseur de 2mm comme l'indique
la figure II-6. Les porte-plateaux sont reliés les uns aux autres par
des barres de mêmes matériaux qu'elles longues de 1240mm, larges
de 25mm et épaisses de 3mm (voir la figure II-8). Le tout est
supporté par un cadre en Fonte grise de type EN-GJL-350 (voir l'annexe
L) de forme tubulaire de 20×20mm, haute de 1710mm, large de 670mm et
épais de 3mm. Sa base est longue de 760mm et large de 708mm comme
illustré à la figure II-7.
" 24 "

Cadre de forme tubulaire creuse
Emplacement du moteur
Figure II-5: Ossature de porte-plateaux
Nous avons choisi l'acier inoxydable ferritique comme
matériau de fabrication des porte-plateaux parce qu'ils coûtent
moins cher que les autres nuances austénitiques, duplex, martensitique
de même résistance à la corrosion et leur coût est
sujet à moins de fluctuations. Ils sont utilisés dans des
applications en intérieur ou dans des atmosphères peu corrosives.
Vu qu'ils seront soudés pour leurs assemblages, nous avons retenu la
nuance ferritique alliée au titane (X3CrTi17) qui améliore leur
soudabilité.

Figure II-6: Dimensions du porte- plateau
~ 25 ~

Figure II-7: Dimensions du cadre de l'ossature des
porte-plateaux
Nous avons choisi la fonte grise comme matériau de
construction du cadre par suite de ses multiples avantages : le prix abordable,
la facilité d'usinage, l'absorption des vibrations et la
stabilité dimensionnelle. Nous avons retenu la nuance EN-GJL-350 pour sa
dureté.

Figure II-8: Dimension de la barre de l'ossature des
porte-plateaux
" 26 "
II.5 Détermination des efforts agissants sur
l'ossature des porte-plateaux
Au moyen du logiciel SolidWorks, nous avons effectué
l'étude statique de l'ossature des porte-plateaux. Comme données,
nous avons considéré les contraintes
générées par le poids des oeufs et le poids du moteur qui
doit être fixé sur un support pour entrainer les plateaux d'oeufs.
Toutes les contraintes agissant sur la structure sont
représentées en rouge sur la figure II-9. Un oeuf a une masse en
moyenne de 63g et 73g pour les gros oeufs ; nous avons considéré
la masse de 73g pour une quantité de 120 oeufs par plateau et pour un
total de 600 oeufs. La masse totale obtenue est de 37,8 kg et 5kg comme masse
du moteur. Après 3 heures de calcul avec une machine ayant un processeur
de 11ième génération Core i5-1145G7 (8 Mo de
cache, jusqu'à 4,40 GHz), le logiciel SolidWorks nous a fourni un
rapport contenant les résultats des calculs de l'étude statique.
Le cadre inférieur est considéré comme encastré,
donc son déplacement est nul.

Figure II-9: Modèle mécanique de l'ossature
des porte-plateaux
II.5.1 Informations sur le maillage de
l'ossature
Le processus commence par la création d'un
modèle géométrique. Pour l'analyse, le modèle doit
être subdivisé en petites entités de formes simples
(éléments), interconnectées en des points communs
(noeuds). Les programmes d'analyse par éléments finis
considèrent le modèle comme un réseau
d'éléments discrets interconnectés (Dassault
Systèmes, 2021). Pour ce faire, le logiciel évalue une taille
d'élément globale en tenant compte du volume du modèle, de
sa surface et d'autres paramètres géométriques. La taille
du maillage généré (nombre de noeuds et
d'éléments) dépend de la géométrie et des
dimensions du modèle, de la taille des éléments, de la
tolérance de maillage, du contrôle du maillage et des
spécifications de contact.
" 27 "
En général, une petite taille
d'élément est nécessaire pour obtenir des résultats
plus précis. Le tableau II-2 donne les différentes informations
sur le maillage utilisé.
Tableau II-2: Informations sur le maillage de l'ossature
des porte-plateaux
Type de maillage
|
Maillage volumique
|
Mailleur utilisé :
|
Maillage standard
|
Points de Jacobien
|
4 Points
|
Taille d'élément
|
15.343 mm
|
Tolérance
|
0.767149 mm
|
Tracé de qualité du maillage
|
Haute
|
Nombre total de noeuds
|
192581
|
Nombre total d'éléments
|
92940
|
Aspect ratio maximum
|
54.858
|
Pourcentage (%) d'éléments ayant un aspect ratio
< 3
|
3.93
|
Pourcentage (%) d'éléments ayant un aspect ratio
> 10
|
8.06
|
Pourcentage (%) d'éléments distordus
(Jacobien)
|
0
|
|
Nous avons utilisé un maillage de haute qualité et
nous n'avons pas obtenu d'éléments distordus car le pourcentage
d'éléments distordus (Jacobien) vaut zéro.
II.5.2 Forces résultantes sur l'ossature de
porte-plateaux
L'étude statique nous a fourni les forces et moments de
réaction résultants qui agissent sur l'ossature de l'incubateur
d'oeufs que voici :
II.5.2.1 Forces de réaction
Les forces de réaction le long des axes X, Y et Z sont
les sommes des forces de réaction nodales individuelles sur les
entités sélectionnées et sur le modèle entier. Le
tableau II-3 donne le résultat final des résultantes des forces
de réactions du système.
Tableau II-3:Résultantes des forces de
réaction sur l'ossature de porte-plateaux
Ensemble de
sélections
|
Unités
|
Somme X
|
Somme Y
|
Somme Z
|
Résultante
|
Modèle entier
|
N
|
-0.000221252
|
914.002
|
-27.6643
|
914.42
|
|

Nom
Contraintes
Figure II-10: Résultat final sur l'état du
système pour les contraintes avec SolidWorks
Type
VON : contrainte de von Mises
0.000 N/mm2 (MPa)
Noeud: 151665
Min
3 140,449 N/mm2 (MPa)
noeud: 147311
Max
" 28 "
II.5.2.2 Moments de réaction
La somme des moments de réaction calculée au
niveau des noeuds de contrainte individuelle est répertoriée par
rapport au système de coordonnées global (axes X, Y et Z). Le
tableau II-4 donne le résultat final des résultantes des moments
de réactions du système.
Tableau II-4:Résultantes des moments de
réaction sur l'ossature de porte-plateaux
Ensemble de sélections
|
Unités
|
Somme X
|
Somme Y
|
Somme Z
|
Résultante
|
Modèle entier
|
N.m
|
0
|
0
|
0
|
0
|
|
Comme nous pouvons le voir dans le tableau II-4, tous les
moments de réaction sont nuls, ce qui veut dire que l'ossature de
l'incubateur d'oeufs a une stabilité dimensionnelle.
II.5.3 Résultats de l'étude statique sur
l'ossature de porte-plateaux
Sur la figure II-10, nous pouvons voir clairement que la
contrainte maximale est largement inférieure aux modules
d'élasticité des matériaux utilisés (le bleu
partout) à l'exception des plateaux d'oeufs que nous considérons
ici fragiles.
" 29 "
Les figures II-11 et figure II-12 nous donnent l'image sur la
déformation transversale et longitudinale de notre système. Il
est normal de constater une déformation au milieu de chaque plateau vu
que nous avons pris une matière très fragile pour les
représentés.

Nom
Déplacements
Figure II-11: Résultat final sur l'état du
système pour les déplacements avec SolidWorks
URES : Déplacement résultant
Type
0, 000.100mm Noeud: 147850
Min
2, 102.101mm Noeud: 105470
Max
II.6 Le système de retournement
d'oeufs
Comme il l'a été dit en introduction, nous nous
sommes également proposés de faire le choix d'un moteur
électrique pouvant entrainer les plateaux d'oeufs afin d'atteindre une
inclinaison de 45 degré des parts et d'autres du plan horizontal. Nous
avons déterminé le poids total développé par 600
oeufs répartis sur cinq plateaux y compris la structure des
porte-plateaux. Nous avons obtenu un poids total de 633,4 N en raison de 429,68
N comme poids des oeufs de poule et 203,72 N pour l'ensemble de la structure
plateaux plus porte-plateaux. Avec un bras de levier de 380mm (780mm/2) en se
référant à la figure II-7, nous avons obtenu un couple
résistant de 240Nm que le moteur devra vaincre pour entrainer le
système. Vu que le
~ 30 ~
retournement d'oeufs doit se faire avec précision, il
nous est recommandé d'utiliser un moteur pas à pas qui sera
commandé par le microcontrôleur afin d'obtenir un
écartement de 45 degré dans le deux sens de rotation et à
intervalle de temps régulier pendant 19 jours d'incubations.

Nom
Déformations
Figure II-12: Résultat final sur l'état du
système pour les déformations avec SolidWorks
ESTRN : Déformation équivalente
Type
0, 000.100 Elément: 71122
Min
4, 230.10-2 Elément: 83544
Max
II.7 Conclusion
Le grief essentiel de ce chapitre était celui de faire
une étude statique de l'ossature des porte-plateaux. Pour faire cette
étude, nous nous sommes servis du modèle théorique de
cette ossature que nous avons réalisé avec le logiciel
SolidWorks. Nous avons placé toutes les contraintes agissant sur ce
dernier ; le logiciel a résolu les différentes équations
statiques et nous a fourni un rapport contenant toutes les données et
résultat concernant cette étude après 3 heures de calcul
avec un processeur Core i5. Grâce aux données obtenues dans le
domaine des contraintes, déplacements et déformations, nous avons
dimensionné le cadre de l'ossature en optant pour une forme tubulaire
creuse afin de minimiser le poids et de gagner en robustesse.
" 31 "
CHAPITRE III : DIMENSIONNEMENT ELECTRIQUE ET
ELECTRONIQUE DE L'INCUBATEUR D'OEUFS
III.1 Introduction
Dans ce chapitre il est question de concevoir et
réaliser le circuit électronique de l'incubateur d'oeufs, donner
brièvement quelques détails fonctionnels sur le schéma
bloc qui résume ce circuit. Ensuite interpréter le code source,
le programme du microcontrôleur qui rend fonctionnel le montage.
III.2 Cahier de charge de la partie
électronique-électrique de l'incubateur
Dans cette partie nous définissons le problème
que doit résoudre le dimensionnement électrique et
électronique de l'incubateur d'oeufs. Nous définissons aussi
l'objectif ainsi que le périmètre (limite) de ce
dimensionnement.
III.2.1 Contexte et définition du problème
de dimensionnement de la partie électrique-
électronique de l'incubateur
d'oeufs
Pour mener à bien l'incubation et s'en passer de la
présence humaine, nous devons rendre l'incubateur capable de
réguler de soit la température, le taux d'humidité et de
retourner automatiquement les oeufs. Il doit également être
capable de fournir les informations relatives à l'incubation et afficher
un message d'alerte en cas de toute baisse ou augmentation dangereuse de l'un
de ces paramètres.
III.2.2 Objectif de dimensionnement électrique
et électronique de l'incubateur d'oeufs
Nous devons concevoir et réaliser le circuit
électronique qui régira l'intelligence de l'incubateur,
écrire le code source du microcontrôleur qui rend fonctionnel le
montage et s'assurer que l'alimentation fournira les tensions continus de 5V,
12V et alternatives de 12V , 220V nécessaires au bon fonctionnement des
différents blocs du circuit électronique de l'incubateur (voir la
figure III-1).
III.2.3 Périmètre d'étude du
dimensionnement électrique et électronique de
l'incubateur
d'oeufs
Ici, nous nous attèlerons plus sur le dimensionnement
électronique, le seul aspect du dimensionnement électrique
concernera le type de transformateur qui sera utilisé dans le circuit
d'alimentation.
~ 32 ~
III.2.4 Description fonctionnelle des besoins pour la
réalisation du circuit électronique
de l'incubateur d'oeufs
Nous aurons à utiliser une alimentation à
découpage 220V AC! 12V DC délivrant un courant de 1A, un
régulateur de tension 12V DC!5V DC, un transformateur abaisseur 220V AC!
12 AC, une pile de 9V, une nomenclature des résistances E12, deux diode
de redressement 1N4007 (qui serviront d'anti-retour), cinq transistors de
puissance 2N2222 (voir l'annexe M), un brumisateur, deux relais bipolaires de
12V DC, trois boutons poussoirs unipolaires, un buzzer de 12V DC (voir l'annexe
N), une sonde de température, un capteur d'humidité, un
écran LCD16×2.
III.3 Circuit électronique de l'incubateur
d'oeufs
La figure III-1 donne le schéma bloc de l'incubateur
avec moins de détails, il regroupe le bloc d'alimentation, du
microcontrôleur, des interfaces de communication, de chauffage et
humidification, de ventilation, capteur de température et
d'humidité. Chaque bloc reçoit une tension d'alimentation
adaptée aux composants électronique du bloc.
La figure III-4 illustre le schéma
détaillé du circuit électronique de l'incubateur. On peut
clairement y voir le microcontrôleur (1), le capteur de
température (2), d'humidité (2), le circuit de chauffage
comportant une lampe à incandescence (3), le moteur de retournement des
plateaux d'oeufs (4), le brumisateur ou humidificateur (5) et le reste des
composants électronique qui constitue le circuit de protection et de
commande.
III.4 Fonctionnement du montage
Expliquer le fonctionnement du montage revient à
expliquer le fonctionnement de chaque bloc fonctionnel du circuit. Ainsi il est
plus pratique de commencer par l'alimentation qui fournit l'énergie
nécessaire au fonctionnement du montage.
III.4.1 Alimentation
Dans le bloc « alimentation », nous retrouvons une
alimentation à découpage (voir la figure III-2) qui fournit une
tension continue de 12 volts pour alimenter les ventilateurs, les diodes
électroluminescentes pour l'éclairage intérieur de
l'incubateur et le système de brumisation (humidification). Pour avoir
une tension continue de 5volts afin d'alimenter le microcontrôleur,
l'afficheur LCD le capteur de température et d'humidité ; la
tension de 12V passe à travers un régulateur de 5V. Le moteur
utilisé pour le retournement est alimenté sous une tension
alternative de 12V abaissée par un transformateur connecté au
réseau électrique.
" 33 "
MICROCONTROLEUR
ALIMENTATION

INTERFACES DE
COMMUNICATION
VENTILATION ET ALARME
CHAUFFAGE ET HUMIDIFICATION
MECANISME DE RETOURNEMENT
CAPTEUR DE TEMPERATURE
CAPTEUR
D'HUMIDITE
Figure III-1:Schéma bloc du circuit
électronique de l'incubateur
~ 34 ~

Figure III-2: Alimentation à découpage
utilisée pour alimenter le circuit électronique de l'incubateur
d'oeufs (Alibaba, 2021)
III.4.2 Capteur d'humidité
Le capteur d'humidité que nous avons utilisé
est le DHT11. Ce dernier comprend un complexe de capteurs de température
et d'humidité avec une sortie de signal numérique
étalonnée. En utilisant la technique exclusive d'acquisition de
signal numérique et la technologie de détection de la
température et de l'humidité, il garantit une grande
fiabilité et une excellente stabilité à long terme. Ce
capteur comprend un composant de mesure d'humidité de type
résistif et un composant de mesure de température NTC, et se
connecte à un microcontrôleur 8 bits haute performance, offrant
une excellente qualité, une réponse rapide, une capacité
antiparasitage et une rentabilité élevée.
Chaque élément DHT11 est strictement
calibré en laboratoire, ce qui est extrêmement précis lors
du calibrage de l'humidité. Les coefficients d'étalonnage sont
stockés sous forme de programmes dans la mémoire OTP, qui sont
utilisés par le processus de détection de signal interne du
capteur. L'interface série mono fil rend l'intégration du
système rapide et facile. Sa petite taille, sa faible consommation
électrique et sa transmission des signaux jusqu'à 20
mètres en font le meilleur choix pour diverses applications, y compris
les plus exigeantes. Le composant est un boîtier de broches à une
rangée à 4 broches comme l'indique la figure III-3 (Cours
Gratuit, s.d.).

Figure III-3:Capteur d'humidité DHT 11
~ 35 ~

1
5
2
4
3
Figure III-4:Circuit électronique de l'incubateur
d'oeuf
" 36 "
III.4.2.1 Processus de communication globale du
capteur d'humidité
Lorsque le microcontrôleur envoie un signal de
démarrage, le DHT11 bascule du mode de consommation basse en mode de
fonctionnement en attendant que ce dernier achève le signal de
démarrage. Une fois cette opération terminée, le DHT11
envoie un signal de réponse sous forme de données sur 40 bits
incluant les informations relatives à l'humidité et à la
température au microcontrôleur. Sans le signal de
démarrage, le DHT11 ne donnera pas le signal de réponse au
microcontrôleur. Une fois les données collectées, le DHT11
passe en mode de consommation réduite jusqu'à ce qu'il
reçoive à nouveau un signal de démarrage. (Cours Gratuit,
s.d.).
III.4.2.2 Le signal de démarrage du
DHT
Lorsque la communication entre le microcontrôleur et le
DHT11 commence, le programme définit le niveau de tension du bus unique
de données de haut en bas et ce processus doit prendre au moins 18 ms
pour assurer la détection du signal par le DHT11, puis le
microcontrôleur augmentera la tension et attendra 40ìs pour la
réponse du DHT (Cours Gratuit, s.d.).
III.4.2.3 Le signal de réponses du
DHT
Une fois que le DHT a détecté le signal de
démarrage, il envoie un signal de réponse de niveau de tension
faible, d'une durée de 80ìs. Ensuite, le programme du DHT
définit le niveau de tension du bus simple de données de bas
à haut et le garde pendant 80ìs pour la préparation du DHT
à l'envoi de données. Lorsque le DATA Single-Bus est au niveau de
tension bas, cela signifie que le DHT envoie le signal de réponse. Une
fois que le signal envoyé, ce dernier tire la tension et la conserve
pendant 80ìs et se prépare à la transmission des
données.
Lorsque le DHT envoie des données au
microcontrôleur, chaque bit de données commence par le niveau de
tension basse 50ìs et la longueur du signal de niveau de tension
élevé suivant détermine si le bit de données est
à "0" ou "1" comme le montre la figure III-5. Si le signal de
réponse du DHT est toujours à un niveau de tension
élevé, cela suggère que le DHT ne répond pas
correctement. Lorsque le dernier bit de données est transmis, le DHT11
abaisse le niveau de tension et le maintien pendant 50ìs. Ensuite, la
tension Single-Bus sera augmentée par la résistance pour la
ramener à l'état libre (Cours Gratuit, s.d.).
" 37 "
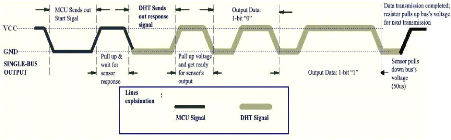
Figure III-5: Signaux de commande du DHT 11
III.4.3 Le capteur de température
Pour notre expérimentation nous avons utilisé
une thermistance. Ce dernier un est capteur de température analogique et
nécessite des lignes de commande appropriées que nous avons
écrites dans le programme pour avoir des résultats assez
précis. Nous avons fait recourt à l'équation de
Steinhart-Hart qui est devenue la méthode généralement
acceptée pour indiquer la relation entre la résistance et la
température. L'équation de Steinhart-Hart pour exprimer la
température en fonction de la résistance est la suivante :
1
??
= ?? + ??[ ????(??)] + ??[????(??)]3
Équation III-1
Où :
A, B et C sont des constantes dérivées de trois
points de test de température, R = Résistance des thermistances
en Ù,
T = Température en Kelvin K (°C + 273,15).
Pour déterminer la résistance de la
thermistance à un point de température spécifique,
l'équation suivante est utilisée :
1 1
?? = ??[??-(?? 2) 3]-{[??+(??
2 ) 3]} Équation III-2
Où :
[?? - (1 ??)]
?? = { ?? }
?? = v{[( ?? 3??)3 + (??2 4 )}
" 38 "
Les constantes A, B et C pour les thermistances
proposées sont indiquées dans le tableau III-1. À l'aide
de ces constantes et des équations III-1 et III-2, nous pouvons
déterminer la température de la thermistance en fonction de sa
résistance, ou déterminer la résistance des thermistances
à une température en particulier.
Tableau III-1: Constantes de Steinhart-Hart
Thermistance
|
Résistance
à 25 °C
|
Constante
A
|
Constante
B
|
Constante
C
|
2252
|
2 252 Ù
|
1,4705x10-3
|
2,3780x10-4
|
1,0389x10-7
|
3K
|
3 000 Ù
|
1,4052x10-3
|
2,3692x10-4
|
1,0125x10-7
|
5K
|
5 000 Ù
|
1,2870x10-3
|
2,3585x10-4
|
9,4346x10-8
|
10K
|
10 000 Ù
|
1,1275x10-3
|
2,3441x10-4
|
8,6482x10-8
|
|
III.4.3.1 Le capteur de température
numérique
Pour plus de facilité, il nous est recommandé
d'utiliser le DS18B20 qui est un capteur de température
numérique. Ce dernier permet la mesure de la température sur la
plage de -55°C à +125°C et son équivalente fahrenheit
-67°F à +257°F est avec un pas de 0,5°C
(#177;0,5°C), avec une tension d'alimentation comprise entre 3,0V et 5,5V.
Le capteur de température DS1820 s'appuie sur le protocole One-wire pour
communiquer avec le microcontrôleur et transmettre sa mesure. Comme son
nom l'indique, un seul fil est nécessaire même si plusieurs
périphériques sont utilisés (IDD, 2016). Un bus 1-Wire est
composé classiquement des trois fils : un fil de masse, un fil
d'alimentation (5 volts) et un fil de données comme on peut le voir sur
la figure III-6.

Figure III-6: Capteur DS18B20 en format "sonde"
étanche (skywodd, 2017)
~ 39 ~
III.4.3.2 Opération de mesure de la
température
La fonctionnalité de base du DS18B20 est son capteur
de température « direct-to-digital ». La résolution du
capteur de température est de 9, 10, 11 ou 12 bits configurable par
l'utilisateur, ce qui correspond respectivement à des incréments
de 0,5 ° C ; 0,25 ° C ; 0,125 ° C, et de 0,0625 ° C ; la
résolution par défaut au démarrage est de 12 bits. Pour
lancer une mesure de la température, le microcontrôleur doit
émettre un signal de commande de conversion T [44 h]. Après la
conversion, les données thermiques résultant (du capteur) sont
stockées dans le registre de température de 2 octets dans la
mémoire cratchpad (de bloc-notes) puis le DS18B20 revient à son
état de repos (Thibodeau, 2018).
Si le DS18B20 est alimenté par une alimentation
externe, le microcontrôleur peut émettre "lire créneaux
horaires" (voir la section Système Bus 1-Wire) après la commande
de conversion T le DS18B20 répondra en transmettant 0 tandis que la
conversion de la température est en cours et 1 lorsque la conversion est
effectuée. Les données de température de sortie du DS18B20
sont étalonnées en degrés Celsius ; pour les applications
Fahrenheit, une table de consultation ou de routine de conversion doit
être utilisée (Thibodeau, 2018).
Les données de température sont stockées
sous forme de16-bit de signe étendu à deux compléments du
registre de température comme indiqué à la figure III-7.
Les bits de signe (S) indiquent si la température est positive ou
négative : pour les nombres positifs S = 0 et pour les nombres
négatifs S = 1. Le DS18B20 est configuré pour une
résolution de 12 bits, tous les bits dans le registre de
température contiennent des données valides. Pour une
résolution de 11 bits, le bit 0 est indéfini. Pour une
résolution de 10 bits, les bits 1 et 0 sont indéfinis, et 9 bits
de résolution les bits 2, 1, et 0 sont indéfinis. Le tableau
III-2 donne des exemples de données de sortie numériques et la
lecture de température correspondant pour les conversions de
résolution de 12 bits (Thibodeau, 2018).

Figure III-7: Format d'enregistrement de la
température
~ 40 ~
Le tableau III-2 donne les différents codes binaires
et hexadécimaux correspondant à quelques températures.
Tableau III-2: Encodage de la température

III.4.4 Interface de communication
L'interface de communication est constituée d'un
clavier organisé autour de trois boutons poussoirs et d'un écran
LDC. Le clavier permet d'introduire les données relatives à
l'incubation comme le nombre des jours et la plage de température. Le
plus complexe est l'écran LCD qui nécessite des instructions
appropriées pour afficher la valeur de la température, du taux
d'humidité, le nombre des jours et quelques messages d'alarmes. Pour la
réalisation, nous avons utilisé un écran LCD 16×2.
III.4.4.1 Présentation de l'écran LCD
16×2
Les afficheurs à cristaux liquides utilisent la
propriété de modulation de lumière des cristaux liquides.
Les écrans à cristaux liquides sont composés de deux
couches de polariseurs, avec des directions de polarisation perpendiculaire,
prenant en sandwich deux plaques de verres entre lesquelles sont placés
les cristaux liquides. Sur les plaques de verre se trouve une matrice
d'électrodes pour chaque pixel. Une tension appliquée entre les
électrodes d'un pixel entraine un changement d'orientation des
molécules et donc la transparence du pixel qui peut alors laisser, ou
non, passer la lumière du rétroéclairage comme on peut le
voir sur la figure III-8 (AranaCorp, 2021).
" 41 "

Figure III-8: Ecran LCD 16×2
L'écran LCD 16×2 présente 16 broches pour
permettre la gestion de l'affichage et du contraste :
· VSS relié à la masse de l'écran ;
· VDD broche d'alimentation typiquement connectée
à la broche 5V de l'Arduino ;
· V0 broche de contraste connectée à une
sortie PWM ou à un potentiomètre.
· RS (Register Select) permet de sélectionner la
zone mémoire ;
· RW (Read or Write) est toujours connecté à
la masse ;
· E (Enable) active ou non l'affichage ;
· D0 mode 8bits, 4 bits de poids fort de la communication
I2C ;
· D1 mode 8bits, 4 bits de poids fort de la communication
I2C ;
· D2 mode 8bits, 4 bits de poids fort de la communication
I2C ;
· D3 mode 8bits, 4 bits de poids fort de la communication
I2C ;
· D4 4 bits de poids faible de la communication I2C ;
· D5 4 bits de poids faible de la communication I2C ;
· D6 4 bits de poids faible de la communication I2C ;
· D7 4 bits de poids faible de la communication I2C ;
· A anode, borne + de la LED de
rétroéclairage et
· K cathode, borne - de la LED de
rétroéclairage.
III.4.4.2 La transmission de données
Sur le schéma de la figure III-9 les deux "modules"
ST7066U et ST7065C sont des puces électroniques utilisées en
particulier pour piloter des matrices d'afficheurs LCD et capables de piloter
40 segments respectivement. Comme un MAX7219 avec une matrice à LED 8X8
(PlaisirArduino, 2021).
" 42 "
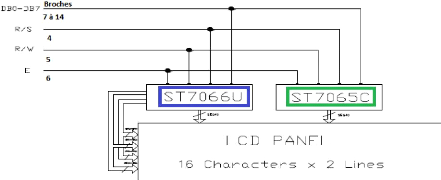
Figure III-9: Schéma de transmission des
données d'un afficheur LCD
En fait, les pilotes reçoivent les données, les
interprètent et affichent les caractères voulus aux positions
souhaitées. Mais pour cela, il faut leur transmettre des données.
D'ailleurs, les deux logigrammes de transmission de données aux figure
III-10 et figure III-11, l'un Writing data pour la
réception de données et l'autre Reading data
pour la transmission de données. Cependant, la seule chose qui
diffère entre ces deux diagrammes, c'est l'état à la
broche "RW" en rouge (PlaisirArduino, 2021).
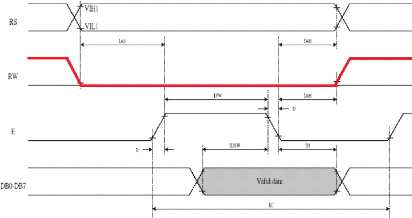
Figure III-10: Diagramme de réception de
données d'un afficheur LCD.
" 43 "
Ainsi, on comprend qu'en fonction de l'état "Haut" ou
"Bas" à la broche "RW", le pilote de la matrice ST7066U est en mode de
réception ou émission de données. Il n'y aura pas
d'émission de données, la broche R/W sera donc par défaut
à l'état bas "LOW" et par conséquent branché au 0V
(PlaisirArduino, 2021).
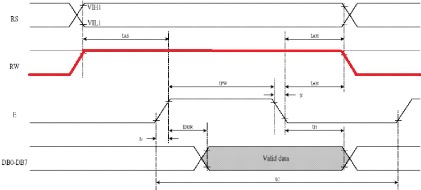
Figure III-11: Diagramme d'émission de
données d'un afficheur LCD.
III.4.4.3 Les fonctions de la
bibliothèque
Des programmeurs ont créé des méthodes
qui nous permettent d'exploiter l'afficheur. D'ailleurs, par simplicité
et plus de flexibilité, ils les ont installés dans une
bibliothèque appelée <LiquidCristal.h>. Ci-dessous un
tableau des méthodes de <LiquidCristal.h>.
Tableau III-3: Méthodes de
<LiquidCristal.h>
Nom de fonction
|
Rôles
|
void clear ( );
|
Efface l'afficheur.
|
void home ( );
|
Retourne le curseur au point d'origine (0,0)
|
void noDisplay ( );
|
Désactive l'affichage.
|
void display ( );
|
Active l'affichage.
|
void noBlink ( );
|
Désactive le clignotement du curseur.
|
void blink ( );
|
Active le clignotement du curseur.
|
void noCursor ( );
|
Désactive le curseur.
|
void cursor ( );
|
Active le curseur.
|
|
~ 44 ~
void scrollDisplayLeft
|
Décale l'affichage vers la gauche.
|
void scrollDisplayRight ( );
|
Décale l'affichage vers la droite.
|
void leftToRight ( );
|
Déplace le curseur vers la droite à l'affichage
d'une donnée.
|
void rightToLeft ( );
|
Déplace le curseur vers la gauche à l'affichage
d'une donnée.
|
void autoscroll ( );
|
Active le défilement automatique de l'affichage vers la
gauche.
|
void noAutoscroll ( );
|
Désactive le défilement automatique de
l'affichage vers la gauche.
|
void createChar (uint8_t, uint8_t[ ]);
|
Permet l'appel de caractères ou symboles pré-
construit dans un tableau.
|
void setCursor (uint8_t, uint8_t);
|
Place le curseur à la position souhaitée.
|
LiquidCrystal lcd (rs, en, d4, d5, d6, d7)
|
Pour définir la communication i2c 4bits.
|
lcd.begin (16, 2);
|
Affiche le texte sur les deux lignes.
|
lcd.print ( );
|
Pour afficher une chaine de caractères en ASCII.
|
lcd.write ( );
|
Pour afficher des données, un octet à la fois.
|
lcd.setCursor (x, y);
|
Pour placer le curseur (colonne x: 0-16, ligne y:0-2).
|
lcd.clear ( );
|
Effacer ce qui est affiché à l'écran.
|
|
III.4.5 Le chauffage et l'humidification
Pour le chauffage, nous avons utilisé des lampes
à incandescences, ces lampes sont alimentées à la tension
du réseau 220V lors de la réalisation. Ces dernières
transforment 95% de l'énergie qu'elles reçoivent en chaleur et ne
transforme que 5% en lumière. On peut aussi utiliser des
résistances chauffantes comme source de chaleur et les placées de
manière à avoir une répartition harmonieuse de la chaleur.
Dès que la température dans l'incubateur est inférieure
à la consigne fixée, le microcontrôleur envoie une
impulsion au circuit de commande des lampes qui seront alimentées.
Lorsque la température dépasse le seuil de 38 degré
centigrade, le microcontrôleur cesse de fournir le signal de commande.
" 45 "
Le contrôle de l'humidité s'effectue
pratiquement de la même façon que la température mais sauf
que cette fois ci dès que l'humidité est inférieure
à 50%, le microcontrôleur fournit un signal pour la commande du
brumisateur qui humidifie l'air chaud de l'incubateur jusqu'à 70% et
s'arrête. Pour redémarrer à nouveau quand l'humidité
sera inférieure au seuil bas.
III.4.6 La ventilation
Le système de ventilation est constitué de deux
ventilateurs. Le premier aspire l'air de l'extérieur vers
l'intérieur de l'incubateur et le second refoule l'air chaud de
l'antichambre vers l'intérieur de l'incubateur. Ainsi, l'air est
renouvelé et se débarrasse du dioxyde de carbone.
III.4.7 Le système de retournement
Le système de retournement est constitué d'un
moteur pas à pas ayant un couple supérieur à 240,691Nm et
son circuit de commande. Vu que le retournement doit être effectué
trois fois le jour, le microcontrôleur fournit toutes les huit heures
pendant 19 jours les impulsions de commande du moteur, et en changeant chaque
fois le précèdent sens de rotation. Le nombre d'impulsions
fournit par le microcontrôleur permettra d'atteindre un écartement
angulaire de 45 degrés par rapport au plan horizontal.
III.4.8 Microcontrôleur
Le microcontrôleur de la carte Arduino UNO que nous
avons utilisé est un ATMega328. C'est un microcontrôleur ATMEL de
la famille AVR 8bits. Les principales caractéristiques sont
:
· FLASH = mémoire programme de 32Ko
· SRAM = données (volatiles) 2Ko
· EEPROM = données (non volatiles) 1Ko, (Cottenceau,
2017).
Nous avons écrit un programme qui figure à
l'annexe B qui contient toutes les instructions nécessaires en rapport
avec l'incubation des oeufs de poules qui permettrons au microcontrôleur
de donner les impulsions nécessaires pour la commande du circuit de
chauffage, ventilation, d'humidification, de retournement d'oeuf, de
contrôle de température et d'humidité.
Au moment de l'allumage, le microcontrôleur est
réinitialisé et envoie des instructions à l'écran
LCD qui affiche le nom du propriétaire et d'autres écrits devant
être affichés qui figurent dans le code source. Après
quelques secondes, les impulsions de commande sont
" 46 "
fournies au circuit de commande du moteur, le premier
retournement s'effectue puis l'écran affichage la valeur de la
température, du taux d'humidité, l'horloge d'incubation ainsi que
quelques messages d'alarme lorsque la température et l'humidité
sont en dehors des consignes fixées. Après sept jours,
l'écran affiche un message de mirage et le vingtième jour est
prévu pour l'éclosion. Voilà brièvement en quoi se
résument les 234 lignes d'instructions contenues dans le code source
(voir annexe B).
III.5 Conclusion
Dans ce chapitre nous avons conçu et
réalisé le circuit électronique de l'incubateur. Nous
avons dimensionné les différents blocs de ce circuit en donnant
quelques spécifications sur leurs caractéristiques
électriques. En se référant au schéma bloc qui
comprend l'alimentation, le microcontrôleur, le capteur de
température, d'humidité, l'interface de communication, le
mécanisme de retournement, le système de chauffage, ventilation
et d'humidification ; nous avons donné quelques explications
fonctionnelles. Nous avons considéré que l'incubateur est
alimenté par le réseau électrique 220V/50Hz qui constitue
sa seule source d'énergie.
" 47 "
CHAPITRE IV : DIMENSIONNEMENT THERMIQUE DE L'INCUBATEUR
D'OEUFS
IV.1 Introduction
Dans ce chapitre, il est premièrement question de
différentes formes de stockage de l'énergie thermique. Une
comparaison de ces types de stockage permettra de mieux choisir le
matériau calorifère approprié pour l'incubateur. Nous
devrons par la suite modéliser le système thermique afin de
déterminer la puissance de chauffage nécessaire ainsi que
l'autonomie thermique de l'incubateur.
IV.2 Stockage thermique
Le stockage de l'énergie thermique permet à la
chaleur d'être utilisée en différé. La chaleur peut
être stockée sous plusieurs formes :
· La chaleur sensible : stockage dans des matériaux
inertes.
· La chaleur latente : utilisation de matériaux
à changement de phase qui emmagasinent l'énergie à mesure
qu'ils changent de phase.
· La chaleur des réactions : thermochimie et
absorption (Soupart, 2015).
IV.2.1 Stockage sensible
Le stockage sensible est le moyen le plus commun de
réutiliser la chaleur. Dans les enceintes de stockage sensible, la
température du moyen de stockage augmente avec la chaleur
transférée. Ce stockage, non isotherme accumule une
quantité de chaleur proportionnelle à sa masse et à sa
capacité calorifique telle que présentée dans
l'équation suivante :
Esensibte = m X ?? X LT
Équation IV-1
Dans ces types de stockage, le matériau de stockage se
présente soit sous forme liquide, soit sous forme solide, soit les deux.
Le solide le plus utilisé est le béton de par son faible
coût, sa facilité d'usage et sa disponibilité, ses
propriétés de résistance mécanique mais surtout sa
capacité calorifique élevée. D'autres matériaux
peuvent être considérés comme les roches, le sable ou
encore les matériaux réfractaires comme la silice ou l'alumine
(E. Oro, 2012).
IV.2.2 Stockage latent
Le stockage de la chaleur latente implique de chauffer un
matériau jusqu'à ce qu'il change de phase, c'est-à-dire
soit de la phase solide à la phase liquide, soit de la phase liquide
à la phase gaz ou encore lors de sa transition solide-solide. Lorsque le
matériau atteint sa
~ 48 ~
température de changement de phase, il absorbe une
quantité de chaleur pour réaliser la transformation, connue sous
le nom de chaleur latente de fusion ou de vaporisation selon le cas. A
l'inverse, lorsque le matériau liquide ou gaz est refroidi, il retourne
à la phase solide ou liquide en restituant sa chaleur latente (Soupart,
2015). La quantité de chaleur stockée et restituée
dépend de la masse du matériau et selon l'équation
ci-dessous :
?????????????? = ? × ?h??-?? ???? ??-?? Équation
IV-2
La quantité de chaleur stockée dans un
système latent est présentée sur le graphe
température - énergie de la figure IV-1 :
Sensible
Température
TFusion
Latent
Energie stockée
Figure IV-1:Graphe de la température-enthalpie
présentant l'énergie stockée dans un système de
stockage latent en comparaison avec un système de stockage sensible
(L.F.Cabeza, 2008) Lorsque le matériau est chauffé, il
accumule d'abord une quantité d'énergie sensible lui permettant
d'atteindre la température de changement de phase. A ce stade,
l'énergie apportée au matériau cesse de le chauffer et est
utilisée à la place pour accomplir le changement de phase. La
chaleur est stockée de façon isotherme à condition que le
corps soit pur sous forme de chaleur latente. Une fois que la transformation
est complète, la température augmente de nouveau
proportionnellement à l'énergie apportée jusqu'à
atteindre la température de la source de chaleur. Il est donc impossible
de ne stocker que la chaleur latente puisque pour arriver au point de
changement de phase, le matériau doit subir une montée en
température, stockant inévitablement une part d'énergie
sensible (Soupart, 2015). La quantité d'énergie stockée
peut être exprimée pour le cas de la transition solide-liquide
selon l'équation ci-dessous :
?? = ? ??????,?????? + ???h??-?? + ? ??????,??????
?????????????? ???????????? Équation IV-3
???????????????? ??????????????
~ 49 ~
Les matériaux utilisés pour le stockage
thermique latent sont connus sous le nom de Matériaux à
Changement de Phase (MCP). Les MCP peuvent être employés pour leur
transition solide-solide, solide-liquide ou liquide-gaz. Cependant, peu de
matériaux ont été identifiés pour la transition
solide-solide, parfois car la chaleur latente de transition solide-solide est
trop faible devant celle de la transition solide-liquide, ou parfois car le
matériau n'est pas stable thermiquement. Les transformations liquide-gaz
sont attractives car elles présentent la plus grande chaleur latente.
Néanmoins, l'énorme changement de volume associé à
l'évaporation du liquide rend le stockage complexe et souvent
inutilisable. C'est pourquoi cette transition est écartée des
systèmes de stockage latent. Bien que la chaleur latente de fusion soit
plus faible que la chaleur latente d'évaporation, la transition
solide-liquide est la plus prometteuse puisqu'elle permet de limiter
l'expansion volumique et ainsi l'augmentation de pression due au changement de
phase (L.F.Cabeza, 2008).
IV.2.3 Stockage thermochimique
La troisième façon de stocker l'énergie
thermique consiste en l'utilisation de l'énergie endothermique des
réactions chimiques réversibles. La chaleur de réaction
qui est stockée est souvent associée à la dissociation des
réactifs chimiques en deux composants. Tout ou une partie de cette
chaleur peut être récupérée plus tard lorsque la
réaction de synthèse a lieu (Soupart, 2015).
IV.3 Comparaison des systèmes de
stockage
Tous les systèmes de stockage sont utilisés
selon trois étapes majeures : la charge, le stockage et la
décharge. Un grand nombre de moyens de stockage peuvent être
identifiés selon leurs propriétés, leur température
d'utilisation, le type de stockage souhaité et le domaine d'application
envisagé. Par exemple, les systèmes latents et sensibles seront
plutôt utilisés comme stockage tampon pour lisser la production ou
différer l'utilisation de l'énergie. Alors que les stockages
thermochimiques seront plus adaptés à un stockage de long terme
ou inter-saisonnier (L.F.Cabeza, 2008). Dans le cadre de ce travail, c'est le
stockage de la chaleur produite dans un incubateur d'oeufs pour suppléer
les déficits qui a été retenu. L'échelle de temps
est donc plutôt celle de la journée et non de la saison. Par
ailleurs, de par sa grande densité énergétique, le
stockage thermochimique est prometteur mais n'est pour l'instant
envisagé qu'à l'échelle de laboratoire étant
donné la complexité de mise en oeuvre.
" 50 "
Ainsi, en raison du faible degré de maturité
technologique et des échelles de temps qui sont plutôt propices au
stockage inter-saisonnier, le stockage thermochimique n'est pas retenu comme
solution de stockage de la chaleur produite dans un incubateur d'oeufs.
D'un point de vue économique, l'évaluation
nécessite de prendre en compte les coûts d'investissement mais
aussi d'exploitation, de maintenance et de recyclage. Ces coûts varient
souvent en fonction du volume de stockage. La densité
énergétique, c'est-à-dire la quantité
d'énergie stockable par unité de volume, est ainsi un
critère primordial. Pour le stockage sensible la densité
énergétique varie souvent entre 52 et 76 kWh/m3.
Cependant, leur coût très élevé limite leur
développement et leur rentabilité. Pour le stockage latent, la
densité énergétique varie entre 72 et 137
kWh/m3. Les volumes de stockage peuvent ainsi être
réduits en utilisant les MCP ce qui implique une réduction des
coûts et constitue un premier avantage en comparaison avec le stockage
sensible. Un autre avantage réside dans la restitution de la chaleur
à température constante. En effet, la quantité
d'énergie stockée et restituée dépend uniquement de
la masse du matériau et de sa chaleur latente. En toute théorie,
avec les MCP, la chaleur est restituée à la température de
fusion du matériau (Soupart, 2015).
Ainsi, on retiendra que le stockage dans les MCP fait son
émergence à l'échelle du démonstrateur et
présente les avantages de réduire le volume de stockage ainsi que
les coûts. De plus, la restitution de la chaleur à
iso-température permet de simplifier son utilisation sur l'incubateur.
Pour toutes ces raisons, c'est ce système de stockage qui est
sélectionné dans le cadre de notre travail.
IV.4 Les Matériaux à Changement de
Phase
IV.4.1 Critère de sélection d'un bon
MCP
La sélection d'un MCP nécessite une
réflexion et une analyse autour de la densité de stockage
souhaitée, des puissances de charge et de décharge mais aussi des
critères économiques et environnementaux sont à
entreprendre pour sélectionner le meilleur MCP. Plusieurs
méthodes ont été proposées par différents
auteurs afin de choisir au mieux un matériau pour une application
spécifique (A. Gil, 2013). Les propriétés
thermo-physiques, propriétés cinétiques et chimiques,
propriétés économiques et propriétés
mécaniques sont considérées comme critères de
sélection.
" 51 "
IV.4.2 Types de MCP
En 1983, Abhat a donné une classification
générale des matériaux, utilisée depuis par la
communauté scientifique du stockage latent. Cette classification est
illustrée sur la figure ci-dessous.

Figure IV-2: Classification des MCP proposée par
(Abhat, 1983)
On peut classer les MCP selon trois catégories :
· Les composés organiques : paraffines, corps non-
paraffiniques.
· Les composés inorganiques : hydrates de sels, sels
et métaux.
· Les eutectiques de corps inorganiques et/ou
organiques.
Les différents sous-groupes de MCP présentent des
propriétés thermiques et chimiques très différentes
qui affectent significativement la conception du système de stockage
thermique pour une application donnée.
IV.4.2.1 Les composés organiques
On trouve dans les composés organiques principalement les
paraffines, les alcools de sucre, les acides gras et d'autres composés
moins utilisés comme les cétones ou les esters.
Cette plage de température est largement
supérieure à notre spectre d'application. Un des
inconvénients les plus connus des alcools de sucre est leur tendance
à la surfusion, qui peut
~ 52 ~
IV.4.2.1.1 Paraffines
Les paraffines sont une famille d'hydrocarbures saturés
de formule brute CnH2n+2, aux propriétés très similaires.
Parmi les MCP solide-liquide, elles sont les plus utilisées, surtout
pour les applications à basse température (de -10 à 100
°C) car elles offrent l'avantage d'avoir une chaleur latente qui
dépend de la masse molaire et des températures de changement de
phase variables, donnant de la flexibilité pour choisir le MCP
approprié à chaque application. Dans cette catégorie, on
peut citer notamment les paraffines n- EICOSANE (Tfusion = 37 °C) (N. S.
Y. U. K. Himran, 1994).
Avantages
Parmi les avantages des paraffines, on peut aussi citer la
faible pression de vapeur saturante qui limite les risques de vaporisation. De
plus, certaines sont considérées comme non toxiques, inoffensives
écologiquement et compatibles avec les réservoirs
métalliques car elles ne provoquent pas ou peu de corrosion. Enfin,
elles sont produites en quantités importantes par l'industrie des
procédés chimiques et sont donc facilement disponibles et peu
coûteuses (Alkan, 2006).
Inconvénients
Cependant, leur conductivité thermique reste
très faible ( 0,25 W/m.K) et elles présentent une expansion
volumique assez élevée ( 15 %) et une densité peu
importante. ( 800 kg/m3). Par ailleurs, des précautions sont
à prendre lors de l'utilisation des réservoirs en plastique, car
les paraffines ont tendance à s'infiltrer dans certains plastiques et
à les ramollir (Hasnain, 1998).
On notera que la gamme de température des paraffines
(-10 à 150 °C) couvre le spectre de l'application sur le stockage
de la chaleur produite par l'incubateur.
IV.4.2.1.2 Acides gras
Les acides gras sont caractérisés par la formule
chimique CH3(CH2)2nCOOH et ont à peu près les
mêmes propriétés thermo-physiques que les paraffines.
L'intérêt d'utiliser les acides gras comme MCP est de couvrir une
gamme de température allant de 40 à 150 °C selon la longueur
de la chaîne carbonée (Y. Yuan, 2014).
Les sels, les métaux et les eutectiques ont des
températures de fusion élevées et ne conviennent pour
notre spectre d'application.
~ 53 ~
d'ailleurs être utilisée pour faire du stockage
inter-saisonnier car elle permet de maintenir le MCP liquide sous le point de
solidification sans qu'il libère ainsi sa chaleur (SAMSSA, 2015)
IV.4.2.2 Les composés inorganiques
Les matériaux inorganiques sont classés en trois
catégories : les sels, les hydrates de sels et les métaux.
IV.4.2.2.1 Hydrates de sels
Les hydrates de sel sont des sels inorganiques qui contiennent
de l'eau et dont la formule générale est AB.nH2O. Pendant la
charge, la déshydratation du sel a lieu. Le produit de cette
déshydratation peut être un hydrate de sel avec moins
molécules d'eau selon la formule : AB. nH2O ?
AB. mH2O + (n - m)H2O
Ou bien le même sel sous sa forme anhydre :
AB. nH2O ? AB + nH2O
Le sel hydraté le plus utilisé par son faible
coût est le CaCl2.6H2O (TFusion = 28 à 30 °C).
Avantages
Les hydrates de sel sont appropriés pour leur
utilisation dans le stockage thermique parce qu'ils présentent une
grande chaleur latente ( 100-300 kJ/kg), une température de fusion
adaptée aux applications à basse température ( 8-100
°C) et sont largement compétitifs en termes de coût et de
rentabilité. Ils sont en effet déjà commercialisés
pour servir comme matériaux de stockage et disponibles en gros volume.
Par ailleurs, ils présentent une conductivité thermique plus
élevée que les paraffines environ 0,5 W/m.K (M. M. Farid,
2004).
Inconvénients
Le principal problème qui se pose lors de l'utilisation
des hydrates de sels est leur fusion non congruente, ce qui veut dire que le
sel n'est pas totalement soluble dans l'eau d'hydratation au niveau du point de
fusion. Certains hydrates de sel peuvent montrer des problèmes de
corrosion des structures métalliques des systèmes de stockage (A.
A. El-Sebaii, 2011).
~ 54 ~
Nous retenons que les MCP organiques paraffinés
présentent des multiples avantages et surtout que la plage de
température de fusion de ces derniers convient pour l'incubateur. Le
tableau ci-dessous présente les propriétés thermiques de
paraffines couramment utilisées.
Tableau IV-1: Propriétés de
différentes paraffines tirées de (KOOENY, 2015)
|
NOM
|
FORMULE CHIMIQUE
|
TEMPÉRATURE DE FUSION (°C)
|
CHALEUR
LATENTE DE
FUSION (J/G)
|
MASSE
MOLÉCULAIRE (G/MOL)
|
|
N-TETRADECANE
|
C14H3
|
6
|
228
|
198.39
|
|
N-PENTADECANE
|
C15H32
|
10
|
205
|
212.42
|
|
N-HEXADECANE
|
C16H34
|
18
|
237
|
226.44
|
|
N-HEPTADECANE
|
C17H36
|
22
|
213
|
240.47
|
|
N-OCTADECANE
|
C18H38
|
28
|
244
|
254.5
|
|
N-NONADECANE
|
C19H40
|
32
|
222
|
268.53
|
|
N-EICOSANE
|
C20H42
|
37
|
246
|
282.55
|
|
N-HENICOSANE
|
C21H44
|
40.5
|
200
|
296.58
|
|
N-DOCOSANE
|
C22H46
|
44.5
|
249
|
310.61
|
|
N-TRICOSANE
|
C23H48
|
47.5
|
232
|
324.63
|
|
N-TETRACOSANE
|
C24H50
|
52
|
255
|
338.66
|
|
N-PENTACOSANE
|
C25H52
|
54
|
238
|
352.69
|
|
N-HEXACOSANE
|
C26H54
|
56.5
|
256
|
366.71
|
Dans le cadre de la conception de l'incubateur, il est
primordial de s'intéresser aux mélanges avec une
température de fusion proche de 37 °C. Dans cette optique,
plusieurs produits commerciaux existent, nous avons recensé des panneaux
à base de bois et contenant des matériaux à changement.
Par exemple, les panneaux commerciaux Energain(c) qui présentent une
chaleur latente de 77 J/g (Achard, 2011) comme on peut le voir à la
figure IV.4.-2. Nous avons également trouvé le CrodaTherm 37
ayant une chaleur latente de 216 KJ/Kg ; c'est un matériau biologique
à changement de phase fabriqué par l'entreprise internationale
CRODA. L'utilisation des MCP CrodaTherm présente plusieurs avantages par
rapport aux technologies actuellement disponibles, telles que les paraffiniques
ou les hydrates de sels métalliques inorganiques parce qu'ils
proviennent de matériaux renouvelables, ont des hautes capacités
de chaleur latente, une stabilité à long terme
éprouvée grâce à des tests en laboratoire,
~ 55 ~
une inflammabilité plus faible que les alternatives
paraffiniques et sont biodégradable. En plus leur prix est encore plus
abordable, 17 Kg net de CrodaTherm 37 reviennent à R226.07 soit
15.46$.

Figure IV-3: Panneau en bois contenant du MCP
Chaque panneau DuPontTM Energain® mesure 1,0 m
x 1,2 m et pèse 5,4 kg. Dans le cadre du dimensionnement thermique, nous
utilisons les propriétés thermiques du CrodaTherm 17 grâce
à ses multiples avantages.
IV.5 Les différents échanges
thermiques
IV.5.1 Echange de chaleur par Conduction
Il s'agit d'un mode de transfert de chaleur au niveau
macroscopique d'un même matériau ou entre plusieurs
matériaux accolés sans déplacement de matière. Ce
mode de transfert se passe spontanément de la surface à la
température la plus élevée vers la surface à
température la moins élevée (Herizo, 2015).
La densité de flux de chaleur est proportionnelle au
gradient de température et régit par la loi de Fourier :
??? = -A.????????
(T) Équation IV-4
??????????
Tels que : A est la conductivité thermique en
watt par mètre-Kelvin et T la température en fonction de
l'épaisseur du matériau, mesuré en Kelvin.
Dans cette étude, toutes les surfaces des
matériaux sont planes. Le flux à travers une surface est
donné par le théorème de Gauss :
?? = ? ?? ??? ?? ? ???? Équation IV-5
~ 56 ~
Avec :
= ??× 1 × cos 0
?
?
??
.n
Or ??? et n? sont de même direction et de même
sens.
Et on a : ?? = 0,
= ??× 1 × cos 0
?
?
??
.n
?
.n = ??
?
??
D'où : ??= ??.S
L'équation IV.5-1 donne : ?? = -A ????
????
En remplaçant ?? par son expression :
??= -A . S = A. S (??1-??2) Équation
IV-6
????
????
La résistance qui caractérise le ralentissement du
transfert de chaleur par conduction est tirée
de l'équation IV.5-3.
??
Nous avons : R =
??.??
Telles que :
R : La résistance thermique par conduction du
matériau d'épaisseur ?? en mètre (m), de
conductivité A en watt par mètre-Kelvin (W/m. K) et
de surface S en mètre carré (m2).
??1-??2 : La différence de température entre deux
surfaces en Kelvin (K)
?? : Le flux de chaleur en Watts (W)
IV.5.2 Echange de chaleur par Convection
La convection est un mode de transfert de chaleur entre un
solide et un fluide (ex : le
contreplaqué et l'air dans le cas de la couveuse). Lorsque
le mouvement du fluide est provoqué
naturellement ou par la différence de températures
de la région, il s'agit d'une convection
naturelle ou convection libre. Par contre, si le mouvement du
fluide est sous l'effet direct des
forces extérieures, il s'agit d'une convection
forcée (Herizo, 2015).
Ce mécanisme de transfert est donné par la loi de
Newton :
~ 57 ~
4)= hc x S x (T1 - T2)
Équation IV-7
Avec :
4): flux de chaleur en watt (W),
hc : le coefficient de transfert thermique en W
· m-2. K-1,
T1: température du fluide loin de la surface en
Kelvin,
T2: température de la surface du matériau.
Et la résistance thermique par convection R est
donné par :
IV.5.3 Echange de chaleur par rayonnement
C'est un transfert d'énergie
électromagnétique entre deux surfaces séparées par
le vide ou par l'air (exemple: rayonnement entre les contre-plaqués).
La puissance rayonnée par un corps est exprimée par
la loi de Stefan-Boltzmann:
4)= ax ex Sx (T14 -
T24) Équation IV-9
Avec :
o : Constante de Stefan-Boltzmann (5,6703.
10-8 W. m-2.
K-4),
E: Émissivité tel que, égale
à 1 pour un corps noir et comprise entre 0 et 1 selon l'état de
surface du matériau,
S: Superficie du corps (m2),
T: Température de la surface du corps (K).
L'équation IV.5-6 peut s'écrire :
4)= ax ex Sx (T12 +
T22)(T1 + T2)(T1 -
T2)
(T1 - T2)
4) =
1
ax ex Sx (T12 +
T22)(T1 + T2)
De la relation ci-dessous, l'expression de la résistance
par rayonnement est égale à :
" 58 "
1
R = 2 Équation IV-10
QxExS(T1
+T22)(T1+T2)
IV.5.4 Inertie thermique
Les matériaux sont capables de stocker et de
dégager de l'énergie sous forme de chaleur par inertie thermique.
Sa valeur dépend de la caractéristique du matériau.
Le flux thermique emmagasiné par inertie d'un
matériau se traduit par :
0 = C. dt Équation IV-11
Avec :
T : la température du matériau (K),
C: la capacité d'inertie du matériau
(Wh. K-1),
Pour un matériau homogène et isotrope : C = p x
e x S x Cp
Telles que :
p: masse volumique,
e: épaisseur,
S: surface du matériau,
Cp: chaleur spécifique du matériau
(Wh. Kg-1. K-1).
IV.6 Echange thermique pour la couveuse
Dans cette étude, les sources de chaleur sont
posées à l'intérieur de l'incubateur dans une antichambre
réchauffant l'air brasé par un ventilateur. La puissance
dégagée par les lampes, sous forme de flux de chaleur, chauffe
l'air intérieur puis ce dernier s'infiltre dans la chambre de dessous
(cage) où se trouve l'emplacement des oeufs et fait un
phénomène de convection à la surface du contre
-plaqué (tôle d'aluminium). Ce phénomène est
dû à la différence de températures entre l'air
intérieur et la tôle. Il y a aussi un échange de chaleur
par rayonnement entre les faces en contre-plaqués qui constituent la
cage. Chaque face est constituée de couches de matières à
savoir une mince tôle d'aluminium, une première couche de, le MCP
et une deuxième couche de bois. Puis, le flux de chaleur traverse le
contre-plaqué par le phénomène de conduction. Enfin, la
convection de l'air extérieur à la surface externe du
contre-plaqué.
~ 59 ~
IV.6.1 Flux de chaleur par convection entre l'air
intérieur et le contre-plaqué Ce flux de chaleur est
donné par l'équation ci-dessous :
???? = h?? X ?? X (????,?? X ??) Équation
IV-12
Avec :
h??: Le coefficient de convection interne de l'air,
Ta,i: La température de l'air intérieur,
??: La température du contre-plaqué,
S: La surface du contre-plaqué.
Et la résistance par convection interne est donnée
par :
1
R?? = Équation IV-13
h??X??
IV.6.2 Flux de chaleur par convection entre l'air
extérieur et le contre-plaqué Le flux de chaleur est par
convection donné par l'équation ci-dessous :
???? = h?? X ?? X (????,?? - ??) Équation
IV-14
Avec :
he: Le coefficient de convection externe de
l'air, Ta,e: La température extérieure.
Et la résistance par convection externe est :
1
R?? = Équation IV-15
h??X??
IV.6.3 Flux de chaleur par conduction à travers le
contreplaqué
Le flux de chaleur de chaleur par conduction est donné par
l'équation ci-dessous :
???? = ????. ??(????,??-??)
?? Équation IV-16
Avec :
??: L'épaisseur du contre-plaqué,
Ac: La conductivité du contre-plaqué
(W. m-'. K-'). Et la
résistance par conduction est :
???? = ???? . ?????? (????,?? - ????,??) Équation
IV-22
' 60 '
???? h1
×?? Équation IV-17
??
IV.6.4 Flux de chaleur par rayonnement à la
surface du contreplaqué Le flux de chaleur par rayonnement est
donné :
|
????=
????
|
??×
= ??
|
??×
× ??
|
??×
× ??
|
4 - (????,??
× (???2 ?,??
|
??4)
+ ??)(????,??
|
Équation IV-18
+ ??)(????,?? - ??)
|
L'expression de la résistance par rayonnement est
égale à :
???? =
1
??× ?? × ??× (????,??
2 + ??2)(????,?? + ??)
1
???? = Équation IV-19
h??.??
??: Émissivité du contre-plaqué.
IV.6.5 Flux de chaleur stocké par inertie du
contre-plaqué Le flux de chaleur stocké est donné
par :
????
?????? = ????. ???? Équation IV-20
Avec :
????: La capacité d'inertie du
contre-plaqué telle que ????= ??. ??. ??. ?????? ,
??????: La chaleur spécifique du contre-plaqué
(??h. ????-1.
??-1). IV.6.6 Flux de chaleur stocké
par inertie de l'air intérieur Le flux de chaleur stocké
est donné par :
????
????,?? = ????. Équation IV-21
????
Avec :
????: La capacité d'inertie de l'air telle que
????= ????. ????. ??. ?????? ,
??????: La chaleur spécifique de l'air
(??h. ????-1.
??-1),
????: L'épaisseur de l'air à
l'intérieur de la couveuse (m). IV.6.7 Puissance
dissipée par l'air du ventilateur La puissance dissipée
est donnée par :
" 61 "
Avec De est le débit d'air qui est
donnée numériquement par De = 930
??3/h. Ce débit a été conçu par
le constructeur du ventilateur et fonction des modèles commerciaux
(Alibaba, 2021). Donc il est fixé pour le volume de notre incubateur.
IV.7 Analogie thermique -
électrique
Pour résoudre plus facilement le problème, nous
avons fait l'analogie entre la thermique et l'électricité,
c'est-à-dire la résistance thermique est analogue à la
résistance électrique, la température est analogue
à la tension électrique, le flux thermique à
l'intensité du courant, l'inertie thermique à la capacité
d'un condensateur. Les polarités indiquent le sens d'écoulement
thermique comme on peut le voir sur la figure IV-4.

Figure IV-4: Analogie électrique du circuit thermique
de l'incubateur Sur la figure ci-dessus, nous retrouvons dans chaque
branche :
· RconvE : résistance thermique dû à la
convection de l'air intérieur et la mince tôle d'aluminium,
· RcondT : résistance thermique par conduction de la
tôle d'aluminium ;
· RcondBe : résistance thermique par conduction de
la première couche de bois ;
~ 62 ~
· RcondMCP : résistance thermique par conduction du
MCP ;
· RcondBs : résistance thermique par conduction de
la deuxième couche de bois ;
· RconvS : résistance thermique dû à la
convection de l'air extérieur et la deuxième couche de bois ;
· RcondBp : résistance thermique par conduction de
la porte en bois ;
· CiAInt : inertie thermique de l'air intérieur ;
· CiT : inertie thermique de la tôle d'aluminium ;
· CiBe : inertie thermique de la première couche de
bois ;
· CiMCP : inertie thermique du MCP ;
· CiBs : inertie thermique de la deuxième couche de
bois ;
· TempInt : température intérieur ;
· TempExt : température extérieur ;
· Plamp : puissance fournie par les lampes ;
· Qoeufs : la chaleur fournit par la respiration des
embryons ;
· Pvent : puissance dissipée par l'air du
ventilateur ;
· QTrouA : chaleur dissipée par le trou
d'aération et
· QconOeufs : chaleur consommée par les oeufs.
IV.7.1 Simplification du schéma
équivalent
Comme en électricité, les résistances en
série (en jaunes sur la figure IV.8-1) peuvent se ramener en une
résistance équivalente :
IRi= Reg
ai = RcondTt + RcondBet-p
Comme on peut le voir sur la figure IV-5 :
°PconvE1 = °Pr1 + °PciT1 +
°Pa1 Équation IV-23
' 63 '
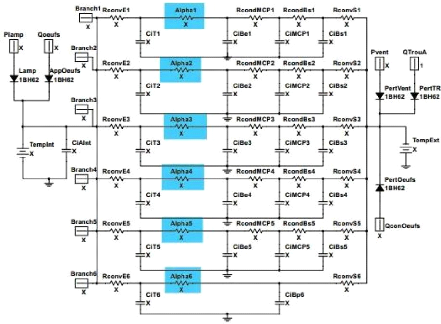
Figure IV-5: Schéma équivalent Thermique
simplifié
Remarque :
Dues à la lourdeur de la présentation des
résistances thermiques par rayonnement entre les six (6) faces, ces
résistances sont omises dans les figures IV-4 et IV-5.
IV.7.2 Mise en équations du
modèle
Pour établir les équations différentielles,
on peut utiliser la loi des noeuds de Kirchhoff à partir de l'analogie
thermique-électricité. Cette loi stipule que la somme des
courants entrant dans un noeud est égale à la somme des courants
sortant.
IV.7.2.1 Mise en place des équations en chaque
noeud
Sur chaque noeud d'une branche, la somme des flux entrants est
égale à la somme des flux sortants, nous avons
Branche 1 Noeud 1
' 64 '
ai = RcondTi + RcondBet-p
Noeud 2
0a1 = 0ciBe1 + 0RcondMCP1 Équation IV-24
Noeud 3
0RcondMCP1 = 0ciMCP1 + 0RcondBs1 Équation
IV-25
Noeud 4
0RcondBs1 = 0ciBs1 + 0RconvS1 Équation IV-26
Branche 2
Noeud 1
0convE2 = 0r2 + 0ciT2 + 0 a2 Équation
IV-27
Noeud 2
0a2 = 0ciBe2 + 0RcondMCP2 Équation IV-28
Noeud 3
0RcondMCP2 = 0ciMCP2 + 0RcondBs2 Équation
IV-29
Noeud 4
0RcondBs2 = 0ciBs2 + 0RconvS2 Équation IV-30
Branche 3
Noeud 1
0convE3 = 0r3 + 0ciT3 + 0a3 Équation
IV-31
Noeud 2
0a3 = 0ciBe3 + 0RcondMCP3 Équation IV-32
Noeud 3
0RcondMCP3 = 0ciMCP3 + 0RcondBs3 Équation
IV-33
Noeud 4
Branche 4
0RcondBs3 = 0ciBs3 + 0RconvS3 Équation IV-34
' 65 '
Noeud 1
OconvE4 = Or4 + OciT4 + Oa4 Équation
IV-35
Noeud 2
Oa4 = OciBe4 + ORcondMCP4 Équation IV-36
Noeud 3
ORcondMCP4 = OciMCP4 + ORcondBs4 Équation
IV-37
Noeud 4
ORcondBs4 = OciBs4 + ORconvS4 Équation IV-38
Branche 5
Noeud 1
OconvE5 = Or5 + OciT5 + Oa5 Équation
IV-39
Noeud 2
Oa5 = OciBe5 + ORcondMCP5 Équation IV-40
Noeud 3
ORcondMCP5 = OciMCP5 + ORcondBs5 Équation
IV-41
Noeud 4
ORcondBs5 = OciBs5 + ORconvS5 Équation IV-42
Branche 6
Noeud 1
OconvE6 = Or6 + OciT6 + Oa6 Équation
IV-43
Noeud 2
Oa6 = OciBp + ORconvs6 Équation IV-44
"lamp + Ooeufs = OconvEl + OconvE2 +
OconvE3 + OconvE4 + OconvE5 +
OconvE6 +
OciAint + "vent + Otrous + Oconoeufs
Équation IV-45
Equation bilan :
" 66 "
En remplaçant l'expression de chaque flux, les
équations en chaque noeud deviennent : Branche 1 (face 1)
Noeud 1
h??11. ??1(??1 - ??2) = h????1.
??1(??1 - ??2) + ??????1. ????2 +
(??2-??3) + (??3-??4)
???? ??????1 ????????1
|
Noeud 2
|
????,?? = ??1, ?????? = ??6
(??2-??3)+ (??3-??4) ????3 (??4-??5)
????????1.
= +
|
Équation IV-46
Équation IV-47
Équation IV-48
Équation IV-49
|
|
Noeud 3
|
|
??????1 ????????1 ???? ??????????1
(??4-??5) ????4 (??5-??6)
= +
|
|
Noeud 4
|
|
??????????1
(??5-??6)
|
??????????1.
???? ????????1
????5
|
|
|
????????1
|
????????1. h??12. ??1(??5
??6)
= + -
????
|
Avec :
T1 : la température intérieure de la couveuse,
T2 : la température de la tôle,
T3 : la température de la première couche de
bois,
T4 : la température de la couche de MCP,
T5 : la température de la deuxième couche de bois
et
T6 : la température extérieure. Branche
2 (face 2)
Noeud 1
??7 (??7-??8)
h??21. ??2(??1 - ??7) = h????2. ??2(??1 - ??7) +
??????2.?????? + ???? ??2 + (??8-??9)
????????2
Équation IV-50
Noeud 3
" 67 "
????,?? = ??1, ?????? = ??6
|
Noeud 2
Noeud 3
|
(??7-??8)+ (??8-??9)
??????2 ????????2
|
????8 + (??9-??10)
= ????????2. Équation IV-51
???? ??????????2
|
|
Noeud 4
|
(??9-??10)
??????????2
|
????9 + (??10-??6)
= ??????????2. Équation IV-52
???? ????????2
|
|
(??10-??6)
????????2
|
= ????????2. ????10 + h??22. ??2(??10 - ??6)
Équation IV-53
????
|
Avec :
T1 : la température intérieure de la couveuse,
T7 : la température de la tôle,
Tg : la température de la première couche de
bois,
T9 : la température de la couche de MCP,
T10 : la température de la deuxième couche de bois
et T6 : la température extérieure.
Branche 3 (face 3)
Noeud 1
????11 (??11 - ??12) (??12 - ??13)
h??31. ??3(??1 - ??11) = h????3. ??3(??1 - ??11) + ??????3. +
+
???? ??????3 ????????3
Équation IV-54

|
Noeud 2
(??11-??12)
|
+ (??12-??13)
????????3
|
????,?? = ??1, ?????? = ??6
3
????????
.???? + (??13-??14)Équation IV-55
???? ??????????3
|
|
??????3
|
' 68 '
|
(??13-??14)
|
????13+ (??14-??6)
= ??????????3. Équation IV-56
???? ????????3
|
|
Noeud 4
|
??????????3
|
|
(??14-??6)
????????3
|
= ????????3. ????14 + h??32. ??3(??14 - ??6)
Équation IV-57
????
|
Avec :
T1 : la température intérieure de la couveuse,
T11 : la température de la tôle,
T12 : la température de la première couche de
bois,
T13 : la température de la couche de MCP,
T14 : la température de la deuxième couche de bois
et T6 : la température extérieure.
Branche 4 (face 4)
Noeud 1
????15 (??15 - ??16) (??16 - ??17)
h??41. ??4(??1 - ??15) = h????4. ??4(??1 - ??15) + ??????4. +
+
???? ??????4 ????????4
Équation IV-58
????,?? = ??1, ?????? = ??6
+ (??16-??17)
????????4
????17 + (??18-??6)
= ??????????4. Équation IV-60
???? ????????4
= ????????4. ????18 + h??42. ??4(??18 - ??6)
Équation IV-61
????
Avec :
Noeud 2
(??15-??16)
??????4
Noeud 3
(??17-??18)
??????????4
Noeud 4
(??18-??6)
????????4
+ (??17-??18)
= ????????4. ????16 Équation IV-59
???? ??????????4
' 69 '
T1 : la température intérieure de la couveuse,
T15 : la température de la tôle,
T16 : la température de la première couche de
bois,
T17 : la température de la couche de MCP,
T18 : la température de la deuxième couche de bois
et T6 : la température extérieure.
Branche 5 (face 5)
Noeud 1
????19 (??19 - ??20) (??20 - ??21)
h??51. ??5(??1 - ??19) = h????5. ??5(??1 - ??19) + ??????5. +
+
???? ??????5 ????????5
Équation IV-62
????,?? = ??1, ?????? = ??6
????21 + (??22-??6)
= ??????????5. Équation IV-64
???? ????????5
Noeud 2
(??19-??20)
??????5
Noeud 3
(??21-??22)
??????????5
Noeud 4
+ (??20-??21)
????????5
+ (??21-??22)
= ????????5. ????20 Équation IV-63
???? ??????????5
|
(??22-??6)
????????5
|
= ????????5. ????22 + h??52. ??5(??22 - ??6)
Équation IV-65
????
|
Avec :
T1 : la température intérieure de la couveuse,
T19 : la température de la tôle,
T20 : la température de la première couche de
bois,
T21 : la température de la couche de MCP,
T22 : la température de la deuxième couche de bois
et
N 70 N
T6 : la température extérieure. Branche
6 (face 6)
Noeud 1
????23 (??23 - ??24) (??24 -
??6)
h??61. ??6(??1 - ??23) = h????6.
??6(??1 - ??23) + ??????6. + +
???? ??????6 ??????
Équation IV-66
????,?? = ??1, ?????? = ??6
Noeud 2
|
(??23-??24)
|
+ (??24-??6) = ????????. ????24 + h??62. ??6(??24
- ??6) Équation IV-67
?????? ????
|
|
??????6
|
Avec :
T1 : la température intérieure de la couveuse,
T23: la température de la tôle,
T24 : la température de la couche de bois,
T6 : la température extérieure.
Equation bilan :
?????????? + ??. ?????????? = h??11. ??1(??1 - ??2) +
h??21. ??2(??1 - ??7) + h??31. ??3(??1 - ??11) +
h??41. ??4(??1 - ??15) + h??51. ??5(??1 - ??19) +
h??61. ??6(??1 - ??23) + ????. ????1
???? +
??????. ???? (??1 - ??6) - ?? ????
?????? ???? + ??. ????. (??1 - ????,??) Équation
IV-68
Après développement nous obtenons un système
de vingt-trois équations différentielles du premier ordre en
fonction du temps que nous pouvons écrire sous forme matricielle :
" 71 "
a??1 at
a??2 at
a??3 at
a??4 at
a??5 at
a??7 at
a??8 at
a??9 at
a??10
at
a??11
at
a??12
at
a??13
at
a??14
at
a??15
at
a??16
at
a??17
at
a??18
at
a??19
at
a??20
at
a??21
at
a??22
at
a??23
at
a??24 at )
A0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 A0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 A0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 A0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 A0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 A0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 A0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 A0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
A0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 A0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 A0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 A0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 A0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 A0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 A0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 A0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 A0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 A0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 A0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 A0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 A0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 A0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 A
BB0 0 0 B0 0 0 B0 0 0 B0 0 0 B0 0 0 B0 BBBB0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 BBBB0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 BB0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 B0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 B0 0 0
0 BBB0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 BBBB0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 BB0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 B0 0 0 0 0 0 0 0 0 0
0 0 0 0 B0 0 0 0 0 0 0 0 BBB0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 BBBB0 0 0 0
0 0 0 0 0 0
|
T1 T2T3
T4
T5
T7
T8
T9
T10
T11
T12
T13
T14
T15
T16
T17
T18
T19
T20
T21
T22
T23 T24)
|
C 00 C C 0 0 C C 0 0 + C C 0 0 C C 0 0 C
C C) C
|
T6 +
|
D
00
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0)
|
0
00
0
0
0
0
0
0
0
0
= 0
0
0
0
0
0
0
0
0
0
0)
0
|
+ 0 0 0 0 0 0 0 0 0 0 0 BB0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 B0 0 0 0 0 0 0 0 0 0 B0 0 0 0 0 0 0 0 0 0 0 0 BBB0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 BBBB0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 BB0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 B0 0 0 0 0 0 B0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
BBB0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 BBBB0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 BB0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 B0 0
(
B0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 BB 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 BB
' 72 '
Les éléments de la première matrice
carré sont donnés par :
A11 = C?? , A22 = C????1,
A33 = C??????1, A44 = C????????1, A55
= C??????1, A66 = C????2, A77 =
C??????2, A88 = C????????2, A99 =
C??????2, A10,10 = C????3, A11,11 =
C??????3, A12,12 = C????????3, A13,13
=
C??????2, A14,14 = C????4, A15,15 =
C??????4, A16,16 = C????????4, A17,17 =
C??????4, A18,18 = C????5,
A19,19 = C??????5,
A20,20 = C????????5, A21,21 = C??????5,
A22,22 = C????6, A23,23 = C??????.
Les éléments de la deuxième matrice
carré sont donnés par :
B11 = (C????. D?? + ??. Co +
1 + 1 + 1 +
1 + 1 + 1 ), B12 = -
1
Ri11 Ri21 Ri31 Ri41 Ri51 Ri61
Ri11,
,
1 1 1 1 1
B16 = -, B1,10 = - , B1,14 , B1,18=-
, B1,22 Ri21 Ri31 R Ri51 Ri61
1 1 1 11 1 1 1
B21 = - B22 = - +B23 = - B24 = -
Rrs1 Ri11 RCT1 Rrs1 Ri11 , RCBe1 RCT1,
RCBe1,
1+
,
1 1 1 1 1 1 - 1
RC??C??4 Ri42 RCBs4 Rrs5 Ri51 RCT5 Rrs5
Ri51,
,
-
B17,17 =
B18,1 =
, B18,18 =
= 1 1 _ 1 _ 1 = 1 1
B18,19 RCBe5 RCT5, B18,20 - RCBe5, B19,18 - RCT5, B19,19
RCT5 RCBe5
,
1 1 1 1 1 1
B32 = - , B33 = - , B34 = + , B35 = - ,B44 =
1 1 1 1 1 1 1
RCT1 RCT1 RCBe1 RC??C??1 RCBe1 RC??C??1
B45 = + , B55 =-,B61 =
, B66 =
RC??C??1 RCBs1 RC??C??1 Ri12 RCBs1 Rrs2 Ri21
1
1 1 1 1 1 1 1
+ , B67 = - , B68 = - , B76 = - , B77 =
RCT2 Rrs2 Ri21 RCBe2 RCT2 RCBe2 RCT2 RCT2
1 1 1 1 1 1
B78 =
B79 = - , B88 = - , B89 = +
RCBe2 RC??C??2 RCBe2 RC??C??2 RCMC??2 RCBs2
+
1
1 1- 1 1 1 1 - 1
1+
RC??C??2 Ri22 RCBs2 Rrs3 Ri31 RCT3 Rrs3
Ri13,
,
-
,,
=
B10,1 =
B99 =

, B10
10
,
_ 1 1 _ 1 _ 1 _ 1 1
B10,,11 - - , B10,12 - - , B11,10
- , B11,11 - -
RCBe3 RCT3 RCBe3 RCT3 RCT3 RCBe3
|
B11,12 =
|
1
RC??C??3 + RCBe3, B11,13 = RC??C??3 , B12,12 = RCMC??3
B12,13 RCBs3 +
|
1 1 1 1 1 1 - 1
1+
RC??C??3 Ri32 RCBs3Rrs4 Ri41 RCT4 Rrs4 Ri14
,
=
=

B13,13
, B14,1 = , B14,14
,
_ 1 1 _ 1 _ 1 _ 1 1
B1415 - , B14,16 - , B15,14-- ,
B15,15-
' RCBe4 RCT4 RCBe4 RCT4 RCT4 RCBe4
|
B15,16 =
|
1 + 1 , B15,17 = 1 , B16,16 = 1 , B16,17 = 1
+
RC??C??4 RCBe4 RC??C??4 RCMC??4 R
|
~ 73 ~
1
??19,20 = + 1
????????5, ??19,21 = - 1
??????????5 , ??20,20 = - ?????1 ?????5, ??20,21 = 1
????????5 +
??????????5
1 1 1 ??????????5, ??21,21 = - ????????5, ??22,1 = 1
??????6 - 1
????61 , ??22,22 = 1
??????6 - ???1 ???6 + 1

????61,
????52
1 1
??22,23 = - ??????6, ??23,22 = - ???1 ???6, ??23,23 = 1
????62 + 1
??????6 - 1
???????? .
????????
Les éléments de la deuxième matrice colonne
sont donnés par :
??1 = -??????. ????, ??4 = ????????1 , ??5
= ( 1
1 ????????1 - 1
????12) , ??8 = 1
????????2 , ??9 = ( 1
????????2 - 1
????22),
??12 = ????????3 , ??13 = ( 1
1 ????????3 - 1
????32) , ??16 = 1
????????4 , ??17 = ( 1
????????4 - 1
????42) , ??20 =
) .
????????5 , ??21 = ( 1
1 ????????5 - 1
????52) , ??22 = 1
???????? , ??23 = ( 1
???????? - 1
????62
L'élément D de la troisième matrice colonne
est donné par :
????
?? = -?????????? - ??. ?????????? - ?? ??? .
??????
En rapport avec les expressions ci-dessus, nous avons :
???? : La capacité d'inertie de l'air telle que ????=
????. ????. ??. ?????? ;
?????? : La chaleur spécifique de l'air (??h.
????-1. ?C -1) ;
????: L'épaisseur de l'air à l'intérieur de
la couveuse (m) ;
???????? : La capacité d'inertie de la tôle
d'aluminium de la unième face intérieur ;
?????????? : La capacité d'inertie de la première
couche de bois de la unième face; ???????????? : La capacité
d'inertie de la couche de MCP de la unième face ;
?D???????? : La capacité d'inertie de la deuxième
couche de bois de la unième face ;
???????? : La capacité d'inertie de la couche de bois qui
constitue la porte de l'incubateur ;
???? : Le débit d'air du ventilateur ;
?? : La masse des oeufs de poule en kg ;
???? : La chaleur massique des oeufs en (KJ/Kg ?C) ;
??????1 : La résistance par convection interne de la
unième face ;
??????2 : La résistance par convection externe de la
unième face ;
~ 74 ~
???????? : La résistance par rayonnement de la
unième face interne ;
???????? : La résistance par conduction de la tôle
d'aluminium de la unième face ;
?????????? : La résistance par conduction de la
première couche de bois de la unième face ; ?????????? : La
résistance par conduction de la deuxième couche de bois de la
unième face ; ???????????? : La résistance par conduction de la
couche de MCP de la unième face ; ???????? : La résistance par
conduction de la couche de bois qui constitue la porte de
l'incubateur ;
?????????? : Chaleur de respiration des oeufs en (KJ/Kg) ;
?? : Taux de renouvellement de l'air extérieur dû au
trou d'aération avec ?? =v?7 ? ;
???? : Volume utile intérieur de notre couveuse en
(??3) qui vaut 1,4234 ;
?????? : Volume spécifique intérieur de la couveuse
en (??3/????) qui vaut 0,944 ;
??? : Différence d'enthalpie entre l'enthalpie
extérieure et l'enthalpie intérieure de la couveuse que nous
considérons par hypothèse égale à-10 kj/kgas.
Pour avoir des résultats correctes, nous avons
travaillé avec les unités internationales, sachant 1Watt-heure
(Wh) =3600 Joules (J) et 1J=1W. Nous avons considéré que la
température initiale est de 25 degré Celsius.
Nous avons écrit un script MATLAB (voir l'annexe A) qui
nous a permis de résoudre le système de 23 équations
différentielles dans lesquelles figure la température
intérieure de l'incubateur. Après calcul avec le logiciel MATLAB
de version R2015a, nous avons obtenu trois courbes qui décrivent
l'évolution de la température intérieure en fonction du
temps pour différentes puissance de chauffage comme on peut le voir sur
la figure IV-6.
~ 75 ~

Figure IV-6: Evolution de la température
intérieur en fonction du temps pour différentes puissance
de
chauffage
En rapport avec la figure IV-6, nous pouvons très bien
voir qu'il faudra au moins 12 lampes de 100W pour réchauffer
l'incubateur au bout de 21 secondes. Nous pouvons également
déterminer la quantité d'énergie thermique qui sera
stocké dans la couveuse sachant qu'il nous faudra en moyenne 105kg de
MCP CrodraTherm 37 pour constituer le réservoir thermique. En utilisant
l'équation IV.2-2 tout considérant la chaleur latente, nous
aurons :
E = m.?????-?? = m. C?? = 105 X 217 = 22785k?? =
6329,17??h.
Où :
C?? : est la chaleur latente du CrodaTherm 37 qui vaut
217kj/kg (voir l'annexe F).
IV.8 Conclusion
Tout au long de ce chapitre, nous avons parlé de
différents types de système de stockage qui existent. Nous avons
fait une étude comparative entre ces derniers et avons choisi le
système de stockage latent qui nous a permis de faire le choix d'un
modèle commerciale, le CrodaTherme 37 qui regorge plusieurs avantages
comme celui d'emmagasiner et restituer la chaleur à une
température constante. Après nous avons fait la
modélisation du circuit thermique qui nous a conduit à la
résolution d'un système d'équation différentielle
pour obtenir l'évolution de la température intérieur de
l'incubateur en fonction du temps pour différentes puissance de
chauffage. Nous avons constaté qu'il nous faudra 1200W comme puissance
de chauffage pour atteindre la température de 38 degré Celsius
dans l'incubateur au bout de 21 secondes.
" 76 "
CHAPITRE V : REALISATION PRATIQUE DE
L'INCUBATEUR
D'OEUFS
V.1 Introduction
Dans ce chapitre, il est question de la réalisation
pratique du modèle expérimentale de l'incubateur. Nous tenons
à préciser que les matériaux de construction du circuit
électronique, de la caisse ainsi que du système de retournement
que nous avons utilisé provient en grande partie du marché local
à l'exception du microcontrôleur et des capteurs que nous avons
acheté depuis la Chine. Nous clôturerons ce chapitre par le
coût estimatif du projet et la détermination du rendement global
de l'incubateur d'oeufs.
V.2 Réalisation de la caisse du modèle
expérimental de l'incubateur d'oeufs
Nous avons découpé cinq planches de bois du type
multi triplex que nous adjointes avec la colle à bois comme nous pouvons
le voir sur la figure V-1.

Figure V-1: Construction de la caisse du modèle
expérimental de l'incubateur d'oeufs
V.3 Isolation thermique de la caisse
Comme nous pouvons le voir sur la figure V-2, nous avons
placé une matière plastique pour l'isolé avec
l'extérieur. Nous avons placé de la mousse en l'intérieur
de la caisse pour accroitre la capacité thermique.
" 77 "

Figure V-2: Isolation de la caisse et amélioration de
la capacité thermique du modèle expérimental de
l'incubateur d'oeufs
| 

